Impurity Controlled near Infrared Surface Plasmonic in AlN
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
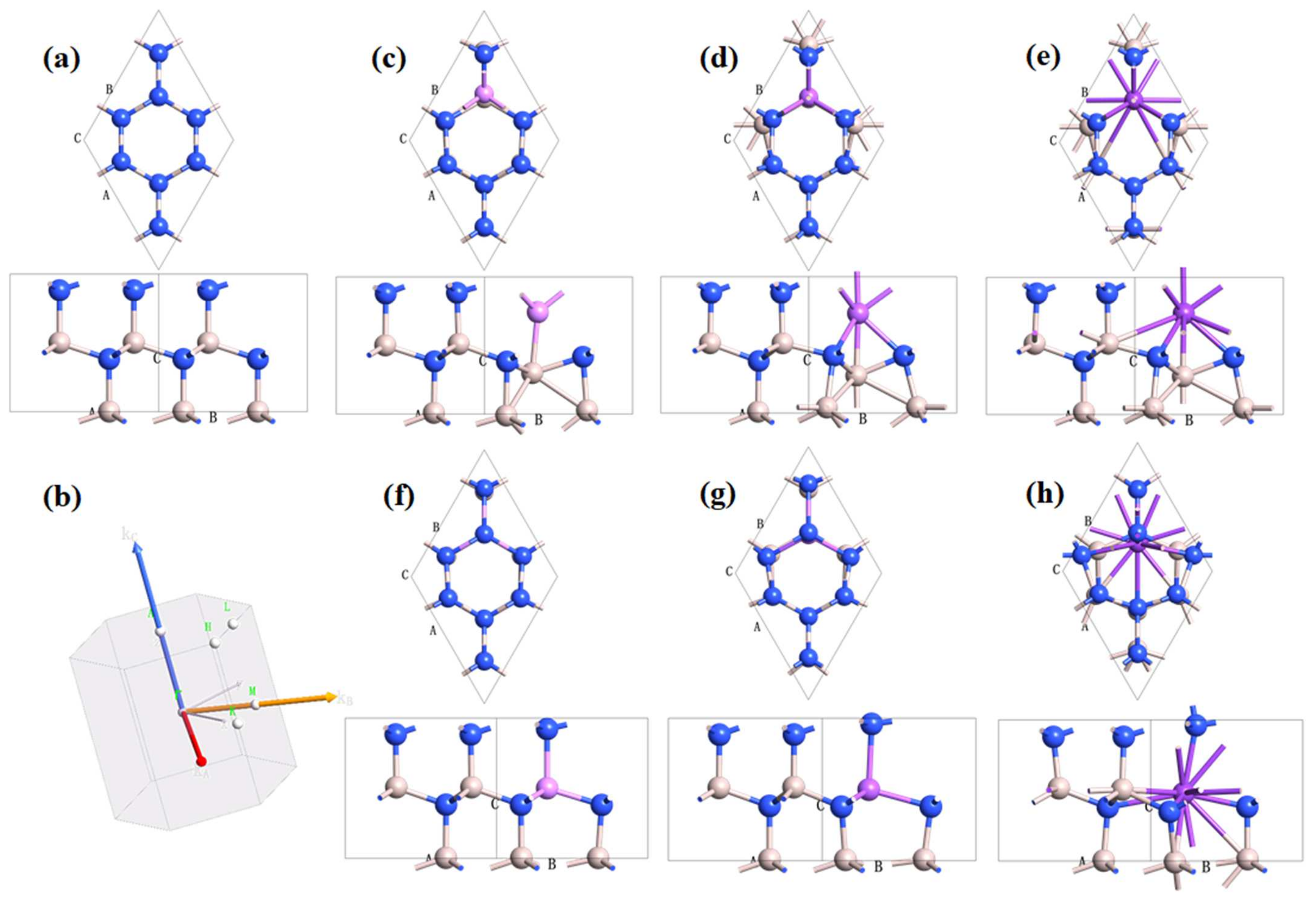
3.1. Crystal Lattice Structures
3.2. Electronic Structure
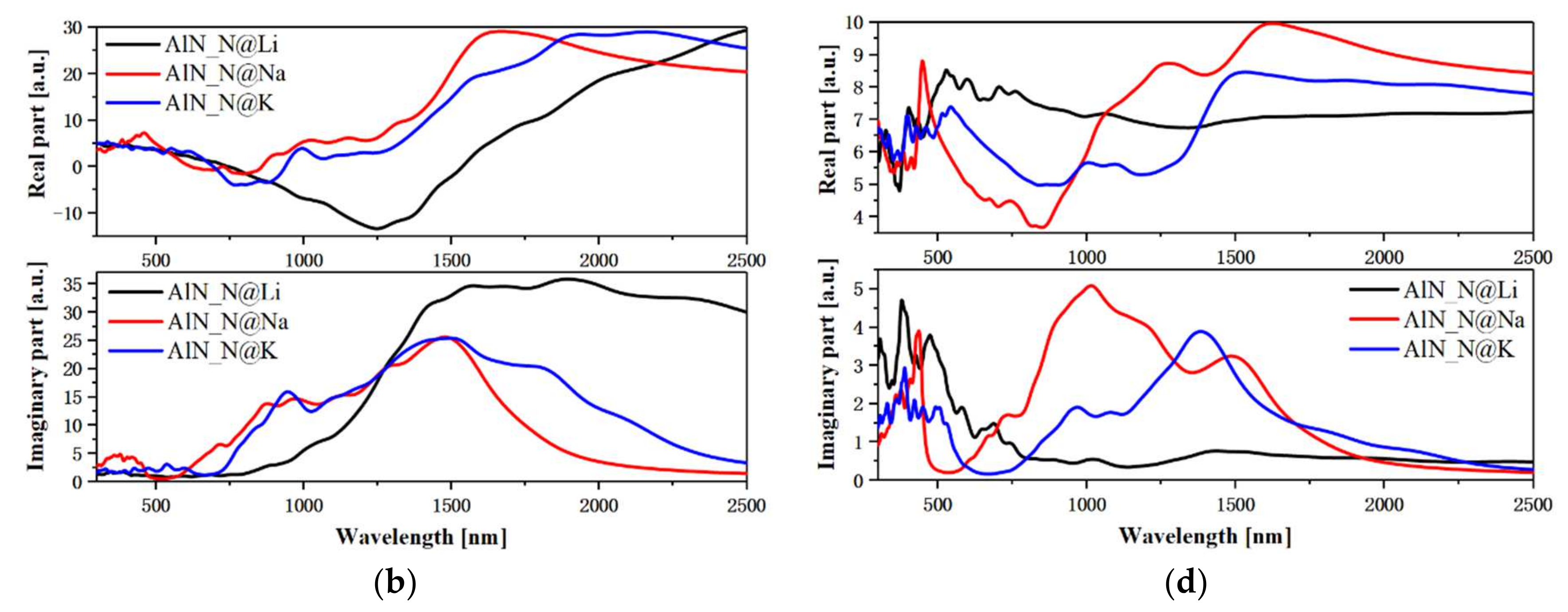
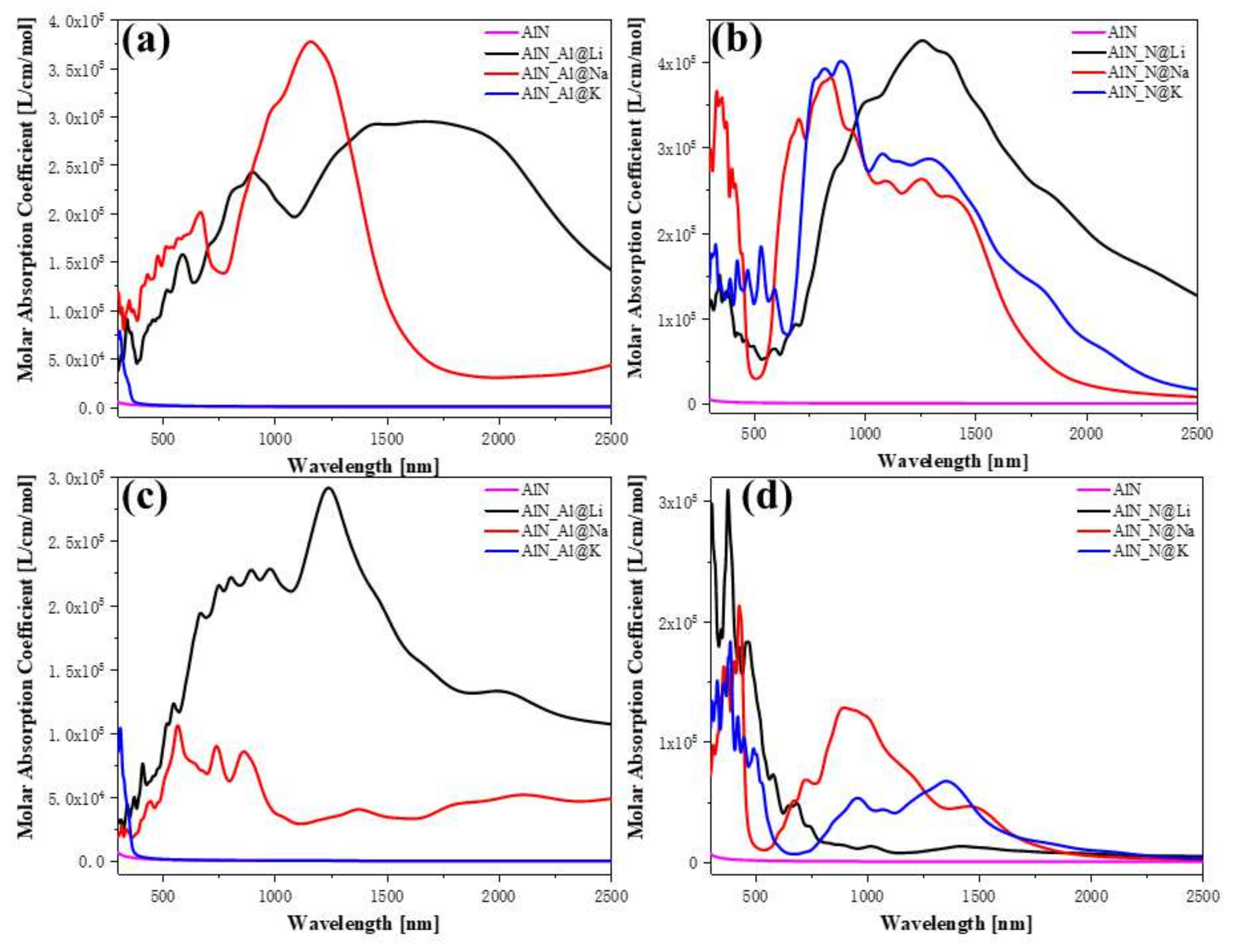
3.3. Optical Properties of Doping AlN
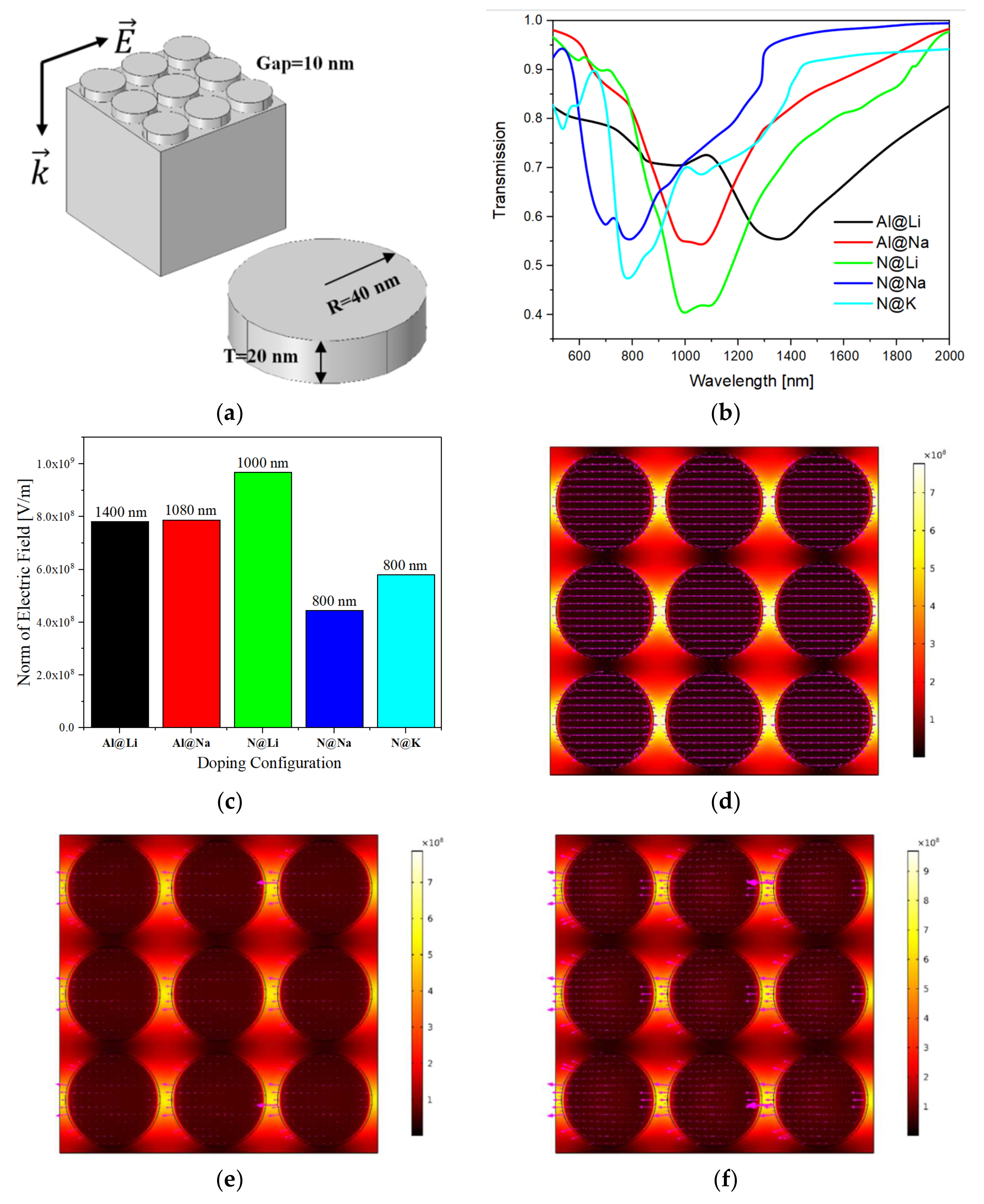
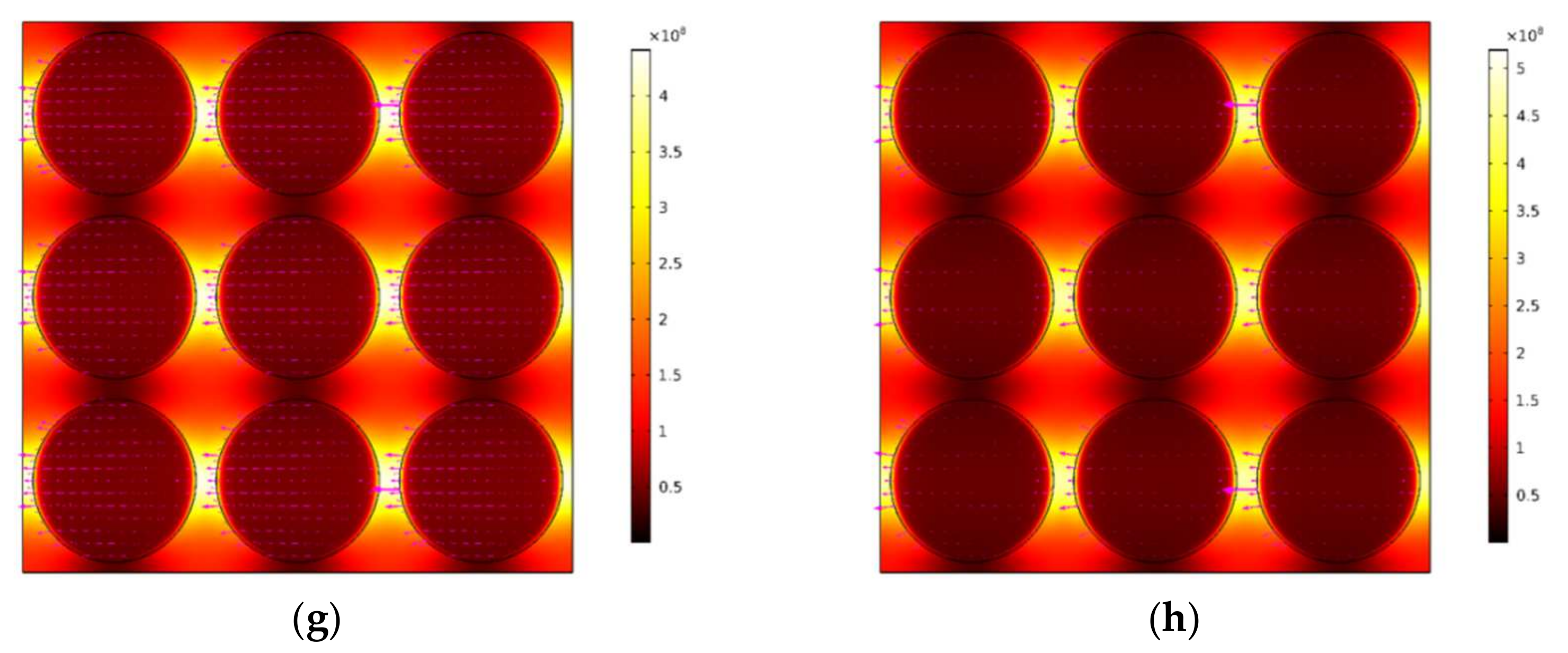
3.4. Plasmonic and Exciton Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ritchie, R.H. Plasma losses by fast electrons in thin films. Phys. Rev. 1957, 106, 874. [Google Scholar] [CrossRef]
- Ozbay, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Hiep, H.M.; Endo, T.; Kerman, K.; Chikae, M.; Kim, D.-K.; Yamamura, S.; Takamura, Y.; Tamiya, E. A localized surface plasmon resonance based immunosensor for the detection of casein in milk. Sci. Technol. Adv. Mater. 2007, 8, 331–338. [Google Scholar] [CrossRef] [Green Version]
- Downing, C.A.; Weick, G. Plasmonic modes in cylindrical nanoparticles and dimers. Proc. R. Soc. A 2020, 476, 20200530. [Google Scholar] [CrossRef]
- Choi, S.; Park, D.; Jeong, Y.; Yun, Y.; Jeong, M.; Byeon, C.; Kang, J.; Park, Q.-H.; Kim, D. Directional control of surface plasmon polariton waves propagating through an asymmetric Bragg resonator. Appl. Phys. Lett. 2009, 94, 063115. [Google Scholar] [CrossRef]
- Krasavin, A.; Zayats, A. Three-dimensional numerical modeling of photonic integration with dielectric-loaded SPP waveguides. Phys. Rev. B 2008, 78, 045425. [Google Scholar] [CrossRef]
- Tong, L.; Xu, H.; Käll, M. Nanogaps for SERS applications. MRS Bull. 2014, 39, 163–168. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Bjerneld, E.J.; Käll, M.; Börjesson, L. Spectroscopy of single hemoglobin molecules by surface enhanced Raman scattering. Phys. Rev. Lett. 1999, 83, 4357. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Aizpurua, J.; Käll, M.; Apell, P. Electromagnetic contributions to single-molecule sensitivity in surface-enhanced Raman scattering. Phys. Rev. E 2000, 62, 4318. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, L.; Sun, M.; Ruan, P.; Zheng, H.; Xu, H. Insights into the nature of plasmon-driven catalytic reactions revealed by HV-TERS. Nanoscale 2013, 5, 3249–3252. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, M.; Ruan, P.; Zheng, H.; Xu, H. Electric field gradient quadrupole Raman modes observed in plasmon-driven catalytic reactions revealed by HV-TERS. Nanoscale 2013, 5, 4151–4155. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Zhang, Z.; Zheng, H.; Xu, H. In-situ plasmon-driven chemical reactions revealed by high vacuum tip-enhanced Raman spectroscopy. Sci. Rep. 2012, 2, 647. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, Y.; Zhang, Z.; Chen, L.; Sun, M. Near field plasmonic gradient effects on high vacuum tip-enhanced Raman spectroscopy. Phys. Chem. Chem. Phys. 2015, 17, 783–794. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Wang, L.; Mu, X.; Chen, M.; Sun, M. Biological nascent evolution of snail bone and collagen revealed by nonlinear optical microscopy. J. Biophotonics 2019, 12, e201900119. [Google Scholar] [CrossRef]
- Kong, L.; Wang, J.; Mu, X.; Li, R.; Li, X.; Fan, X.; Song, P.; Ma, F.; Sun, M. Porous size dependent g-C3N4 for efficient photocatalysts: Regulation synthesizes and physical mechanism. Mater. Today Energy 2019, 13, 11–21. [Google Scholar] [CrossRef]
- Mu, X.; Cai, K.; Wei, W.; Li, Y.; Wang, Z.; Wang, J. Dependence of UV–Visible Absorption Characteristics on the Migration Distance and the Hyperconjugation Effect of a Methine Chain. J. Phys. Chem. C 2018, 122, 7831–7837. [Google Scholar] [CrossRef]
- Mu, X.; Chen, X.; Wang, J.; Sun, M. Visualizations of Electric and Magnetic Interactions in Electronic Circular Dichroism and Raman Optical Activity. J. Phys. Chem. A 2019, 123, 8071–8081. [Google Scholar] [CrossRef]
- Mu, X.; Wang, J.; Sun, M. Visualizations of Photoinduced Charge Transfer and Electron-Hole Coherence in Two-Photon Absorptions. J. Phys. Chem. C 2019, 123, 14123–14143. [Google Scholar] [CrossRef]
- Valev, V. Characterization of nanostructured plasmonic surfaces with second harmonic generation. Langmuir 2012, 28, 15454–15471. [Google Scholar] [CrossRef]
- Wu, R.-L.; Quan, J.; Tian, C.; Sun, M. Transformation from Quantum to Classical Mode: The Size Effect of Plasmon in 2D Atomic Cluster System. Sci. Rep. 2019, 9, 6641. [Google Scholar] [CrossRef]
- Borah, R.; Verbruggen, S.W. Coupled Plasmon Modes in 2D Gold Nanoparticle Clusters and their Effect on Local Temperature Control. J. Phys. Chem. C 2019. [Google Scholar] [CrossRef]
- Shibayama, J.; Ando, R.; Nomura, A.; Yamauchi, J.; Nakano, H. Simple trapezoidal recursive convolution technique for the frequency-dependent FDTD analysis of a Drude–Lorentz model. IEEE Photon. Technol. Lett. 2008, 21, 100–102. [Google Scholar] [CrossRef]
- Tip, A. Linear dispersive dielectrics as limits of Drude-Lorentz systems. Phys. Rev. E 2004, 69, 016610. [Google Scholar] [CrossRef] [PubMed]
- Sabah, C.; Uckun, S. Multilayer system of Lorentz/Drude type metamaterials with dielectric slabs and its application to electromagnetic filters. Prog. Electromagn. Res. 2009, 91, 349–364. [Google Scholar] [CrossRef] [Green Version]
- Choy, T.C. Effective Medium Theory: Principles and Applications; Oxford University Press: Oxford, UK, 2015; Volume 165. [Google Scholar]
- Bohren, C.F. Applicability of effective-medium theories to problems of scattering and absorption by nonhomogeneous atmospheric particles. J. Atmos. Sci 1986, 43, 468–475. [Google Scholar] [CrossRef] [Green Version]
- Koschny, T.; Kafesaki, M.; Economou, E.; Soukoulis, C. Effective medium theory of left-handed materials. Phys. Rev. Lett. 2004, 93, 107402. [Google Scholar] [CrossRef] [Green Version]
- Szabó, B.; Babuška, I. Finite Element Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Strite, S.; Morkoç, H. GaN, AlN, and InN: A review. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 1992, 10, 1237–1266. [Google Scholar] [CrossRef]
- Yim, W.; Paff, R. Thermal expansion of AlN, sapphire, and silicon. J. Appl. Phys. 1974, 45, 1456–1457. [Google Scholar] [CrossRef]
- Shen, L.; Heikman, S.; Moran, B.; Coffie, R.; Zhang, N.-Q.; Buttari, D.; Smorchkova, I.; Keller, S.; DenBaars, S.; Mishra, U. AlGaN/AlN/GaN high-power microwave HEMT. IEEE Electron Device Lett. 2001, 22, 457–459. [Google Scholar] [CrossRef]
- Ching, W.; Harmon, B. Electronic structure of AlN. Phys. Rev. B 1986, 34, 5305. [Google Scholar] [CrossRef] [PubMed]
- Amano, H.; Sawaki, N.; Akasaki, I.; Toyoda, Y. Metalorganic vapor phase epitaxial growth of a high quality GaN film using an AlN buffer layer. Appl. Phys. Lett. 1986, 48, 353–355. [Google Scholar] [CrossRef] [Green Version]
- Gerlich, D.; Dole, S.; Slack, G. Elastic properties of aluminum nitride. J. Phys. Chem. Solids 1986, 47, 437–441. [Google Scholar] [CrossRef]
- Iqbal, J.; Ayub, K. Theoretical study of the non linear optical properties of alkali metal (Li, Na, K) doped aluminum nitride nanocages. RSC Adv. 2016, 6, 94228–94235. [Google Scholar]
- Gueorguiev, G.K.; Goyenola, C.; Schmidt, S.; Hultman, L. CFx: A first-principles study of structural patterns arising during synthetic growth. Chem. Phys. Lett. 2011, 516, 62–67. [Google Scholar] [CrossRef] [Green Version]
- Kakanakova-Georgieva, A.; Gueorguiev, G.K.; Yakimova, R.; Janzén, E. Effect of impurity incorporation on crystallization in AlN sublimation epitaxy. J. Appl. Phys. 2004, 96, 5293–5297. [Google Scholar] [CrossRef]
- Dos Santos, R.B.; Rivelino, R.; de Brito Mota, F.; Gueorguiev, G.K.; Kakanakova-Georgieva, A. Dopant species with Al–Si and N–Si bonding in the MOCVD of AlN implementing trimethylaluminum, ammonia and silane. J. Phys. D Appl. Phys. 2015, 48, 295104. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
- Smidstrup, S.; Stradi, D.; Wellendorff, J.; Khomyakov, P.A.; Vej-Hansen, U.G.; Lee, M.-E.; Ghosh, T.; Jónsson, E.; Jónsson, H.; Stokbro, K. First-principles Green’s-function method for surface calculations: A pseudopotential localized basis set approach. Phys. Rev. B 2017, 96, 195309. [Google Scholar] [CrossRef] [Green Version]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G.; et al. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter. 2019, 32, 015901. [Google Scholar] [CrossRef] [PubMed]
- Dev, P.; Agrawal, S.; English, N.J. Functional Assessment for Predicting Charge-Transfer Excitations of Dyes in Complexed State: A Study of Triphenylamine–Donor Dyes on Titania for Dye-Sensitized Solar Cells. J. Phys. Chem. A 2013, 117, 2114–2124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Städele, M.; Moukara, M.; Majewski, J.A.; Vogl, P.; Görling, A. Exact exchange Kohn-Sham formalism applied to semiconductors. Phys. Rev. B 1999, 59, 10031. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wang, J.; Chen, S.; Wang, M. Impurity Controlled near Infrared Surface Plasmonic in AlN. Nanomaterials 2022, 12, 459. https://doi.org/10.3390/nano12030459
Li Q, Wang J, Chen S, Wang M. Impurity Controlled near Infrared Surface Plasmonic in AlN. Nanomaterials. 2022; 12(3):459. https://doi.org/10.3390/nano12030459
Chicago/Turabian StyleLi, Quanjiang, Jingang Wang, Shenghui Chen, and Meishan Wang. 2022. "Impurity Controlled near Infrared Surface Plasmonic in AlN" Nanomaterials 12, no. 3: 459. https://doi.org/10.3390/nano12030459
APA StyleLi, Q., Wang, J., Chen, S., & Wang, M. (2022). Impurity Controlled near Infrared Surface Plasmonic in AlN. Nanomaterials, 12(3), 459. https://doi.org/10.3390/nano12030459






