Application of the Photoacoustic Approach in the Characterization of Nanostructured Materials
Abstract
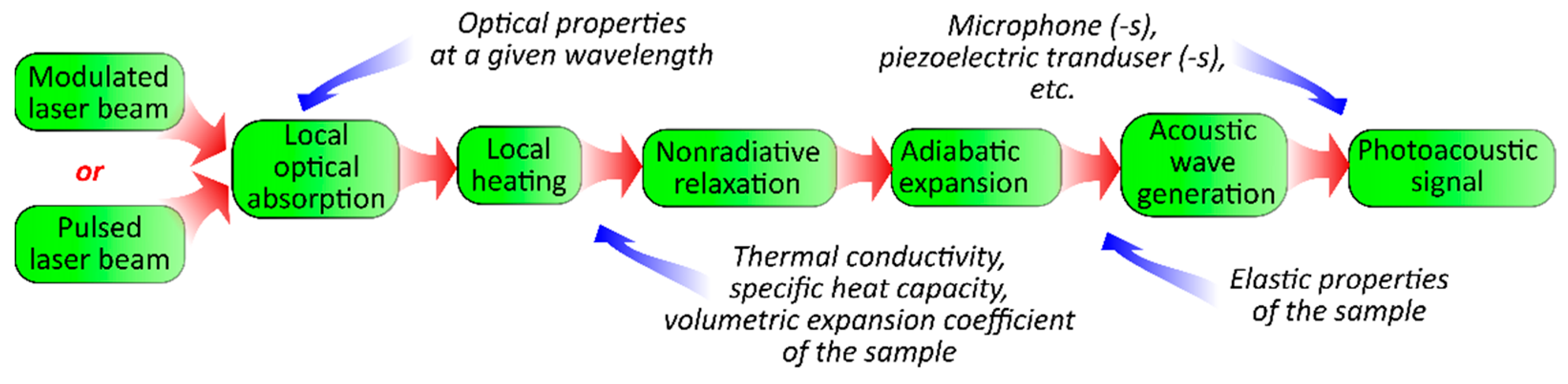
1. Introduction
- Section 1 (this section) provides a brief introduction to the history and physical background of the photoacoustic effect.
- Section 2 is devoted to the gas–microphone photoacoustic technique. In this, the first section describes the background, status, and future prospects of the approach. The second section is devoted to the mathematical basis that allows us to describe the signal formation. The third section provides insight into the main configurations of the gas–microphone photoacoustic cells. The last section provides examples of the application of the photoacoustic approaches in the evaluation of thermal and optical properties of nanostructured materials.
- Section 3 reports the features of photoacoustic signal formation by implementing the PA technique with the configuration of piezoelectric detection. The first section gives a short overview of the theoretical basis for the description of the signal’s formation in this case, and the second section gives some examples of the application of the piezoelectric approaches in the characterization of nanomaterials.
- Section 4 provides a short description of the application of the photoacoustic methods in imaging (the first section) and visualization (the second section) with respect to biomedical and materials research applications.
- Section 5 provides an overview of the use of the photoacoustic approach for FT-IR spectroscopy with a gas–microphone configuration (the first subsection) and its application in the nanosystem investigation in different phases.
2. Photoacoustic Gas–Microphone Technique
2.1. PA Gas–Microphone Technique: Background, Status, and Future Prospects
2.2. Main Concepts of PA Signal Analysis Obtained by the Gas–Microphone Technique
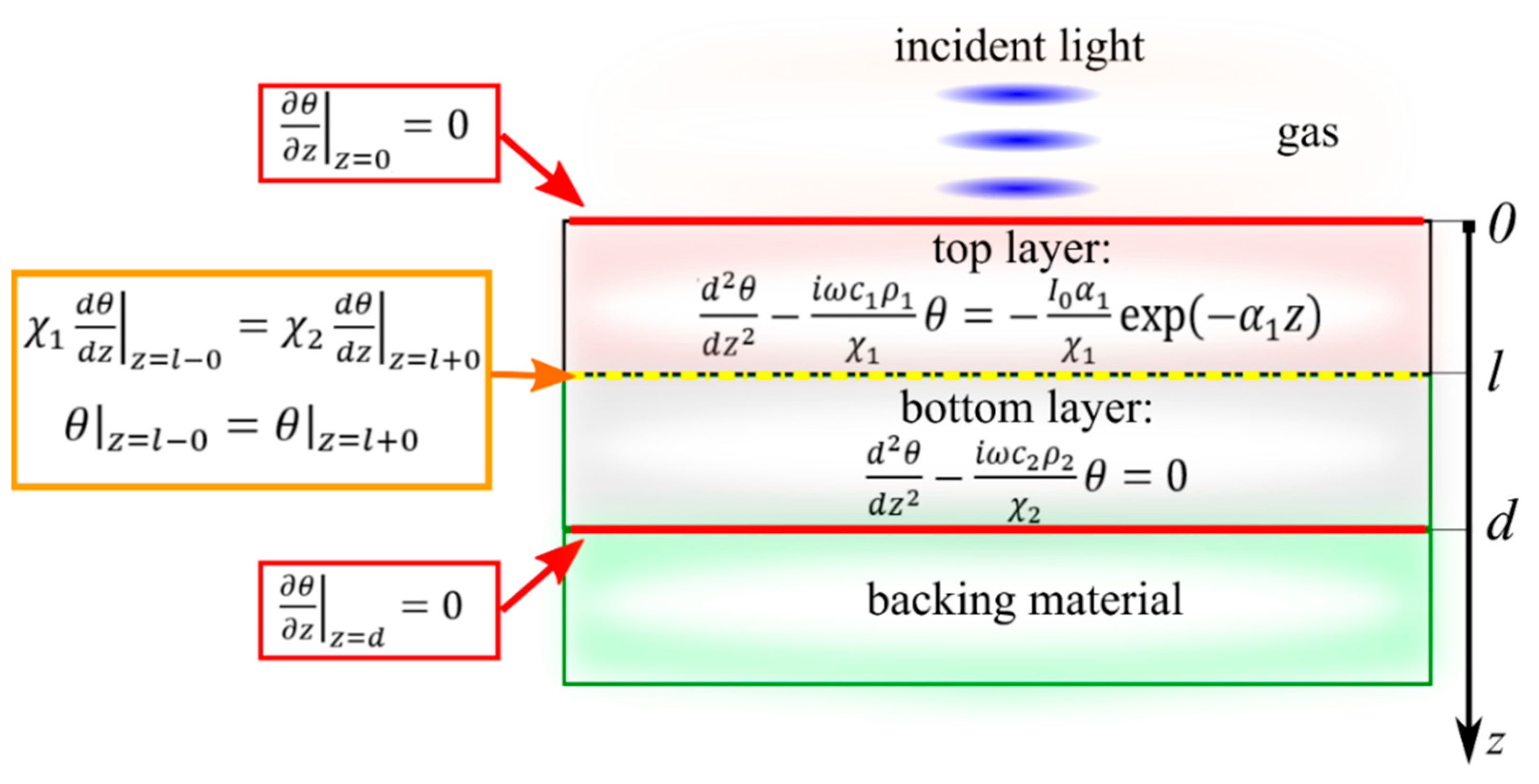
2.2.1. Thermal Diffusivity Measurements
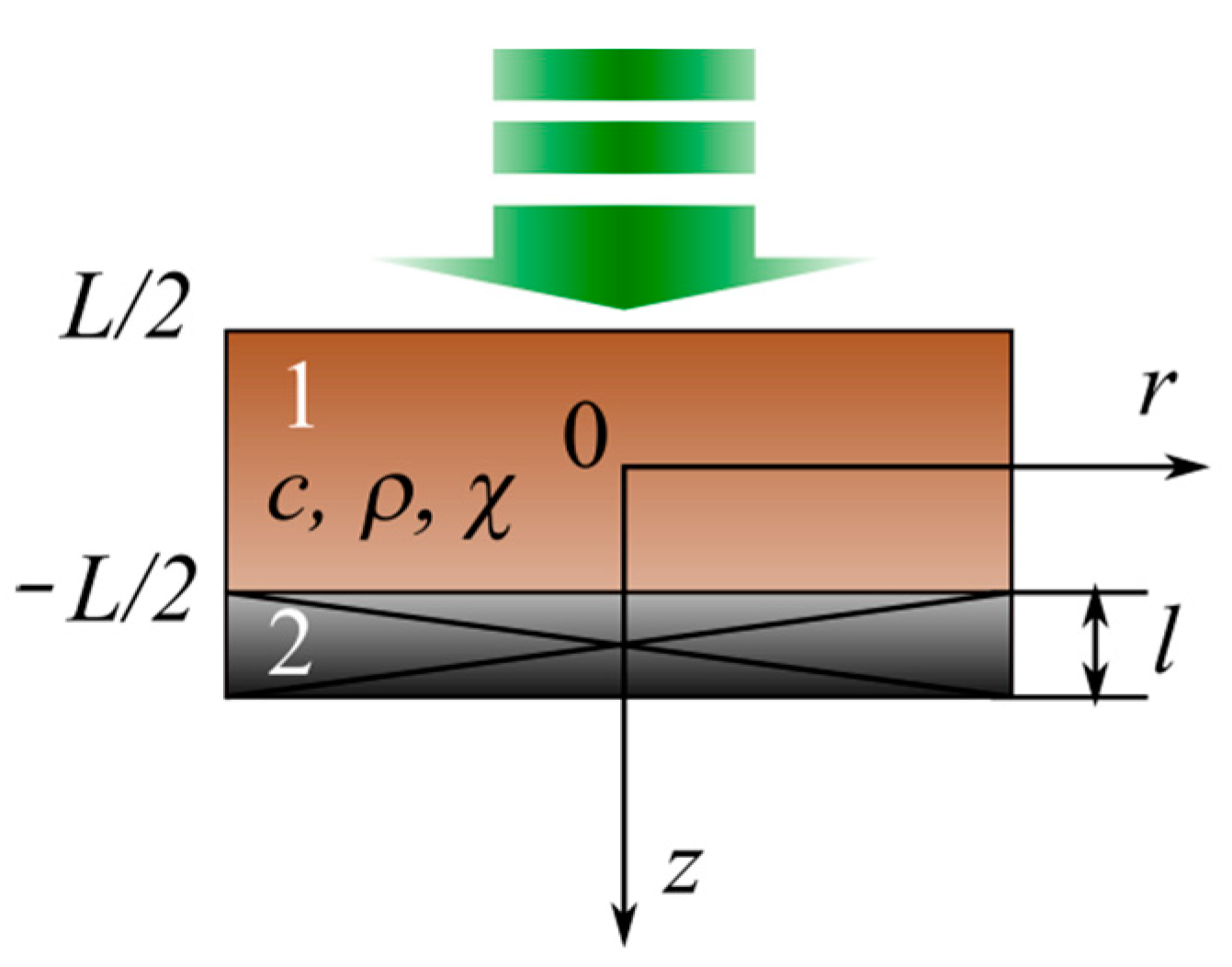
2.2.2. Characterization of Low-Dimensional Semiconductor Materials by Variable Temperature Component Distribution Modeling
- The absence of heat outflow at the lower and upper boundaries of the studied structure;
- The continuity conditions for both temperature and heat flow at the interface between the two layers of the system.
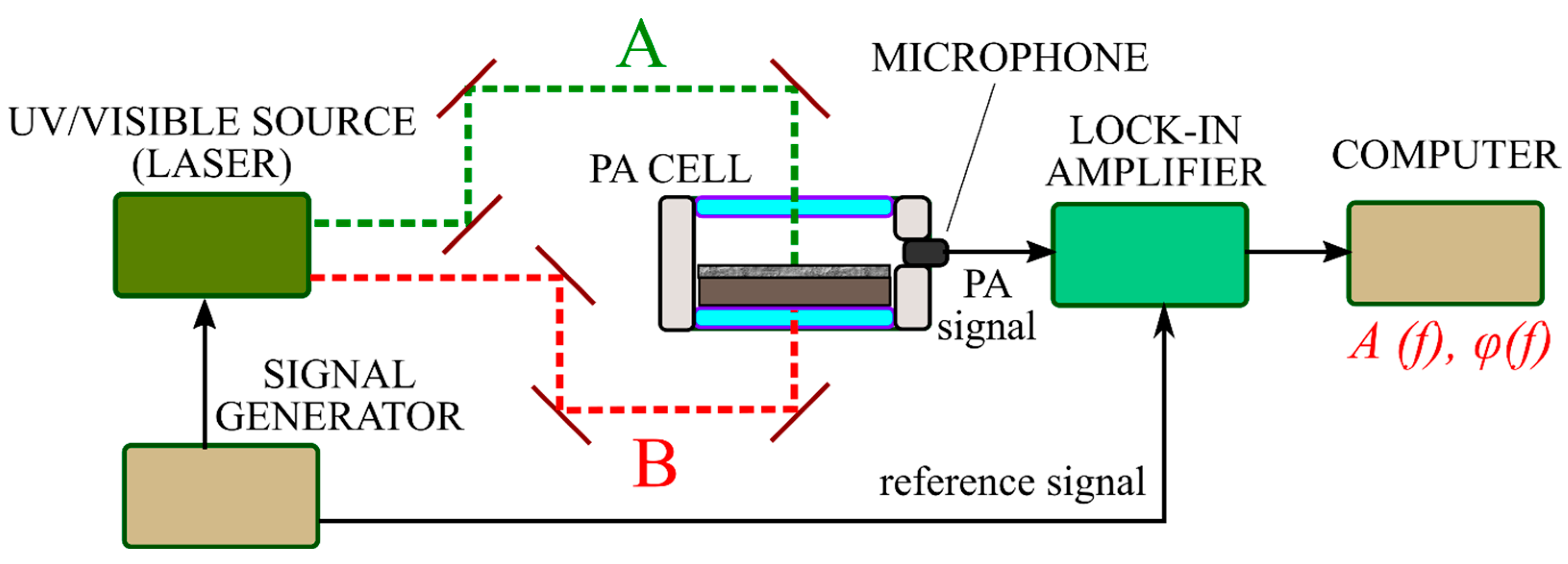
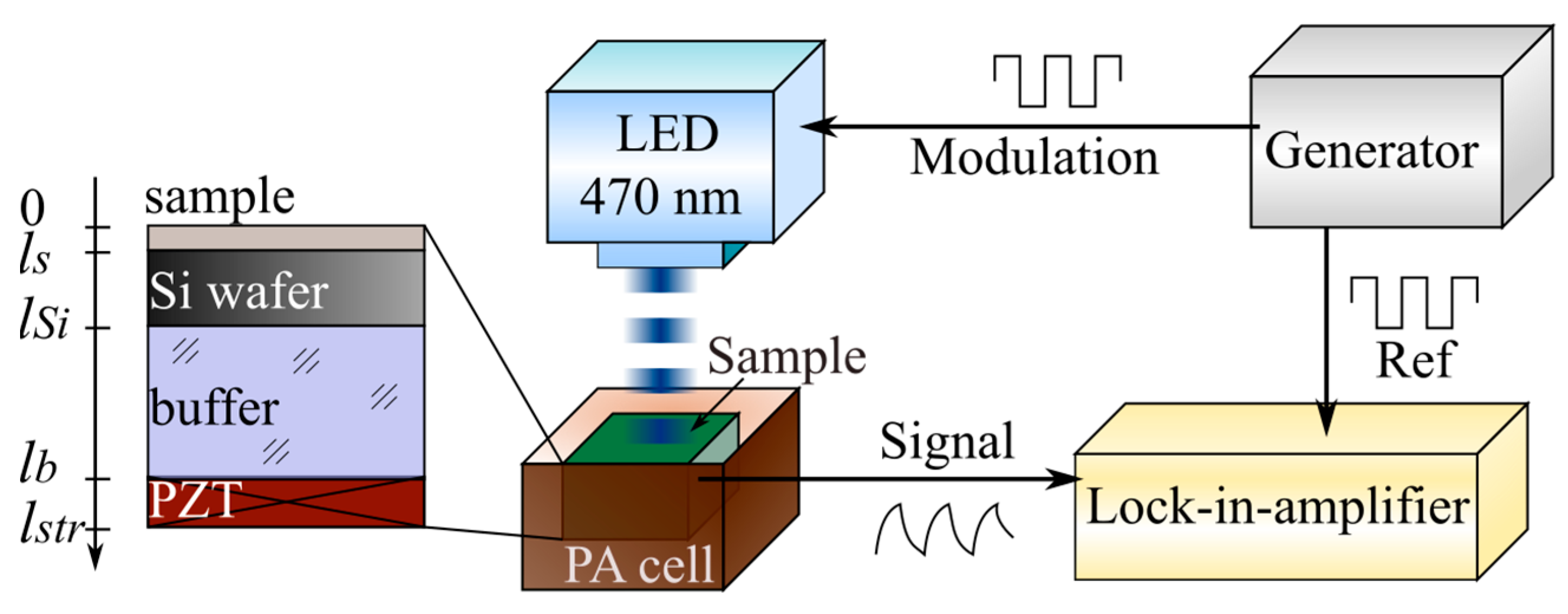
2.3. Experimental Setup of the PA GM Technique
2.4. The Application of the Photoacoustic Approaches in the Evaluation of Thermal and Optical Properties of Nanostructured Materials
2.4.1. Features of PA Response Formation in Porous Multilayered Structures
- Calculation of the complex dielectric permittivity using Bruggeman’s approximation;
- Numerical evaluation of the volumetric heat source from Maxwell equation’s resolution;
- Calculation of the temperature profiles of the photoexcited sample and the fitting procedure with the experimentally obtained PA response using the developed model’s calculations.
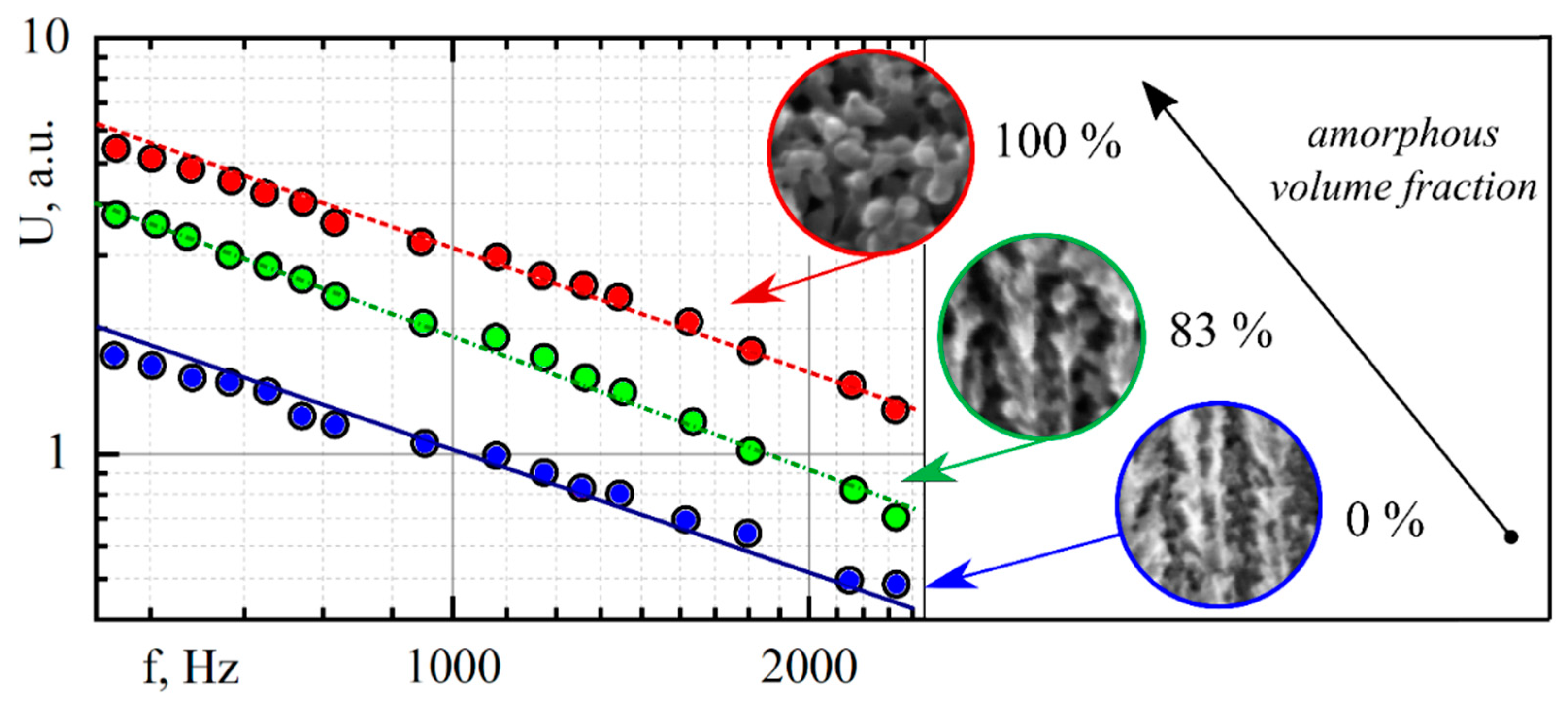
2.4.2. Comparative Magnitude Analysis of the Thin, Porous Films Using the PA Technique
3. Piezoelectric Photoacoustic Detection
3.1. Photoacoustic Signal Formation in Solids with the Piezoelectric Technique
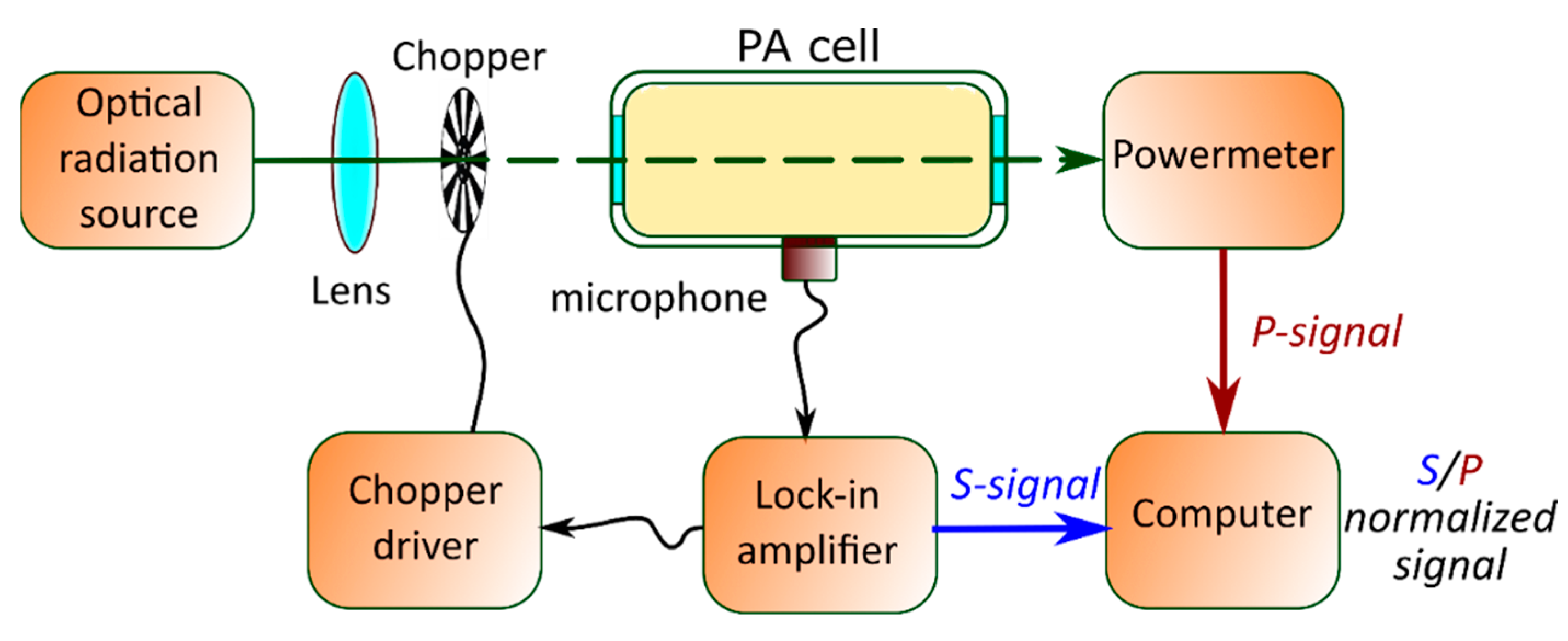
3.2. Experimental Setup of PA with a Piezoelectric Registration Technique
3.3. Application of PA in Piezoelectric Detection Configuration
3.3.1. Thermal Property Characterization of Nanostructured Materials with the Photoacoustic Piezoelectric Technique
3.3.2. Characterization of Colloids, Liquid Food, and Nanofluids Using the Piezoelectric Photoacoustic Technique
4. Physical Principles of Photoacoustic Imaging
- (a)
- Photoacoustic microscopy (PAM), a common low-cost method where a focused modulated laser beam is used to achieve high-spatial-resolution imaging at small depths;
- (b)
- Photoacoustic tomography (PAT), a hybrid imaging technique that combines optical excitation and acoustic detection to realize imaging with relatively deep penetration in the studied object.
4.1. Photoacoustic Microscopy: Areas of Application, Advantages, and Drawbacks
4.2. Adaptation of Photoacoustic Tomography for Preclinical and Clinical Applications
5. Physical Principles of Photoacoustic FT-IR Spectroscopy
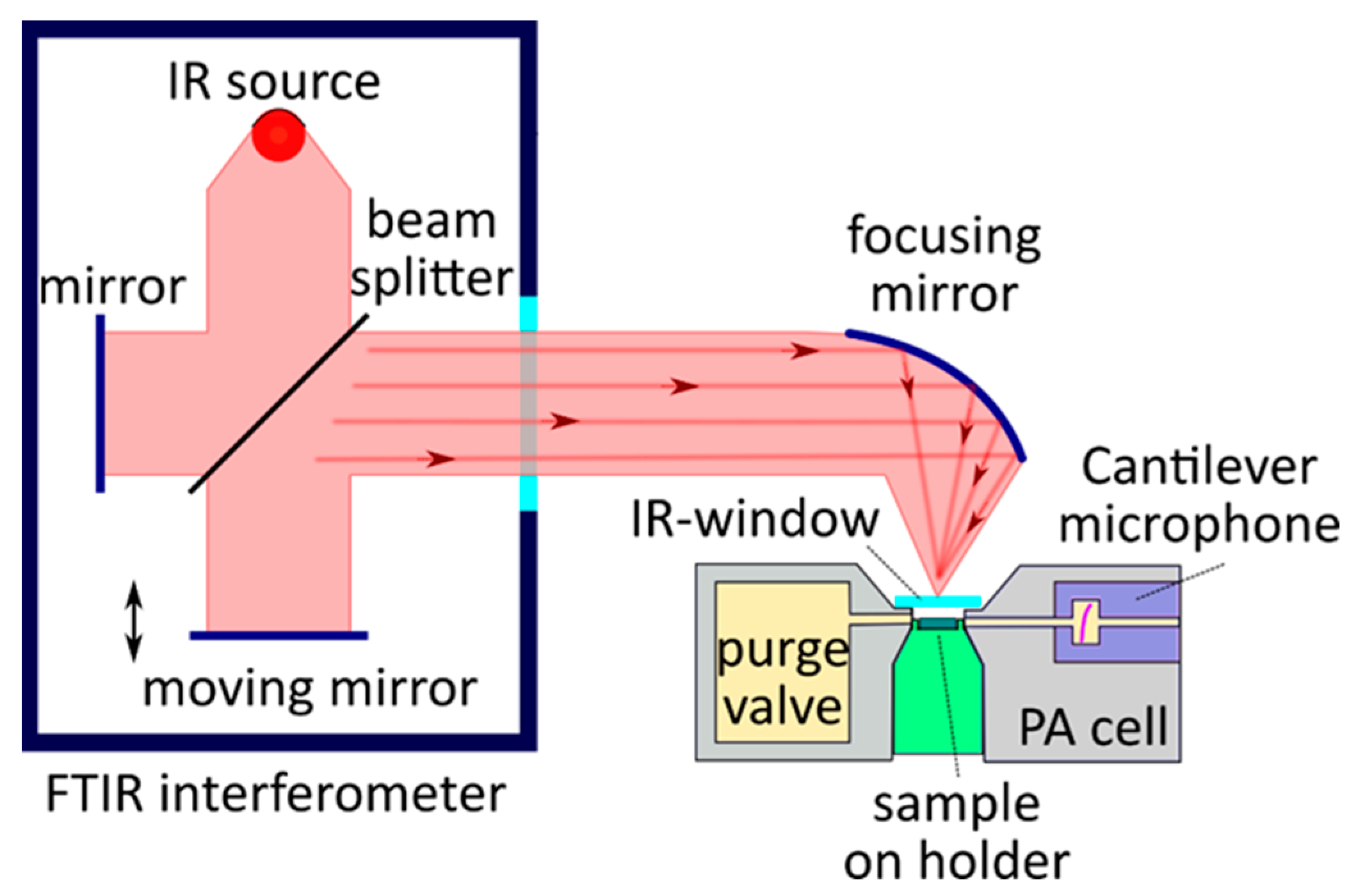
5.1. Gas-Phase Photoacoustic FT-IR Spectroscopy
5.2. Solid- and Liquid-Phase Photoacoustic FT-IR Spectroscopy
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haisch, C. Photoacoustic spectroscopy for analytical measurements. Meas. Sci. Technol. 2012, 23, 012001. [Google Scholar] [CrossRef]
- Palzer, S. Photoacoustic-Based Gas Sensing: A Review. Sensors 2020, 20, 2745. [Google Scholar] [CrossRef] [PubMed]
- Usoltseva, L.O.; Korobov, M.V.; Proskurnin, M.A. Photothermal spectroscopy: A promising tool for nanofluids. J. Appl. Phys. 2020, 128, 190901. [Google Scholar] [CrossRef]
- Volkov, D.S.; Krivoshein, P.K.; Proskurnin, M.A. Detonation nanodiamonds: A comparison study by photoacoustic, diffuse reflectance, and attenuated total reflection FTIR spectroscopies. Nanomaterials 2020, 10, 2501. [Google Scholar] [CrossRef]
- Krishnaswamy, S. Photoacoustic Characterization of Materials. In Springer Handbook of Experimental Solid Mechanics; Sharpe, W., Ed.; Springer: Boston, MA, USA, 2008; pp. 769–800. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, K.; Chen, Y.; Yang, B.; Guo, M.; Deng, H.; Ma, F.; Zhu, F.; Gong, Z.; Peng, W.; et al. High-sensitivity photoacoustic gas detector by employing multi-pass cell and fiber-optic microphone. Opt. Express 2020, 28, 6618–6630. [Google Scholar] [CrossRef]
- Abad, B. Non-contact methods for thermal properties measurement. Renew. Sustain. Energy Rev. 2017, 76, 1348–1370. [Google Scholar] [CrossRef]
- Skvortsov, L.A. Laser photothermal spectroscopy of light-induced absorption. Quantum Electron. 2013, 43, 1–13. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, Y.; Tiao, M.; Xia, J. Review of methods to improve the performance of linear array-based photoacoustic tomography. J. Innov. Opt. Health Sci. 2020, 13, 2030003. [Google Scholar] [CrossRef]
- Rosencwaig, A. Photoacoustics and Photoacoustic Spectroscopy; John Wiley & Sons: New York, NY, USA, 1980; pp. 1–309. [Google Scholar]
- Lysenko, V.; Perichon, S.; Remaki, B.; Barbier, D.; Champagnon, B. Thermal conductivity of thick meso-porous silicon layers by micro-Raman scattering. J. Appl. Phys. 1999, 86, 6841. [Google Scholar] [CrossRef]
- Hochbaum, A.I.; Chen, R.; Diaz Delgado, R.; Liang, W.; Garnett, E.C.; Najarian, M.; Majumdar, A.; Yang, P. Enhanced thermoelectric performance of rough silicon nanowires. Nature 2008, 451, 163–167. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, S.; Zheng, R.; Cheng, G. Significant reduction of thermal conductivity in silicon nanowire arrays. Nanotechnology 2013, 24, 505718. [Google Scholar] [CrossRef] [PubMed]
- Stoib, B.; Filser, S.; Petermann, N.; Wiggers, H.; Stutzmann, M.; Brandt, M.S. Thermal conductivity of mesoporous films measured by Raman spectroscopy. Appl. Phys. Lett. 2014, 104, 161907. [Google Scholar] [CrossRef]
- Sailor, M.J. Porous Silicon in Practice; Wiley-VCH Verlag &Co.: Weinheim, Germany, 2012; pp. 1–254. [Google Scholar]
- Han, H.; Huang, Z.; Lee, W. Metal-assisted chemical etching of silicon and nanotechnology applications. Nano Today 2014, 9, 271–304. [Google Scholar] [CrossRef]
- Gasera. Available online: https://www.gasera.fi/technology/solid-phase-pas (accessed on 16 May 2021).
- Da Costa, A.C.R.; Siqueira, A.F. Thermal diffusivity of conducting polypyrrole. J. Appl. Phys. 1996, 80, 5579–5582. [Google Scholar] [CrossRef]
- Lishchuk, P.; Andrusenko, D.; Isaiev, M.; Lysenko, V.; Burbelo, R. Investigation of thermal transport properties of porous silicon by photoacoustic technique. Int. J. Thermophys. 2015, 36, 2428–2433. [Google Scholar] [CrossRef]
- Gurevich, Y.G.; Logvinov, G.N.; De, G.G.; Espejo, G. Physics of thermal waves in homogeneous and inhomogeneous (two-layer) samples. Int. J. Therm. Sci. 2003, 42, 63–69. [Google Scholar] [CrossRef]
- De La Cruz, G.G.; Gurevich, Y.G. Thermal diffusion of a two-layer system. Phys. Rev. B 1995, 51, 2188–2192. [Google Scholar] [CrossRef]
- Andrusenko, D.; Isaiev, M.; Tytarenko, A.; Lysenko, V.; Burbelo, R. Size evaluation of the fine morphological features of porous nanostructures from the perturbation of heat transfer by a pore filling agent. Microporous Mesoporous Mater. 2014, 194, 79–82. [Google Scholar] [CrossRef]
- Rosencwaig, A.; Gersho, A. Theory of the photoacoustic effect with solids. J. Appl. Phys. 1976, 47, 64–69. [Google Scholar] [CrossRef]
- Todorovic, D.M.; Rabasovic, M.D.; Markushev, D.D.; Jovic, V.; Radulovic, K.T.; Sarajlic, M. Photoacoustic elastic bending method: Characterization of thin films on silicon membranes. Int. J. Thermophys. 2015, 36, 1016–1028. [Google Scholar] [CrossRef]
- Šoškić, Z.; Ćirić-Kostić, S.; Galović, S. An extension to the methodology for characterization of thermal properties of thin solid samples by photoacoustic techniques. Int. J. Therm. Sci. 2016, 109, 217–230. [Google Scholar] [CrossRef]
- Balderas-López, J.A.; Mandelis, A. Thermal diffusivity measurements in the photoacoustic open-cell configuration using simple signal normalization techniques. J. Appl. Phys. 2001, 90, 2273–2279. [Google Scholar] [CrossRef]
- Burbelo, R.; Andrusenko, D.; Isaiev, M.; Kuzmich, A. Laser photoacoustic diagnostics of advanced materials with different structure and dimensions. Arch. Met. Mater. 2011, 56, 1157–1162. [Google Scholar] [CrossRef][Green Version]
- Benedetto, G.; Boarino, L.; Spagnolo, R. Evaluation of thermal conductivity of porous silicon layers by a photoacoustic method. Appl. Phys. A Mater. Sci. Process. 1997, 64, 155–159. [Google Scholar] [CrossRef]
- Tytarenko, A.I.; Andrusenko, D.A.; Kuzmich, A.G.; Gavril’chenko, I.V.; Skryshevskii, V.A.; Isaiev, M.; Burbelo, R.M. Features of photoacoustic transformation in microporous nanocrystalline silicon. Tech. Phys. Lett. 2014, 40, 188–191. [Google Scholar] [CrossRef]
- Isaiev, M.; Tutashkonko, S.; Jean, V.; Termentzidis, K.; Nychyporuk, T.; Andrusenko, D.; Marty, O.; Burbelo, R.M.; Lacroix, D.; Lysenko, V. Thermal conductivity of meso-porous germanium. Appl. Phys. Lett. 2014, 105, 031912. [Google Scholar] [CrossRef]
- Lishchuk, P.; Isaiev, M.; Osminkina, L.; Burbelo, R.; Nychyporuk, T.; Timoshenko, V. Photoacoustic characterization of nanowire arrays formed by metal-assisted chemical etching of crystalline silicon substrates with different doping level. Phys. E Low Dimens. Syst. Nanostructures 2019, 107, 131–136. [Google Scholar] [CrossRef]
- Lishchuk, P.; Dekret, A.; Pastushenko, A.; Kuzmich, A.; Burbelo, R.; Belarouci, A.; Lysenko, V.; Isaiev, M. Interfacial thermal resistance between porous layers: Impact on thermal conductivity of a multilayered porous structure. Int. J. Therm. Sci. 2018, 134, 317–320. [Google Scholar] [CrossRef]
- Lishchuk, P.; Isaiev, M. Characterization of porous silicon based composite nanostructures by means of photoacoustic technique. In Proceedings of the 2018 IEEE 8th International Conference on Nanomaterials: Applications & Properties (NAP-2018), Odesa, Ukraine, 9–14 September 2018; p. 01SPN11(1–5). [Google Scholar] [CrossRef]
- Dubyk, K.; Chepela, L.; Lishchuk, P.; Belarouci, A.; Lacroix, D.; Isaiev, M. Features of photothermal transformation in porous silicon based multilayered structures. Appl. Phys. Lett. 2019, 115, 021902. [Google Scholar] [CrossRef]
- Lishchuk, P.; Belarouci, A.; Tkach, R.; Dubyk, K.; Ostapenko, R.; Kuryliuk, V.; Castanet, G.; Naumenko, S.; Kuzmich, A.; Lemoine, F.; et al. Impact of thermal annealing on photoacoustic response and heat transport in porous silicon based nanostructured materials. AIP Conf. Proc. 2019, 2170, 020008. [Google Scholar] [CrossRef]
- Ramirez-Gutierrez, C.F.; Lujan-Cabrera, I.A.; Isaza, C.; Anaya Rivera, E.K.; Rodriguez-Garcia, M.E. In situ photoacoustic study of optical properties of p-type (111) porous silicon thin films. Nanomaterials 2021, 11, 1314. [Google Scholar] [CrossRef]
- Ramirez-Gutierrez, C.F.; Martinez-Hernandez, H.D.; Lujan-Cabrera, I.A.; Rodriguez-García, M.E. Design, fabrication, and optical characterization of one-dimensional photonic crystals based on porous silicon assisted by in-situ photoacoustics. Sci. Rep. 2019, 9, 14732. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Gutierrez, C.F.; Castaño-Yepes, J.D.; Rodriguez-García, M.E. Modeling the photoacoustic signal during the porous silicon formation. J. Appl. Phys. 2017, 121, 025103. [Google Scholar] [CrossRef]
- Isaiev, M.; Newby, P.; Canut, B.; Tytarenko, A.; Lishchuk, P.; Andrusenko, D.; Gomès, S.; Bluet, J.-M.; Fréchette, L.G.; Lysenko, V.; et al. Thermal conductivity of partially amorphous porous silicon by photoacoustic technique. Mater. Lett. 2014, 128, 71–74. [Google Scholar] [CrossRef]
- Newby, P.; Canut, B.; Bluet, J.-M.; Gomès, S.; Isaiev, M.; Burbelo, R.; Termentzidis, K.; Chantrenne, P.; Fréchette, L.G.; Lysenko, V. Amorphization and reduction of thermal conductivity in porous silicon by irradiation with swift heavy ions. J. Appl. Phys. 2013, 114, 014903. [Google Scholar] [CrossRef]
- Massoud, A.M.; Chapuis, P.O.; Canut, B.; Bluet, J.M. Thermal conductivity of irradiated porous silicon down to the oxide limit investigated by Raman thermometry and scanning thermal microscopy. J. Appl. Phys. 2020, 128, 175109. [Google Scholar] [CrossRef]
- Jackson, W.; Amer, N.M. Piezoelectric photoacoustic detection: Theory and experiment. J. Appl. Phys. 1980, 51, 3343–3353. [Google Scholar] [CrossRef]
- Blonskij, I.V.; Tkhoryk, V.A.; Shendeleva, M.L. Thermal diffusivity of solids determination by photoacoustic piezoelectric technique. J. Appl. Phys. 1996, 79, 3512–3516. [Google Scholar] [CrossRef]
- Isaiev, M.; Andrusenko, D.; Tytarenko, A.; Kuzmich, A.; Lysenko, V.; Burbelo, R. Photoacoustic signal formation in heterogeneous multilayer systems with piezoelectric detection. Int. J. Thermophys. 2014, 35, 2341–2351. [Google Scholar] [CrossRef]
- Maliński, M. Application of the temperature distribution formula for the photoacoustic investigations of layer systems. Eur. Phys. J. Spec. Top. 2008, 153, 291–293. [Google Scholar] [CrossRef]
- Zakrzewski, J.; Maliński, M.; Strzałkowski, K. Temperature distributions in piezoelectric photothermal spectroscopy. Int. J. Thermophys. 2013, 34, 725–735. [Google Scholar] [CrossRef]
- Andrusenko, D.A.; Kucherov, I.Y. Photothermoacoustic effect in solids with piezoelectric recording. JETP 1999, 44, 1397–1401. [Google Scholar]
- Sun, Q.; Gao, C.; Zhao, B.; Bi, Y. A modified photoacoustic piezoelectric model for thermal diffusivity determination of solids. Int. J. Thermophys. 2010, 31, 1157–1164. [Google Scholar] [CrossRef]
- Yan, L.; Gao, C.; Zhao, B.; Ma, X.; Zhuang, N.; Duan, H. Non-destructive imaging of standard cracks of railway by photoacoustic piezoelectric technology. Int. J. Thermophys. 2012, 33, 2001–2005. [Google Scholar] [CrossRef]
- Sun, Q.-M.; Gao, C.-M.; Zhao, B.-X.; Rao, H.-B. Thermal diffusivity of light-emitting diode packaging material determined by photoacoustic piezoelectric technique. Chin. Phys. B 2010, 19, 118103. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, Y.; Gao, C.; Liu, T.; Sun, Q. Thermal properties of porcine tissues determined by modified photoacoustic piezoelectric technique. Int. J. Thermophys. 2013, 34, 1513–1518. [Google Scholar] [CrossRef]
- Dubyk, K.; Pastushenko, A.; Nychyporuk, T.; Burbelo, R.; Isaiev, M.; Lysenko, V. Thermal conductivity of silicon nanomaterials measured using the photoacoustic technique in a piezoelectric configuration. J. Phys. Chem. Solids 2019, 126, 267–273. [Google Scholar] [CrossRef]
- Dubyk, K.; Nychyporuk, T.; Lysenko, V.; Termentzidis, K.; Castanet, G.; Lemoine, F.; Lacroix, D.; Isaiev, M. Thermal properties study of silicon nanostructures by photoacoustic techniques. J. Appl. Phys. 2020, 127, 225101. [Google Scholar] [CrossRef]
- Glazov, A.L.; Morozov, N.F.; Muratikov, K.L. Photoacoustic microscopy of vickers indentations in metals with piezoelectric detection. Int. J. Thermophys. 2017, 38, 113. [Google Scholar] [CrossRef]
- Sun, Q.; Gao, C.; Zhao, B.; Rao, H. Thermal diffusivity of light-emitting material determination by photoacoustic piezoelectric technique. Photonics Optoelectron. Meet. Laser Technol. Appl. 2008, 7276, 72761. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, S.Y.; Zhao, Y.Z.; Li, Z.Q.; Cheng, L.P. Thermal diffusivity of composites determined by photoacoustic piezoelectric technique. Rev. Sci. Instrum. 2003, 74, 834–836. [Google Scholar] [CrossRef]
- Andrusenko, D.; Isaiev, M.; Kuzmich, A.; Lysenko, V.; Burbelo, R. Photoacoustic effects in nanocomposite structure porous silicon-liquid. Nanoscale Res. Lett. 2012, 7, 411. [Google Scholar] [CrossRef] [PubMed]
- Voitenko, K.; Andrusenko, D.; Pastushenko, A.; Isaiev, M.; Kuzmich, A.G.; Burbelo, R.M. Photoacoustic response formation in nanostructured composite systems «porous matrix—liquid. J. Nano Electron. Phys. 2017, 9, 04021. [Google Scholar] [CrossRef]
- Saidur, R.; Leong, K.Y.; Mohammad, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Dadfar, S.M.; Roemhild, K.; Drude, N.; von Stillfried, S.; Knüchel, R.; Kiessling, F.; Lammers, T. Iron oxide nanoparticles: Diagnostic, therapeutic and theranostic applications. Adv. Drug Deliv. Rev. 2019, 138, 302–325. [Google Scholar] [CrossRef]
- Sharma, A.K.; Tiwari, A.K.; Dixit, A.R. Progress of nanofluid application in machining: A review. Mater. Manuf. Process. 2015, 30, 813–828. [Google Scholar] [CrossRef]
- Potisk, T.; Svenšek, D.; Brand, H.R.; Pleiner, H.; Lisjak, D.; Osterman, N.; Mertelj, A. Dynamic magneto-optic coupling in a ferromagnetic nematic liquid crystal. Phys. Rev. Lett. 2017, 119, 97802. [Google Scholar] [CrossRef]
- Aldama-Reyna, W.; Agreda Delgado, J.F.; Valverde-Alva, M.A.; Angelats-Silva, L.M. Photoacoustic study of changes in optical properties of colloids with silver nanoparticles produced by laser ablation. Int. J. Appl. Eng. Res. 2018, 13, 1408–1414. [Google Scholar]
- Li, Y.; Zhang, H.; Yang, Z.; Yuan, B.; Yuan, Z.; Xue, H. Incident-power-dependent optical transmission properties of magnetic fluid films. Optik 2018, 172, 730–735. [Google Scholar] [CrossRef]
- Suriyanto, N.; Ng, E.Y.K.; Kumar, S.D. Physical mechanism and modeling of heat generation and transfer in magnetic fluid hyperthermia through Néelian and Brownian relaxation: A review. Biomed. Eng. Online 2017, 16, 36. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Colombo, M.; Prosperi, D. Recent advances in magnetic fluid hyperthermia for cancer therapy. Colloids Surf. B Biointerfaces 2019, 174, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Sokolovskaya, Y.G.; Podymova, N.B.; Karabutov, A.A. Laser optoacoustic method for measurement of light extinction coefficient and investigation of its spatial distribution in colloidal media. Int. J. Thermophys. 2020, 41, 86. [Google Scholar] [CrossRef]
- Sokolovskaya, Y.G.; Podymova, N.B.; Karabutov, A.A. Laser optoacoustic study of the structural inhomogeneity of a magnetic fluid by reconstruction of the spatial distribution of the light extinction coefficient. Phys. Acoust. 2020, 66, 268–276. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Parekh, K.; Jain, N. In vitro hyperthermic effect of magnetic fluid on cervical and breast cancer cells. Sci. Rep. 2020, 10, 15249. [Google Scholar] [CrossRef]
- Chua, H.L.; Huong, A. Piezoelectric photoacoustic system for fluid flow monitoring. Int. J. Integr. Eng. 2020, 12, 204–210. [Google Scholar] [CrossRef]
- Dubyk, K.; Isaiev, M.; Alekseev, S.; Burbelo, R.; Lysenko, V. Thermal conductivity of nanofluids formed by carbon flurooxide mesoparticles. SN Appl. Sci. 2019, 1, 1440. [Google Scholar] [CrossRef]
- Alekseev, S.; Korytko, D.; Iazykov, M.; Khainakov, S.; Lysenko, V. Electrochemical synthesis of carbon fluorooxide nanoparticles from 3C-SiC substrates. J. Phys. Chem. C 2015, 119, 20503–20514. [Google Scholar] [CrossRef]
- Rahman, T.; Adams, A.T.; Schein, P.; Jain, A.; Erickson, D.; Choudhury, T. Nutrilyzer: A mobile system for characterizing liquid food with photoacoustic effect. In Proceedings of the 14th ACM Conference on Embedded Network Sensor Systems CD-ROM, Stanford, CA, USA, 14–16 November 2016; pp. 123–136. [Google Scholar] [CrossRef]
- Kishor, R.; Gao, F.; Sreejith, S.; Feng, X.; Seah, Y.P.; Wang, Z.; Stuparu, M.C.; Lim, T.-T.; Chen, X.; Zheng, Y. Photoacoustic induced surface acoustic wave sensor for concurrent opto-mechanical microfluidic sensing of dyes and plasmonic nanoparticles. RSC Adv. 2016, 6, 50238–50244. [Google Scholar] [CrossRef]
- Manohar, S.; Razansky, D. Photoacoustics: A historical review. Adv. Opt. Photonics 2016, 8, 586–617. [Google Scholar] [CrossRef]
- Wong, Y.H.; Thomas, R.L.; Hawkins, G.F. Surface and subsurface structure of solids by laser photoacoustic spectroscopy. Appl. Phys. Lett. 1978, 32, 538–539. [Google Scholar] [CrossRef]
- Liu, W. Photoacoustic microscopy: Principles and biomedical applications. Biomed. Eng. Lett. 2018, 2, 203–213. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.Y.; Jeon, S.; Baik, J.W.; Cho, S.H.; Kim, C. Super-resolution localization photoacoustic microscopy using intrinsic red blood cells as contrast absorbers. Light Sci. Appl. 2019, 8, 103. [Google Scholar] [CrossRef] [PubMed]
- Jeon, S.; Kim, J.; Lee, D.; Baik, J.W.; Kim, C. Review on practical photoacoustic microscopy. Photoacoustics 2019, 15, 100141. [Google Scholar] [CrossRef]
- Hysi, E.; Moore, M.J.; Strohm, E.M.; Kolios, M.C. A tutorial in photoacoustic microscopy and tomography signal processing methods. J. Appl. Phys. 2021, 129, 141102. [Google Scholar] [CrossRef]
- Litvinenko, S.; Lishchuk, P.; Lysenko, V.; Isaiev, M. Bi-modal photothermal/optical microscopy for complementary bio-imaging with high resolution and contrast. Appl. Phys. B 2021, 127, 139–143. [Google Scholar] [CrossRef]
- Burbelo, R.M.; Kuz’mich, A.G.; Kucherov, I.Y. Atomic structure and non-electronic properties of semiconductors: Photothermoacoustic and photoelectric microscopy of silicon. Semiconductors 1999, 33, 630–635. [Google Scholar] [CrossRef]
- Proskurnin, M.A.; Usoltseva, L.O.; Volkov, D.S.; Nedosekin, D.A.; Korobov, M.V.; Zharov, V.F. Photothermal and Heat-Transfer Properties of Aqueous Detonation Nanodiamonds by Photothermal Microscopy and Transient Spectroscopy. J. Phys. Chem. C 2021, 125, 7808–7823. [Google Scholar] [CrossRef]
- Dubyk, K.; Chepela, L.; Alekseev, S.; Kuzmich, A.; Zousman, B.; Levinson, O.; Rozhin, A.; Geloen, A.; Isaiev, M.; Lysenko, V. Some Types of Carbon-based Nanomaterials as Contrast Agents for Photoacoustic Tomography. J. Nano Electron. Phys. 2020, 12, 04033. [Google Scholar] [CrossRef]
- Razansky, D.; Buehler, A.; Ntziachristos, V. Volumetric real-time multispectral optoacoustic tomography of biomarkers. Nat. Protoc. 2011, 6, 1121–1129. [Google Scholar] [CrossRef]
- Acosta, S. Solvability for photoacoustic imaging with idealized piezoelectric sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 2413–2422. [Google Scholar] [CrossRef] [PubMed]
- Deán-Ben, X.L.; Sela, G.; Lauri, A.; Kneipp, M.; Ntziachristos, V.; Westmeyer, G.G.; Shoham, S.; Razansky, D. Functional optoacoustic neuro-tomography for scalable whole-brain monitoring of calcium indicators. Light Sci. Appl. 2016, 5, e16201. [Google Scholar] [CrossRef] [PubMed]
- Brecht, H.-P.; Su, R.; Fronheiser, M.; Ermilov, S.A.; Conjusteau, A.; Oraevsky, A.A. Whole-body three-dimensional optoacoustic tomography system for small animals. J. Biomed. Opt. 2009, 14, 064007. [Google Scholar] [CrossRef] [PubMed]
- Buehler, A.; Herzog, E.; Razansky, D.; Ntziachristos, V. Video rate optoacoustic tomography of mouse kidney perfusion. Opt. Lett. 2010, 35, 2475–2477. [Google Scholar] [CrossRef] [PubMed]
- Gamelin, J.; Maurudis, A.; Aguirre, A.; Huang, F.; Guo, P.; Wang, L.; Zhu, Q. A real-time photoacoustic tomography system for small animals. Opt. Express 2009, 17, 10489–10498. [Google Scholar] [CrossRef] [PubMed]
- Nuster, R.; Paltauf, G. Comparison of piezoelectric and optical projection imaging for three-dimensional in vivo photoacoustic tomography. J. Imaging 2019, 5, 15. [Google Scholar] [CrossRef]
- Paltauf, G.; Hartmair, P.; Kovachev, G.; Nuster, R. Piezoelectric line detector array for photoacoustic tomography. Photoacoustics 2017, 8, 28–36. [Google Scholar] [CrossRef]
- Kolkman, R.G.M.; Blomme, E.; Cool, T.; Bilcke, M.; van Leeuwen, T.; Steenbergen, W.; Grimbergen, K.A.; Heeten, G.J.D. Feasibility of noncontact piezoelectric detection of photoacoustic signals in tissue-mimicking phantoms. J. Biomed. Opt. 2010, 15, 055011. [Google Scholar] [CrossRef][Green Version]
- Gao, C. Thermal property of biological tissues characterized by piezoelectric photoacoustic technique. Chin. Sci. Bull. 2004, 49, 2115–2119. [Google Scholar] [CrossRef]
- Kolkman, R.G.M.; Hondebrink, E.; Steenbergen, W.; De Mul, F.F.M. In vivo photoacoustic imaging of blood vessels using an extreme-narrow aperture sensor. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 343–346. [Google Scholar] [CrossRef]
- Kudryashov, S.I.; Allen, S.D.; Galanzha, E.I.; Galitovskaya, E.; Zharov, V.P. Photoacoustics of individual live cells and particles. In Proceedings of the Photons Plus Ultrasound: Imaging and Sensing 2006: The Seventh Conference on Biomedical Thermoacoustics, Optoacoustics, and Acousto-Optics, San Jose, CA, USA, 21–26 January 2006; Volume 6086, p. 60860. [Google Scholar] [CrossRef]
- Kottmann, J.; Rey, J.M.; Sigrist, M.W. New photoacoustic cell design for studying aqueous solutions and gels. Rev. Sci. Instrum. 2011, 82, 84903. [Google Scholar] [CrossRef] [PubMed]
- Kottmann, J.; Rey, J.M.; Luginbühl, J.; Reichmann, E.; Sigrist, M.W. Glucose sensing in human epidermis using mid-infrared photoacoustic detection. Biomed. Opt. Express 2012, 3, 667. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Liu, G.; Huang, Z.; Zhao, D.; Xiong, Z. Exploration and practice in photoacoustic measurement for glucose concentration based on tunable pulsed laser induced ultrasound. Int. J. Optomechatronics 2015, 9, 221–237. [Google Scholar] [CrossRef]
- Bayrakli, I.; Erdogan, Y.K. Photo-acoustic sensor based on an inexpensive piezoelectric film transducer and an amplitude-stabilized single-mode external cavity diode laser for in vitro measurements of glucose concentration. Opt. Laser Technol. 2018, 102, 180–183. [Google Scholar] [CrossRef]
- Zhao, S.; Tao, W.; He, Q.; Zhao, H.; Yang, H. Glucose solution determination based on liquid photoacoustic resonance. Appl. Opt. 2017, 56, 193. [Google Scholar] [CrossRef]
- Coleman, P.B. Practical Sampling Techniques for Infrared Analysis; CRC Press: New York, NY, USA, 1993; pp. 1–316. [Google Scholar]
- Canivet, J.; Lysenko, V.; Lehtinen, J.; Legrand, A.; Wisser, F.M.; Quadrelli, E.A.; Farrusseng, D. Sensitive photoacoustic IR spectroscopy for the characterization of amino/azido mixed-linker metal-organic frameworks. ChemPhysChem 2017, 18, 2855–2858. [Google Scholar] [CrossRef] [PubMed]
- Dumitras, D.C.; Petrus, M.; Bratu, A.-M.; Popa, C. Applications of near infrared photoacoustic spectroscopy for analysis of human respiration: A review. Molecules 2020, 25, 1728. [Google Scholar] [CrossRef]
- Dumitras, D.C.; Dutu, D.C.; Matei, C.; Magureanu, A.M.; Petrus, M.; Popa, C. Laser photoacoustic spectroscopy: Principles, instrumentation, and characterization. J. Optoelectron. Adv. Mater. 2007, 9, 3655–3701. [Google Scholar]
- Kuusela, T.; Peura, J.; Matveev, B.A.; Remennyy, M.A.; Stus’, N.M. Photoacoustic gas detection using a cantilever microphone and III–V mid-IR LEDs. Vib. Spectrosc. 2009, 51, 289–293. [Google Scholar] [CrossRef]
- Pan, Y.; Dong, L.; Yin, X.; Wu, H. Compact and highly sensitive NO2 photoacoustic sensor for environmental monitoring. Molecules 2020, 25, 1201. [Google Scholar] [CrossRef]
- Uotila, J.; Kauppinen, J. Fourier transform infrared measurement of solid-, liquid-, and gas-phase samples with a single photoacoustic cell. Appl. Spectrosc. 2008, 62, 655–660. [Google Scholar] [CrossRef] [PubMed]
- Kapitanov, V.A.; Zeninari, V.; Parvitte, B.; Courtois, D.; Ponomarev, Y.N. Optimisation of photoacoustic resonant cells with commercial microphones for diode laser gas detection. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2002, 58, 2397–2404. [Google Scholar] [CrossRef]
- Kauppinen, J.; Wilcken, K.; Kauppinen, I.; Koskinen, V. High sensitivity in gas analysis with photoacoustic detection. Microchem. J. 2004, 76, 151–159. [Google Scholar] [CrossRef]
- Wilcken, K.; Kauppinen, J. Optimization of a microphone for photoacoustic spectroscopy. Appl. Spectrosc. 2003, 57, 1087–1092. [Google Scholar] [CrossRef] [PubMed]
- Koskinen, V.; Fonsen, J.; Kauppinen, J.; Kauppinen, I. Extremely sensitive trace gas analysis with modern photoacoustic spectroscopy. Vib. Spectrosc. 2006, 42, 239–242. [Google Scholar] [CrossRef]
- Uotila, J. Use of the optical cantilever microphone in photoacoustic spectroscopy. Ph.D. Thesis, University of Turku, Turku, Finland, 2009. [Google Scholar]
- Sievilä, P.; Rytkönen, V.-P.; Hahtela, O.; Chekurov, N.; Kauppinen, J.; Tittonen, I. Fabrication and characterization of an ultrasensitive acousto-optical cantilever. J. Micromechanics Microeng. 2007, 17, 852–859. [Google Scholar] [CrossRef]
- Koskinen, V.; Fonsen, J.; Roth, K.; Kauppinen, J. Progress in cantilever enhanced photoacoustic spectroscopy. Vib. Spectrosc. 2008, 48, 16–21. [Google Scholar] [CrossRef]
- Gasera. Available online: https://www.gasera.fi/technology/optical-microphone (accessed on 16 May 2021).




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaiev, M.; Mussabek, G.; Lishchuk, P.; Dubyk, K.; Zhylkybayeva, N.; Yar-Mukhamedova, G.; Lacroix, D.; Lysenko, V. Application of the Photoacoustic Approach in the Characterization of Nanostructured Materials. Nanomaterials 2022, 12, 708. https://doi.org/10.3390/nano12040708
Isaiev M, Mussabek G, Lishchuk P, Dubyk K, Zhylkybayeva N, Yar-Mukhamedova G, Lacroix D, Lysenko V. Application of the Photoacoustic Approach in the Characterization of Nanostructured Materials. Nanomaterials. 2022; 12(4):708. https://doi.org/10.3390/nano12040708
Chicago/Turabian StyleIsaiev, Mykola, Gauhar Mussabek, Pavlo Lishchuk, Kateryna Dubyk, Nazym Zhylkybayeva, Gulmira Yar-Mukhamedova, David Lacroix, and Vladimir Lysenko. 2022. "Application of the Photoacoustic Approach in the Characterization of Nanostructured Materials" Nanomaterials 12, no. 4: 708. https://doi.org/10.3390/nano12040708
APA StyleIsaiev, M., Mussabek, G., Lishchuk, P., Dubyk, K., Zhylkybayeva, N., Yar-Mukhamedova, G., Lacroix, D., & Lysenko, V. (2022). Application of the Photoacoustic Approach in the Characterization of Nanostructured Materials. Nanomaterials, 12(4), 708. https://doi.org/10.3390/nano12040708







