Temperature-Dependent Fractional Dynamics in Pseudo-Capacitors with Carbon Nanotube Array/Polyaniline Electrodes
Abstract
:1. Introduction
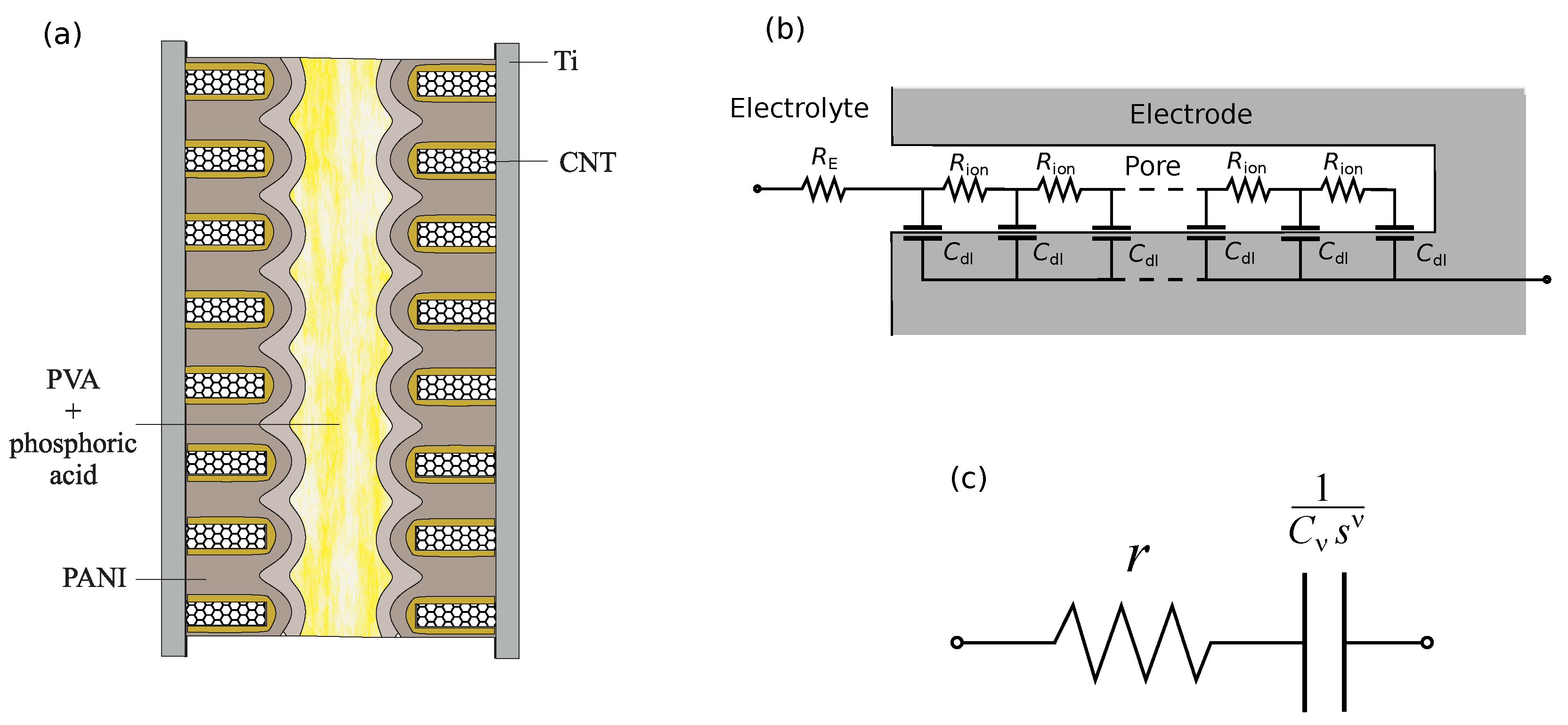
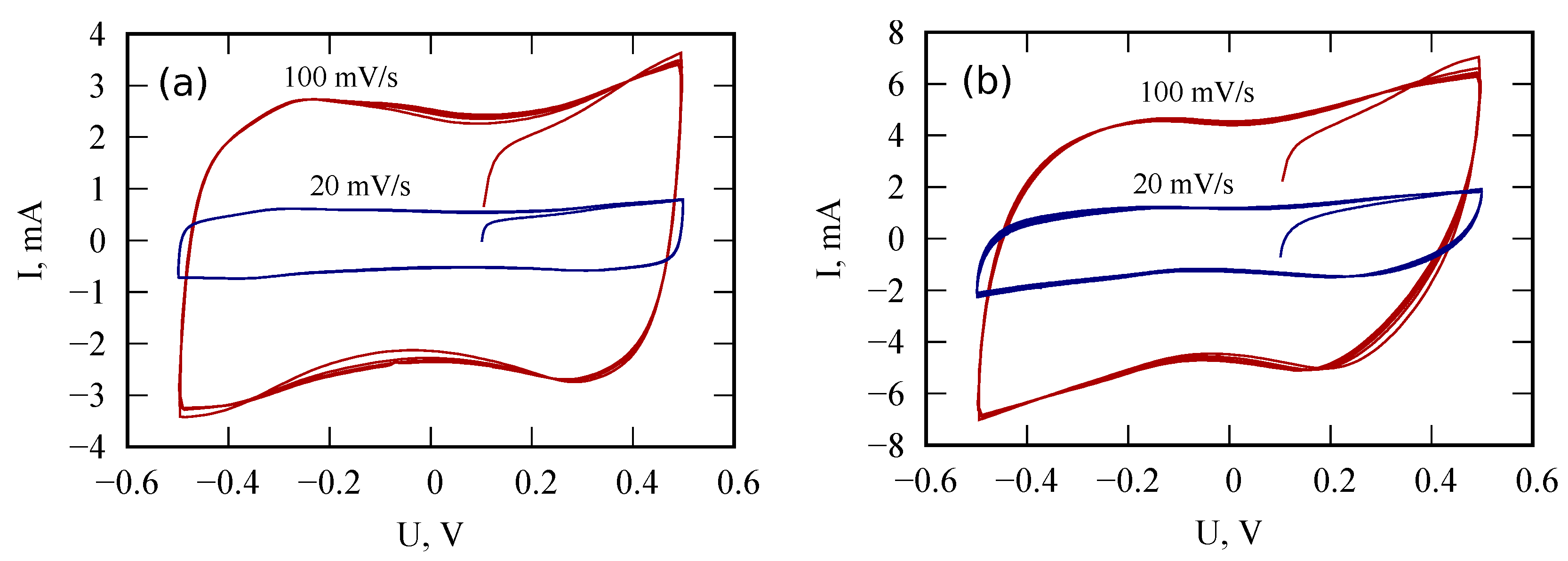
2. Materials and Experimental Methods
3. Fractional Differential Models of Supercapacitors
3.1. Havriliak–Negami Response
3.2. Phase-Field Model
3.3. Linearized Model
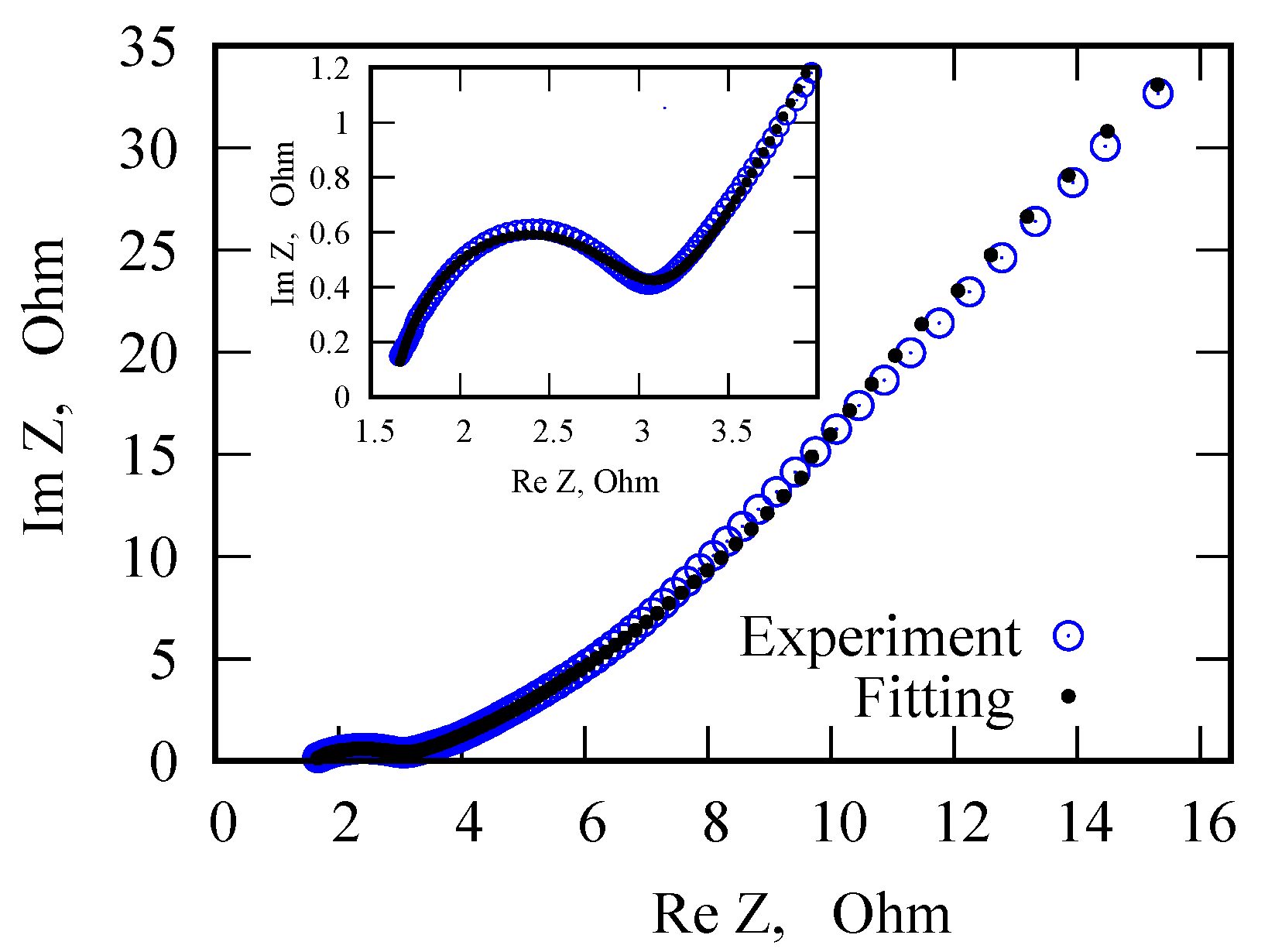
4. Temperature-Dependent Fractional Dynamics in PANI/VA-MWCNT Pseudo-Capacitors
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, T.M.; Lin, Y.W.; Liao, C.S. Preparation and characterization of polyaniline/multi-walled carbon nanotube composites. Carbon 2005, 43, 734–740. [Google Scholar] [CrossRef]
- Eftekhari, A.; Li, L.; Yang, Y. Polyaniline supercapacitors. J. Power Sources 2017, 347, 86–107. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef] [Green Version]
- Gupta, V.; Miura, N. Polyaniline/single-wall carbon nanotube (PANI/SWCNT) composites for high performance supercapacitors. Electrochim. Acta 2006, 52, 1721–1726. [Google Scholar] [CrossRef]
- Aydinli, A.; Yuksel, R.; Unalan, H.E. Vertically aligned carbon nanotube–polyaniline nanocomposite supercapacitor electrodes. Int. J. Hydrog. Energy 2018, 43, 18617–18625. [Google Scholar] [CrossRef]
- Kitsyuk, E.P.; Sibatov, R.T.; Svetukhin, V.V. Memory effect and fractional differential dynamics in planar microsupercapacitors based on multiwalled carbon nanotube arrays. Energies 2020, 13, 213. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Tan, P.; Wang, D.; Li, Z.; Peng, L.; Hu, Y.; Wang, C.; Zhu, W.; Chen, S.; Chen, W. High-performance supercapacitors based on electrochemical-induced vertical-aligned carbon nanotubes and polyaniline nanocomposite electrodes. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-order models of supercapacitors, batteries and fuel cells: A survey. Mater. Renew. Sustain. Energy 2015, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Biswas, K.; Bohannan, G.; Caponetto, R.; Lopes, A.M.; Machado, J.A.T. Fractional-Order Devices; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Martynyuk, V.; Ortigueira, M. Fractional model of an electrochemical capacitor. Signal Process. 2015, 107, 355–360. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A.; Lopes, A.M.; de Camposinhos, R. Fractional-order modelling of epoxy resin. Philos. Trans. R. Soc. A 2020, 378, 20190292. [Google Scholar] [CrossRef]
- Uchaikin, V.V.; Ambrozevich, A.S.; Sibatov, R.T.; Ambrozevich, S.A.; Morozova, E.V. Memory and nonlinear transport effects in charging-discharging of a supercapacitor. Tech. Phys. 2016, 61, 250–259. [Google Scholar] [CrossRef]
- Sabatier, J. Fractional order models for electrochemical devices. In Fractional Dynamics; De Gruyter Open: Warsaw, Poland, 2016; pp. 141–160. [Google Scholar]
- Allagui, A.; Freeborn, T.J.; Elwakil, A.S.; Fouda, M.E.; Maundy, B.J.; Radwan, A.G.; Said, Z.; Abdelkareem, M.A. Review of fractional-order electrical characterization of supercapacitors. J. Power Sources 2018, 400, 457–467. [Google Scholar] [CrossRef]
- Sibatov, R.T.; Uchaikin, V.V. Fractional kinetics of charge carriers in supercapacitors. In Volume 8: Applications in Engineering, Life and Social Sciences, Part B; De Gruyter: Vienna, Austria, 2019; pp. 87–118. [Google Scholar]
- L’vov, P.E.; Sibatov, R.T.; Yavtushenko, I.O.; Kitsyuk, E.P. Time-Fractional Phase Field Model of Electrochemical Impedance. Fractal Fract. 2021, 5, 191. [Google Scholar] [CrossRef]
- Kopka, R. Changes in derivative orders for fractional models of supercapacitors as a function of operating temperature. IEEE Access 2019, 7, 47674–47681. [Google Scholar] [CrossRef]
- De Levie, R. On porous electrodes in electrolyte solutions: I. capacitance effects. Electrochim. Acta 1963, 8, 751–780. [Google Scholar] [CrossRef]
- Vicentini, R.; Nunes, W.G.; da Costa, L.H.; Da Silva, L.M.; Freitas, B.; Pascon, A.M.; Vilas-Boas, O.; Zanin, H. Multi-walled carbon nanotubes and activated carbon composite material as electrodes for electrochemical capacitors. J. Energy Storage 2021, 33, 100738. [Google Scholar] [CrossRef]
- Stepień, M.; Handzlik, P.; Fitzner, K. Electrochemical synthesis of oxide nanotubes on Ti6Al7Nb alloy and their interaction with the simulated body fluid. J. Solid State Electrochem. 2016, 20, 2651–2661. [Google Scholar] [CrossRef] [Green Version]
- Kötz, R.; Carlen, M. Principles and applications of electrochemical capacitors. Electrochim. Acta 2000, 45, 2483–2498. [Google Scholar] [CrossRef]
- Mahon, P.J.; Paul, G.L.; Keshishian, S.M.; Vassallo, A.M. Measurement and modelling of the high-power performance of carbon-based supercapacitors. J. Power Sources 2000, 91, 68–76. [Google Scholar] [CrossRef]
- Quintana, J.J.; Ramos, A.; Nuez, I. Identification of the fractional impedance of ultracapacitors. IFAC Proc. Vol. 2006, 39, 432–436. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Measurement of supercapacitor fractional-order model parameters from voltage-excited step response. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 367–376. [Google Scholar] [CrossRef]
- Bisquert, J. Theory of the impedance of electron diffusion and recombination in a thin layer. J. Phys. Chem. B 2002, 106, 325–333. [Google Scholar] [CrossRef]
- Augustyn, V.; Simon, P.; Dunn, B. Pseudocapacitive oxide materials for high-rate electrochemical energy storage. Energy Environ. Sci. 2014, 7, 1597–1614. [Google Scholar] [CrossRef] [Green Version]
- Parveen, N.; Ansari, S.A.; Ansari, M.Z.; Ansari, M.O. Manganese oxide as an effective electrode material for energy storage: A review. Environ. Chem. Lett. 2022, 20, 283–309. [Google Scholar] [CrossRef]
- Ansari, S.A.; Parveen, N.; Al-Othoum, M.A.S.; Ansari, M.O. Effect of washing on the electrochemical performance of a three-dimensional current collector for energy storage applications. Nanomaterials 2021, 11, 1596. [Google Scholar] [CrossRef] [PubMed]
- Gil’mutdinov, A.K.; Ushakov, P.A.; El-Khazali, R. Fractal Elements and Their Applications; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993; Volume 1. [Google Scholar]
- Bisquert, J.; Compte, A. Theory of the electrochemical impedance of anomalous diffusion. J. Electroanal. Chem. 2001, 499, 112–120. [Google Scholar] [CrossRef]
- Lee, G.J.; Pyun, S.I.; Kim, C.H. Kinetics of double-layer charging/discharging of the activated carbon fiber cloth electrode: Effects of pore length distribution and solution resistance. J. Solid State Electrochem. 2004, 8, 110–117. [Google Scholar] [CrossRef]
- Itagaki, M.; Suzuki, S.; Shitanda, I.; Watanabe, K.; Nakazawa, H. Impedance analysis on electric double layer capacitor with transmission line model. J. Power Sources 2007, 164, 415–424. [Google Scholar] [CrossRef]
- Garcia, B.B.; Feaver, A.M.; Zhang, Q.; Champion, R.D.; Cao, G.; Fister, T.T.; Nagle, K.P.; Seidler, G.T. Effect of pore morphology on the electrochemical properties of electric double layer carbon cryogel supercapacitors. J. Appl. Phys. 2008, 104, 014305. [Google Scholar] [CrossRef]
- Batalla, B.; Sinha, G.; Aliev, F. Dynamics of molecular motion of nematic liquid crystal confined in cylindrical pores. Mol. Cryst. Liq. Cryst. 1999, 331, 121–128. [Google Scholar] [CrossRef]
- Prasad, R.; Mehta, U.; Kothari, K. Various analytical models for supercapacitors: A mathematical study. Resour.-Effic. Technol. 2020, 1, 1–15. [Google Scholar]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag-Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Jonscher, A.K. Dielectric relaxation in solids. J. Phys. D Appl. Phys. 1999, 32, R57. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. On the theory of relaxation for systems with “remnant” memory. Phys. Status Solidi (b) 1984, 124, 389–393. [Google Scholar] [CrossRef]
- Weron, K. A probabilistic mechanism hidden behind the universal power law for dielectric relaxation: General relaxation equation. J. Phys. Condens. Matter 1991, 3, 9151. [Google Scholar] [CrossRef]
- Uchaikin, V.V.; Sibatov, R. Fractional Kinetics in Solids: Anomalous Charge Transport in Semiconductors, Dielectrics, and Nanosystems; World Scientific: Singapore, 2013. [Google Scholar]
- Khamzin, A.A. Trap-controlled fractal diffusion model of the Havriliak–Negami dielectric relaxation. J. Non-Cryst. Solids 2019, 524, 119636. [Google Scholar] [CrossRef]
- Uchaikin, V.; Sibatov, R.; Uchaikin, D. Memory regeneration phenomenon in dielectrics: The fractional derivative approach. Phys. Scr. 2009, T136, 014002. [Google Scholar] [CrossRef]
- Sibatov, R.T.; Uchaikin, V.V.; Uchaikin, D.V. Fractional wave equation for dielectric medium with Havriliak–Negami response. In Fractional Dynamics and Control; Springer: New York, NY, USA, 2012; pp. 293–301. [Google Scholar]
- Sibatov, R.; Shulezhko, V.; Svetukhin, V. Fractional derivative phenomenology of percolative phonon-assisted hopping in two-dimensional disordered systems. Entropy 2017, 19, 463. [Google Scholar] [CrossRef]
- Uchaikin, V.V.; Sibatov, R.T. Fractional theory for transport in disordered semiconductors. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 715–727. [Google Scholar] [CrossRef]


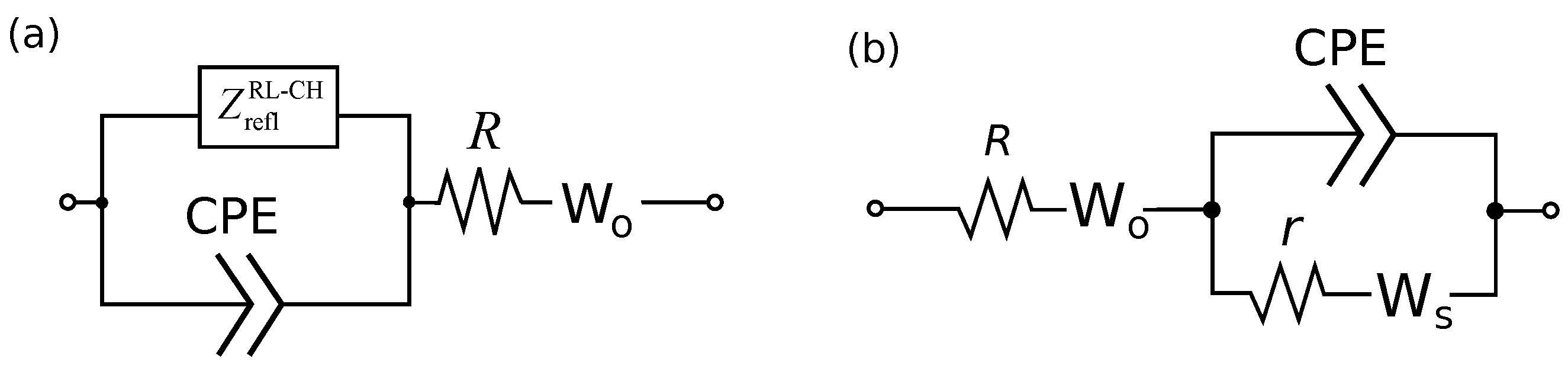
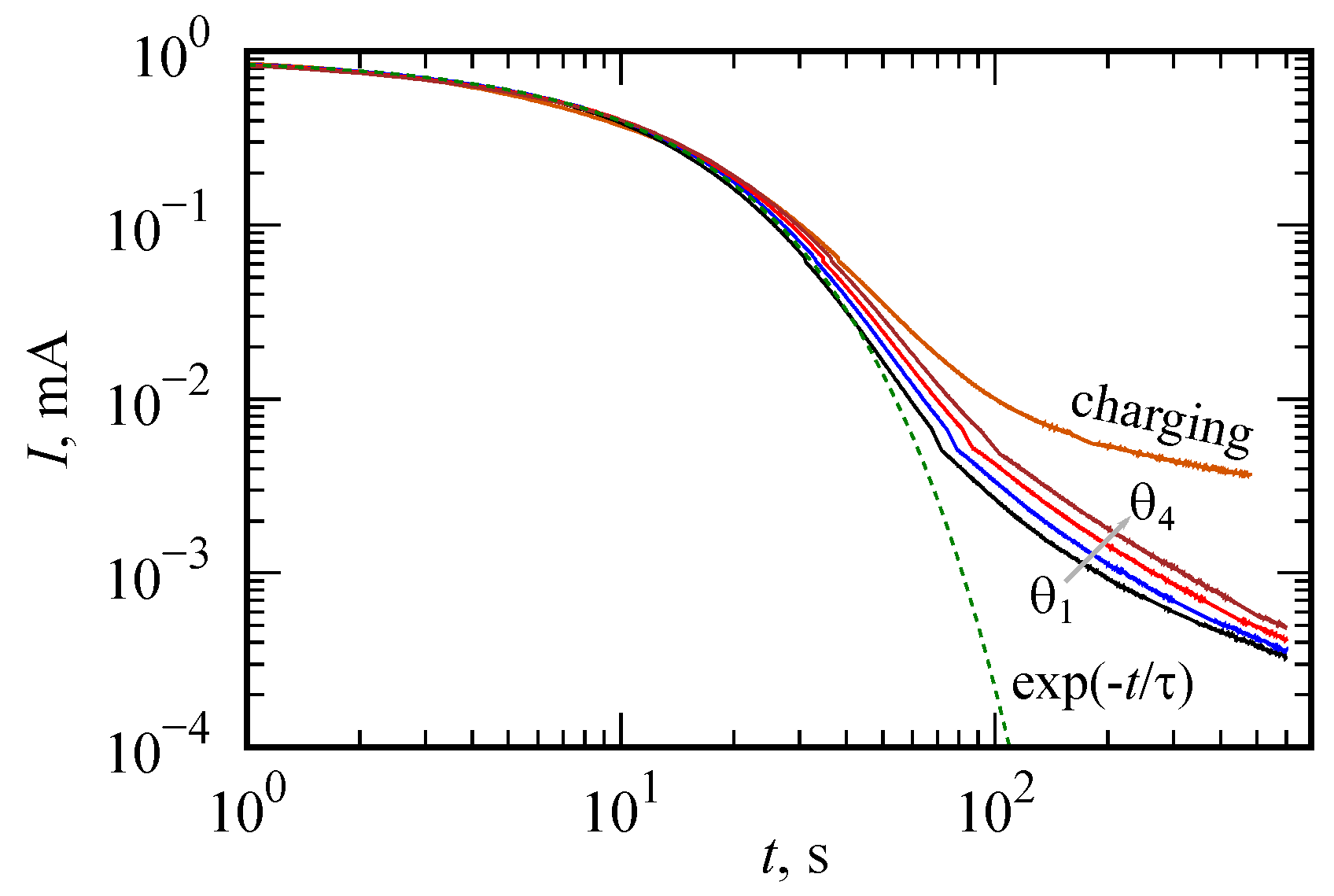

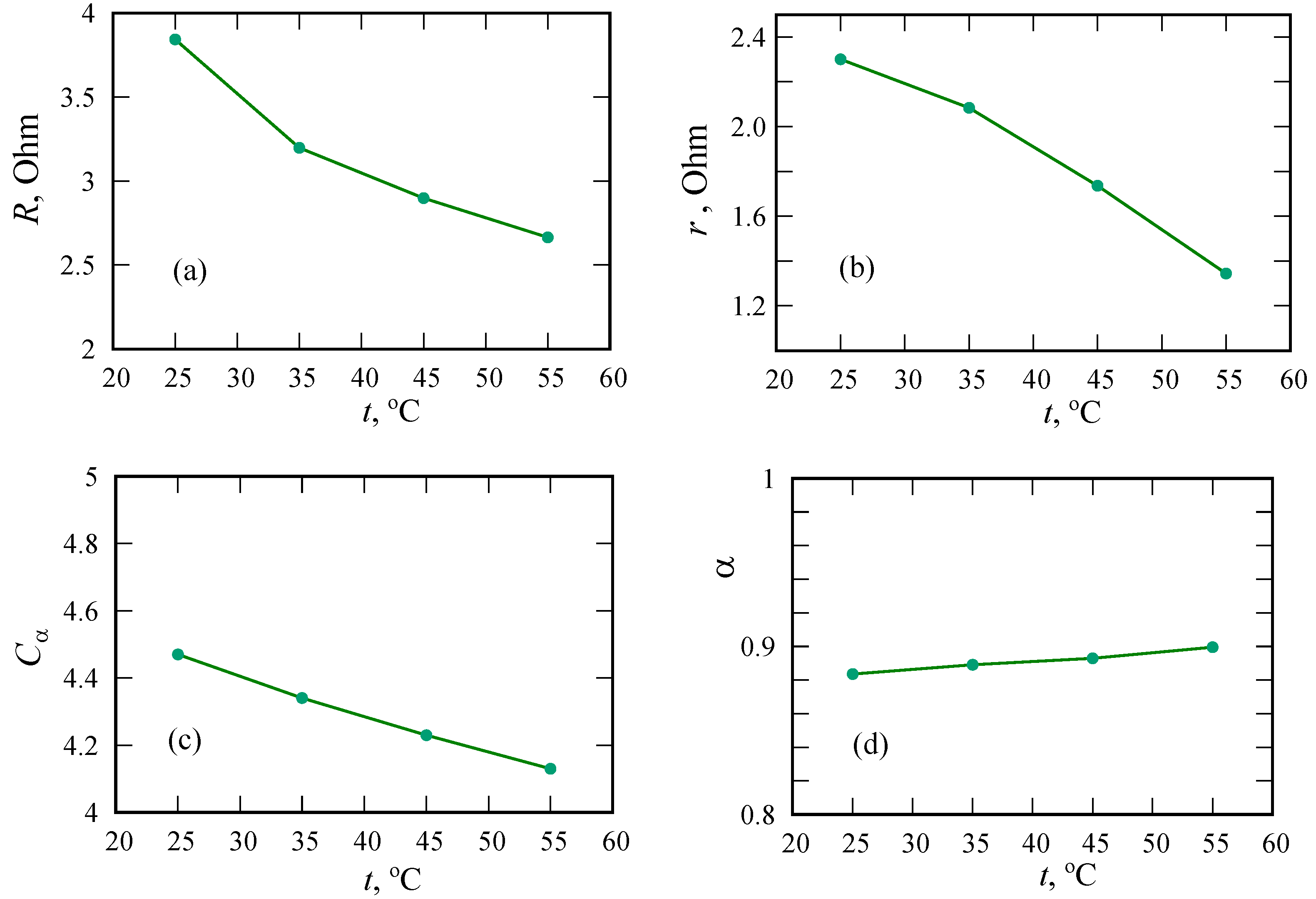
| Parameter | PANI/VA-MWCNT 1 | PANI/VA-MWCNT 2 |
|---|---|---|
| R, Ohm | 4.124 | 1.623 |
| r, Ohm | 0.704 | 1.360 |
| , sOhm | 5.558 | 1.270 |
| 0.8068 | 0.8654 | |
| , Ohm·s | 6.497 | 10.513 |
| , s | 2.408 | 2.272 |
| , Ohm·s | 8.081 | 0.348 |
| , s | 0.238 | 0.0263 |
| Parameter | C | C | C | C |
|---|---|---|---|---|
| R, Ohm | 3.8431 | 3.1989 | 2.8983 | 2.6658 |
| r, Ohm | 2.301 | 2.085 | 1.737 | 1.345 |
| , sOhm | 4.47 | 4.34 | 4.23 | 4.13 |
| 0.88363 | 0.88906 | 0.89299 | 0.89952 | |
| , Ohm·s | 40.478 | 39.609 | 38.988 | 35.463 |
| , s | 6.7649 | 18.647 | 25.284 | 7.0558 |
| , Ohm·s | 3.1208 | 2.3203 | 0.54176 | 1.656 |
| , s | 0.0907 | 0.085134 | 0.020342 | 0.066649 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavtushenko, I.O.; Makhmud-Akhunov, M.Y.; Sibatov, R.T.; Kitsyuk, E.P.; Svetukhin, V.V. Temperature-Dependent Fractional Dynamics in Pseudo-Capacitors with Carbon Nanotube Array/Polyaniline Electrodes. Nanomaterials 2022, 12, 739. https://doi.org/10.3390/nano12050739
Yavtushenko IO, Makhmud-Akhunov MY, Sibatov RT, Kitsyuk EP, Svetukhin VV. Temperature-Dependent Fractional Dynamics in Pseudo-Capacitors with Carbon Nanotube Array/Polyaniline Electrodes. Nanomaterials. 2022; 12(5):739. https://doi.org/10.3390/nano12050739
Chicago/Turabian StyleYavtushenko, Igor O., Marat Yu. Makhmud-Akhunov, Renat T. Sibatov, Evgeny P. Kitsyuk, and Vyacheslav V. Svetukhin. 2022. "Temperature-Dependent Fractional Dynamics in Pseudo-Capacitors with Carbon Nanotube Array/Polyaniline Electrodes" Nanomaterials 12, no. 5: 739. https://doi.org/10.3390/nano12050739
APA StyleYavtushenko, I. O., Makhmud-Akhunov, M. Y., Sibatov, R. T., Kitsyuk, E. P., & Svetukhin, V. V. (2022). Temperature-Dependent Fractional Dynamics in Pseudo-Capacitors with Carbon Nanotube Array/Polyaniline Electrodes. Nanomaterials, 12(5), 739. https://doi.org/10.3390/nano12050739






