Next Article in Journal
Simultaneously Enhancing the Strength, Plasticity, and Conductivity of Copper Matrix Composites with Graphene-Coated Submicron Spherical Copper
Next Article in Special Issue
Graphene Oxide Thin Films with Drug Delivery Function
Previous Article in Journal
Improved Performance of NbOx Resistive Switching Memory by In-Situ N Doping
Previous Article in Special Issue
High-Yield Production of Selected 2D Materials by Understanding Their Sonication-Assisted Liquid-Phase Exfoliation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Nanomaterials
Volume 12
Issue 6
10.3390/nano12061028
nanomaterials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

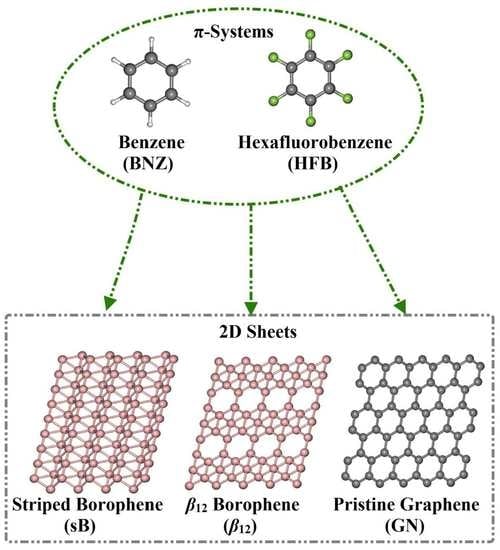
Borophene and Pristine Graphene 2D Sheets as Potential Surfaces for the Adsorption of Electron-Rich and Electron-Deficient π-Systems: A Comparative DFT Study

by
Mahmoud A. A. Ibrahim
1,*,
Amna H. M. Mahmoud
1,
Kamal A. Soliman
2,
Gamal A. H. Mekhemer
1,
Muhammad Naeem Ahmed
3,
Ahmed M. Shawky
4,
Mohammed A. S. Abourehab
5,
Eslam B. Elkaeed
6,
Mahmoud E. S. Soliman
7,* and
Nayra A. M. Moussa
1
1
Computational Chemistry Laboratory, Chemistry Department, Faculty of Science, Minia University, Minia 61519, Egypt
2
Department of Chemistry, Faculty of Science, Benha University, Benha 13518, Egypt
3
Department of Chemistry, The University of Azad Jammu and Kashmir, Muzaffarabad 13100, Pakistan
4
Science and Technology Unit (STU), Umm Al-Qura University, Makkah 21955, Saudi Arabia
5
Department of Pharmaceutics, Faculty of Pharmacy, Umm Al-Qura University, Makkah 21955, Saudi Arabia
6
Department of Pharmaceutical Sciences, College of Pharmacy, AlMaarefa University, Riyadh 13713, Saudi Arabia
7
Molecular Modelling and Drug Design Research Group, School of Health Sciences, University of KwaZulu-Natal, Westville, Durban 4000, South Africa
*
Authors to whom correspondence should be addressed.
Nanomaterials 2022, 12(6), 1028; https://doi.org/10.3390/nano12061028
Submission received: 26 February 2022 / Revised: 13 March 2022 / Accepted: 17 March 2022 / Published: 21 March 2022
(This article belongs to the Special Issue Graphene and Related 2D Materials)
Browse Figures
Versions Notes

Abstract

:
The versatility of striped borophene (sB), β12 borophene (β12), and pristine graphene (GN) to adsorb π-systems was comparatively assessed using benzene (BNZ) and hexafluorobenzene (HFB) as electron-rich and electron-deficient aromatic π-systems, respectively. Using the density functional theory (DFT) method, the adsorption process of the π-systems on the investigated 2D sheets in the parallel configuration was observed to have proceeded more favorably than those in the vertical configuration. According to the observations of the Bader charge transfer analysis, the π-system∙∙∙sB complexes were generally recorded with the largest contributions of charge transfer, followed by the π-system∙∙∙β12 and ∙∙∙GN complexes. The band structures of the pure sheets signaled the metallic and semiconductor characters of the sB/β12 and GN surfaces, respectively. In the parallel configuration, the adsorption of both BNZ and HFB showed more valence and conduction bands compared to the adsorption in the vertical configuration, revealing the prominent preferentiality of the anterior configuration. The density-of-states (DOSs) results also affirmed that the adsorption process of the BNZ and HFB on the surface of the investigated 2D sheets increased their electrical properties. In all instances, the sB and β12 surfaces demonstrated higher adsorptivity towards the BNZ and HFB than the GN analog. The findings of this work could make a significant contribution to the deep understanding of the adsorption behavior of aromatic π-systems toward 2D nanomaterials, leading, in turn, to their development of a wide range of applications.

Graphical Abstract

1. Introduction

Graphene, a single-atom-thick layer of sp2-bonded carbon atoms tightly packed into a two-dimensional (2D) honeycomb lattice, has been become the linchpin of a variety of fields in science and technology, especially electronics [1,2], condensed-matter physics [3], biomedical research [4,5,6], and energy storage [7,8,9]. Immense efforts were therefore undertaken to fully uncover the characteristics of graphene and its derivatives. For graphene, or, to be more precise, pristine graphene (GN), various superior physical and chemical properties, including large surface area, mechanical strength, fascinating thermal and electrical conductivity, have hitherto been deeply understood and well established through significant studies [10,11,12]. Consequently, GN has been widely used in various industrial applications, such as sensors, lithium-ion batteries, and catalysis [13,14,15,16]. The utilization of GN in removing toxic volatile organic compounds (VOCs) such as benzene, pyridine, and thiophene from the air was also reported [17,18].
Soon after the recognition of GN, sustained interest developed in the detailed investigation of the features of elemental 2D materials, including germanene [19,20], phosphorene [21,22], transition metal dichalcogenides [23,24], and silicone [25,26], using advanced experimental and computational techniques. Crucially, borophene—a two-dimensional boron sheet—has recently drawn an upsurge in attention from the scholar community due to its promising properties, such as its preferential surface reactivity, unique electronic properties, and high electrical conductivity [18,27,28,29,30]. Moreover, some borophene structures have been predicted to host Dirac fermions [31]. The applications of borophene have been extended to lithium-ion batteries, hydrogen detection, and hydrogen storage [32,33,34]. Experimentally, borophene was successfully grown on an Ag(111) surface under ultra-high-vacuum conditions [27,29].
Using high-resolution scanning tunneling microscopy (STM), different borophene phases were noticed, such as striped (sB), β12, and χ3 phases [27]. As previously demonstrated, the β12 and χ3 phases of borophene showed more obvious stability than the sB phase, which was interpreted as a consequence of their planar structures, which had 1/6 and 1/5 vacancies, respectively [35,36,37,38,39,40,41]. Upon examining its mechanical and thermodynamical features, β12 borophene was found to be the most stable phase of borophene [38,42]. Significantly, the sB phase of borophene demonstrated anisotropic metallic behavior through its unique buckled structure [27,28]. Owing to its anisotropic character, the sB was found to be stiffer than GN along one axis (i.e., a direction) [27,42,43]. Nonetheless, along a direction, the sB demonstrated phonon instability [28], while elastic instability was observed along the b direction [43].
As an essential issue, the aromatic π-systems were recorded as volatile organic compounds (VOCs) that were emitted from vehicle exhaust, petrochemical technologies, and thinners [44,45]. These compounds were found to have significant toxicity and carcinogenic effects on public health [46,47]. Numerous studies were accordingly designed to limit the existence of π-systems through the adsorption process on the surfaces of efficient 2D nanomaterials, such as stanene, CrI3, GN, χ3 borophene, β12 borophene, and germanene [48,49,50,51,52,53,54,55,56]. A careful literature search revealed that the adsorption of electron-rich and electron-deficient aromatic π-systems in different borophene phases and GN sheets has not been sufficiently studied yet. Accordingly, the present work is devoted to thoroughly investigating the adsorption of the electron-rich and electron-deficient aromatic π-systems on anchoring 2D sheets by means of the density functional theory (DFT) method. To pursue the aim of the current work, benzene (BNZ) and hexafluorobenzene (HFB) were utilized as electron-rich and electron-deficient aromatic π-systems to be adsorbed at all possible sites of adsorption on the surface of the sB, β12, and GN sheets in vertical and parallel configurations (Figure 1). For the studied π-system∙∙∙2D sheet complexes, the analyses of geometric structures and the adsorption energies were performed. Furthermore, the electronic properties, including charge transfer, band structures, and density of states (DOSs), were precisely assessed for the 2D sheets before and after the adsorption process. The obtained findings will serve as the foundation for future research pertinent to the application of borophene and graphene as adsorbent materials.

2. Computational Methods

All calculations were performed with Quantum ESPRESSO 6.4.1 package [57,58] using density functional theory (DFT) [59,60]. Generalized gradient approximation (GGA) was employed using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation function [61]. The ultrasoft pseudopotential was adopted for treating electron–ion interactions [62]. The DFT-D2 method of the Grimme scheme [63] was applied to account for the van der Waals interactions in all computations. The cutoffs of energy and charge density were set to be 50 Ry and 500 Ry, respectively. All structures were fully optimized with respect to the energy convergence threshold of 10−5 eV and force convergence threshold of 10−4 eV/Å. Monkhorst–Pack grids of 6 × 6 × 1 and 12 × 12 × 1 k-points were used to sample the first Brillouin zone for geometric optimization and electronic structure calculations, respectively, combined with the Marzari–Vanderbilt smearing technique [64]. A vacuum of 20 Å was settled along the vertical direction of the borophene and the graphene surfaces for all calculations to avoid spurious interactions between the periodic cells in the z-direction. The corresponding space groups of the studied sB and β12 sheets were Pmmn and P2mm, respectively.
The potential of sB, β12, and GN to adsorb BNZ/HFB as electron-rich/electron-deficient aromatic π-systems was comparatively assessed. For adsorption energy calculations, supercells of 9 × 4 × 1, 3 × 4 × 1, and 6 × 5 × 1 were constructed for sB, β12, and GN, respectively. The number of atoms in the supercells of sB, β12, and GN was 72, 60, and 60, respectively. On the designed 2D sheets, BNZ and HFB were subjected to adsorption process as electron-rich and electron-deficient aromatic π-systems, respectively, within vertical and parallel configurations (Figure 1). Adsorption energy (Ead) was computed according to the following equation:
E ad   = E π − system · · · 2 D   sheet − E π − system + E 2 D   sheet
where E π − system · · · 2 D   sheet , E π − system , and E 2 D   sheet were the energies of complex, adsorbed π-system, and anchoring 2D sheet, respectively. Using Bader charge analysis [65,66], the charge transfer (Qt) to or from the 2D sheets was assessed as follows:
Q t   = Q combined   2 D   sheet   − Q isolated   2 D   sheet  
where the Qcombined 2D sheet and Qisolated 2D sheet were the charges of the 2D sheet after and before the adsorption process, respectively. Based on Bader charge analysis, the charge density difference (∆ρ) was evaluated according to the following equation:
Δ ρ = ρ π − system · · · 2 D   sheet − ρ π − system + ρ 2 D   sheet
where ρ π − system · · · 2 D   sheet , ρ π − system , and ρ 2 D   sheet were the charge of the complex, adsorbed π-system, and anchoring 2D sheet, respectively. The charge density difference maps were visualized using the VESTA [67] package. Furthermore, the electronic band structure, total density of states (TDOSs), and projected density-of-states (PDOSs) calculations were thoroughly studied to understand the electronic properties of the studied 2D sheets.

3. Results and Discussion

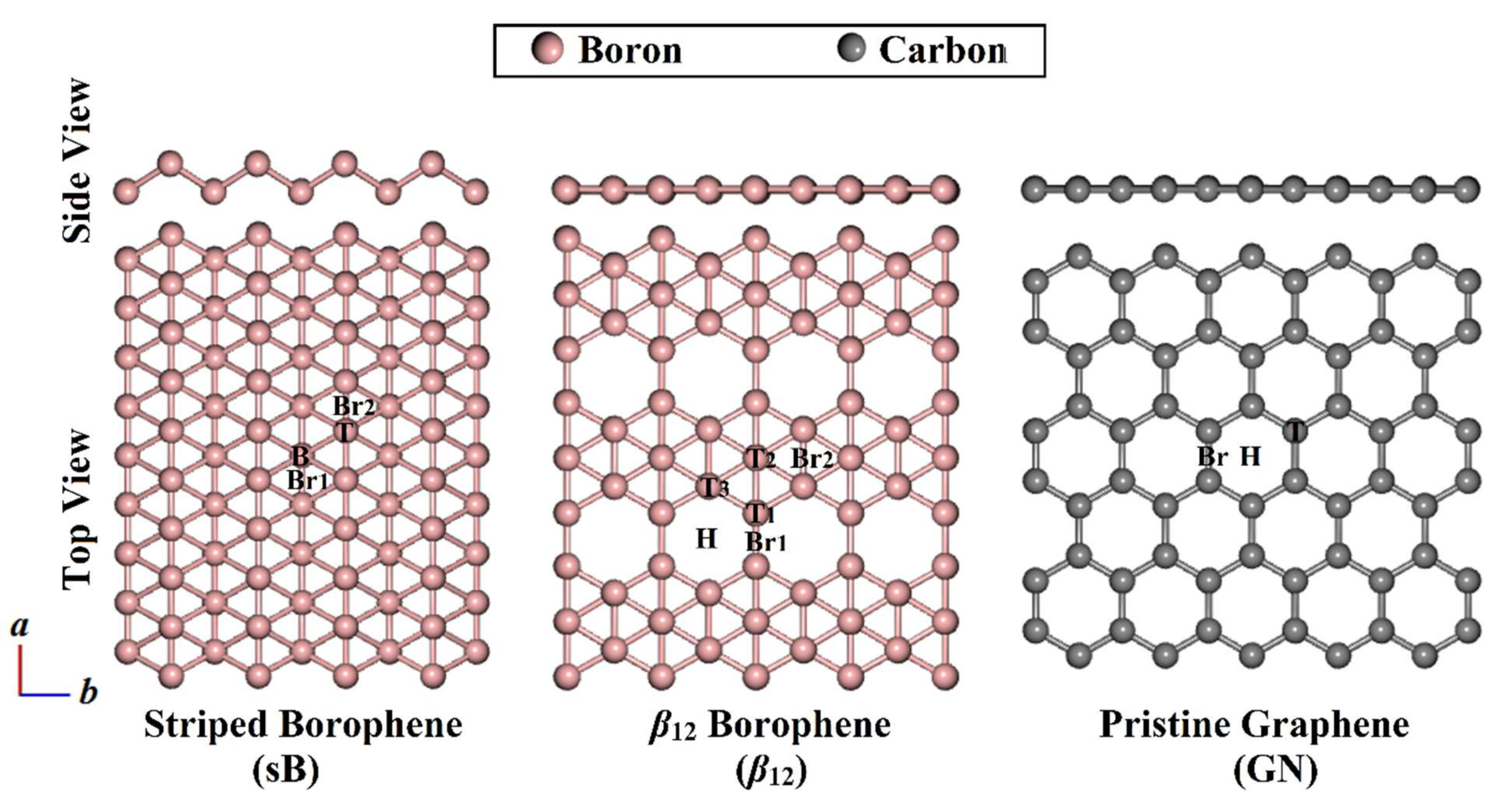
3.1. Geometric Structures

Prior to the adsorption calculations of the aromatic π-systems on the 2D sheets, the structures of the striped sB, β12, and GN were constructed and geometrically minimized to obtain the equilibrium geometries. The optimized structures of the 2D sheets are illustrated in Figure 2.
According to the optimized structures demonstrated in Figure 2, the equilibrium lattice constants (a × b) of sB and β12 were 1.64 Å × 2.93 Å and 5.06 Å × 2.93 Å, respectively. For GN, the calculated lattice constant values of the unit cell were 2.47 Å × 2.47 Å. The abovementioned values of the equilibrium lattice constants of sB/β12 and GN were consistent with the values reported by the literature, which were 1.61 Å × 2.86 Å/5.0 Å × 3.0 Å [27,28,29] and 2.46 Å × 2.46 Å [17,51], respectively.
Because of the buckled structure of the sB with corrugations along the b direction, two types of boron atoms, namely, T and B atoms, were observed, as depicted in Figure 2. The calculated T–T and B–B distances were 1.61 Å. The T–B distance was 1.88 Å, and the buckling height was 0.92 Å. All the measured distances were consistent with the literature [28,32,43]. Accordingly, the sB sheet was found to have four different adsorption sites, termed the top site (T@sB), bottom site (B@sB), and bridge sites (Br1@sB and Br2@sB) (Figure 2).
Based on the geometrical position of the boron atoms, three different boron atoms –namely, T1, T2, and T3—were observed in the β12 sheet (Figure 2). The T1–T1, T1–T2, and T1–T3 bond lengths were 1.65, 1.71, and 1.68 Å, respectively. These different bonds led in turn to the existence of six possible adsorption sites on the β12 sheet; three top (T1@β12, T2@β12, and T3@β12), one hollow (H@β12), and two bridge sites (Br1@β12 and Br2@β12). When observing the GN sheet, a symmetric carbon–carbon bond was detected with a distance of 1.42 Å, resulting in three adsorption sites—namely, top (T@GN), hollow (H@GN), and bridge (Br@GN).

3.2. Adsorption Energy Calculations

To obtain a better understanding of the adsorption process within the π-system∙∙∙2D sheet complexes, BNZ and HFB were placed at versatile sites on the surfaces of sB, β12, and GN in both vertical and parallel configurations (Figure 1). Upon the relaxed structures, the adsorption energies were computed according to Equation (1) (see Computational Methods section), and the equilibrium distances were assessed (Table 1). The obtained relaxed structures for all the studied π-system∙∙∙2D sheet complexes are depicted in Figure S1. Figure 3 illustrates the relaxed π-systems at the most favorable energetic sites on the studied 2D sheets.
At first glance, the considered aromatic electron-rich and electron-deficient π-systems demonstrated an obvious tendency to be adsorbed on the relaxed 2D sheets (Figure S1), producing considerable negative adsorption energies (Table 1). The π-system∙∙∙sB, ∙∙∙β12, and ∙∙∙GN intermolecular distances were found to have values in the range of 2.54–4.06 Å, 2.15–3.30 Å, and 2.27–3.40 Å, respectively.
With regard to the adsorption process of the π-system on the surface of the sB sheet in a vertical configuration, the most prominent adsorption energy was detected in the case of the π-system∙∙∙B@sB complexes, followed by the π-system∙∙∙Br1@sB, π-system∙∙∙Br2@sB, and, finally, π-system∙∙∙T@sB complexes. For instance, the adsorption energies of the BNZ on the surface of the sB sheet at the B@sB, Br1@sB, Br2@sB, and T@sB sites were −5.66, −5.64, −4.40, and −4.35 kcal/mol, respectively. For parallel configuration, the T@sB and Br1@sB sites were found to be the most preferential adsorption sites for the BNZ and HFB, with adsorption energies of −14.93 and −15.76 kcal/mol, respectively.
According to the data registered in Table 1, the adsorption of the BNZ and HFB on the β12 surface was occurred significantly at the H@β12 site in the vertical configuration with adsorption energy values of −6.40 and −4.54 kcal/mol, respectively. Turning to the parallel configuration of the π-system∙∙∙β12 complexes, the T2@β12 and H@β12 sites were found to have significantly negative adsorption energy values in the interactions with BNZ and HFB, respectively.
Similar to the π-system∙∙∙β12 interactions, the H@GN site was documented as the most promising site for the adsorption of both BNZ and HFB on the GN surface in the vertical configuration. In comparison, the T@GN site was found to have the largest negative adsorption energies of the π-system∙∙∙GN complexes in the parallel configuration, followed by the Br@GN and, finally, H@GN sites. For example, the adsorption energies of the BNZ–GN complexes in the parallel configuration were −9.97, −9.89, and −8.78 kcal/mol for the BNZ–T@GN, BNZ∙∙∙Br@GN, and BNZ∙∙∙H@GN complexes, respectively. The obtained results were found to be compatible with those of an earlier study, demonstrating that the T@GN site was the most favorable site for the adsorption process of BNZ with an adsorption energy of −5.53 kcal/mol [50]. The slight difference between the adsorption energy values in the present study and the preceding study might be ascribed to the different chosen cutoff energies in the calculations.
Notably, the adsorption process of the aromatic π-systems∙∙∙sB/β12/GN complexes within the parallel configuration was observed to have greater favorability than those in the vertical configuration. For instance, the adsorption energies of the BNZ∙∙∙B@sB complex were −5.66 and −11.46 kcal/mol in vertical and parallel configurations, respectively.

3.3. Charge Transfer Calculations

Bader charge analysis has been documented as a powerful tool to precisely obtain an in-depth theoretical insight into the charge transfer during the adsorption process [65,66]. Utilizing Bader charge analysis, the charge transfer differences (Qt) of the relaxed π-system∙∙∙2D sheet complexes at all possible adsorption sites were calculated as illustrated in Equation (2) in the Computational Methods section, and they are compiled in Table 1. In the context of Bader charge analysis, the negative values of the charge transfer differences (Qt) outline the transfer of charge from the π-systems to the 2D sheets, and the positive values mean the opposite.
As can be seen from the data in Table 1, the adsorption of HFB on the sB surface had higher negative values of Qt, compared to BNZ, in the vertical configuration. For example, the Qt values were −0.0275 and −0.0154 e within the adsorption process of the HFB and BNZ, respectively, at the T@sB site in the vertical configuration. Although the adsorption of BNZ in the vertical configuration at the B@sB site exhibited the largest negative adsorption energy value of −5.66 kcal/mol, it had a small Qt value of −0.0136 e. This observation c confirmed that the charge transfer contributed little to the adsorption process within the BNZ∙∙∙sB complexes in the vertical configuration. On the other hand, the charge transfer in the HFB∙∙∙B@sB complex in the vertical configuration was shown to play the main dominant role in the interaction by the largest Qt value (i.e., −0.0318 e). Furthermore, a direct correlation between the Qt and the adsorption energy values was observed for the π-system∙∙∙sB complexes in the parallel configuration. For example, the BNZ∙∙∙T@sB and HFB–Br1@sB complexes, the most stable complexes in the parallel configuration with adsorption energy values of −14.93 and −15.76 kcal/mol, showed Qt values of 0.0735 and −0.0813 e, respectively.
In general, the charge transfer’s contribution to the adsorption process of BNZ and HFB on the β12 surface, in both vertical and parallel configurations, was signaled by smaller values of Qt compared to the π-system∙∙∙sB complexes. For instance, the Qt values were −0.0318 and −0.0261 e in the case of the HFB∙∙∙Br1@sB and ∙∙∙Br1@β12 complexes, respectively, in the vertical configuration. Moreover, it was noted that the adsorption of HFB on the β12 surface resulted from the transfer of a larger amount of the Qt compared to the BNZ analog. For example, the BNZ∙∙∙ and HFB∙∙∙H@β12 complexes in the vertical configuration had Qt values of −0.0199 and −0.0274 e, respectively.
Notably, the Qt showed small values, ranging from −0.0058 e for the BNZ∙∙∙GN complexes to −0.0124 e for HFB∙∙∙GN complexes, indicating the small contributions of charge transfer to the adsorption process on the GN surface in the vertical configuration.
Interestingly, in the case of parallel configuration, the adsorption of BNZ on all the studied 2D sheets showed positive Qt values. For example, the Qt values were 0.0735, 0.0436, and 0.0065 e for the BNZ∙∙∙T@sB, ∙∙∙T2@β12, and ∙∙∙T@GN, respectively. The latter observation emphasized that the charge was transferred from the 2D sheets to the BNZ. Similar findings of small positive Qt values in the case of the adsorption of BNZ on the GN surface in the parallel configuration were observed in prior theoretical studies [49,50].
To deeply understand the adsorption process, the charge density difference maps for the π-system∙∙∙2D sheet complexes at the most energetically favorable sites were generated based on Equation (3) in the Computational Methods section (Figure 4). With this in mind, the cyan- and yellow-colored-areas referred to increases and decreases in the charge density around the adsorption systems, respectively.
For the π-system∙∙∙2D sheet complexes in the vertical configuration, charge accumulation regions were observed around the BNZ and HFB systems and at the interface sites located over the 2D sheets (Figure 4). According to the latter observation, the charge transfer occurred from the investigated π-systems to the surfaces of the sB, β12, and GN sheets, confirmed by the negative sign of the estimated Qt values (Table 1). Evident accumulated charge regions were denoted by more prominent cyan colors in the case of the adsorption of HFB on the investigated 2D sheets compared with BNZ analog. Accordingly, the 2D sheets exhibited greater potential to attract electrons from HFB than from BNZ analog.
For the BNZ∙∙∙2D sheet complexes in the parallel configuration, the accumulated charge regions were noticed over the 2D sheets, designating the charge transfer from 2D sheets to BNZ. The latter findings were in agreement with the positive Qt values listed in Table 1. By contrast, in the case of the adsorption of HFB on the 2D sheets, the electron depletion regions were observed over the 2D sheets, signifying the transfer of charge from HFB to the 2D sheets.
In sum, the current Bader charge analysis generally demonstrated that the π-system∙∙∙sB complexes had the largest charge transfer difference (Qt) values, followed by the π-system∙∙∙β12 and, finally, the π-system∙∙∙GN complexes.

3.4. Band Structure Calculations

Electronic band structure analyses were performed to illuminate further the effects of the adsorbed π-systems (i.e., BNZ and HFB) on the electronic properties of the investigated 2D sheets. Using the PBE function, the band structure calculations of the pure 2D sheets were carried out along the high-symmetry points of the Brillouin zone and are depicted in Figure 5. Moreover, the band structures were investigated for the π-system∙∙∙2D sheet complexes at the most energetically favorable adsorption sites to determine the effect of the adsorption process on the electronic properties of the 2D sheets (Figure 6).
As shown in Figure 5, many bands crossing the Fermi level along the Г-Y-S-X-Г path were apparently detected in the case of the pure sB and β12 sheets. Accordingly, the electrons in the valence band could easily move to the conduction band through these bands. In the case of GN surface, the bands along the Y-S-X-Г-Y direction met at a point along the Fermi level (i.e., Dirac point), where the bandgap value was zero (Figure 5). Consequently, the findings emphasized that the sB and the β12 surfaces showed metallic properties, while the GN had semiconductor characters.
For the pure surface of the sB sheet, the bands touched at the Y, Г, and X points at 0.0, −2.0, and 1.6 eV, respectively (Figure 5). Following the adsorption of the BNZ and HFB on the surface of the sB sheet, it was observed that the bands shifted far away from each other, confirming the prominent effect of the adsorption of the π-systems on the electronic properties of the sB sheet (Figure 6). Simultaneously, the adsorption of the BNZ on the sB sheet resulted in the appearance of new valence and conduction bands at roughly −1.0/–2.0 eV, and 1.4/1.7 eV, respectively, demonstrating the interference of the BNZ bands with the sB bands. Extra bands were also found in the valence region of −1.5 and −2.0 eV at Г point after the adsorption of HFB on the sB surface in the vertical and parallel configurations.
Similarly, the obtained band structures of the π-system∙∙∙β12 complexes showed additional bands after the adsorption of the BNZ in both configurations at around −1.5 and −2.0 eV, which might be attributed to the contribution of the orbitals of BNZ in the adsorption process. In comparison, new conduction and valence bands appeared after the adsorption of the HFB in both configurations at 2.3 and −2.0 eV at Г point, respectively. Conspicuously, the adsorption of both BNZ and HFB had more valence and conduction bands in the parallel configuration than the vertical configuration, revealing the favorability of the parallel configuration over the vertical configuration. The latter results were in line with the adsorption energy results (Table 1).
The band structure analyses indicated that the adsorption of the electron-rich and electron-deficient π-systems on the GN barely affected the electronic properties of the pure surface and that the Dirac point remained. As shown in Figure 6, the adsorption of BNZ on the surface of the GN in both configurations gave rise to the appearance of a new valence band at −2.0 eV. At the same time, new conduction bands appeared at 1.6 and 2.1 eV for the HFB∙∙∙H@GN complex in the vertical configuration, exhibiting the HFB and GN surface interaction. Overall, the obtained band structures highlighted the occurrence of interactions between the aromatic π-systems and the GN.

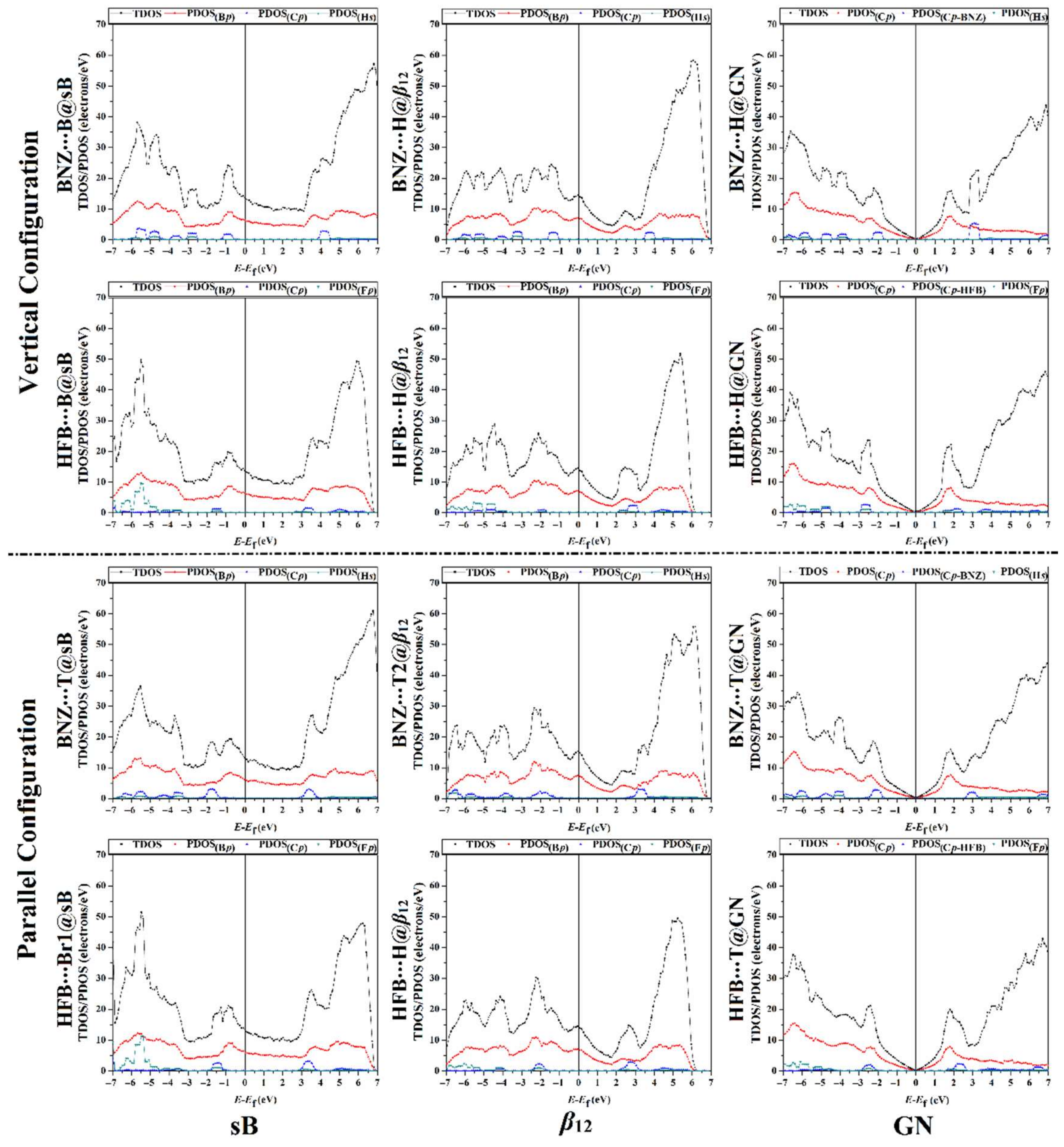
3.5. Density of State Calculations

The total and projected density-of-states (TDOS/PDOS) analyses were performed to reveal the nature of the interaction between the electron-rich/deficient π-systems and the sB/β12/GN 2D sheets. The TDOS and PDOS plots were generated for the studied 2D sheets before and after the adsorption process (Figure 7 and Figure 8, respectively).
As illustrated in Figure 7, the TDOS peaks at the Fermi level in the case of both pure sB and β12 surfaces were not zero, highlighting the metallic property of the examined sheets. In addition, the peaks of the pure sB and β12 surfaces were found to have a high value of TDOS near the Fermi level, ensuring the conductivity of the surfaces.
With regard to the TDOS of the pure GN surface, there was a Dirac point at the Fermi level (Figure 7), which was consistent with that of the band structure affirmations. From the PDOS results illustrated in Figure 7, the p-orbital of the B and C atoms showed the main contribution in the TDOS peaks of the pure sB/β12 and GN sheets, respectively.
Based on the PDOS peaks of the sB and β12 surfaces shown in Figure 8, the peaks of the p-orbital of the B atoms exhibited the dominant contribution to the TDOS near the Fermi level. In comparison, the s-orbital of hydrogen atoms made a frail contribution in the adsorption process.
Notably, the Hsin the BNZ exhibited a minor contribution in the adsorption process on the surface of the sB sheet, with energy values ranging from −6.0 to −2.5 eV in the vertical configuration and from −6.5 to −3.3 eV in the parallel one. Accordingly, the PDOS findings outlined that the adsorption of the BNZ on the sB surface in the vertical and parallel configurations was dominated by the contribution of the Cp in the BNZ. Turning to the HFB∙∙∙sB complexes in both vertical and parallel configurations, the Fpshowed the most prevalent contribution to the occurrence of the adsorption process and was found with energy values ranging from −7.0 to −4.5 eV. Remarkably, for the HFB∙∙∙Br1@sB in the parallel configuration, the adsorption process was dominated by the Fp and Bp hybridization, which was located at −5.4 eV. Obviously, the adsorption of HFB on the surface of the sB sheet in the parallel configuration showed higher PDOS peaks than in the vertical configuration, which was in agreement with the adsorption energy results (Table 1).
Concerning the β12 results, the PDOS analyses of the BNZ∙∙∙H@β12 and BNZ∙∙∙T2@β12 complexes in the vertical and parallel configurations, respectively, showed that the Cp in BNZ had the main role in the adsorption process on the β12 surface. Besides, the Hs made a tiny contribution to the adsorption process, with the PDOS peaks appearing at the valence region below the energy value of −3.0 eV. In addition, the Cp of the HFB displayed considerable hybridization with the Bp in the β12 sheet, producing a peak in the conduction area at about 3.0 eV. The DOS analyses were compatible with the findings of the adsorption energy and charge transfer calculations (Table 1).
For the GN surface, the adsorption of BNZ at the H@GN and T@GN sites in the vertical and parallel configurations, respectively, originated from the contribution of the Cpof the BNZ, which showed prominent peaks at energy values of −2.0 and 3.0 eV. Prominent Cpand Fp peaks were noted for the adsorption of HFB on the GN surface in both studied configurations, at energy values of −2.5 and 3.0 eV, in the valence and conduction regions, respectively.
Conclusively, the DOS peaks of all the examined π-system∙∙∙2D sheet complexes shifted towards the Fermi level compared to the pure surfaces, highlighting the enhancement of the electrical properties of the investigated 2D sheets after the adsorption process.

4. Conclusions

In the current study, the adsorption of electron-rich and electron-deficient π-systems (BNZ and HFB) on borophene and graphene sheets was comparatively investigated using DFT calculations. Adsorption energies, charge transfer analyses, electronic band structures, and DOS calculations were performed for the π-system∙∙∙2D sheet in the vertical and parallel configurations. The BNZ and HFB adsorption on the sB, β12, and GN surfaces in the parallel configuration demonstrated more favorable amplitude than that in the vertical configuration. The adsorption of BNZ and HFB over the sB and β12 sheets enhanced the electronic properties of their surfaces. On the other hand, the adsorption of BNZ and HFB on the GN sheet exhibited nominal change in the electronic properties of the GN surface. Based on Bader charge analysis, the charge was transferred from BNZ and HFB to the investigated 2D sheets, with the exception of the adsorption of BNZ in the parallel configuration, in which the charge was transferred from the 2D sheets to BNZ. Crucially, the band structure and the density-of-states (DOSs) results confirmed that the adsorption process of the π-system on the surface of the investigated 2D sheets bolstered their electrical properties. The results of this research could provide a base of information for fields relevant to the application of 2D nanomaterials.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano12061028/s1. Figure S1: Side and top views of the relaxed structures of the vertical and parallel configurations of the π-system∙∙∙2D sheet complexes where π-system = benzene (BNZ)/hexafluorobenzene (HFB) and the 2D sheet = striped borophene (sB)/β12 borophene (β12)/pristine graphene (GN) at all possible adsorption sites.

Author Contributions

Conceptualization, M.A.A.I.; data curation, A.H.M.M.; formal analysis, A.H.M.M.; investigation, A.H.M.M.; methodology, M.A.A.I., N.A.M.M. and A.M.S.; project administration, M.A.A.I., M.N.A. and M.E.S.S.; resources, M.A.A.I. and E.B.E.; software, M.A.A.I. and K.A.S.; supervision, M.A.A.I. and G.A.H.M.; visualization, A.H.M.M.; writing—original draft, A.H.M.M.; writing—review and editing, K.A.S., G.A.H.M., M.N.A., A.M.S., M.A.S.A., E.B.E., M.E.S.S. and N.A.M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

Ahmed M. Shawky would like to thank the Scientific Research at Umm Al-Qura University for supporting this work with grant No. 22UQU433174DSR05. The computational work was completed with resources provided by the Science and Technology Development Fund (STDF), Egypt, grants No. 5480 and 7972. Eslam B. Elkaeed extends his appreciation to the Research Center at AlMaarefa University for funding this work under TUMA project agreement No. TUMA-2021-4. Mahmoud A. A. Ibrahim extends his appreciation to the Academy of Scientific Research and Technology (ASRT, Egypt) for funding the Graduation Projects conducted at CompChem Lab, Egypt.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jariwala, D.; Sangwan, V.K.; Lauhon, L.J.; Marks, T.J.; Hersam, M.C. Carbon nanomaterials for electronics, optoelectronics, photovoltaics, and sensing. Chem. Soc. Rev. 2013, 42, 2824–2860. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Yung, K.C.; Wu, W.M.; Pierpoint, M.P.; Kusmartsev, F.V. Introduction to graphene electronics—A new era of digital transistors and devices. Contemp. Phys. 2013, 54, 233–251. [Google Scholar] [CrossRef] [Green Version]
  3. Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
  4. Yang, K.; Li, Y.; Tan, X.; Peng, R.; Liu, Z. Behavior and toxicity of graphene and its functionalized derivatives in biological systems. Small 2013, 9, 1492–1503. [Google Scholar] [CrossRef] [PubMed]
  5. Feng, L.; Wu, L.; Qu, X. New horizons for diagnostics and therapeutic applications of graphene and graphene oxide. Adv. Mater. 2013, 25, 168–186. [Google Scholar] [CrossRef]
  6. Liu, Y.; Dong, X.; Chen, P. Biological and chemical sensors based on graphene materials. Chem. Soc. Rev. 2012, 41, 2283–2307. [Google Scholar] [CrossRef]
  7. Zhang, J.; Zhao, F.; Zhang, Z.; Chen, N.; Qu, L. Dimension-tailored functional graphene structures for energy conversion and storage. Nanoscale 2013, 5, 3112–3126. [Google Scholar] [CrossRef]
  8. Sun, Y.Q.; Wu, Q.O.; Shi, G.Q. Graphene based new energy materials. Energy Environ. Sci. 2011, 4, 1113–1132. [Google Scholar] [CrossRef]
  9. Mahmood, N.; Zhang, C.Z.; Yin, H.; Hou, Y.L. Graphene-based nanocomposites for energy storage and conversion in lithium batteries, supercapacitors and fuel cells. J. Mater. Chem. A 2014, 2, 15–32. [Google Scholar] [CrossRef] [Green Version]
  10. Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
  11. Leenaerts, O.; Partoens, B.; Peeters, F.M. Adsorption of H2O, NH3, CO, NO2, and NO on graphene: A first-principles study. Phys. Rev. B Condens. Matter 2008, 77, 125416. [Google Scholar] [CrossRef] [Green Version]
  12. Elgengehi, S.M.; El-Taher, S.; Ibrahim, M.A.A.; Desmarais, J.K.; El-Kelany, K.E. Graphene and graphene oxide as adsorbents for cadmium and lead heavy metals: A theoretical investigation. Appl. Surf. Sci. 2020, 507, 145038. [Google Scholar] [CrossRef]
  13. Varghese, S.S.; Lonkar, S.; Singh, K.K.; Swaminathan, S.; Abdala, A. Recent advances in graphene based gas sensors. Sens. Actuators B-Chem. 2015, 218, 160–183. [Google Scholar] [CrossRef]
  14. Raccichini, R.; Varzi, A.; Wei, D.; Passerini, S. Critical insight into the relentless progression toward graphene and graphene-containing materials for lithium-ion battery anodes. Adv. Mater. 2017, 29, 1603421. [Google Scholar] [CrossRef] [PubMed]
  15. Hou, Y.; Wen, Z.H.; Cui, S.M.; Ci, S.Q.; Mao, S.; Chen, J.H. An advanced nitrogen-doped graphene/cobalt-embedded porous carbon polyhedron hybrid for efficient catalysis of oxygen reduction and water splitting. Adv. Funct. Mater. 2015, 25, 872–882. [Google Scholar] [CrossRef]
  16. Ayatollahi, A.; Roknabadi, M.R.; Behdani, M.; Shahtahmassebi, N.; Sanyal, B. Adsorption characteristics of amino acids on graphene and germanene using dispersion-corrected density functional theory. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 127, 114498. [Google Scholar] [CrossRef]
  17. Li, K.; Li, N.; Yan, N.N.; Wang, T.Y.; Zhang, Y.T.; Song, Q.; Li, H.J. Adsorption of small hydrocarbons on pristine, N-doped and vacancy graphene by DFT study. Appl. Surf. Sci. 2020, 515, 146028. [Google Scholar] [CrossRef]
  18. Kulish, V.V. Surface reactivity and vacancy defects in single-layer borophene polymorphs. Phys. Chem. Chem. Phys. 2017, 19, 11273–11281. [Google Scholar] [CrossRef]
  19. Cahangirov, S.; Topsakal, M.; Akturk, E.; Sahin, H.; Ciraci, S. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 2009, 102, 236804. [Google Scholar] [CrossRef] [Green Version]
  20. Derivaz, M.; Dentel, D.; Stephan, R.; Hanf, M.C.; Mehdaoui, A.; Sonnet, P.; Pirri, C. Continuous germanene layer on Al(111). Nano Lett. 2015, 15, 2510–2516. [Google Scholar] [CrossRef]
  21. Popov, I.; Seifert, G.; Tomanek, D. Designing electrical contacts to MoS2 monolayers: A computational study. Phys. Rev. Lett. 2012, 108, 156802. [Google Scholar] [CrossRef] [Green Version]
  22. Qiao, J.; Kong, X.; Hu, Z.X.; Yang, F.; Ji, W. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 2014, 5, 4475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef]
  24. Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147–150. [Google Scholar] [CrossRef]
  25. Aufray, B.; Kara, A.; Vizzini, S.; Oughaddou, H.; Leandri, C.; Ealet, B.; Le Lay, G. Graphene-like silicon nanoribbons on Ag(110): A possible formation of silicene. Appl. Phys. Lett. 2010, 96, 183102. [Google Scholar] [CrossRef] [Green Version]
  26. Du, Y.; Zhuang, J.; Liu, H.; Xu, X.; Eilers, S.; Wu, K.; Cheng, P.; Zhao, J.; Pi, X.; See, K.W.; et al. Tuning the band gap in silicene by oxidation. ACS Nano 2014, 8, 10019–10025. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Mannix, A.J.; Zhou, X.F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Peng, B.; Zhang, H.; Shao, H.Z.; Xu, Y.F.; Zhang, R.J.; Zhua, H.Y. The electronic, optical, and thermodynamic properties of borophene from first-principles calculations. J. Mater. Chem. C 2016, 4, 3592–3598. [Google Scholar] [CrossRef] [Green Version]
  29. Feng, B.; Zhang, J.; Zhong, Q.; Li, W.; Li, S.; Li, H.; Cheng, P.; Meng, S.; Chen, L.; Wu, K. Experimental realization of two-dimensional boron sheets. Nat. Chem. 2016, 8, 563–568. [Google Scholar] [CrossRef] [Green Version]
  30. Ranjan, P.; Lee, J.M.; Kumar, P.; Vinu, A. Borophene: New sensation in flatland. Adv. Mater. 2020, 32, e2000531. [Google Scholar] [CrossRef]
  31. Zhou, X.F.; Dong, X.; Oganov, A.R.; Zhu, Q.; Tian, Y.J.; Wang, H.T. Semimetallic two-dimensional boron allotrope with massless dirac fermions. Phys. Rev. Lett. 2014, 112, 085502. [Google Scholar] [CrossRef] [Green Version]
  32. Jiang, H.R.; Lu, Z.H.; Wu, M.C.; Ciucci, F.; Zhao, T.S. Borophene: A promising anode material offering high specific capacity and high rate capability for lithium-ion batteries. Nano Energy 2016, 23, 97–104. [Google Scholar] [CrossRef]
  33. Novotny, M.; Dominguez-Gutierrez, F.J.; Krstic, P. A computational study of hydrogen detection by borophene. J. Mater. Chem. C 2017, 5, 5426–5433. [Google Scholar] [CrossRef]
  34. Chen, X.F.; Wang, L.F.Z.; Zhang, W.T.; Zhang, J.L.; Yuan, Y.Q. Ca-decorated borophene as potential candidates for hydrogen storage: A first-principle study. Int. J. Hydrog. Energy 2017, 42, 20036–20045. [Google Scholar] [CrossRef]
  35. Xu, S.G.; Zhao, Y.J.; Liao, J.H.; Yang, X.B.; Xu, H. The nucleation and growth of borophene on the Ag (111) surface. Nano Res. 2016, 9, 2616–2622. [Google Scholar] [CrossRef] [Green Version]
  36. Yang, X.B.; Ding, Y.; Ni, J. Ab initio prediction of stable boron sheets and boron nanotubes: Structure, stability, and electronic properties. Phys. Rev. B Condens. Matter 2008, 77, 041402. [Google Scholar] [CrossRef]
  37. Li, X.B.; Xie, S.Y.; Zheng, H.; Tian, W.Q.; Sun, H.B. Boron based two-dimensional crystals: Theoretical design, realization proposal and applications. Nanoscale 2015, 7, 18863–18871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  38. Zhang, Z.; Yang, Y.; Gao, G.; Yakobson, B.I. Two-dimensional boron monolayers mediated by metal substrates. Angew. Chem. Int. Ed. Engl. 2015, 54, 13022–13026. [Google Scholar] [CrossRef] [PubMed]
  39. Tang, H.; Ismail-Beigi, S. Novel precursors for boron nanotubes: The competition of two-center and three-center bonding in boron sheets. Phys. Rev. Lett. 2007, 99, 115501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Liu, H.; Gao, J.; Zhao, J. From boron cluster to two-dimensional boron sheet on Cu(111) surface: Growth mechanism and hole formation. Sci. Rep. 2013, 3, 3238. [Google Scholar] [CrossRef] [Green Version]
  41. Lu, H.; Mu, Y.; Bai, H.; Chen, Q.; Li, S.D. Binary nature of monolayer boron sheets from ab initio global searches. J. Chem. Phys. 2013, 138, 024701. [Google Scholar] [CrossRef] [Green Version]
  42. Peng, B.; Zhang, H.; Shao, H.Z.; Ning, Z.Y.; Xu, Y.F.; Ni, G.; Lu, H.L.; Zhang, D.W.; Zhu, H.Y. Stability and strength of atomically thin borophene from first principles calculations. Mater. Res. Lett. 2017, 5, 399–407. [Google Scholar] [CrossRef]
  43. Wang, H.; Li, Q.; Gao, Y.; Miao, F.; Zhou, X.-F.; Wan, X.G. Strain effects on borophene: Ideal strength, negative Possion’s ratio and phonon instability. New J. Phys. 2016, 18, 073016. [Google Scholar] [CrossRef]
  44. He, C.; Cheng, J.; Zhang, X.; Douthwaite, M.; Pattisson, S.; Hao, Z. Recent advances in the catalytic oxidation of volatile organic compounds: A review based on pollutant sorts and sources. Chem. Rev. 2019, 119, 4471–4568. [Google Scholar] [CrossRef]
  45. Scire, S.; Liotta, L.F. Supported gold catalysts for the total oxidation of volatile organic compounds. Appl. Catal. B-Environ. 2012, 125, 222–246. [Google Scholar] [CrossRef]
  46. Woodruff, T.J.; Axelrad, D.A.; Caldwell, J.; Morello-Frosch, R.; Rosenbaum, A. Public health implications of 1990 air toxics concentrations across the United States. Environ. Health Perspect. 1998, 106, 245–251. [Google Scholar] [CrossRef]
  47. Cohen, A.J.; Pope, C.A. 3rd. Lung cancer and air pollution. Environ. Health Perspect. 1995, 103 (Suppl. 8), 219–224. [Google Scholar] [CrossRef] [Green Version]
  48. Lu, M.; Yao, Q.S.; Li, Q.Y.; Xiao, C.Y.; Huang, C.X.; Kan, E.J. Tuning electronic and magnetic properties of two-dimensional ferromagnetic semiconductor CrI3 through adsorption of benzene. J. Phys. Chem. C 2020, 124, 22143–22149. [Google Scholar] [CrossRef]
  49. AlZahrani, A.Z. First-principles study on the structural and electronic properties of graphene upon benzene and naphthalene adsorption. Appl. Surf. Sci. 2010, 257, 807–810. [Google Scholar] [CrossRef]
  50. Zhang, Y.H.; Zhou, K.G.; Xie, K.F.; Zeng, J.; Zhang, H.L.; Peng, Y. Tuning the electronic structure and transport properties of graphene by noncovalent functionalization: Effects of organic donor, acceptor and metal atoms. Nanotechnology 2010, 21, 065201. [Google Scholar] [CrossRef]
  51. Chakarova-Kack, S.D.; Schroder, E.; Lundqvist, B.I.; Langreth, D.C. Application of van der Waals density functional to an extended system: Adsorption of benzene and naphthalene on graphite. Phys. Rev. Lett. 2006, 96, 146107. [Google Scholar] [CrossRef] [Green Version]
  52. Li, Y.S.; Yu, C.M. DFT study of the adsorption of C6H6 and C6H5OH molecules on stanene nanosheets: Applications to sensor devices. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 127, 114533. [Google Scholar] [CrossRef]
  53. Sabokdast, S.; Horri, A.; Azar, Y.T.; Momeni, M.; Tavakoli, M.b. Adsorption of adenine molecule on χ3 borophene nanosheets: A density functional theory study. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 119, 114026. [Google Scholar] [CrossRef]
  54. Li, Q.X.; Liu, H.Y.; Tian, Y.G.; Guo, J.H.; Chen, G.; Lee, J.Y. Methylation detection and DNA sequencing based on adsorption of nucleobases on silicene nanoribbon. J. Phys. Chem. C 2020, 124, 10823–10831. [Google Scholar] [CrossRef]
  55. Wang, Y.P.; Ji, W.X.; Zhang, C.W.; Li, S.S.; Li, F.; Li, P.; Ren, M.J.; Chen, X.L.; Yuan, M.; Wang, P.J. Enhanced band gap opening in germanene by organic molecule adsorption. Mater. Chem. Phys. 2016, 173, 379–384. [Google Scholar] [CrossRef]
  56. Li, W.; Jiang, Q.; Li, D.; Ao, Z.; An, T. Density functional theory investigation on selective adsorption of VOCs on borophene. Chin. Chem. Lett. 2021, 32, 2803–2806. [Google Scholar] [CrossRef]
  57. Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
  58. Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
  59. Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  60. Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  61. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
  62. Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B Condens. Matter 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
  63. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  64. Marzari, N.; Vanderbilt, D.; De Vita, A.; Payne, M.C. Thermal contraction and disordering of the Al(110) surface. Phys. Rev. Lett. 1999, 82, 3296–3299. [Google Scholar] [CrossRef] [Green Version]
  65. Henkelman, G.; Arnaldsson, A.; Jonsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comp. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
  66. Bader, R.F.W. Atoms in Molecules: A Quantum Theory, 1st ed.; Clarendon Press: Oxford, UK, 1990; Volume XVIII, p. 438. [Google Scholar]
  67. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
Nanomaterials 12 01028 g001 550
Figure 1. Side and top views of the vertical and parallel configurations of the π-system∙∙∙2D sheet complexes where π-system = BNZ/HFB and the 2D sheet = sB/β12/GN.
Figure 1. Side and top views of the vertical and parallel configurations of the π-system∙∙∙2D sheet complexes where π-system = BNZ/HFB and the 2D sheet = sB/β12/GN.
Nanomaterials 12 01028 g001
Nanomaterials 12 01028 g002 550
Figure 2. Side and top views of the sB-, β12-, and GN-optimized 2D sheets. Top (T), bottom (B), and two bridge (Br1 and Br2) sites are labeled on the surface of the sB sheet. On the β12 surface, three top (T1, T2, and T3), one hollow (H), and two bridge sites (Br1 and Br2) are depicted. Three adsorption sites, namely, top (T), hollow (H), and bridge (Br) sites are illustrated on the GN surface.
Figure 2. Side and top views of the sB-, β12-, and GN-optimized 2D sheets. Top (T), bottom (B), and two bridge (Br1 and Br2) sites are labeled on the surface of the sB sheet. On the β12 surface, three top (T1, T2, and T3), one hollow (H), and two bridge sites (Br1 and Br2) are depicted. Three adsorption sites, namely, top (T), hollow (H), and bridge (Br) sites are illustrated on the GN surface.
Nanomaterials 12 01028 g002
Nanomaterials 12 01028 g003 550
Figure 3. Side and top views of the relaxed structures of the vertical and parallel configurations of the π-system∙∙∙2D sheet complexes where π-system = BNZ/HFB and the 2D sheet = sB/β12/GN at the most energetically favorable adsorption sites. The π-system–2D sheet equilibrium distances (d) are given in Å.
Figure 3. Side and top views of the relaxed structures of the vertical and parallel configurations of the π-system∙∙∙2D sheet complexes where π-system = BNZ/HFB and the 2D sheet = sB/β12/GN at the most energetically favorable adsorption sites. The π-system–2D sheet equilibrium distances (d) are given in Å.
Nanomaterials 12 01028 g003
Nanomaterials 12 01028 g004 550
Figure 4. Charge density difference maps of the relaxed structures of the vertical and parallel configurations of the π-system∙∙∙2D sheet complexes where π-system = BNZ/HFB and the 2D sheet = sB/β12/GN at the most energetically favorable adsorption sites. Cyan and yellow colors represent the charge accumulation (negative) and depletion (positive), respectively. Green, pink, Gray, and brown balls refer to boron, hydrogen, fluorine, and carbon atoms.
Figure 4. Charge density difference maps of the relaxed structures of the vertical and parallel configurations of the π-system∙∙∙2D sheet complexes where π-system = BNZ/HFB and the 2D sheet = sB/β12/GN at the most energetically favorable adsorption sites. Cyan and yellow colors represent the charge accumulation (negative) and depletion (positive), respectively. Green, pink, Gray, and brown balls refer to boron, hydrogen, fluorine, and carbon atoms.
Nanomaterials 12 01028 g004
Nanomaterials 12 01028 g005 550
Figure 5. Band structure plots for the pure surfaces of sB, β12, and GN along the high-symmetry points of the Brillouin zone. The Fermi energy is set to zero-energy.
Figure 5. Band structure plots for the pure surfaces of sB, β12, and GN along the high-symmetry points of the Brillouin zone. The Fermi energy is set to zero-energy.
Nanomaterials 12 01028 g005
Nanomaterials 12 01028 g006 550
Figure 6. Band structure plots for the sB, β12, and GN after the adsorption process of BNZ and HFB at the most energetically favorable adsorption sites in the vertical and parallel configurations. The Fermi energy was set to zero-energy.
Figure 6. Band structure plots for the sB, β12, and GN after the adsorption process of BNZ and HFB at the most energetically favorable adsorption sites in the vertical and parallel configurations. The Fermi energy was set to zero-energy.
Nanomaterials 12 01028 g006
Nanomaterials 12 01028 g007 550
Figure 7. The total and projected density-of-states (TDOS/PDOS) plots for the pure surfaces of the sB, β12, and GN, assuming the Fermi level as the reference level. The values Bp and Cp represent the p-orbital of boron (B) and carbon (C) atoms, respectively.
Figure 7. The total and projected density-of-states (TDOS/PDOS) plots for the pure surfaces of the sB, β12, and GN, assuming the Fermi level as the reference level. The values Bp and Cp represent the p-orbital of boron (B) and carbon (C) atoms, respectively.
Nanomaterials 12 01028 g007
Nanomaterials 12 01028 g008 550
Figure 8. The total and projected density-of-states (TDOS/PDOS) plots for the sB, β12, and GN after the adsorption process of BNZ and HFB at the most energetically favorable adsorption sites in the vertical and parallel configurations. The Bp/Cp/Fp and Hs represent the p-orbital and s-orbital of boron (B)/carbon (C)/fluorine (F) and hydrogen (H) atoms, respectively.
Figure 8. The total and projected density-of-states (TDOS/PDOS) plots for the sB, β12, and GN after the adsorption process of BNZ and HFB at the most energetically favorable adsorption sites in the vertical and parallel configurations. The Bp/Cp/Fp and Hs represent the p-orbital and s-orbital of boron (B)/carbon (C)/fluorine (F) and hydrogen (H) atoms, respectively.
Nanomaterials 12 01028 g008
Table
Table 1. Adsorption energies (Ead, kcal/mol) and equilibrium distances (d, Å) of the relaxed structures of BNZ and HFB on the sB, β12, and GN sheets in the vertical and parallel configurations at all studied adsorption sites, as well as the charge transfer difference (Qt, e) for the 2D sheets before and after the adsorption process.
Table 1. Adsorption energies (Ead, kcal/mol) and equilibrium distances (d, Å) of the relaxed structures of BNZ and HFB on the sB, β12, and GN sheets in the vertical and parallel configurations at all studied adsorption sites, as well as the charge transfer difference (Qt, e) for the 2D sheets before and after the adsorption process.
2D SheetAdsorption
Site a		π-System
Benzene (BNZ)Hexafluorobenzene (HFB)
Ead (kcal/mol)d (Å)Qtb (e)Ead (kcal/mol)d (Å)Qtb (e)
Vertical Configuration c
sBT−4.352.57−0.0154−3.992.95−0.0275
B−5.663.02−0.0136−4.833.52−0.0318
Br1−5.643.02−0.0132−4.793.53−0.0318
Br2−4.402.54−0.0169−4.002.93−0.0274
β12T1−5.072.54−0.0176−3.943.02−0.0219
T2−4.352.62−0.0157−4.392.94−0.0219
T3−4.842.53−0.0165−4.222.96−0.0220
H−6.402.15−0.0199−4.542.72−0.0274
Br1−5.652.38−0.0177−4.202.90−0.0261
Br2−4.952.47−0.0157−4.502.91−0.0215
GNT−4.302.52−0.0067−3.742.89−0.0124
H−5.042.27−0.0058−3.972.79−0.0117
Br−4.472.45−0.0074−3.762.88−0.0121
Parallel Configuration c
sBT−14.933.090.0735−14.663.23−0.0733
B−11.464.000.0469−15.744.04−0.0812
Br1−11.434.030.0454−15.764.06−0.0813
Br2−14.503.010.0572−14.753.18−0.0730
β12T1−11.453.260.0184−16.183.27−0.0672
T2−12.163.240.0436−16.053.27−0.0520
T3−10.503.300.0066−15.803.27−0.0652
H−11.733.230.0385−16.553.23−0.0534
Br1−11.553.250.0184−16.193.22−0.0608
Br2−10.773.300.0099−15.663.27−0.0645
GNT−9.973.280.0065−14.343.21−0.0378
H−8.783.400.0080−12.513.33−0.0325
Br−9.893.280.0050−14.083.22−0.0357
a All adsorption sites on the surface of the studied 2D sheets are illustrated in Figure 2. b   Q t was estimated by Equation (2) (see Computational Methods section for details). c All the relaxed structures of the π-system∙∙∙2D sheet complexes are displayed in Figure S1.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Ibrahim, M.A.A.; Mahmoud, A.H.M.; Soliman, K.A.; Mekhemer, G.A.H.; Ahmed, M.N.; Shawky, A.M.; Abourehab, M.A.S.; Elkaeed, E.B.; Soliman, M.E.S.; Moussa, N.A.M. Borophene and Pristine Graphene 2D Sheets as Potential Surfaces for the Adsorption of Electron-Rich and Electron-Deficient π-Systems: A Comparative DFT Study. Nanomaterials 2022, 12, 1028. https://doi.org/10.3390/nano12061028

AMA Style

Ibrahim MAA, Mahmoud AHM, Soliman KA, Mekhemer GAH, Ahmed MN, Shawky AM, Abourehab MAS, Elkaeed EB, Soliman MES, Moussa NAM. Borophene and Pristine Graphene 2D Sheets as Potential Surfaces for the Adsorption of Electron-Rich and Electron-Deficient π-Systems: A Comparative DFT Study. Nanomaterials. 2022; 12(6):1028. https://doi.org/10.3390/nano12061028

Chicago/Turabian Style

Ibrahim, Mahmoud A. A., Amna H. M. Mahmoud, Kamal A. Soliman, Gamal A. H. Mekhemer, Muhammad Naeem Ahmed, Ahmed M. Shawky, Mohammed A. S. Abourehab, Eslam B. Elkaeed, Mahmoud E. S. Soliman, and Nayra A. M. Moussa. 2022. "Borophene and Pristine Graphene 2D Sheets as Potential Surfaces for the Adsorption of Electron-Rich and Electron-Deficient π-Systems: A Comparative DFT Study" Nanomaterials 12, no. 6: 1028. https://doi.org/10.3390/nano12061028

APA Style

Ibrahim, M. A. A., Mahmoud, A. H. M., Soliman, K. A., Mekhemer, G. A. H., Ahmed, M. N., Shawky, A. M., Abourehab, M. A. S., Elkaeed, E. B., Soliman, M. E. S., & Moussa, N. A. M. (2022). Borophene and Pristine Graphene 2D Sheets as Potential Surfaces for the Adsorption of Electron-Rich and Electron-Deficient π-Systems: A Comparative DFT Study. Nanomaterials, 12(6), 1028. https://doi.org/10.3390/nano12061028

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop