Analytical Investigation of the Time-Dependent Stagnation Point Flow of a CNT Nanofluid over a Stretching Surface
Abstract
:1. Introduction
2. Mathematical Formulation
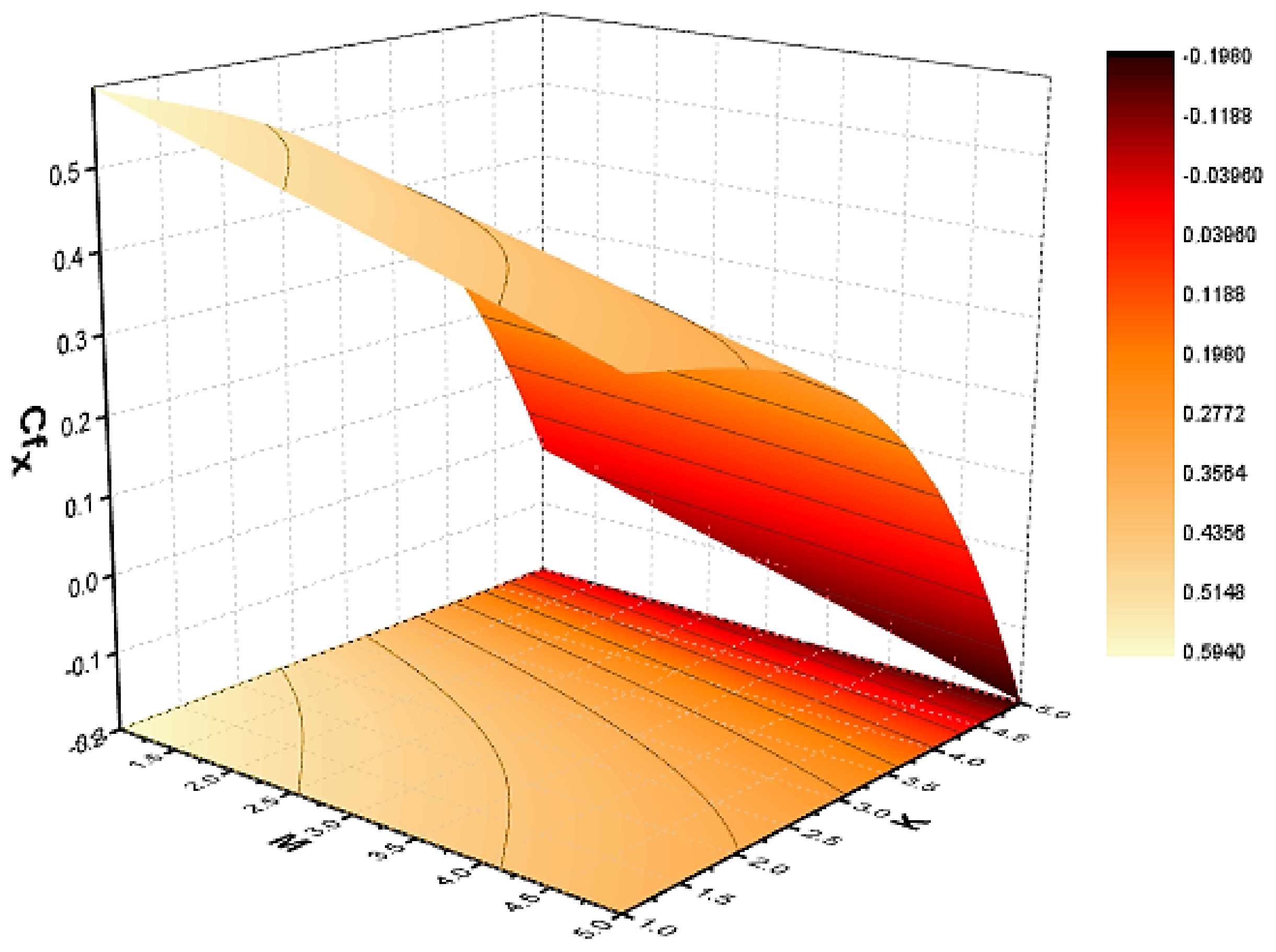
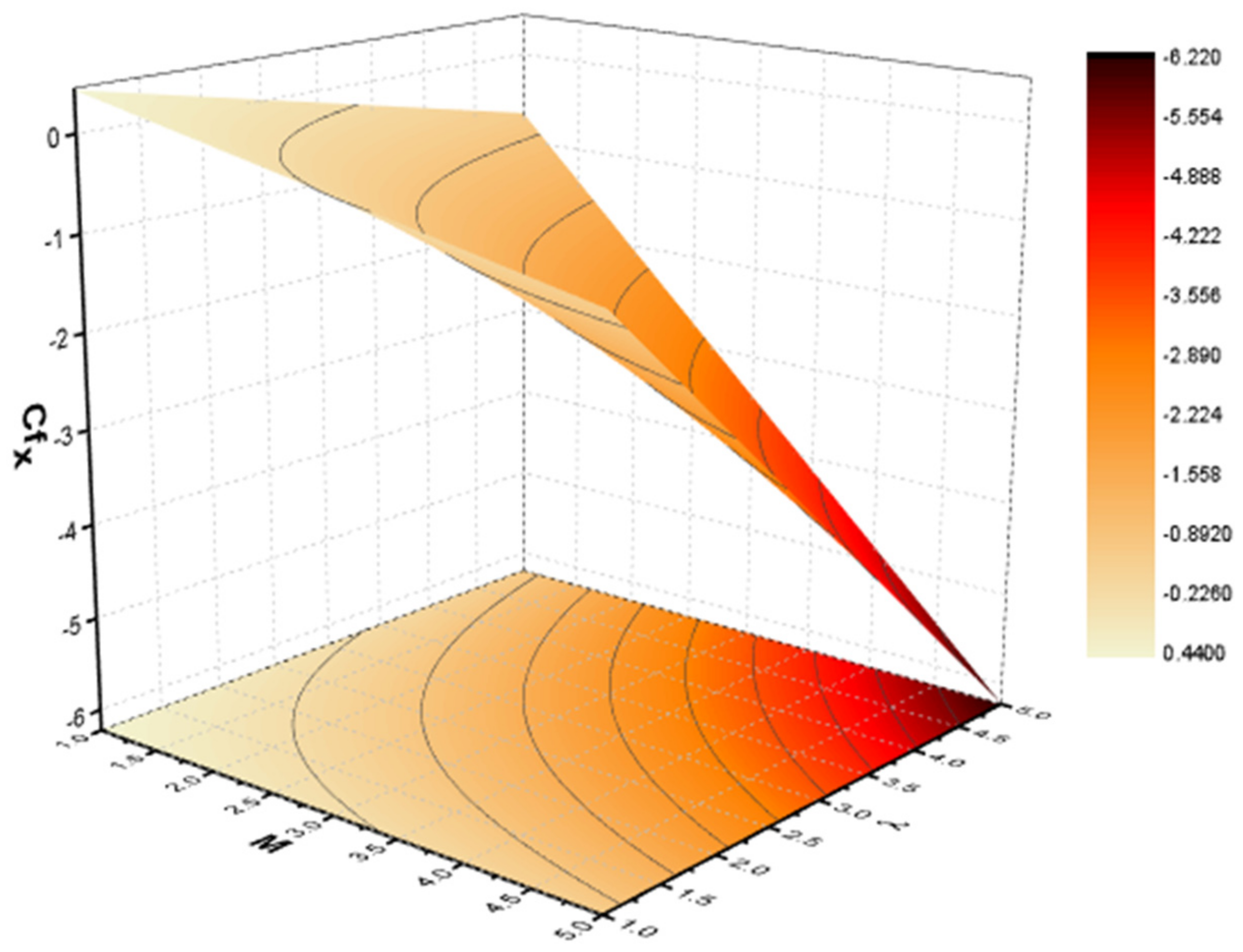
The Skin Friction and Nusselt Number
3. Method of Solution
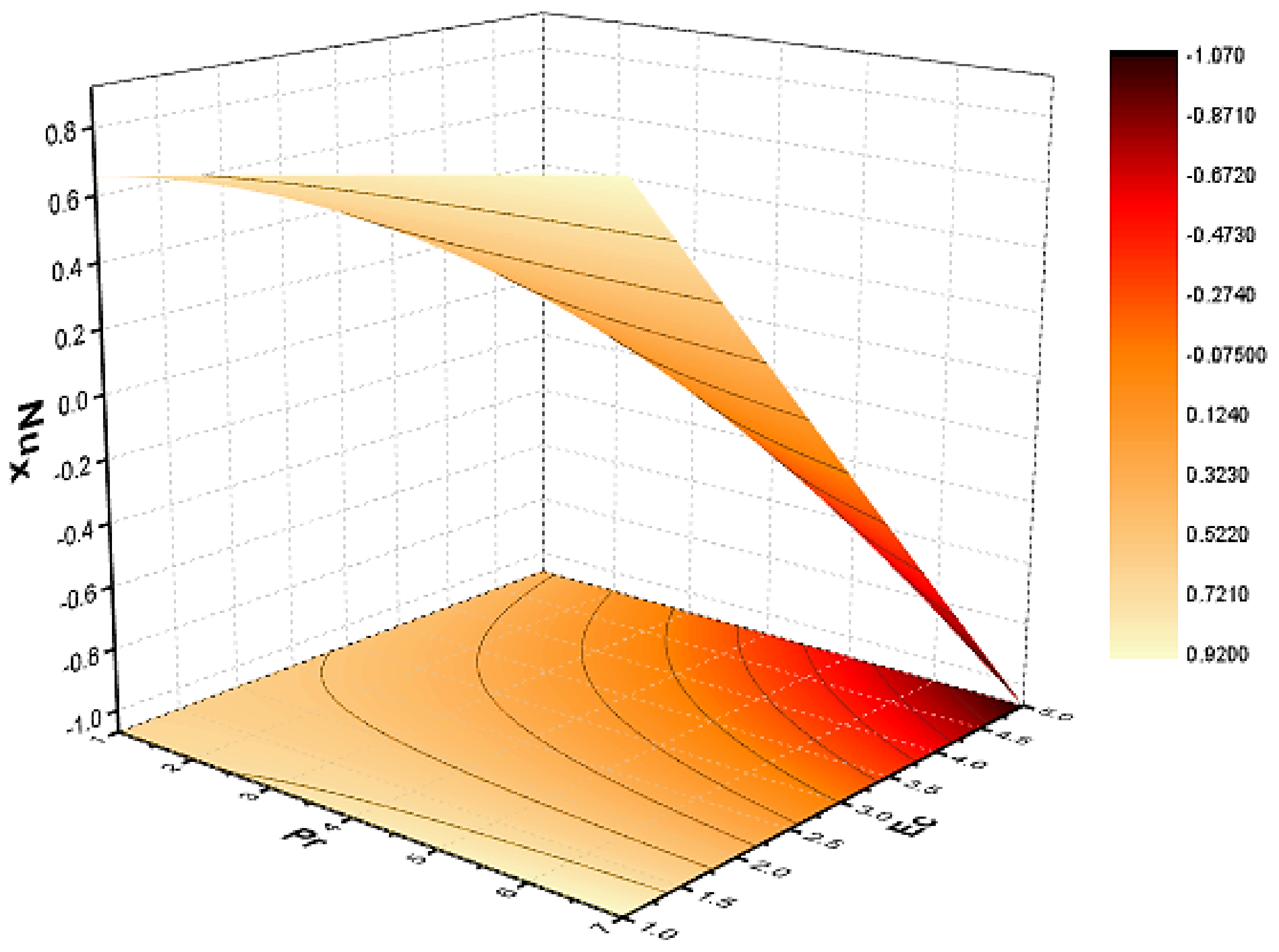
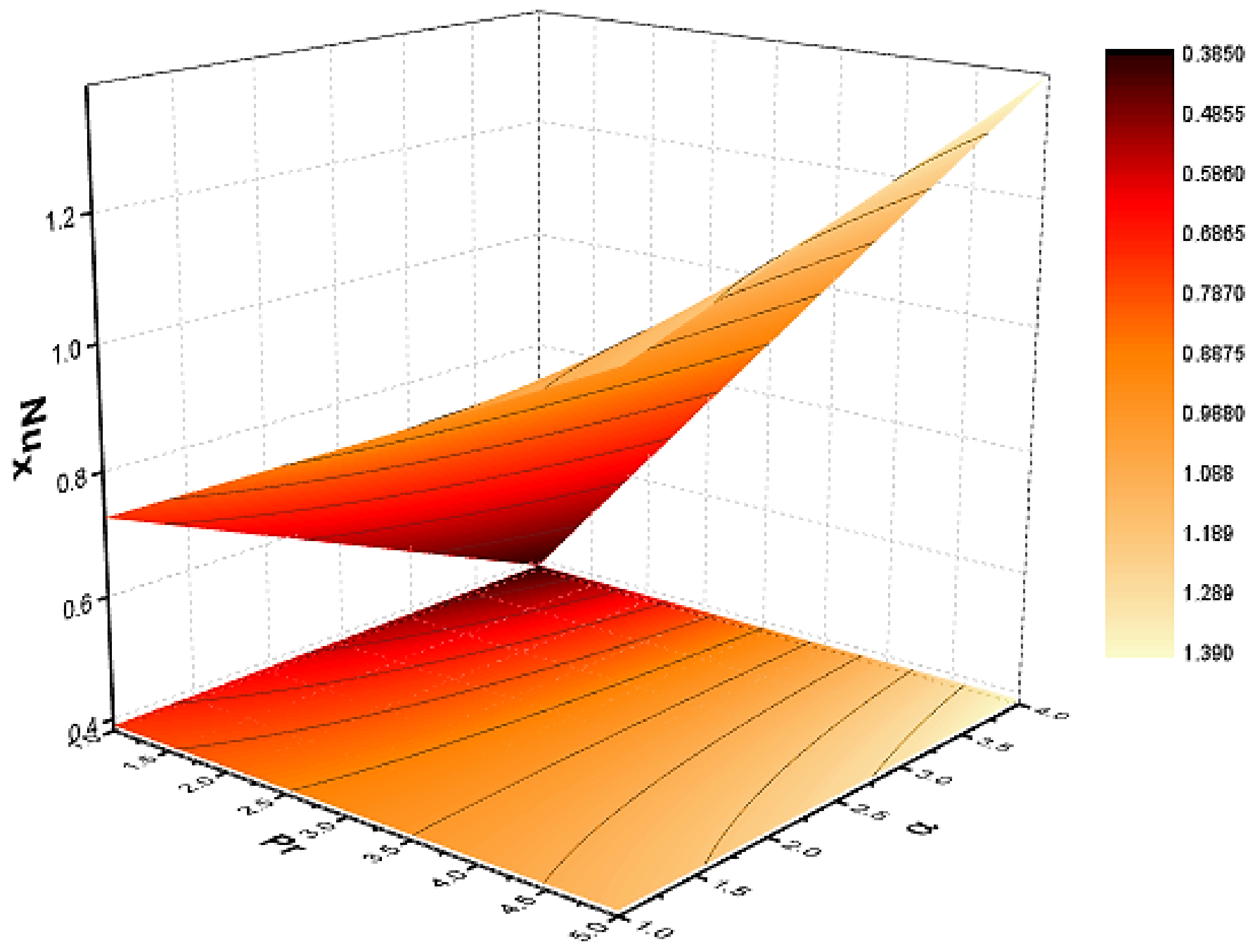
4. Results and Discussion
5. Conclusions
- 1.
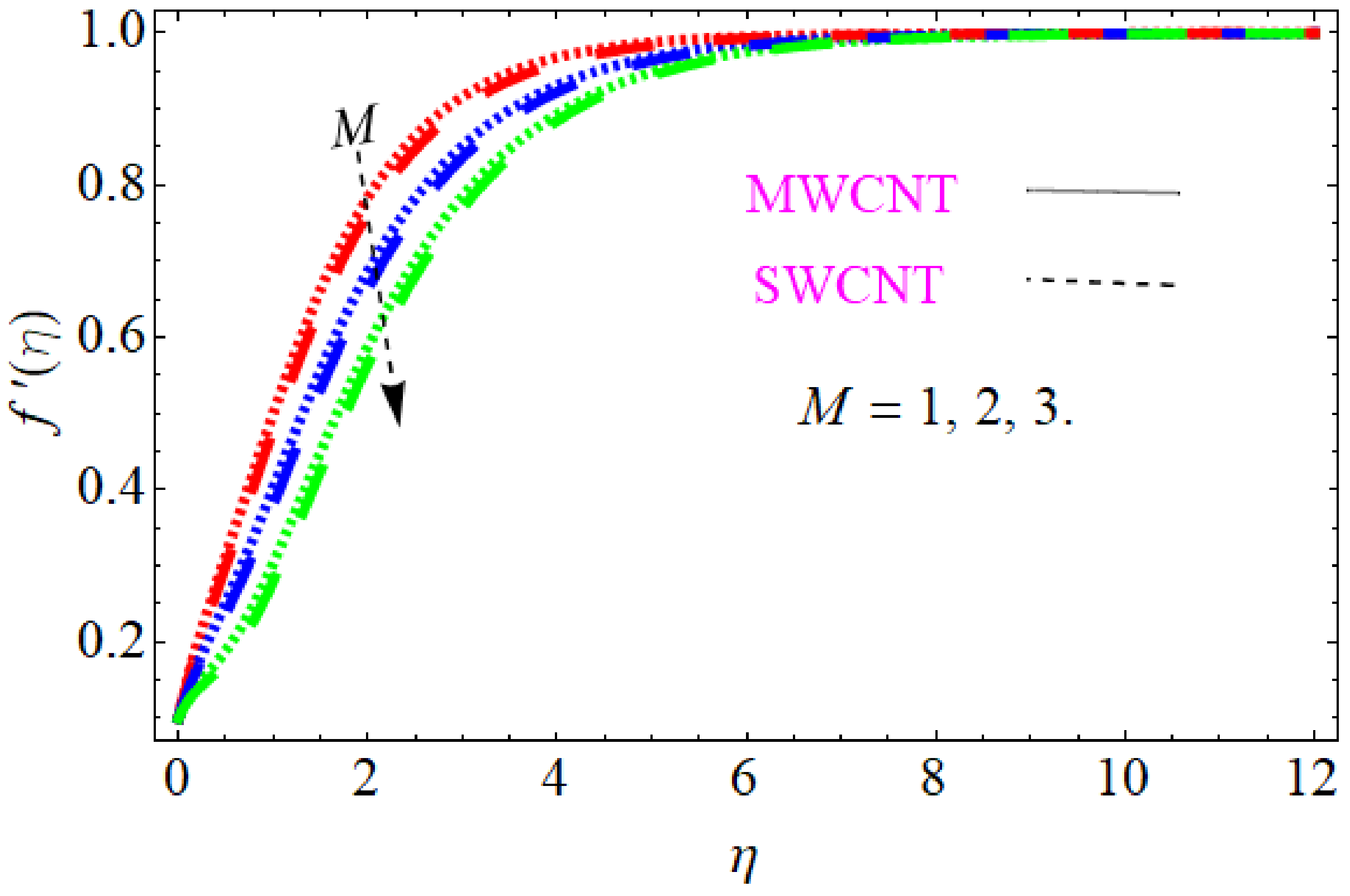
- Increasing the value of the dimensionless nanoparticle volume fraction parameter reduces velocity.
- 2.
- Increasing the value of the magnetic field parameter reduces velocity
- 3.
- Increasing the value of the unsteady parameter reduces velocity
- 4.
- Increasing the value of the Prandtl number reduces the temperature profile
- 5.
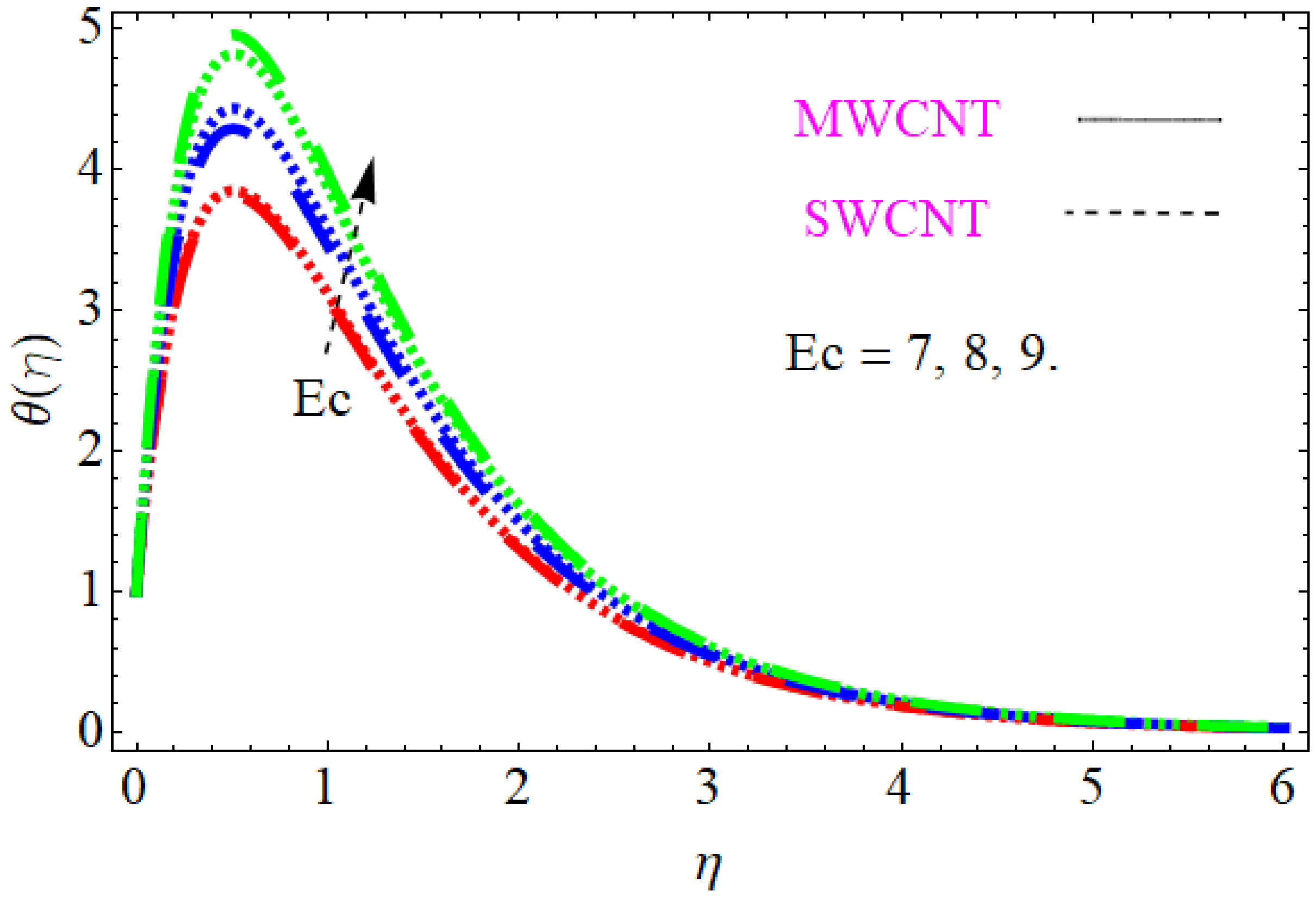
- Increasing the value of the Eckert number increases the temperature profile
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| x, y, | Cartesian coordinates |
| u, v, | Velocity components |
| Uw, Vw | Velocities of the stretching sheet |
| S | Time dependent parameter |
| T | Local Temperature |
| M | Magnetic field |
| Nux | Local Nusselt number |
| pr | Prandtl number |
| Tw | Surface temperature |
| B0 | Constant magnetic field |
| T∞ | Ambient temperature- |
| Ec | Eckert number |
| Cfx | Skin friction coefficient in x− direction- |
| θ | Dimensionless temperature |
| Density of the fluid | |
| Fluid viscosity | |
| Independent variable | |
| Spatial scale parameter | |
| Thermal conductivity | |
| Specific heat |
References
- Pop, I.; Postelnicu, A.; Grosan, T. Thermo-solutal Marangoni forced convection boundarylayers. Meccanica 2001, 36, 555–571. [Google Scholar]
- Al-Mudhaf, A.; Chamkha, A.J. Similarity solutions for MHD thermo-solutal Marangoni convection over a flat surface in the presence of heat generation or absorption effects. Heat Mass Transf. 2005, 42, 112–121. [Google Scholar]
- Wang, C.Y. Liquid film sprayed on a stretching surface. Chem. Eng. Commun. 2006, 193, 869–878. [Google Scholar]
- Chen, C.-H. Marangoni effects on forced convection of power-law liquids in a thin film over a stretching surface. Phys. Lett. A 2007, 370, 51–57. [Google Scholar] [CrossRef]
- Magyari, E.; Chamkha, A.J. Exact analytical solutions for thermo-solutal Marangoni convection in the presence of heat and mass generation or consumption. Heat Mass Transf. 2007, 43, 965–974. [Google Scholar]
- Lin, Y.; Zheng, L.; Zhang, X. Magneto-hydrodynamics thermo-capillary Marangoni convection heat transfer of power-law fluids driven by temperature gradient. J. Heat Transf. 2013, 135, 051702. [Google Scholar]
- Lin, Y.; Zheng, L.; Zhang, X. Radiation effects on Marangoni convection flow and heat transfer in pseudo-plastic non-Newtonian nanofluids with variable thermal conductivity. Int. J. Heat Mass Transf. 2014, 77, 708–716. [Google Scholar] [CrossRef]
- Aly, E.; Ebaid, A. Exact analysis for the effect of heat transfer on MHD and radiation Marangoni boundary layer nanofluid flow past a surface embedded in a porous medium. J. Mol. Liq. 2016, 215, 625–639. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hassan, M. Particle shape effects on Marangoni convection boundary layer flow of a nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2160–2174. [Google Scholar] [CrossRef]
- Jiao, C.; Zheng, L.; Lin, Y.; Ma, L.; Chen, G. Marangoni abnormal convection heat transfer of power-law fluid driven by temperature gradient in porous medium with heat generation. Int. J. Heat Mass Transf. 2016, 92, 700–707. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Chamkha, A.J. Influence of Lorentz forces on nanofluid forced convection considering Marangoni convection. J. Mol. Liq. 2017, 225, 750–757. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Influence of magnetic field on CuOeH2O nanofluid flow considering Marangoni boundary layer. Int. J. Hydrog. Energy 2017, 42, 2748–2755. [Google Scholar]
- Mahanthesh, B.; Gireesha, B.J.; PrasannaKumara, B.C.; Shashikumar, N.S. Marangoni convection radiative flow of dusty nanoliquid with exponential space dependent heat source. Nucl. Eng. Technol. 2017, 49, 1660–1668. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Analytical investigation for Lorentz forces effect on nanofluid Marangoni boundary layer hydrothermal behavior using HAM. Indian J. Phys. 2017, 91, 1581–1587. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B. Thermal Marangoni convection in two-phase flow of dusty Casson fluid. Results Phys. 2018, 8, 537–544. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J. Scrutinization of thermal radiation, viscous dissipation and Joule heating effects on Ma-rangoni convective two-phase flow of Casson fluid with fluid particle suspension. Results Phys. 2018, 8, 869–878. [Google Scholar]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME-Publ. Fed 1995, 231, 99–106. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.L.; Thompson, J. Anomalously increased effective thermal conductivities of ethylene glycol-based nano-fluids containing copper nanoparticles. Appl. Phys. 2001, 78, 718–720. [Google Scholar]
- Khamis, S.; Makinde, O.D.; Nkansah-Gyekye, Y. Unsteady flow of variable viscosity Cu-water and Al2O3-water nanofluids in a porous pipe with buoyancy force. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1638–1657. [Google Scholar] [CrossRef]
- Malvandi, A.; Ganji, D.D. Mixed Convection of Alumina/Water Nanofluid in Microchannels using Modified Buongiorno’s Model in Presence of Heat Source/Sink. J. Appl. Fluid Mech. 2016, 9, 2277–2289. [Google Scholar] [CrossRef]
- Reddy, S.; Chamkha, A.J. Heat and mass transfer characteristics of Al2O3-water and Ag-water nanofluid through porous media over a vertical cone with heat generation/absorption. J. Porous Media 2017, 20, 1–17. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D. Numerical investigation of laminar flow and heat transfer of non-Newtonian nanofluid within a porous medium. Powder Technol. 2018, 325, 78–91. [Google Scholar] [CrossRef]
- Hosseini, S.; Sheikholeslami, M.; Ghasemian, M.; Ganji, D. Nanofluid heat transfer analysis in a microchannel heat sink (MCHS) under the effect of magnetic field by means of KKL model. Powder Technol. 2018, 324, 36–47. [Google Scholar] [CrossRef]
- Xie, H.; Lee, H.; Youn, W.; Choi, M. Nanofluids containing multiwalled carbon nanotubes and their enhanced thermal conductivities. J. Appl. Phys. 2003, 94, 4967. [Google Scholar] [CrossRef]
- Ding, Y.; Alias, H.; Wen, D.; Williams, R.A. Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids). Int. J. Heat Mass Transf. 2006, 49, 240–250. [Google Scholar] [CrossRef]
- Haq, R.U.; Khan, Z.H.; Khan, W.A. Thermo-physical effects of carbon nanotubes on MHD flow over a stretching surface. Phys. E Low-Dimens. Syst. Nanostruct. 2014, 63, 215–222. [Google Scholar]
- Ueki, Y.; Aoki, T.; Ueda, K.; Shibahara, M. Thermophysical properties of carbon-based material nanofluid. Int. J. Heat Mass Transf. 2017, 113, 1130–1134. [Google Scholar] [CrossRef]
- Rehman, A.; Mehmood, R.; Nadeem, S.; Akbar, N.S.; Motsa, S.S. Effects of single and multi-walled carbon nanotubes on water and engine oil based rotating fluids with internal heating. Adv. Powder Technol. 2017, 28, 1991–2002. [Google Scholar]
- Sreedevi, P.; Reddy, P.S.; Chamkha, A.J. Magneto-hydrodynamics heat and mass transfer analysis of single and multi-wall carbon nanotubes over vertical cone with convective boundary condition. Int. J. Mech. Sci. 2018, 135, 646–655. [Google Scholar] [CrossRef]
- Jyothi, K.; Reddy, P.S.; Reddy, M.S. Influence of magnetic field and thermal radiation on convective flow of SWCNTs-water and MWCNTs-water nanofluid between rotating stretchable disks with convective boundary conditions. Powder Technol. 2018, 331, 326–337. [Google Scholar] [CrossRef]
- Rahmati, A.; Reiszadeh, M. An experimental study on the effects of the use of multi-walled carbon nanotubes in ethylene glycol/water-based fluid with indirect heaters in gas pressure reducing stations. Appl. Therm. Eng. 2018, 134, 107–117. [Google Scholar] [CrossRef]
- Muhammad, T.; Lu, D.-C.; Mahanthesh, B.; Eid, M.R.; Ramzan, M.; Dar, A. Significance of Darcy-Forchheimer Porous Medium in Nanofluid Through Carbon Nanotubes. Commun. Theor. Phys. 2018, 70, 361. [Google Scholar] [CrossRef]
- Gau, H.; Herminghaus, S.; Lenz, P.; Lipowsky, R. Liquid morphologies on structured surfaces: From microchannels to mi-crochips. Science 1999, 283, 46–49. [Google Scholar] [PubMed] [Green Version]
- Binda, M.; Natali, D.; Iacchetti, A.; Sampietro, M. Integration of an organic photo-detector onto a plastic optical fiber by means of spray coating technique. Adv. Mater. 2013, 25, 4335–4339. [Google Scholar]
- Kundan, A.; Nguyen, T.T.T.; Plawsky, J.L.; Wayner, J.P.C.; Chao, D.F.; Sicker, R.J. Condensation on Highly Superheated Surfaces: Unstable Thin Films in a Wickless Heat Pipe. Phys. Rev. Lett. 2017, 118, 094501. [Google Scholar] [CrossRef] [Green Version]
- Frenkel, A.L. Nonlinear Theory of Strongly Undulating Thin Films Flowing Down Vertical Cylinders. Eur. Lett. 1992, 18, 583–588. [Google Scholar] [CrossRef]
- Chang, H.-C.; Demekhin, E.A. Mechanism for drop formation on a coated vertical fibre. J. Fluid Mech. 1999, 380, 233–255. [Google Scholar] [CrossRef]
- Kliakhandler, I.L.; Davis, S.H.; Bankoff, S.G. Viscous beads on vertical fibre. J. Fluid Mech. 2001, 429, 381–390. [Google Scholar] [CrossRef]
- Duprat, C.; Giorgiutti-Dauphiné, F.; Tseluiko, D.; Saprykin, S.; Kalliadasis, S. Liquid film coating a fiber as a model system for the formation of bound states in active dispersive-dissipative noninear media. Phys. Rev. Lett. 2009, 103, 234501. [Google Scholar]
- Ding, Z.; Wong, T.N. Three-dimensional dynamics of thin liquid films on vertical cylinders with Marangoni effect. Phys. Fluids 2017, 29, 011701. [Google Scholar] [CrossRef]
- Alshomrani, A.S.; Gul, T. A convective study of Al2O3-H2O and Cu-H2Onano-liquid films sprayed over a stretching cyl-inder with viscous dissipation. Eur. Phys. J. Plus 2017, 132, 1–16. [Google Scholar]
- AlSagri, A.S.; Nasir, S.; Gul, T.; Islam, S.; Nisar, K.; Shah, Z.; Khan, I. MHD Thin Film Flow and Thermal Analysis of Blood with CNTs Nanofluid. Coatings 2019, 9, 175. [Google Scholar] [CrossRef] [Green Version]
- Chao, Y.; Ding, Z.; Liu, R. Dynamics of thin liquid films flowing down the non-isothermal cylinder with wall slippage. Chem. Eng. Sci. 2018, 175, 354–364. [Google Scholar]
- Liao, S.-J. A kind of approximate solution technique which does not depend upon small parameters—II. An application in fluid mechanics. Int. J. Non-Linear Mech. 1997, 32, 815–822. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S.J. Homotopy Analysis Method in Non-Linear Differential Equations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gul, T.; Ferdous, K. The experimental study to examine the stable dispersion of the graphene nanoparticles and to look at the GO–H2O nanofluid flow between two rotating disks. Appl. Nanosci. 2018, 8, 1711–1728. [Google Scholar]
- Gul, T.; Nasir, S.; Islam, S.; Shah, Z.; Khan, M.A. Effective Prandtl Number Model Influences on the γAl2O3–AH2O and γAl2O3–C2H6O2 Nanofluids Spray Along a Stretching Cylinder. Arab. J. Sci. Eng. 2018, 44, 1–16. [Google Scholar]
- Gohar, T.; Gul, W.; Khan, M.; Shuaib, M.; Khan, M.; Bonyah, E. MWCNTs/SWCNTs Nanofluid Thin Film Flow over a Non-linear Extending Disc: OHAM Solution. J. Therm. Sci. 2019, 28, 115–122. [Google Scholar]
- Gul, T.; Haleem, I.; Ullah, I.; Khan, M.A.; Bonyah, E.; Khan, I.; Shuaib, M. The study of the entropy generation in a thin film flow with variable fluid properties past over a stretching sheet. Adv. Mech. Eng. 2018, 10, 1687814018789522. [Google Scholar] [CrossRef] [Green Version]
- Khan, W.; Idress, M.; Gul, T.; Khan, A.M.; Bonyah, E. Three non-Newtonian fluids flow considering thin film over an un-steady stretching surface with variable fluid properties. Adv. Mech. Eng. 2018, 10, 1687814018807361. [Google Scholar]



| 5 | ||
| 10 | ||
| 15 | ||
| 20 | ||
| 25 |
| 5 | ||
| 10 | ||
| 15 | ||
| 20 | ||
| 25 |
| Numerical | OHAM | ||
|---|---|---|---|
| 1 | 1.00…. | 1.00…. | 0.0…. |
| 2 | 1.72…. | 1.70…. | …. |
| 3 | 1.71…. | 1.69…. | …. |
| 4 | 1.96…. | 1.94…. | …. |
| 5 | 0.87…. | 0.83…. | …. |
| 6 | 0.23…. | 0.21…. | …. |
| 7 | 0.29…. | 0.27…. | …. |
| 8 | 0.39…. | 0.38…. | …. |
| 9 | 0.42…. | 0.37…. | …. |
| 10 | 0.92…. | 0.90…. | …. |
| Numerical | OHAM | ||
|---|---|---|---|
| 1 | 1.00…. | 1.00…. | 0.0…. |
| 2 | 1.31…. | 1.29…. | …. |
| 3 | 1.12…. | 1.10…. | …. |
| 4 | 1.70…. | 1.65…. | …. |
| 5 | 1.44…. | 1.41…. | …. |
| 6 | 1.34…. | 1.30…. | …. |
| 7 | 1.95…. | 1.90…. | …. |
| 8 | 1.90…. | 1.80…. | …. |
| 9 | 1.54…. | 1.50…. | …. |
| 10 | 1.35…. | 1.30…. | …. |
| Physical Properties | Thermal Conduct | |||
|---|---|---|---|---|
| Solid particles | SWCNTs | 6600 | 2600 | 2600 |
| MWCNTs | 3000 | 1600 | 1600 | |
| 0.0 | 0.01 | 0.02 | 0.03 | 0.04 | |
|---|---|---|---|---|---|
| 0.145 | 0.147 | 0.204 | 0.235 | 0.266 | |
| 0.145 | 0.172 | 0.2 | 0.228 | 0.2257 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, A.; Saeed, A.; Salleh, Z.; Jan, R.; Kumam, P. Analytical Investigation of the Time-Dependent Stagnation Point Flow of a CNT Nanofluid over a Stretching Surface. Nanomaterials 2022, 12, 1108. https://doi.org/10.3390/nano12071108
Rehman A, Saeed A, Salleh Z, Jan R, Kumam P. Analytical Investigation of the Time-Dependent Stagnation Point Flow of a CNT Nanofluid over a Stretching Surface. Nanomaterials. 2022; 12(7):1108. https://doi.org/10.3390/nano12071108
Chicago/Turabian StyleRehman, Ali, Anwar Saeed, Zabidin Salleh, Rashid Jan, and Poom Kumam. 2022. "Analytical Investigation of the Time-Dependent Stagnation Point Flow of a CNT Nanofluid over a Stretching Surface" Nanomaterials 12, no. 7: 1108. https://doi.org/10.3390/nano12071108
APA StyleRehman, A., Saeed, A., Salleh, Z., Jan, R., & Kumam, P. (2022). Analytical Investigation of the Time-Dependent Stagnation Point Flow of a CNT Nanofluid over a Stretching Surface. Nanomaterials, 12(7), 1108. https://doi.org/10.3390/nano12071108







