Heat Transfer Analysis of Nanostructured Material Flow over an Exponentially Stretching Surface: A Comparative Study
Abstract
:1. Introduction
2. Statement of Problem
3. Quantities of Physical Interest
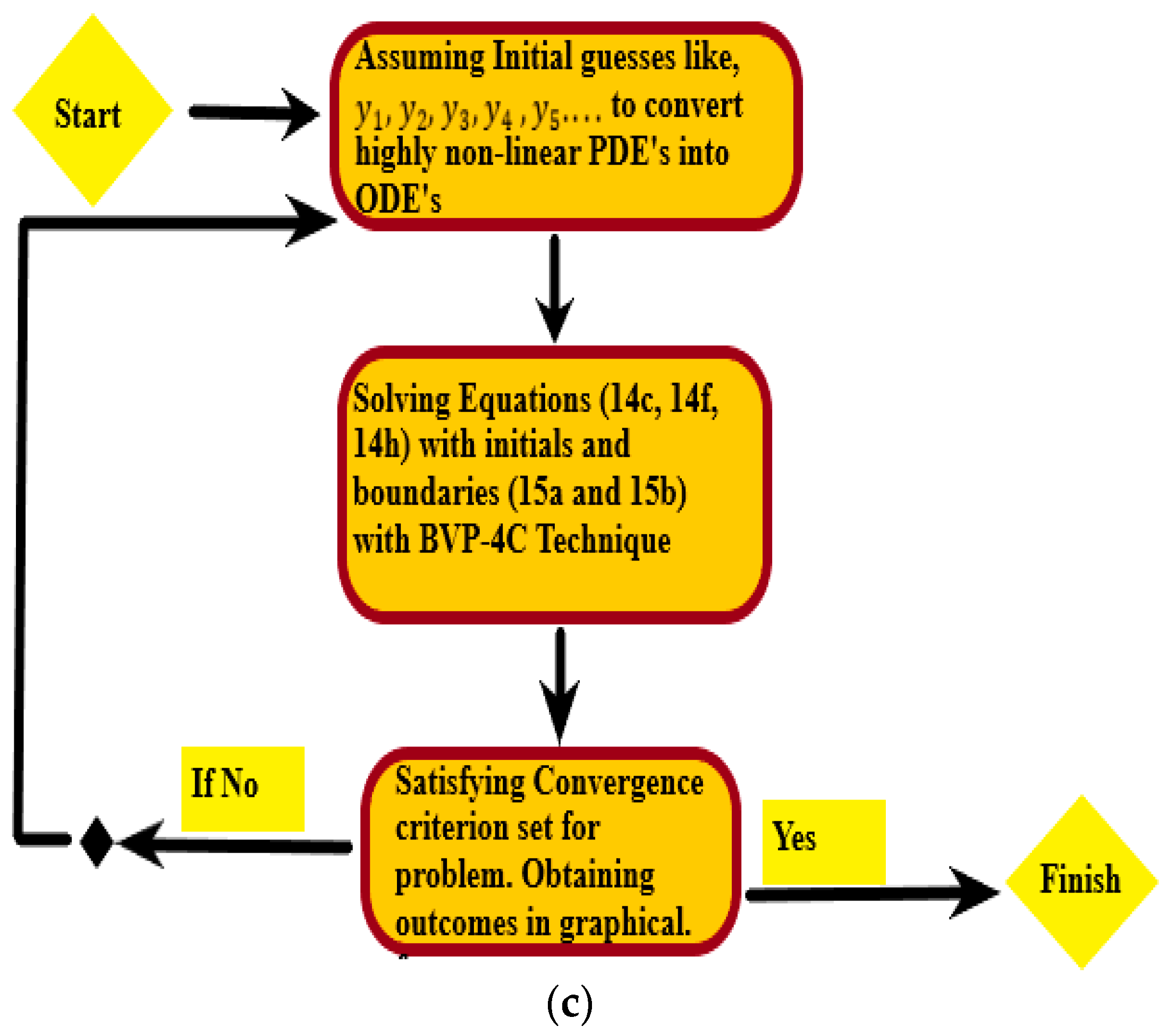
4. Numerical Procedure
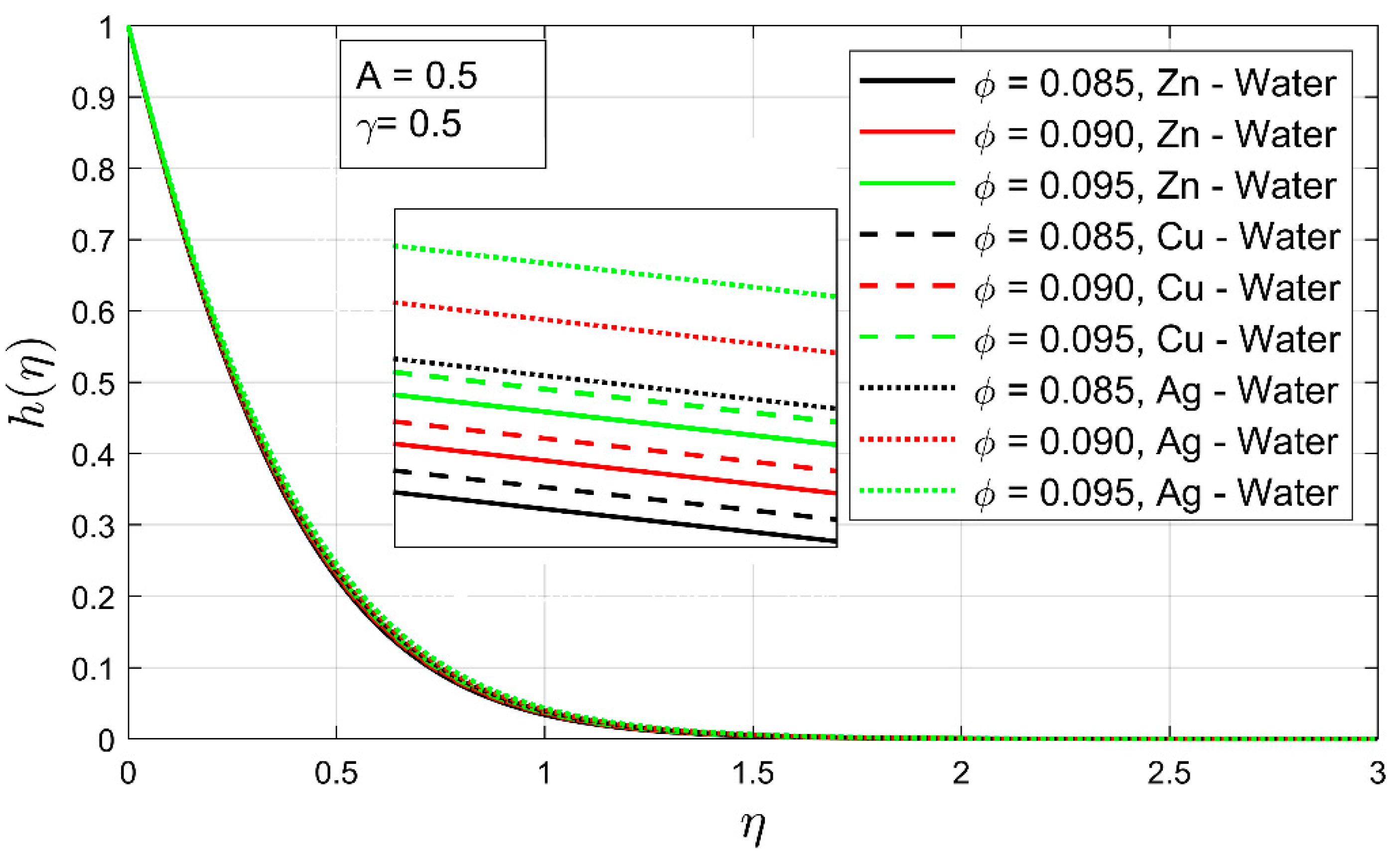
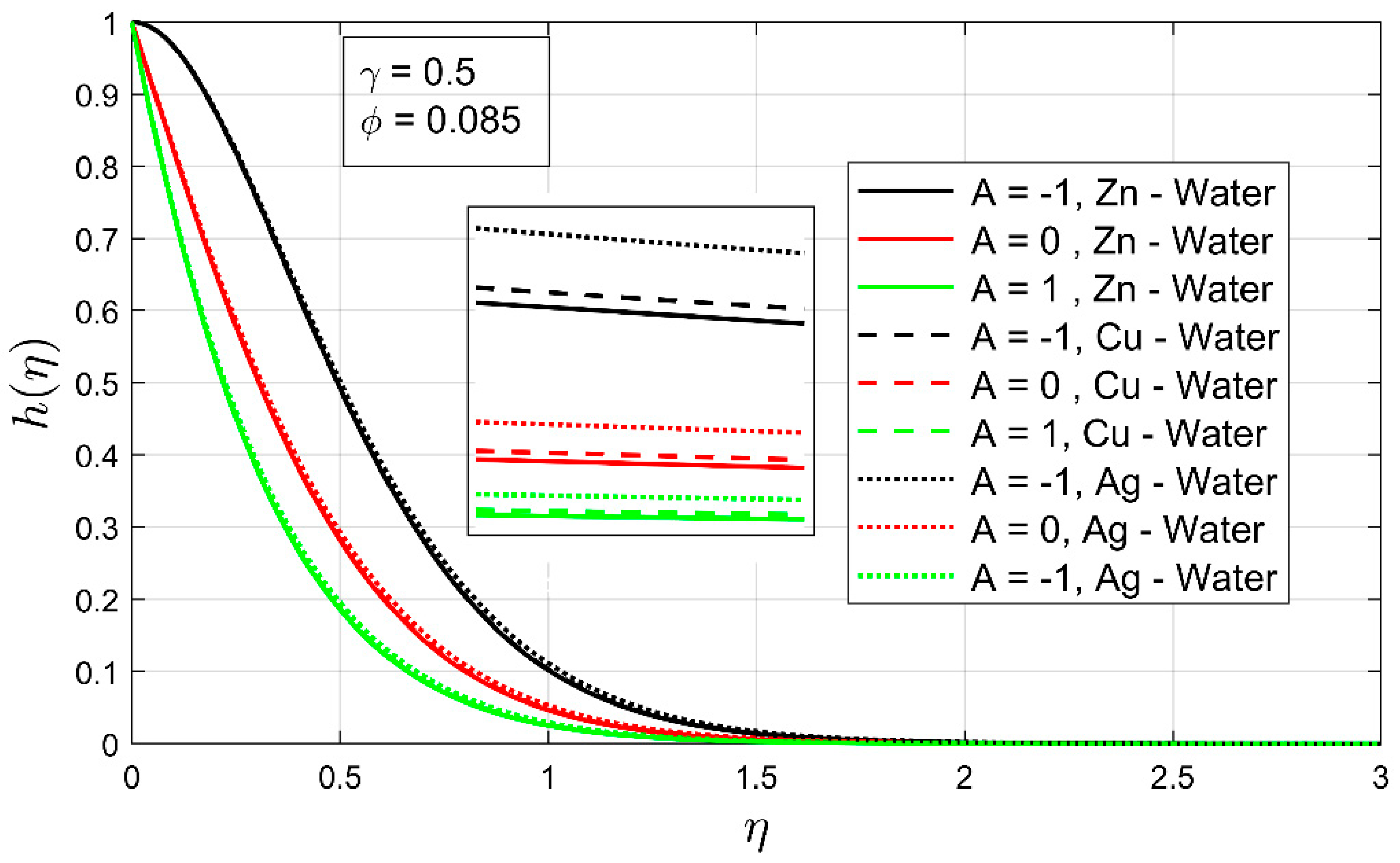
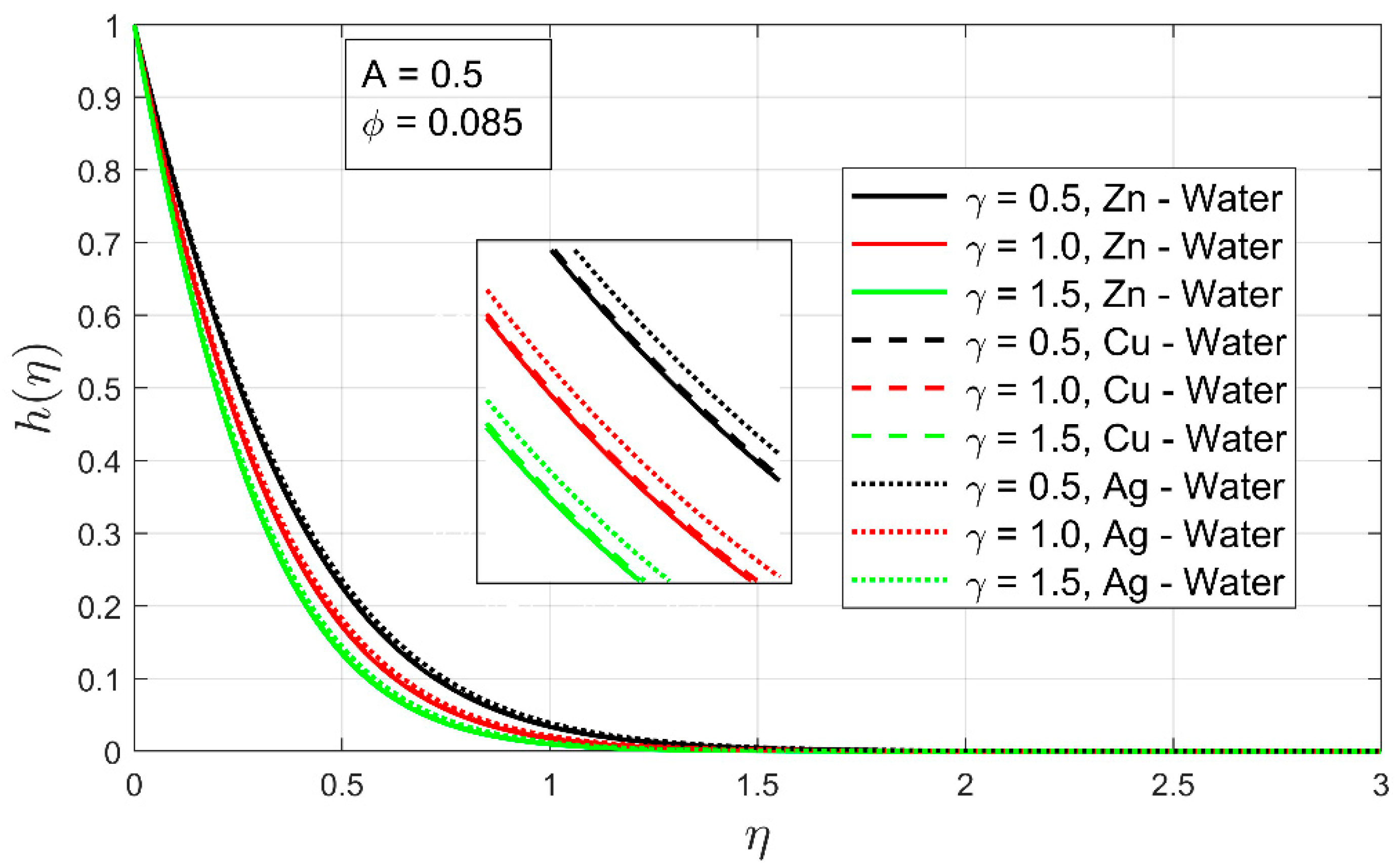
5. Results and Discussion
6. Conclusions
- (a)
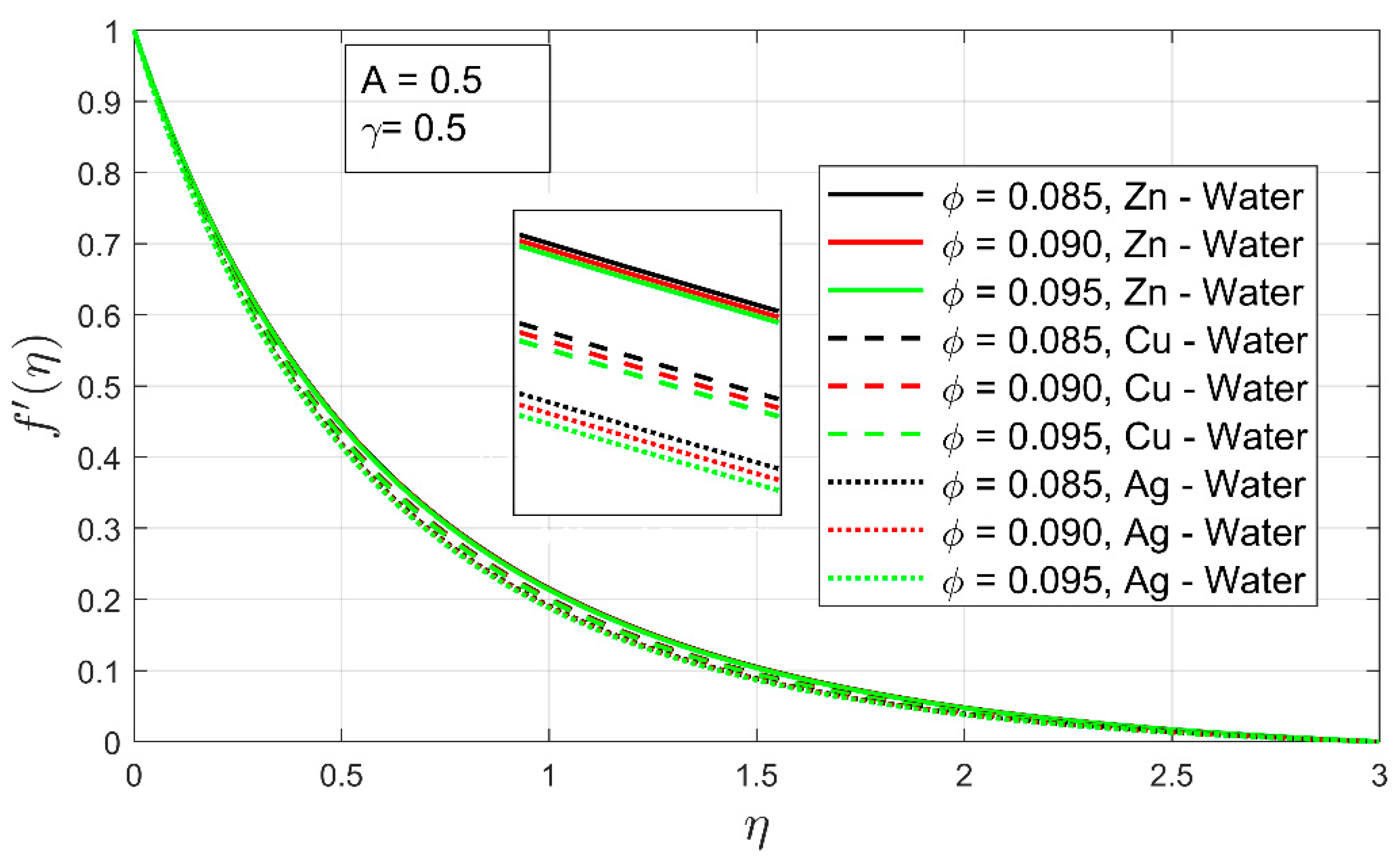
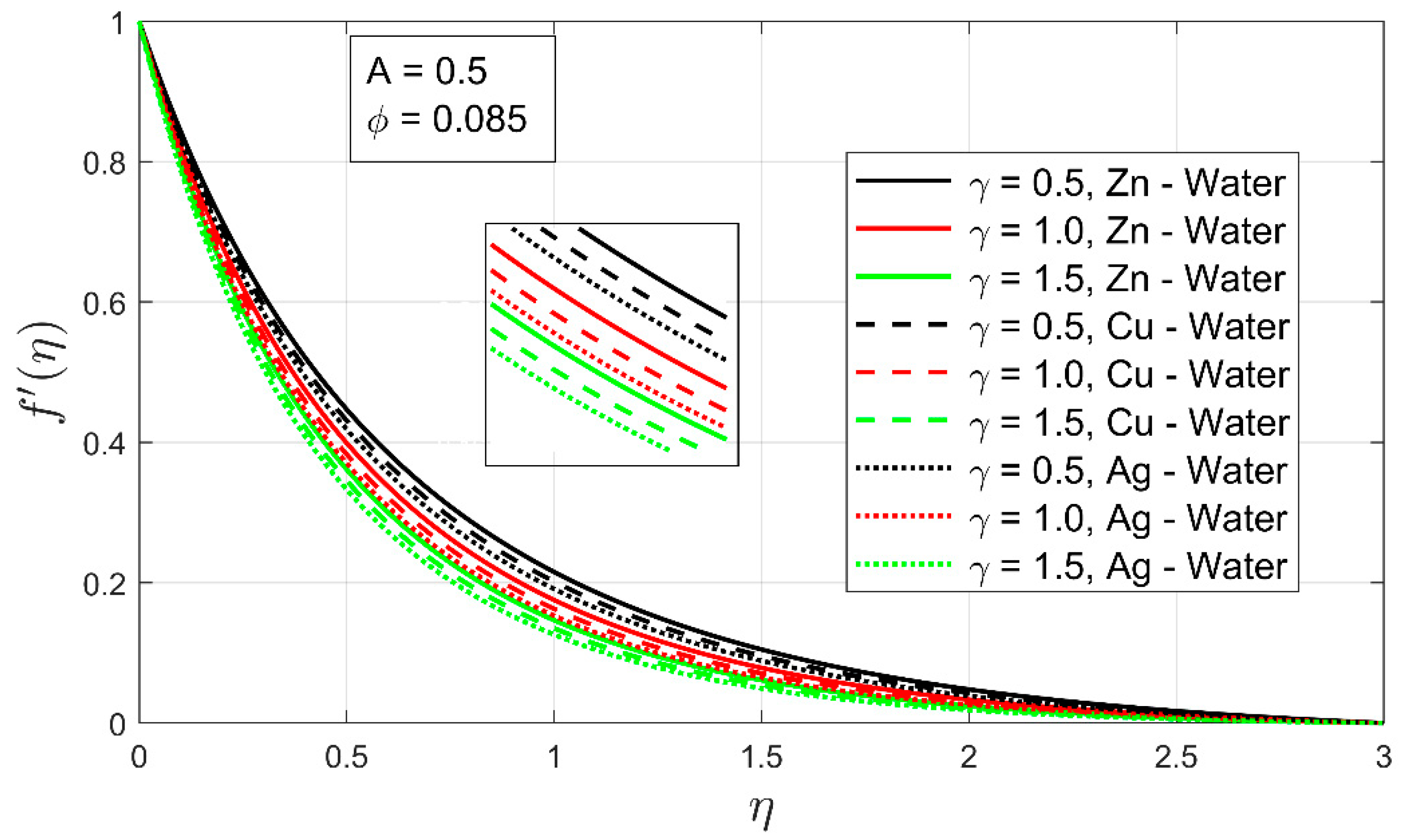
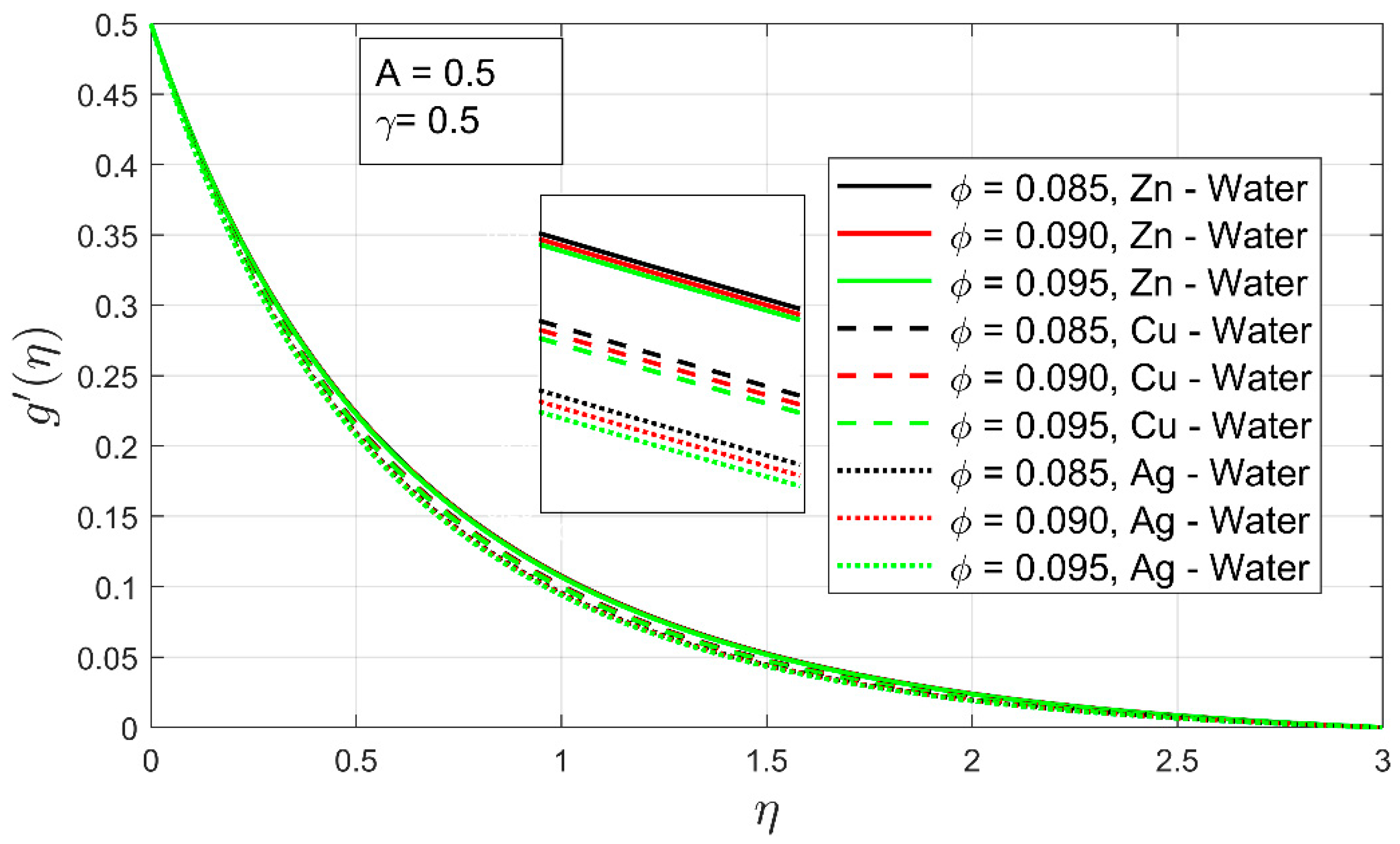
- Boundary layer thickness has decreased more rapidly in the secondary velocity profile as compared to the primary velocity profile
- (b)
- An increment in temperature exponent results in the enhancement of heat transfer for all examined nanofluid and is highly noted for nanofluid.
- (c)
- Reduced skin friction coefficients , are obtained in y-direction compared to x-direction under different increasing study parameters.
- (d)
- Skins frictions , and heat transfer coefficients have increased under the increasing influence of the stretching ratio.
- (e)
- The porosity decreases the skin friction and increases the fluid flow.
- (f)
- Out of all examined nanofluids, namely, -water, -water, and -water, reduced skin frictions and high heat transfer rates were observed for -water under the different parametric influences.
7. Recommendations
8. Practical Significance
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Stretching rates of surface | |
| 3D | Three dimensional |
| Skin friction alongside x-axis and y-axis | |
| Specific heat capacity | |
| Volumetric heat capacity | |
| Thermal conductivity | |
| Dynamic viscosity of nanofluid | |
| Reference length | |
| Surface stretching ratio parameter | |
| Wall shear stress | |
| Nusselt number | |
| Pr | Prandtl number |
| Re | Reynolds number |
| T | Temperature of fluid |
| MHD | Magneto hydrodynamic |
| Temperature at wall | |
| The temperature outside the surface | |
| Velocity constituents of x-, y-, and z-axis, respectively | |
| Thermal diffusivity of nanofluid | |
| vnf | Kinematics viscosity of nanofluid |
| Dimensionless variable | |
| Density of nanofluid | |
| Wall temperature flux | |
| volume concentration of nanoparticles | |
| Subscripts for fluid, solid nanoparticles, and nanofluid, respectively | |
| Temperature exponent |
References
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: II. The boundary layer on a continuous flat surface. AiChE J. 1961, 7, 221–225. [Google Scholar]
- Crane, L.J. Flow past a stretching plate. Zeitschrift für Angewandte Mathematik und Physik ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Hussain, A.; Elkotb, M.A.; Arshad, M.; Rehman, A.; Sooppy Nisar, K.; Hassan, A.; Saleel, C.A. Computational Investigation of the Combined Impact of Nonlinear Radiation and Magnetic Field on Three-Dimensional Rotational Nanofluid Flow across a Stretchy Surface. Processes 2021, 9, 1453. [Google Scholar] [CrossRef]
- Nandeppanavar, M.M.; Vaishali, S.; Kemparaju, M.C.; Raveendra, N. Theoretical analysis of thermal characteristics of casson nano fluid flow past an exponential stretching sheet in Darcy porous media. Case Stud. Therm. Eng. 2020, 21, 100717. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Hassan, A.; Haider, Q.; Ibrahim, A.H.; Alqurashi, M.S.; Abdussattar, A. Thermophoresis and Brownian Effect for Chemically Reacting Magneto-Hydrodynamic Nanofluid Flow across an Exponentially Stretching Sheet. Energies 2022, 15, 143. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Rehman, A.; Hassan, A.; Elagan, S.K.; Ahmad, H.; Ishan, A. Three-Dimensional Water-Based Magneto-Hydrodynamic Rotating Nanofluid Flow over a Linear Extending Sheet and Heat Transport Analysis: A Numerical Approach. Energies 2021, 14, 5133. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Sheikholeslami, M.; Sheykholeslami, F.B.; Khoshhal, S.; Mola-Abasia, H.; Ganji, D.D.; Rokni, H.B. Effect of magnetic field on Cu–water nanofluid heat transfer using GMDH-type neural network. Neural Comput. Appl. 2014, 25, 171–178. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Sheikholeslami, M.; Alsaedi, A. Three-dimensional flow of nanofluid induced by an exponentially stretching sheet: An application to solar energy. PLoS ONE 2015, 10, e0116603. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A. Model for flow of Casson nanofluid past a non-linearly stretching sheet considering magnetic field effects. AIP Adv. 2015, 5, 077148. [Google Scholar] [CrossRef] [Green Version]
- Rashidi, M.M.; Freidoonimehr, N.; Hosseini, A.; Bég, O.A.; Hung, T.K. Homotopy simulation of nanofluid dynamics from a non-linearly stretching isothermal permeable sheet with transpiration. Meccanica 2014, 49, 469–482. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Alsulami, R.A.; Rawa, M.J.; Alazwari, M.A.; Goodarzi, M.; Safaei, M.R. A Significant Solar Energy Note on Powell-Eyring Nanofluid with Thermal Jump Conditions: Implementing Cattaneo-Christov Heat Flux Model. Mathematics 2021, 9, 2669. [Google Scholar] [CrossRef]
- Aouinet, H.; Dhahri, M.; Safaei, M.R.; Sammouda, H.; Anqi, A.E. Turbulent boundary layers and hydrodynamic flow analysis of nanofluids over a plate. J. Cent. South Univ. 2021, 28, 3340–3353. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Alshehri, H.M.; Goodarzi, M. Marangoni-bioconvectional flow of Reiner—Philippoff nanofluid with melting phenomenon and nonuniform heat source/sink in the presence of a swimming microorganisms. Math. Methods Appl. Sci. 2021, 1–19. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Abu-Hamdeh, N.H.; Goodarzi, M. Entropy Optimization of First-Grade Viscoelastic Nanofluid Flow over a Stretching Sheet by Using Classical Keller-Box Scheme. Mathematics 2021, 9, 2563. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical solutions of magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J. Phys. 2013, 87, 1121–1124. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Rehman, A.; Hassan, A.; Elagan, S.K.; Alshehri, N.A. Heat Transmission of Engine-Oil-Based Rotating Nanofluids Flow with Influence of Partial Slip Condition: A Computational Model. Energies 2021, 14, 3859. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Arifin, N.M.; Rosali, H. Effect of suction/injection on stagnation point flow of hybrid nanofluid over an exponentially shrinking sheet with stability analysis. CFD Lett. 2019, 11, 21–33. [Google Scholar]
- Hussain, T.; Shehzad, S.A.; Hayat, T.; Alsaedi, A.; Al-Solamy, F.; Ramzan, M. Radiative hydromagnetic flow of Jeffrey nanofluid by an exponentially stretching sheet. PLoS ONE 2014, 9, e103719. [Google Scholar] [CrossRef]
- Malvandi, A.; Hedayati, F.; Domairry, G. Stagnation point flow of a nanofluid toward an exponentially stretching sheet with nonuniform heat generation/absorption. J. Thermodyn. 2013, 2013, 764827. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Nazar, R.; Pop, I. Flow and heat transfer at a general three-dimensional stagnation point in a nanofluid. Phys. B Condens. Matter 2010, 405, 4914–4918. [Google Scholar] [CrossRef]
- Krishna, C.; ViswanathaReddy, G.; Souayeh, B.; Raju, C.S.K.; Rahimi-Gorji, M.; Raju, S. Thermal convection of MHD Blasius and Sakiadis flow with thermal convective conditions and variable properties. Microsyst. Technol. 2019, 25, 3735–3746. [Google Scholar] [CrossRef]
- Veera Krishna, M. Heat transport on steady MHD flow of copper and alumina nanofluids past a stretching porous surface. Heat Transf. 2020, 49, 1374–1385. [Google Scholar] [CrossRef]
- Gangadhar, K.; Bhargavi, D.N.; Kannan, T.; Venkata Subba Rao, M.; Chamkha, A.J. Transverse MHD flow of Al2O3-Cu/H2O hybrid nanofluid with active radiation: A novel hybrid model. Math. Methods Appl. Sci. 2020, 1–19. [Google Scholar] [CrossRef]
- Prasad, K.V.; Vaidya, H.; Rajashekhar, C.; Khan, S.U.; Manjunatha, G.; Viharika, J.U. Slip flow of MHD Casson fluid in an inclined channel with variable transport properties. Commun. Theor. Phys. 2020, 72, 095004. [Google Scholar] [CrossRef]
- Salahuddin, T.; Khan, M.; Saeed, T.; Ibrahim, M.; Chu, Y.M. Induced MHD impact on exponentially varying viscosity of Williamson fluid flow with variable conductivity and diffusivity. Case Stud. Therm. Eng. 2021, 25, 100895. [Google Scholar] [CrossRef]
- Rehman, A.U.; Riaz, M.B.; Akgül, A.; Saeed, S.T.; Baleanu, D. Heat and mass transport impact on MHD second-grade fluid: A comparative analysis of fractional operators. Heat Transf. 2021, 50, 7042–7064. [Google Scholar] [CrossRef]
- Kumar, D.; Sinha, S.; Sharma, A.; Agrawal, P.; Kumar Dadheech, P. Numerical study of chemical reaction and heat transfer of MHD slip flow with Joule heating and Soret–Dufour effect over an exponentially stretching sheet. Heat Transf. 2022, 51, 1939–1963. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, M.N.; Nadeem, S. Unsteady three dimensional bioconvective flow of Maxwell nanofluid over an exponentially stretching sheet with variable thermal conductivity and chemical reaction. Int. J. Ambient. Energy, 2022; just-accepted. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Mdallal, Q.A.; Ahmad, H.; Sherif, E.S.M.; Rehman, A.; Arshad, M. Comsolic solution of an elliptic cylindrical compressible fluid flow. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Hassan, A.; Hussain, A.; Arshad, M.; Alanazi, M.M.; Zahran, H.Y. Numerical and Thermal Investigation of Magneto-Hydrodynamic Hybrid Nanoparticles (SWCNT-Ag) under Rosseland Radiation: A Prescribed Wall Temperature Case. Nanomaterials 2022, 12, 891. [Google Scholar] [CrossRef] [PubMed]
- Hussain, A.; Hassan, A.; Al Mdallal, Q.; Ahmad, H.; Rehman, A.; Altanji, M.; Arshad, M. Heat transportation enrichment and elliptic cylindrical solution of time-dependent flow. Case Stud. Therm. Eng. 2021, 27, 101248. [Google Scholar]
- Hassan, A.; Hussain, A.; Arshad, M.; Haider, Q.; Althobaiti, A.; Elagan, S.K.; Alqurashi, M.S.; Abdelmohimen, M.A. Heat transport investigation of hybrid nanofluid (Ag-CuO) porous medium flow: Under magnetic field and Rosseland radiation. Ain Shams Engi. J. 2022, 13, 101667. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Al Mdallal, Q.; Ahmad, H.; Rehman, A.; Altanji, M.; Arshad, M. Heat transport investigation of magneto-hydrodynamics (SWCNT-MWCNT) hybrid nanofluid under the thermal radiation regime. Case Stud. Therm. Eng. 2021, 27, 101244. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Arshad, M.; Rehman, A.; Matoog, R.T.; Abdeljawad, T. Numerical simulation and thermal enhancement of multi-based nanofluid over an embrittled cone. Case Stud. Therm. Eng. 2021, 28, 101614. [Google Scholar] [CrossRef]
- Ahmad, F.; Tang, X.W.; Qiu, J.N.; Wróblewski, P.; Ahmad, M.; Jamil, I. Prediction of slope stability using Tree Augmented Naive-Bayes classifier: Modeling and performance evaluation. Math. Biosci. Eng. 2022, 19, 4526–4546. [Google Scholar] [CrossRef]
- Hussain, A.; Arshad, M.; Hassan, A.; Rehman, A.; Ahmad, H.; Baili, J.; Gia, T.N. Heat transport investigation of engine oil based rotating nanomaterial liquid flow in the existence of partial slip effect. Case Stud. Therm. Eng. 2021, 28, 101500. [Google Scholar]
- Eid, M.R. Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. J. Mol. Fluids 2016, 220, 718–725. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Ahmadian, A.; Senu, N.; Ali, L.; Haider, A. Significance of Lorentz and Coriolis forces on dynamics of water based silver tiny particles via finite element simulation. Ain. Shams Eng. J. 2022, 13, 101572. [Google Scholar] [CrossRef]
- Gopal, D.; Jagadha, S.; Sreehari, P.; Kishan, N.; Mahendar, D. A numerical study of viscous dissipation with first order chemical reaction and ohmic effects on MHD nanofluid flow through an exponential stretching sheet. Mater. Today Proc. 2022. In Press, Corrected Proof. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577. [Google Scholar] [CrossRef]
- Liu, I.C.; Wang, H.H.; Peng, Y.F. Flow and heat transfer for three-dimensional flow over an exponentially stretching surface. Chem. Eng. Commun. 2013, 200, 253–268. [Google Scholar] [CrossRef]




[43] | [44] | |||
|---|---|---|---|---|
[44] | Results | Liu et al. [44] | [44] | ||||
|---|---|---|---|---|---|---|---|
| 0.6236 | |||||||
| 07 | 5.94689 | ||||||
| −0.535008 | |||||||
| 1 | −0.610684 | ||||||
| −4.56615 (Ag) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshad, M.; Hussain, A.; Hassan, A.; Khan, I.; Badran, M.; Mehrez, S.; Elfasakhany, A.; Abdeljawad, T.; Galal, A.M. Heat Transfer Analysis of Nanostructured Material Flow over an Exponentially Stretching Surface: A Comparative Study. Nanomaterials 2022, 12, 1204. https://doi.org/10.3390/nano12071204
Arshad M, Hussain A, Hassan A, Khan I, Badran M, Mehrez S, Elfasakhany A, Abdeljawad T, Galal AM. Heat Transfer Analysis of Nanostructured Material Flow over an Exponentially Stretching Surface: A Comparative Study. Nanomaterials. 2022; 12(7):1204. https://doi.org/10.3390/nano12071204
Chicago/Turabian StyleArshad, Mubashar, Azad Hussain, Ali Hassan, Ilyas Khan, Mohamed Badran, Sadok Mehrez, Ashraf Elfasakhany, Thabet Abdeljawad, and Ahmed M. Galal. 2022. "Heat Transfer Analysis of Nanostructured Material Flow over an Exponentially Stretching Surface: A Comparative Study" Nanomaterials 12, no. 7: 1204. https://doi.org/10.3390/nano12071204
APA StyleArshad, M., Hussain, A., Hassan, A., Khan, I., Badran, M., Mehrez, S., Elfasakhany, A., Abdeljawad, T., & Galal, A. M. (2022). Heat Transfer Analysis of Nanostructured Material Flow over an Exponentially Stretching Surface: A Comparative Study. Nanomaterials, 12(7), 1204. https://doi.org/10.3390/nano12071204









