Constrained DFT for Molecular Junctions
Abstract
:1. Introduction
2. Methods
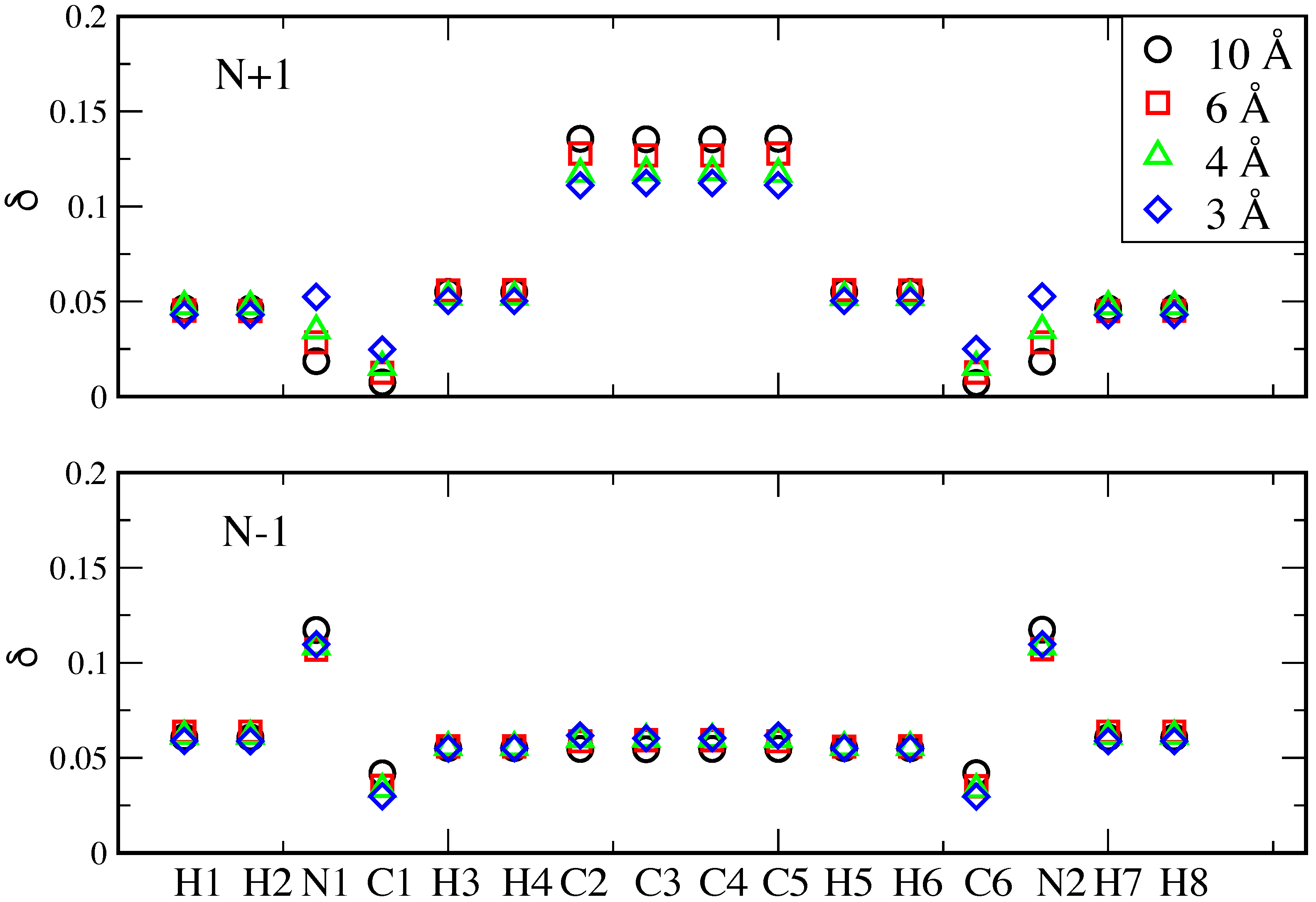
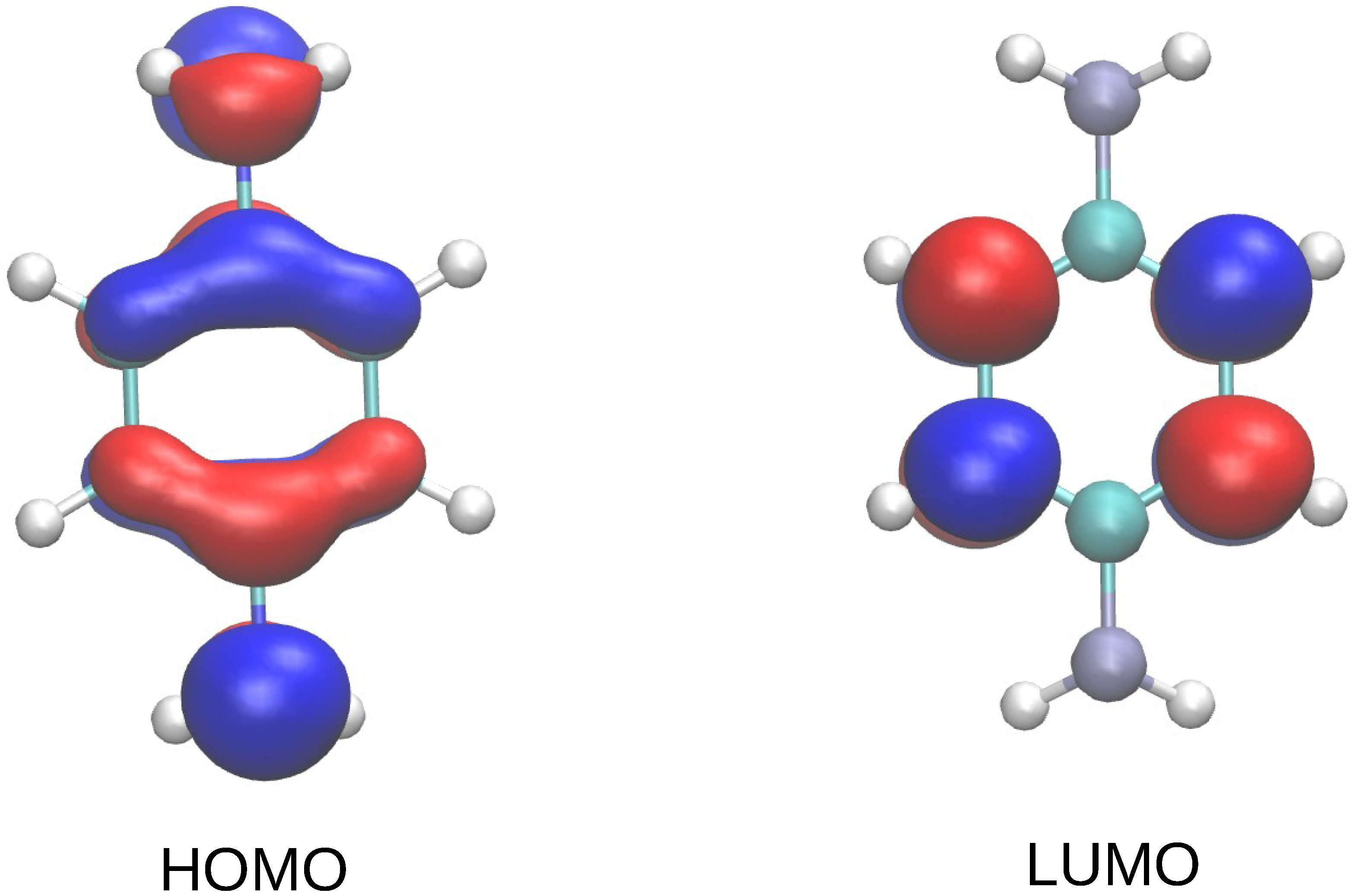
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BDA | benzene diamine |
| cDFT | constrained density functional theory |
| HOMO | highest occupied molecular orbital |
| LUMO | lowest occupied molecular orbital |
References
- Blumberger, J.; McKenna, K.P. Constrained density functional theory applied to electron tunnelling between defects in MgO. Phys. Chem. Chem. Phys. 2013, 15, 2184–2196. [Google Scholar] [CrossRef] [PubMed]
- Difley, S.; Beljonne, D.; Van Voorhis, T. On the singlet-triplet splitting of geminate electron-hole pairs in organic semiconductors. J. Am. Chem. Soc. 2008, 130, 3420–3427. [Google Scholar] [CrossRef] [PubMed]
- Cedillo, A.; Neck, D.V.; Bultinck, P. Self-consistent methods constrained to a fixed number of particles in a given fragment and its relation to the electronegativity equalization method. In Theoretical Chemistry in Belgium; Springer: Berlin/Heidelberg, Germany, 2014; pp. 27–33. [Google Scholar]
- Kaduk, B.; Kowalczyk, T.; Van Voorhis, T. Constrained Density Functional Theory. Chem. Rev. 2012, 112, 321–370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, G.; Rosta, E.; Warshel, A. Using the constrained DFT approach in generating diabatic surfaces and off diagonal empirical valence bond terms for modeling reactions in condensed phases. J. Phys. Chem. B 2006, 110, 19570–19574. [Google Scholar] [CrossRef]
- Behler, J.; Delley, B.; Reuter, K.; Scheffler, M. Nonadiabatic potential-energy surfaces by constrained density-functional theory. Phys. Rev. B 2007, 75, 115409. [Google Scholar] [CrossRef] [Green Version]
- Cioslowski, J.; Stefanov, B.B. Electron flow and electronegativity equalization in the process of bond formation. J. Chem. Phys. 1993, 99, 5151–5162. [Google Scholar] [CrossRef]
- Dederichs, P.H.; Blügel, S.; Zeller, R.; Akai, H. Ground States of Constrained Systems: Application to Cerium Impurities. Phys. Rev. Lett. 1984, 53, 2512–2515. [Google Scholar] [CrossRef]
- Shao, Y.; Molnar, L.F.; Jung, Y.; Kussmann, J.; Ochsenfeld, C.; Brown, S.T.; Gilbert, A.T.; Slipchenko, L.V.; Levchenko, S.V.; O’Neill, D.P.; et al. Advances in methods and algorithms in a modern quantum chemistry program package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. [Google Scholar] [CrossRef]
- Sena, A.M.P.; Miyazaki, T.; Bowler, D.R. Linear Scaling Constrained Density Functional Theory in CONQUEST. J. Chem. Theory Comput. 2011, 7, 884–889. [Google Scholar] [CrossRef]
- Oberhofer, H.; Blumberger, J. Charge constrained density functional molecular dynamics for simulation of condensed phase electron transfer reactions. J. Chem. Phys. 2009, 131, 064101. [Google Scholar] [CrossRef] [Green Version]
- O’Regan, D.D.; Teobaldi, G. Optimization of constrained density functional theory. Phys. Rev. B 2016, 94, 035159. [Google Scholar] [CrossRef] [Green Version]
- Brooke, C.; Vezzoli, A.; Higgins, S.J.; Zotti, L.A.; Palacios, J.J.; Nichols, R.J. Resonant Transport and Electrostatic Effects in Single-Molecule Electrical Junctions. Phys. Rev. B 2015, 91, 195438. [Google Scholar] [CrossRef] [Green Version]
- Palacios, J.J.; Jacob, D.; Perez-Jimenez, A.J.; Fabian, E.S.; Louis, E.; Verges, J.A.; Soriano, M.; Zotti, L.A.; Dednam, W. Available online: https://www.simuneatomistics.com/; https://github.com/juanjosepalacios/ANT.Gaussian (accessed on 1 May 2021).
- Jacob, D.; Palacios, J.J. Critical comparison of electrode models in density functional theory based quantum transport calculations. J. Chem. Phys. 2011, 134, 044118. [Google Scholar] [CrossRef] [Green Version]
- Palacios, J.J.; Pérez-Jiménez, A.J.; Louis, E.; Vergés, J.A. Fullerene-based molecular nanobridges: A first-principles study. Phys. Rev. B 2001, 64, 115411. [Google Scholar] [CrossRef] [Green Version]
- Palacios, J.J.; Pérez-Jiménez, A.J.; Louis, E.; SanFabián, E.; Vergés, J.A. First-principles approach to electrical transport in atomic-scale nanostructures. Phys. Rev. B 2002, 66, 035322. [Google Scholar] [CrossRef] [Green Version]
- Palacios, J.J.; Pérez-Jiménez, A.J.; Louis, E.; Vergés, J.A. Electronic transport through C60 molecules. Nanotechnology 2001, 12, 160. [Google Scholar] [CrossRef]
- Souza, A.M.; Rungger, I.; Pemmaraju, C.D.; Schwingenschloegl, U.; Sanvito, S. Constrained-DFT method for accurate energy-level alignment of metal/molecule interfaces. Phys. Rev. B 2013, 88, 165112. [Google Scholar] [CrossRef] [Green Version]
- Koch, N. Organic electronic devices and their functional interfaces. ChemPhysChem 2007, 8, 1438–1455. [Google Scholar] [CrossRef]
- Repp, J.; Meyer, G.; Stojković, S.M.; Gourdon, A.; Joachim, C. Molecules on Insulating Films: Scanning-Tunneling Microscopy Imaging of Individual Molecular Orbitals. Phys. Rev. Lett. 2005, 94, 026803. [Google Scholar] [CrossRef] [Green Version]
- Greiner, M.T.; Helander, M.G.; Tang, W.M.; Wang, Z.B.; Qiu, J.; Lu, Z.H. Universal energy-level alignment of molecules on metal oxides. Nat. Mater. 2011, 11, 76–81. [Google Scholar] [CrossRef]
- Lu, X.; Grobis, M.; Khoo, K.H.; Louie, S.G.; Crommie, M.F. Charge transfer and screening in individual C60 molecules on metal substrates: A scanning tunneling spectroscopy and theoretical study. Phys. Rev. B 2004, 70, 115418. [Google Scholar] [CrossRef]
- Perrin, M.L.; Verzijl, C.J.; Martin, C.A.; Shaikh, A.J.; Eelkema, R.; van Esch, J.H.; van Ruitenbeek, J.M.; Thijssen, J.M.; van der Zant, H.S.; Dulić, D. Large tunable image-charge effects in single-molecule junctions. Nat. Nanotechnol. 2013, 8, 282–287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thygesen, K.S.; Rubio, A. Renormalization of Molecular Quasiparticle Levels at metal–molecule Interfaces: Trends across Binding Regimes. Phys. Rev. Lett. 2009, 102, 046802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Myöhänen, P.; Tuovinen, R.; Korhonen, T.; Stefanucci, G.; van Leeuwen, R. Image charge dynamics in time-dependent quantum transport. Phys. Rev. B 2012, 85, 075105. [Google Scholar] [CrossRef] [Green Version]
- Tamblyn, I.; Darancet, P.; Quek, S.Y.; Bonev, S.A.; Neaton, J.B. Electronic energy level alignment at metal–molecule interfaces with a GW approach. Phys. Rev. B 2011, 84, 201402. [Google Scholar] [CrossRef] [Green Version]
- Durrant, T.R.; Murphy, S.T.; Watkins, M.B.; Shluger, A.L. Relation between image charge and potential alignment corrections for charged defects in periodic boundary conditions. J. Chem. Phys. 2018, 149, 024103. [Google Scholar] [CrossRef] [Green Version]
- Quek, S.Y.; Choi, H.J.; Louie, S.G.; Neaton, J.B. Length Dependence of Conductance in Aromatic Single-Molecule Junctions. Nano Lett. 2009, 9, 3949–3953. [Google Scholar] [CrossRef]
- Darancet, P.; Widawsky, J.R.; Choi, H.J.; Venkataraman, L.; Neaton, J.B. Quantitative Current–Voltage Characteristics in Molecular Junctions from First Principles. Nano Lett. 2012, 12, 6250–6254. [Google Scholar] [CrossRef] [Green Version]
- Brisendine, J.M.; Refaely-Abramson, S.; Liu, Z.F.; Cui, J.; Ng, F.; Neaton, J.B.; Koder, R.L.; Venkataraman, L. Probing Charge Transport through Peptide Bonds. J. Phys. Chem. Lett. 2018, 9, 763–767. [Google Scholar] [CrossRef]
- Markussen, T.; Jin, C.; Thygesen, K.S. Quantitatively accurate calculations of conductance and thermopower of molecular junctions. Phys. Status Solidi (B) 2013, 250, 2394–2402. [Google Scholar] [CrossRef] [Green Version]
- Neaton, J.B.; Hybertsen, M.S.; Louie, S.G. Renormalization of Molecular Electronic Levels at metal–molecule Interfaces. Phys. Rev. Lett. 2006, 97, 216405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaasbjerg, K.; Flensberg, K. Strong Polarization-Induced Reduction of Addition Energies in Single-Molecule Nanojunctions. Nano Lett. 2008, 8, 3809–3814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frish, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. GAUSSIAN 03, Revision B.01; Gaussian, Inc.: Pittsburg, PA, USA, 2003. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wadt, W.R.; Hay, P.J. Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi. J. Chem. Phys. 1985, 82, 284–298. [Google Scholar] [CrossRef]
- Ross, R.B.; Powers, J.M.; Atashroo, T.; Ermler, W.C.; LaJohn, L.A.; Christiansen, P.A. Ab initio relativistic effective potentials with spin–orbit operators. IV. Cs through Rn. J. Chem. Phys. 1990, 93, 6654–6670. [Google Scholar] [CrossRef]
- Dell’Angela, M.; Kladnik, G.; Cossaro, A.; Verdini, A.; Kamenetska, M.; Tamblyn, I.; Quek, S.Y.; Neaton, J.B.; Cvetko, D.; Morgante, A.; et al. Relating Energy Level Alignment and Amine-Linked Single Molecule Junction Conductance. Nano Lett. 2010, 10, 2470–2474. [Google Scholar] [CrossRef] [Green Version]
- Biller, A.; Tamblyn, I.; Neaton, J.B.; Kronik, L. Electronic level alignment at a metal–molecule interface from a short-range hybrid functional. J. Chem. Phys. 2011, 135, 164706. [Google Scholar] [CrossRef]
- Zotti, L.A.; Bürkle, M.; Pauly, F.; Lee, W.; Kim, K.; Jeong, W.; Asai, Y.; Reddy, P.; Cuevas, J.C. Heat dissipation and its relation to thermopower in single-molecule junctions. New J. Phys. 2014, 16, 015004. [Google Scholar] [CrossRef]
- Quek, S.Y.; Venkataraman, L.; Choi, H.J.; Louie, S.G.; Hybertsen, M.S.; Neaton, J.B. Amine–Gold Linked Single-Molecule Circuits: Experiment and Theory. Nano Lett. 2007, 7, 3477–3482. [Google Scholar] [CrossRef] [Green Version]
- Soriano, M.; Palacios, J.J. Theory of projections with nonorthogonal basis sets: Partitioning techniques and effective Hamiltonians. Phys. Rev. B 2014, 90, 075128. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Li, S.L.; Truhlar, D.G. Modeling the Partial Atomic Charges in Inorganometallic Molecules and Solids and Charge Redistribution in Lithium-Ion Cathodes. J. Chem. Theory Comput. 2014, 10, 5640–5650. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zotti, L.A.; Dednam, W.; Lombardi, E.B.; Palacios, J.J. Constrained DFT for Molecular Junctions. Nanomaterials 2022, 12, 1234. https://doi.org/10.3390/nano12071234
Zotti LA, Dednam W, Lombardi EB, Palacios JJ. Constrained DFT for Molecular Junctions. Nanomaterials. 2022; 12(7):1234. https://doi.org/10.3390/nano12071234
Chicago/Turabian StyleZotti, Linda Angela, Wynand Dednam, Enrico B. Lombardi, and Juan Jose Palacios. 2022. "Constrained DFT for Molecular Junctions" Nanomaterials 12, no. 7: 1234. https://doi.org/10.3390/nano12071234
APA StyleZotti, L. A., Dednam, W., Lombardi, E. B., & Palacios, J. J. (2022). Constrained DFT for Molecular Junctions. Nanomaterials, 12(7), 1234. https://doi.org/10.3390/nano12071234






