Insights on Shear Transfer Efficiency in “Brick-and-Mortar” Composites Made of 2D Carbon Nanoparticles
Abstract
:1. Introduction
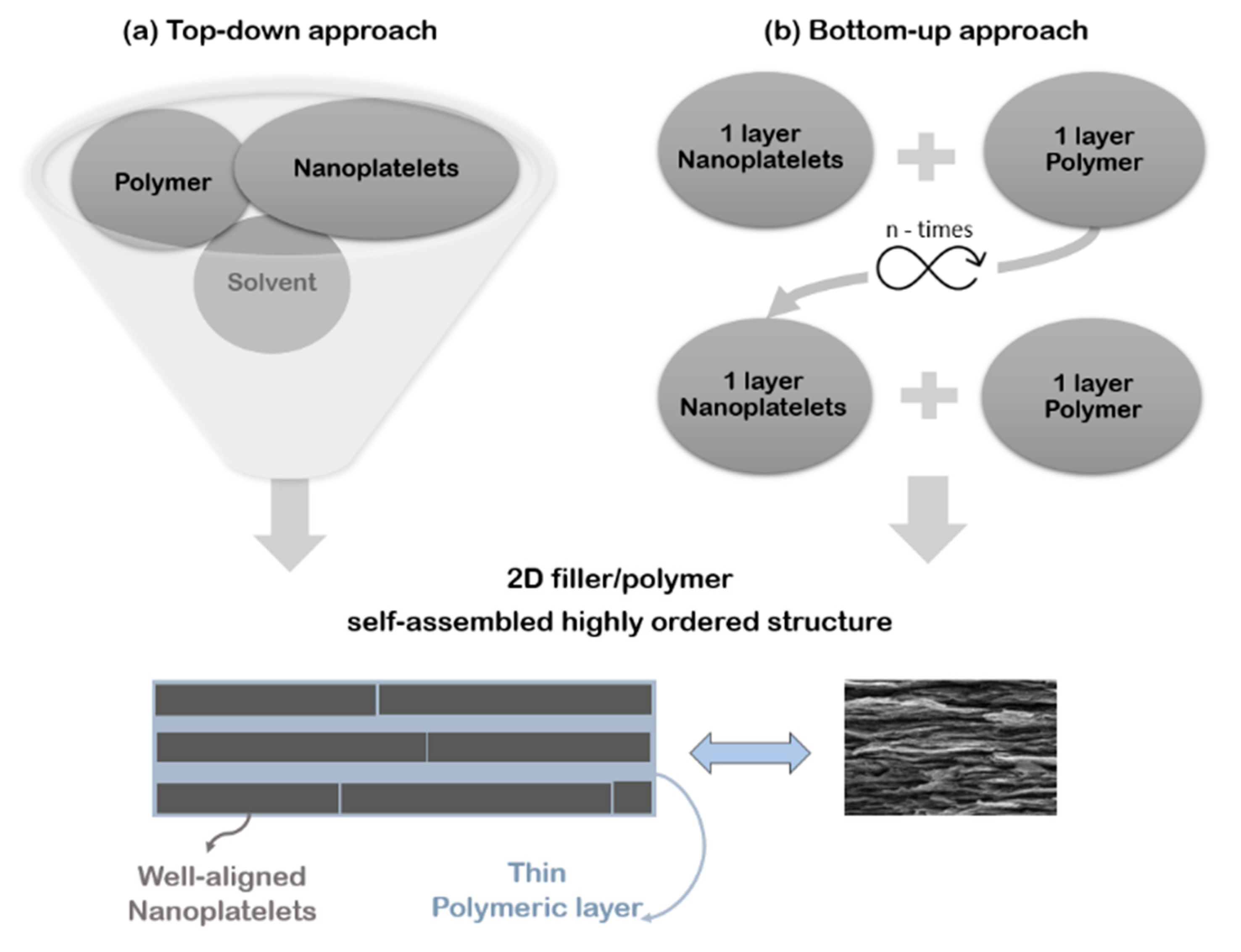
1.1. Mimicking Nature: Nacre-Inspired Materials
1.2. Engineering Materials Based on 2D Nanoparticles
1.3. Technologies Enabling Industry Applications
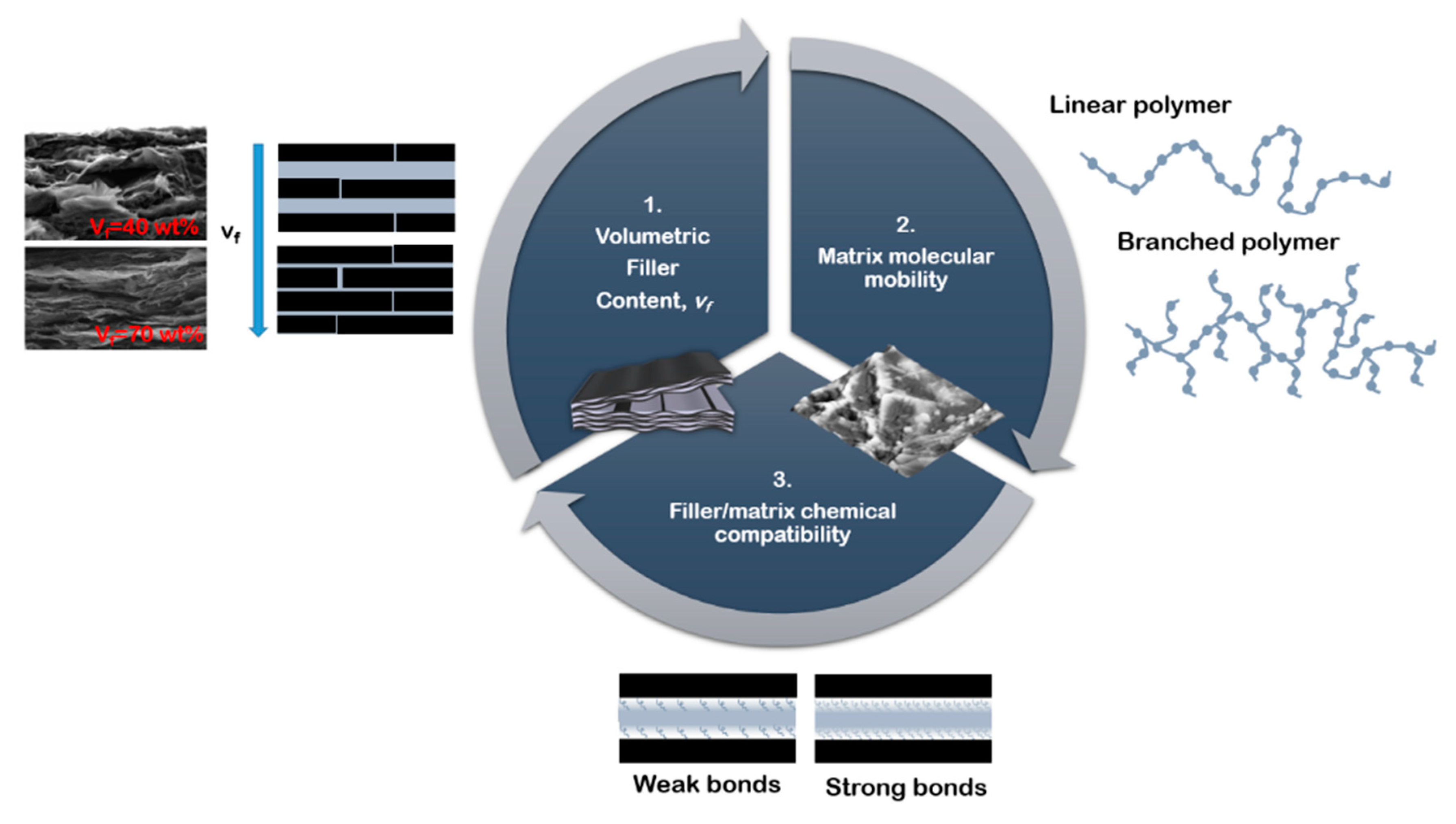
2. Mechanical Performances—Experimental Observation of Literature Data

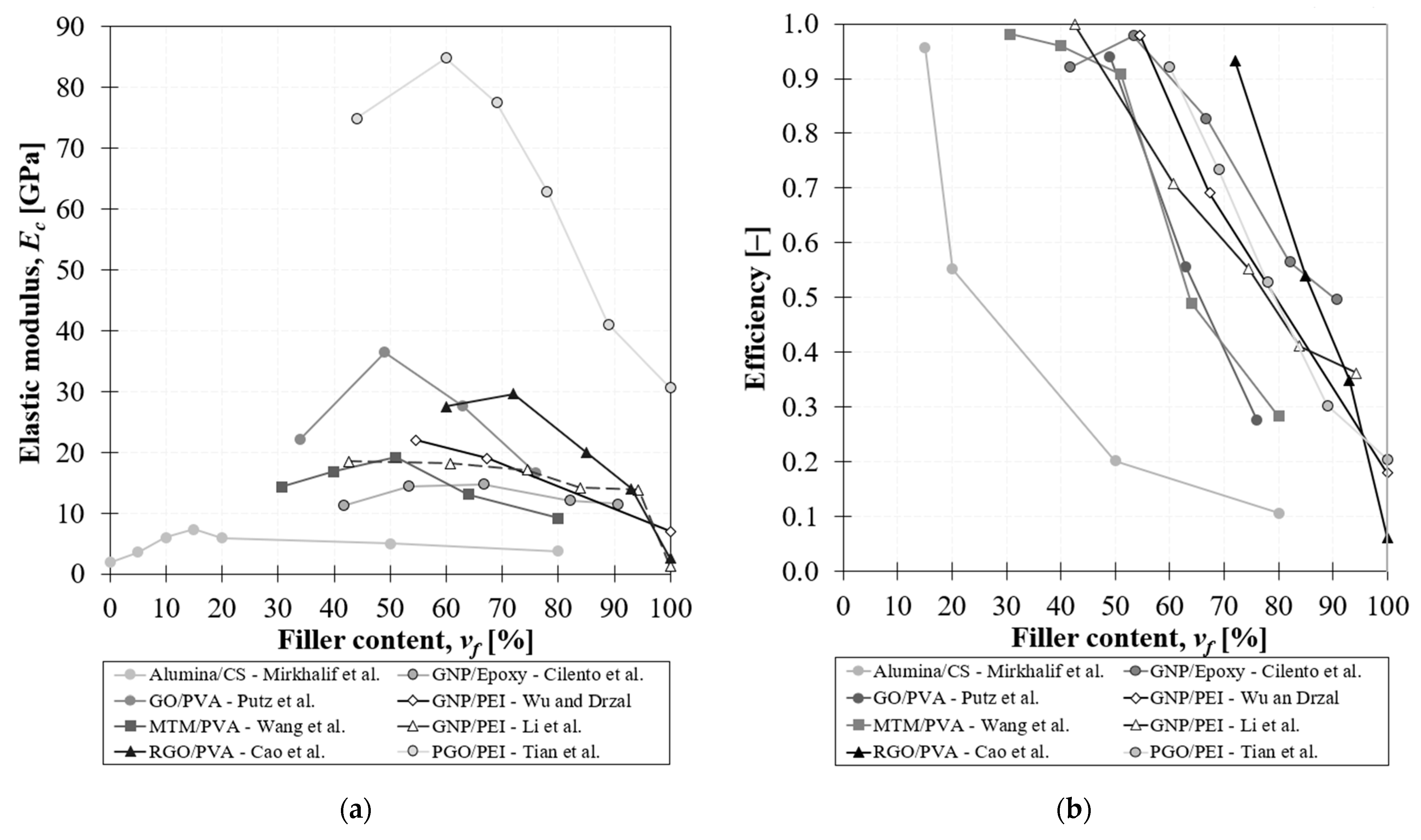
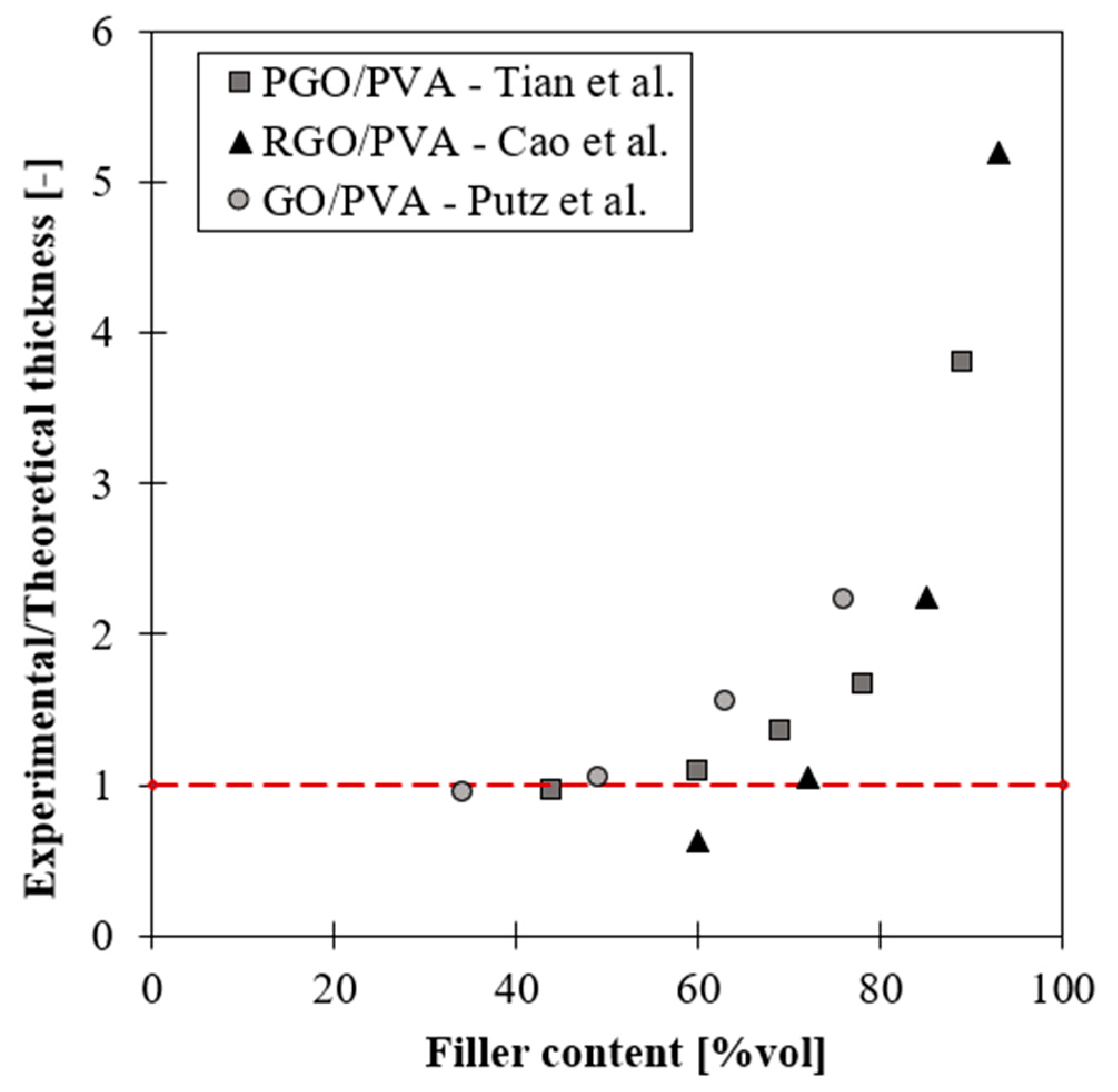
2.1. Influence of Filler Content
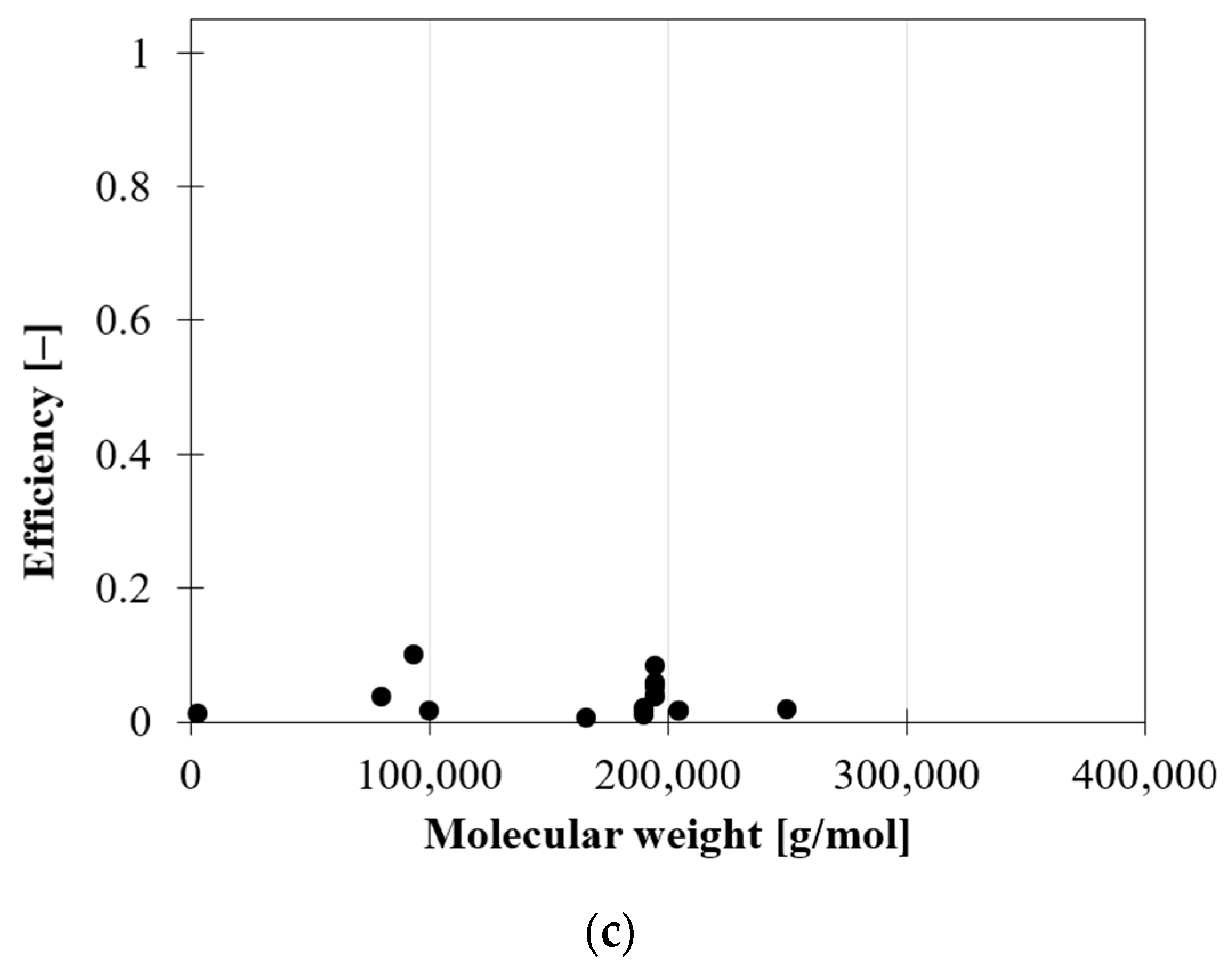
2.2. Influence of Matrix—Effect of Matrix Molecular Weight
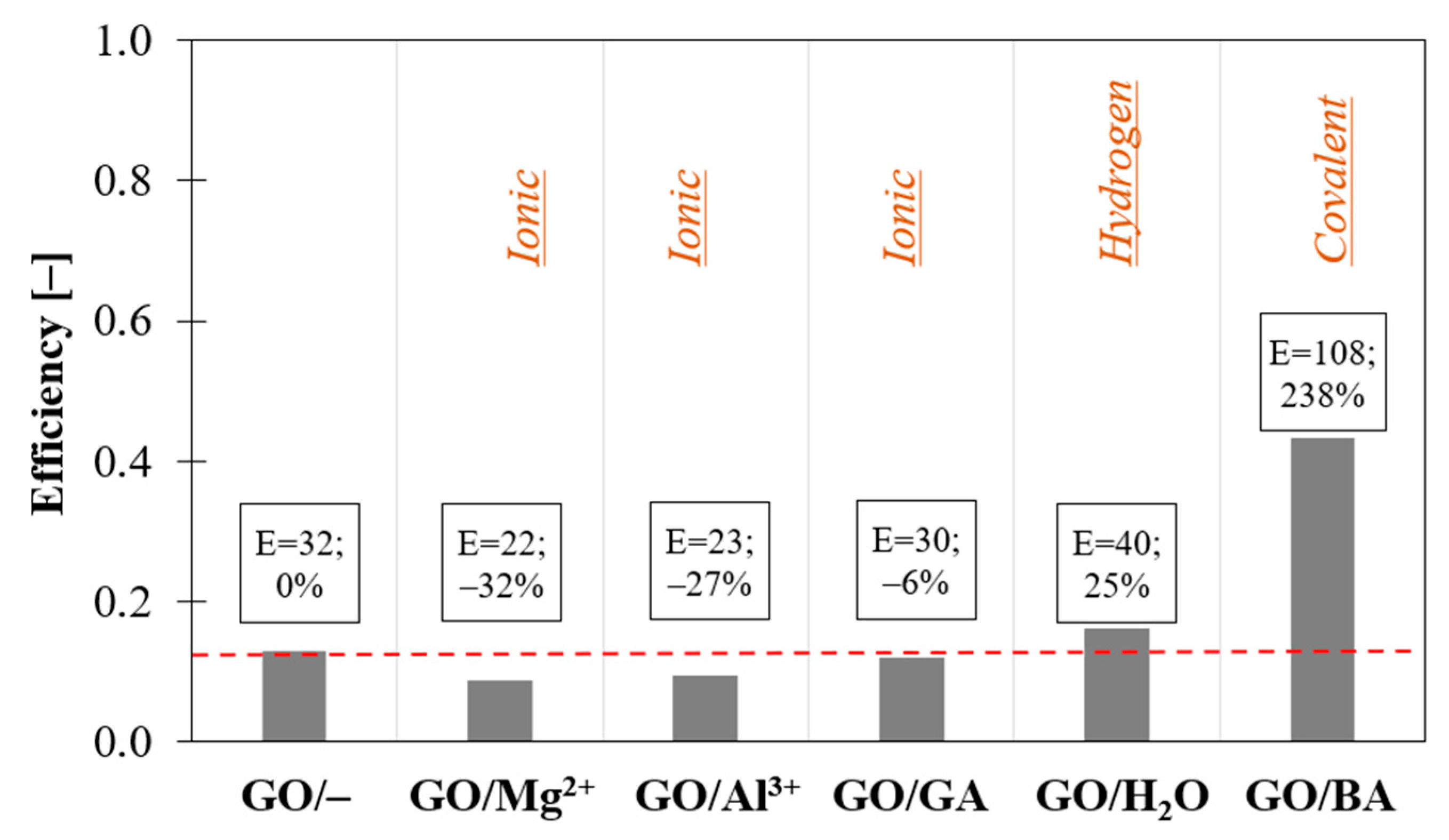
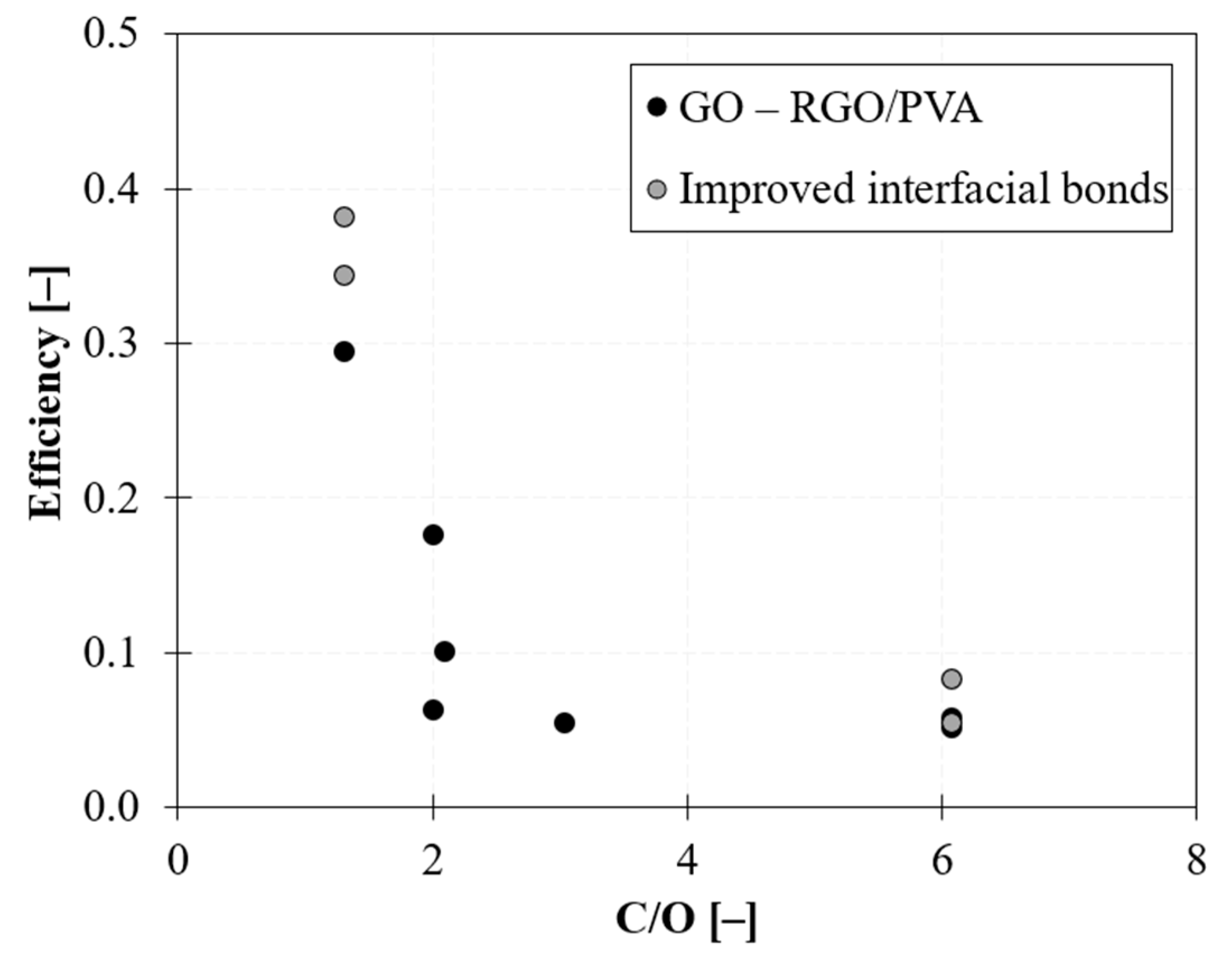
2.3. Filler/Matrix Compatibility—Chemical Bonding
2.4. Interfacial Shear Strength
3. Analytical Models for the Prediction of Mechanical Properties
4. Discussion
5. Conclusions
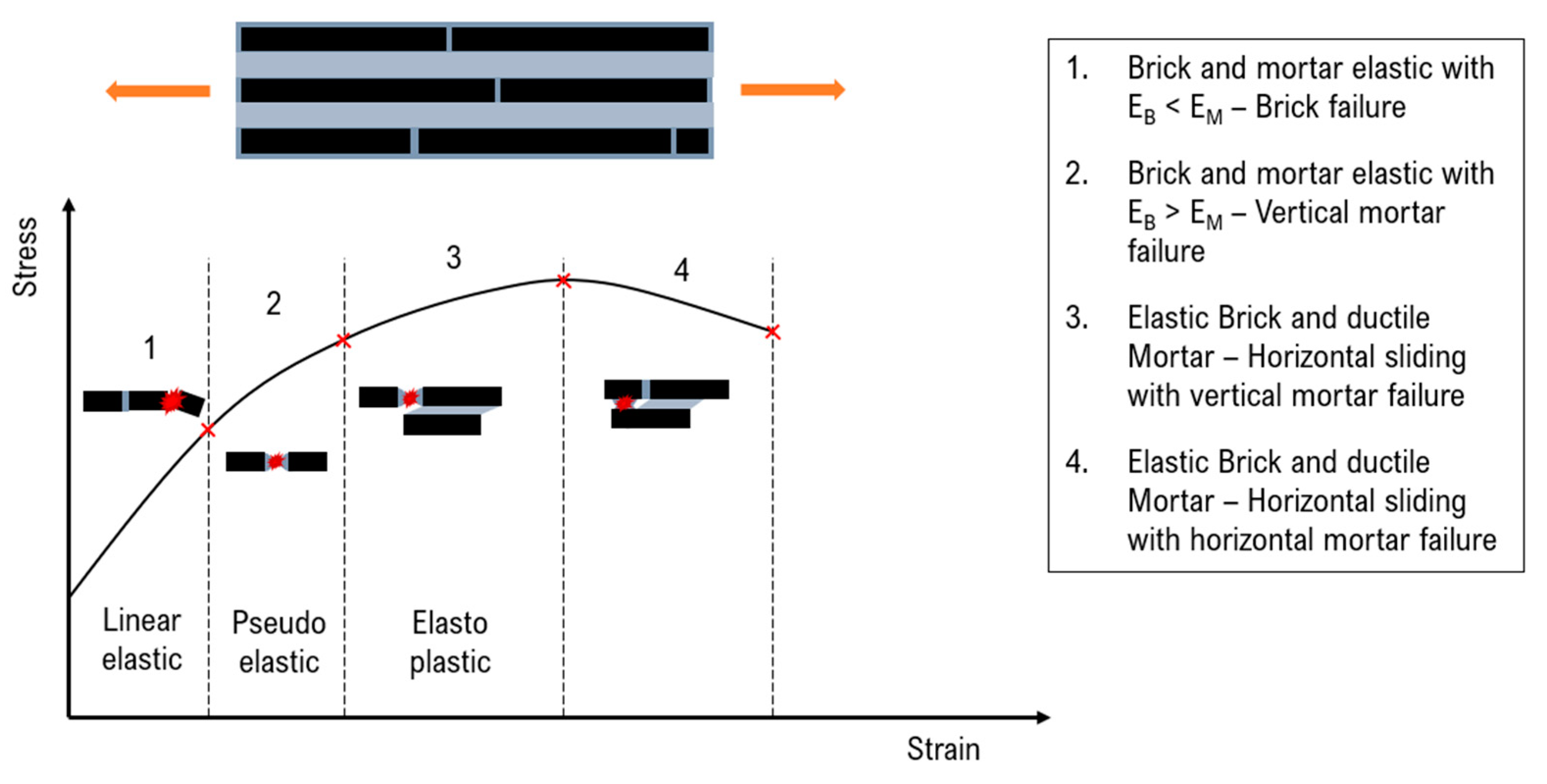
- −
- Drops at high filler content.Starting from a critical volumetric fraction, the elastic modulus B&M composites deviate from the expected behaviour dictated by the rule of mixture due to the partial coverage of the nanoplatelets at the nanoscopic level.
- −
- Decreases as the molecular weight increases.The higher the molecular mobility of the polymer and the capacity to intercalate between nanoplatelets, the better the stress transfer at the interface.
- −
- Improves when a high interfacial attraction between nanoparticles and the surrounding matrix is guaranteed.Strong chemical bonding and molecular interactions between nanoparticles and the polymer ensure self-assemblies with a tendency toward forming intercalated morphologies, with a stable layer of polymer between flakes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Peng, J.; Cheng, Q. High-Performance Nanocomposites Inspired by Nature. Adv. Mater. 2017, 29, 1702959. [Google Scholar] [CrossRef] [PubMed]
- George, J.; Ishida, H. A Review on the Very High Nanofiller-Content Nanocomposites: Their Preparation Methods and Properties with High Aspect Ratio Fillers. Prog. Polym. Sci. 2018, 86, 1–39. [Google Scholar] [CrossRef]
- Schmidt, D.F. Nanolaminates-Bioinspired and Beyond. Mater. Lett. 2013, 108, 328–335. [Google Scholar] [CrossRef]
- Sun, J.; Bhushan, B. Hierarchical Structure and Mechanical Properties of Nacre: A Review. RSC Adv. 2012, 2, 7617. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Rim, J.E.; Barthelat, F.; Buehler, M.J.; Espinosa, H.D. Merger of Structure and Material in Nacre and Bone-Perspectives on de Novo Biomimetic Materials. Prog. Mater. Sci. 2009, 54, 1059–1100. [Google Scholar] [CrossRef]
- Niebel, T.P.; Bouville, F.; Kokkinis, D.; Studart, A.R. Journal of the Mechanics and Physics of Solids Role of the Polymer Phase in the Mechanics of Nacre-like Composites. J. Mech. Phys. Solids 2016, 96, 133–146. [Google Scholar] [CrossRef] [Green Version]
- Balandin, A.A. Thermal Properties of Graphene and Nanostructured Carbon Materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [Green Version]
- Cilento, F.; Martone, A.; Cristiano, F.; Fina, A.; Giordano, M. Effect of Matrix Content on Mechanical and Thermal Properties of High Graphene Content Composites. MATEC Web Conf. 2019, 303, 01002. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Suk, J.W.; Piner, R.D.; An, J.; Ruoff, R.S. Mechanical Properties of Monolayer Graphene Oxide. ACS Nano 2010, 4, 6557–6564. [Google Scholar] [CrossRef]
- Chen, J.; Li, L. Thermal Conductivity of Graphene Oxide: A Molecular Dynamics Study. JETP Lett. 2020, 112, 117–121. [Google Scholar] [CrossRef]
- Chen, H.; Müller, M.B.; Gilmore, K.J.; Wallace, G.G.; Li, D. Mechanically Strong, Electrically Conductive, and Biocompatible Graphene Paper. Adv. Mater. 2008, 20, 3557–3561. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.; Zhao, J.; Liu, F. Mechanical Properties of Graphene Oxides. Nanoscale 2012, 4, 5910–5916. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; Li, M.; Liu, J.; Wang, B.; Zhang, C.; Yiang, L.; Cheng, Q. A Strong Integrated Strength and Toughness Artificial Nacre Based on Dopamine Cross-Linked Graphene Oxide. ACS Nano 2014, 8, 9511–9517. [Google Scholar] [CrossRef] [PubMed]
- Cost, J.R.; Janowski, K.R.; Rossi, R.C. Elastic Properties of Isotropic Graphite. Philos. Mag. 1968, 17, 851–854. [Google Scholar] [CrossRef]
- Wu, H.; Drzal, L.T. Graphene Nanoplatelet Paper as a Light-Weight Composite with Excellent Electrical and Thermal Conductivity and Good Gas Barrier Properties. Carbon N. Y. 2012, 50, 1135–1145. [Google Scholar] [CrossRef]
- Rafiee, R.; Shahzadi, R. Mechanical Properties of Nanoclay and Nanoclay Reinforced Polymers: A Review. Polym. Compos. 2019, 40, 431–445. [Google Scholar] [CrossRef]
- Uddin, F. Montmorillonite: An Introduction to Properties and Utilization. In Current Topics in the Utilization of Clay in Industrial and Medical Applications; Zoveidavianpoor, M., Ed.; IntechOpen: London, UK, 2018; pp. 3–24. [Google Scholar]
- Tsoukleri, G.; Parthenios, J.; Papagelis, K.; Jalil, R.; Ferrari, A.C.; Geim, A.K.; Novoselov, K.S.; Galiotis, C. Subjecting a Graphene Monolayer to Tension and Compression. Small 2009, 5, 2397–2402. [Google Scholar] [CrossRef] [Green Version]
- Wassei, J.K.; Kaner, R.B. Graphene, a Promising Transparent Conductor. Mater. Today 2010, 13, 52–59. [Google Scholar] [CrossRef]
- Kuzmenko, A.B.; Van Heumen, E.; Carbone, F.; Van Der Marel, D. Universal Optical Conductance of Graphite. Phys. Rev. Lett. 2008, 100, 117401. [Google Scholar] [CrossRef] [Green Version]
- Wick, P.; Louw-gaume, A.E.; Kucki, M.; Krug, H.F.; Kostarelos, K.; Fadeel, B.; Dawson, K.A.; Salvati, A.; Vµzquez, E.; Ballerini, L.; et al. Classification Framework for Graphene-Based Materials. Angew. Chem. Int. Ed 2014, 53, 7714–7718. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohan, V.B.; Brown, R.; Jayaraman, K.; Bhattacharyya, D. Characterisation of Reduced Graphene Oxide: Effects of Reduction Variables on Electrical Conductivity. Mater. Sci. Eng. B 2015, 193, 49–60. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The Rise of Graphene. In Nanoscience and Technology: A Collection of Reviews from Nature Journals; World Scientific: Singapore, 2010; pp. 11–19. [Google Scholar]
- Uddin, F. Clays, Nanoclays, and Montmorillonite Minerals. Metall. Mater. Trans. A 2008, 39, 2804–2814. [Google Scholar] [CrossRef]
- Corni, I.; Harvey, T.J.; Wharton, J.A.; Stokes, K.R.; Walsh, F.C.; Wood, R.J.K. A Review of Experimental Techniques to Produce a Nacre-like Structure. Bioinspir. Biomim. 2012, 7, 031001. [Google Scholar] [CrossRef] [PubMed]
- Richardson, J.J.; Björnmalm, M.; Caruso, F. Technology-Driven Layer-by-Layer Assembly of Nanofilms. Science 2015, 348, aaa2491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suter, J.L.; Sinclair, R.C.; Coveney, P.V. Principles Governing Control of Aggregation and Dispersion of Graphene and Graphene Oxide in Polymer Melts. Adv. Mater. 2020, 32, 2003213. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Zhu, S.; Mao, L. Graphene Nanoarchitectonics: Approaching the Excellent Properties of Graphene from Microscale to Macroscale. J. Inorg. Organomet. Polym. Mater. 2015, 25, 179–188. [Google Scholar] [CrossRef]
- Huang, C.; Cheng, Q. Learning from Nacre: Constructing Polymer Nanocomposites. Compos. Sci. Technol. 2017, 150, 141–166. [Google Scholar] [CrossRef]
- Wan, S.; Cheng, Q. Role of Interface Interactions in the Construction of GO-Based Artificial Nacres. Adv. Mater. Interfaces 2018, 5, 1800107. [Google Scholar] [CrossRef]
- Podsiadlo, P.; Kaushik, A.K.; Arruda, E.M.; Waas, A.M.; Shim, B.S.; Xu, J.; Nandivada, H.; Pumplin, B.G.; Lahann, J.; Ramamoorthy, A.; et al. Ultrastrong and Stiff Layered Polymer Nanocomposites. Science 2007, 318, 80–83. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, H.; Kotov, N.A. Thermodynamic and Structural Insights into Nanocomposites Engineering by Comparing Two Materials Assembly Techniques for Graphene. ACS Nano 2013, 7, 4818–4829. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Gao, Y.; Liu, Q.; Kuang, J.; Zhou, D.; Ju, S.; Han, B.; Zhang, Z. High Mechanical Performance of Layered Graphene Oxide/Poly(Vinyl Alcohol) Nanocomposite Films. Small 2013, 9, 2466–2472. [Google Scholar] [CrossRef] [PubMed]
- Compton, O.C.; Cranford, S.W.; Putz, K.W.; An, Z.; Brinson, L.C.; Buehler, M.J.; Nguyen, S.T. Tuning the Mechanical Properties of Graphene Oxide Paper and Its Associated Polymer Nanocomposites by Controlling Cooperative Intersheet Hydrogen Bonding. ACS Nano 2012, 6, 2008–2019. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Cao, Y.; Wang, Y.; Yang, W.; Feng, J. Realizing Ultrahigh Modulus and High Strength of Macroscopic Graphene Oxide Papers Through Crosslinking of Mussel-Inspired Polymers. Adv. Mater. 2013, 25, 2980–2983. [Google Scholar] [CrossRef]
- Patro, T.U.; Wagner, H.D. Influence of Graphene Oxide Incorporation and Chemical Cross-Linking on Structure and Mechanical Properties of Layer-by-Layer Assembled Poly (Vinyl Alcohol)-Laponite Free-Standing Films. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 2377–2387. [Google Scholar] [CrossRef]
- Wan, S.; Peng, J.; Li, Y.; Hu, H.; Jiang, L.; Cheng, Q. Use of Synergistic Interactions to Fabricate Strong, Tough, and Conductive Arti Fi Cial Nacre Based on Graphene Oxide and Chitosan. ACS Nano 2015, 9, 9830–9836. [Google Scholar] [CrossRef]
- Wu, Y.; Cao, R.; Ji, L.; Huang, W.; Yang, X.; Tu, Y. Synergistic Toughening of Bioinspired Artificial Nacre by Polystyrene Grafted Graphene Oxide. RSC Adv. 2015, 5, 28085–28091. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Ma, P.; Zhang, S.; Zhang, H.; Du, M.; Xie, Y.; Chen, M.; Dong, W.; Ming, W. Artificial Nacre from Supramolecular Assembly of Graphene Oxide. ACS Nano 2018, 12, 6228–6235. [Google Scholar] [CrossRef]
- Cheng, Q.; Wu, M.; Li, M.; Jiang, L.; Tang, Z. Ultratough Artificial Nacre Based on Conjugated Cross-Linked Graphene Oxide. Angew. Chem. Int. Ed. 2013, 52, 3750–3755. [Google Scholar] [CrossRef]
- Li, Y.; Xue, Z.; Luan, Y.; Wang, L.; Zhao, D.; Xu, F.; Xiao, Y.; Guo, Z.; Wang, Z. Improved Mechanical Performance of Graphene Oxide Based Arti Fi Cial Nacre Composites by Regulating the Micro-Laminated Structure and Interface Bonding. Compos. Sci. Technol. 2019, 179, 63–68. [Google Scholar] [CrossRef]
- Wan, S.; Li, Y.; Peng, J.; Hu, H.; Cheng, Q.; Jiang, L. Synergistic Toughening of Graphene Oxide-Molybdenum Disulfide-Thermoplastic Polyurethane Ternary Artificial Nacre. ACS Nano 2015, 9, 708–714. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Dikin, D.A.; Nguyen, S.T.; Ruoff, R.S. Graphene Oxide Sheets Chemically Cross-Linked by Polyallylamine. J. Phys. Chem. C 2009, 113, 15801–15804. [Google Scholar] [CrossRef]
- Putz, B.K.W.; Compton, O.C.; Palmeri, M.J.; Nguyen, S.T.; Brinson, L.C. High-Nanofiller-Content Graphene Oxide–Polymer Nanocomposites via Vacuum-Assisted Self-Assembly. Adv. Funct. Mater. 2010, 20, 3322–3329. [Google Scholar] [CrossRef]
- Li, Y.; Yu, T.; Yang, T.; Zheng, L.; Liao, K. Bio-Inspired Nacre-like Composite Films Based on Graphene with Superior Mechanical, Electrical, and Biocompatible Properties. Adv. Mater. 2012, 24, 3426–3431. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Q.; Liang, L.; Ding, H.; Liang, X.; Sun, G. High-Content Graphene-Reinforced Polymer with Bioinspired Multilayer Structure. J. Mater. Sci. 2020, 55, 16836–16845. [Google Scholar] [CrossRef]
- Wan, S.; Xu, F.; Jiang, L.; Cheng, Q. Superior Fatigue Resistant Bioinspired Graphene-Based Nanocomposite via Synergistic Interfacial Interactions. Adv. Funct. Mater. 2017, 27, 1703459. [Google Scholar] [CrossRef]
- Gong, S.; Zhang, Q.; Wang, R.; Jiang, L.; Cheng, Q. Synergistically Toughening Nacre-like Graphene Nanocomposites via Gel-Film Transformation. J. Mater. Chem. A 2017, 5, 16386–16392. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, Z.; Wu, K.; Huang, R.; Liu, T.; Jiang, H.; Chen, F.; Fu, Q. Ultrathin Flexible Reduced Graphene Oxide / Cellulose Nanofiber Composite Films with Strongly Anisotropic Thermal Conductivity and Efficient. J. Mater. Chem. C 2017, 5, 3748–3756. [Google Scholar] [CrossRef]
- Hu, K.; Tolentino, L.S.; Kulkarni, D.D.; Ye, C.; Kumar, S.; Tsukruk, V. V Written-in Conductive Patterns on Robust Graphene Oxide Biopaper by Electrochemical Microstamping. Angew. Chem. Int. Ed. 2013, 52, 13784–13788. [Google Scholar] [CrossRef]
- Ni, H.; Xu, F.; Tomsia, A.P.; Saiz, E.; Jiang, L.; Cheng, Q. Robust Bioinspired Graphene Film via π−π Cross-Linking. ACS Appl. Mater. Interfaces 2017, 9, 29. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, L.; Chen, J.; Li, C.; Shi, G. Ultratough, Ultrastrong, and Highly Conductive Graphene Films with Arbitrary Sizes. Adv. Mater. 2014, 26, 7588–7592. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Chen, C.; Chen, K.; Lu, Q.; Wang, Q.; Zhou, P.; Liu, D.; Song, L.; Niu, Z.; Chen, J. High-Strength Graphene Composite Films by Molecular Level Couplings for Flexible Supercapacitors with High Volumetric Capacitance. J. Mater. Chem. A 2017, 5, 15008–15016. [Google Scholar] [CrossRef]
- Wan, S.; Hu, H.; Peng, J.; Li, Y.; Fan, Y.; Jiang, L.; Cheng, Q. Nacre-Inspired Integrated Strong and Tough Reduced Graphene Oxide–Poly(Acrylic Acid) Nanocomposites. Nanoscale 2016, 8, 5649–5656. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.; Yang, M.; Zhao, Q.; Gao, W.; Xie, T.; Bai, H. Superstretchable Nacre-Mimetic Graphene/Poly(Vinyl Alcohol) Composite Film Based on Interfacial Architectural Engineering. ACS Nano 2017, 11, 4777–4784. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, H.; Ma, P.; Bai, H.; Chen, M.; Dong, W.; Xie, Y.; Deshmukh, Y.S. Superior Performance of Artificial Nacre Based on Graphene Oxide Nanosheets. ACS Appl. Mater. Interfaces 2017, 9, 4215–4222. [Google Scholar] [CrossRef]
- Tang, Z.; Kotov, N.A.; Magonov, S.; Ozturk, B. Nanostructured Artificial Nacre. Nat. Mater. 2003, 2, 413–418. [Google Scholar] [CrossRef]
- Das, P.; Malho, J.M.; Rahimi, K.; Schacher, F.H.; Wang, B.; Demco, D.E.; Walther, A. Nacre-Mimetics with Synthetic Nanoclays up to Ultrahigh Aspect Ratios. Nat. Commun. 2015, 6, 5967. [Google Scholar] [CrossRef] [Green Version]
- Liu, A.; Walther, A.; Ikkala, O.; Belova, L.; Berglund, L.A. Clay Nanopaper with Tough Cellulose Nanofiber Matrix for Fire Retardancy and Gas Barrier Functions. Biomacromolecules 2011, 12, 633–641. [Google Scholar] [CrossRef]
- Walther, A.; Bjurhager, I.; Malho, J.M.; Pere, J.; Ruokolainen, J.; Berglund, L.A.; Ikkala, O. Large-Area, Lightweight and Thick Biomimetic Composites with Superior Material Properties via Fast, Economic, and Green Pathways. Nano Lett. 2010, 10, 2742–2748. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, Q.; Lin, L.; Chen, L.; Jiang, L. Understanding the Relationship of Performance with Nanofiller Content in the Biomimetic Layered Nanocomposites. Nanoscale 2013, 5, 6356–6362. [Google Scholar] [CrossRef]
- Yao, H.B.; Tan, Z.H.; Fang, H.Y.; Yu, S.H. Artificial Nacre-like Bionanocomposite Films from the Self-Assembly of Chitosan-Montmorillonite Hybrid Building Blocks. Angew. Chem. Int. Ed. 2010, 49, 10127–10131. [Google Scholar] [CrossRef]
- Debelak, B.; Lafdi, K. Use of Exfoliated Graphite Filler to Enhance Polymer Physical Properties. Carbon N. Y. 2007, 45, 1727–1734. [Google Scholar] [CrossRef]
- Li, X.; Manasrah, A.; Al-ostaz, A.; Alkhateb, H.; Lincoln, D.; Rushing, G.; Cheng, A.H. Preparation and Characterization of High Content Graphene Nanoplatelet-Polyetherimide Paper. J. Nanosci. Nanoeng. 2015, 1, 252–258. [Google Scholar]
- Mirkhalaf, M.; Barthelat, F. Nacre-like Materials Using a Simple Doctor Blading Technique: Fabrication, Testing and Modeling. J. Mech. Behav. Biomed. Mater. 2016, 56, 23–33. [Google Scholar] [CrossRef]
- Cilento, F.; Martone, A.; Carbone, M.G.P.; Giordano, M.; Galiotis, C. Load Transfer in High Content Graphite Nanoplateles Composites. In AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MD, USA, 2019; Volume 2196. [Google Scholar]
- Cilento, F.; Martone, A.; Pastore Carbone, M.G.; Galiotis, C.; Giordano, M. Nacre-like GNP/Epoxy Composites: Reinforcement Efficiency Vis-à-Vis Graphene Content. Compos. Sci. Technol. 2021, 211, 108873. [Google Scholar] [CrossRef]
- Putz, K.W.; Compton, O.C.; Segar, C.; An, Z.; Nguyen, S.T.; Brinson, L.C. Evolution of Order during Vacuum-Assisted Self-Assembly of Graphene Oxide Paper and Associated Polymer Nanocomposites. ACS Nano 2011, 5, 6601–6609. [Google Scholar] [CrossRef]
- Podsiadlo, P.; Tang, Z.; Shim, B.S.; Kotov, N.A. Counterintuitive Effect of Molecular Strength and Role of Molecular Rigidity on Mechanical Properties of Layer-by-Layer Assembled Nanocomposites. Nano Lett. 2007, 7, 1224–1231. [Google Scholar] [CrossRef] [PubMed]
- Rehse, N.; Wang, C.; Hund, M.; Geoghegan, M.; Magerle, R.; Krausch, G. Stability of Thin Polymer Films on a Corrugated Substrate. Eur. Phys. J. E 2001, 4, 69–76. [Google Scholar] [CrossRef]
- Yang, M.H.; Hou, S.Y.; Chang, Y.L.; Yang, A.C.M. Molecular Recoiling in Polymer Thin Film Dewetting. Phys. Rev. Lett. 2006, 96, 066105. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, S.; Wang, Q.; Liu, X.; Ji, X.; Jiang, B. Effects of Molecular Weight, Solvent and Substrate on the Dewetting Morphology of Polystyrene Films. Appl. Surf. Sci. 2004, 236, 131–140. [Google Scholar] [CrossRef]
- An, Z.; Compton, O.C.; Putz, K.W.; Brinson, L.C.; Nguyen, S.T. Bio-Inspired Borate Cross-Linking in Ultra-Stiff Graphene Oxide Thin Films. Adv. Mater. 2011, 23, 3842–3846. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Lee, K.S.; Bozoklu, G.; Cai, W.; Nguyen, S.B.T.; Ruoff, R.S. Graphene Oxide Papers Modified by Divalent Ions—Enhancing Mechanical Properties via Chemical Cross-Linking. ACS Nano 2008, 2, 572–578. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Liu, L.Q.; Zu, S.Z.; Peng, K.; Zhou, D.; Han, B.H.; Zhang, Z. The Effect of Interlayer Adhesion on the Mechanical Behaviors of Macroscopic Graphene Oxide Papers. ACS Nano 2011, 5, 2134–2141. [Google Scholar] [CrossRef] [PubMed]
- Krishnamoorthy, K.; Veerapandian, M.; Yun, K.; Kim, S.-J. The Chemical and Structural Analysis of Graphene Oxide with Different Degrees of Oxidation. Carbon N. Y. 2013, 53, 38–49. [Google Scholar] [CrossRef]
- Wagner, H.D.; Vaia, R.A. Nanocomposites: Issues at the Interface. Mater. Today 2004, 7, 38–42. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; Zheng, M.; Park, C.; Wang, X.; Ke, C. Quantitative Nanomechanical Characterization of the van Der Waals Interfaces between Carbon Nanotubes and Epoxy. Carbon N. Y. 2015, 82, 214–228. [Google Scholar] [CrossRef]
- Ding, W.; Eitan, A.; Fisher, F.T.; Chen, X.; Dikin, D.A.; Andrews, R.; Brinson, L.C.; Schadler, L.S.; Ruoff, R.S. Direct Observation of Polymer Sheathing in Carbon Nanotube−Polycarbonate Composites. Nano Lett. 2003, 3, 1593–1597. [Google Scholar] [CrossRef]
- Kranbuehl, D.E.; Cai, M.; Glover, A.J.; Schniepp, H.C. Measurement of the Interfacial Attraction between Graphene Oxide Sheets and the Polymer in a Nanocomposite. Appl. Polym. Sci. 2011, 122, 3739–3743. [Google Scholar] [CrossRef]
- Liu, Y.; Hamon, A.-L.; Bai, J. Directly Measuring Interfacial Shear Strength between Polymethyl Methacrylate and Graphene Nanoplatelets. Mater. Lett. 2016, 182, 244–247. [Google Scholar] [CrossRef]
- Jang, C.; Lacy, T.E.; Gwaltney, S.R.; Toghiani, H.; Pittman, C.U. Interfacial Shear Strength of Cured Vinyl Ester Resin-Graphite Nanoplatelet from Molecular Dynamics Simulations. Polymer 2013, 54, 3282–3289. [Google Scholar] [CrossRef]
- Safaei, M.; Sheidaei, A.; Baniassadi, M.; Ahzi, S.; Mosavi Mashhadi, M.; Pourboghrat, F. An Interfacial Debonding-Induced Damage Model for Graphite Nanoplatelet Polymer Composites. Comput. Mater. Sci. 2015, 96, 191–199. [Google Scholar] [CrossRef]
- He, Z.Z.; Zhu, Y.B.; Xia, J.; Wu, H.A. Optimization Design on Simultaneously Strengthening and Toughening Graphene-Based Nacre-like Materials through Noncovalent Interaction. J. Mech. Phys. Solids 2019, 133, 103706. [Google Scholar] [CrossRef]
- Gao, E.; Cao, Y.; Liu, Y.; Xu, Z. Optimizing Interfacial Cross-Linking in Graphene-Derived Materials, Which Balances Intralayer and Interlayer Load Transfer. ACS Appl. Mater. Interfaces 2017, 9, 24830–24839. [Google Scholar] [CrossRef] [PubMed]
- Galiotis, C.; Young, R.J.; Batchelder, D.N. A Resonance Raman Spectroscopic Study of the Strength of the Bonding between an Epoxy Resin and a Polydiacetylene Fibre. J. Mater. Sci. Lett. 1983, 2, 263–266. [Google Scholar] [CrossRef]
- Melanitis, N.; Galiotis, C. Interfacial Micromechanics in Model Composites Using Laser Raman Spectroscopy. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1993, 440, 379–398. [Google Scholar]
- Mohiuddin, T.M.G.; Lombardo, A.; Nair, R.R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.M.; Galiotis, C.; Marzari, N. Uniaxial Strain in Graphene by Raman Spectroscopy: G Peak Splitting, Grüneisen Parameters, and Sample Orientation. Phys. Rev. B 2009, 79, 205433. [Google Scholar] [CrossRef]
- Bretzlaff, R.S.; Wool, R.P. Frequency Shifting and Asymmetry in Infrared Bands of Stressed Polymers. Macromolecules 1983, 16, 1907–1917. [Google Scholar] [CrossRef]
- Gouadec, G.; Colomban, P. Raman Spectroscopy of Nanomaterials: How Spectra Relate to Disorder, Particle Size and Mechanical Properties. Prog. Cryst. Growth Charact. Mater. 2007, 53, 1–56. [Google Scholar] [CrossRef] [Green Version]
- Tashiro, K.; Gang, W.; Kobayashi, M. Quasiharmonic Treatment of Infrared and Raman Vibrational Frequency Shifts Induced by Tensile Deformation of Polymer Chains. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 2527–2553. [Google Scholar] [CrossRef]
- Mitra, V.K.; Risen, W.M., Jr.; Baughman, R.H. A Laser Raman Study of the Stress Dependence of Vibrational Frequencies of a Monocrystalline Polydiacetylene. J. Chem. Phys. 1977, 66, 2731–2736. [Google Scholar] [CrossRef]
- Young, R.J. Polymer Single Crystal Fibres. In Developments in Oriented Polymers—2; Springer: Berlin/Heidelberg, Germany, 1987; pp. 1–38. [Google Scholar]
- Schrader, B. Infrared and Raman Spectroscopy: Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 3527615423. [Google Scholar]
- Robinson, I.M.; Zakikhani, M.J.; Day, R.J.; Young, R.J.; Galiotis, C. Strain Dependence of the Raman Frequencies for Different Types of Carbon Fibres. J. Mater. Sci. Lett. 1987, 6, 1212–1214. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman Spectrum of Graphene and Graphene Layers. Phys. Rev. Lett. 2006, 187401, 1–4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vidano, R.P.; Fischbach, D.B.; Willis, L.J.; Loehr, T.M. Observation of Raman Band Shifting with Excitation Wavelength for Carbons and Graphites. Solid State Commun. 1981, 39, 341–344. [Google Scholar] [CrossRef]
- Kaniyoor, A.; Ramaprabhu, S. A Raman Spectroscopic Investigation of Graphite Oxide Derived Graphene. AIP Adv. 2012, 2, 32183. [Google Scholar] [CrossRef] [Green Version]
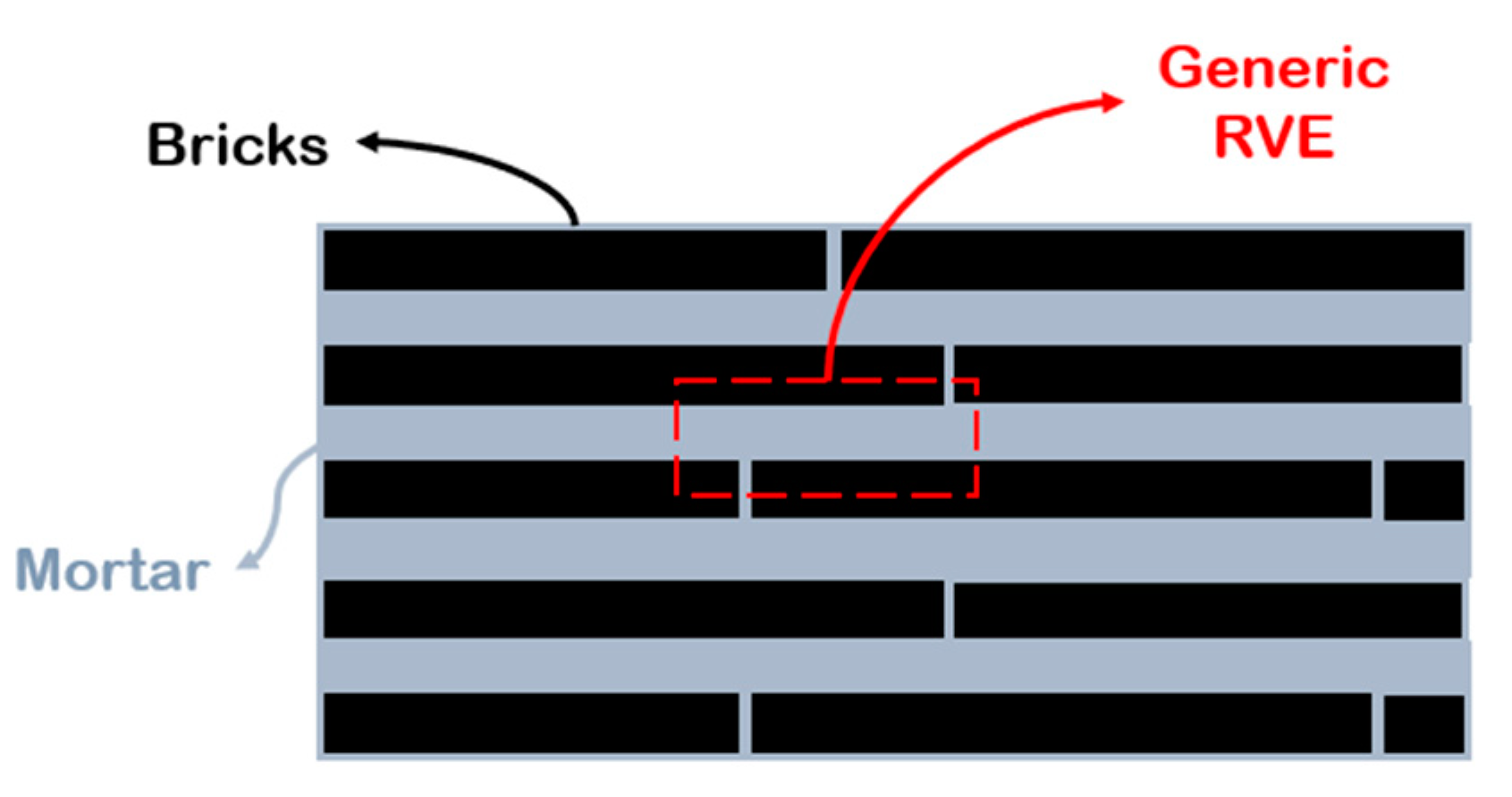
- Begley, M.R.; Philips, N.R.; Compton, B.G.; Wilbrink, D.V.; Ritchie, R.O.; Utz, M. Micromechanical Models to Guide the Development of Synthetic “brick and Mortar” Composites. J. Mech. Phys. Solids 2012, 60, 1545–1560. [Google Scholar] [CrossRef]
- Cox, H.L. The Elasticity and Strength of Paper and Other Fibrous Materials. Br. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Kotha, S.P.; Kotha, S.; Guzelsu, N. A Shear-Lag Model to Account for Interaction Effects between Inclusions in Composites Reinforced with Rectangular Platelets. Compos. Sci. Technol. 2000, 60, 2147–2158. [Google Scholar] [CrossRef]
- Barthelat, F. Designing Nacre-like Materials for Simultaneous Stiffness, Strength and Toughness: Optimum Materials, Composition, Microstructure and Size. J. Mech. Phys. Solids 2014, 73, 22–37. [Google Scholar] [CrossRef]
- Wu, W.; Sadeghipour, K.; Boberick, K.; Baran, G. Predictive Modeling of Elastic Properties of Particulate-Reinforced Composites. Mater. Sci. Eng. 2002, 332, 362–370. [Google Scholar] [CrossRef]
- Pimenta, S.; Robinson, P. An Analytical Shear-Lag Model for Composites with “brick-and-Mortar” Architecture Considering Non-Linear Matrix Response and Failure. Compos. Sci. Technol. 2014, 104, 111–124. [Google Scholar] [CrossRef]
- Wei, X.; Naraghi, M.; Espinosa, H.D. Optimal Length Scales Emerging from Shear Load Transfer in Natural Materials: Application to Carbon-Based Nanocomposite Design. ACS Nano 2012, 6, 2333–2344. [Google Scholar] [CrossRef] [PubMed]
- Abid, N.; Mirkhalaf, M.; Barthelat, F. Discrete-Element Modeling of Nacre-like Materials: Effects of Random Microstructures on Strain Localization and Mechanical Performance. J. Mech. Phys. Solids 2018, 112, 385–402. [Google Scholar] [CrossRef]
- Barthelat, F.; Dastjerdi, A.K.; Rabiei, R. An Improved Failure Criterion for Biological and Engineered Staggered Composites. J. R. Soc. Interface 2013, 10, 20120849. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, B. Biomimetics: Bioinspired Hierarchical-Structured Surfaces for Green Science and Technology; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 3319282840. [Google Scholar]
- Carbone, M.G.P.; Tammaro, D.; Manikas, A.C.; Paterakis, G.; Di Maio, E.; Galiotis, C. Wettability of Graphene by Molten Polymers. Polymer 2019, 180, 121708. [Google Scholar] [CrossRef]
- Cheng-An, T.; Hao, Z.; Fang, W.; Hui, Z.; Xiaorong, Z.; Jianfang, W. Mechanical Properties of Graphene Oxide/Polyvinyl Alcohol Composite Film. Polym. Polym. Compos. 2017, 25, 11–16. [Google Scholar] [CrossRef]
- Liang, J.; Huang, Y.; Zhang, L.; Wang, Y.; Ma, Y.; Cuo, T.; Chen, Y. Molecular-Level Dispersion of Graphene into Poly(Vinyl Alcohol) and Effective Reinforcement of Their Nanocomposites. Adv. Funct. Mater. 2009, 19, 2297–2302. [Google Scholar] [CrossRef]




| Filler | Matrix Type | Composite Mechanical Behaviour | Composite Conductivities |
|---|---|---|---|
| Graphitic (GO, RGO, GNP, Pyrolytic Graphite…) | Brittle | Pseudo-elastic | Electrically Conductive in plane High ratio in plane/trough thickness thermal conductivity |
| Ductile | Plastic | ||
| Ceramic (MTM, Alumina, Silica…) | Brittle | Pseudo-elastic | Isolating |
| Ductile | Plastic |
| Particle | Costs | Geometry | Elastic Modulus | In Plane—Therm. Cond. | Elec. Cond. |
|---|---|---|---|---|---|
| Graphene | EUR 200–300 per flake | Monolayer | 1 TPa [9] | 5000 W/mK [9] | 107–108 S/m [9] |
| GO | 2–5 layers 48 EUR/g | 2–5 layer BET 420 m2/g | 250 GPa [10] | 72 W/mK with an oxidation degree of 0.35 [11] | 270 S/m [12] |
| RGO | 2–5 layers 68 EUR/g | 2–5 layer BET 1562 m2/g | 250–350 GPa [13] | 670 W/mK with an oxidation degree of 0.05 [11] | 4480 S/m [14] |
| GNP | 6–10 EUR/g | >10 layer BET 30 m2/g | 25–40 GPa [15] | 300–470 W/mK [8] | 2 × 106 S/m [16] |
| MTM | <1 EUR/g | BET 750 m2 very high (nm × µm) aspect ratio | 207 GPa [17] | 16 W/m [18] | 25 to 100 mS/m [18] |
| Authors | RVE | Elastic Modulus |
|---|---|---|
| (a) Cox et al. [101] | 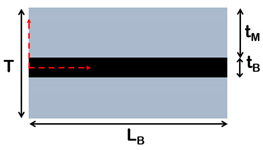 | |
| (b) Kotha et al. [102] |  | |
| (c) Barthelat et al. [103]. | 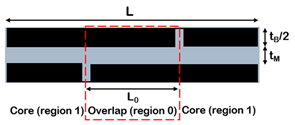 | |
| (d) Begley et al. [100] | 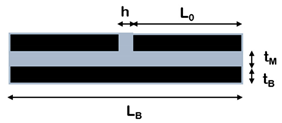 | |
| (e) Wei et al. [104] |  | |
| (f) Cilento et al. [68] |  | with |
| Thick Platelets (AR < 10) | Slender Platelets (AR > 30) | |
|---|---|---|
| Strength | Increase with AR | Independent from AR |
| Stress–Strain curve | Resembles the matrix constitutive law | Does not depend on the matrix behaviour |
| Behaviour | Ductile (Yield criterion) | Fragile (Fracture criterion) |
| Fracture | - | Matrix fracture with crack tip at the platelets’ ends |
| Distribution of shear stresses | Homogeneous | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cilento, F.; Martone, A.; Giordano, M. Insights on Shear Transfer Efficiency in “Brick-and-Mortar” Composites Made of 2D Carbon Nanoparticles. Nanomaterials 2022, 12, 1359. https://doi.org/10.3390/nano12081359
Cilento F, Martone A, Giordano M. Insights on Shear Transfer Efficiency in “Brick-and-Mortar” Composites Made of 2D Carbon Nanoparticles. Nanomaterials. 2022; 12(8):1359. https://doi.org/10.3390/nano12081359
Chicago/Turabian StyleCilento, Fabrizia, Alfonso Martone, and Michele Giordano. 2022. "Insights on Shear Transfer Efficiency in “Brick-and-Mortar” Composites Made of 2D Carbon Nanoparticles" Nanomaterials 12, no. 8: 1359. https://doi.org/10.3390/nano12081359
APA StyleCilento, F., Martone, A., & Giordano, M. (2022). Insights on Shear Transfer Efficiency in “Brick-and-Mortar” Composites Made of 2D Carbon Nanoparticles. Nanomaterials, 12(8), 1359. https://doi.org/10.3390/nano12081359








