High-FOM Temperature Sensing Based on Hg-EIT-Like Liquid Metamaterial Unit
Abstract
:1. Introduction
2. Structure Design and Numerical Investigations
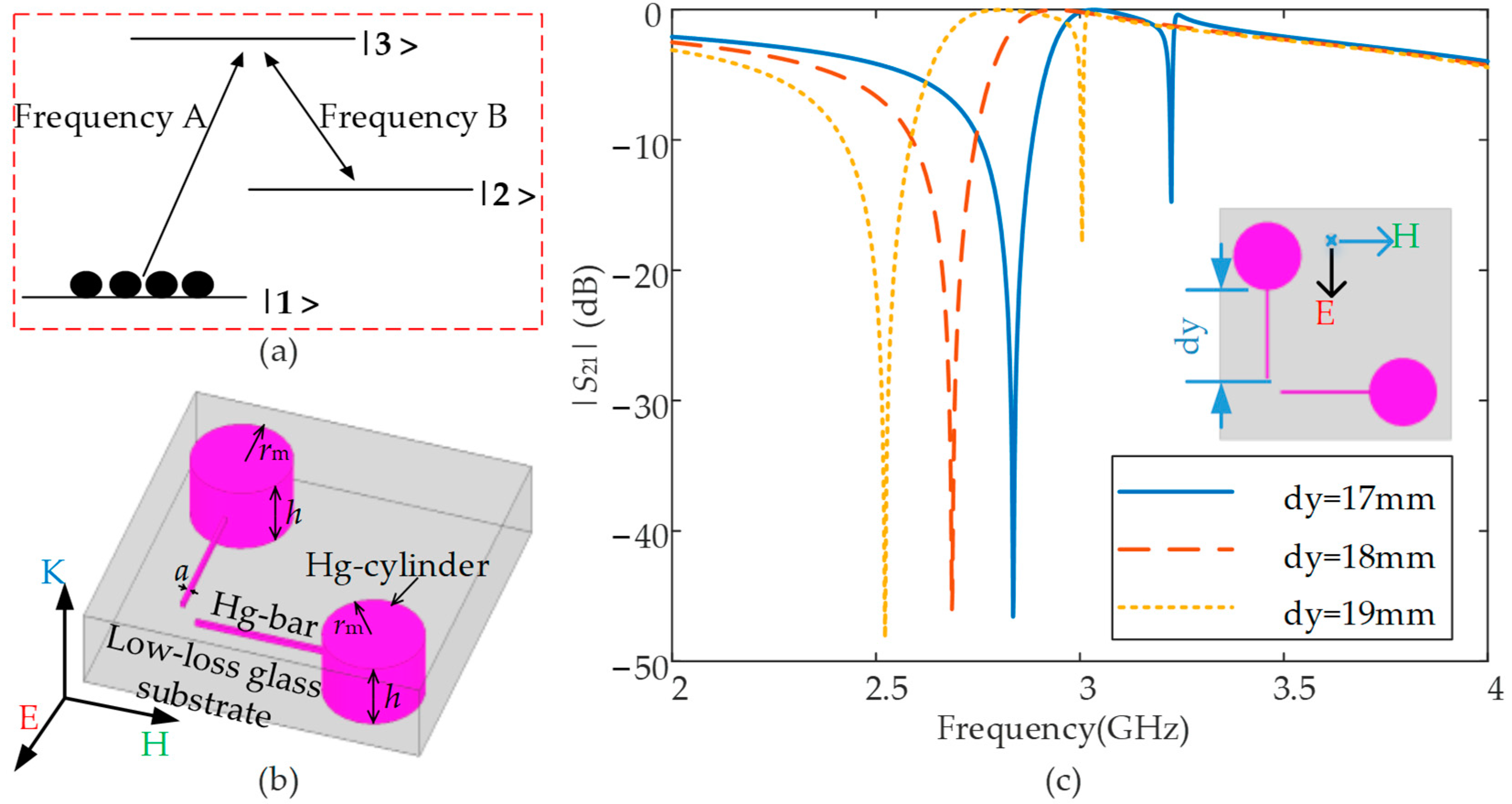
2.1. Operating Mechanism
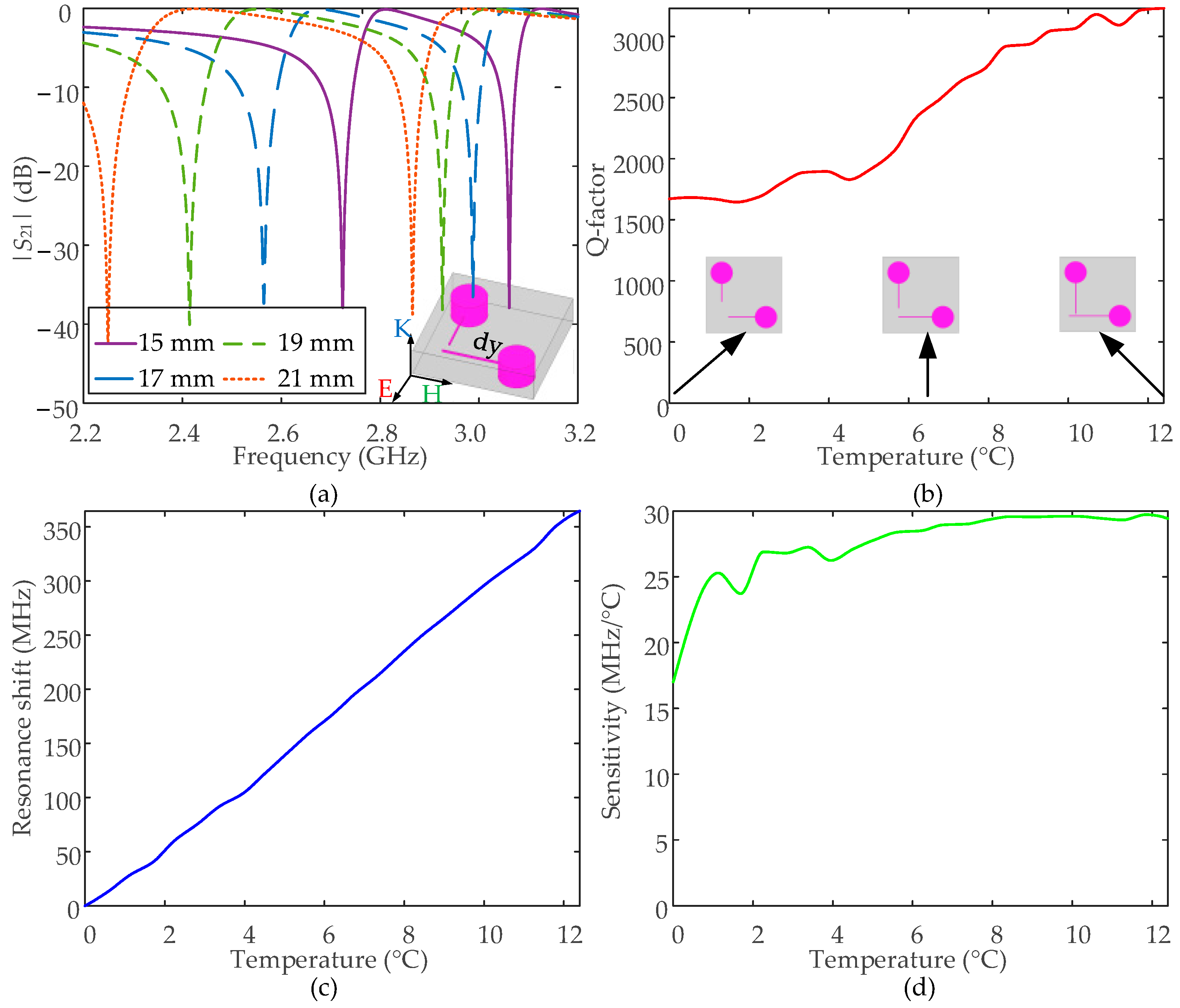
2.2. Initial Strucure Design and Numerical Anslysis
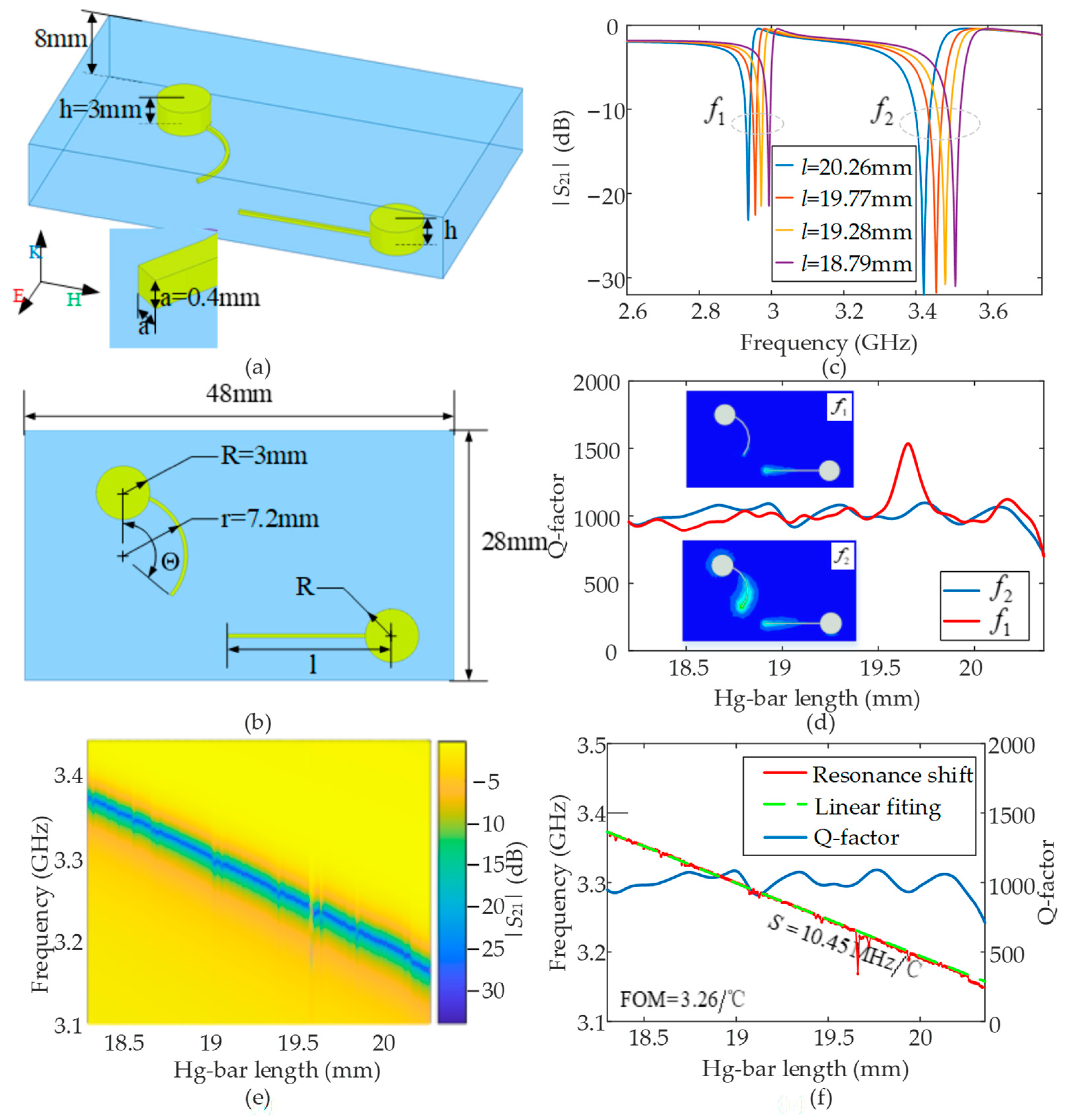
2.3. Structure Optimizations
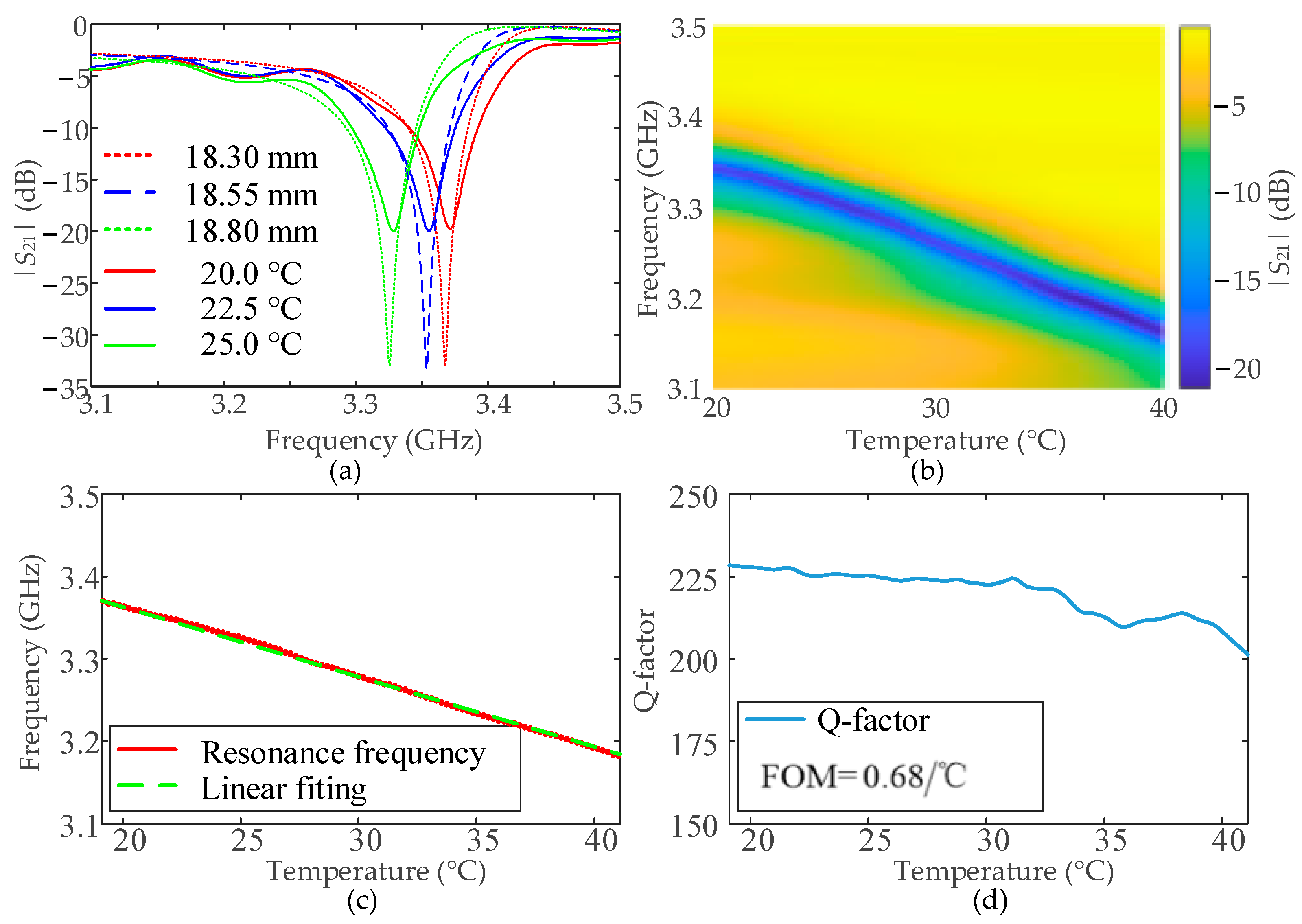
3. Experimental Demonstrations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, T.J.; Smith, D.R.; Liu, R. Metamaterials: Theory, Design and Applications; Spring: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Jung, J.; Park, H.; Park, J.; Chang, T.; Shin, J. Broadband metamaterials and metasurfaces: A review from the perspectives of materials and devices. Nanophotonics 2020, 9, 3165–3196. [Google Scholar] [CrossRef]
- Wang, J.; Lang, T.; Hong, Z.; Xiao, M.; Yu, J. Design and fabrication of a triple-band terahertz metamaterial absorber. Nanomaterials 2021, 11, 1110. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.; Cui, T.J. Information metamaterials: Bridging the physical world and digital world. PhotoniX 2020, 1, 1. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Chen, X.; Thakur, Y.; Lu, B.; Zhang, Q.; Runt, J.; Zhang, Q.M. A highly scalable dielectric metamaterial with superior capacitor performance over a broad temperature. Sci. Adv. 2020, 6, eaax6622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, S.; Qian, Z.; Rajaram, V.; Calisgan, S.D.; Alù, A.; Rinaldi, M. Ultra-narrowband metamaterial absorbers for high spectral resolution infrared spectroscopy. Adv. Opt. Mater. 2019, 7, 1801236. [Google Scholar] [CrossRef]
- Li, Z.; Sun, X.; Ma, C.; Li, J.; Li, X.; Guan, B.-O.; Chen, K. Ultra-narrow-band metamaterial perfect absorber based on surface lattice resonance in a WS 2 nanodisk array. Opt. Express 2021, 29, 27084–27091. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, L.; Li, J.; Wang, Y.; Wen, G. Polarization conversion of metasurface for the application of wide band low-profile circular polarization slot antenna. Appl. Phys. Lett. 2016, 109, 054101. [Google Scholar] [CrossRef]
- Akram, M.R.; Ding, G.; Chen, K.; Feng, Y.; Zhu, W. Ultrathin single layer metasurfaces with ultra-wideband operation for both transmission and reflection. Adv. Mater. 2020, 32, 1907308. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.; Wang, C.; Wang, M.; Wang, S.; Ding, F.; Huang, Y.; Zhang, X.; Liu, H.; Ling, X.; et al. Deterministic approach to achieve full-polarization cloak. Research 2021, 2021, 6382172. [Google Scholar] [CrossRef]
- Zhu, W.; Xiao, F.; Rukhlenko, I.D.; Geng, J.; Liang, X.; Premaratne, M.; Jin, R. Wideband visible-light absorption in an ultrathin silicon nanostructure. Opt. Express 2017, 25, 5781–5786. [Google Scholar] [CrossRef]
- Xie, J.; Quader, S.; Xiao, F.; He, C.; Liang, X.; Geng, J.; Jin, R.; Zhu, W.; Rukhlenko, I.D. Truly all-dielectric ultrabroadband metamaterial absorber: Water-based and ground-free. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 536–540. [Google Scholar] [CrossRef]
- Huang, Y.; Wen, G.; Zhu, W.; Li, J.; Si, L.; Premaratne, M. Experimental demonstration of a magnetically tunable ferrite based metamaterial absorber. Opt. Express 2014, 22, 16408–16417. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wei, X.; Rukhlenko, I.D.; Chen, H.-T.; Zhu, W. Electrically tunable metasurface with independent frequency and amplitude modulations. ACS Photonics 2019, 7, 265–271. [Google Scholar] [CrossRef]
- Lee, M.; Lee, E.; So, S.; Byun, S.; Son, J.; Ge, B.; Lee, H.; Park, H.S.; Shim, W.; Pee, J.H.; et al. Bulk metamaterials exhibiting chemically tunable hyperbolic responses. J. Am. Chem. Soc. 2021, 143, 20725–20734. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Lin, F.; Liu, F.; Zhang, H. Investigation of phonon scattering on the tunable mechanisms of terahertz graphene metamaterials. Nanomaterials 2020, 10, 39. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Xue, T.; Zhang, J.; Liu, L.; Xie, J.; Wang, G.; Yao, J.Q.; Zhu, W.; Ye, X. Terahertz toroidal metasurface biosensor for sensitive distinction of lung cancer cells. Nanophotonics 2022, 11, 101–109. [Google Scholar] [CrossRef]
- Zhang, J.; Mu, N.; Liu, L.; Xie, J.; Feng, H.; Yao, J.; Chen, T.; Zhu, W. Highly sensitive detection of malignant glioma cells using metamaterial-inspired THz biosensor based on electromagnetically induced transparency. Biosens. Bioelectron. 2021, 185, 113241. [Google Scholar] [CrossRef]
- Gao, F.; Yuan, P.; Gao, S.; Deng, J.; Sun, Z.; Jin, G.; Zeng, G.; Yan, B. Active electromagnetically induced transparency effect in graphene-dielectric hybrid metamaterial and its high-performance sensor application. Nanomaterials 2021, 11, 2032. [Google Scholar] [CrossRef]
- Yang, J.; Lin, Y.-S. Design of tunable terahertz metamaterial sensor with single- and dual-resonance characteristic. Nanomaterials 2021, 11, 2212. [Google Scholar] [CrossRef]
- Lochbaum, A.; Dorodnyy, A.; Koch, U.; Koepfli, S.M.; Volk, S.; Fedoryshyn, Y.; Wood, V.; Leuthold, J. Compact mid-infrared gas sensing enabled by an all-metamaterial design. Nano Lett. 2020, 20, 4169–4176. [Google Scholar] [CrossRef]
- Xu, R.; Lin, Y.-S. Tunable infrared metamaterial emitter for gas sensing application. Nanomaterials 2020, 10, 1442. [Google Scholar] [CrossRef] [PubMed]
- Shang, W.; Xiao, F.; Zhu, W.; Han, L.; Premaratne, M.; Mei, T.; Zhao, J. Unidirectional scattering exploited transverse displacement sensor with tunable measuring range. Opt. Express 2019, 27, 4944–4955. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Liu, Y.; Fu, Y. Transmit-Array, Metasurface-based tunable polarizer and high-performance biosensor in the visible regime. Nanomaterials 2019, 9, 603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kairm, H.; Delfin, D.; Shuvo, M.A.I.; Chavez, L.A.; Garcia, C.R.; Barton, J.H.; Gaytan, S.M.; Cadena, M.A.; Rumpf, R.C.; Wicker, R.B.; et al. Concept and model of a metamaterial-based passive wireless temperature sensor for harsh environment applications. IEEE Sens. J. 2014, 15, 1445–1452. [Google Scholar] [CrossRef]
- Zou, H.; Cheng, Y. Design of a six-band terahertz metamaterial absorber for temperature sensing application. Opt. Mater. 2019, 88, 674–679. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Olifierczuk, M.; Parka, J. Thermally induced tunability of a terahertz metamaterial by using a specially designed nematic liquid crystal mixture. Opt. Express 2018, 26, 2443–2452. [Google Scholar] [CrossRef]
- Keshavarz, A.; Zakery, A. Ultrahigh sensitive temperature sensor based on graphene-semiconductor metamaterial. Appl. Phys. A 2017, 123, 797. [Google Scholar] [CrossRef]
- Yang, F.; Fan, Y.; Yang, R.; Xu, J.; Fu, Q.; Zhang, F.; Wei, Z.; Li, H. Controllable coherent perfect absorber made of liquid metal-based metasurface. Opt. Express 2019, 27, 25974–25982. [Google Scholar] [CrossRef]
- Xu, J.; Fan, Y.; Yang, R.; Fu, Q.; Zhang, F. Realization of switchable EIT metamaterial by exploiting fluidity of liquid metal. Opt. Express 2019, 27, 2837–2843. [Google Scholar] [CrossRef]
- Xie, X.; Pu, M.; Liu, K.; Ma, X.; Li, X.; Yang, J.; Luo, X. High-efficiency and tunable circular-polarization beam splitting with a liquid-filled all-metallic catenary meta-mirror. Adv. Mater. Technol. 2019, 4, 1900334. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, Z.; Li, J.; Lv, W.; Xie, F.; Wen, G.; Yu, P.; Chen, Z. Dynamics analysis of a pair of ring resonators in liquid media. Phys. Rev. Appl. 2018, 10, 044026. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Huang, Y.; Ma, L.; Yu, P.; Wen, G. Experimental investigations of wave-DSRR interactions in liquid-phase media. Appl. Phys. Lett. 2019, 114, 144101. [Google Scholar] [CrossRef]
- Chen, L.; Ruan, Y.; Cui, H.Y. Liquid metal metasurface for flexible beam-steering. Opt. Express 2019, 27, 23282–23292. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Chen, D.; Zheng, W.; Li, J.; Wang, W.; Liu, Y.; Zhou, Y.; Huang, Y.; Wen, G. Thermally tunable high-Q metamaterial and sensing application based on liquid metals. Opt. Express 2021, 29, 6069–6079. [Google Scholar] [CrossRef]
- Ma, L.; Chen, D.; Zheng, W.; Li, J.; Wang, W.; Liu, Y.; Zhou, Y.; Huang, Y.; Wen, G. High-Q liquid metamaterial unit for the temperature sensing application in microstrip line plate form. Results Phys. 2021, 24, 104172. [Google Scholar] [CrossRef]
- Ling, K.; Kim, K.; Lim, S. Flexible liquid metal-filled metamaterial absorber on polydimethylsiloxane (PDMS). Opt. Express 2015, 23, 21375–21383. [Google Scholar] [CrossRef]
- Wu, P.C.; Zhu, W.; Shen, Z.X.; Chong, P.H.J.; Ser, W.; Tsai, D.P.; Liu, A.Q. Broadband wide-angle multifunctional polarization converter via liquid-metal-based metasurface. Adv. Opt. Mater. 2017, 5, 1600938. [Google Scholar] [CrossRef]
- Fedotov, V.A.; Rose, M.; Prosvirnin, S.L.; Papasimakis, N.; Zheludev, N.I. Sharp trapped-mode resonances in planar metamaterials with a broken structural symmetry. Phys. Rev. Lett. 2007, 99, 147401. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liu, W.; Li, Z.; Li, Z.; Cheng, H.; Chen, S.; Tian, J. High-quality-factor multiple Fano resonances for refractive index sensing. Opt. Lett. 2018, 43, 1842–1845. [Google Scholar] [CrossRef]
- Kaelberer, T.; Fedotov, V.A.; Papasimakis, N.; Tsai, D.P.; Zheludev, N.I. Toroidal dipolar response in a metamaterial. Science 2010, 330, 1510–1512. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Du, S.; Cui, A.; Li, Z.; Fan, Y.; Chen, S.; Li, W.; Li, J.; Gu, C. High-quality-factor mid-infrared toroidal excitation in folded 3D metamaterials. Adv. Mater. 2017, 29, 1606298. [Google Scholar] [CrossRef] [PubMed]
- Miroshnichenko, A.E.; Evlyukhin, A.B.; Yu, Y.F.; Bakker, R.M.; Chipouline, A.; Kuznetsov, A.I.; Luk’yanchuk, B.; Chichkov, B.N.; Kivshar, Y.S. Nonradiating anapole modes in dielectric nanoparticles. Nat. Commun. 2015, 6, 8069. [Google Scholar] [CrossRef] [PubMed]
- Basharin, A.A.; Chuguevsky, V.; Volsky, N.; Kafesaki, M.; Economou, E.N. Extremely high Q-factor metamaterials due to anapole excitation. Phys. Rev. B 2017, 95, 035104. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Liu, Y.; Wang, W.; Chen, D.; Wei, X.; Li, J.; Huang, Y.; Wen, G. Research on the reflection-type ELC-based optomechanical metamaterial. Opt. Express 2022, 30, 5498–5511. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valagiannopoulos, C.A.; Uzunoglu, N.K. Rigorous analysis of a metallic circular post in a rectangular waveguide with step discontinuity of sidewalls. IEEE Trans. Microw. Theory Tech. 2007, 55, 1673–1684. [Google Scholar] [CrossRef]
- Valagiannopoulos, C.A. Electromagnetic propagation into parallel-plate waveguide in the presence of a skew metallic surface. Electromagnetics 2011, 31, 593–605. [Google Scholar] [CrossRef]
- Mollah, M.A.; Islam, S.R.; Yousufali, M.; Abdulrazak, L.F.; Hossain, M.B.; Amiri, I.S. Plasmonic temperature sensor using D-shaped photonic crystal fiber. Results Phys. 2020, 16, 102966. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.; Chen, H.; Li, J.; Fan, Z. High-sensitivity plasmonic temperature sensor based on photonic crystal fiber coated with nanoscale gold film. Appl. Phys. Express 2015, 8, 046701. [Google Scholar] [CrossRef]
- Peng, Y.; Hou, J.; Zhang, Y.; Huang, Z.; Xiao, R.; Lu, Q. Temperature sensing using the bandgap-like effect in a selectively liquid-filled photonic crystal fiber. Opt. Lett. 2013, 38, 263–265. [Google Scholar] [CrossRef]
- Chen, H.; Li, S.; Li, J.; Han, Y.; Wu, Y. High sensitivity of temperature sensor based on ultracompact photonics crystal fibers. IEEE Photonics J. 2014, 6, 1–6. [Google Scholar] [CrossRef]
- Gieseler, J.; Novotny, L.; Quidant, R. Thermal nonlinearities in a nanomechanical oscillator. Nat. Phys. 2013, 9, 806–810. [Google Scholar] [CrossRef] [Green Version]
- Lapine, M.; Shadrivov, I.V.; Powell, D.A.; Kivshar, Y.S. Magnetoelastic metamaterials. Nat. Mater. 2012, 11, 30–33. [Google Scholar] [CrossRef] [PubMed]
- Lv, W.; Xie, F.; Huang, Y.; Li, J.; Fang, X.; Rashid, A.; Zhu, W.; Rukhlenko, I.D.; Wen, G. Nonlinear coupling states study of electromagnetic force actuated plasmonic nonlinear metamaterials. Opt. Express 2018, 26, 3211–3220. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Pei, L.; Wang, J.; Ruan, Z.; Zheng, J.; Li, J.; Ning, T. Magnetic field and temperature dual-parameter sensor based on magnetic fluid materials filled photonic crystal fiber. Opt. Express 2020, 28, 1456–1471. [Google Scholar] [CrossRef]
- Ferreira, R.A.; Mamontova, E.; Botas, A.M.; Shestakov, M.; Vanacken, J.; Moshchalkov, V.; Guari, Y.; Chibotaru, L.F.; Luneau, D.; André, P.S.; et al. Synchronous temperature and magnetic field dual-sensing by luminescence in a dysprosium single-molecule magnet. Adv. Opt. Mater. 2021, 9, 2101495. [Google Scholar] [CrossRef]

| Resonant Structure | Sensitivity | Q-Factor | FOM (/°C) | |||
|---|---|---|---|---|---|---|
| Sim. | Mea. | Sim. | Mea. | Sim. | Mea. | |
| Fano [35] | 15.7 MHz/°C | 16.4 MHz/°C | ~800 | ~80 | ~6.3 | ~0.59 |
| Anapole [36] | 16 MHz/°C | 17.14 MHz/°C | ~230 | ~65 | ~1.53 | ~0.3 |
| Benzene-PCF [49] | 12 nm/°C | – | ~90 | – | ~0.4 | – |
| LM-PCF [50] | 2.15 nm/°C | – | ~50 | – | ~0.061 | – |
| DS-PCF [51] | – | 5.55 nm/°C | – | ~70 | – | ~0.076 |
| LC-PCF [52] | 2.82 nm/°C | – | ~20 | – | ~0.048 | – |
| EIT-like | 10.45 MHz/°C | 9.5 MHz/°C | ~1000 | ~210 | ~3.26 | ~0.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhou, Y.; Peng, F.; Chen, D.; Xian, C.; Kuang, P.; Ma, L.; Wei, X.; Huang, Y.; Wen, G. High-FOM Temperature Sensing Based on Hg-EIT-Like Liquid Metamaterial Unit. Nanomaterials 2022, 12, 1395. https://doi.org/10.3390/nano12091395
Li J, Zhou Y, Peng F, Chen D, Xian C, Kuang P, Ma L, Wei X, Huang Y, Wen G. High-FOM Temperature Sensing Based on Hg-EIT-Like Liquid Metamaterial Unit. Nanomaterials. 2022; 12(9):1395. https://doi.org/10.3390/nano12091395
Chicago/Turabian StyleLi, Jian, Yuedan Zhou, Fengwei Peng, Dexu Chen, Chengwei Xian, Pengjun Kuang, Liang Ma, Xueming Wei, Yongjun Huang, and Guangjun Wen. 2022. "High-FOM Temperature Sensing Based on Hg-EIT-Like Liquid Metamaterial Unit" Nanomaterials 12, no. 9: 1395. https://doi.org/10.3390/nano12091395
APA StyleLi, J., Zhou, Y., Peng, F., Chen, D., Xian, C., Kuang, P., Ma, L., Wei, X., Huang, Y., & Wen, G. (2022). High-FOM Temperature Sensing Based on Hg-EIT-Like Liquid Metamaterial Unit. Nanomaterials, 12(9), 1395. https://doi.org/10.3390/nano12091395







