Microstructure and Intrinsic Strain of Nanocrystals in Ferroelectric (Na,K)NbO3 Nanofibers
Abstract
:1. Introduction
2. Experimental Section
3. Results and Discussion
3.1. Crystallized Fibers’ Morphology
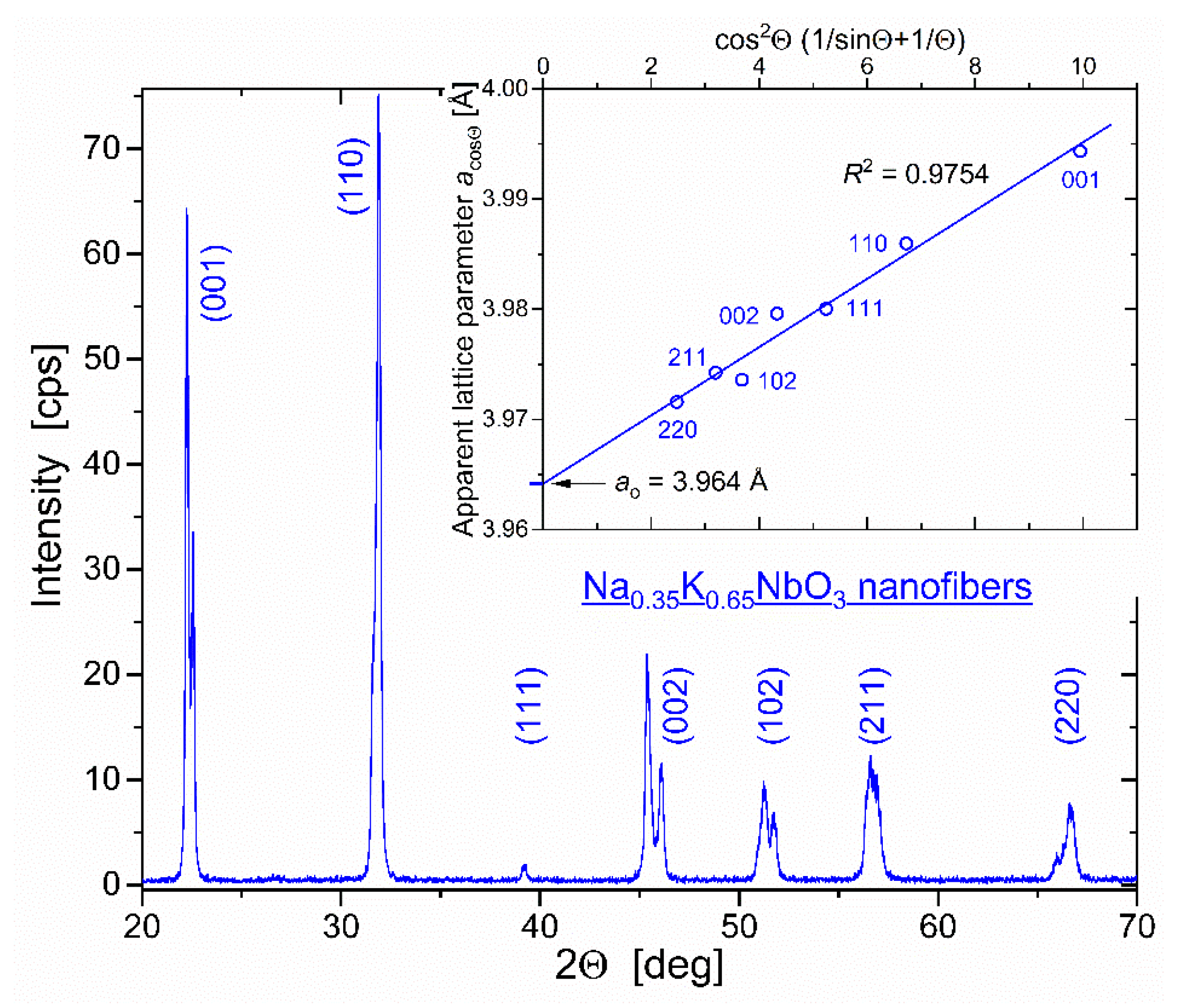
3.2. Lattice Parameter
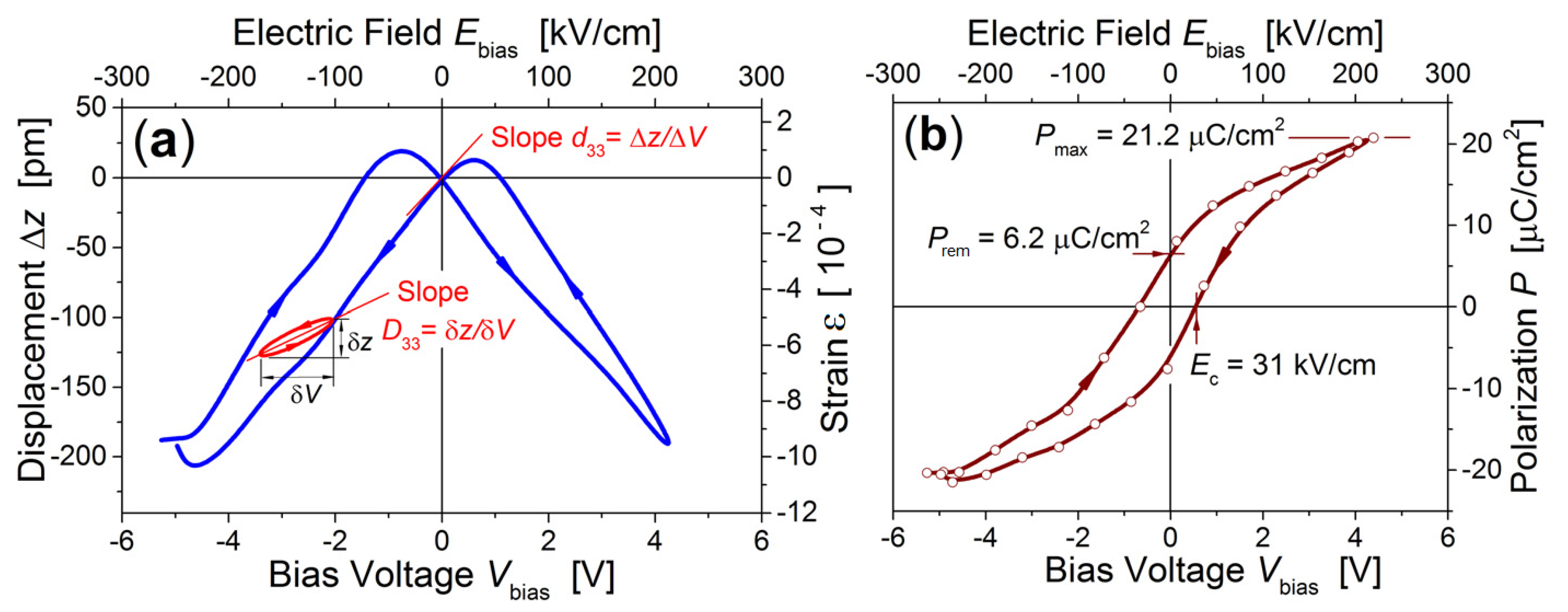
3.3. Ferroelectricity
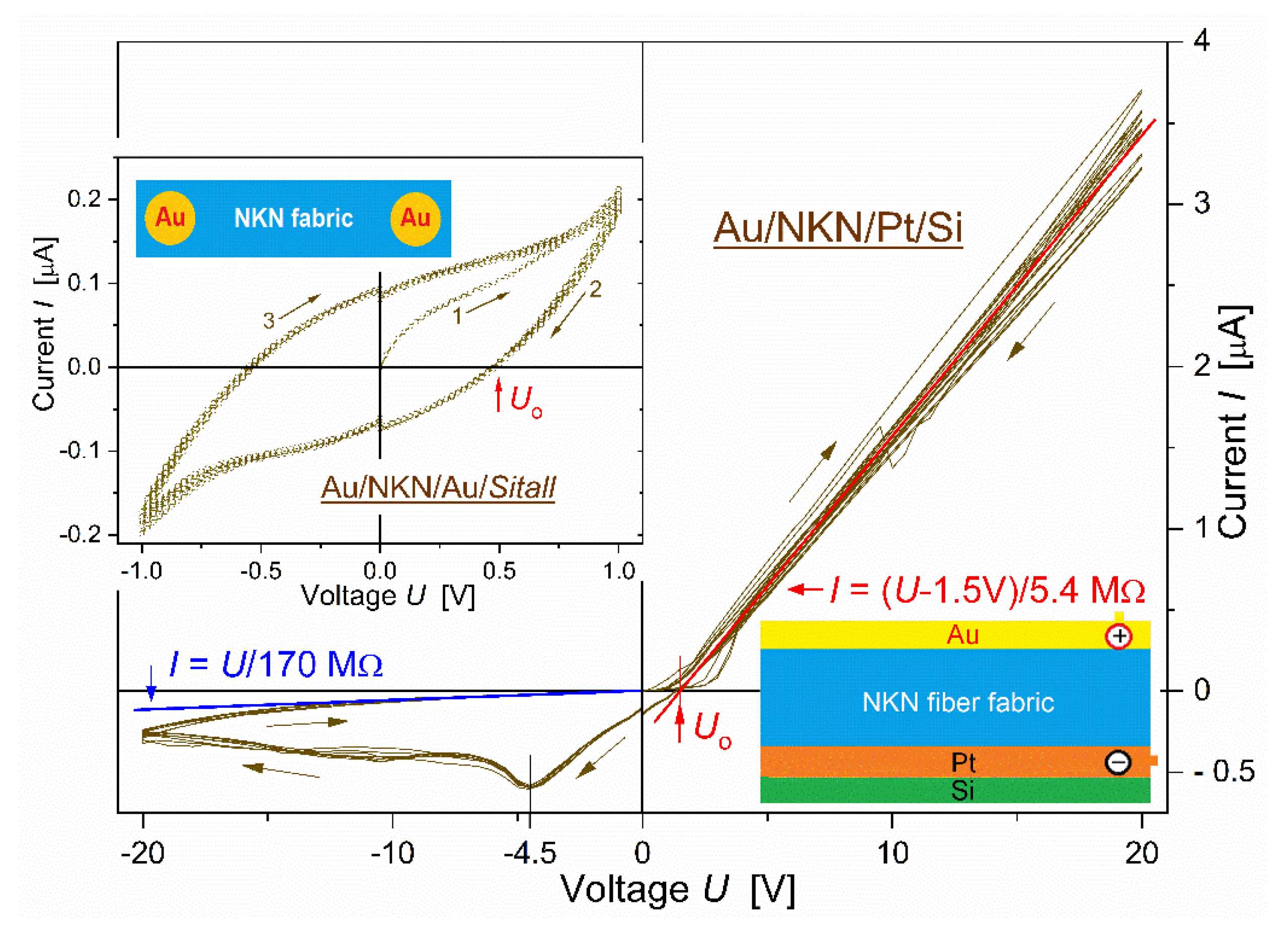
3.4. Electrical Switching
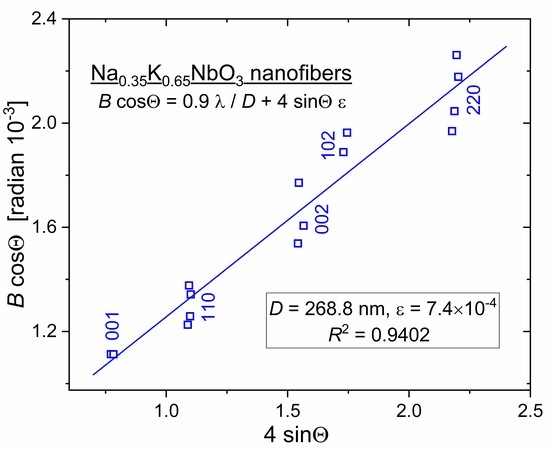
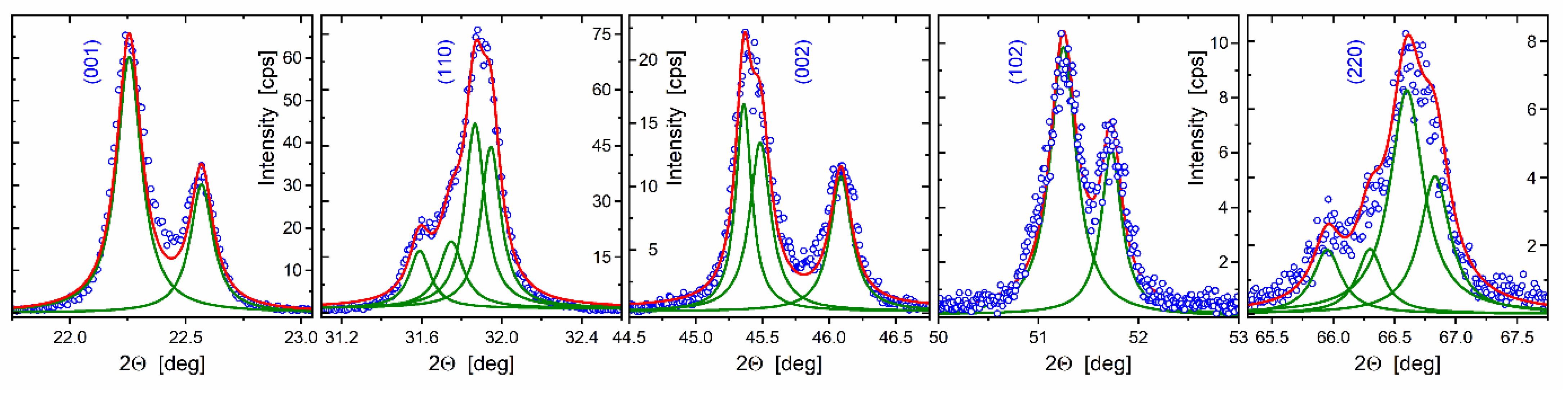
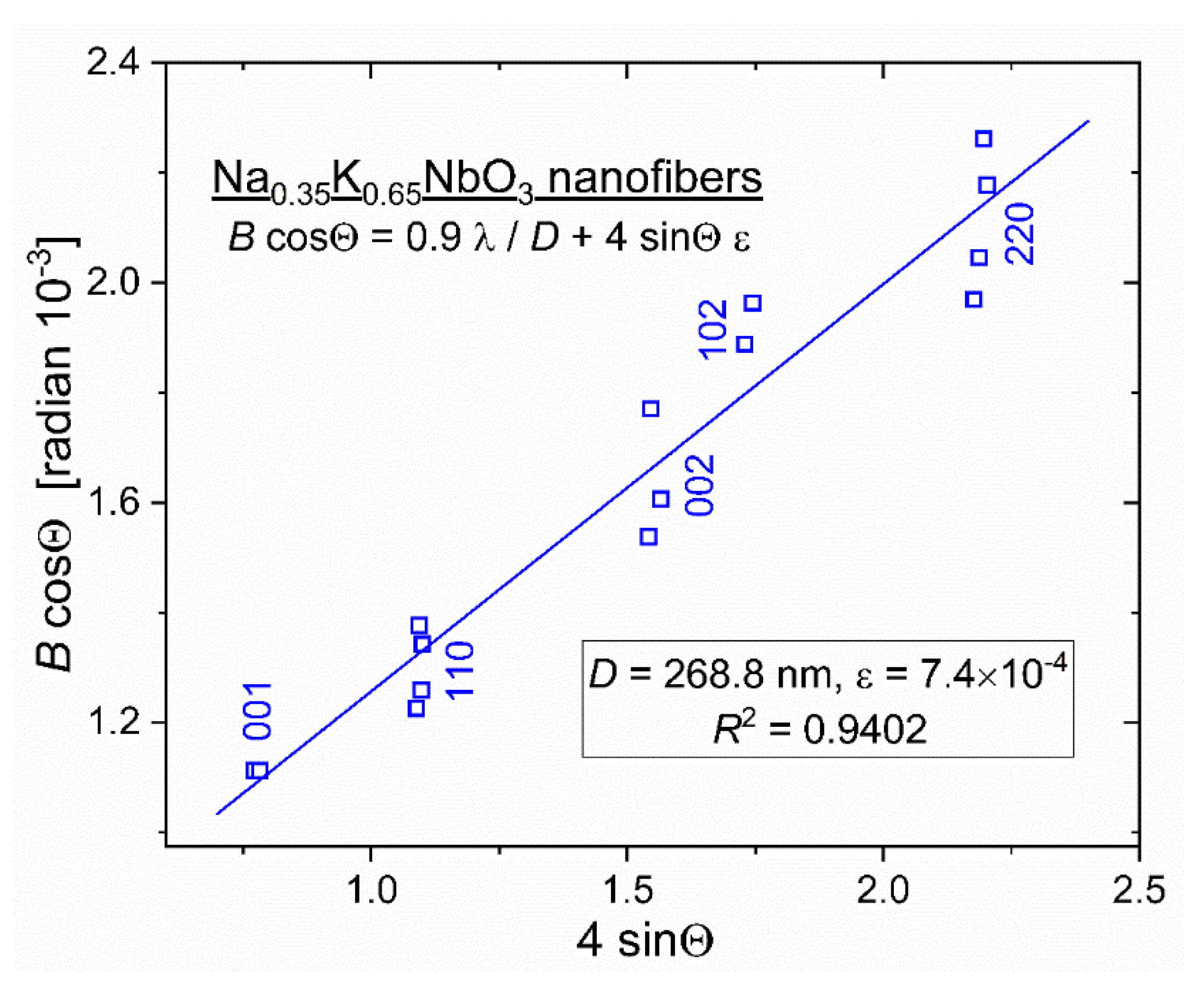
3.5. Size and Intrinsic Strain of Nanocrystals
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matthias, B.T. New Ferroelectric Crystals. Phys. Rev. 1949, 75, 1771. [Google Scholar] [CrossRef]
- Shirane, G.; Danner, H.; Pavlovic, A.; Pepinsky, R. Phase Transitions in Ferroelectric KNbO3. Phys. Rev. 1954, 93, 672–673. [Google Scholar] [CrossRef]
- Shirane, G.; Newnham, R.; Pepinsky, R. Dielectric properties and phase transitions of NaNbO3 and (Na,K)NbO3. Phys Rev. 1954, 96, 581–588. [Google Scholar] [CrossRef]
- Egerton, L.; Dillon, D.M. Piezoelectric and Dielectric Properties of Ceramics in the System Potassium-Sodium Niobate. J. Am. Ceram. Soc. 1959, 42, 438–442. [Google Scholar] [CrossRef]
- Dungan, R.H.; Golding, R.D. Polarization of NaNbO3–KNbO3 ceramic solid solutions. J. Am. Ceram. Soc. 1965, 48, 601. [Google Scholar] [CrossRef]
- Nilsson, K.; Lidman, J.; Ljungstrom, K.; Kjellman, C. Biocompatible Material for Implants. U.S. Patent 6,526,984, 4 March 2003. [Google Scholar]
- Margolin, A.M.; Surovyak, Z.S.; Zacharchenko, I.N.; Alyoshin, V.A.; Chernusheva, L.K.; Radchenko, M.G.; Dudukevich, V.P. (K,Na)NbO3 ferroelectric films formed under HF cathode sputtering. Zhurnal Tekhnicheskoi Fiz. 1988, 58, 2355–2359. [Google Scholar]
- Wang, X.; Helmersson, U.; Olafsson, S.; Rudner, S.; Wernlund, L.-D.; Gevorgian, S. Growth and field dependent dielectric properties of epitaxial Na0.5K0.5NbO3 thin films. Appl. Phys. Lett. 1998, 73, 927–929. [Google Scholar] [CrossRef]
- Blomqvist, M.; Koh, J.-H.; Khartsev, S.; Grishin, A.; Andreasson, J. High-performance epitaxial Na0.5K0.5NbO3 thin films by magnetron sputtering. Appl. Phys. Lett. 2002, 81, 337–339. [Google Scholar] [CrossRef]
- Khartsev, S.I.; Grishin, A.M.; Andréasson, J.; Koh, J.-H.; Song, J.-S. Comparative characteristics of Na0.5K0.5NbO3 films on Pt by pulsed laser deposition and magnetron sputtering. Integr. Ferroelectr. 2003, 55, 769–779. [Google Scholar] [CrossRef]
- Cho, C.-R.; Grishin, A. Self-assembling ferroelectric Na0.5K0.5NbO3 thin films by pulsed-laser deposition. Appl. Phys. Lett. 1999, 75, 268–270. [Google Scholar] [CrossRef]
- Cho, C.-R.; Grishin, A.M. Background oxygen effects on pulsed laser deposited Na0.5K0.5NbO3 films: From superparaelectric state to ferroelectricity. J. Appl. Phys. 2000, 87, 4439–4448. [Google Scholar] [CrossRef]
- Setter, N.; Damjanovic, D.; Eng, L.; Fox, G.; Gevorgian, S.; Hong, S.; Kingon, A.; Kohlstedt, H.; Park, N.Y.; Stephenson, G.B.; et al. Ferroelectric thin films: Review of materials, properties, and applications. J. Appl. Phys. 2006, 100, 051606. [Google Scholar] [CrossRef]
- Damjanovic, D.; Klein, N.; Li, J.; Porokhonskyy, V. What can be expected from lead-free piezoelectric materials? Funct. Mater. Lett. 2010, 3, 5–13. [Google Scholar] [CrossRef]
- Zhang, S.-W.; Zhou, Z.; Luo, J.; Li, J.-F. Potassium-sodium-niobate-based thin films: Lead free for micro-piezoelectrics. Ann. Phys. 2019, 531, 1800525. [Google Scholar] [CrossRef] [Green Version]
- Burns, S.R.; Dolgos, M.R. Sizing up (K1-xNax)NbO3 films: A review of synthesis routes, properties & applications. New J. Chem. 2021, 45, 7408–7436. [Google Scholar]
- Gupta, A.; Sharma, S.; Gupta, R.; Sharma, A.; Tomar, M. Exploitation of electric field assisted optical signal amplification in ferroelectric photorefractive K0.50Na0.50NbO3 thin film. Opt. Mater. 2021, 121, 111599. [Google Scholar] [CrossRef]
- Grishin, A.M.; Markova, N.P. Broadband luminescent ferroelectric biocompatible Er: (Na,K)NbO3 nanofibers. J. Am. Ceram. Soc. 2016, 100, 1051–1056. [Google Scholar] [CrossRef]
- Gao, X.; Cheng, Z.; Chen, Z.; Liu, Y.; Meng, X.; Zhang, X.; Wang, J.; Guo, Q.; Li, B.; Sun, H.; et al. The mechanism for the enhanced piezoelectricity in multi-elements doped (K,Na)NbO3 ceramics. Nat. Commun. 2021, 12, 881. [Google Scholar] [CrossRef]
- Hussain, F.; Khesro, A.; Lu, Z.; Alotaibi, N.; Mohamad, A.A.; Wang, G.; Wang, D.; Zhou, D. Acceptor and Donor Dopants in Potassium Sodium Niobate Based Ceramics. Front. Mater. 2020, 7, 160. [Google Scholar] [CrossRef]
- Jalalian, A.; Grishin, A.M. Biocompatible ferroelectric (Na,K)NbO3 nanofibers. Appl. Phys. Lett. 2012, 100, 012904. [Google Scholar] [CrossRef] [Green Version]
- Jalalian, A.; Grishin, A.M. Piezoelectricity and electrostriction in biocompatible (Na,K)NbO3 nanofiber scaffolds. Appl. Phys. Lett. 2014, 104, 243701. [Google Scholar] [CrossRef]
- Anton, F. Process and Apparatus for Preparing Artificial Threads. U.S. Patent 1,975,504, 2 October 1934. [Google Scholar]
- De Vrieze, S.; De Clerck, K. 80 Years of Electrospinning. In Proceedings of the International conference on Latest Advances in High-Tech Textiles and Textile-Based Materials, Ghent, Belgium, 23–25 September 2009; pp. 60–63. [Google Scholar]
- Grishin, A.M.; Velichko, A.A.; Jalalian, A. Nb2O5 nanofiber memristor. Appl. Phys. Lett. 2013, 103, 053111. [Google Scholar] [CrossRef]
- Liu, Y.; Sreenivasulu, G.; Zhou, P.; Fu, J.; Filippov, D.; Zhang, W.; Zhou, T.; Zhang, T.; Shah, P.; Page, M.R.; et al. Converse magneto-electric effects in a core–shell multiferroic nanofiber by electric field tuning of ferromagnetic resonance. Sci. Rep. 2020, 10, 20170. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhou, P.; Ge, B.; Liu, J.; Zhang, J.; Zhang, W.; Zhang, T.; Srinivasan, G. Strain-mediated magneto-electric effects in coaxial nanofibers of Y/W-type hexagonal ferrites and ferroelectrics. J. Compos. Sci. 2021, 5, 268. [Google Scholar] [CrossRef]
- Choopani, S.; Samavat, F.; Kolobova, E.N.; Grishin, A.M. Ferromagnetic resonance and magnetic anisotropy in biocompatible Y3Fe5O12@Na0.5K0.5NbO3 core-shell nanofibers. Ceram. Int. 2020, 46, 2072–2078. [Google Scholar] [CrossRef]
- Grishin, A.M.; Jalalian, A.; Tsindlekht, M.I. Gadolinia nanofibers as a multimodal bioimaging and potential radiation therapy agent. AIP Adv. 2015, 5, 057104. [Google Scholar] [CrossRef] [Green Version]
- Yousry, Y.M.; Yao, K.; Tan, X.; Mohamed, A.M.; Wang, Y.; Chen, S.; Ramakrishna, S. Structure and high performance of lead-free (K0.5Na0.5)NbO3 piezoelectric nanofibers with surface-induced crystallization at lowered temperature. ACS Appl. Mater. Interfaces 2019, 11, 23503–23511. [Google Scholar] [CrossRef] [Green Version]
- Azimi, B.; Milazzo, M.; Lazzeri, A.; Berrettini, S.; Uddin, M.J.; Qin, Z.; Buehler, M.J.; Danti, S. Electrospinning Piezoelectric Fibers for Biocompatible Devices. Adv. Healthc. Mater. 2020, 9, e1901287. [Google Scholar] [CrossRef]
- Khare, D.; Basu, B.; Dubey, A.K. Electrical stimulation and piezoelectric biomaterials for bone tissue engineering applications. Biomaterials 2020, 258, 120280. [Google Scholar]
- Ichangi, A.; Shvartsman, V.V.; Lupascu, D.C.; Lê, K.; Grosch, M.; Schmidt-Verma, A.K.; Bohr, C.; Verma, A.; Fischer, T.; Mathur, S. Li and Ta-modified KNN piezoceramic fibers for vibrational energy harvesters. J. Eur. Ceram. Soc. 2021, 41, 7662–7669. [Google Scholar] [CrossRef]
- Jalalian, A.; Kavrik, M.S.; Khartsev, S.I.; Grishin, A.M. Ferromagnetic resonance in Y3Fe5O12 nanofibers. Appl. Phys. Lett. 2011, 99, 102501. [Google Scholar] [CrossRef]
- Ohbayashi, K. Piezoelectric Properties and Microstructure of (K,Na)NbO3–KTiNbO5 Composite Lead-Free Piezoelectric Ceramic. In Piezoelectric Materials; Ogawa, T., Ed.; IntechOpen: London, UK, 2016. [Google Scholar] [CrossRef] [Green Version]
- Gibbons, D.F.; Chirba, V.G. Acoustical loss and Young’s modulus of yttrium iron garnet. Phys. Rev. 1958, 110, 770–771. [Google Scholar] [CrossRef]
- Hereinafter we Notify NKN Bragg Reflections Using Miller Indices in Pseudo-Cubic Na0.35K0.65NbO3 Crystal System. This unit Cell is Twice Downsized Monoclinic Bravais Lattice from Inorganic Crystal Structure Database (ICSD-38004). Available online: https://icsd.products.fiz-karlsruhe.de/ (accessed on 27 April 2022).
- Nelson, J.B.; Riley, D.P. An experimental investigation of extrapolation methods in the derivation of accurate unit-cell dimen-sions of crystals. Proc. Phys. Soc. 1945, 57, 160–177. [Google Scholar] [CrossRef]
- Ahn, C.W.; Lee, S.Y.; Lee, H.J.; Ullah, A.; Bae, J.S.; Jeong, E.D.; Choi, J.S.; Park, B.H.; Kim, I.W. The effect of K and Na excess on the ferroelectric and piezoelectric properties of K0.5Na0.5NbO3 thin films. J. Phys. D Appl. Phys. 2009, 42, 215304. [Google Scholar] [CrossRef]
- Bobnar, V.; Malič, B.; Holc, J.; Kosec, M.; Steinhausen, R.; Beige, H. Electrostrictive effect in lead-free relaxor K0.5Na0.5NbO3–SrTiO3 ceramic system. J. Appl. Phys. 2005, 98, 024113. [Google Scholar] [CrossRef]
- Stokes, A.R.; Wilson, A.J.C. A method of calculating the integral breadths of Debye-Scherrer lines. Math. Proc. Camb. Philos. Soc. 1942, 38, 313–322. [Google Scholar] [CrossRef]
- Stokes, A.R.; Wilson, A.J.C. The diffraction of X rays by distorted crystal aggregates. Proc. Phys. Soc. 1944, 56, 174–181. [Google Scholar] [CrossRef]
- Williamson, G.K.; Hall, W.H. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grishin, A.M. Microstructure and Intrinsic Strain of Nanocrystals in Ferroelectric (Na,K)NbO3 Nanofibers. Nanomaterials 2022, 12, 1541. https://doi.org/10.3390/nano12091541
Grishin AM. Microstructure and Intrinsic Strain of Nanocrystals in Ferroelectric (Na,K)NbO3 Nanofibers. Nanomaterials. 2022; 12(9):1541. https://doi.org/10.3390/nano12091541
Chicago/Turabian StyleGrishin, Alexander M. 2022. "Microstructure and Intrinsic Strain of Nanocrystals in Ferroelectric (Na,K)NbO3 Nanofibers" Nanomaterials 12, no. 9: 1541. https://doi.org/10.3390/nano12091541