Thermal and Hydraulic Performances of Carbon and Metallic Oxides-Based Nanomaterials
Abstract
:1. Introduction
2. Materials and Methods
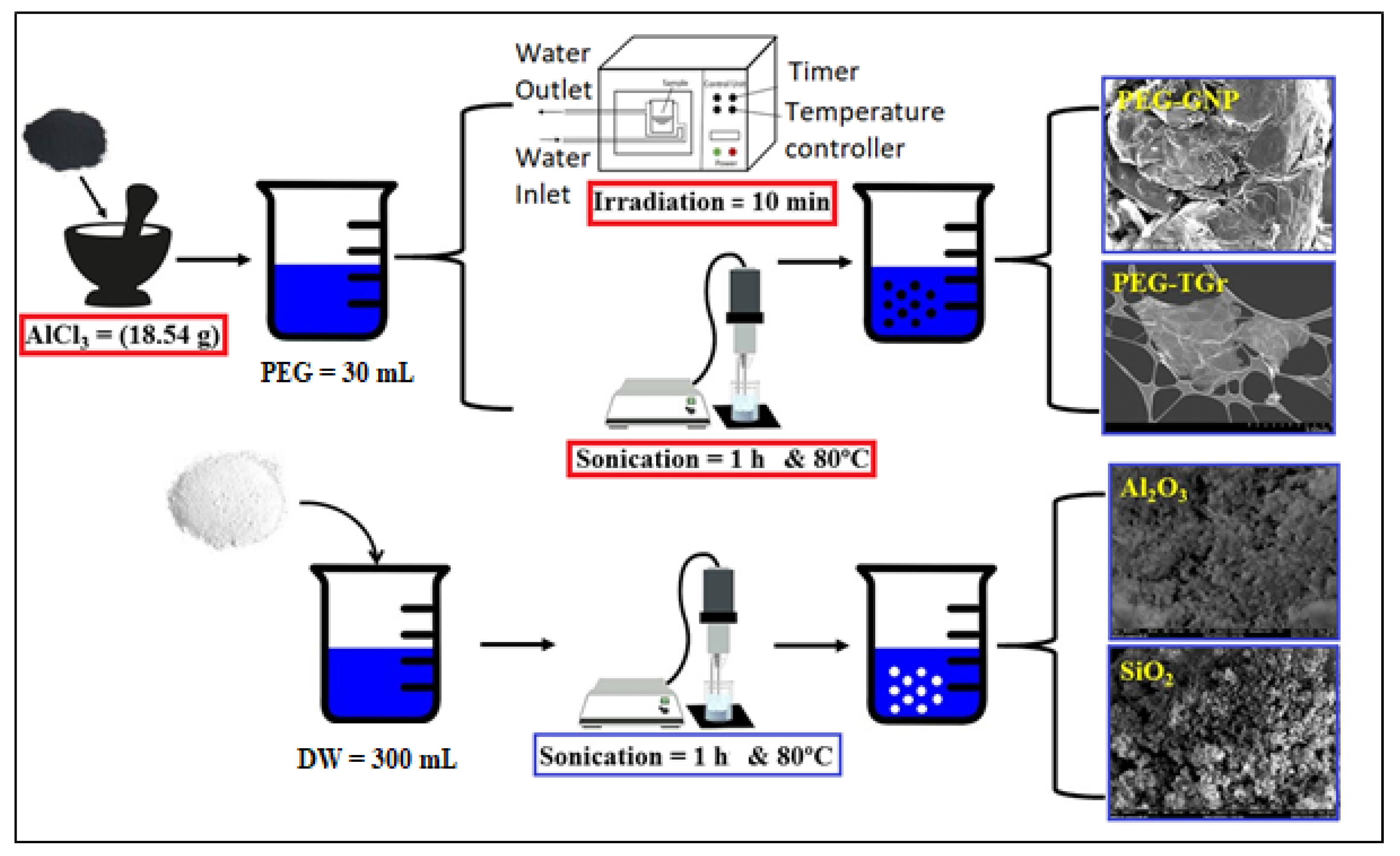
2.1. Functionalization and Preparation Process
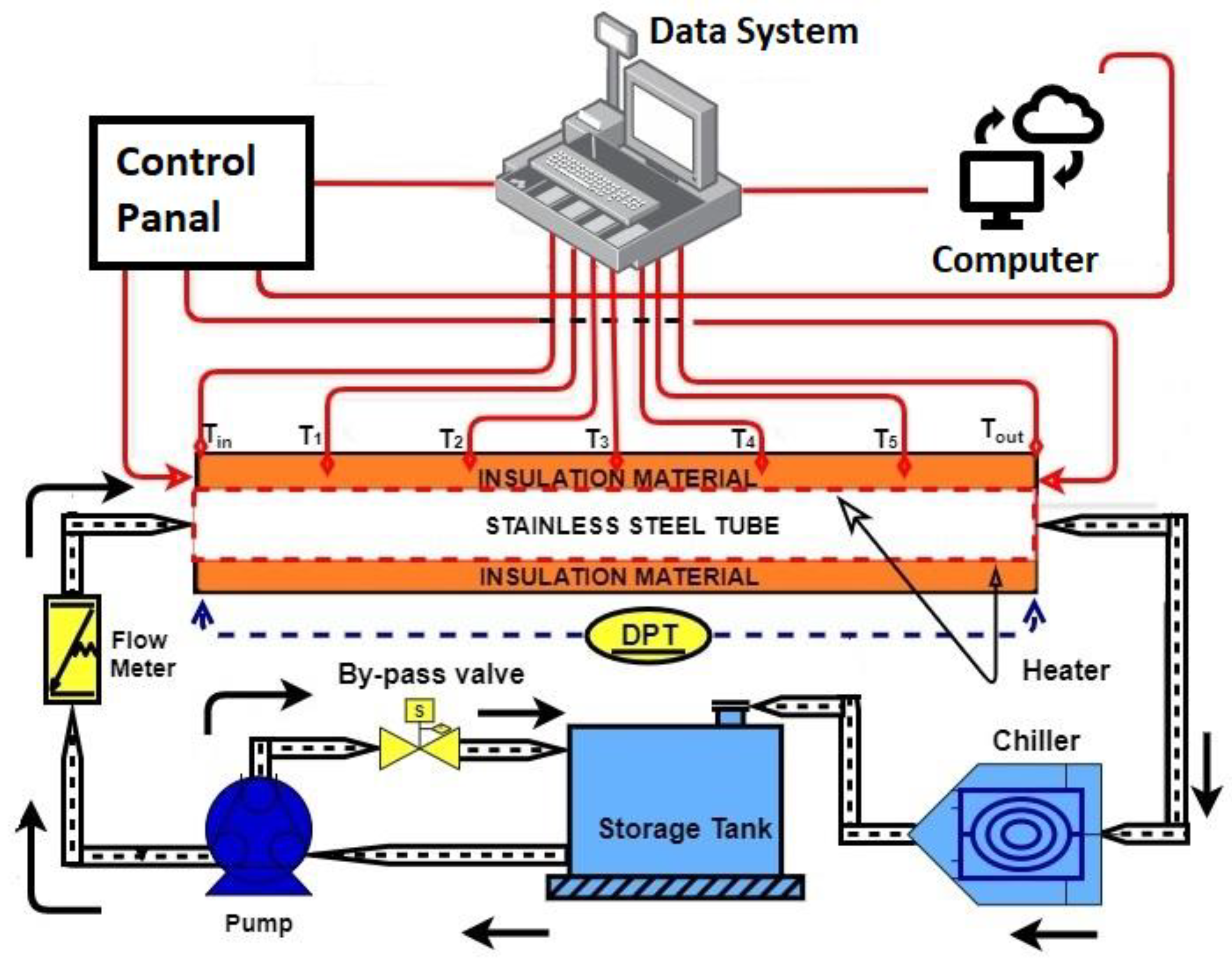
2.2. Experimental Methodologies
2.3. Data Processing
| Heat flux (q″) | (1) | |
| Heat transfer coefficient (h) | (2) | |
| Nusselt number (Nu) | (3) | |
| Friction factor (f) | (4) | |
| Reynolds Number (Re) | (5) | |
| Prandtl number (Pr) | (6) |
3. Results and Discussion
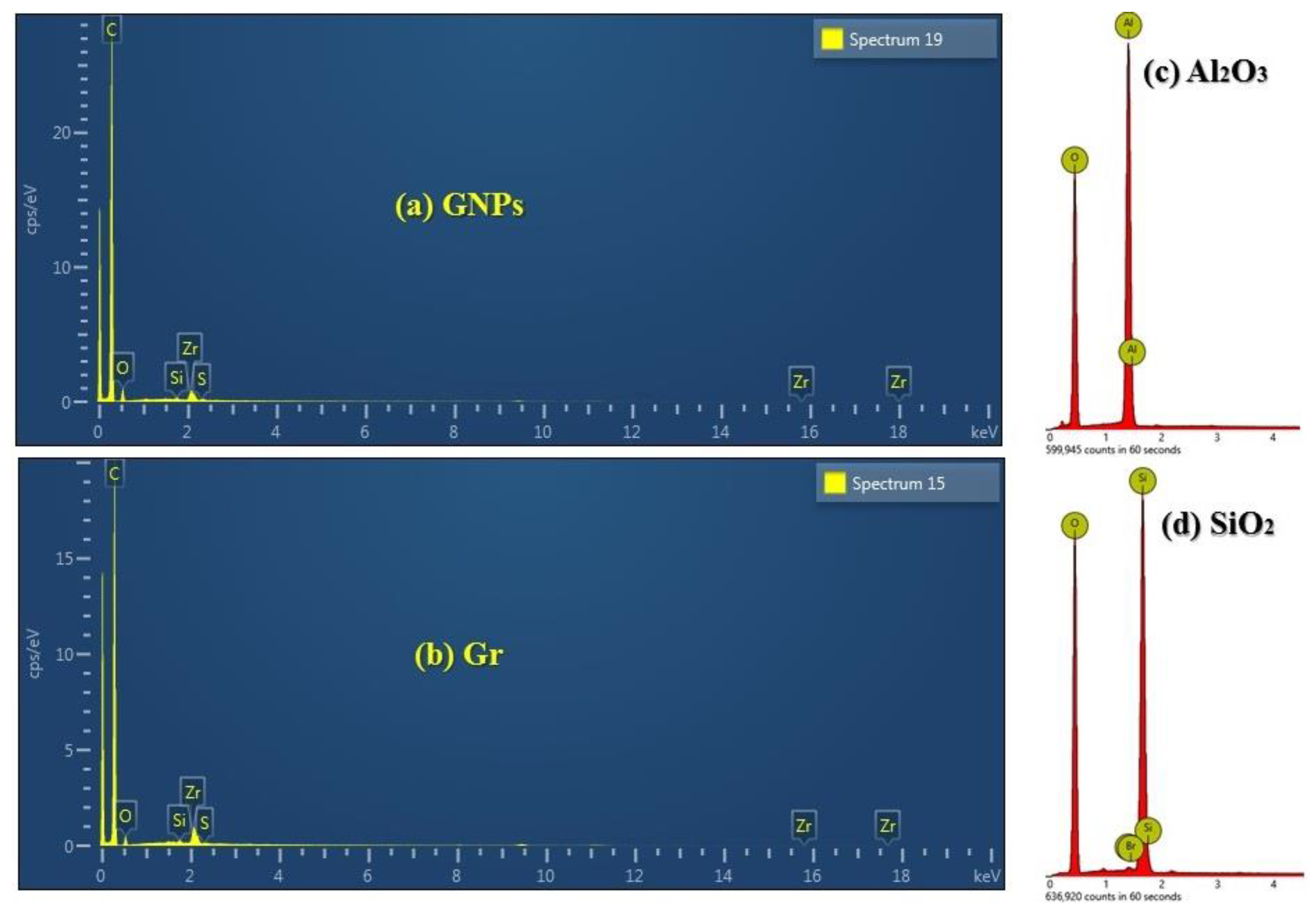
3.1. Characterization of Nanofluids
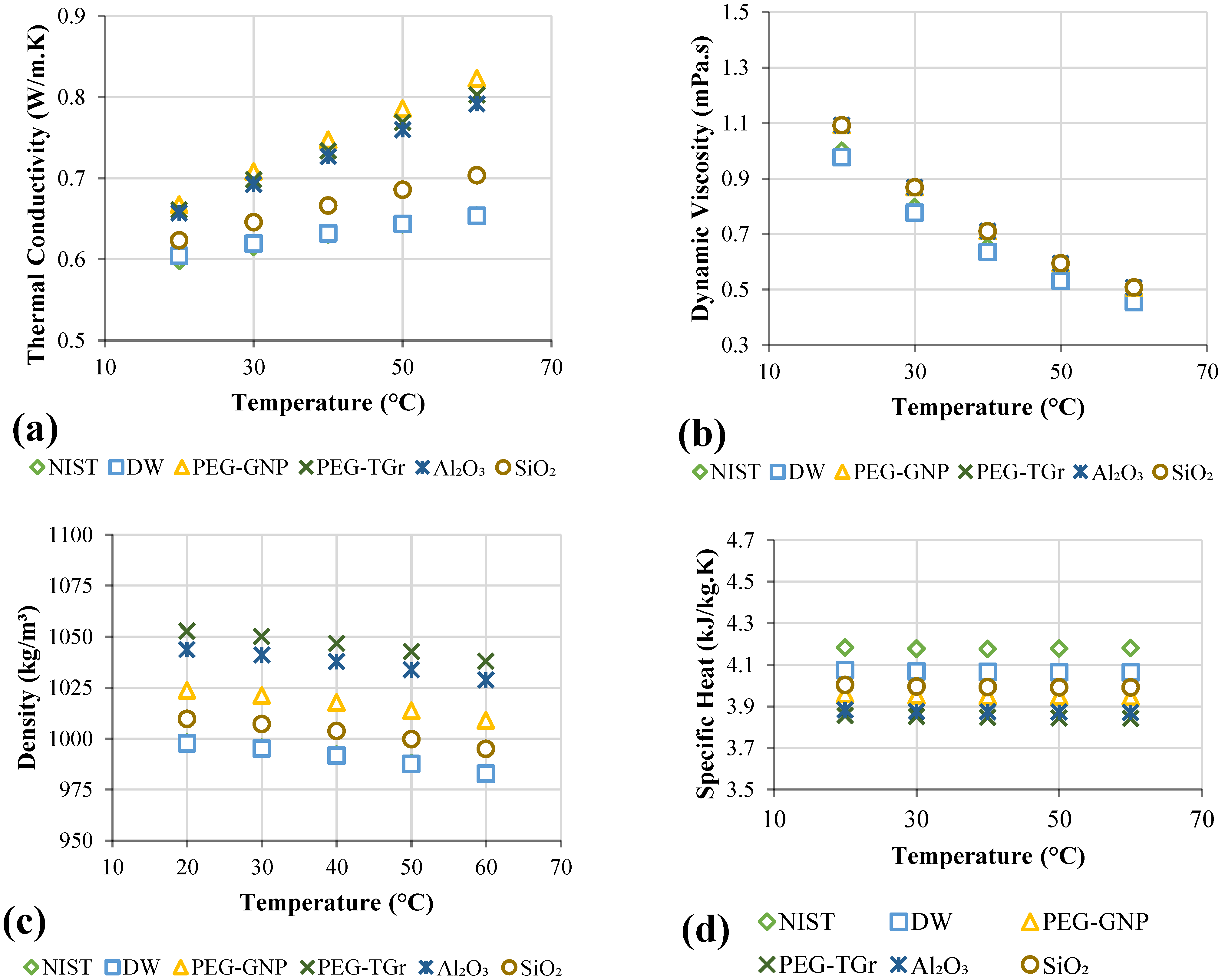
3.2. Thermophysical Properties Measurements
3.3. Validation Test for Distilled Water
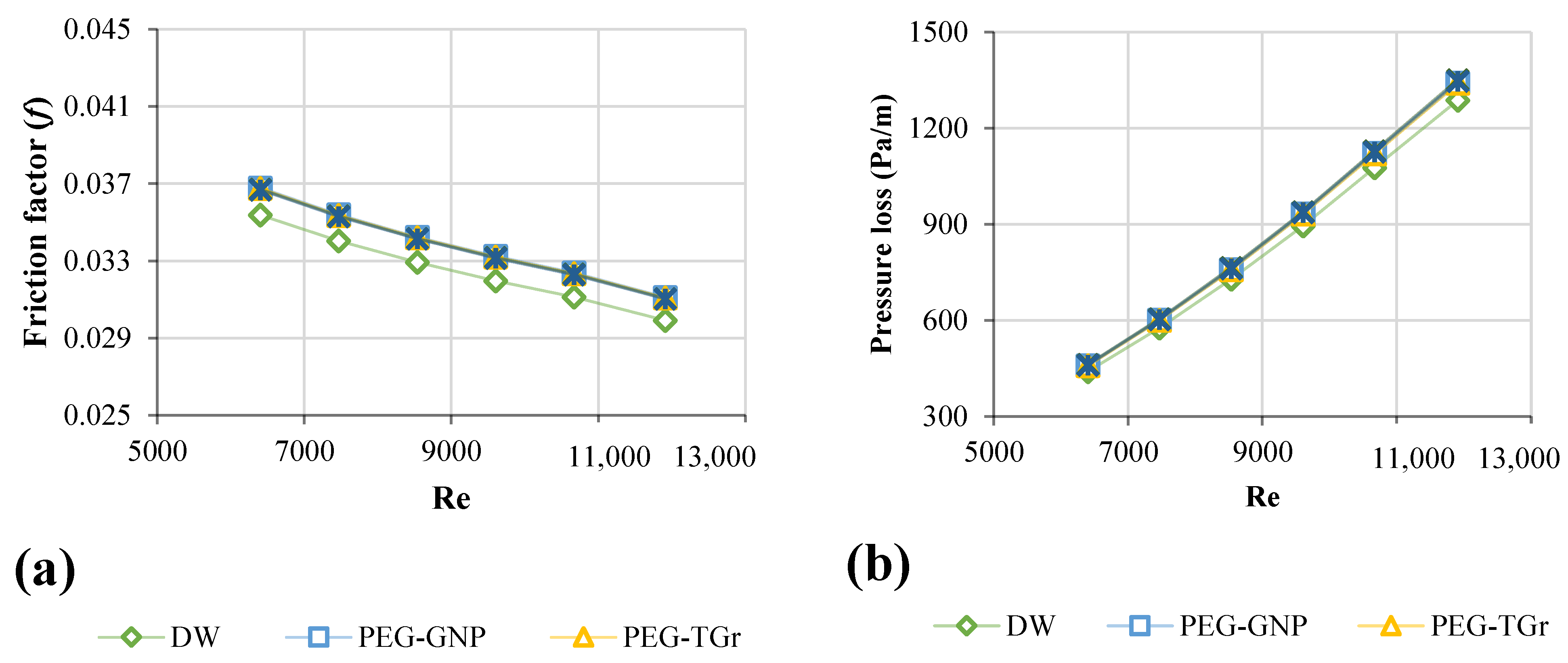
3.4. Convective Heat Transfer of Functionalized Nanofluids
3.5. Friction Factor of Nanofluids
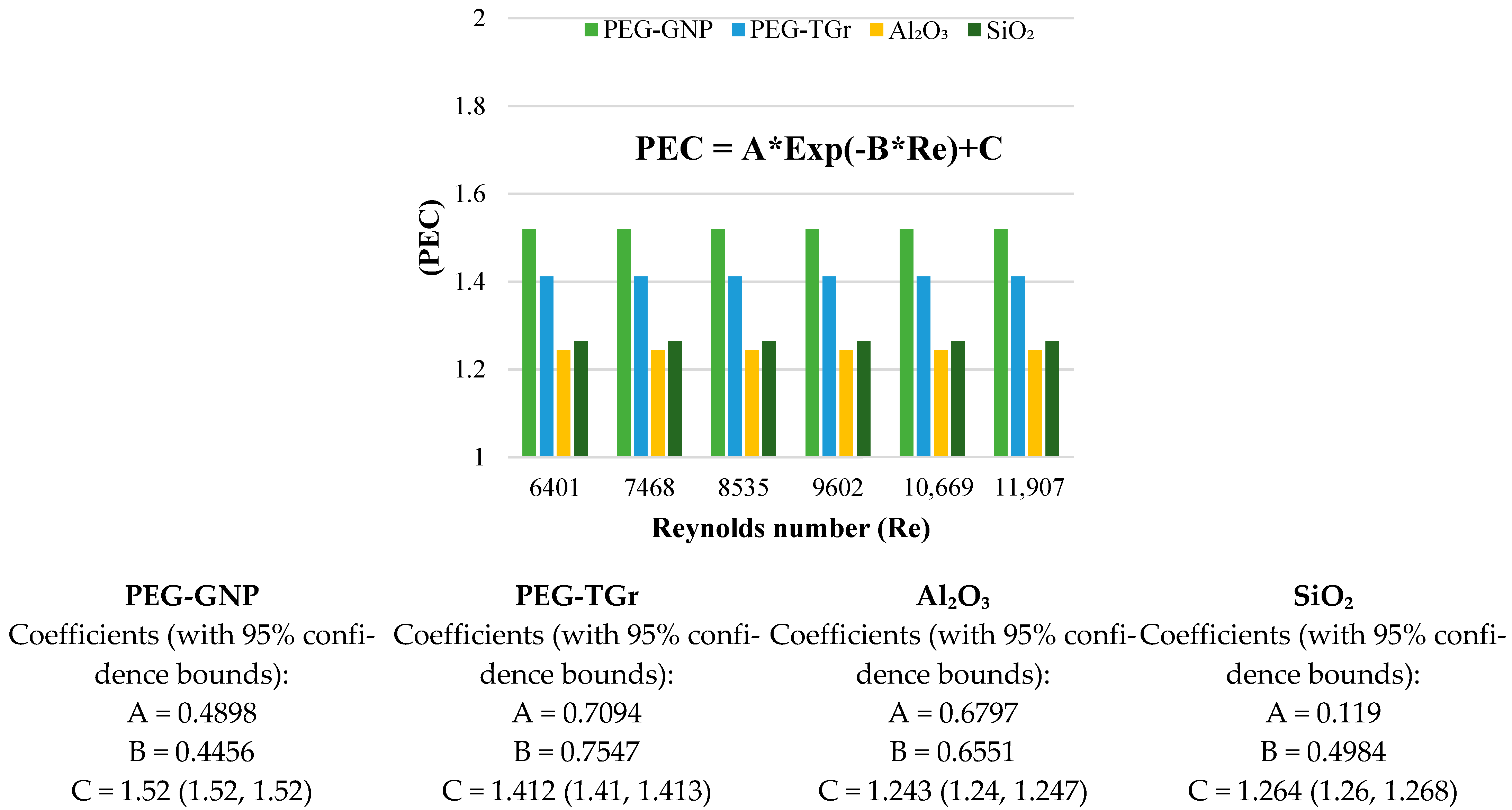
3.6. Performance Index and Performance Evaluation Criterion
3.7. Pumping Power of Different Nanofluids
4. Conclusions
- The nanofluids exhibited the greatest thermal conductivity improvements as follows: PEG@GNPs = 31.6%, PEG@TGr = 29.74%, Al2O3 = 10.44%, and SiO2 = 9.32% at 60 °C and 0.1 wt.%.
- The highest improvement in heat transfer coefficients of the nanofluids was as follows: PEG@GNPs = 44.4%, PEG@TGr = 41.2%, Al2O3 = 22.5%, and SiO2 = 24 % at 0.1 wt.%. Meanwhile, the maximum enhancement in the Nu of the nanofluids was as follows: PEG@GNPs = 35%, PEG@TGr = 30.1%, Al2O3 = 20.6%, and SiO2 = 21.9% at 11,205 W/m2.
- The most significant pressure loss and friction factor increases were 20.8–23.7% and 3.57–3.85%, respectively. The effective dynamic viscosity significantly impacts the pressure drop for different nanofluids.
- The PI and PEC values of the tested samples were >1 and increased with the Reynolds number.
- Although the required pumping power was slightly increased, this was advantageous for the industrial application of these new working fluids.
- The nonlinear regression was developed for a relative pumping power of different nanofluids against temperature at different mass fractions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ac | Square Cross-section area of pipe, m2 |
| Al2O3 | Alumina |
| AlCl3 | Aluminum chloride |
| CNTs | Carbon nanotubes |
| Cp | Specific heat capacity, kJ/kg K |
| Cu | Copper nanomaterials |
| CuO | Copper oxide |
| Dh | Hydraulic Diameter of pipe, m |
| DMF | Dimethylformamide |
| DPT | Differential Pressure Transmitter |
| DSC | Differential Scanning Calorimeter |
| DW | Distilled water |
| f | Friction factor |
| GNP | Graphene Nanoplatelets |
| GO | Graphite oxide |
| h | Heat transfer coefficient, W/m2-K |
| HCl | Hydrochloric acid |
| I | Electric current, A |
| k | Thermal conductivity, W/m-K |
| L | Tube total-length, m |
| Mass flow rate, kg/s | |
| MWCNT | Multi-Walled Carbon Nanotube |
| NIST | National Institute of Standards and Technology |
| Nu | Average Nusselt number |
| P | Power supply, W |
| P | Perimeter of square pipe, m |
| PEC | Performance Evaluation Criterion |
| PEG | Pentaethylene Glycol |
| PG | Propylene Glycol |
| Pr | Prandtl number |
| q″ | Constant Heat flux, W/m2 |
| Q | Heat transfer amount, W |
| RGO | Reduced Graphene Oxide |
| Re | Reynolds number |
| RTD | Resistance Temperature Detector |
| SiO2 | Silica nanomaterials |
| T | Temperature, °C |
| T-Gr | Thermally Treated Graphene |
| THF | Tetrahydrofuran |
| TiO2 | Titanium dioxide |
| U | Velocity vector, m/s |
| V | Voltage, V |
| v | Working fluid velocity, m/s |
| W | Pumping power, W |
| Greek symbols | |
| ρ | Density, kg/m3 |
| μ | Dynamic Viscosity, Pa·s |
| ε | Performance index |
| ΔP | Pressure loss |
| φ | Mass fraction, % |
| Subscripts | |
| bf | Base fluid |
| nf | Nanofluid |
| np | Particles in nanosize |
| w | Wall of pipe |
| i | Inlet |
| o | Output |
| b | Bulk fluid |
References
- Sadri, R.; Mallah, A.R.; Hosseini, M.; Ahmadi, G.; Kazi, S.N.; Dabbagh, A.; Yeong, C.H.; Ahmad, R.; Yaakup, N.A. CFD Modeling of Turbulent Convection Heat Transfer of Nanofluids Containing Green Functionalized Graphene Nanoplatelets Flowing in a Horizontal Tube: Comparison with Experimental Data. J. Mol. Liq. 2018, 269, 152–159. [Google Scholar] [CrossRef]
- Mohammad, R.S.; Aldlemy, M.S.; Al Hassan, S.; Abdulla, A.I.; Scholz, M.; Yaseen, Z.M. Frictional Pressure Drop and Cost Savings for Graphene Nanoplatelets Nanofluids in Turbulent Flow Environments. Nanomaterials 2021, 11, 3094. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, H.M.R.; Pereira, R.F.P.; Lepleux, E.; Pacheco, L.; Valente, A.J.M.; Duarte, A.J.; de Zea Bermudez, V. Non-Newtonian Thermosensitive Nanofluid Based on Carbon Dots Functionalized with Ionic Liquids. Small 2020, 16, 1907661. [Google Scholar] [CrossRef]
- MR Gonçalves, H.; Neves, S.A.F.; Duarte, A.; de Zea Bermudez, V. Nanofluid Based on Carbon Dots Functionalized with Ionic Liquids for Energy Applications. Energies 2020, 13, 649. [Google Scholar] [CrossRef] [Green Version]
- Sofiah, A.G.N.; Samykano, M.; Pandey, A.K.; Kadirgama, K.; Sharma, K.; Saidur, R. Immense Impact from Small Particles: Review on Stability and Thermophysical Properties of Nanofluids. Sustain. Energy Technol. Assess. 2021, 48, 101635. [Google Scholar] [CrossRef]
- Esfe, M.H.; Kamyab, M.H.; Toghraie, D. Statistical Review of Studies on the Estimation of Thermophysical Properties of Nanofluids Using Artificial Neural Network (ANN). Powder Technol. 2022, 400, 117210. [Google Scholar] [CrossRef]
- Adun, H.; Kavaz, D.; Dagbasi, M. Review of Ternary Hybrid Nanofluid: Synthesis, Stability, Thermophysical Properties, Heat Transfer Applications, and Environmental Effects. J. Clean. Prod. 2021, 328, 129525. [Google Scholar] [CrossRef]
- Bumataria, R.K.; Chavda, N.K.; Panchal, H. Current Research Aspects in Mono and Hybrid Nanofluid Based Heat Pipe Technologies. Heliyon 2019, 5, e01627. [Google Scholar] [CrossRef] [Green Version]
- Ambreen, T.; Kim, M.-H. Heat Transfer and Pressure Drop Correlations of Nanofluids: A State of Art Review. Renew. Sustain. Energy Rev. 2018, 91, 564–583. [Google Scholar] [CrossRef]
- Alawi, O.A.; Kamar, H.M.; Hussein, O.A.; Mallah, A.R.; Mohammed, H.A.; Khiadani, M.; Roomi, A.B.; Kazi, S.N.; Yaseen, Z.M. Effects of Binary Hybrid Nanofluid on Heat Transfer and Fluid Flow in a Triangular-Corrugated Channel: An Experimental and Numerical Study. Powder Technol. 2022, 395, 267–279. [Google Scholar] [CrossRef]
- Abdelrazek, A.H.; Alawi, O.A.; Kazi, S.N.; Yusoff, N.; Chowdhury, Z.; Sarhan, A.A.D. A New Approach to Evaluate the Impact of Thermophysical Properties of Nanofluids on Heat Transfer and Pressure Drop. Int. Commun. Heat Mass Transf. 2018, 95, 161–170. [Google Scholar] [CrossRef]
- Murshed, S.M.S.; Estellé, P. A State of the Art Review on Viscosity of Nanofluids. Renew. Sustain. Energy Rev. 2017, 76, 1134–1152. [Google Scholar] [CrossRef]
- Azmi, W.H.; Sharma, K.V.; Mamat, R.; Najafi, G.; Mohamad, M.S. The Enhancement of Effective Thermal Conductivity and Effective Dynamic Viscosity of Nanofluids—A Review. Renew. Sustain. Energy Rev. 2016, 53, 1046–1058. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. A Critical Synthesis of Thermophysical Characteristics of Nanofluids. Int. J. Heat Mass Transf. 2011, 54, 4410–4428. [Google Scholar] [CrossRef]
- Alawi, O.A.; Kamar, H.M.; Mallah, A.R.; Mohammed, H.A.; Sabrudin, M.A.S.; Newaz, K.M.S.; Najafi, G.; Yaseen, Z.M. Experimental and Theoretical Analysis of Energy Efficiency in a Flat Plate Solar Collector Using Monolayer Graphene Nanofluids. Sustainability 2021, 13, 5416. [Google Scholar] [CrossRef]
- Sadeghinezhad, E.; Togun, H.; Mehrali, M.; Sadeghi Nejad, P.; Tahan Latibari, S.; Abdulrazzaq, T.; Kazi, S.N.; Metselaar, H.S.C. An Experimental and Numerical Investigation of Heat Transfer Enhancement for Graphene Nanoplatelets Nanofluids in Turbulent Flow Conditions. Int. J. Heat Mass Transf. 2015, 81, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Zubir, M.N.M.; Badarudin, A.; Kazi, S.N.; Huang, N.M.; Misran, M.; Sadeghinezhad, E.; Mehrali, M.; Syuhada, N.I.; Gharehkhani, S. Experimental Investigation on the Use of Reduced Graphene Oxide and Its Hybrid Complexes in Improving Closed Conduit Turbulent Forced Convective Heat Transfer. Exp. Therm. Fluid Sci. 2015, 66, 290–303. [Google Scholar] [CrossRef]
- Solangi, K.H.; Amiri, A.; Luhur, M.R.; Ghavimi, S.A.A.; Zubir, M.N.M.; Kazi, S.N.; Badarudin, A. Experimental Investigation of the Propylene Glycol-Treated Graphene Nanoplatelets for the Enhancement of Closed Conduit Turbulent Convective Heat Transfer. Int. Commun. Heat Mass Transf. 2016, 73, 43–53. [Google Scholar] [CrossRef]
- Yarmand, H.; Gharehkhani, S.; Shirazi, S.F.S.; Amiri, A.; Alehashem, M.S.; Dahari, M.; Kazi, S.N. Experimental Investigation of Thermo-Physical Properties, Convective Heat Transfer and Pressure Drop of Functionalized Graphene Nanoplatelets Aqueous Nanofluid in a Square Heated Pipe. Energy Convers. Manag. 2016, 114, 38–49. [Google Scholar] [CrossRef]
- Sadri, R.; Hosseini, M.; Kazi, S.N.; Bagheri, S.; Abdelrazek, A.H.; Ahmadi, G.; Zubir, N.; Ahmad, R.; Abidin, N.I.Z. A Facile, Bio-Based, Novel Approach for Synthesis of Covalently Functionalized Graphene Nanoplatelet Nano-Coolants toward Improved Thermo-Physical and Heat Transfer Properties. J. Colloid Interface Sci. 2018, 509, 140–152. [Google Scholar] [CrossRef]
- Qi, C.; Wang, G.; Yan, Y.; Mei, S.; Luo, T. Effect of Rotating Twisted Tape on Thermo-Hydraulic Performances of Nanofluids in Heat-Exchanger Systems. Energy Convers. Manag. 2018, 166, 744–757. [Google Scholar] [CrossRef]
- Qi, C.; Fan, F.; Pan, Y.; Liu, M.; Yan, Y. Effects of Turbulator with Round Hole on the Thermo-Hydraulic Performance of Nanofluids in a Triangle Tube. Int. J. Heat Mass Transf. 2020, 146, 118897. [Google Scholar] [CrossRef]
- Kaood, A.; Hassan, M.A. Thermo-Hydraulic Performance of Nanofluids Flow in Various Internally Corrugated Tubes. Chem. Eng. Process. Process Intensif. 2020, 154, 108043. [Google Scholar] [CrossRef]
- Alawi, O.A.; Sidik, N.A.C.; Kazi, S.N.; Najafi, G. Graphene Nanoplatelets and Few-Layer Graphene Studies in Thermo-Physical Properties and Particle Characterization. J. Therm. Anal. Calorim. 2019, 135, 1081–1093. [Google Scholar] [CrossRef]
- Alawi, O.A.; Mallah, A.R.; Kazi, S.N.; Sidik, N.A.C.; Najafi, G. Thermophysical Properties and Stability of Carbon Nanostructures and Metallic Oxides Nanofluids: Experimental Approach. J. Therm. Anal. Calorim. 2018, 135, 1545–1562. [Google Scholar] [CrossRef]
- Buongiorno, J.; Venerus, D.C.; Prabhat, N.; McKrell, T.; Townsend, J.; Christianson, R.; Tolmachev, Y.V.; Keblinski, P.; Hu, L.; Alvarado, J.L. A Benchmark Study on the Thermal Conductivity of Nanofluids. J. Appl. Phys. 2009, 106, 94312. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Seara, J.; Uhía, F.J.; Sieres, J.; Campo, A. A General Review of the Wilson Plot Method and Its Modifications to Determine Convection Coefficients in Heat Exchange Devices. Appl. Therm. Eng. 2007, 27, 2745–2757. [Google Scholar] [CrossRef] [Green Version]
- Gnielinski, V. New Equations for Heat and Mass Transfer in the Turbulent Flow in Pipes and Channels. NASA STI/Recon Tech. Rep. A 1975, 75, 8–16. [Google Scholar]
- Colebrook, C.F. Turbulent Flow in Pipes, with Particular Reference to the Transition Region between the Smooth and Rough Pipe Laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Petukhov, B.S. Heat Transfer and Friction in Turbulent Pipe Flow with Variable Physical Properties. Adv. Heat Transf. 1970, 6, 503–564. [Google Scholar] [CrossRef]
- Sadeghinezhad, E.; Mehrali, M.; Tahan Latibari, S.; Mehrali, M.; Kazi, S.N.; Oon, C.S.; Metselaar, H.S.C. Experimental Investigation of Convective Heat Transfer Using Graphene Nanoplatelet Based Nanofluids under Turbulent Flow Conditions. Ind. Eng. Chem. Res. 2014, 53, 12455–12465. [Google Scholar] [CrossRef]
- Blasius, H. Grenzschichten in Flussigkeiten Mit Kleiner Reibung. Z. Math. Phys. 1908, 56, 1–37. [Google Scholar]
- Das, S.K.; Putra, N.; Thiesen, P.; Roetzel, W. Temperature Dependence of Thermal Conductivity Enhancement for Nanofluids. J. Heat Transfer 2003, 125, 567–574. [Google Scholar] [CrossRef]
- Amiri, A.; Ahmadi, G.; Shanbedi, M.; Etemadi, M.; Mohd Zubir, M.N.; Chew, B.T.; Kazi, S.N. Heat Transfer Enhancement of Water-Based Highly Crumpled Few-Layer Graphene Nanofluids. RSC Adv. 2016, 6, 105508–105527. [Google Scholar] [CrossRef]
- Taylor, J. Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Books: New York, NY, USA, 1997; ISBN 9780935702750. [Google Scholar]
- Ramires, M.L.V.; Nieto de Castro, C.A.; Nagasaka, Y.; Nagashima, A.; Assael, M.J.; Wakeham, W.A. Standard Reference Data for the Thermal Conductivity of Water. J. Phys. Chem. Ref. Data 1995, 24, 1377–1381. [Google Scholar] [CrossRef]
- Aravind, S.S.J.; Baskar, P.; Baby, T.T.; Sabareesh, R.K.; Das, S.; Ramaprabhu, S. Investigation of Structural Stability, Dispersion, Viscosity, and Conductive Heat Transfer Properties of Functionalized Carbon Nanotube Based Nanofluids. J. Phys. Chem. C 2011, 115, 16737–16744. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, L.; Liu, J.; Fang, X.; Zhang, Z. Effect of Morphology of Carbon Nanomaterials on Thermo-Physical Characteristics, Optical Properties and Photo-Thermal Conversion Performance of Nanofluids. Renew. Energy 2016, 99, 888–897. [Google Scholar] [CrossRef]
- Elias, M.M.; Mahbubul, I.M.; Saidur, R.; Sohel, M.R.; Shahrul, I.M.; Khaleduzzaman, S.S.; Sadeghipour, S. Experimental Investigation on the Thermo-Physical Properties of Al2O3 Nanoparticles Suspended in Car Radiator Coolant. Int. Commun. Heat Mass Transf. 2014, 54, 48–53. [Google Scholar] [CrossRef]
- Khajeh Arzani, H.; Amiri, A.; Arzani, H.K.; Rozali, S.B.; Kazi, S.N.; Badarudin, A. Toward Improved Heat Transfer Performance of Annular Heat Exchangers with Water/Ethylene Glycol-Based Nanofluids Containing Graphene Nanoplatelets. J. Therm. Anal. Calorim. 2016, 126, 1427–1436. [Google Scholar] [CrossRef]
- Selvam, C.; Mohan Lal, D.; Harish, S. Thermal Conductivity and Specific Heat Capacity of Water–Ethylene Glycol Mixture-Based Nanofluids with Graphene Nanoplatelets. J. Therm. Anal. Calorim. 2017, 129, 947–955. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Klein, S.; Beckman, W. Heat Transfer: A Practical Approach; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Kazi, S.N.; Duffy, G.G.; Chen, X.D. Validation of Heat Transfer and Friction Loss Data for Fibre Suspensions in a Circular and a Coaxial Pipe Heat Exchanger. Int. J. Therm. Sci. 2014, 79, 146–160. [Google Scholar] [CrossRef]
- Mehrali, M.; Sadeghinezhad, E.; Rosen, M.A.; Tahan Latibari, S.; Mehrali, M.; Metselaar, H.S.C.; Kazi, S.N. Effect of Specific Surface Area on Convective Heat Transfer of Graphene Nanoplatelet Aqueous Nanofluids. Exp. Therm. Fluid Sci. 2015, 68, 100–108. [Google Scholar] [CrossRef]
- Wensel, J.; Wright, B.; Thomas, D.; Douglas, W.; Mannhalter, B.; Cross, W.; Hong, H.; Kellar, J.; Smith, P.; Roy, W. Enhanced Thermal Conductivity by Aggregation in Heat Transfer Nanofluids Containing Metal Oxide Nanoparticles and Carbon Nanotubes. Appl. Phys. Lett. 2008, 92, 023110. [Google Scholar] [CrossRef]
- Michaelides, E.E. Brownian Movement and Thermophoresis of Nanoparticles in Liquids. Int. J. Heat Mass Transf. 2015, 81, 179–187. [Google Scholar] [CrossRef]
- Shanbedi, M.; Amiri, A.; Rashidi, S.; Heris, S.Z.; Baniadam, M. Thermal Performance Prediction of Two-Phase Closed Thermosyphon Using Adaptive Neuro-Fuzzy Inference System. Heat Transf. Eng. 2015, 36, 315–324. [Google Scholar] [CrossRef]

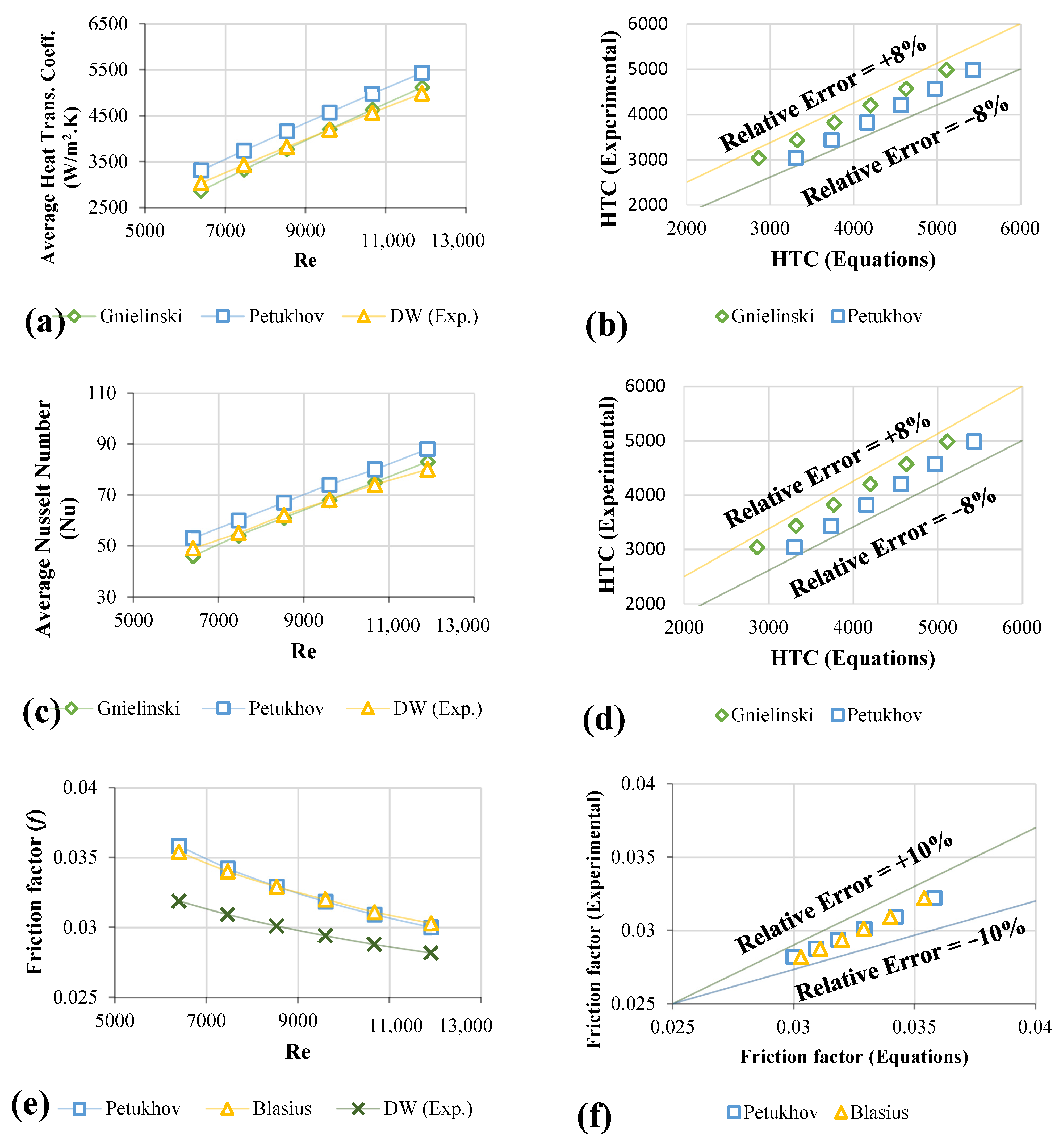
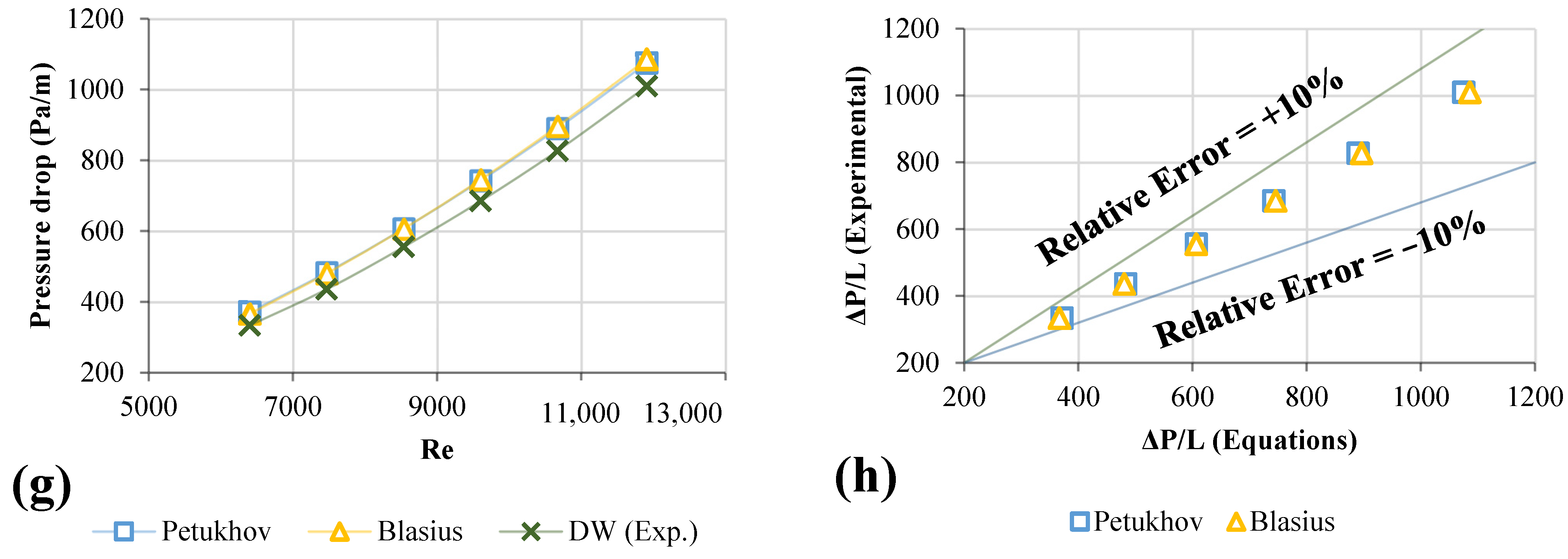

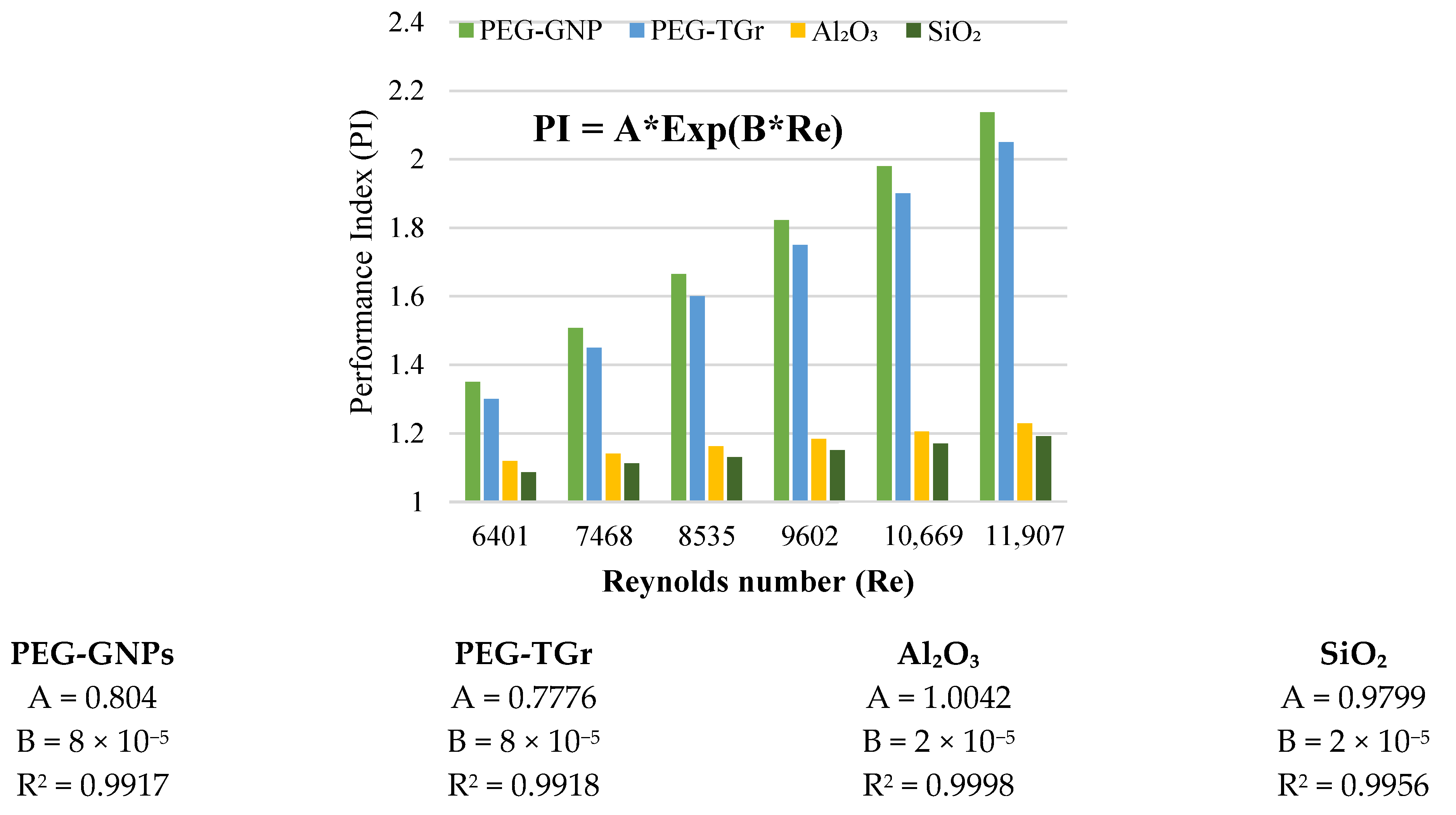
| Variable | Uncertainty Equations | Uncertainty Values |
|---|---|---|
| Reynolds number, Re | ±1.73% | |
| Constant Heat flux, q | ±1.51% | |
| Heat transfer coefficient, h | ±1.52% | |
| Nusselt number, Nu | ±5.23% | |
| Friction factor, f | ±1.60% |
| Study | Nanofluid | Mass/Volume % | Base Fluid | Temp. Range | Tool | Remarks |
|---|---|---|---|---|---|---|
| [39] | Graphene (Gr) | 0.005 and 0.01 | Ionic Liquid | From 20 °C to 145 °C | Hot Disc-thermal constant analyzer | Thermal conductivity enhanced by 9.4% at 0.01 wt.% |
| [40] | Al2O3 | 0.2–1 | DW+EG | From 10 °C to 50 °C | KD2pro | Thermal conductivity was enhanced by 8.3% at 1 vol.% |
| [41] | Graphene (Gr) | 0.02–0.2 | DW+EG | From 25–65 °C | KD2pro | Thermal conductivity enhanced by 64% at 0.2 wt.% |
| [42] | Graphene (Gr) | 0.5–0.45 | DW+EG | 30 °C | KD2pro | Thermal conductivity enhanced by 18% at 0.45 vol.% |
| Current study | PEG@GNP, PEG@TGr, Al2O3, and SiO2 | 0.1 | DW | From 20 °C to 60 °C | KD2pro | PEG@GNP = 31.6%, PEG@TGr = 29.74%, SiO2 = 11.4%, & Al2O3 = 8.04% at 60 °C |
| Study | Nanofluid | Mass/Volume% | Base Fluid | Temp. Range | Tool | Remarks |
|---|---|---|---|---|---|---|
| [39] | Graphene (Gr) | 0.005 and 0.01 | Ionic Liquid | From 25 °C to 150 °C | Viscometer | Viscosity enhanced by 29.1% and 13.4% raised for 0.005 and 0.01 wt.% |
| [40] | Al2O3 | 0.2–1 | DW+EG | From 10 °C to 50 °C | Brookfield Viscometer | Viscosity and temperature were in opposite correlation |
| [41] | Graphene (Gr) | 0.02–0.2 | DW+EG | From 25–65 °C | Brookfield Viscometer | Viscosity decreases as temperature rises and increases as nanoparticle concentration rises. |
| Current study | PEG@GNP, PEG@TGr, Al2O3, and SiO2 | 0.1 | DW | From 20 °C to 60 °C | Anton Paar Rheometer | A minor increase in the nanofluids’ dynamic viscosity relative to DW. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afan, H.A.; Aldlemy, M.S.; Ahmed, A.M.; Jawad, A.H.; Naser, M.H.; Homod, R.Z.; Mussa, Z.H.; Abdulkadhim, A.H.; Scholz, M.; Yaseen, Z.M. Thermal and Hydraulic Performances of Carbon and Metallic Oxides-Based Nanomaterials. Nanomaterials 2022, 12, 1545. https://doi.org/10.3390/nano12091545
Afan HA, Aldlemy MS, Ahmed AM, Jawad AH, Naser MH, Homod RZ, Mussa ZH, Abdulkadhim AH, Scholz M, Yaseen ZM. Thermal and Hydraulic Performances of Carbon and Metallic Oxides-Based Nanomaterials. Nanomaterials. 2022; 12(9):1545. https://doi.org/10.3390/nano12091545
Chicago/Turabian StyleAfan, Haitham Abdulmohsin, Mohammed Suleman Aldlemy, Ali M. Ahmed, Ali H. Jawad, Maryam H. Naser, Raad Z. Homod, Zainab Haider Mussa, Adnan Hashim Abdulkadhim, Miklas Scholz, and Zaher Mundher Yaseen. 2022. "Thermal and Hydraulic Performances of Carbon and Metallic Oxides-Based Nanomaterials" Nanomaterials 12, no. 9: 1545. https://doi.org/10.3390/nano12091545
APA StyleAfan, H. A., Aldlemy, M. S., Ahmed, A. M., Jawad, A. H., Naser, M. H., Homod, R. Z., Mussa, Z. H., Abdulkadhim, A. H., Scholz, M., & Yaseen, Z. M. (2022). Thermal and Hydraulic Performances of Carbon and Metallic Oxides-Based Nanomaterials. Nanomaterials, 12(9), 1545. https://doi.org/10.3390/nano12091545










