Theory of Excitons in Atomically Thin Semiconductors: Tight-Binding Approach
Abstract
:1. General Overview
1.1. 2D van der Waals Materials
1.2. Optical Properties of TMDs and Their Heterostructures
1.3. Review of Theory of Correlated Optical Excitations
2. Electronic Structure of MX Semiconductors
2.1. Ab Initio Insight into Electronic Structure
2.2. Minimal Tight-Binding Hamiltonian
3. Tight-Binding Theory of Optical Excitations
3.1. Bethe–Salpeter Equation
3.2. Coulomb Matrix Elements
3.3. Screening of Coulomb Interactions
4. Mechanisms of the Renormalization of the X Spectrum
5. Summary
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TMDs | Transition metal dichalcogenides |
| X | Exciton |
| hBN | Hexagonal boron nitride |
| BSE | Bethe–Salpeter equation |
| VB | Valence band |
| CB | Conduction band |
| DFT | Density functional theory |
| SOC | Spin-orbit coupling |
| TB | Tight-binding |
| BZ | Brillouin zone |
| EMA | Effective mass approximation |
| mDF | Massive Dirac fermion |
| R.-K. | Rytova–Keldysh |
References
- Wallace, P.R. The Band Theory of Graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Connell, G.; Wilson, J.; Yoffe, A. Effects of pressure and temperature on exciton absorption and band structure of layer crystals: Molybdenum disulphide. J. Phys. Chem. Solids 1969, 30, 287–296. [Google Scholar] [CrossRef]
- Wilson, J.; Yoffe, A. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [Green Version]
- Mounet, N.; Gibertini, M.; Schwaller, P.; Campi, D.; Merkys, A.; Marrazzo, A.; Sohier, T.; Castelli, I.E.; Cepellotti, A.; Pizzi, G.; et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat. Nanotechnol. 2018, 13, 246–252. [Google Scholar] [CrossRef] [Green Version]
- Chhowalla, M.; Shin, H.S.; Eda, G.; Li, L.J.; Loh, K.P.; Zhang, H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263–275. [Google Scholar] [CrossRef]
- Duan, X.; Wang, C.; Pan, A.; Yu, R.; Duan, X. Two-dimensional transition metal dichalcogenides as atomically thin semiconductors: Opportunities and challenges. Chem. Soc. Rev. 2015, 44, 8859–8876. [Google Scholar] [CrossRef]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef]
- Lien, D.H.; Kang, J.S.; Amani, M.; Chen, K.; Tosun, M.; Wang, H.P.; Roy, T.; Eggleston, M.S.; Wu, M.C.; Dubey, M.; et al. Engineering Light Outcoupling in 2D Materials. Nano Lett. 2015, 15, 1356–1361. [Google Scholar] [CrossRef]
- Lin, Y.; Ling, X.; Yu, L.; Huang, S.; Hsu, A.L.; Lee, Y.H.; Kong, J.; Dresselhaus, M.S.; Palacios, T. Dielectric Screening of Excitons and Trions in Single-Layer MoS2. Nano Lett. 2014, 14, 5569. [Google Scholar] [CrossRef]
- Raja, A.; Chaves, A.; Yu, J.; Arefe, G.; Hill, H.M.; Rigosi, A.F.; Berkelbach, T.C.; Nagler, P.; Schüller, C.; Korn, T.; et al. Coulomb engineering of the bandgap and excitons in two-dimensional materials. Nat. Commun. 2017, 8, 15251. [Google Scholar] [CrossRef] [Green Version]
- Ajayi, O.A.; Ardelean, J.V.; Shepard, G.D.; Wang, J.; Antony, A.; Taniguchi, T.; Watanabe, K.; Heinz, T.F.; Strauf, S.; Zhu, X.Y.; et al. Approaching the intrinsic photoluminescence linewidth in transition metal dichalcogenide monolayers. 2D Mater. 2017, 4, 031011. [Google Scholar] [CrossRef] [Green Version]
- Cadiz, F.; Courtade, E.; Robert, C.; Wang, G.; Shen, Y.; Cai, H.; Taniguchi, T.; Watanabe, K.; Carrere, H.; Lagarde, D.; et al. Excitonic Linewidth Approaching the Homogeneous Limit in MoS2-Based van der Waals Heterostructures. Phys. Rev. X 2017, 7, 021026. [Google Scholar] [CrossRef] [Green Version]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.Y.; Galli, G.; Wang, F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271. [Google Scholar] [CrossRef]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Eda, G.; Yamaguchi, H.; Voiry, D.; Fujita, T.; Chen, M.; Chhowalla, M. Photoluminescence from Chemically Exfoliated MoS2. Nano Lett. 2011, 11, 5111–5116. [Google Scholar] [CrossRef]
- Tonndorf, P.; Schmidt, R.; Böttger, P.; Zhang, X.; Börner, J.; Liebig, A.; Albrecht, M.; Kloc, C.; Gordan, O.; Zahn, D.R.T.; et al. Photoluminescence emission and Raman response of monolayer MoS2, MoSe2, and WSe2. Opt. Express 2013, 21, 4908–4916. [Google Scholar] [CrossRef]
- Zhao, W.; Ghorannevis, Z.; Chu, L.; Toh, M.; Kloc, C.; Tan, P.H.; Eda, G. Evolution of Electronic Structure in Atomically Thin Sheets of WS2 and WSe2. ACS Nano 2013, 7, 791–797. [Google Scholar] [CrossRef] [Green Version]
- Ruppert, C.; Aslan, O.B.; Heinz, T.F. Optical Properties and Band Gap of Single- and Few-Layer MoTe2 Crystals. Nano Lett. 2014, 14, 6231–6236. [Google Scholar] [CrossRef]
- Lezama, I.G.; Arora, A.; Ubaldini, A.; Barreteau, C.; Giannini, E.; Potemski, M.; Morpurgo, A.F. Indirect-to-Direct Band Gap Crossover in Few-Layer MoTe2. Nano Lett. 2015, 15, 2336–2342. [Google Scholar] [CrossRef] [Green Version]
- Kadantsev, E.S.; Hawrylak, P. Electronic structure of a single MoS2 monolayer. Solid State Commun. 2012, 152, 909. [Google Scholar] [CrossRef]
- Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 2012, 86, 115409. [Google Scholar] [CrossRef] [Green Version]
- Jin, W.; Yeh, P.C.; Zaki, N.; Zhang, D.; Sadowski, J.T.; Al-Mahboob, A.; van der Zande, A.M.; Chenet, D.A.; Dadap, J.I.; Herman, I.P.; et al. Direct Measurement of the Thickness-Dependent Electronic Band Structure of MoS2 Using Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 2013, 111, 106801. [Google Scholar] [CrossRef] [Green Version]
- Coehoorn, R.; Haas, C.; de Groot, R.A. Electronic structure of MoSe2, MoS2, and WSe2. II. The nature of the optical band gaps. Phys. Rev. B 1987, 35, 6203–6206. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Liu, G.B.; Feng, W.; Xu, X.; Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef] [Green Version]
- Cao, T.; Wang, G.; Han, W.; Ye, H.; Zhu, C.; Shi, J.; Niu, Q.; Tan, P.; Wang, E.; Liu, B.; et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat. Commun. 2012, 3, 887. [Google Scholar] [CrossRef] [Green Version]
- Mak, K.F.; He, K.; Shan, J.; Heinz, T.F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 2012, 7, 494–498. [Google Scholar] [CrossRef]
- Sallen, G.; Bouet, L.; Marie, X.; Wang, G.; Zhu, C.R.; Han, W.P.; Lu, Y.; Tan, P.H.; Amand, T.; Liu, B.L.; et al. Robust optical emission polarization in MoS2 monolayers through selective valley excitation. Phys. Rev. B 2012, 86, 081301. [Google Scholar] [CrossRef] [Green Version]
- Zeng, H.; Dai, J.; Yao, W.; Xiao, D.; Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechnol. 2012, 7, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Palleau, E.; Amand, T.; Tongay, S.; Marie, X.; Urbaszek, B. Polarization and time-resolved photoluminescence spectroscopy of excitons in MoSe2 monolayers. Appl. Phys. Lett. 2015, 106, 112101. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Oka, T.; Suzuki, R.; Ye, J.; Iwasa, Y. Electrically switchable chiral light-emitting transistor. Science 2014, 344, 725–728. [Google Scholar] [CrossRef]
- Kioseoglou, G.; Hanbicki, A.T.; Currie, M.; Friedman, A.L.; Gunlycke, D.; Jonker, B.T. Valley polarization and intervalley scattering in monolayer MoS2. Appl. Phys. Lett. 2012, 101, 221907. [Google Scholar] [CrossRef] [Green Version]
- Jones, A.M.; Yu, H.; Ghimire, N.J.; Wu, S.; Aivazian, G.; Ross, J.S.; Zhao, B.; Yan, J.; Mandrus, D.G.; Xiao, D.; et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 2013, 8, 634–638. [Google Scholar] [CrossRef]
- Wang, G.; Marie, X.; Liu, B.L.; Amand, T.; Robert, C.; Cadiz, F.; Renucci, P.; Urbaszek, B. Control of Exciton Valley Coherence in Transition Metal Dichalcogenide Monolayers. Phys. Rev. Lett. 2016, 117, 187401. [Google Scholar] [CrossRef]
- Hao, K.; Moody, G.; Wu, F.; Dass, C.K.; Xu, L.; Chen, C.H.; Sun, L.; Li, M.Y.; Li, L.J.; MacDonald, A.H.; et al. Direct measurement of exciton valley coherence in monolayer WSe2. Nat. Phys. 2016, 12, 677–682. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, A.; Sidler, M.; Allain, A.V.; Lembke, D.S.; Kis, A.; Imamoglu, A. Valley Zeeman effect in elementary optical excitations of monolayer WSe2. Nat. Phys. 2015, 11, 141–147. [Google Scholar] [CrossRef] [Green Version]
- Aivazian, G.; Gong, Z.; Jones, A.M.; Chu, R.L.; Yan, J.; Mandrus, D.G.; Zhang, C.; Cobden, D.; Yao, W.; Xu, X. Magnetic control of valley pseudospin in monolayer WSe2. Nat. Phys. 2015, 11, 148–152. [Google Scholar] [CrossRef] [Green Version]
- Scrace, T.; Tsai, Y.; Barman, B.; Schweidenback, L.; Petrou, A.; Kioseoglou, G.; Ozfidan, I.; Korkusiński, M.; Hawrylak, P. Magnetoluminescence and valley polarized state of a two-dimensional electron gas in WS2 monolayers. Nat. Nanotechnol. 2015, 10, 603–607. [Google Scholar] [CrossRef] [PubMed]
- Braz, J.E.H.; Amorim, B.; Castro, E.V. Valley-polarized magnetic state in hole-doped monolayers of transition-metal dichalcogenides. Phys. Rev. B 2018, 98, 161406. [Google Scholar] [CrossRef] [Green Version]
- Roch, J.G.; Froehlicher, G.; Leisgang, N.; Makk, P.; Watanabe, K.; Taniguchi, T.; Warburton, R.J. Spin-polarized electrons in monolayer MoS2. Nat. Nanotechnol. 2019, 14, 432–436. [Google Scholar] [CrossRef] [PubMed]
- Miserev, D.; Klinovaja, J.; Loss, D. Exchange intervalley scattering and magnetic phase diagram of transition metal dichalcogenide monolayers. Phys. Rev. B 2019, 100, 014428. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Kumar, N.; Zhao, L.; Wang, Z.; Mak, K.F.; Zhao, H.; Shan, J. Tightly Bound Excitons in Monolayer WSe2. Phys. Rev. Lett. 2014, 113, 026803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arora, A.; Koperski, M.; Nogajewski, K.; Marcus, J.; Faugeras, C.; Potemski, M. Excitonic resonances in thin films of WSe2: From monolayer to bulk material. Nanoscale 2015, 7, 10421–10429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chernikov, A.; Berkelbach, T.C.; Hill, H.M.; Rigosi, A.; Li, Y.; Aslan, O.B.; Reichman, D.R.; Hybertsen, M.S.; Heinz, T.F. Exciton Binding Energy and Nonhydrogenic Rydberg Series in Monolayer WS2. Phys. Rev. Lett. 2014, 113, 076802. [Google Scholar] [CrossRef] [Green Version]
- Hill, H.M.; Rigosi, A.F.; Roquelet, C.; Chernikov, A.; Berkelbach, T.C.; Reichman, D.R.; Hybertsen, M.S.; Brus, L.E.; Heinz, T.F. Observation of Excitonic Rydberg States in Monolayer MoS2 and WS2 by Photoluminescence Excitation Spectroscopy. Nano Lett. 2015, 15, 2992–2997. [Google Scholar] [CrossRef]
- Arora, A.; Nogajewski, K.; Molas, M.; Koperski, M.; Potemski, M. Exciton band structure in layered MoSe2: From a monolayer to the bulk limit. Nanoscale 2015, 7, 20769–20775. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Marie, X.; Gerber, I.; Amand, T.; Lagarde, D.; Bouet, L.; Vidal, M.; Balocchi, A.; Urbaszek, B. Giant Enhancement of the Optical Second-Harmonic Emission of WSe2 Monolayers by Laser Excitation at Exciton Resonances. Phys. Rev. Lett. 2015, 114, 097403. [Google Scholar] [CrossRef] [Green Version]
- Stier, A.V.; McCreary, K.M.; Jonker, B.T.; Kono, J.; Crooker, S.A. Exciton diamagnetic shifts and valley Zeeman effects in monolayer WS2 and MoS2 to 65 Tesla. Nat. Commun. 2016, 7, 10643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stier, A.V.; Wilson, N.P.; Velizhanin, K.A.; Kono, J.; Xu, X.; Crooker, S.A. Magnetooptics of Exciton Rydberg States in a Monolayer Semiconductor. Phys. Rev. Lett. 2018, 120, 057405. [Google Scholar] [CrossRef] [Green Version]
- Molas, M.R.; Slobodeniuk, A.O.; Nogajewski, K.; Bartos, M.; Bala, L.; Babiński, A.; Watanabe, K.; Taniguchi, T.; Faugeras, C.; Potemski, M. Energy Spectrum of Two-Dimensional Excitons in a Nonuniform Dielectric Medium. Phys. Rev. Lett. 2019, 123, 136801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goryca, M.; Li, J.; Stier, A.; Crooker, S.; Taniguchi, T.; Watanabe, K.; Courtade, E.; Shree, S.; Robert, C.; Urbaszek, B.; et al. Revealing exciton masses and dielectric properties of monolayer semiconductors with high magnetic fields. Nat. Commun. 2019, 10, 4172. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delhomme, A.; Butseraen, G.; Zheng, B.; Marty, L.; Bouchiat, V.; Molas, M.R.; Pan, A.; Watanabe, K.; Taniguchi, T.; Ouerghi, A.; et al. Magneto-spectroscopy of exciton Rydberg states in a CVD grown WSe2 monolayer. Appl. Phys. Lett. 2019, 114, 232104. [Google Scholar] [CrossRef] [Green Version]
- Bieniek, M.; Korkusiński, M.; Szulakowska, L.; Potasz, P.; Ozfidan, I.; Hawrylak, P. Band nesting, massive Dirac fermions, and valley Landé and Zeeman effects in transition metal dichalcogenides: A tight-binding model. Phys. Rev. B 2018, 97, 085153. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.X.; You, Y.; Zhao, S.Y.F.; Heinz, T.F. Experimental Evidence for Dark Excitons in Monolayer WSe2. Phys. Rev. Lett. 2015, 115, 257403. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Robert, C.; Suslu, A.; Chen, B.; Yang, S.; Alamdari, S.; Gerber, I.C.; Amand, T.; Marie, X.; Tongay, S.; et al. Spin-orbit engineering in transition metal dichalcogenide alloy monolayers. Nat. Commun. 2015, 6, 10110. [Google Scholar] [CrossRef]
- Wang, G.; Robert, C.; Glazov, M.M.; Cadiz, F.; Courtade, E.; Amand, T.; Lagarde, D.; Taniguchi, T.; Watanabe, K.; Urbaszek, B.; et al. In-Plane Propagation of Light in Transition Metal Dichalcogenide Monolayers: Optical Selection Rules. Phys. Rev. Lett. 2017, 119, 047401. [Google Scholar] [CrossRef] [Green Version]
- Robert, C.; Amand, T.; Cadiz, F.; Lagarde, D.; Courtade, E.; Manca, M.; Taniguchi, T.; Watanabe, K.; Urbaszek, B.; Marie, X. Fine structure and lifetime of dark excitons in transition metal dichalcogenide monolayers. Phys. Rev. B 2017, 96, 155423. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Mak, K.F.; Shan, J. Long valley lifetime of dark excitons in single-layer WSe2. Nat. Commun. 2019, 10, 4047. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, K.D.; Jiang, T.; Clark, G.; Xu, X.; Raschke, M.B. Radiative control of dark excitons at room temperature by nano-optical antenna-tip Purcell effect. Nat. Nanotechnol. 2018, 13, 59–64. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Scuri, G.; Wild, D.S.; High, A.A.; Dibos, A.; Jauregui, L.A.; Shu, C.; De Greve, K.; Pistunova, K.; Joe, A.Y.; et al. Probing dark excitons in atomically thin semiconductors via near-field coupling to surface plasmon polaritons. Nat. Nanotechnol. 2017, 12, 856–860. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molas, M.R.; Slobodeniuk, A.O.; Kazimierczuk, T.; Nogajewski, K.; Bartos, M.; Kapuściński, P.; Oreszczuk, K.; Watanabe, K.; Taniguchi, T.; Faugeras, C.; et al. Probing and Manipulating Valley Coherence of Dark Excitons in Monolayer WSe2. Phys. Rev. Lett. 2019, 123, 096803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Withers, F.; Del Pozo-Zamudio, O.; Schwarz, S.; Dufferwiel, S.; Walker, P.M.; Godde, T.; Rooney, A.P.; Gholinia, A.; Woods, C.R.; Blake, P.; et al. WSe2 Light-Emitting Tunneling Transistors with Enhanced Brightness at Room Temperature. Nano Lett. 2015, 15, 8223–8228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.X.; Cao, T.; Lu, Z.; Lin, Y.C.; Zhang, F.; Wang, Y.; Li, Z.; Hone, J.C.; Robinson, J.A.; Smirnov, D.; et al. Magnetic brightening and control of dark excitons in monolayer WSe2. Nat. Nanotechnol. 2017, 12, 883–888. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molas, M.R.; Faugeras, C.; Slobodeniuk, A.O.; Nogajewski, K.; Bartos, M.; Basko, D.M.; Potemski, M. Brightening of dark excitons in monolayers of semiconducting transition metal dichalcogenides. 2D Mater. 2017, 4, 021003. [Google Scholar] [CrossRef]
- Lu, Z.; Rhodes, D.; Li, Z.; Tuan, D.V.; Jiang, Y.; Ludwig, J.; Jiang, Z.; Lian, Z.; Shi, S.F.; Hone, J.; et al. Magnetic field mixing and splitting of bright and dark excitons in monolayer MoSe2. 2D Mater. 2019, 7, 015017. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wang, T.; Jin, C.; Lu, Z.; Lian, Z.; Meng, Y.; Blei, M.; Gao, S.; Taniguchi, T.; Watanabe, K.; et al. Emerging photoluminescence from the dark-exciton phonon replica in monolayer WSe2. Nat. Commun. 2019, 10, 2469. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.; Cao, T.; O’Brien, K.; Zhu, H.; Yin, X.; Wang, Y.; Louie, S.G.; Zhang, X. Probing excitonic dark states in single-layer tungsten disulphide. Nature 2014, 513, 214–218. [Google Scholar] [CrossRef] [Green Version]
- Berghauser, G.; Knorr, A.; Malic, E. Optical fingerprint of dark 2p-states in transition metal dichalcogenides. 2D Mater. 2017, 4, 015029. [Google Scholar] [CrossRef] [Green Version]
- Pöllmann, C.; Steinleitner, P.; Leierseder, U.; Nagler, P.; Plechinger, G.; Porer, M.; Bratschitsch, R.; Schüller, C.; Korn, T.; Huber, R. Resonant internal quantum transitions and femtosecond radiative decay of excitons in monolayer WSe2. Nat. Mater. 2015, 14, 889. [Google Scholar] [CrossRef] [PubMed]
- Cha, S.; Sung, J.H.; Sim, S.; Park, J.; Heo, H.; Jo, M.H.; Choi, H. 1s-intraexcitonic dynamics in monolayer MoS2 probed by ultrafast mid-infrared spectroscopy. Nat. Commun. 2016, 7, 10768. [Google Scholar] [CrossRef] [Green Version]
- Steinleitner, P.; Merkl, P.; Graf, A.; Nagler, P.; Watanabe, K.; Taniguchi, T.; Zipfel, J.; Schüller, C.; Korn, T.; Chernikov, A.; et al. Dielectric Engineering of Electronic Correlations in a van der Waals Heterostructure. Nano Lett. 2018, 18, 1402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berghäuser, G.; Steinleitner, P.; Merkl, P.; Huber, R.; Knorr, A.; Malic, E. Mapping of the dark exciton landscape in transition metal dichalcogenides. Phys. Rev. B 2018, 98, 020301. [Google Scholar] [CrossRef] [Green Version]
- Brem, S.; Zipfel, J.; Selig, M.; Raja, A.; Waldecker, L.; Ziegler, J.D.; Taniguchi, T.; Watanabe, K.; Chernikov, A.; Malic, E. Intrinsic lifetime of higher excitonic states in tungsten diselenide monolayers. Nanoscale 2019, 11, 12381–12387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merkl, P.; Mooshammer, F.; Steinleitner, P.; Girnghuber, A.; Lin, K.Q.; Nagler, P.; Holler, J.; Schüller, C.; Lupton, J.M.; Korn, T.; et al. Ultrafast transition between exciton phases in van der Waals heterostructures. Nat. Mater. 2019, 18, 691. [Google Scholar] [CrossRef] [Green Version]
- Yong, C.K.; Utama, M.I.B.; Ong, C.S.; Cao, T.; Regan, E.C.; Horng, J.; Shen, Y.; Cai, H.; Watanabe, K.; Taniguchi, T.; et al. Valley-dependent exciton fine structure and Autler–Townes doublets from Berry phases in monolayer MoSe2. Nat. Mater. 2019, 18, 1065–1070. [Google Scholar] [CrossRef] [Green Version]
- Berkelbach, T.C.; Hybertsen, M.S.; Reichman, D.R. Bright and dark singlet excitons via linear and two-photon spectroscopy in monolayer transition-metal dichalcogenides. Phys. Rev. B 2015, 92, 085413. [Google Scholar] [CrossRef] [Green Version]
- Feierabend, M.; Berghäuser, G.; Knorr, A.; Malic, E. Proposal for dark exciton based chemical sensors. Nat. Commun. 2017, 8, 14776. [Google Scholar] [CrossRef] [Green Version]
- Christiansen, D.; Selig, M.; Berghäuser, G.; Schmidt, R.; Niehues, I.; Schneider, R.; Arora, A.; de Vasconcellos, S.M.; Bratschitsch, R.; Malic, E.; et al. Phonon Sidebands in Monolayer Transition Metal Dichalcogenides. Phys. Rev. Lett. 2017, 119, 187402. [Google Scholar] [CrossRef] [Green Version]
- Selig, M.; Berghäuser, G.; Raja, A.; Nagler, P.; Schüller, C.; Heinz, T.F.; Korn, T.; Chernikov, A.; Malic, E.; Knorr, A. Excitonic linewidth and coherence lifetime in monolayer transition metal dichalcogenides. Nat. Commun. 2016, 7, 13279. [Google Scholar] [CrossRef] [PubMed]
- Peng, G.H.; Lo, P.Y.; Li, W.H.; Huang, Y.C.; Chen, Y.H.; Lee, C.H.; Yang, C.K.; Cheng, S.J. Distinctive Signatures of the Spin- and Momentum-Forbidden Dark Exciton States in the Photoluminescence of Strained WSe2 Monolayers under Thermalization. Nano Lett. 2019, 19, 2299–2312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lampert, M.A. Mobile and Immobile Effective-Mass-Particle Complexes in Nonmetallic Solids. Phys. Rev. Lett. 1958, 1, 450–453. [Google Scholar] [CrossRef]
- Kheng, K.; Cox, R.T.; d’ Aubigné, M.Y.; Bassani, F.; Saminadayar, K.; Tatarenko, S. Observation of negatively charged excitons X− in semiconductor quantum wells. Phys. Rev. Lett. 1993, 71, 1752–1755. [Google Scholar] [CrossRef] [PubMed]
- Hawrylak, P. Optical properties of a two-dimensional electron gas: Evolution of spectra from excitons to Fermi-edge singularities. Phys. Rev. B 1991, 44, 3821–3828. [Google Scholar] [CrossRef] [PubMed]
- Narvaez, G.A.; Hawrylak, P.; Brum, J.A. The role of finite hole mass in the negatively charged exciton in two dimensions. Phys. E Low-Dimens. Syst. Nanostruct. 2001, 9, 716–722. [Google Scholar] [CrossRef]
- Mak, K.F.; He, K.; Lee, C.; Lee, G.H.; Hone, J.; Heinz, T.F.; Shan, J. Tightly bound trions in monolayer MoS2. Nat. Mater. 2013, 12, 207–211. [Google Scholar] [CrossRef]
- Mitioglu, A.A.; Plochocka, P.; Jadczak, J.N.; Escoffier, W.; Rikken, G.L.J.A.; Kulyuk, L.; Maude, D.K. Optical manipulation of the exciton charge state in single-layer tungsten disulfide. Phys. Rev. B 2013, 88, 245403. [Google Scholar] [CrossRef] [Green Version]
- Lui, C.H.; Frenzel, A.J.; Pilon, D.V.; Lee, Y.H.; Ling, X.; Akselrod, G.M.; Kong, J.; Gedik, N. Trion-Induced Negative Photoconductivity in Monolayer MoS2. Phys. Rev. Lett. 2014, 113, 166801. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Moody, G.; Tran, K.; Scott, M.E.; Overbeck, V.; Berghäuser, G.; Schaibley, J.; Seifert, E.J.; Pleskot, D.; Gabor, N.M.; et al. Trion formation dynamics in monolayer transition metal dichalcogenides. Phys. Rev. B 2016, 93, 041401. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Wang, H.; Chan, W.; Manolatou, C.; Rana, F. Absorption of light by excitons and trions in monolayers of metal dichalcogenide MoS2: Experiments and theory. Phys. Rev. B 2014, 89, 205436. [Google Scholar] [CrossRef] [Green Version]
- Rezk, A.R.; Carey, B.; Chrimes, A.F.; Lau, D.W.M.; Gibson, B.C.; Zheng, C.; Fuhrer, M.S.; Yeo, L.Y.; Kalantar-zadeh, K. Acoustically-Driven Trion and Exciton Modulation in Piezoelectric Two-Dimensional MoS2. Nano Lett. 2016, 16, 849–855. [Google Scholar] [CrossRef] [PubMed]
- Plechinger, G.; Nagler, P.; Kraus, J.; Paradiso, N.; Strunk, C.; Schüller, C.; Korn, T. Identification of excitons, trions and biexcitons in single-layer WS2. Phys. Status Solidi (RRL)—Rapid Res. Lett. 2015, 9, 457–461. [Google Scholar] [CrossRef] [Green Version]
- Cuadra, J.; Baranov, D.G.; Wersall, M.; Verre, R.; Antosiewicz, T.J.; Shegai, T. Observation of Tunable Charged Exciton Polaritons in Hybrid Monolayer WS2 Plasmonic Nanoantenna System. Nano Lett. 2018, 18, 1777–1785. [Google Scholar] [CrossRef] [Green Version]
- Jadczak, J.; Delgado, A.; Bryja, L.; Huang, Y.S.; Hawrylak, P. Robust high-temperature trion emission in monolayers of Mo(SySe1−y)2 alloys. Phys. Rev. B 2017, 95, 195427. [Google Scholar] [CrossRef]
- Jadczak, J.; Kutrowska-Girzycka, J.; Kapuściński, P.; Huang, Y.S.; Wójs, A.; Bryja, L. Probing of free and localized excitons and trions in atomically thin WSe2, WS2, MoSe2 and MoS2 in photoluminescence and reflectivity experiments. Nanotechnology 2017, 28, 395702. [Google Scholar] [CrossRef]
- Nan, H.; Wang, Z.; Wang, W.; Liang, Z.; Lu, Y.; Chen, Q.; He, D.; Tan, P.; Miao, F.; Wang, X.; et al. Strong Photoluminescence Enhancement of MoS2 through Defect Engineering and Oxygen Bonding. ACS Nano 2014, 8, 5738–5745. [Google Scholar] [CrossRef] [Green Version]
- Mouri, S.; Miyauchi, Y.; Matsuda, K. Tunable Photoluminescence of Monolayer MoS2 via Chemical Doping. Nano Lett. 2013, 13, 5944–5948. [Google Scholar] [CrossRef] [Green Version]
- Scheuschner, N.; Ochedowski, O.; Kaulitz, A.M.; Gillen, R.; Schleberger, M.; Maultzsch, J. Photoluminescence of freestanding single- and few-layer MoS2. Phys. Rev. B 2014, 89, 125406. [Google Scholar] [CrossRef] [Green Version]
- Godde, T.; Schmidt, D.; Schmutzler, J.; Aßmann, M.; Debus, J.; Withers, F.; Alexeev, E.M.; Del Pozo-Zamudio, O.; Skrypka, O.V.; Novoselov, K.S.; et al. Exciton and trion dynamics in atomically thin MoSe2 and WSe2: Effect of localization. Phys. Rev. B 2016, 94, 165301. [Google Scholar] [CrossRef] [Green Version]
- Ross, J.S.; Wu, S.; Yu, H.; Ghimire, N.J.; Jones, A.M.; Aivazian, G.; Yan, J.; Mandrus, D.G.; Xiao, D.; Yao, W.; et al. Electrical control of neutral and charged excitons in a monolayer semiconductor. Nat. Commun. 2013, 4, 1474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ross, J.S.; Klement, P.; Jones, A.M.; Ghimire, N.J.; Yan, J.; Mandrus, D.G.; Taniguchi, T.; Watanabe, K.; Kitamura, K.; Yao, W.; et al. Electrically tunable excitonic light-emitting diodes based on monolayer WSe2 p-n junctions. Nat. Nanotechnol. 2014, 9, 268–272. [Google Scholar] [CrossRef] [PubMed]
- Shang, J.; Shen, X.; Cong, C.; Peimyoo, N.; Cao, B.; Eginligil, M.; Yu, T. Observation of Excitonic Fine Structure in a 2D Transition-Metal Dichalcogenide Semiconductor. ACS Nano 2015, 9, 647–655. [Google Scholar] [CrossRef] [PubMed]
- Yao, K.; Yan, A.; Kahn, S.; Suslu, A.; Liang, Y.; Barnard, E.S.; Tongay, S.; Zettl, A.; Borys, N.J.; Schuck, P.J. Optically Discriminating Carrier-Induced Quasiparticle Band Gap and Exciton Energy Renormalization in Monolayer MoS2. Phys. Rev. Lett. 2017, 119, 087401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Lü, T.; Myint, Y.W.; Pei, J.; Macdonald, D.; Zheng, J.C.; Lu, Y. Robust Excitons and Trions in Monolayer MoTe2. ACS Nano 2015, 9, 6603–6609. [Google Scholar] [CrossRef] [PubMed]
- Courtade, E.; Semina, M.; Manca, M.; Glazov, M.M.; Robert, C.; Cadiz, F.; Wang, G.; Taniguchi, T.; Watanabe, K.; Pierre, M.; et al. Charged excitons in monolayer WSe2: Experiment and theory. Phys. Rev. B 2017, 96, 085302. [Google Scholar] [CrossRef] [Green Version]
- Liu, E.; van Baren, J.; Lu, Z.; Altaiary, M.M.; Taniguchi, T.; Watanabe, K.; Smirnov, D.; Lui, C.H. Gate Tunable Dark Trions in Monolayer WSe2. Phys. Rev. Lett. 2019, 123, 027401. [Google Scholar] [CrossRef] [Green Version]
- Back, P.; Sidler, M.; Cotlet, O.; Srivastava, A.; Takemura, N.; Kroner, M.; Imamoğlu, A. Giant Paramagnetism-Induced Valley Polarization of Electrons in Charge-Tunable Monolayer MoSe2. Phys. Rev. Lett. 2017, 118, 237404. [Google Scholar] [CrossRef] [Green Version]
- Plechinger, G.; Nagler, P.; Arora, A.; Schmidt, R.; Chernikov, A.; del Águila, A.G.; Christianen, P.C.M.; Bratschitsch, R.; Schüller, C.; Korn, T. Trion fine structure and coupled spin-valley dynamics in monolayer tungsten disulfide. Nat. Commun. 2016, 7, 12715. [Google Scholar] [CrossRef] [Green Version]
- Vaclavkova, D.; Wyzula, J.; Nogajewski, K.; Bartos, M.; Slobodeniuk, A.O.; Faugeras, C.; Potemski, M.; Molas, M.R. Singlet and triplet trions in WS2 monolayer encapsulated in hexagonal boron nitride. Nanotechnology 2018, 29, 325705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boulesbaa, A.; Huang, B.; Wang, K.; Lin, M.W.; Mahjouri-Samani, M.; Rouleau, C.; Xiao, K.; Yoon, M.; Sumpter, B.; Puretzky, A.; et al. Observation of two distinct negative trions in tungsten disulfide monolayers. Phys. Rev. B 2015, 92, 115443. [Google Scholar] [CrossRef] [Green Version]
- Orsi Gordo, V.; Balanta, M.A.G.; Galvão Gobato, Y.; Covre, F.S.; Galeti, H.V.A.; Iikawa, F.; Couto, O.D.D.; Qu, F.; Henini, M.; Hewak, D.W.; et al. Revealing the nature of low-temperature photoluminescence peaks by laser treatment in van der Waals epitaxially grown WS2 monolayers. Nanoscale 2018, 10, 4807–4815. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molas, M.R.; Nogajewski, K.; Slobodeniuk, A.O.; Binder, J.; Bartos, M.; Potemski, M. The optical response of monolayer, few-layer and bulk tungsten disulfide. Nanoscale 2017, 9, 13128–13141. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wang, T.; Lu, Z.; Khatoniar, M.; Lian, Z.; Meng, Y.; Blei, M.; Taniguchi, T.; Watanabe, K.; McGill, S.A.; et al. Direct Observation of Gate-Tunable Dark Trions in Monolayer WSe2. Nano Lett. 2019, 19, 6886–6893. [Google Scholar] [CrossRef] [Green Version]
- Jadczak, J.; Kutrowska-Girzycka, J.; Bieniek, M.; Kazimierczuk, T.; Kossacki, P.; Schindler, J.; Debus, J.; Watanabe, K.; Taniguchi, T.; Ho, C.; et al. Probing negatively charged and neutral excitons in MoS2/hBN and hBN/MoS2/hBN van der Waals heterostructures. Nanotechnology 2021, 32, 145717. [Google Scholar] [CrossRef] [PubMed]
- Arora, A.; Deilmann, T.; Reichenauer, T.; Kern, J.; Michaelis de Vasconcellos, S.; Rohlfing, M.; Bratschitsch, R. Excited-State Trions in Monolayer WS2. Phys. Rev. Lett. 2019, 123, 167401. [Google Scholar] [CrossRef]
- Jones, A.M.; Yu, H.; Schaibley, J.R.; Yan, J.; Mandrus, D.G.; Taniguchi, T.; Watanabe, K.; Dery, H.; Yao, W.; Xu, X. Excitonic luminescence upconversion in a two-dimensional semiconductor. Nat. Phys. 2016, 12, 323–327. [Google Scholar] [CrossRef]
- Jadczak, J.; Bryja, L.; Kutrowska-Girzycka, J.; Kapuscinski, P.; Bieniek, M.; Huang, Y.S.; Hawrylak, P. Room temperature multi-phonon upconversion photoluminescence in monolayer semiconductor WS2. Nat. Commun. 2019, 10, 107. [Google Scholar] [CrossRef] [Green Version]
- Mai, C.; Barrette, A.; Yu, Y.; Semenov, Y.G.; Kim, K.W.; Cao, L.; Gundogdu, K. Many-Body Effects in Valleytronics: Direct Measurement of Valley Lifetimes in Single-Layer MoS2. Nano Lett. 2014, 14, 202–206. [Google Scholar] [CrossRef]
- You, Y.; Zhang, X.X.; Berkelbach, T.C.; Hybertsen, M.S.; Reichman, D.R.; Heinz, T.F. Observation of biexcitons in monolayer WSe2. Nat. Phys. 2015, 11, 477–481. [Google Scholar] [CrossRef]
- Sie, E.J.; Frenzel, A.J.; Lee, Y.H.; Kong, J.; Gedik, N. Intervalley biexcitons and many-body effects in monolayer MoS2. Phys. Rev. B 2015, 92, 125417. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.S.; Kim, M.S.; Kim, H.; Lee, Y.H. Identifying multiexcitons in MoS2 monolayers at room temperature. Phys. Rev. B 2016, 93, 140409. [Google Scholar] [CrossRef]
- Okada, M.; Miyauchi, Y.; Matsuda, K.; Taniguchi, T.; Watanabe, K.; Shinohara, H.; Kitaura, R. Observation of biexcitonic emission at extremely low power density in tungsten disulfide atomic layers grown on hexagonal boron nitride. Sci. Rep. 2017, 7, 322. [Google Scholar] [CrossRef]
- Nagler, P.; Ballottin, M.V.; Mitioglu, A.A.; Durnev, M.V.; Taniguchi, T.; Watanabe, K.; Chernikov, A.; Schüller, C.; Glazov, M.M.; Christianen, P.C.M.; et al. Zeeman Splitting and Inverted Polarization of Biexciton Emission in Monolayer WS2. Phys. Rev. Lett. 2018, 121, 057402. [Google Scholar] [CrossRef] [Green Version]
- Paradisanos, I.; Germanis, S.; Pelekanos, N.T.; Fotakis, C.; Kymakis, E.; Kioseoglou, G.; Stratakis, E. Room temperature observation of biexcitons in exfoliated WS2 monolayers. Appl. Phys. Lett. 2017, 110, 193102. [Google Scholar] [CrossRef] [Green Version]
- Pei, J.; Yang, J.; Wang, X.; Wang, F.; Mokkapati, S.; Lü, T.; Zheng, J.C.; Qin, Q.; Neshev, D.; Tan, H.H.; et al. Excited State Biexcitons in Atomically Thin MoSe2. ACS Nano 2017, 11, 7468–7475. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T.; Lu, Z.; Jin, C.; Chen, Y.; Meng, Y.; Lian, Z.; Taniguchi, T.; Watanabe, K.; Zhang, S.; et al. Revealing the biexciton and trion-exciton complexes in BN encapsulated WSe2. Nat. Commun. 2018, 9, 3719. [Google Scholar] [CrossRef] [Green Version]
- Barbone, M.; Montblanch, A.R.P.; Kara, D.M.; Palacios-Berraquero, C.; Cadore, A.R.; De Fazio, D.; Pingault, B.; Mostaani, E.; Li, H.; Chen, B.; et al. Charge-tuneable biexciton complexes in monolayer WSe2. Nat. Commun. 2018, 9, 3721. [Google Scholar] [CrossRef]
- Paur, M.; Molina-Mendoza, A.J.; Bratschitsch, R.; Watanabe, K.; Taniguchi, T.; Mueller, T. Electroluminescence from multi-particle exciton complexes in transition metal dichalcogenide semiconductors. Nat. Commun. 2019, 10, 1709. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.Y.; Goldstein, T.; Taniguchi, T.; Watanabe, K.; Yan, J. Coulomb-bound four- and five-particle intervalley states in an atomically-thin semiconductor. Nat. Commun. 2018, 9, 3717. [Google Scholar] [CrossRef] [PubMed]
- Hao, K.; Specht, J.F.; Nagler, P.; Xu, L.; Tran, K.; Singh, A.; Dass, C.K.; Schüller, C.; Korn, T.; Richter, M.; et al. Neutral and charged inter-valley biexcitons in monolayer MoSe2. Nat. Commun. 2017, 8, 15552. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Lee, B.; Naylor, C.H.; Ee, H.S.; Park, J.; Johnson, A.T.C.; Agarwal, R. Strong Exciton–Plasmon Coupling in MoS2 Coupled with Plasmonic Lattice. Nano Lett. 2016, 16, 1262–1269. [Google Scholar] [CrossRef] [Green Version]
- Van Tuan, D.; Scharf, B.; Žutić, I.; Dery, H. Marrying Excitons and Plasmons in Monolayer Transition-Metal Dichalcogenides. Phys. Rev. X 2017, 7, 041040. [Google Scholar] [CrossRef] [Green Version]
- Sidler, M.; Back, P.; Cotlet, O.; Srivastava, A.; Fink, T.; Kroner, M.; Demler, E.; Imamoglu, A. Fermi polaron-polaritons in charge-tunable atomically thin semiconductors. Nat. Phys. 2017, 13, 255–261. [Google Scholar] [CrossRef]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419. [Google Scholar] [CrossRef]
- Ponomarenko, L.A.; Geim, A.K.; Zhukov, A.A.; Jalil, R.; Morozov, S.V.; Novoselov, K.S.; Grigorieva, I.V.; Hill, E.H.; Cheianov, V.V.; Fal’ko, V.I.; et al. Tunable metal-insulator transition in double-layer graphene heterostructures. Nat. Phys. 2011, 7, 958–961. [Google Scholar] [CrossRef]
- Georgiou, T.; Jalil, R.; Belle, B.D.; Britnell, L.; Gorbachev, R.V.; Morozov, S.V.; Kim, Y.J.; Gholinia, A.; Haigh, S.J.; Makarovsky, O.; et al. Vertical field-effect transistor based on graphene-WS2 heterostructures for flexible and transparent electronics. Nat. Nanotechnol. 2013, 8, 100–103. [Google Scholar] [CrossRef]
- Robert, C.; Semina, M.A.; Cadiz, F.; Manca, M.; Courtade, E.; Taniguchi, T.; Watanabe, K.; Cai, H.; Tongay, S.; Lassagne, B.; et al. Optical spectroscopy of excited exciton states in MoS2 monolayers in van der Waals heterostructures. Phys. Rev. Mater. 2018, 2, 011001. [Google Scholar] [CrossRef]
- Jin, C.; Ma, E.Y.; Karni, O.; Regan, E.C.; Wang, F.; Heinz, T.F. Ultrafast dynamics in van der Waals heterostructures. Nat. Nanotechnol. 2018, 13, 994–1003. [Google Scholar] [CrossRef]
- Fang, H.; Battaglia, C.; Carraro, C.; Nemsak, S.; Ozdol, B.; Kang, J.S.; Bechtel, H.A.; Desai, S.B.; Kronast, F.; Unal, A.A.; et al. Strong interlayer coupling in van der Waals heterostructures built from single-layer chalcogenides. Proc. Natl. Acad. Sci. USA 2014, 111, 6198–6202. [Google Scholar] [CrossRef] [Green Version]
- Rivera, P.; Schaibley, J.R.; Jones, A.M.; Ross, J.S.; Wu, S.; Aivazian, G.; Klement, P.; Seyler, K.; Clark, G.; Ghimire, N.J.; et al. Observation of long-lived interlayer excitons in monolayer MoSe2-WSe2 heterostructures. Nat. Commun. 2015, 6, 6242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.; Wen, X.; Zhang, J.; Wu, T.; Gong, Y.; Zhang, X.; Yuan, J.; Yi, C.; Lou, J.; Ajayan, P.M.; et al. Ultrafast formation of interlayer hot excitons in atomically thin MoS2/WS2 heterostructures. Nat. Commun. 2016, 7, 12512. [Google Scholar] [CrossRef] [PubMed]
- Baranowski, M.; Surrente, A.; Klopotowski, L.; Urban, J.M.; Zhang, N.; Maude, D.K.; Wiwatowski, K.; Mackowski, S.; Kung, Y.C.; Dumcenco, D.; et al. Probing the Interlayer Exciton Physics in a MoS2/MoSe2/MoS2 van der Waals Heterostructure. Nano Lett. 2017, 17, 6360–6365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, B.; Steinhoff, A.; Pano, B.; Klein, J.; Jahnke, F.; Holleitner, A.; Wurstbauer, U. Long-Lived Direct and Indirect Interlayer Excitons in van der Waals Heterostructures. Nano Lett. 2017, 17, 5229–5237. [Google Scholar] [CrossRef] [Green Version]
- Nagler, P.; Plechinger, G.; Ballottin, M.V.; Mitioglu, A.; Meier, S.; Paradiso, N.; Strunk, C.; Chernikov, A.; Christianen, P.C.M.; Schüller, C.; et al. Interlayer exciton dynamics in a dichalcogenide monolayer heterostructure. 2D Mater. 2017, 4, 025112. [Google Scholar] [CrossRef]
- Wang, T.; Miao, S.; Li, Z.; Meng, Y.; Lu, Z.; Lian, Z.; Blei, M.; Taniguchi, T.; Watanabe, K.; Tongay, S.; et al. Giant Valley-Zeeman Splitting from Spin-Singlet and Spin-Triplet Interlayer Excitons in WSe2/MoSe2 Heterostructure. Nano Lett. 2020, 20, 694–700. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Florian, M.; Steinhoff, A.; Erben, D.; Tran, K.; Kim, D.S.; Sun, L.; Quan, J.; Claassen, R.; Majumder, S.; et al. Twist Angle-Dependent Interlayer Exciton Lifetimes in van der Waals Heterostructures. Phys. Rev. Lett. 2021, 126, 047401. [Google Scholar] [CrossRef]
- Nagler, P.; Ballottin, M.V.; Mitioglu, A.A.; Mooshammer, F.; Paradiso, N.; Strunk, C.; Huber, R.; Chernikov, A.; Christianen, P.C.; Schüller, C.; et al. Giant magnetic splitting inducing near-unity valley polarization in van der Waals heterostructures. Nat. Commun. 2017, 8, 1551. [Google Scholar] [CrossRef]
- Hsu, W.T.; Lu, L.S.; Wu, P.H.; Lee, M.H.; Chen, P.J.; Wu, P.Y.; Chou, Y.C.; Jeng, H.T.; Li, L.J.; Chu, M.W.; et al. Negative circular polarization emissions from WSe2/MoSe2 commensurate heterobilayers. Nat. Commun. 2018, 9, 1356. [Google Scholar] [CrossRef]
- Hanbicki, A.T.; Chuang, H.J.; Rosenberger, M.R.; Hellberg, C.S.; Sivaram, S.V.; McCreary, K.M.; Mazin, I.I.; Jonker, B.T. Double indirect interlayer exciton in a MoSe2/WSe2 van der Waals heterostructure. Acs Nano 2018, 12, 4719–4726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Ardelean, J.; Bai, Y.; Steinhoff, A.; Florian, M.; Jahnke, F.; Xu, X.; Kira, M.; Hone, J.; Zhu, X.Y. Optical generation of high carrier densities in 2D semiconductor heterobilayers. Sci. Adv. 2019, 5, eaax0145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ciarrocchi, A.; Unuchek, D.; Avsar, A.; Watanabe, K.; Taniguchi, T.; Kis, A. Polarization switching and electrical control of interlayer excitons in two-dimensional van der Waals heterostructures. Nat. Photonics 2019, 13, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Gogna, R.; Burg, G.W.; Horng, J.; Paik, E.; Chou, Y.H.; Kim, K.; Tutuc, E.; Deng, H. Highly valley-polarized singlet and triplet interlayer excitons in van der Waals heterostructure. Phys. Rev. B 2019, 100, 041402. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Lu, X.; Dubey, S.; Devenica, L.; Srivastava, A. Dipolar interactions between localized interlayer excitons in van der Waals heterostructures. Nat. Mater. 2020, 19, 624–629. [Google Scholar] [CrossRef]
- Joe, A.Y.; Jauregui, L.A.; Pistunova, K.; Mier Valdivia, A.M.; Lu, Z.; Wild, D.S.; Scuri, G.; De Greve, K.; Gelly, R.J.; Zhou, Y.; et al. Electrically controlled emission from singlet and triplet exciton species in atomically thin light-emitting diodes. Phys. Rev. B 2021, 103, L161411. [Google Scholar] [CrossRef]
- Sigl, L.; Sigger, F.; Kronowetter, F.; Kiemle, J.; Klein, J.; Watanabe, K.; Taniguchi, T.; Finley, J.J.; Wurstbauer, U.; Holleitner, A.W. Signatures of a degenerate many-body state of interlayer excitons in a van der Waals heterostack. Phys. Rev. Res. 2020, 2, 042044. [Google Scholar] [CrossRef]
- Rivera, P.; Seyler, K.L.; Yu, H.; Schaibley, J.R.; Yan, J.; Mandrus, D.G.; Yao, W.; Xu, X. Valley-polarized exciton dynamics in a 2D semiconductor heterostructure. Science 2016, 351, 688–691. [Google Scholar] [CrossRef] [Green Version]
- Lorchat, E.; Selig, M.; Katsch, F.; Yumigeta, K.; Tongay, S.; Knorr, A.; Schneider, C.; Höfling, S. Excitons in Bilayer MoS2 Displaying a Colossal Electric Field Splitting and Tunable Magnetic Response. Phys. Rev. Lett. 2021, 126, 037401. [Google Scholar] [CrossRef]
- Jauregui, L.A.; Joe, A.Y.; Pistunova, K.; Wild, D.S.; High, A.A.; Zhou, Y.; Scuri, G.; De Greve, K.; Sushko, A.; Yu, C.H.; et al. Electrical control of interlayer exciton dynamics in atomically thin heterostructures. Science 2019, 366, 870–875. [Google Scholar] [CrossRef] [Green Version]
- Calman, E.V.; Fowler-Gerace, L.H.; Choksy, D.J.; Butov, L.V.; Nikonov, D.E.; Young, I.A.; Hu, S.; Mishchenko, A.; Geim, A.K. Indirect Excitons and Trions in MoSe2/WSe2 van der Waals Heterostructures. Nano Lett. 2020, 20, 1869–1875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rivera, P.; Yu, H.; Seyler, K.L.; Wilson, N.P.; Yao, W.; Xu, X. Interlayer valley excitons in heterobilayers of transition metal dichalcogenides. Nat. Nanotechnol. 2018, 13, 1004–1015. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; He, J.; Zhang, R.; Cong, C.; Zheng, Y.; Zhang, H.; Zhang, S.; Chen, L. Effects of dielectric screening on the excitonic and critical points properties of WS2/MoS2 heterostructures. Nanoscale 2020, 12, 23732–23739. [Google Scholar] [CrossRef]
- Fogler, M.M.; Butov, L.V.; Novoselov, K.S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 2014, 5, 4555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Calman, E.V.; Fogler, M.M.; Butov, L.V.; Hu, S.; Mishchenko, A.; Geim, A.K. Indirect excitons in van der Waals heterostructures at room temperature. Nat. Commun. 2018, 9, 1895. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mouri, S.; Zhang, W.; Kozawa, D.; Miyauchi, Y.; Eda, G.; Matsuda, K. Thermal dissociation of inter-layer excitons in MoS2/MoSe2 hetero-bilayers. Nanoscale 2017, 9, 6674–6679. [Google Scholar] [CrossRef] [PubMed]
- Deilmann, T.; Thygesen, K.S. Interlayer Trions in the MoS2/WS2 van der Waals Heterostructure. Nano Lett. 2018, 18, 1460–1465. [Google Scholar] [CrossRef] [Green Version]
- Vialla, F.; Danovich, M.; Ruiz-Tijerina, D.A.; Massicotte, M.; Schmidt, P.; Taniguchi, T.; Watanabe, K.; Hunt, R.J.; Szyniszewski, M.; Drummond, N.D.; et al. Tuning of impurity-bound interlayer complexes in a van der Waals heterobilayer. 2D Mater. 2019, 6, 035032. [Google Scholar] [CrossRef]
- Baek, H.; Brotons-Gisbert, M.; Campbell, A.; Vitale, V.; Lischner, J.; Watanabe, K.; Taniguchi, T.; Gerardot, B.D. Optical read-out of Coulomb staircases in a moiré superlattice via trapped interlayer trions. Nat. Nanotechnol. 2021, 16, 1237–1243. [Google Scholar] [CrossRef]
- Wang, Z.; Rhodes, D.A.; Watanabe, K.; Taniguchi, T.; Hone, J.C.; Shan, J.; Mak, K.F. Evidence of high-temperature exciton condensation in two-dimensional atomic double layers. Nature 2019, 574, 76–80. [Google Scholar] [CrossRef]
- Van der Zande, A.M.; Kunstmann, J.; Chernikov, A.; Chenet, D.A.; You, Y.; Zhang, X.; Huang, P.Y.; Berkelbach, T.C.; Wang, L.; Zhang, F.; et al. Tailoring the Electronic Structure in Bilayer Molybdenum Disulfide via Interlayer Twist. Nano Lett. 2014, 14, 3869–3875. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhang, L.; Cao, T.; Jin, C.; Qiu, D.; Zhou, Q.; Zettl, A.; Yang, P.; Louie, S.G.; Wang, F. Evolution of interlayer coupling in twisted molybdenum disulfide bilayers. Nat. Commun. 2014, 5, 4966. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Ling, X.; Liang, L.; Kong, J.; Terrones, H.; Meunier, V.; Dresselhaus, M.S. Probing the Interlayer Coupling of Twisted Bilayer MoS2 Using Photoluminescence Spectroscopy. Nano Lett. 2014, 14, 5500–5508. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.C.; Jin, W.; Zaki, N.; Kunstmann, J.; Chenet, D.; Arefe, G.; Sadowski, J.T.; Dadap, J.I.; Sutter, P.; Hone, J.; et al. Direct Measurement of the Tunable Electronic Structure of Bilayer MoS2 by Interlayer Twist. Nano Lett. 2016, 16, 953–959. [Google Scholar] [CrossRef]
- Huang, S.; Liang, L.; Ling, X.; Puretzky, A.A.; Geohegan, D.B.; Sumpter, B.G.; Kong, J.; Meunier, V.; Dresselhaus, M.S. Low-Frequency Interlayer Raman Modes to Probe Interface of Twisted Bilayer MoS2. Nano Lett. 2016, 16, 1435–1444. [Google Scholar] [CrossRef]
- Liao, M.; Wei, Z.; Du, L.; Wang, Q.; Tang, J.; Yu, H.; Wu, F.; Zhao, J.; Xu, X.; Han, B.; et al. Precise control of the interlayer twist angle in large scale MoS2 homostructures. Nat. Commun. 2020, 11, 2153. [Google Scholar] [CrossRef]
- Grzeszczyk, M.; Szpakowski, J.; Slobodeniuk, A.; Kazimierczuk, T.; Bhatnagar, M.; Taniguchi, T.; Watanabe, K.; Kossacki, P.; Potemski, M.; Babiński, A.; et al. The optical response of artificially twisted MoS2 bilayers. Sci. Rep. 2021, 11, 17037. [Google Scholar] [CrossRef]
- Tran, K.; Choi, J.; Singh, A. Moiré and beyond in transition metal dichalcogenide twisted bilayers. 2D Mater. 2020, 8, 022002. [Google Scholar] [CrossRef]
- Brotons-Gisbert, M.; Baek, H.; Campbell, A.; Watanabe, K.; Taniguchi, T.; Gerardot, B. Moire-Trapped Interlayer Trions in a Charge-Tunable WSe2/MoSe2 Heterobilayer. Phys. Rev. X 2021, 11, 031033. [Google Scholar] [CrossRef]
- Ruiz-Tijerina, D.A.; Fal’ko, V.I. Interlayer hybridization and moiré superlattice minibands for electrons and excitons in heterobilayers of transition-metal dichalcogenides. Phys. Rev. B 2019, 99, 125424. [Google Scholar] [CrossRef] [Green Version]
- Kunstmann, J.; Mooshammer, F.; Nagler, P.; Chaves, A.; Stein, F.; Paradiso, N.; Plechinger, G.; Strunk, C.; Schüller, C.; Seifert, G.; et al. Momentum-space indirect interlayer excitons in transition-metal dichalcogenide van der Waals heterostructures. Nat. Phys. 2018, 14, 801–805. [Google Scholar] [CrossRef] [Green Version]
- Tran, K.; Moody, G.; Wu, F.; Lu, X.; Choi, J.; Kim, K.; Rai, A.; Sanchez, D.A.; Quan, J.; Singh, A.; et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 2019, 567, 71–75. [Google Scholar] [CrossRef] [Green Version]
- Seyler, K.L.; Rivera, P.; Yu, H.; Wilson, N.P.; Ray, E.L.; Mandrus, D.G.; Yan, J.; Yao, W.; Xu, X. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 2019, 567, 66–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, C.; Regan, E.C.; Yan, A.; Iqbal Bakti Utama, M.; Wang, D.; Zhao, S.; Qin, Y.; Yang, S.; Zheng, Z.; Shi, S.; et al. Observation of moiré excitons in WSe2/WS2 heterostructure superlattices. Nature 2019, 567, 76–80. [Google Scholar] [CrossRef]
- Alexeev, E.M.; Ruiz-Tijerina, D.A.; Danovich, M.; Hamer, M.J.; Terry, D.J.; Nayak, P.K.; Ahn, S.; Pak, S.; Lee, J.; Sohn, J.I.; et al. Resonantly hybridized excitons in moiré superlattices in van der Waals heterostructures. Nature 2019, 567, 81–86. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Hsu, W.T.; Lu, L.S.; Sun, L.; Cheng, H.Y.; Lee, M.H.; Quan, J.; Tran, K.; Wang, C.Y.; Staab, M.; et al. Moiré potential impedes interlayer exciton diffusion in van der Waals heterostructures. Sci. Adv. 2020, 6, eaba8866. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Li, L.; Li, T.; Xu, Y.; Liu, S.; Barmak, K.; Watanabe, K.; Taniguchi, T.; MacDonald, A.H.; Shan, J.; et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 2020, 579, 353–358. [Google Scholar] [CrossRef]
- Regan, E.C.; Wang, D.; Jin, C.; Bakti Utama, M.I.; Gao, B.; Wei, X.; Zhao, S.; Zhao, W.; Zhang, Z.; Yumigeta, K.; et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 2020, 579, 359–363. [Google Scholar] [CrossRef]
- Zheng, Z.; Ma, Q.; Bi, Z.; de la Barrera, S.; Liu, M.H.; Mao, N.; Zhang, Y.; Kiper, N.; Watanabe, K.; Taniguchi, T.; et al. Unconventional ferroelectricity in moiré heterostructures. Nature 2020, 588, 71–76. [Google Scholar] [CrossRef]
- Kennes, D.M.; Claassen, M.; Xian, L.; Georges, A.; Millis, A.J.; Hone, J.; Dean, C.R.; Basov, D.N.; Pasupathy, A.N.; Rubio, A. Moiré heterostructures as a condensed-matter quantum simulator. Nat. Phys. 2021, 17, 155–163. [Google Scholar] [CrossRef]
- Jin, C.; Tao, Z.; Li, T.; Xu, Y.; Tang, Y.; Zhu, J.; Liu, S.; Watanabe, K.; Taniguchi, T.; Hone, J.C.; et al. Stripe phases in WSe2/WS2 moiré superlattices. Nat. Mater. 2021, 20, 940–944. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Wang, T.; Miao, S.; Wang, C.; Li, Z.; Lian, Z.; Taniguchi, T.; Watanabe, K.; Okamoto, S.; Xiao, D.; et al. Correlated insulating states at fractional fillings of the WS2/WSe2 moiré lattice. Nat. Phys. 2021, 17, 715–719. [Google Scholar] [CrossRef]
- Salpeter, E.E.; Bethe, H.A. A Relativistic Equation for Bound-State Problems. Phys. Rev. 1951, 84, 1232–1242. [Google Scholar] [CrossRef]
- Sham, L.J.; Rice, T.M. Many-Particle Derivation of the Effective-Mass Equation for the Wannier Exciton. Phys. Rev. 1966, 144, 708–714. [Google Scholar] [CrossRef]
- Strinati, G. Dynamical Shift and Broadening of Core Excitons in Semiconductors. Phys. Rev. Lett. 1982, 49, 1519–1522. [Google Scholar] [CrossRef]
- Strinati, G. Effects of dynamical screening on resonances at inner-shell thresholds in semiconductors. Phys. Rev. B 1984, 29, 5718–5726. [Google Scholar] [CrossRef]
- Hanke, W.; Sham, L.J. Many-Particle Effects in the Optical Excitations of a Semiconductor. Phys. Rev. Lett. 1979, 43, 387–390. [Google Scholar] [CrossRef]
- Albrecht, S.; Onida, G.; Reining, L. Ab initio calculation of the quasiparticle spectrum and excitonic effects in Li2O. Phys. Rev. B 1997, 55, 10278–10281. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, S.; Reining, L.; Del Sole, R.; Onida, G. Ab Initio Calculation of Excitonic Effects in the Optical Spectra of Semiconductors. Phys. Rev. Lett. 1998, 80, 4510–4513. [Google Scholar] [CrossRef] [Green Version]
- Rohlfing, M.; Louie, S.G. Electron-hole excitations and optical spectra from first principles. Phys. Rev. B 2000, 62, 4927–4944. [Google Scholar] [CrossRef]
- Deslippe, J.; Samsonidze, G.; Strubbe, D.A.; Jain, M.; Cohen, M.L.; Louie, S.G. BerkeleyGW: A massively parallel computer package for the calculation of the quasiparticle and optical properties of materials and nanostructures. Comput. Phys. Commun. 2012, 183, 1269–1289. [Google Scholar] [CrossRef] [Green Version]
- Gillet, Y.; Giantomassi, M.; Gonze, X. Efficient on-the-fly interpolation technique for Bethe–Salpeter calculations of optical spectra. Comput. Phys. Commun. 2016, 203, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Sangalli, D.; Ferretti, A.; Miranda, H.; Attaccalite, C.; Marri, I.; Cannuccia, E.; Melo, P.; Marsili, M.; Paleari, F.; Marrazzo, A.; et al. Many-body perturbation theory calculations using the yambo code. J. Phys. Condens. Matter 2019, 31, 325902. [Google Scholar] [CrossRef] [PubMed]
- Ono, S.; Noguchi, Y.; Sahara, R.; Kawazoe, Y.; Ohno, K. TOMBO: All-electron mixed-basis approach to condensed matter physics. Comput. Phys. Commun. 2015, 189, 20–30. [Google Scholar] [CrossRef]
- Vorwerk, C.; Aurich, B.; Cocchi, C.; Draxl, C. Bethe–Salpeter equation for absorption and scattering spectroscopy: Implementation in the exciting code. Electron. Struct. 2019, 1, 037001. [Google Scholar] [CrossRef]
- Sander, T.; Maggio, E.; Kresse, G. Beyond the Tamm-Dancoff approximation for extended systems using exact diagonalization. Phys. Rev. B 2015, 92, 045209. [Google Scholar] [CrossRef]
- Marini, A.; Hogan, C.; Grüning, M.; Varsano, D. Yambo: An ab initio tool for excited state calculations. Comput. Phys. Commun. 2009, 180, 1392–1403. [Google Scholar] [CrossRef] [Green Version]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Cheiwchanchamnangij, T.; Lambrecht, W.R.L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 2012, 85, 205302. [Google Scholar] [CrossRef] [Green Version]
- Komsa, H.P.; Krasheninnikov, A.V. Effects of confinement and environment on the electronic structure and exciton binding energy of MoS2 from first principles. Phys. Rev. B 2012, 86, 241201. [Google Scholar] [CrossRef] [Green Version]
- Qiu, D.Y.; da Jornada, F.H.; Louie, S.G. Optical Spectrum of MoS2: Many-Body Effects and Diversity of Exciton States. Phys. Rev. Lett. 2013, 111, 216805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, H.; Pan, H.; Zhang, Y.W.; Yakobson, B.I. Quasiparticle band structures and optical properties of strained monolayer MoS2 and WS2. Phys. Rev. B 2013, 87, 155304. [Google Scholar] [CrossRef] [Green Version]
- Bernardi, M.; Palummo, M.; Grossman, J.C. Extraordinary Sunlight Absorption and One Nanometer Thick Photovoltaics Using Two-Dimensional Monolayer Materials. Nano Lett. 2013, 13, 3664–3670. [Google Scholar] [CrossRef]
- Conley, H.J.; Wang, B.; Ziegler, J.I.; Haglund, R.F.; Pantelides, S.T.; Bolotin, K.I. Bandgap Engineering of Strained Monolayer and Bilayer MoS2. Nano Lett. 2013, 13, 3626–3630. [Google Scholar] [CrossRef] [Green Version]
- Klots, A.R.; Newaz, A.K.M.; Wang, B.; Prasai, D.; Krzyzanowska, H.; Lin, J.; Caudel, D.; Ghimire, N.J.; Yan, J.; Ivanov, B.L.; et al. Probing excitonic states in suspended two-dimensional semiconductors byphotocurrent spectroscopy. Sci. Rep. 2014, 4, 6608. [Google Scholar] [CrossRef]
- Soklaski, R.; Liang, Y.; Yang, L. Temperature effect on optical spectra of monolayer molybdenum disulfide. Appl. Phys. Lett. 2014, 104, 193110. [Google Scholar] [CrossRef] [Green Version]
- Ugeda, M.M.; Bradley, A.J.; Shi, S.F.; da Jornada, F.H.; Zhang, Y.; Qiu, D.Y.; Ruan, W.; Mo, S.K.; Hussain, Z.; Shen, Z.X.; et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 2014, 13, 1091. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, H.; Liu, G.B.; Gong, P.; Xu, X.; Yao, W. Dirac cones and Dirac saddle points of bright excitons in monolayer transition metal dichalcogenides. Nat. Commun. 2014, 5, 3876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, D.Y.; Cao, T.; Louie, S.G. Nonanalyticity, Valley Quantum Phases, and Lightlike Exciton Dispersion in Monolayer Transition Metal Dichalcogenides: Theory and First-Principles Calculations. Phys. Rev. Lett. 2015, 115, 176801. [Google Scholar] [CrossRef]
- Latini, S.; Olsen, T.; Thygesen, K.S. Excitons in van der Waals heterostructures: The important role of dielectric screening. Phys. Rev. B 2015, 92, 245123. [Google Scholar] [CrossRef] [Green Version]
- Qiu, D.Y.; da Jornada, F.H.; Louie, S.G. Screening and many-body effects in two-dimensional crystals: Monolayer MoS2. Phys. Rev. B 2016, 93, 235435. [Google Scholar] [CrossRef] [Green Version]
- Molina-Sánchez, A.; Palummo, M.; Marini, A.; Wirtz, L. Temperature-dependent excitonic effects in the optical properties of single-layer MoS2. Phys. Rev. B 2016, 93, 155435. [Google Scholar] [CrossRef] [Green Version]
- Robert, C.; Picard, R.; Lagarde, D.; Wang, G.; Echeverry, J.P.; Cadiz, F.; Renucci, P.; Högele, A.; Amand, T.; Marie, X.; et al. Excitonic properties of semiconducting monolayer and bilayer MoTe2. Phys. Rev. B 2016, 94, 155425. [Google Scholar] [CrossRef] [Green Version]
- Despoja, V.; Rukelj, Z.; Marušić, L. Ab initio study of electronic excitations and the dielectric function in molybdenum disulfide monolayer. Phys. Rev. B 2016, 94, 165446. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Wu, M.; Cao, T.; Monahan, D.M.; Lee, Y.H.; Louie, S.G.; Fleming, G.R. Exchange-driven intravalley mixing of excitons in monolayer transition metal dichalcogenides. Nat. Phys. 2019, 15, 228. [Google Scholar] [CrossRef]
- Molina-Sánchez, A.; Sangalli, D.; Hummer, K.; Marini, A.; Wirtz, L. Effect of spin-orbit interaction on the optical spectra of single-layer, double-layer, and bulk MoS2. Phys. Rev. B 2013, 88, 045412. [Google Scholar] [CrossRef] [Green Version]
- Echeverry, J.P.; Urbaszek, B.; Amand, T.; Marie, X.; Gerber, I.C. Splitting between bright and dark excitons in transition metal dichalcogenide monolayers. Phys. Rev. B 2016, 93, 121107. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Laurien, M.; Hu, Z.; Rubel, O. Exploration of the bright and dark exciton landscape and fine structure of MoS2 using G0W0-BSE. Phys. Rev. B 2019, 100, 125413. [Google Scholar] [CrossRef] [Green Version]
- Druppel, M.; Deilmann, T.; Kruger, P.; Rohlfing, M. Diversity of trion states and substrate effects in the optical properties of an MoS2 monolayer. Nat. Commun. 2017, 8, 2117. [Google Scholar] [CrossRef]
- Torche, A.; Bester, G. First-principles many-body theory for charged and neutral excitations: Trion fine structure splitting in transition metal dichalcogenides. Phys. Rev. B 2019, 100, 201403. [Google Scholar] [CrossRef]
- Zhumagulov, Y.V.; Vagov, A.; Senkevich, N.Y.; Gulevich, D.R.; Perebeinos, V. Three-particle states and brightening of intervalley excitons in a doped MoS2 monolayer. Phys. Rev. B 2020, 101, 245433. [Google Scholar] [CrossRef]
- Zibouche, N.; Schlipf, M.; Giustino, F. GW band structure of monolayer MoS2 using the SternheimerGW method and effect of dielectric environment. Phys. Rev. B 2021, 103, 125401. [Google Scholar] [CrossRef]
- He, J.; Hummer, K.; Franchini, C. Stacking effects on the electronic and optical properties of bilayer transition metal dichalcogenides MoS2, MoSe2, WS2, and WSe2. Phys. Rev. B 2014, 89, 075409. [Google Scholar] [CrossRef]
- Gao, S.; Yang, L.; Spataru, C.D. Interlayer coupling and gate-tunable excitons in transition metal dichalcogenide heterostructures. Nano Lett. 2017, 17, 7809–7813. [Google Scholar] [CrossRef] [PubMed]
- Gillen, R.; Maultzsch, J. Interlayer excitons in MoSe2/WSe2 heterostructures from first principles. Phys. Rev. B 2018, 97, 165306. [Google Scholar] [CrossRef] [Green Version]
- Torun, E.; Miranda, H.P.; Molina-Sánchez, A.; Wirtz, L. Interlayer and intralayer excitons in MoS2/WS2 and MoSe2/WSe2 heterobilayers. Phys. Rev. B 2018, 97, 245427. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Li, X.; Yang, L. Modulated interlayer exciton properties in a two-dimensional moiré crystal. Phys. Rev. B 2019, 100, 155416. [Google Scholar] [CrossRef] [Green Version]
- Gerber, I.C.; Courtade, E.; Shree, S.; Robert, C.; Taniguchi, T.; Watanabe, K.; Balocchi, A.; Renucci, P.; Lagarde, D.; Marie, X.; et al. Interlayer excitons in bilayer MoS2 with strong oscillator strength up to room temperature. Phys. Rev. B 2019, 99, 035443. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Zhang, X.; Lu, G. Shedding light on moiré excitons: A first-principles perspective. Sci. Adv. 2020, 6, eabc5638. [Google Scholar] [CrossRef]
- Suzuki, Y.; Watanabe, K. Excitons in two-dimensional atomic layer materials from time-dependent density functional theory: Mono-layer and bi-layer hexagonal boron nitride and transition-metal dichalcogenides. Phys. Chem. Chem. Phys. 2020, 22, 2908–2916. [Google Scholar] [CrossRef]
- Li, Z.; Lu, X.; Cordovilla Leon, D.F.; Lyu, Z.; Xie, H.; Hou, J.; Lu, Y.; Guo, X.; Kaczmarek, A.; Taniguchi, T.; et al. Interlayer Exciton Transport in MoSe2/WSe2 Heterostructures. ACS Nano 2021, 15, 1539–1547. [Google Scholar] [CrossRef] [PubMed]
- Deilmann, T.; Rohlfing, M.; Wurstbauer, U. Light–matter interaction in van der Waals hetero-structures. J. Phys. Condens. Matter 2020, 32, 333002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palummo, M.; Bernardi, M.; Grossman, J.C. Exciton radiative lifetimes in two-dimensional transition metal dichalcogenides. Nano Lett. 2015, 15, 2794–2800. [Google Scholar] [CrossRef] [Green Version]
- Steinhoff, A.; Rösner, M.; Jahnke, F.; Wehling, T.O.; Gies, C. Influence of Excited Carriers on the Optical and Electronic Properties of MoS2. Nano Lett. 2014, 14, 3743–3748. [Google Scholar] [CrossRef] [PubMed]
- Berghäuser, G.; Malic, E. Analytical approach to excitonic properties of MoS2. Phys. Rev. B 2014, 89, 125309. [Google Scholar] [CrossRef] [Green Version]
- Konabe, S.; Okada, S. Effect of Coulomb interactions on optical properties of monolayer transition-metal dichalcogenides. Phys. Rev. B 2014, 90, 155304. [Google Scholar] [CrossRef]
- Wu, F.; Qu, F.; MacDonald, A.H. Exciton band structure of monolayer MoS2. Phys. Rev. B 2015, 91, 075310. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, A.; Sidler, M.; Allain, A.V.; Lembke, D.S.; Kis, A.; Imamoğlu, A. Optically active quantum dots in monolayer WSe2. Nat. Nanotechnol. 2015, 10, 491–496. [Google Scholar] [CrossRef]
- Scharf, B.; Frank, T.; Gmitra, M.; Fabian, J.; Žutić, I.; Perebeinos, V. Excitonic Stark effect in MoS2 monolayers. Phys. Rev. B 2016, 94, 245434. [Google Scholar] [CrossRef] [Green Version]
- Ridolfi, E.; Lewenkopf, C.H.; Pereira, V.M. Excitonic structure of the optical conductivity in MoS2 monolayers. Phys. Rev. B 2018, 97, 205409. [Google Scholar] [CrossRef] [Green Version]
- Steinhoff, A.; Kim, J.H.; Jahnke, F.; Rösner, M.; Kim, D.S.; Lee, C.; Han, G.H.; Jeong, M.S.; Wehling, T.O.; Gies, C. Efficient Excitonic Photoluminescence in Direct and Indirect Band Gap Monolayer MoS2. Nano Lett. 2015, 15, 6841–6847. [Google Scholar] [CrossRef] [PubMed]
- Glazov, M.M.; Amand, T.; Marie, X.; Lagarde, D.; Bouet, L.; Urbaszek, B. Exciton fine structure and spin decoherence in monolayers of transition metal dichalcogenides. Phys. Rev. B 2014, 89, 201302. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Shan, W.Y.; Yao, W.; Xiao, D. Berry Phase Modification to the Energy Spectrum of Excitons. Phys. Rev. Lett. 2015, 115, 166803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glazov, M.M.; Ivchenko, E.L.; Wang, G.; Amand, T.; Marie, X.; Urbaszek, B.; Liu, B.L. Spin and valley dynamics of excitons in transition metal dichalcogenide monolayers. Phys. Status Solidi (B) 2015, 252, 2349–2362. [Google Scholar] [CrossRef] [Green Version]
- Van der Donck, M.; Peeters, F.M. Spectrum of exciton states in monolayer transition metal dichalcogenides: Angular momentum and Landau levels. Phys. Rev. B 2019, 99, 115439. [Google Scholar] [CrossRef] [Green Version]
- Chaves, A.J.; Ribeiro, R.M.; Frederico, T.; Peres, N.M.R. Excitonic effects in the optical properties of 2D materials: An equation of motion approach. 2D Mater. 2017, 4, 025086. [Google Scholar] [CrossRef] [Green Version]
- Trushin, M.; Goerbig, M.O.; Belzig, W. Optical absorption by Dirac excitons in single-layer transition-metal dichalcogenides. Phys. Rev. B 2016, 94, 041301. [Google Scholar] [CrossRef] [Green Version]
- Glazov, M.M.; Golub, L.E.; Wang, G.; Marie, X.; Amand, T.; Urbaszek, B. Intrinsic exciton-state mixing and nonlinear optical properties in transition metal dichalcogenide monolayers. Phys. Rev. B 2017, 95, 035311. [Google Scholar] [CrossRef] [Green Version]
- Trushin, M.; Goerbig, M.O.; Belzig, W. Model Prediction of Self-Rotating Excitons in Two-Dimensional Transition-Metal Dichalcogenides. Phys. Rev. Lett. 2018, 120, 187401. [Google Scholar] [CrossRef] [Green Version]
- Berkelbach, T.C.; Hybertsen, M.S.; Reichman, D.R. Theory of neutral and charged excitons in monolayer transition metal dichalcogenides. Phys. Rev. B 2013, 88, 045318. [Google Scholar] [CrossRef] [Green Version]
- Kylänpää, I.; Komsa, H.P. Binding energies of exciton complexes in transition metal dichalcogenide monolayers and effect of dielectric environment. Phys. Rev. B 2015, 92, 205418. [Google Scholar] [CrossRef] [Green Version]
- Mayers, M.Z.; Berkelbach, T.C.; Hybertsen, M.S.; Reichman, D.R. Binding energies and spatial structures of small carrier complexes in monolayer transition-metal dichalcogenides via diffusion Monte Carlo. Phys. Rev. B 2015, 92, 161404. [Google Scholar] [CrossRef] [Green Version]
- Velizhanin, K.A.; Saxena, A. Excitonic effects in two-dimensional semiconductors: Path integral Monte Carlo approach. Phys. Rev. B 2015, 92, 195305. [Google Scholar] [CrossRef] [Green Version]
- Olsen, T.; Latini, S.; Rasmussen, F.; Thygesen, K.S. Simple Screened Hydrogen Model of Excitons in Two-Dimensional Materials. Phys. Rev. Lett. 2016, 116, 056401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kidd, D.W.; Zhang, D.K.; Varga, K. Binding energies and structures of two-dimensional excitonic complexes in transition metal dichalcogenides. Phys. Rev. B 2016, 93, 125423. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, T.G. Exciton Stark shift and electroabsorption in monolayer transition-metal dichalcogenides. Phys. Rev. B 2016, 94, 125424. [Google Scholar] [CrossRef] [Green Version]
- Cho, Y.; Berkelbach, T.C. Environmentally sensitive theory of electronic and optical transitions in atomically thin semiconductors. Phys. Rev. B 2018, 97, 041409. [Google Scholar] [CrossRef] [Green Version]
- Selig, M.; Berghäuser, G.; Richter, M.; Bratschitsch, R.; Knorr, A.; Malic, E. Dark and bright exciton formation, thermalization, and photoluminescence in monolayer transition metal dichalcogenides. 2D Mater. 2018, 5, 035017. [Google Scholar] [CrossRef] [Green Version]
- Cavalcante, L.S.R.; da Costa, D.R.; Farias, G.A.; Reichman, D.R.; Chaves, A. Stark shift of excitons and trions in two-dimensional materials. Phys. Rev. B 2018, 98, 245309. [Google Scholar] [CrossRef] [Green Version]
- Feierabend, M.; Khatibi, Z.; Berghäuser, G.; Malic, E. Dark exciton based strain sensing in tungsten-based transition metal dichalcogenides. Phys. Rev. B 2019, 99, 195454. [Google Scholar] [CrossRef] [Green Version]
- Hsu, W.T.; Quan, J.; Wang, C.Y.; Lu, L.S.; Campbell, M.; Chang, W.H.; Li, L.J.; Li, X.; Shih, C.K. Dielectric impact on exciton binding energy and quasiparticle bandgap in monolayer WS2 and WSe2. 2D Mater. 2019, 6, 025028. [Google Scholar] [CrossRef]
- Rytova, N.S. Screened potential of a point charge in a thin film. Proc. MSU Phys. Astron. 1967, 3, 30. [Google Scholar]
- Keldysh, L.V. Coulomb interaction in thin semiconduc-tor and semimetal films. JETP Lett. 1979, 29, 658. [Google Scholar]
- Slobodeniuk, A.O.; Bala, Ł.; Koperski, M.; Molas, M.R.; Kossacki, P.; Nogajewski, K.; Bartos, M.; Watanabe, K.; Taniguchi, T.; Faugeras, C.; et al. Fine structure of K-excitons in multilayers of transition metal dichalcogenides. 2D Mater. 2019, 6, 025026. [Google Scholar] [CrossRef]
- Arora, A.; Koperski, M.; Slobodeniuk, A.; Nogajewski, K.; Schmidt, R.; Schneider, R.; Molas, M.R.; de Vasconcellos, S.M.; Bratschitsch, R.; Potemski, M. Zeeman spectroscopy of excitons and hybridization of electronic states in few-layer WSe2, MoSe2 and MoTe2. 2D Mater. 2018, 6, 015010. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Gupta, G.; Majumdar, K. Layer degree of freedom for excitons in transition metal dichalcogenides. Phys. Rev. B 2019, 99, 165411. [Google Scholar] [CrossRef] [Green Version]
- Berman, O.L.; Kezerashvili, R.Y. High-temperature superfluidity of the two-component Bose gas in a transition metal dichalcogenide bilayer. Phys. Rev. B 2016, 93, 245410. [Google Scholar] [CrossRef] [Green Version]
- Van der Donck, M.; Peeters, F. Interlayer excitons in transition metal dichalcogenide heterostructures. Phys. Rev. B 2018, 98, 115104. [Google Scholar] [CrossRef] [Green Version]
- Kormányos, A.; Zólyomi, V.; Fal’ko, V.I.; Burkard, G. Tunable Berry curvature and valley and spin Hall effect in bilayer MoS2. Phys. Rev. B 2018, 98, 035408. [Google Scholar] [CrossRef] [Green Version]
- Berman, O.L.; Kezerashvili, R.Y. Superfluidity of dipolar excitons in a transition metal dichalcogenide double layer. Phys. Rev. B 2017, 96, 094502. [Google Scholar] [CrossRef] [Green Version]
- Bieniek, M.; Szulakowska, L.; Hawrylak, P. Band nesting and exciton spectrum in monolayer MoS2. Phys. Rev. B 2020, 101, 125423. [Google Scholar] [CrossRef] [Green Version]
- Bieniek, M. Electronic and Optical Properties of Two-Dimensional Transition Metal Dichalcogenide Crystals. Ph.D. Thesis, Wroclaw University of Science and Technology, Wroclaw, Poland, October 2021. [Google Scholar]
- Clementi, E.; Raimondi, D.L. Atomic Screening Constants from SCF Functions. J. Chem. Phys. 1963, 38, 2686. [Google Scholar] [CrossRef]
- Clementi, E.; Raimondi, D.L.; Reinhardt, W.P. Atomic Screening Constants from SCF Functions. II. Atoms with 37 to 86 Electrons. J. Chem. Phys. 1967, 47, 1300. [Google Scholar] [CrossRef]
- Cappelluti, E.; Roldan, R.; Silva-Guillen, J.A.; Ordejon, P.; Guinea, F. Tight-binding model and direct-gap/indirect-gap transition in single-layer and multilayer MoS2. Phys. Rev. B 2013, 88, 075409. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.B.; Shan, W.Y.; Yao, Y.; Yao, W.; Xiao, D. Three-band tight-binding model for monolayers of group-VIB transition metal dichalcogenides. Phys. Rev. B 2013, 88, 085433. [Google Scholar] [CrossRef] [Green Version]
- Rostami, H.; Moghaddam, A.G.; Asgari, R. Effective lattice Hamiltonian for monolayer MoS2: Tailoring electronic structure with perpendicular electric and magnetic fields. Phys. Rev. B 2013, 88, 085440. [Google Scholar] [CrossRef] [Green Version]
- Zahid, F.; Liu, L.; Zhu, Y.; Wang, J.; Guo, H. A generic tight-binding model for monolayer, bilayer and bulk MoS2. AIP Adv. 2013, 3, 052111. [Google Scholar] [CrossRef] [Green Version]
- Fang, S.; Kuate Defo, R.; Shirodkar, S.N.; Lieu, S.; Tritsaris, G.A.; Kaxiras, E. Ab initio tight-binding Hamiltonian for transition metal dichalcogenides. Phys. Rev. B 2015, 92, 205108. [Google Scholar] [CrossRef] [Green Version]
- Ho, Y.H.; Wang, Y.H.; Chen, H.Y. Magnetoelectronic and optical properties of a MoS2 monolayer. Phys. Rev. B 2014, 89, 155316. [Google Scholar] [CrossRef]
- Liu, G.B.; Xiao, D.; Yao, Y.; Xu, X.; Yao, W. Electronic structures and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides. Chem. Soc. Rev. 2015, 44, 2643–2663. [Google Scholar] [CrossRef] [Green Version]
- Ridolfi, E.; Le, D.; Rahman, T.S.; Mucciolo, E.R.; Lewenkopf, C.H. A tight-binding model for MoS2 monolayers. J. Phys. Condens. Matter 2015, 27, 365501. [Google Scholar] [CrossRef] [Green Version]
- Shanavas, K.V.; Satpathy, S. Effective tight-binding model for MX2 under electric and magnetic fields. Phys. Rev. B 2015, 91, 235145. [Google Scholar] [CrossRef] [Green Version]
- Silva-Guillen, J.A.; San-Jose, P.; Roldan, R. Electronic Band Structure of Transition Metal Dichalcogenides from Ab Initio and Slater—Koster Tight-Binding Model. Appl. Sci. 2016, 6, 284. [Google Scholar] [CrossRef] [Green Version]
- Pearce, A.J.; Mariani, E.; Burkard, G. Tight-binding approach to strain and curvature in monolayer transition-metal dichalcogenides. Phys. Rev. B 2016, 94, 155416. [Google Scholar] [CrossRef] [Green Version]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498. [Google Scholar] [CrossRef]
- Koskinen, P.; Mäkinen, V. Density-functional tight-binding for beginners. Comput. Mater. Sci. 2009, 47, 237–253. [Google Scholar] [CrossRef] [Green Version]
- Urban, A.; Reese, M.; Mrovec, M.; Elsässer, C.; Meyer, B. Parameterization of tight-binding models from density functional theory calculations. Phys. Rev. B 2011, 84, 155119. [Google Scholar] [CrossRef]
- Kormányos, A.; Zólyomi, V.; Drummond, N.D.; Rakyta, P.; Burkard, G.; Fal’ko, V.I. Monolayer MoS2: Trigonal warping, the Γ valley, and spin-orbit coupling effects. Phys. Rev. B 2013, 88, 045416. [Google Scholar] [CrossRef] [Green Version]
- Kormányos, A.; Burkard, G.; Gmitra, M.; Fabian, J.; Zólyomi, V.; Drummond, N.D.; Fal’ko, V. Kp theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2015, 2, 022001. [Google Scholar] [CrossRef]
- Pedersen, T.G.; Pedersen, K.; Brun Kriestensen, T. Optical matrix elements in tight-binding calculations. Phys. Rev. B 2001, 63, 201101. [Google Scholar] [CrossRef]
- Zhang, X.; Shan, W.Y.; Xiao, D. Optical Selection Rule of Excitons in Gapped Chiral Fermion Systems. Phys. Rev. Lett. 2018, 120, 077401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, T.; Wu, M.; Louie, S.G. Unifying Optical Selection Rules for Excitons in Two Dimensions: Band Topology and Winding Numbers. Phys. Rev. Lett. 2018, 120, 087402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, 1st ed.; Dover Publications Inc.: Mignola, NY, USA, 1989. [Google Scholar]
- Shavitt, I.; Bartlett, R.J. Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory; Cambridge Molecular Science, Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef] [Green Version]
- Hawrylak, P. Single-electron capacitance spectroscopy of few-electron artificial atoms in a magnetic field: Theory and experiment. Phys. Rev. Lett. 1993, 71, 3347–3350. [Google Scholar] [CrossRef] [PubMed]
- Hawrylak, P.; Pfannkuche, D. Magnetoluminescence from correlated electrons in quantum dots. Phys. Rev. Lett. 1993, 70, 485–488. [Google Scholar] [CrossRef]
- Wojs, A.; Hawrylak, P. Negatively charged magnetoexcitons in quantum dots. Phys. Rev. B 1995, 51, 10880–10885. [Google Scholar] [CrossRef]
- Wojs, A.; Hawrylak, P.; Fafard, S.; Jacak, L. Electronic structure and magneto-optics of self-assembled quantum dots. Phys. Rev. B 1996, 54, 5604–5608. [Google Scholar] [CrossRef] [Green Version]
- Wojs, A.; Hawrylak, P. Theory of photoluminescence from modulation-doped self-assembled quantum dots in a magnetic field. Phys. Rev. B 1997, 55, 13066–13071. [Google Scholar] [CrossRef] [Green Version]
- Hawrylak, P.; Narvaez, G.A.; Bayer, M.; Forchel, A. Excitonic Absorption in a Quantum Dot. Phys. Rev. Lett. 2000, 85, 389–392. [Google Scholar] [CrossRef]
- Güçlü, A.D.; Potasz, P.; Voznyy, O.; Korkusinski, M.; Hawrylak, P. Magnetism and Correlations in Fractionally Filled Degenerate Shells of Graphene Quantum Dots. Phys. Rev. Lett. 2009, 103, 246805. [Google Scholar] [CrossRef] [Green Version]
- Zieliński, M.; Korkusiński, M.; Hawrylak, P. Atomistic tight-binding theory of multiexciton complexes in a self-assembled InAs quantum dot. Phys. Rev. B 2010, 81, 085301. [Google Scholar] [CrossRef] [Green Version]
- Güçlü, A.D.; Potasz, P.; Hawrylak, P. Excitonic absorption in gate-controlled graphene quantum dots. Phys. Rev. B 2010, 82, 155445. [Google Scholar] [CrossRef] [Green Version]
- Bayer, M.; Stern, O.; Hawrylak, P.; Fafard, S.; Forchel, A. Hidden symmetries in the energy levels of excitonic ‘artificial atoms’. Nature 2000, 405, 923–926. [Google Scholar] [CrossRef] [PubMed]
- Korkusinski, M.; Voznyy, O.; Hawrylak, P. Theory of highly excited semiconductor nanostructures including Auger coupling: Exciton-biexciton mixing in CdSe nanocrystals. Phys. Rev. B 2011, 84, 155327. [Google Scholar] [CrossRef] [Green Version]
- Potasz, P.; Güçlü, A.D.; Wójs, A.; Hawrylak, P. Electronic properties of gated triangular graphene quantum dots: Magnetism, correlations, and geometrical effects. Phys. Rev. B 2012, 85, 075431. [Google Scholar] [CrossRef] [Green Version]
- Korkusinski, M.; Hawrylak, P. Atomistic theory of emission from dark excitons in self-assembled quantum dots. Phys. Rev. B 2013, 87, 115310. [Google Scholar] [CrossRef]
- Ozfidan, I.; Korkusinski, M.; Hawrylak, P. Theory of biexcitons and biexciton-exciton cascade in graphene quantum dots. Phys. Rev. B 2015, 91, 115314. [Google Scholar] [CrossRef] [Green Version]
- Güçlü, A.D.; Potasz, P.; Korkusinski, M.; Hawrylak, P. Graphene Quantum Dots; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Fan, F.; Voznyy, O.; Sabatini, R.P.; Bicanic, K.T.; Adachi, M.M.; McBride, J.R.; Reid, K.R.; Park, Y.S.; Li, X.; Jain, A.; et al. Continuous-wave lasing in colloidal quantum dot solids enabled by facet-selective epitaxy. Nature 2017, 544, 75–79. [Google Scholar] [CrossRef]
- Cygorek, M.; Otten, M.; Korkusinski, M.; Hawrylak, P. Accurate and efficient description of interacting carriers in quantum nanostructures by selected configuration interaction and perturbation theory. Phys. Rev. B 2020, 101, 205308. [Google Scholar] [CrossRef]
- Wójs, A.; Quinn, J.J.; Hawrylak, P. Charged excitons in a dilute two-dimensional electron gas in a high magnetic field. Phys. Rev. B 2000, 62, 4630–4637. [Google Scholar] [CrossRef] [Green Version]
- Wójs, A.; Quinn, J.J. Photoluminescence from fractional quantum Hall systems: Role of separation between electron and hole layers. Phys. Rev. B 2000, 63, 045304. [Google Scholar] [CrossRef] [Green Version]
- Benedict, L.X. Screening in the exchange term of the electron-hole interaction of the Bethe-Salpeter equation. Phys. Rev. B 2002, 66, 193105. [Google Scholar] [CrossRef]
- Qiu, D.Y.; da Jornada, F.H.; Louie, S.G. Solving the Bethe-Salpeter equation on a subspace: Approximations and consequences for low-dimensional materials. Phys. Rev. B 2021, 103, 045117. [Google Scholar] [CrossRef]
- Sauer, M.O.; Nielsen, C.E.M.; Merring-Mikkelsen, L.; Pedersen, T.G. Optical emission from light-like and particle-like excitons in monolayer transition metal dichalcogenides. Phys. Rev. B 2021, 103, 205404. [Google Scholar] [CrossRef]
- Ozfidan, I.; Korkusinski, M.; Güçlü, A.D.; McGuire, J.A.; Hawrylak, P. Microscopic theory of the optical properties of colloidal graphene quantum dots. Phys. Rev. B 2014, 89, 085310. [Google Scholar] [CrossRef] [Green Version]
- Sundararaman, R.; Arias, T.A. Regularization of the Coulomb singularity in exact exchange by Wigner-Seitz truncated interactions: Towards chemical accuracy in nontrivial systems. Phys. Rev. B 2013, 87, 165122. [Google Scholar] [CrossRef] [Green Version]
- Trolle, M.L.; Seifert, G.; Pedersen, T.G. Theory of excitonic second-harmonic generation in monolayer MoS2. Phys. Rev. B 2014, 89, 235410. [Google Scholar] [CrossRef] [Green Version]
- Cudazzo, P.; Tokatly, I.V.; Rubio, A. Dielectric screening in two-dimensional insulators: Implications for excitonic and impurity states in graphane. Phys. Rev. B 2011, 84, 085406. [Google Scholar] [CrossRef] [Green Version]
- Quintela, M.F.M.; Peres, N.M. A colloquium on the variational method applied to excitons in 2D materials. Eur. Phys. J. B 2020, 93, 1–16. [Google Scholar]
- Tamulewicz, M.; Kutrowska-Girzycka, J.; Gajewski, K.; Serafińczuk, J.; Sierakowski, A.; Jadczak, J.; Bryja, L.; Gotszalk, T.P. Layer number dependence of the work function and optical properties of single and few layers MoS2: Effect of substrate. Nanotechnology 2019, 30, 245708. [Google Scholar] [CrossRef]
- Berkelbach, T.C.; Reichman, D.R. Optical and Excitonic Properties of Atomically Thin Transition-Metal Dichalcogenides. Annu. Rev. Condens. Matter Phys. 2018, 9, 379. [Google Scholar] [CrossRef]
- Ovesen, S.; Brem, S.; Linderälv, C.; Kuisma, M.; Korn, T.; Erhart, P.; Selig, M.; Malic, E. Interlayer exciton dynamics in van der Waals heterostructures. Commun. Phys. 2019, 2, 23. [Google Scholar] [CrossRef]
- Kamban, H.C.; Pedersen, T.G. Interlayer excitons in van der Waals heterostructures: Binding energy, Stark shift, and field-induced dissociation. Sci. Rep. 2020, 10, 5537. [Google Scholar] [CrossRef] [PubMed]
- Kezerashvili, R.Y.; Spiridonova, A. Magnetoexcitons in transition metal dichalcogenides monolayers, bilayers, and van der Waals heterostructures. Phys. Rev. Res. 2021, 3, 033078. [Google Scholar] [CrossRef]
- Garate, I.; Franz, M. Excitons and optical absorption on the surface of a strong topological insulator with a magnetic energy gap. Phys. Rev. B 2011, 84, 045403. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, A.; Imamoglu, A. Signatures of Bloch-Band Geometry on Excitons: Nonhydrogenic Spectra in Transition-Metal Dichalcogenides. Phys. Rev. Lett. 2015, 115, 166802. [Google Scholar] [CrossRef] [PubMed]
- Sadecka, K. Inter- and Intralayer Excitonic Spectrum of MoSe2/WSe2 Heterostructure. Acta Phys. Pol. A 2022, 141, 110–115. [Google Scholar] [CrossRef]






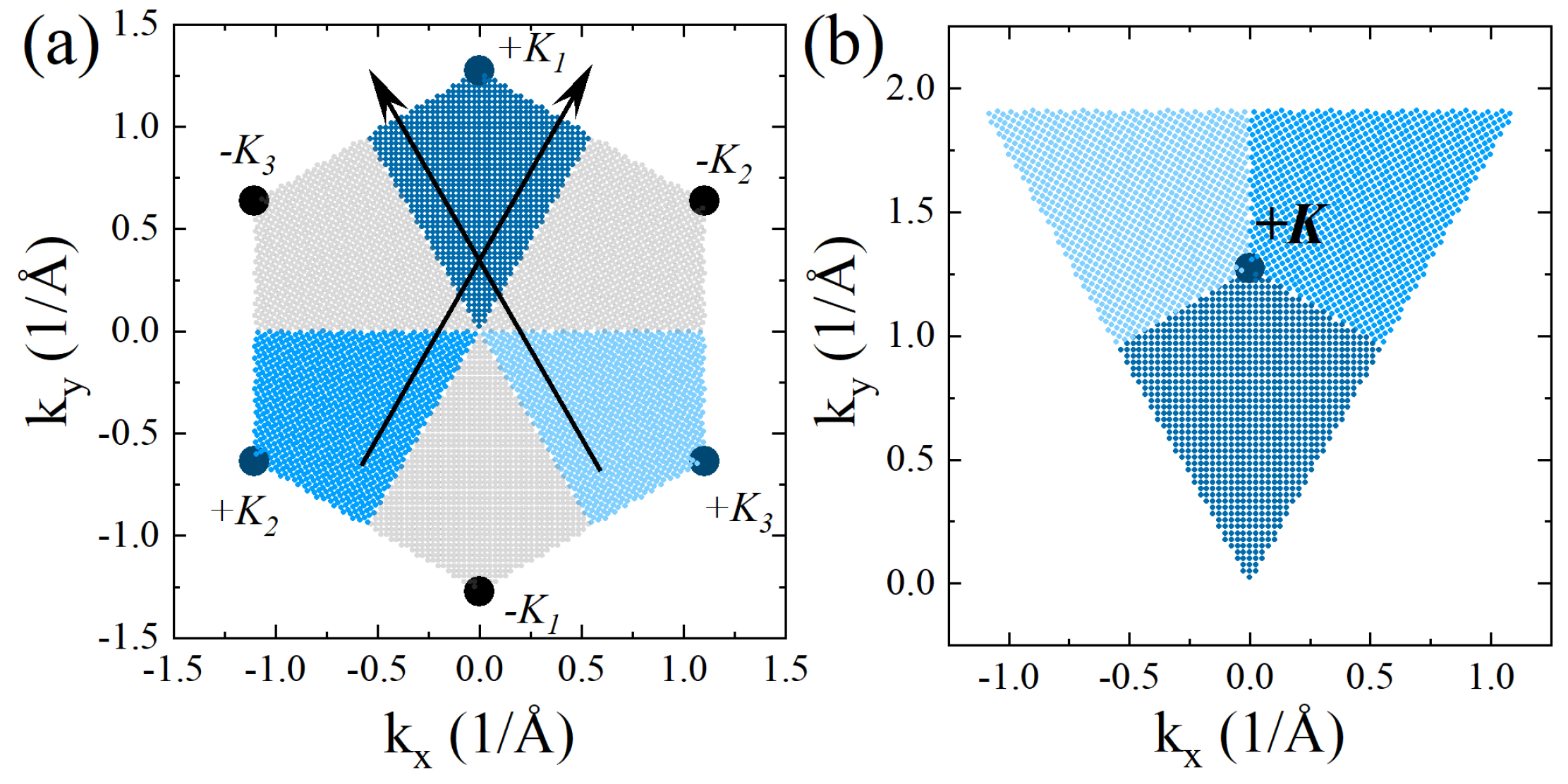

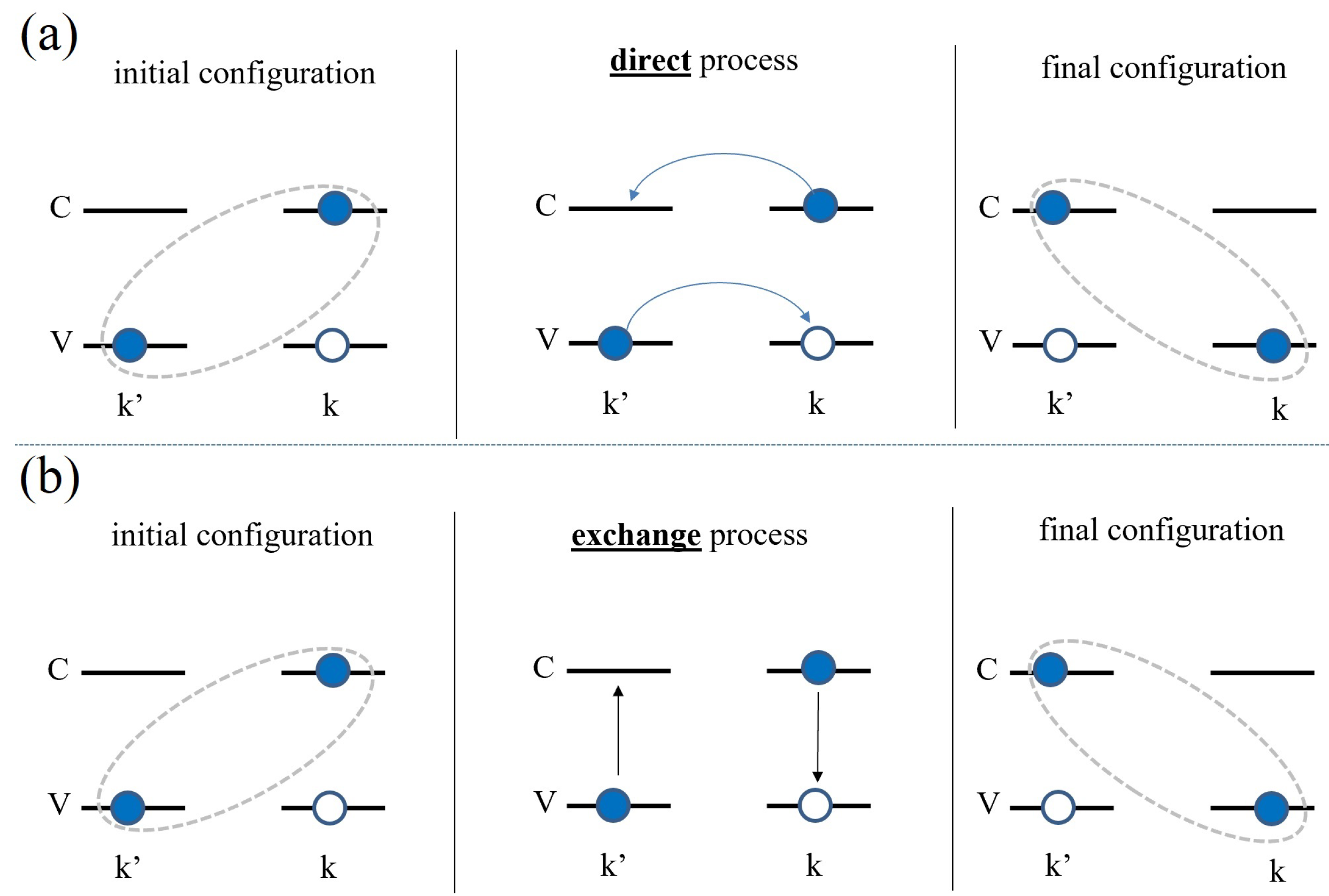




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bieniek, M.; Sadecka, K.; Szulakowska, L.; Hawrylak, P. Theory of Excitons in Atomically Thin Semiconductors: Tight-Binding Approach. Nanomaterials 2022, 12, 1582. https://doi.org/10.3390/nano12091582
Bieniek M, Sadecka K, Szulakowska L, Hawrylak P. Theory of Excitons in Atomically Thin Semiconductors: Tight-Binding Approach. Nanomaterials. 2022; 12(9):1582. https://doi.org/10.3390/nano12091582
Chicago/Turabian StyleBieniek, Maciej, Katarzyna Sadecka, Ludmiła Szulakowska, and Paweł Hawrylak. 2022. "Theory of Excitons in Atomically Thin Semiconductors: Tight-Binding Approach" Nanomaterials 12, no. 9: 1582. https://doi.org/10.3390/nano12091582
APA StyleBieniek, M., Sadecka, K., Szulakowska, L., & Hawrylak, P. (2022). Theory of Excitons in Atomically Thin Semiconductors: Tight-Binding Approach. Nanomaterials, 12(9), 1582. https://doi.org/10.3390/nano12091582





