Computational NEXAFS Characterization of Molecular Model Systems for 2D Boroxine Frameworks
Abstract
:1. Introduction
2. Methods
2.1. Geometry Optimization
2.2. NEXAFS Spectra Calculation
3. Results and Discussion
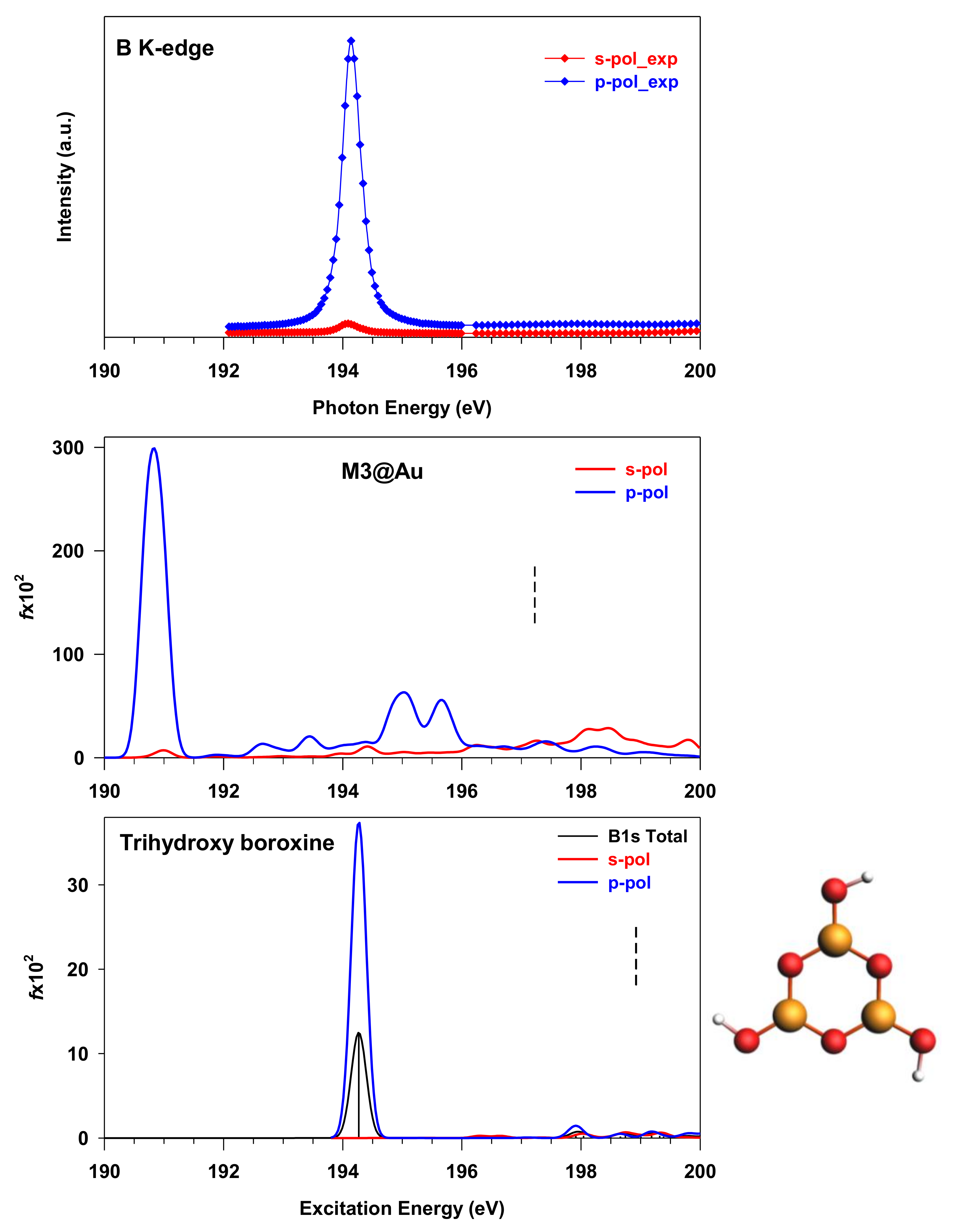
3.1. THDB Molecule
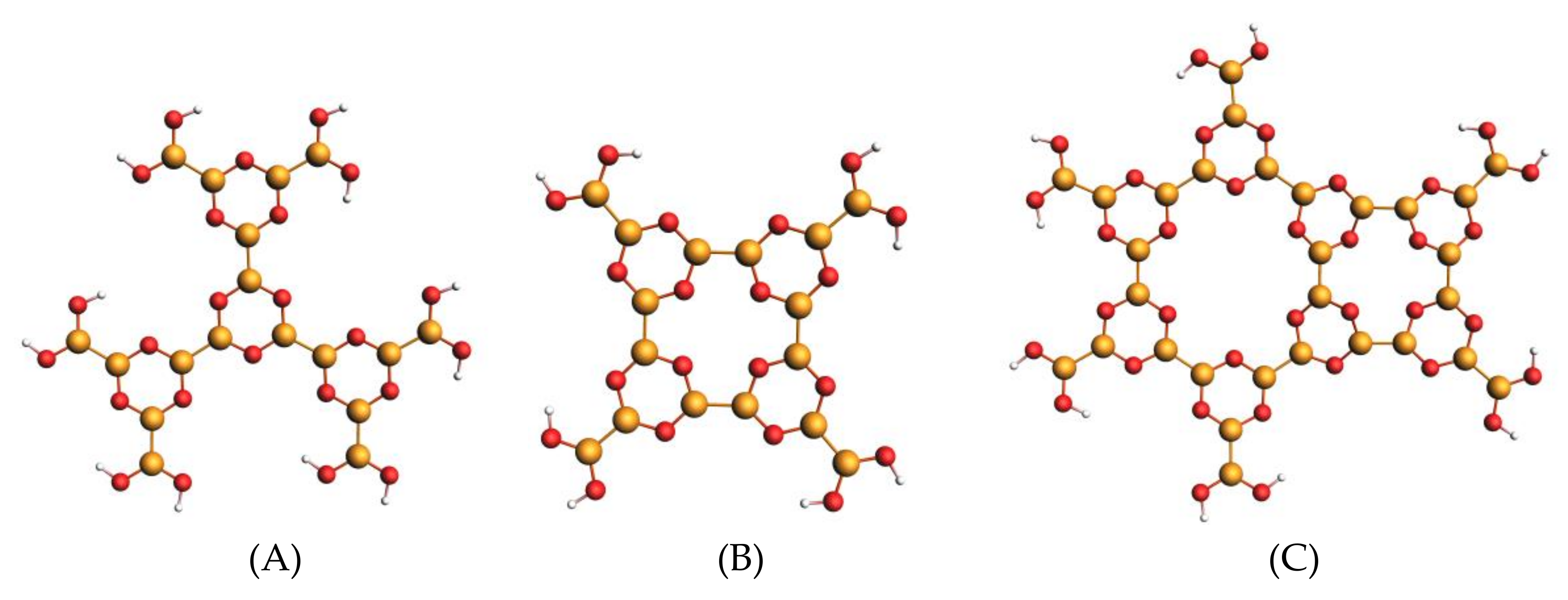
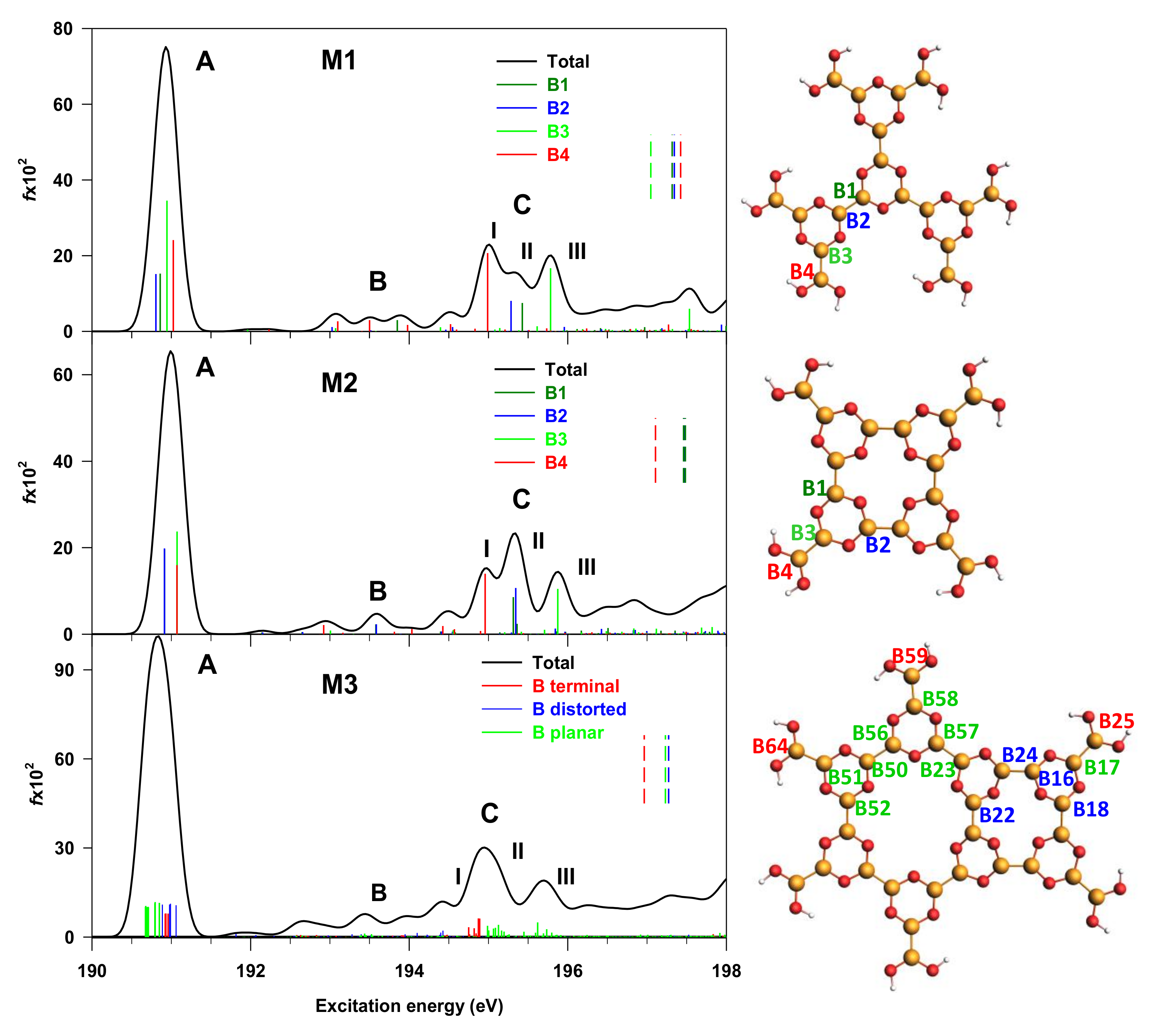
3.2. M1, M2 and M3 Molecular Models
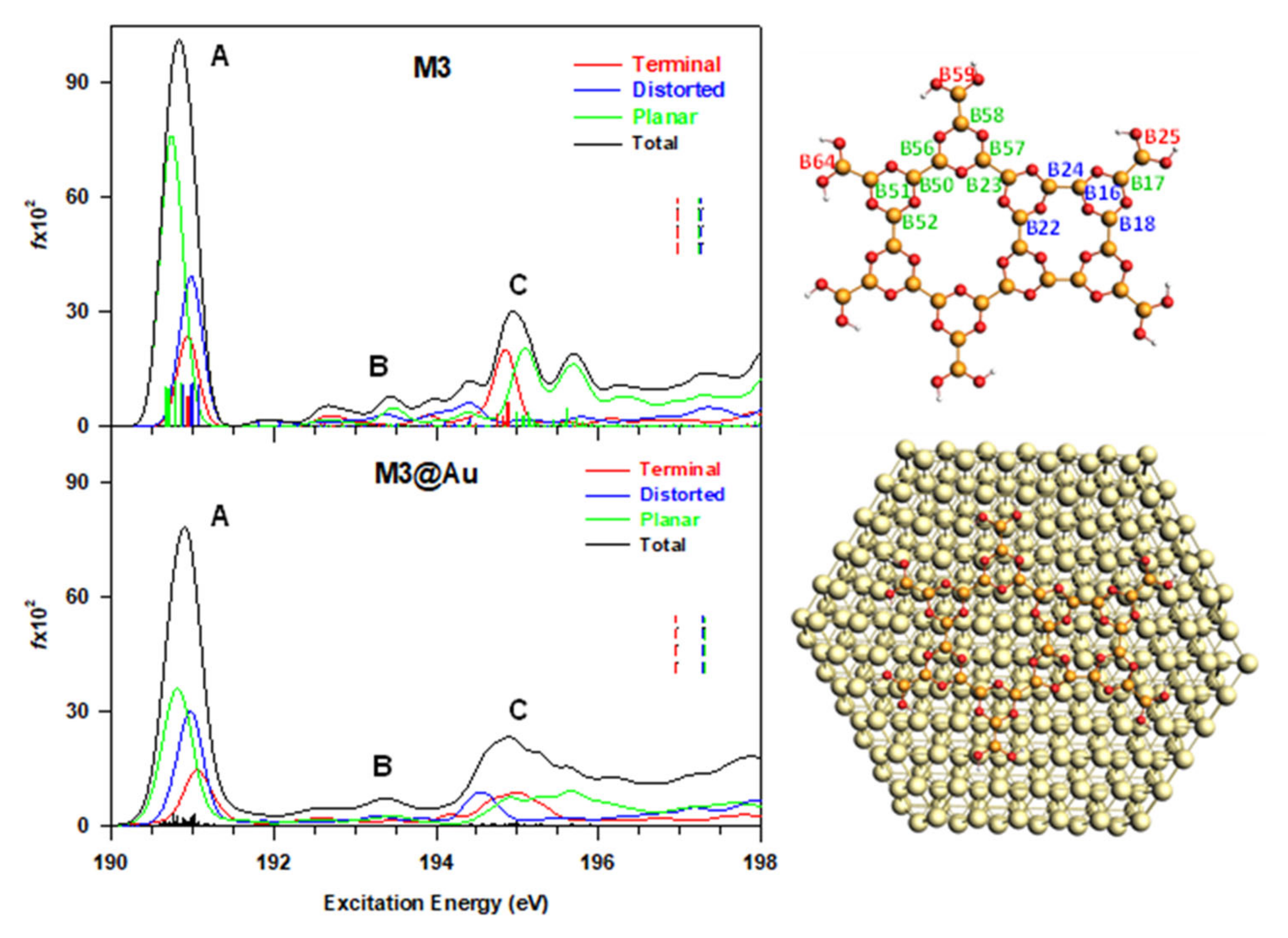
3.3. M3@Au(111) Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cote, A.P.; Benin, A.I.; Ockwig, N.W.; O’Keeffe, M.; Matzger, A.J.; Yaghi, O.M. Porous, crystalline, covalent organic frameworks. Science 2005, 310, 1166–1170. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartels, L. Tailoring molecular layers at metal surfaces. Nat. Chem. 2010, 2, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Plas, J.; Ivasenko, O.; Martsinovich, N.; Lackinger, M.; De Feyter, S. Nanopatterning of a covalent organic framework host–guest system. Chem. Commun. 2016, 52, 68–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dienstmaier, J.F.; Gigler, A.M.; Goetz, A.J.; Knochel, P.; Bein, T.; Lyapin, A.; Reichlmaier, S.; Heckl, M.; Lackinger, W.M. Synthesis of Well-Ordered COF Monolayers: Surface Growth of Nanocrystalline Precursors versus Direct On-Surface Polycondensation. ACS Nano 2011, 5, 9737–9745. [Google Scholar] [CrossRef]
- Feng, B.; Zhang, J.; Zhong, Q.; Li, W.; Li, S.; Li, H.; Cheng, P.; Meng, S.; Chen, L.; Wu, K. Experimental Realization of Two-Dimensional Boron Sheets. Nat. Chem. 2016, 8, 563–568. [Google Scholar] [CrossRef] [Green Version]
- Toffoli, D.; Stredansky, M.; Feng, Z.; Balducci, G.; Furlan, S.; Stener, M.; Ustunel, H.; Cvetko, D.; Kladnik, G.; Morgante, A.; et al. Electronic properties of the boroxine–gold interface: Evidence of ultra-fast charge delocalization. Chem. Sci. 2017, 8, 3789–3798. [Google Scholar] [CrossRef] [Green Version]
- Stredansky, M.; Sala, A.; Fontanot, T.; Costantini, R.; Africh, C.; Comelli, G.; Floreano, L.; Morgante, A.; Cossaro, A. On-surface synthesis of a 2D boroxine framework: A route to a novel 2D material? Chem. Commun. 2018, 54, 3971–3973. [Google Scholar] [CrossRef]
- Lin, S.; Gu, J.; Zhang, H.; Wang, Y.; Chen, Z. Porous hexagonal boron oxide monolayer with robust wide band gap: A computational study. FlatChem 2018, 9, 27–32. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, H.; Mathe, S.D.R.; Dong, A.; Zhang, J. Covalent Organic Frameworks: From Materials Design to Biomedical Application. Nanomaterials 2017, 8, 15. [Google Scholar] [CrossRef] [Green Version]
- Ullah, S.; Denis, P.A.; Sato, F. Theoretical investigation of various aspects of two dimensional holey boroxine, B3O3. RSC Adv. 2019, 9, 37526–37536. [Google Scholar] [CrossRef] [Green Version]
- Rahimi, R.; Solimannejad, M. B3O3 monolayer: An emerging 2D material for CO2 capture. New J. Chem. 2021, 45, 15328–15335. [Google Scholar] [CrossRef]
- Rahimi, R.; Solimannejad, M.; Ehsanfar, Z. First-principles studies on two-dimensional B3O3 adsorbent as a potential drug delivery platform for TEPA anticancer drug. J. Mol. Model. 2021, 27, 347–357. [Google Scholar] [CrossRef] [PubMed]
- Rahman, N.U.; Adnan, A.A.; Ullah, R.; Ahmad, R.; Ahmad, I. Selective sensing of NH3 and CH2O molecules by novel 2D porous hexagonal boron oxide (B3O3) monolayer: A DFT approach. Surf. Interfaces 2022, 29, 101767–101779. [Google Scholar] [CrossRef]
- Toffoli, D.; Grazioli, C.; Monti, M.; Stener, M.; Totani, R.; Richter, R.; Schio, L.; Fronzoni, G.; Cossaro, A. Revealing the electronic Ok. Phys. Chem. 2021, 23, 23517–23525. [Google Scholar]
- Slater, J.C. Statistical Exchange-Correlation in the Self-Consistent Field. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1972; Volume 6, pp. 1–92. [Google Scholar] [CrossRef]
- Triguero, L.; Pettersson, L.G.M.; Ågren, H. Calculations of Near-Edge X-ray-Absorption Spectra of Gas-Phase and Chemisorbed Molecules by Means of Density-Functional and Transition-Potential Theory. Phys. Rev. B 1998, 58, 8097–8110. [Google Scholar] [CrossRef] [Green Version]
- Toffoli, D.; Ponzi, A.; Bernes, E.; de Simone, M.; Grazioli, C.; Coreno, M.; Stredansky, M.; Cossaro, A.; Fronzoni, G. Correlation effects in B1s core-excited states of boronic-acid derivatives: An experimental and computational study. J. Chem. Phys. 2019, 151, 134306. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Fonseca Guerra, C.; Snijders, J.G.; te Velde, G.; Baerends, E.J. Towards an Order-N DFT Method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ellis, D.E.; Roos, P. Self-Consistent Molecular Hartree-Fock-Slater Calculations I. The Computational Procedure. Chem. Phys. 1973, 2, 41–51. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-Functional Approximation for The Correlation Energy of The Inhomogeneous Electron Gas. Phys. Rev. B Condens. Matter Mater. Phys. 1986, 33, 8822–8824. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, T.; Rauk, A.; Baerends, E.J. On the calculation of multiplet energies by the Hartree-Fock-slater method. Theor. Chim. Acta 1977, 43, 261–271. [Google Scholar] [CrossRef]
- Löwdin, P.-O. Quantum Theory of Many-Particle Systems. I. Physical Interpretations by Means of Density Matrices, Natural Spin-Orbitals, and Convergence Problems in the Method of Configurational Interaction. Phys. Rev. 1955, 97, 1474–1489. [Google Scholar] [CrossRef]
- Bourne Worster, S.; Feighan, O.; Manby, F.R. Reliable transition properties from excited-state mean-field calculations. J. Chem. Phys. 2021, 154, 124106. [Google Scholar] [CrossRef]
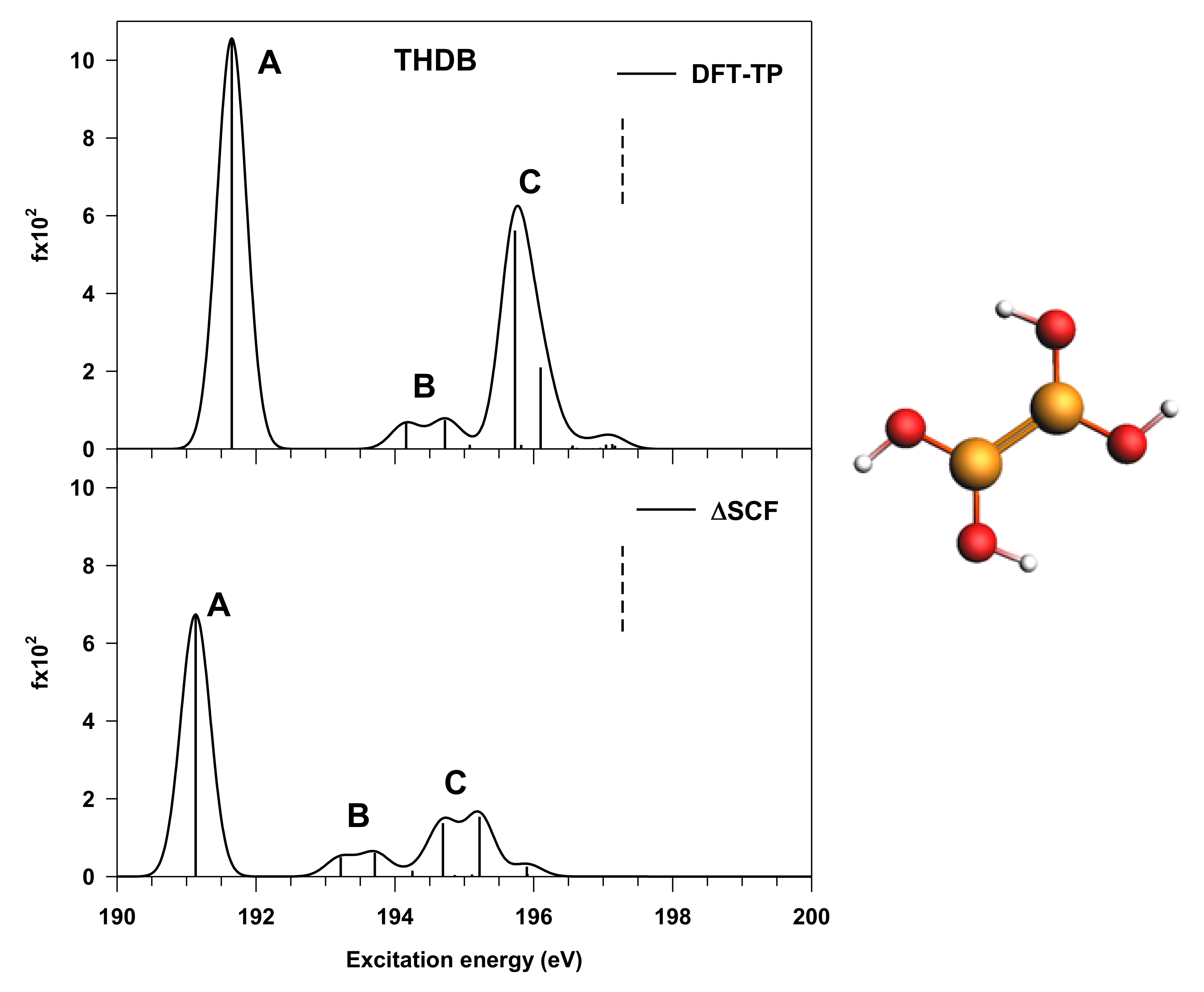
| Peak | Transition | ΔSCF Results | DFT-TP Results | Assignment, Main Character of the Final MO | ||
|---|---|---|---|---|---|---|
| E(eV) | f × 102 a | E(eV) | f × 102 a | |||
| A | B1s → 5a” | 191.13 | 6.74 | 191.65 | 10.56 | π(B–B) + π*(B–O) |
| B | B1s → 15a’ | 193.22 | 0.50 | 194.16 | 0.66 | mixed valence σ*(B–B), σ*(O–H)/Rydberg |
| B1s → 16a’ | 193.71 | 0.61 | 194.72 | 0.74 | mixed valence σ*(O–H)/Rydberg | |
| C | B1s → 6a” | 194.69 | 1.37 | 195.73 | 5.62 | π*(B–B) + π*(B–O) |
| B1s → 7a” | 195.22 | 1.54 | 196.10 | 2.10 | π*(B–B) + π*(B–O) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toffoli, D.; Bernes, E.; Cossaro, A.; Balducci, G.; Stener, M.; Mauri, S.; Fronzoni, G. Computational NEXAFS Characterization of Molecular Model Systems for 2D Boroxine Frameworks. Nanomaterials 2022, 12, 1610. https://doi.org/10.3390/nano12091610
Toffoli D, Bernes E, Cossaro A, Balducci G, Stener M, Mauri S, Fronzoni G. Computational NEXAFS Characterization of Molecular Model Systems for 2D Boroxine Frameworks. Nanomaterials. 2022; 12(9):1610. https://doi.org/10.3390/nano12091610
Chicago/Turabian StyleToffoli, Daniele, Elisa Bernes, Albano Cossaro, Gabriele Balducci, Mauro Stener, Silvia Mauri, and Giovanna Fronzoni. 2022. "Computational NEXAFS Characterization of Molecular Model Systems for 2D Boroxine Frameworks" Nanomaterials 12, no. 9: 1610. https://doi.org/10.3390/nano12091610
APA StyleToffoli, D., Bernes, E., Cossaro, A., Balducci, G., Stener, M., Mauri, S., & Fronzoni, G. (2022). Computational NEXAFS Characterization of Molecular Model Systems for 2D Boroxine Frameworks. Nanomaterials, 12(9), 1610. https://doi.org/10.3390/nano12091610







