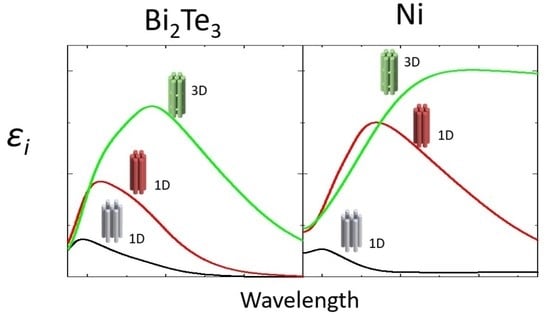
Plasmon Resonances in 1D Nanowire Arrays and 3D Nanowire Networks of Topological Insulators and Metals
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of the 1D Nanowire Arrays and 3D Nanowire Networks
2.2. Characterization of the 1D Nanowire Arrays and 3D Nanowire Networks
3. Results and Discussion
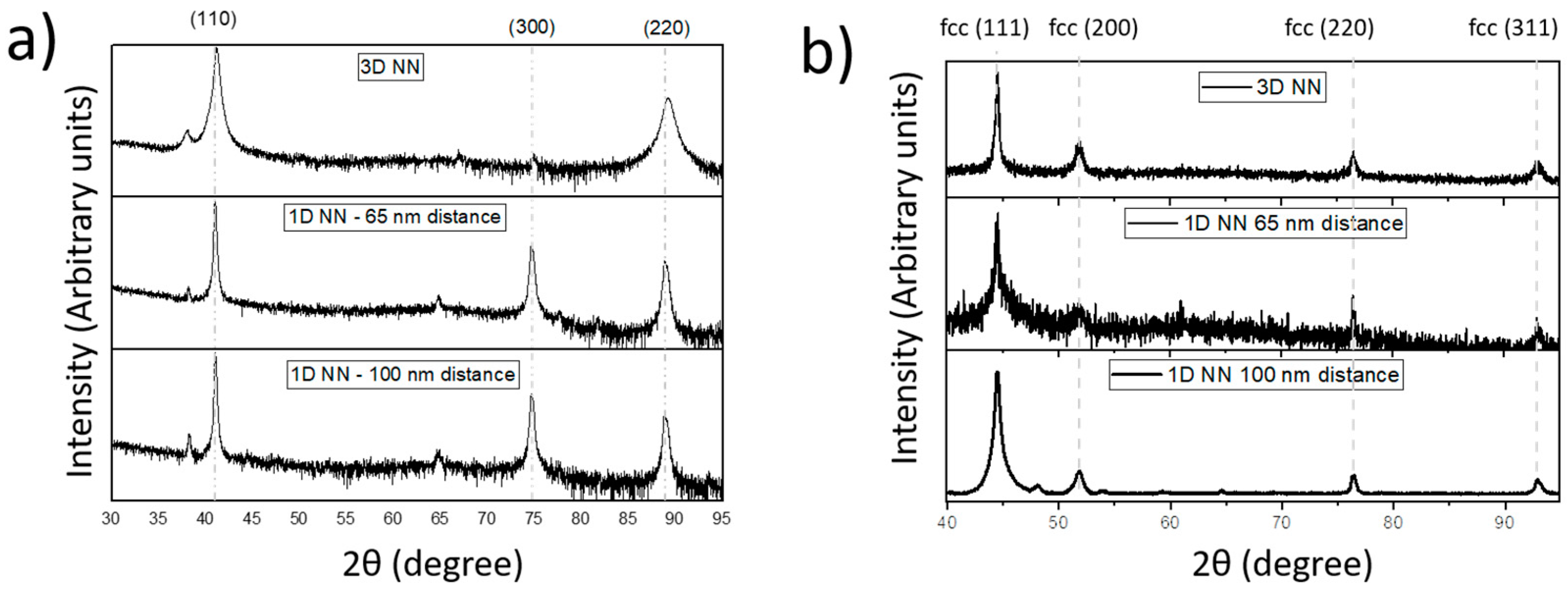
3.1. Morphological and Structural Characterization of the 1D Nanowire Arrays and 3D Nanowire Networks
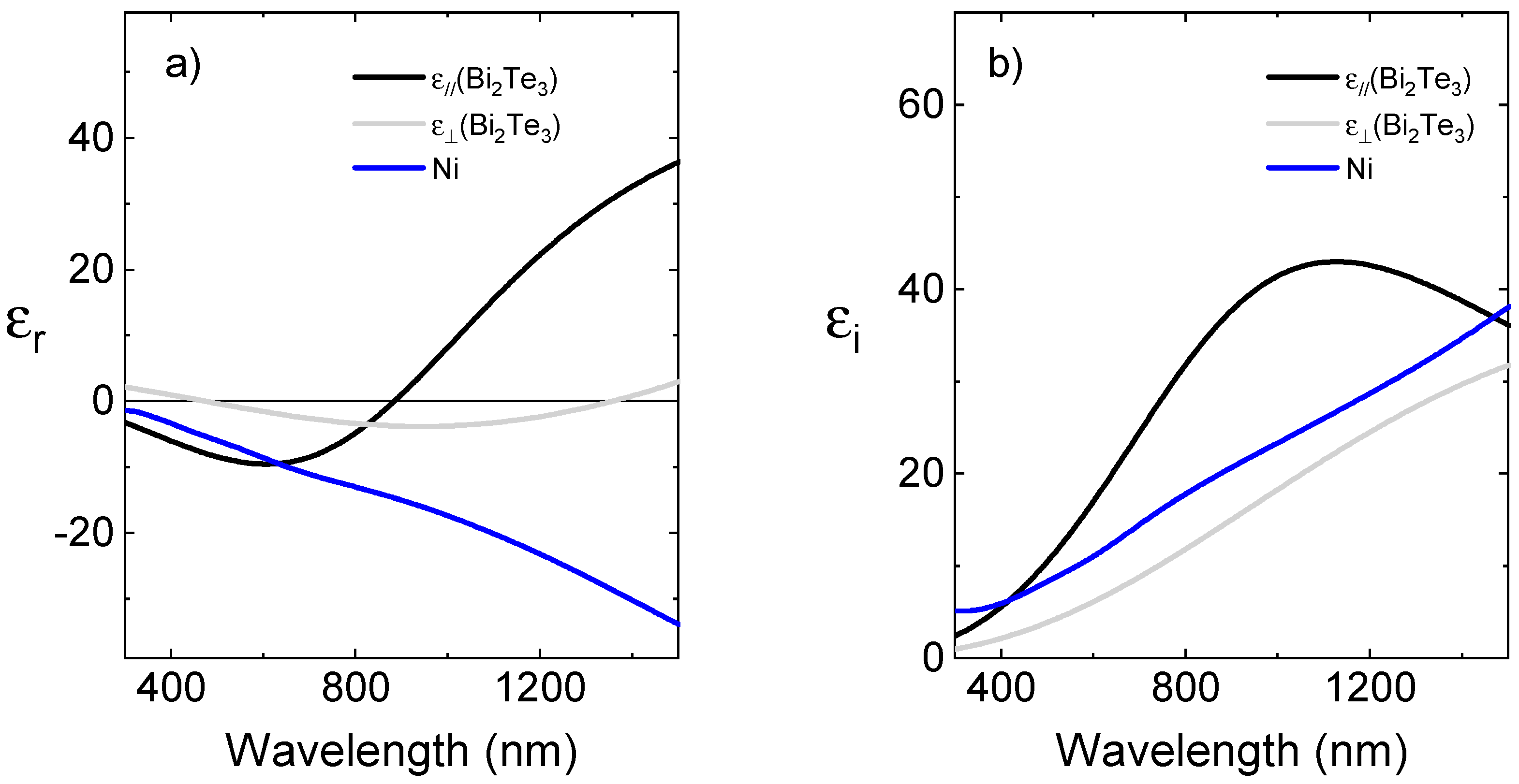
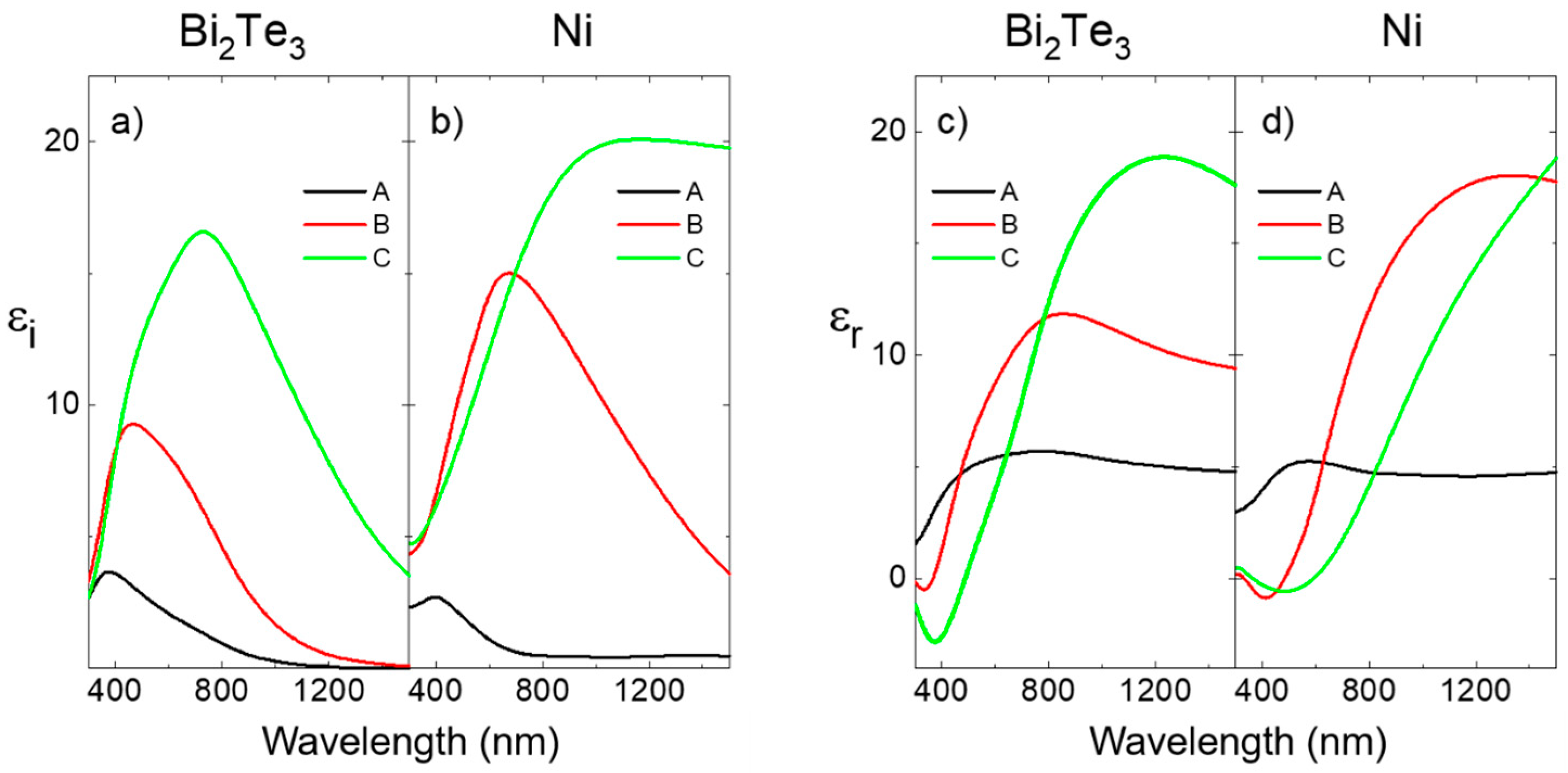
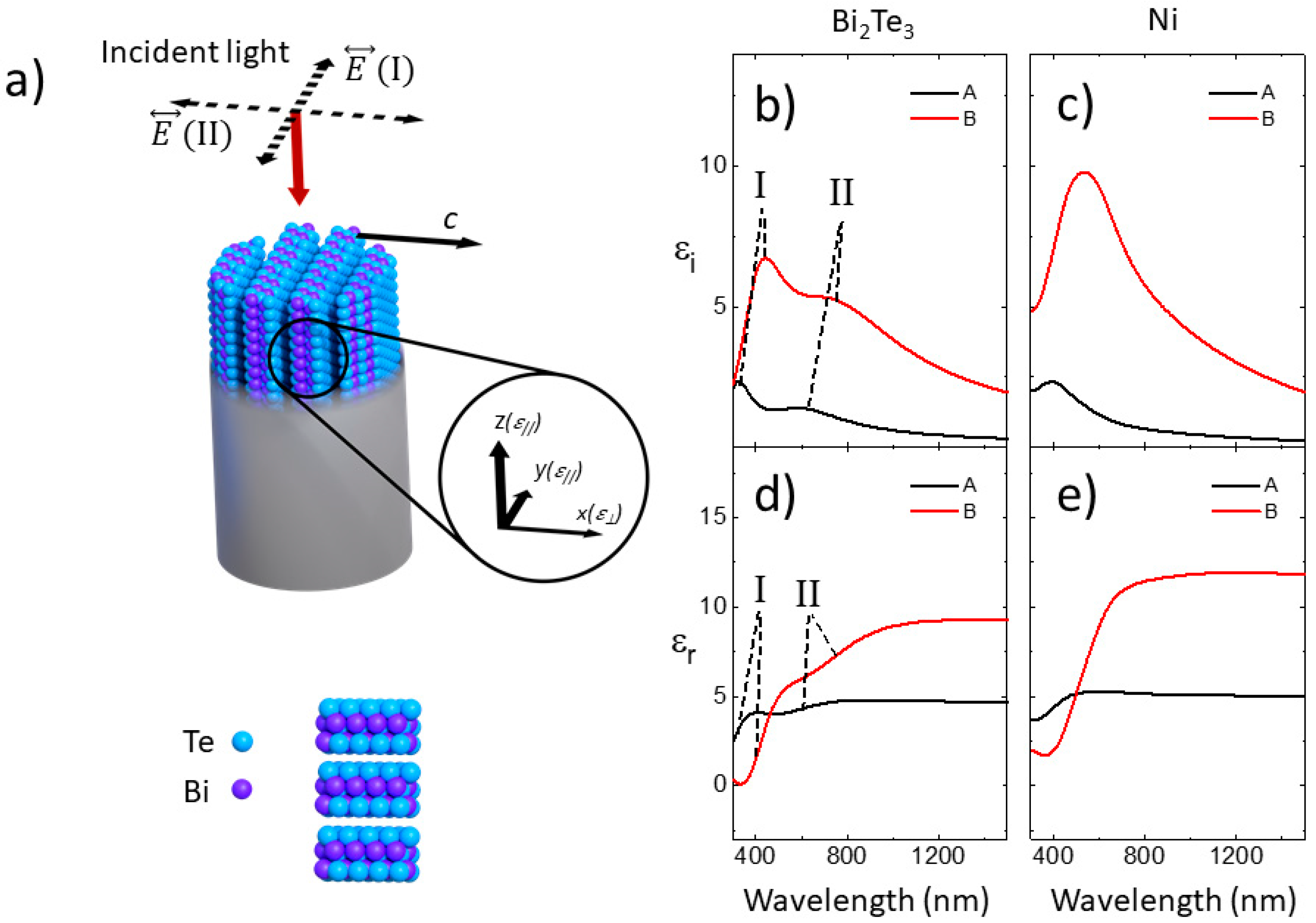
3.2. Optical Characterization of the 1D Nanowire Arrays and 3D Nanowire Networks
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B. Details of the Optical Model

References
- Ahmadivand, A.; Gerislioglu, B. Photonic and Plasmonic Metasensors. Laser Photonics Rev. 2022, 16, 2100328. [Google Scholar] [CrossRef]
- Chen, J.; Yang, C.; Gu, P.; Kuang, Y.; Tang, C.; Chen, S.; Liu, Z. High sensing properties of magnetic plasmon resonance by strong coupling in three-dimensional metamaterials. J. Light. Technol. 2021, 39, 562–565. [Google Scholar] [CrossRef]
- Chen, J.; Kuang, Y.; Gu, P.; Feng, S.; Zhu, Y.; Tang, C.; Guo, Y.; Liu, Z.; Gao, F. Strong magnetic plasmon resonance in a simple metasurface for high-quality sensing. J. Light. Technol. 2021, 39, 4525–4528. [Google Scholar] [CrossRef]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
- Boltasseva, A.; Atwater, H.A. Low-loss plasmonic metamaterials. Science 2011, 331, 290–291. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Krishnamoorthy, H.N.; Adamo, G.; Dubrovkin, A.M.; Chong, Y.; Zheludev, N.I.; Soci, C. Plasmonics of topological insulators at optical frequencies. NPG Asia Mater. 2017, 9, e425. [Google Scholar] [CrossRef]
- Caballero-Calero, O.; Díaz-Chao, P.; Abad, B.; Manzano, C.V.; Ynsa, M.D.; Romero, J.J.; Rojo, M.M.; Martín-González, M.S. Improvement of Bismuth Telluride electrodeposited films by the addition of Sodium Lignosulfonate. Electrochim. Acta 2014, 123, 117–126. [Google Scholar] [CrossRef]
- Yamashita, O.; Tomiyoshi, S.; Makita, K. Bismuth telluride compounds with high thermoelectric figures of merit. J. Appl. Phys. 2003, 93, 368–374. [Google Scholar] [CrossRef]
- Greenaway, D.L.; Harbeke, G. Band structure of bismuth telluride, bismuth selenide and their respective alloys. J. Phys. Chem. Solids 1965, 26, 1585–1604. [Google Scholar] [CrossRef]
- Esslinger, M.; Vogelgesang, R.; Talebi, N.; Khunsin, W.; Gehring, P.; De Zuani, S.; Gompf, B.; Kern, K. Tetradymites as natural hyperbolic materials for the near-infrared to visible. Acs Photonics 2014, 1, 1285–1289. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.-X.; Qi, X.-L.; Dai, X.; Fang, Z.; Zhang, S.-C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438–442. [Google Scholar] [CrossRef]
- Gehring, P.; Gaul, A.; Hoyer, A.; Vaklinova, K.; Mehta, R.J.; Burghard, M.; Borca-Tasciuc, T.; Singh, D.J.; Kern, K.; Ramanath, G. Harnessing Topological Band Effects in Bismuth Telluride Selenide for Large Enhancements in Thermoelectric Properties through Isovalent Doping. Adv. Mater. 2016, 28, 6436–6441. [Google Scholar]
- Di Pietro, P.; Ortolani, M.; Limaj, O.; Di Gaspare, A.; Giliberti, V.; Giorgianni, F.; Brahlek, M.; Bansal, N.; Koirala, N.; Oh, S. Observation of Dirac plasmons in a topological insulator. Nat. Nanotechnol. 2013, 8, 556–560. [Google Scholar] [CrossRef] [PubMed]
- Falsetti, E.; Nucara, A.; Shibayev, P.P.; Salehi, M.; Moon, J.; Oh, S.; Brubach, J.-B.; Roy, P.; Ortolani, M.; Calvani, P. Infrared spectroscopy of the topological surface states of Bi 2 Se 3 by use of the Berreman effect. Phys. Rev. Lett. 2018, 121, 176803. [Google Scholar] [CrossRef]
- Wang, Z.; Ginley, T.P.; Mambakkam, S.V.; Chandan, G.; Zhang, Y.; Ni, C.; Law, S. Plasmon coupling in topological insulator multilayers. Phys. Rev. Mater. 2020, 4, 115202. [Google Scholar] [CrossRef]
- Di Pietro, P.; Adhlakha, N.; Piccirilli, F.; Di Gaspare, A.; Moon, J.; Oh, S.; Di Mitri, S.; Spampinati, S.; Perucchi, A.; Lupi, S. Terahertz tuning of Dirac plasmons in Bi 2 Se 3 topological insulator. Phys. Rev. Lett. 2020, 124, 226403. [Google Scholar] [CrossRef]
- Venuthurumilli, P.K.; Wen, X.; Iyer, V.; Chen, Y.P.; Xu, X. Near-field imaging of surface plasmons from the bulk and surface state of topological insulator Bi2Te2Se. ACS Photonics 2019, 6, 2492–2498. [Google Scholar] [CrossRef]
- Yuan, J.; Ma, W.; Zhang, L.; Lu, Y.; Zhao, M.; Guo, H.; Zhao, J.; Yu, W.; Zhang, Y.; Zhang, K. Infrared nanoimaging reveals the surface metallic plasmons in topological insulator. ACS Photonics 2017, 4, 3055–3062. [Google Scholar] [CrossRef]
- Lu, X.; Hao, Q.; Cen, M.; Zhang, G.; Sun, J.; Mao, L.; Cao, T.; Zhou, C.; Jiang, P.; Yang, X. Observation and manipulation of visible edge plasmons in Bi2Te3 nanoplates. Nano Lett. 2018, 18, 2879–2884. [Google Scholar] [CrossRef]
- Eddrief, M.; Vidal, F.; Gallas, B. Optical properties of Bi2Se3: From bulk to ultrathin films. J. Phys. D: Appl. Phys. 2016, 49, 505304. [Google Scholar] [CrossRef]
- Ou, J.-Y.; So, J.-K.; Adamo, G.; Sulaev, A.; Wang, L.; Zheludev, N.I. Ultraviolet and visible range plasmonics in the topological insulator Bi1. 5Sb0. 5Te1. 8Se1. 2. Nat. Commun. 2014, 5, 6139. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Bosman, M.; Danesh, M.; Zeng, M.; Song, P.; Darma, Y.; Rusydi, A.; Lin, H.; Qiu, C.-W.; Loh, K.P. Visible surface plasmon modes in single Bi2Te3 nanoplate. Nano Lett. 2015, 15, 8331–8335. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Zhang, J.; Gao, N.; Song, P.; Bosman, M.; Peng, B.; Sun, B.; Qiu, C.W.; Xu, Q.H.; Bao, Q. Actively Tunable Visible Surface Plasmons in Bi2Te3 and their Energy-Harvesting Applications. Adv. Mater. 2016, 28, 3138–3144. [Google Scholar] [CrossRef] [PubMed]
- Aigner, A.; Maier, S.A.; Ren, H. Topological-insulator-based gap-surface plasmon metasurfaces. Photonics 2021, 8, 40. [Google Scholar] [CrossRef]
- Yue, Z.; Cai, B.; Wang, L.; Wang, X.; Gu, M. Intrinsically core-shell plasmonic dielectric nanostructures with ultrahigh refractive index. Sci. Adv. 2016, 2, e1501536. [Google Scholar] [CrossRef] [PubMed]
- Krishnamoorthy, H.; Adamo, G.; Yin, J.; Savinov, V.; Zheludev, N.; Soci, C. Infrared dielectric metamaterials from high refractive index chalcogenides. Nat. Commun. 2020, 11, 1692. [Google Scholar] [CrossRef]
- Chen, J.; Albella, P.; Pirzadeh, Z.; Alonso-González, P.; Huth, F.; Bonetti, S.; Bonanni, V.; Åkerman, J.; Nogués, J.; Vavassori, P. Plasmonic nickel nanoantennas. Small 2011, 7, 2341–2347. [Google Scholar] [CrossRef]
- Ruiz-Clavijo, A.; Caballero-Calero, O.; Martin-Gonzalez, M. Revisiting anodic alumina templates: From fabrication to applications. Nanoscale 2021, 13, 2227–2265. [Google Scholar] [CrossRef]
- Martín, J.; Martín-González, M.; Francisco Fernández, J.; Caballero-Calero, O. Ordered three-dimensional interconnected nanoarchitectures in anodic porous alumina. Nat. Commun. 2014, 5, 5130. [Google Scholar] [CrossRef]
- Donnelly, C.; Guizar-Sicairos, M.; Scagnoli, V.; Holler, M.; Huthwelker, T.; Menzel, A.; Vartiainen, I.; Müller, E.; Kirk, E.; Gliga, S. Element-specific X-ray phase tomography of 3D structures at the nanoscale. Phys. Rev. Lett. 2015, 114, 115501. [Google Scholar] [CrossRef]
- Williams, G.; Hunt, M.; Boehm, B.; May, A.; Taverne, M.; Ho, D.; Giblin, S.; Read, D.; Rarity, J.; Allenspach, R. Two-photon lithography for 3D magnetic nanostructure fabrication. Nano Res. 2018, 11, 845–854. [Google Scholar] [CrossRef]
- Bielinski, A.R.; Gayle, A.J.; Lee, S.; Dasgupta, N.P. Geometric Optimization of Bismuth Vanadate Core–Shell Nanowire Photoanodes using Atomic Layer Deposition. ACS Appl. Mater. Interfaces 2021, 13, 52063–52072. [Google Scholar] [CrossRef] [PubMed]
- Rojo, M.M.; Abad, B.; Manzano, C.; Torres, P.; Cartoixà, X.; Alvarez, F.; Gonzalez, M.M. Thermal conductivity of Bi 2 Te 3 nanowires: How size affects phonon scattering. Nanoscale 2017, 9, 6741–6747. [Google Scholar] [CrossRef]
- Ruiz-Clavijo, A.; Caballero-Calero, O.; Manzano, C.V.; Maeder, X.; Beardo, A.; Cartoixà, X.; Álvarez, F.X.; Martín-González, M. Metamaterials to increase the thermoelectric efficiency. 2021; sent to publication. [Google Scholar]
- Abad, B.; Maiz, J.; Ruiz-Clavijo, A.; Caballero-Calero, O.; Martin-Gonzalez, M. Tailoring thermal conductivity via three-dimensional porous alumina. Sci. Rep. 2016, 6, 38595. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Clavijo, A.; Ruiz-Gomez, S.; Caballero-Calero, O.; Perez, L.; Martin-Gonzalez, M. Tailoring magnetic anisotropy at will in 3D interconnected nanowire networks. Phys. Status Solidi RRL Rapid Res. Lett. 2019, 13, 1900263. [Google Scholar] [CrossRef]
- Abad, B.a.; Maiz, J.; Martin-Gonzalez, M. Rules to determine thermal conductivity and density of Anodic Aluminum Oxide (AAO) membranes. J. Phys. Chem. C 2016, 120, 5361–5370. [Google Scholar] [CrossRef]
- Vera-Londono, L.; Ruiz-Clavijo, A.; Caballero-Calero, O.; Martín-González, M. Understanding the thermal conductivity variations in nanoporous anodic aluminum oxide. Nanoscale Adv. 2020, 2, 4591–4603. [Google Scholar] [CrossRef]
- Ruiz-Clavijo, A.; Caballero-Calero, O.; Martín-González, M. Three-dimensional Bi2Te3 networks of interconnected nanowires: Synthesis and optimization. Nanomaterials 2018, 8, 345. [Google Scholar] [CrossRef]
- Ruiz-Clavijo, A.; Caballero-Calero, O.; Manzano, C.V.; Maeder, X.; Beardo, A.; Cartoixà, X.; Álvarez, F.X.; Martín-González, M. 3D Bi2Te3 Interconnected Nanowire Networks to Increase Thermoelectric Efficiency. ACS Appl. Energy Mater. 2021, 4, 13556–13566. [Google Scholar] [CrossRef]
- Lingstädt, R.; Talebi, N.; Hentschel, M.; Mashhadi, S.; Gompf, B.; Burghard, M.; Giessen, H.; van Aken, P.A. Interaction of edge exciton polaritons with engineered defects in the hyperbolic material Bi2Se3. Commun. Mater. 2021, 2, 5. [Google Scholar] [CrossRef]
- Mauser, K.W.; Kim, S.; Mitrovic, S.; Fleischman, D.; Pala, R.; Schwab, K.; Atwater, H.A. Resonant thermoelectric nanophotonics. Nat. Nanotechnol. 2017, 12, 770–775. [Google Scholar] [CrossRef] [PubMed]
- Humlicek, J. Data analysis for nanomaterials: Effective medium approximation, its limits and implementations. In Ellipsometry at the Nanoscale; Springer: Berlin/Heidelberg, Germany, 2013; pp. 145–178. [Google Scholar]
- Shekhar, P.; Atkinson, J.; Jacob, Z. Hyperbolic metamaterials: Fundamentals and applications. Nano Converg. 2014, 1, 14. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caballero-Calero, O.; Ruiz-Clavijo, A.; Manzano, C.V.; Martín-González, M.; Armelles, G. Plasmon Resonances in 1D Nanowire Arrays and 3D Nanowire Networks of Topological Insulators and Metals. Nanomaterials 2023, 13, 154. https://doi.org/10.3390/nano13010154
Caballero-Calero O, Ruiz-Clavijo A, Manzano CV, Martín-González M, Armelles G. Plasmon Resonances in 1D Nanowire Arrays and 3D Nanowire Networks of Topological Insulators and Metals. Nanomaterials. 2023; 13(1):154. https://doi.org/10.3390/nano13010154
Chicago/Turabian StyleCaballero-Calero, Olga, Alejandra Ruiz-Clavijo, Cristina V. Manzano, Marisol Martín-González, and Gaspar Armelles. 2023. "Plasmon Resonances in 1D Nanowire Arrays and 3D Nanowire Networks of Topological Insulators and Metals" Nanomaterials 13, no. 1: 154. https://doi.org/10.3390/nano13010154
APA StyleCaballero-Calero, O., Ruiz-Clavijo, A., Manzano, C. V., Martín-González, M., & Armelles, G. (2023). Plasmon Resonances in 1D Nanowire Arrays and 3D Nanowire Networks of Topological Insulators and Metals. Nanomaterials, 13(1), 154. https://doi.org/10.3390/nano13010154