Tunable Light Field Modulations with Chip- and Fiber-Compatible Monolithic Dielectric Metasurfaces
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussions
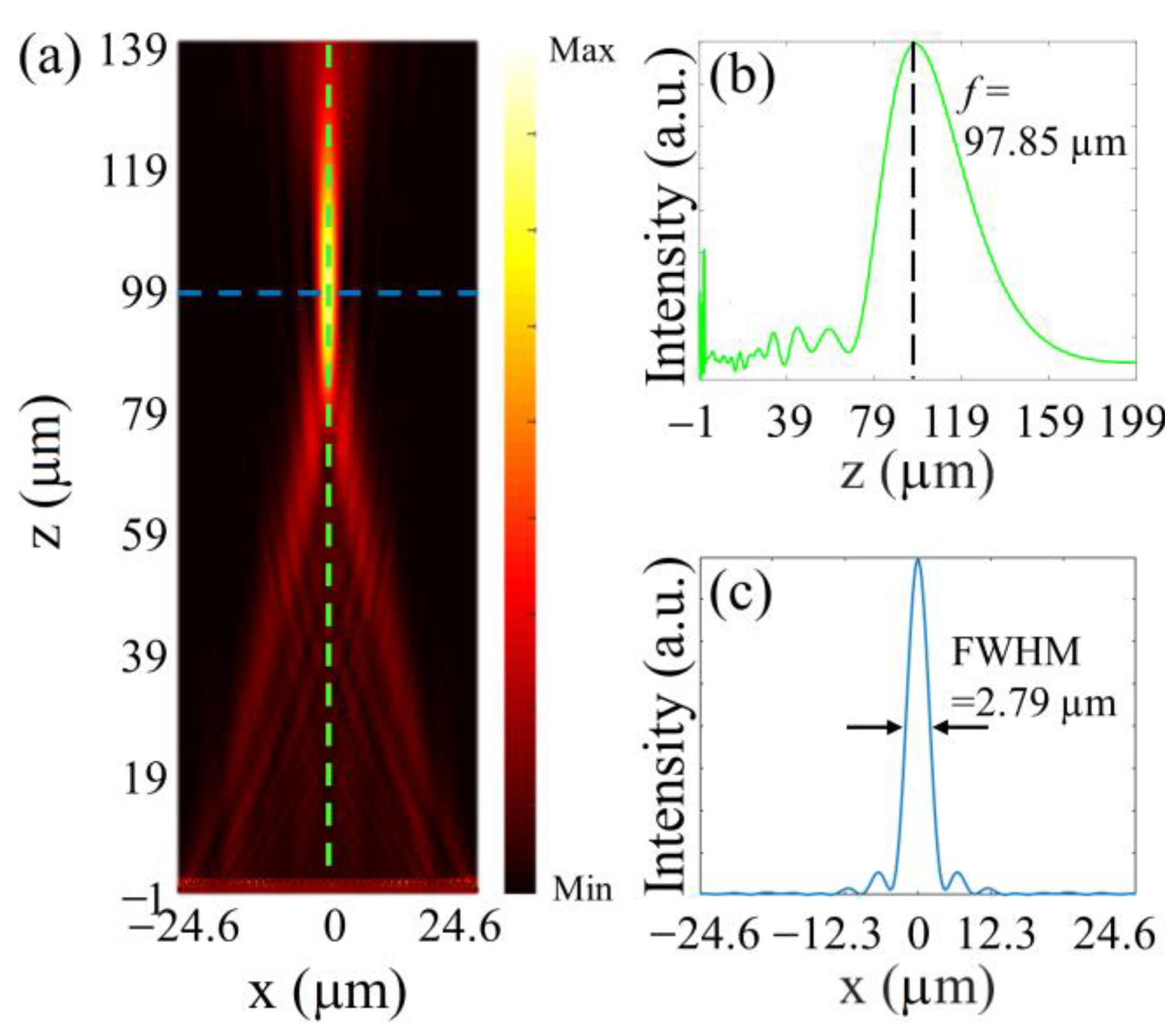
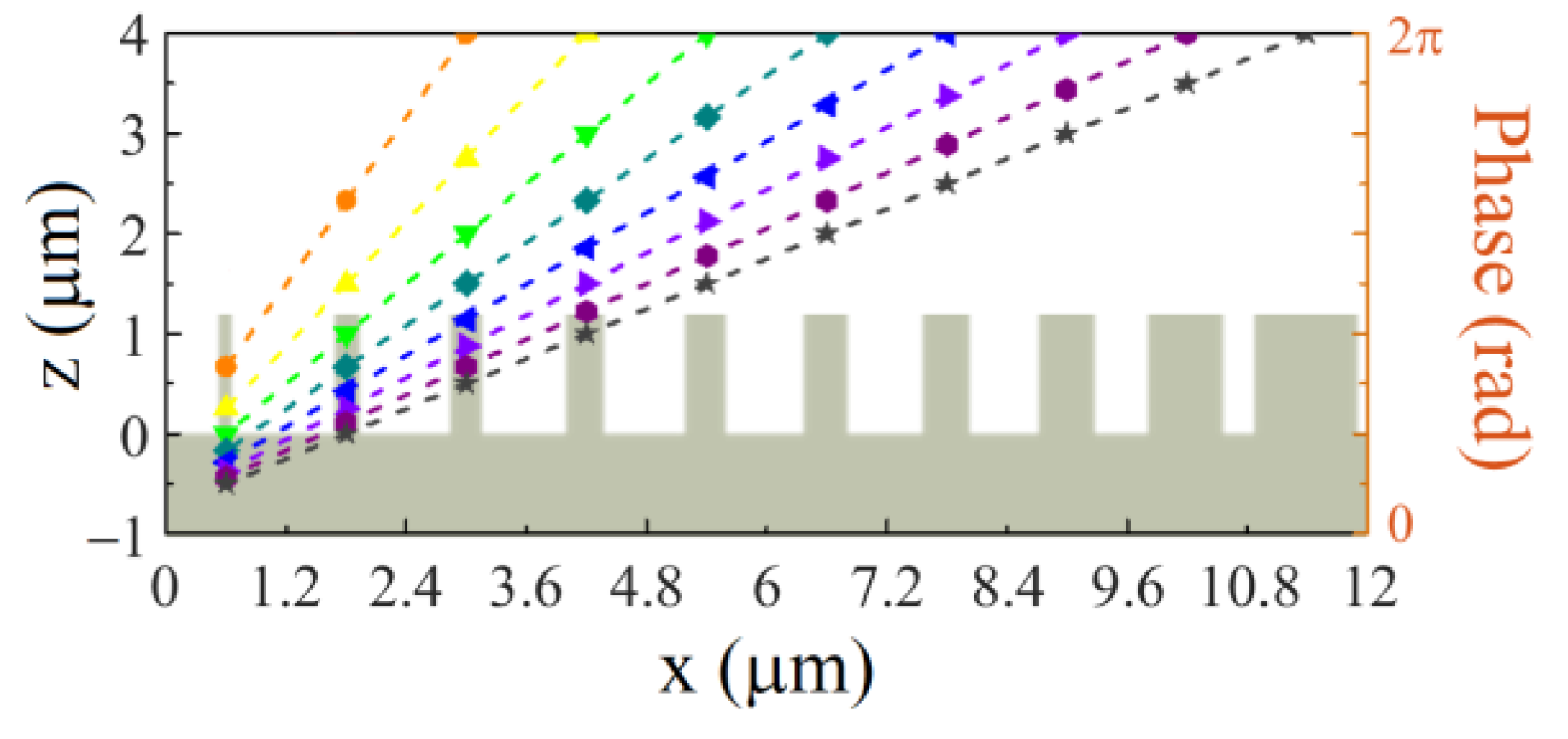
3.1. Continuously Tunable Metalens
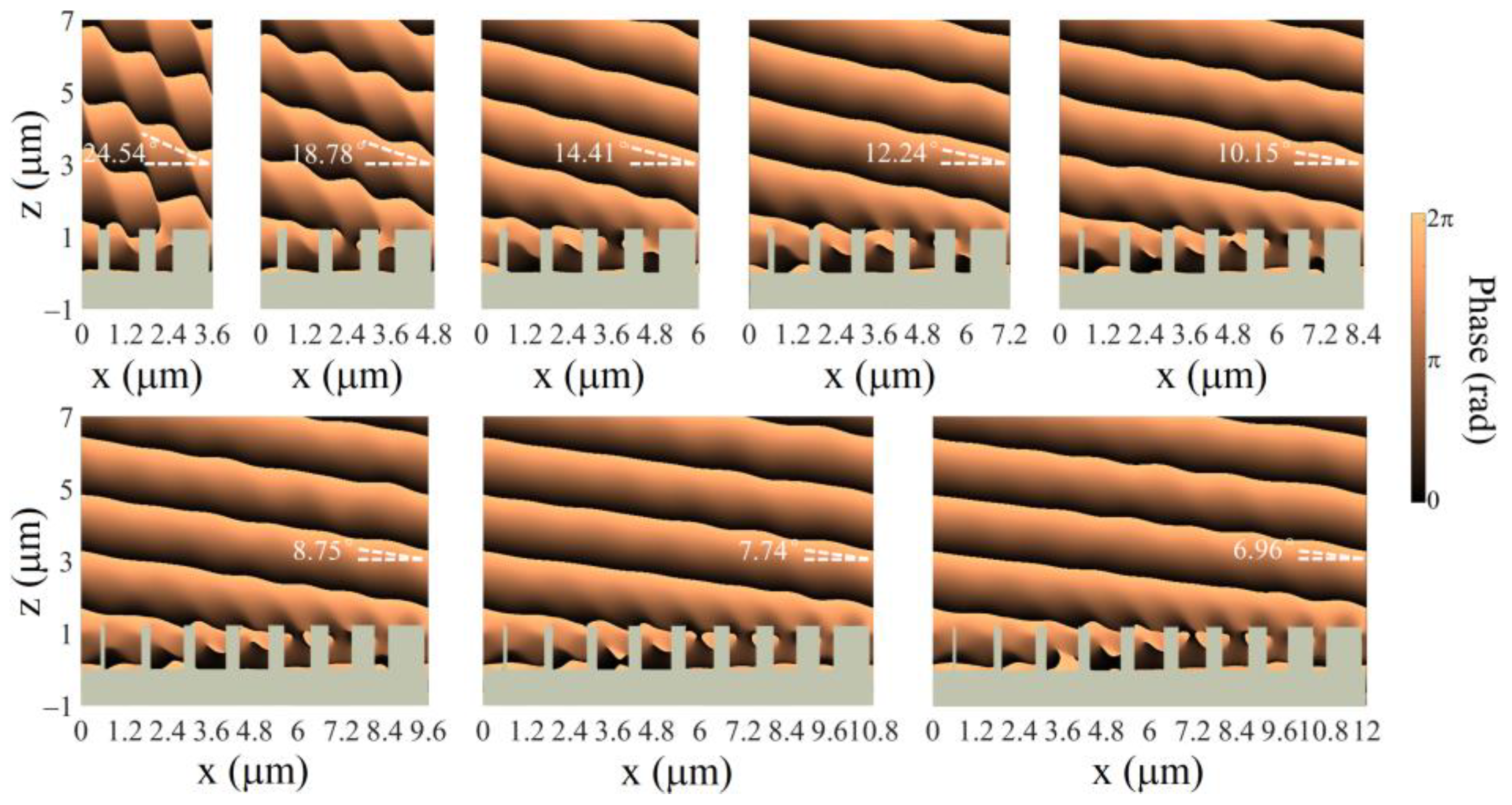
3.2. Discretely Tunable Beam Deflectors
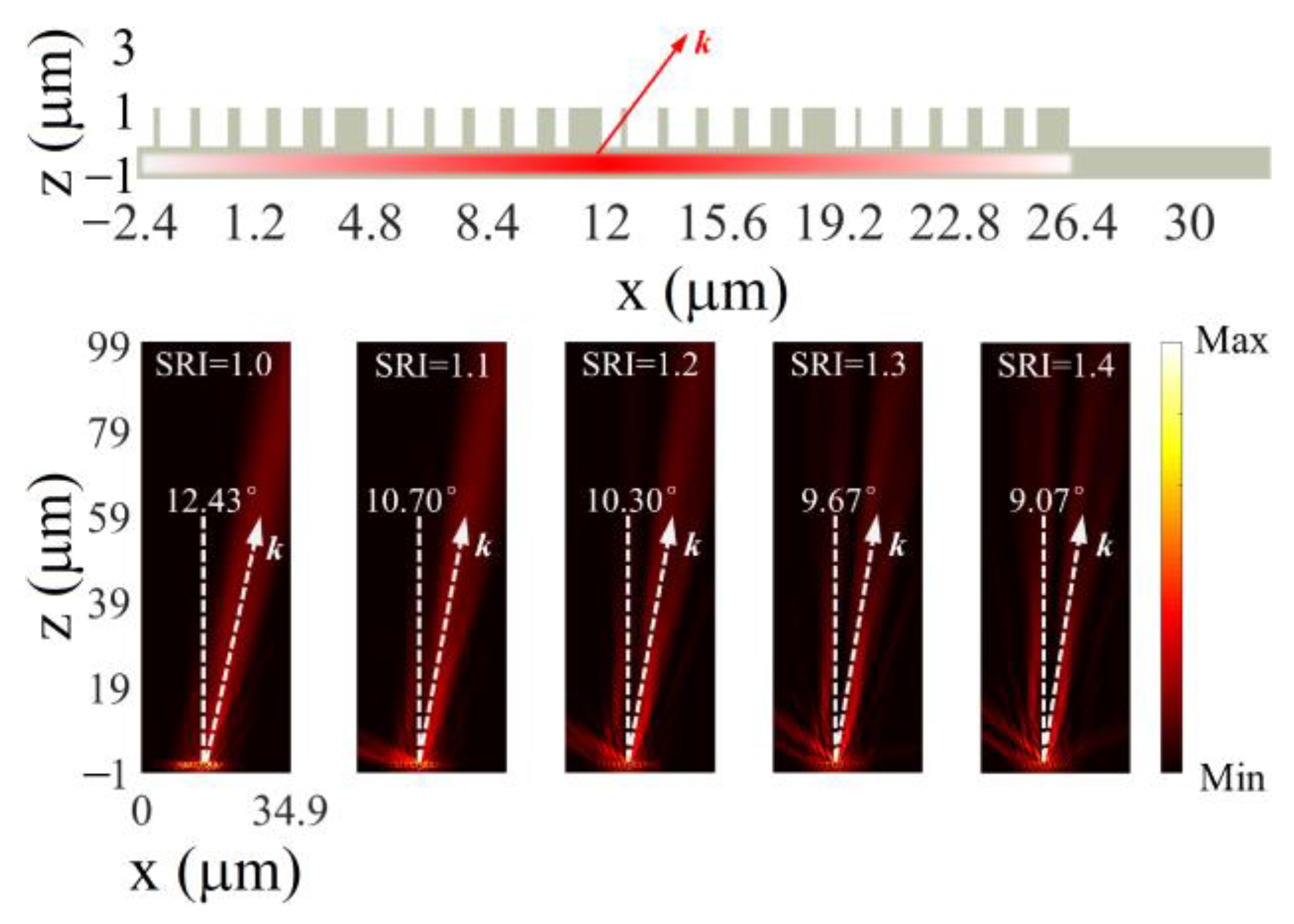
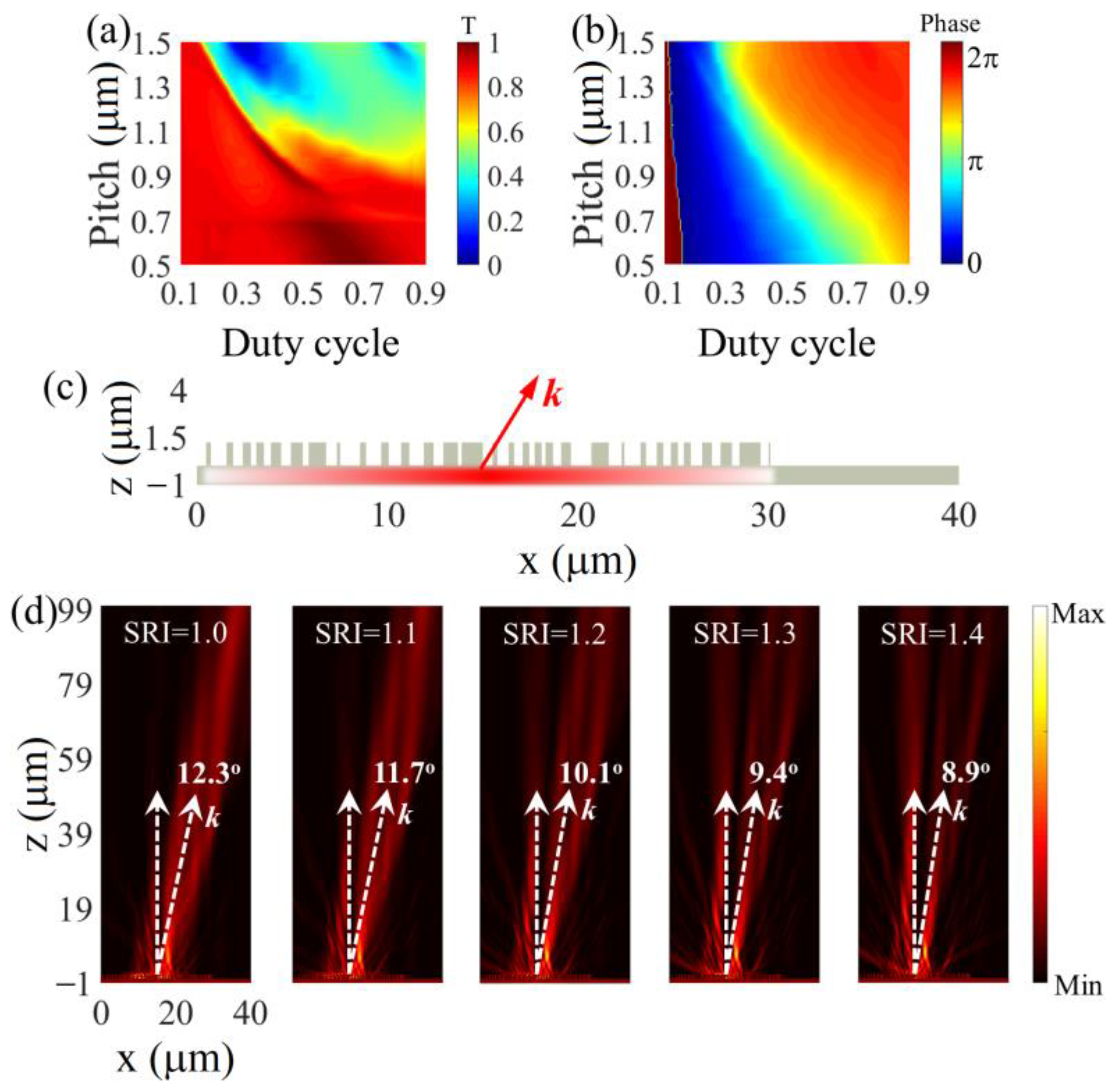
3.3. Continuously Tunable Beam Deflectors
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333. [Google Scholar] [CrossRef]
- Sun, S.; He, Q.; Xiao, S.; Xu, Q.; Li, X.; Zhou, L. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 2012, 11, 426–431. [Google Scholar] [CrossRef] [PubMed]
- Qiu, C.-W.; Zhang, T.; Hu, G.; Kivshar, Y. Quo Vadis, Metasurfaces? Nano Lett. 2021, 21, 5461–5474. [Google Scholar] [CrossRef]
- Fu, R.; Chen, K.; Li, Z.; Yu, S.; Zheng, G. Metasurface-based nanoprinting: Principle, design and advances. Opto-Electron. Sci. 2022, 1, 220011–220041. [Google Scholar] [CrossRef]
- Colburn, S.; Zhan, A.; Majumdar, A. Metasurface optics for full-color computational imaging. Sci. Adv. 2018, 4, eaar2114. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Pu, M.; Jin, J.; Xu, M.; Guo, Y.; Li, X.; Gao, P.; Ma, X.; Luo, X. Generalized Pancharatnam-Berry Phase in Rotationally Symmetric Meta-Atoms. Phys. Rev. Lett. 2021, 126, 183902. [Google Scholar] [CrossRef]
- Saifullah, Y.; He, Y.; Boag, A.; Yang, G.-M.; Xu, F. Recent Progress in Reconfigurable and Intelligent Metasurfaces: A Comprehensive Review of Tuning Mechanisms, Hardware Designs, and Applications. Adv. Sci. 2022, 9, 2203747. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Hung Chu, C.; Chen, J.-W.; Lu, S.-H.; Chen, J.; Xu, B.; Kuan, C.-H.; et al. Broadband achromatic optical metasurface devices. Nat. Commun. 2017, 8, 187. [Google Scholar] [CrossRef]
- Kim, Y.; Wu, P.C.; Sokhoyan, R.; Mauser, K.; Glaudell, R.; Kafaie Shirmanesh, G.; Atwater, H.A. Phase Modulation with Electrically Tunable Vanadium Dioxide Phase-Change Metasurfaces. Nano Lett. 2019, 19, 3961–3968. [Google Scholar] [CrossRef]
- Chen, S.; Li, Z.; Liu, W.; Cheng, H.; Tian, J. From Single-Dimensional to Multidimensional Manipulation of Optical Waves with Metasurfaces. Adv. Mater. 2019, 31, 1802458. [Google Scholar] [CrossRef]
- Deng, L.; Deng, J.; Guan, Z.; Tao, J.; Chen, Y.; Yang, Y.; Zhang, D.; Tang, J.; Li, Z.; Li, Z.; et al. Malus-metasurface-assisted polarization multiplexing. Light Sci. Appl. 2020, 9, 101. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190. [Google Scholar] [CrossRef] [PubMed]
- Tseng, M.L.; Hsiao, H.-H.; Chu, C.H.; Chen, M.K.; Sun, G.; Liu, A.-Q.; Tsai, D.P. Metalenses: Advances and Applications. Adv. Opt. Mater. 2018, 6, 1800554. [Google Scholar] [CrossRef]
- Li, G.; Chen, S.; Pholchai, N.; Reineke, B.; Wong, P.W.H.; Pun, E.Y.B.; Cheah, K.W.; Zentgraf, T.; Zhang, S. Continuous control of the nonlinearity phase for harmonic generations. Nat. Mater. 2015, 14, 607–612. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Fu, Y.H.; Dong, Y.; Hu, T.; Xu, Z.; Zhong, Q.; Li, D.; Lai, K.H.; Zhu, S.; Lin, Q.; et al. Large-area pixelated metasurface beam deflector on a 12-inch glass wafer for random point generation. Nanophotonics 2019, 8, 1855–1861. [Google Scholar] [CrossRef]
- Meng, C.; Tang, S.; Ding, F.; Bozhevolnyi, S.I. Optical Gap-Surface Plasmon Metasurfaces for Spin-Controlled Surface Plasmon Excitation and Anomalous Beam Steering. ACS Photonics 2020, 7, 1849–1856. [Google Scholar] [CrossRef]
- Cheng, H.; Fang, B.; Huang, W.; Li, R.; Shen, C.; Ke, L.; Jing, X.; Li, C.; Hong, Z. Far-field steering of beams based on dynamic encoding metasurface. Opt. Laser Technol. 2022, 156, 108520. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Ding, F.; Chang, B.; Wei, Q.; Huang, L.; Guan, X.; Bozhevolnyi, S.I. Versatile Polarization Generation and Manipulation Using Dielectric Metasurfaces. Laser Photonics Rev. 2020, 14, 2000116. [Google Scholar] [CrossRef]
- Hu, Q.; Chen, K.; Zhang, N.; Zhao, J.; Jiang, T.; Zhao, J.; Feng, Y. Arbitrary and Dynamic Poincaré Sphere Polarization Converter with a Time-Varying Metasurface. Adv. Opt. Mater. 2022, 10, 2101915. [Google Scholar] [CrossRef]
- Yuan, Q.; Fang, L.; Fang, H.; Li, J.; Wang, T.; Jie, W.; Zhao, J.; Gan, X. Second Harmonic and Sum-Frequency Generations from a Silicon Metasurface Integrated with a Two-Dimensional Material. ACS Photonics 2019, 6, 2252–2259. [Google Scholar] [CrossRef]
- Cui, T.; Bai, B.; Sun, H.-B. Tunable Metasurfaces Based on Active Materials. Adv. Funct. Mater. 2019, 29, 1806692. [Google Scholar] [CrossRef]
- Abdelraouf, O.A.M.; Wang, Z.; Liu, H.; Dong, Z.; Wang, Q.; Ye, M.; Wang, X.R.; Wang, Q.J.; Liu, H. Recent Advances in Tunable Metasurfaces: Materials, Design, and Applications. ACS Nano 2022, 16, 13339–13369. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.; Gao, W.; Xiao, Q.; Ding, L.; Gao, T.; Zhou, Y.; Gao, X.; Yan, T.; Liu, C.; Gu, Z.; et al. Directly wireless communication of human minds via non-invasive brain-computer-metasurface platform. ELight 2022, 2, 11. [Google Scholar] [CrossRef]
- Zhu, R.; Wang, J.; Qiu, T.; Han, Y.; Fu, X.; Shi, Y.; Liu, X.; Liu, T.; Zhang, Z.; Chu, Z.; et al. Remotely mind-controlled metasurface via brainwaves. ELight 2022, 2, 10. [Google Scholar] [CrossRef]
- Buchnev, O.; Podoliak, N.; Kaczmarek, M.; Zheludev, N.I.; Fedotov, V.A. Electrically Controlled Nanostructured Metasurface Loaded with Liquid Crystal: Toward Multifunctional Photonic Switch. Adv. Opt. Mater. 2015, 3, 674–679. [Google Scholar] [CrossRef]
- Park, J.; Jeong, B.G.; Kim, S.I.; Lee, D.; Kim, J.; Shin, C.; Lee, C.B.; Otsuka, T.; Kyoung, J.; Kim, S.; et al. All-solid-state spatial light modulator with independent phase and amplitude control for three-dimensional LiDAR applications. Nat. Nanotechnol. 2021, 16, 69–76. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B. Photonic and Plasmonic Metasensors. Laser Photonics Rev. 2022, 16, 2100328. [Google Scholar] [CrossRef]
- Huang, T.-Y.; Grote, R.R.; Mann, S.A.; Hopper, D.A.; Exarhos, A.L.; Lopez, G.G.; Klein, A.R.; Garnett, E.C.; Bassett, L.C. A monolithic immersion metalens for imaging solid-state quantum emitters. Nat. Commun. 2019, 10, 2392. [Google Scholar] [CrossRef]
- Thomaschewski, M.; Zenin, V.A.; Wolff, C.; Bozhevolnyi, S.I. Plasmonic monolithic lithium niobate directional coupler switches. Nat. Commun. 2020, 11, 748. [Google Scholar] [CrossRef]
- West, P.R.; Stewart, J.L.; Kildishev, A.V.; Shalaev, V.M.; Shkunov, V.V.; Strohkendl, F.; Zakharenkov, Y.A.; Dodds, R.K.; Byren, R. All-dielectric subwavelength metasurface focusing lens. Opt. Express 2014, 22, 26212–26221. [Google Scholar] [CrossRef] [PubMed]
- Carletti, L.; Zilli, A.; Moia, F.; Toma, A.; Finazzi, M.; De Angelis, C.; Neshev, D.N.; Celebrano, M. Steering and Encoding the Polarization of the Second Harmonic in the Visible with a Monolithic LiNbO3 Metasurface. ACS Photonics 2021, 8, 731–737. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Xu, R.; Lin, Y.-S.; Chen, C.-H. Tunable electromagnetic characteristics of suspended nanodisk metasurface. Opt. Laser Technol. 2020, 128, 106214. [Google Scholar] [CrossRef]
- Schaeper, O.; Yang, Z.; Kianinia, M.; Fröch, J.E.; Komar, A.; Mu, Z.; Gao, W.; Neshev, D.N.; Aharonovich, I. Monolithic Silicon Carbide Metalenses. ACS Photonics 2022, 9, 1409–1414. [Google Scholar] [CrossRef]
- Gao, B.; Ren, M.; Wu, W.; Hu, H.; Cai, W.; Xu, J. Lithium Niobate Metasurfaces. Laser Photonics Rev. 2019, 13, 1800312. [Google Scholar] [CrossRef]
- Hu, Y.; Ou, X.; Zeng, T.; Lai, J.; Zhang, J.; Li, X.; Luo, X.; Li, L.; Fan, F.; Duan, H. Electrically Tunable Multifunctional Polarization-Dependent Metasurfaces Integrated with Liquid Crystals in the Visible Region. Nano Lett. 2021, 21, 4554–4562. [Google Scholar] [CrossRef]
- Komar, A.; Paniagua-Domínguez, R.; Miroshnichenko, A.E.; Yu, Y.F.; Kivshar, Y.S.; Kuznetsov, A.I.; Neshev, D.N. Dynamic Beam Switching by Liquid Crystal Tunable Dielectric Metasurfaces. ACS Photonics 2018, 5, 1742–1748. [Google Scholar] [CrossRef]
- Du, B.; Ruan, Y.; Ly, T.-T.; Jia, P.; Sun, Q.; Feng, Q.; Yang, D.; Ebendorff-Heidepriem, H. MoS2-enhanced Epoxy-based Plasmonic Fiber-optic Sensor for Selective and Sensitive Detection of Methanol. Sens. Actuators B Chem. 2020, 305, 127513. [Google Scholar] [CrossRef]
- Zhou, C.; Lee, W.-B.; Gao, S.; Li, H.; Park, C.-S.; Choi, D.-Y.; Lee, S.-S. All-Dielectric Fiber Meta-Tip Enabling Vortex Generation and Beam Collimation for Optical Interconnect. Laser Photonics Rev. 2021, 15, 2000581. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-Insensitive Metalenses at Visible Wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef]
- Zelmon, D.E.; Small, D.L.; Jundt, D. Infrared corrected Sellmeier coefficients for congruently grown lithium niobate and 5 mol. % magnesium oxide–doped lithium niobate. J. Opt. Soc. Am. B 1997, 14, 3319–3322. [Google Scholar] [CrossRef]
- Kim, S.-J.; Kim, C.; Kim, Y.; Jeong, J.; Choi, S.; Han, W.; Kim, J.; Lee, B. Dielectric Metalens: Properties and Three-Dimensional Imaging Applications. Sensors 2021, 21, 4584. [Google Scholar] [CrossRef] [PubMed]
- Carletti, L.; Malureanu, R.; Mørk, J.; Chung, I.-S. High-index-contrast grating reflector with beam steering ability for the transmitted beam. Opt. Express 2011, 19, 23567–23572. [Google Scholar] [CrossRef] [PubMed]
- Principe, M.; Consales, M.; Micco, A.; Crescitelli, A.; Castaldi, G.; Esposito, E.; La Ferrara, V.; Cutolo, A.; Galdi, V.; Cusano, A. Optical fiber meta-tips. Light Sci. Appl. 2017, 6, e16226. [Google Scholar] [CrossRef] [PubMed]
- Consales, M.; Quero, G.; Spaziani, S.; Principe, M.; Micco, A.; Galdi, V.; Cutolo, A.; Cusano, A. Metasurface-Enhanced Lab-on-Fiber Biosensors. Laser Photonics Rev. 2020, 14, 2000180. [Google Scholar] [CrossRef]
- Du, B.; Ruan, Y.; Yang, D.; Jia, P.; Gao, S.; Wang, Y.; Wang, P.; Ebendorff-Heidepriem, H. Freestanding metal nanohole array for high-performance applications. Photonics Res. 2020, 8, 1749–1756. [Google Scholar] [CrossRef]
- Ren, H.; Jang, J.; Li, C.; Aigner, A.; Plidschun, M.; Kim, J.; Rho, J.; Schmidt, M.A.; Maier, S.A. An achromatic metafiber for focusing and imaging across the entire telecommunication range. Nat. Commun. 2022, 13, 4183. [Google Scholar] [CrossRef]
- Li, S.-Q.; Xu, X.; Maruthiyodan Veetil, R.; Valuckas, V.; Paniagua-Domínguez, R.; Kuznetsov, A.I. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface. Science 2019, 364, 1087–1090. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Shen, Z.; Ge, S.; Chen, B.; Shen, Z.; Wang, T.; Zhang, C.; Hu, W.; Fan, K.; Padilla, W.; et al. Liquid crystal programmable metasurface for terahertz beam steering. Appl. Phys. Lett. 2020, 116, 131104. [Google Scholar] [CrossRef]
- Shirmanesh, G.K.; Sokhoyan, R.; Wu, P.C.; Atwater, H.A. Electro-optically Tunable Multifunctional Metasurfaces. ACS Nano 2020, 14, 6912–6920. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Yang, J.; Huang, J.; Zhang, Z.; Xie, W.; Jiang, X.; He, X.; Han, Y.; Zhang, Z.; Yu, Y. Continuously tunable metasurfaces controlled by single electrode uniform bias-voltage based on nonuniform periodic rectangular graphene arrays. Opt. Express 2020, 28, 29306–29317. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.C.; Pala, R.A.; Shirmanesh, G.K.; Cheng, W.-H.; Sokhoyan, R.; Grajower, M.; Alam, M.Z.; Lee, D.; Atwater, H.A. Dynamic beam steering with all-dielectric electro-optic III–V multiple-quantum-well metasurfaces. Nat. Commun. 2019, 10, 3654. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Fowler, C.; Liang, J.; Azhar, B.; Shalaginov, M.Y.; Deckoff-Jones, S.; An, S.; Chou, J.B.; Roberts, C.M.; Liberman, V.; et al. Electrically reconfigurable non-volatile metasurface using low-loss optical phase-change material. Nat. Nanotechnol. 2021, 16, 661–666. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Hong, X.; Wang, K.; Wu, J.; Xu, H.-X.; Zhao, W.; Liu, W.; Zhang, S.; Garcia-Vidal, F.; Wang, B.; et al. Coherent steering of nonlinear chiral valley photons with a synthetic Au–WS2 metasurface. Nat. Photonics 2019, 13, 467–472. [Google Scholar] [CrossRef]
- Ee, H.-S.; Agarwal, R. Tunable Metasurface and Flat Optical Zoom Lens on a Stretchable Substrate. Nano Lett. 2016, 16, 2818–2823. [Google Scholar] [CrossRef]
- Luo, Y.; Chu, C.H.; Vyas, S.; Kuo, H.Y.; Chia, Y.H.; Chen, M.K.; Shi, X.; Tanaka, T.; Misawa, H.; Huang, Y.-Y.; et al. Varifocal Metalens for Optical Sectioning Fluorescence Microscopy. Nano Lett. 2021, 21, 5133–5142. [Google Scholar] [CrossRef]



| Applications | Operation Wavelength | Tunability Range | Tunability Continuity | Compatibility | Ref. |
|---|---|---|---|---|---|
| Beam steering | 0.65 μm | 11° | No | Low | [48] |
| 0.672 THz | 32° | No | Low | [49] | |
| 1.522 μm | 22° | No | Low | [50] | |
| 5 THz | 35.5° | Yes | Low | [51] | |
| 0.917 μm | 9.66° | No | Moderate | [52] | |
| 1.55 μm | 32° | No | Moderate | [53] | |
| 0.124 μm | 8.5° | No | High | [54] | |
| 1.55 μm | 27.58° | No | High | This work | |
| 1.55 μm | 3.4° | Yes | High | ||
| Varifocal lens | 1.522 μm | 10 μm | No | Low | [50] |
| 0.633 μm | 100 μm | Yes | Low | [55] | |
| 0.532 μm | 115 mm | Yes | Low | [56] | |
| 1.55 μm | 61.6 μm | Yes | High | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Xu, Y.; Ding, H.; Jiang, W.; Zhang, L.; Zhang, Y. Tunable Light Field Modulations with Chip- and Fiber-Compatible Monolithic Dielectric Metasurfaces. Nanomaterials 2023, 13, 69. https://doi.org/10.3390/nano13010069
Du B, Xu Y, Ding H, Jiang W, Zhang L, Zhang Y. Tunable Light Field Modulations with Chip- and Fiber-Compatible Monolithic Dielectric Metasurfaces. Nanomaterials. 2023; 13(1):69. https://doi.org/10.3390/nano13010069
Chicago/Turabian StyleDu, Bobo, Yunfan Xu, Huimin Ding, Weitao Jiang, Lei Zhang, and Yanpeng Zhang. 2023. "Tunable Light Field Modulations with Chip- and Fiber-Compatible Monolithic Dielectric Metasurfaces" Nanomaterials 13, no. 1: 69. https://doi.org/10.3390/nano13010069
APA StyleDu, B., Xu, Y., Ding, H., Jiang, W., Zhang, L., & Zhang, Y. (2023). Tunable Light Field Modulations with Chip- and Fiber-Compatible Monolithic Dielectric Metasurfaces. Nanomaterials, 13(1), 69. https://doi.org/10.3390/nano13010069








