Three-Channel Near-Field Display and Encryption Based on a Polarization Multiplexed Metasurface
Abstract
1. Introduction
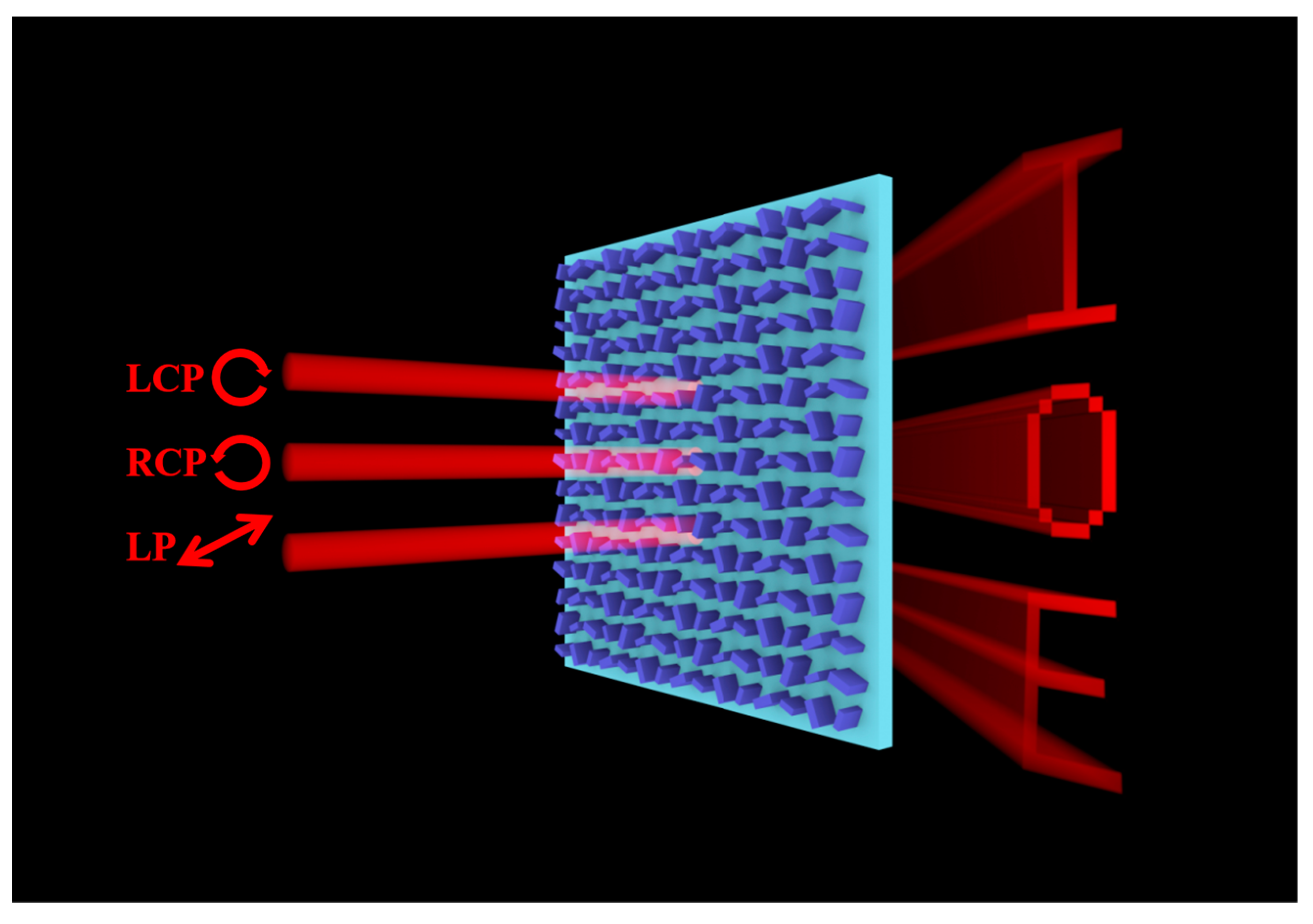
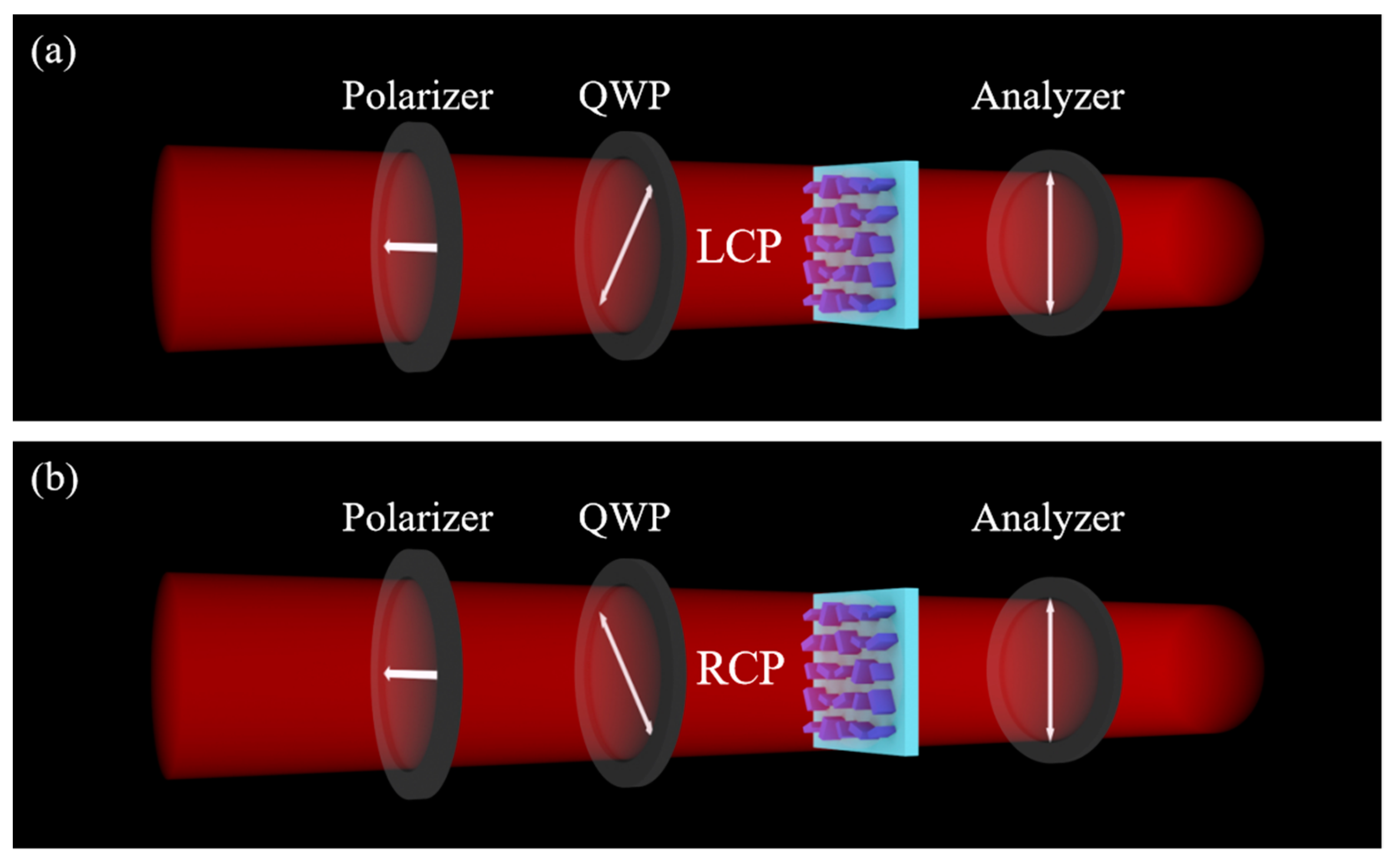
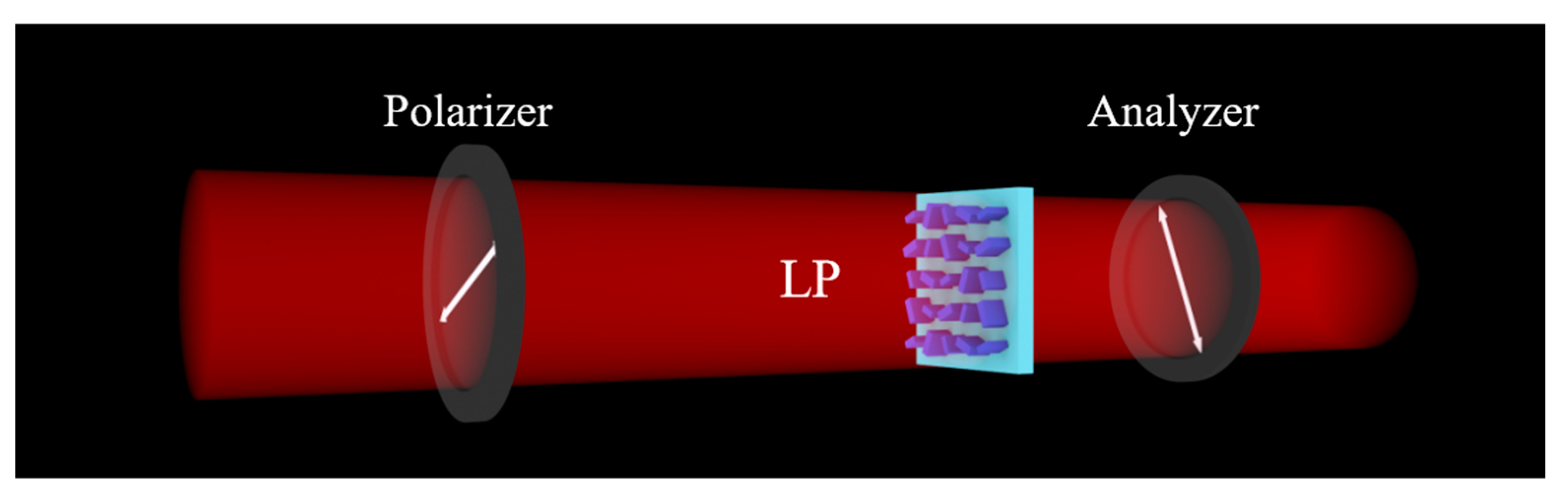
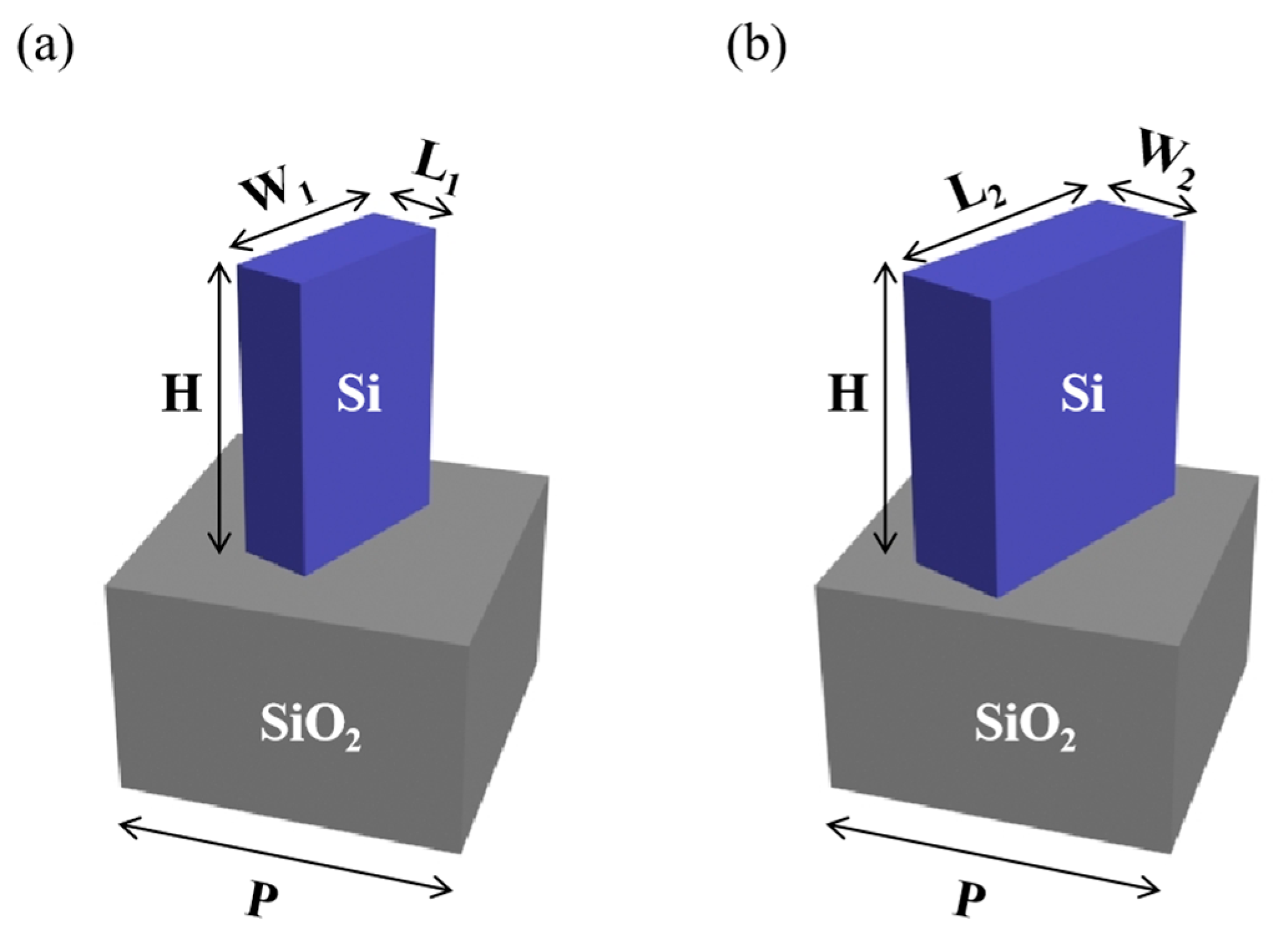
2. Principle and Design
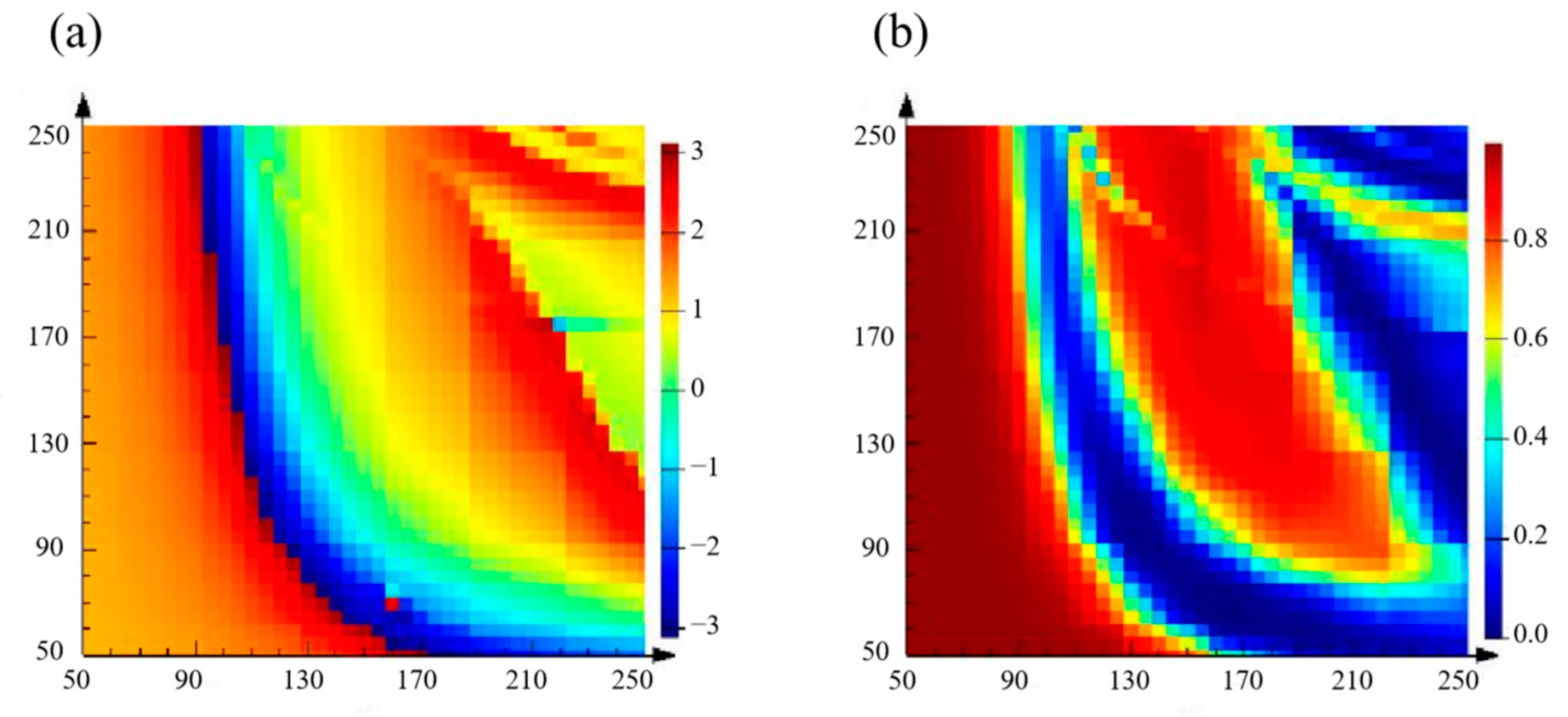
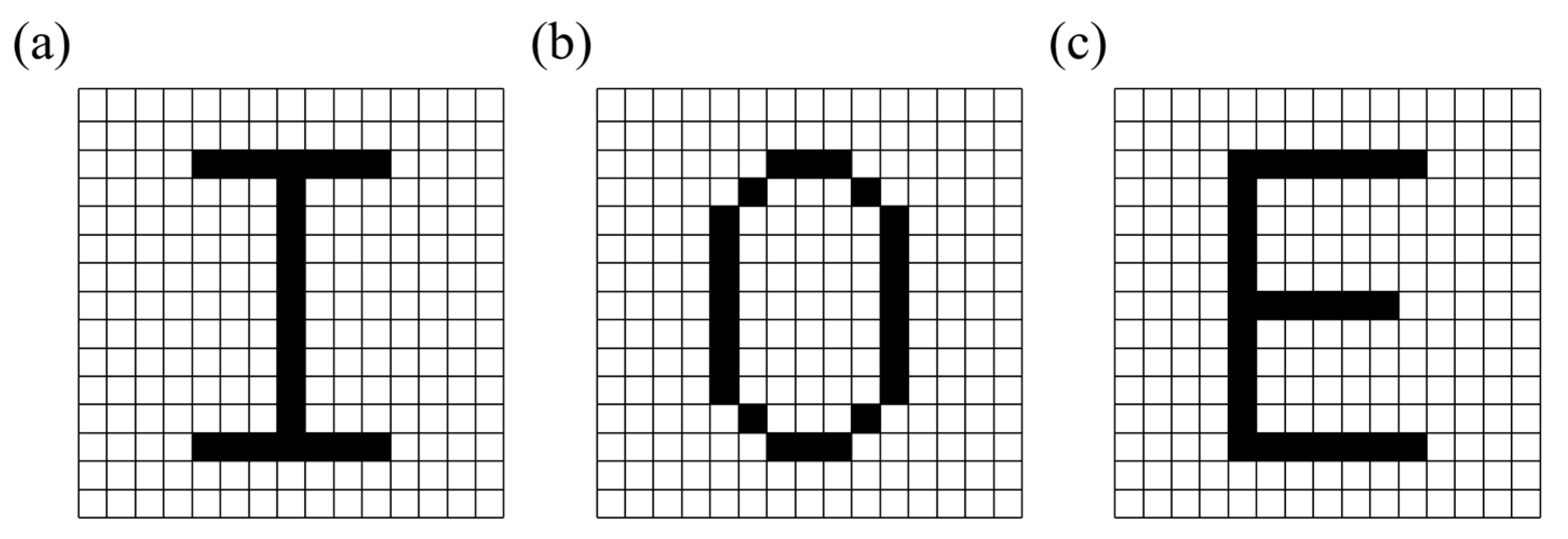
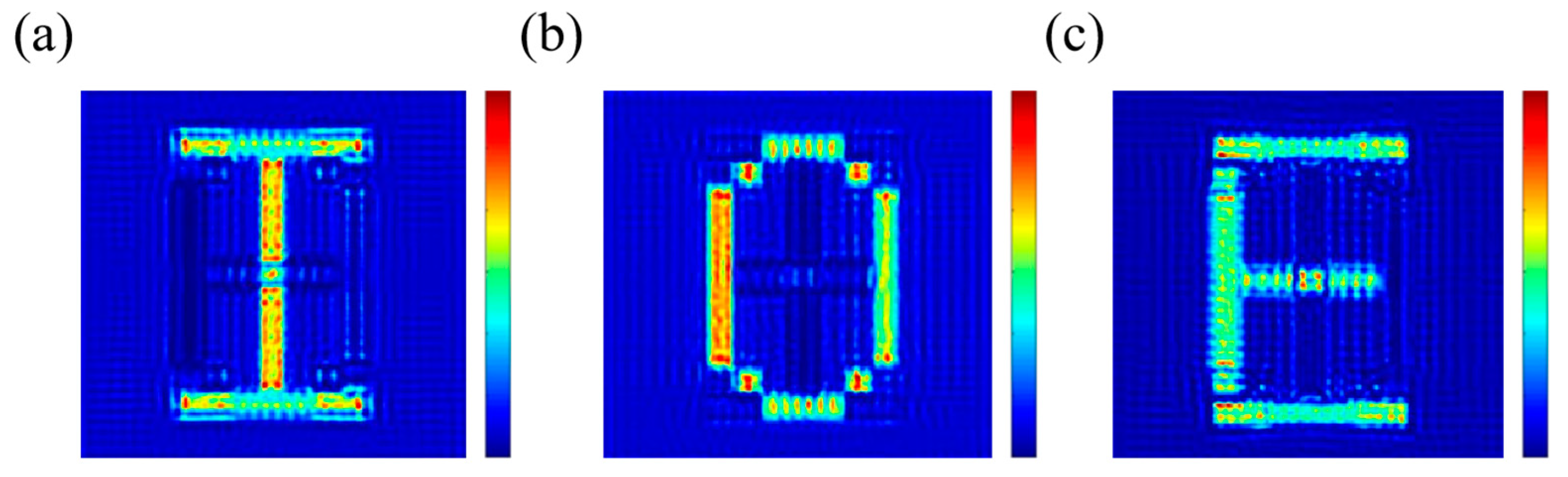
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [PubMed]
- Fu, R.; Chen, K.; Li, Z.; Yu, S.; Zheng, G. Metasurface-based nanoprinting: Principle, design and advances. Opto-Electron. Sci. 2022, 1, 220011–220041. [Google Scholar] [CrossRef]
- Yue, F.; Zhang, C.; Zang, X.F.; Wen, D.; Gerardot, B.D.; Zhang, S.; Chen, X. High-resolution grayscale image hidden in a laser beam. Light Sci. Appl. 2018, 7, 17129. [Google Scholar] [CrossRef]
- Dai, Q.; Deng, L.; Deng, J.; Tao, J.; Yang, Y.; Chen, M.; Li, Z.; Li, Z.; Zheng, G. Ultracompact, high-resolution and continuous grayscale image display based on resonant dielectric metasurfaces. Opt. Express 2019, 27, 27927–27935. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Y.; Chen, M.; Xu, R.; Yuan, L. Ultracompact metaimage display and encryption with a silver nanopolarizer based metasurface. Appl. Phys. Lett. 2020, 117, 021105. [Google Scholar] [CrossRef]
- Tang, J.; Li, Z.; Wan, S.; Wang, Z.; Wan, C.; Dai, C.; Li, Z. Angular multiplexing nanoprinting with independent amplitude encryption based on visible-frequency metasurfaces. ACS Appl. Mater. Interfaces. 2021, 13, 38623–38628. [Google Scholar] [CrossRef]
- Wan, S.; Tang, J.; Wan, C.; Li, Z.; Li, Z. Angular-encrypted quad-fold display of nanoprinting and meta-holography for optical information storage. Adv. Opt. Mater. 2022, 10, 2102820. [Google Scholar] [CrossRef]
- Deng, J.; Gao, F.; Yuan, P.; Li, Y.; Yan, B. Bidirectional nanoprinting based on bilayer metasurfaces. Opt. Express 2022, 30, 377–388. [Google Scholar] [CrossRef]
- Cao, Y.; Tang, L.; Li, J.; Lee, C.; Dong, Z.G. Four-channel display and encryption by near-field reflection on nanoprinting metasurface. Nanophotonics 2022, 11, 3365–3374. [Google Scholar] [CrossRef]
- Cao, Y.; Tang, L.; Li, J.; Wang, J.; Dong, Z.G. Dual-wavelength complementary grayscale imaging by an ultrathin metasurface. Opt. Lett. 2020, 45, 5181–5184. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Dai, Q.; Deng, L.; Zheng, G.; Li, G. Structural-color nanoprinting with hidden watermarks. Opt. Lett. 2021, 46, 480–483. [Google Scholar] [CrossRef]
- Ren, R.; Li, Z.; Deng, L.; Shan, X.; Dai, Q.; Guan, Z.; Zheng, G.; Yu, S. Non-orthogonal polarization multiplexed metasurfaces for tri-channel polychromatic image displays and information encryption. Nanophotonics 2021, 10, 2903–2914. [Google Scholar] [CrossRef]
- Li, Z.; Deng, L.; Deng, J.; He, Z.; Tao, J.; Zheng, G.; Yu, S. Metasurface-enabled three-in-one nanoprints by multifunctional manipulations of light. Iscience 2021, 24, 103510. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Deng, J.; Guan, Z.; Tao, J.; Chen, Y.; Yang, Y.; Zhang, D.; Tang, J.; Li, Z.; Li, Z.; et al. Malus-metasurface-assisted polarization multiplexing. Light Sci. Appl. 2020, 9, 101. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ren, R.; Deng, J.; Deng, L.; Li, G.; Zheng, G. Non-orthogonal-polarization multiplexed metasurfaces for tri-channel gray-imaging. Opt. Express 2021, 29, 134–144. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Gao, J.; Yang, X. Chiral grayscale imaging with plasmonic metasurfaces of stepped nanoapertures. Adv. Opt. Mater. 2019, 7, 1801467. [Google Scholar] [CrossRef]
- Hu, S.; Du, S.; Li, J.; Gu, C. Multidimensional image and beam splitter based on hyperbolic metamaterials. Nano Lett. 2021, 21, 1792–1799. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.; Gao, J. 3D Janus plasmonic helical nanoapertures for polarization-encrypted data storage. Light Sci. Appl. 2019, 8, 45. [Google Scholar] [CrossRef]
- Dai, Q.; Zhou, N.; Deng, L.; Deng, J.; Li, Z.; Zheng, G. Dual-channel binary gray-image display enabled with malus-assisted metasurfaces. Phys. Rev. Appl. 2020, 14, 034002. [Google Scholar] [CrossRef]
- Zheng, P.; Dai, Q.; Li, Z.; Ye, Z.; Xiong, J.; Liu, H.-C.; Zheng, G.; Zhang, S. Metasurface-Based Key for Computational Imaging Encryption. Sci. Adv. 2021, 7, eabg0363. [Google Scholar] [CrossRef] [PubMed]
- Dai, Q.; Zhu, G.; Zhang, W.; Li, J.; Li, Z.; Cui, H.; Wei, K.; He, Z.; Guan, Z.; Zheng, G. Dual-channel anticounterfeiting color-nanoprinting with a single-size nanostructured metasurface. Opt. Express 2022, 30, 33574–33587. [Google Scholar] [CrossRef]
- Guo, J.; Wang, T.; Quan, B.; Zhao, H.; Gu, C.; Li, J.; Wang, X.; Situ, G.; Zhang, Y. Polarization multiplexing for double images display. Opto Electron. Adv. 2019, 2, 07180029. [Google Scholar] [CrossRef]
- Li, Z.; Yu, S.; Zheng, G. Advances in exploiting the degrees of freedom in nanostructured metasurface design: From 1 to 3 to more. Nanophotonics 2020, 9, 3699–3731. [Google Scholar] [CrossRef]
- Xiong, B.; Deng, L.; Peng, R.; Liu, Y. Controlling the degrees of freedom in metasurface designs for multi-functional optical devices. Nanoscale Adv. 2019, 1, 3786–3806. [Google Scholar] [CrossRef] [PubMed]
- Bao, Y.; Wen, L.; Chen, Q.; Qiu, C.W.; Li, B. Toward the capacity limit of 2D planar Jones matrix with a single-layer metasurface. Sci. Adv. 2021, 7, eabh0365. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Zhou, C.; Yue, W.; Li, Y.; Zhang, C.; Kan, H.; Li, C.; Lee, S.S.; Choi, D.Y. Efficient all-dielectric diatomic metasurface for linear polarization generation and 1-bit phase control. ACS Appl. Mater. Interfaces 2021, 13, 14497–14506. [Google Scholar] [CrossRef]
- Yu, N.; Aieta, F.; Genevet, P.; Kats, M.A.; Gaburro, Z.; Capasso, F. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 2012, 12, 6328–6333. [Google Scholar] [CrossRef]
- Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Liu, M.; Zhu, W.; Huo, P.; Feng, L.; Song, M.; Zhang, C.; Chen, L.; Lezec, H.J.; Lu, Y.; Agrawal, A.; et al. Multifunctional metasurfaces enabled by simultaneous and independent control of phase and amplitude for orthogonal polarization states. Light Sci. Appl. 2021, 10, 107. [Google Scholar] [CrossRef] [PubMed]




| Rotation Angle | ||||||||
|---|---|---|---|---|---|---|---|---|
| Nanostructure 1 | Nanostructure 2 | |||||||
| Incident light | 22.5° | 67.5° | 112.5° | 157.5° | 22.5° | 67.5° | 112.5° | 157.5° |
| LCP | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| RCP | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| Rotation Angle | ||||||||
|---|---|---|---|---|---|---|---|---|
| Nanostructure 1 | Nanostructure 2 | |||||||
| Incident light | 22.5° | 67.5° | 112.5° | 157.5° | 22.5° | 67.5° | 112.5° | 157.5° |
| LCP | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| RCP | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| LP | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Li, Z.; Hong, Y.; Zhang, Y.; Liu, H.; Wei, Z. Three-Channel Near-Field Display and Encryption Based on a Polarization Multiplexed Metasurface. Nanomaterials 2023, 13, 1638. https://doi.org/10.3390/nano13101638
Yuan J, Li Z, Hong Y, Zhang Y, Liu H, Wei Z. Three-Channel Near-Field Display and Encryption Based on a Polarization Multiplexed Metasurface. Nanomaterials. 2023; 13(10):1638. https://doi.org/10.3390/nano13101638
Chicago/Turabian StyleYuan, Jiadong, Zuyu Li, Yuhan Hong, Yuhang Zhang, Hongzhan Liu, and Zhongchao Wei. 2023. "Three-Channel Near-Field Display and Encryption Based on a Polarization Multiplexed Metasurface" Nanomaterials 13, no. 10: 1638. https://doi.org/10.3390/nano13101638
APA StyleYuan, J., Li, Z., Hong, Y., Zhang, Y., Liu, H., & Wei, Z. (2023). Three-Channel Near-Field Display and Encryption Based on a Polarization Multiplexed Metasurface. Nanomaterials, 13(10), 1638. https://doi.org/10.3390/nano13101638







