Insights into Structural, Electronic, and Transport Properties of Pentagonal PdSe2 Nanotubes Using First-Principles Calculations
Abstract
1. Introduction
2. Computational Details
3. Results
3.1. Effect of Size on the Structural and Electronic Properties of Pentagonal Palladium Diselenide Nanotubes
3.1.1. Structure and Energetic Stability
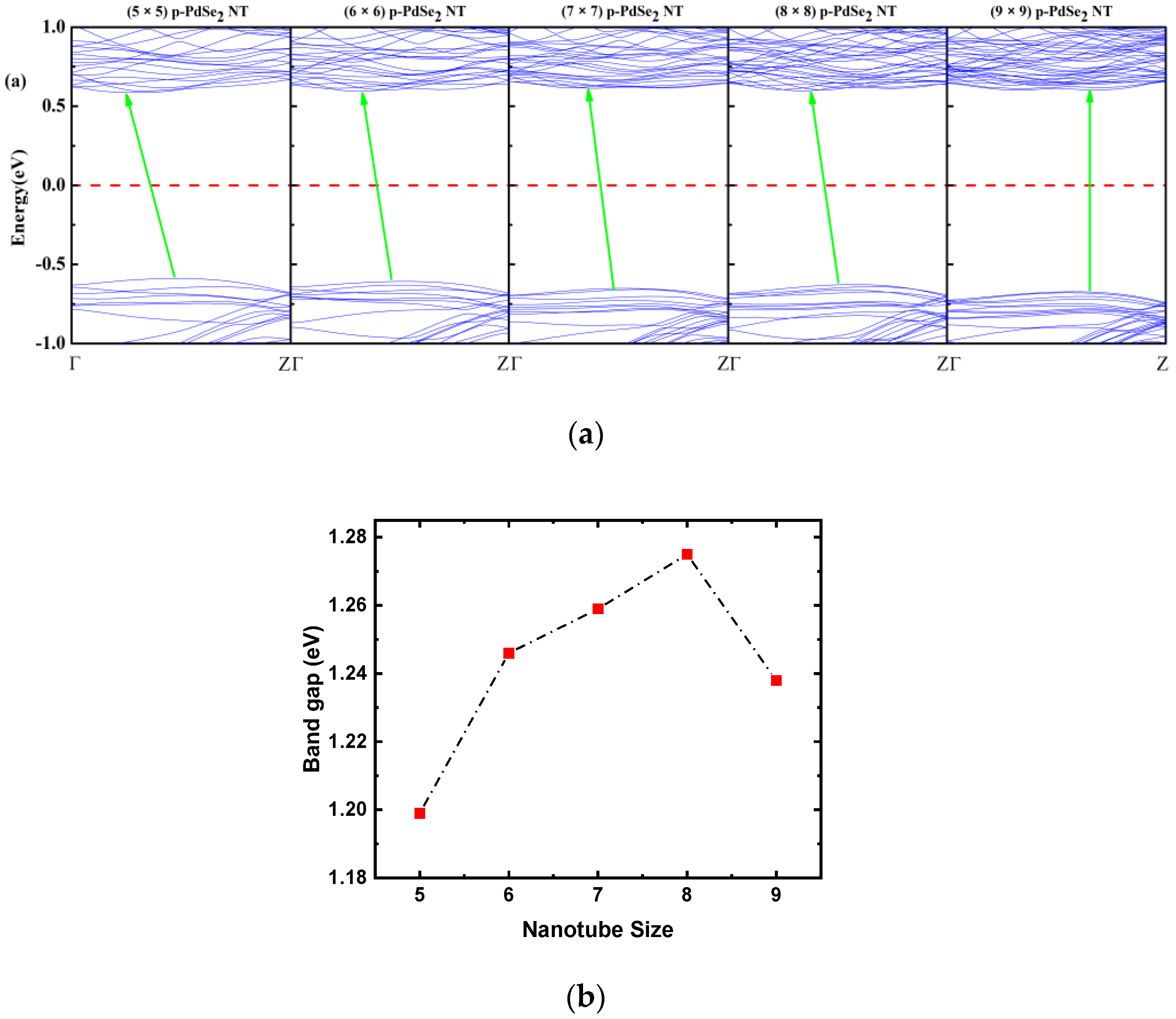
3.1.2. Electronic Properties
3.2. Effect of Strain on the Structural and Electronic Properties of p-PdSe2 Nanotubes
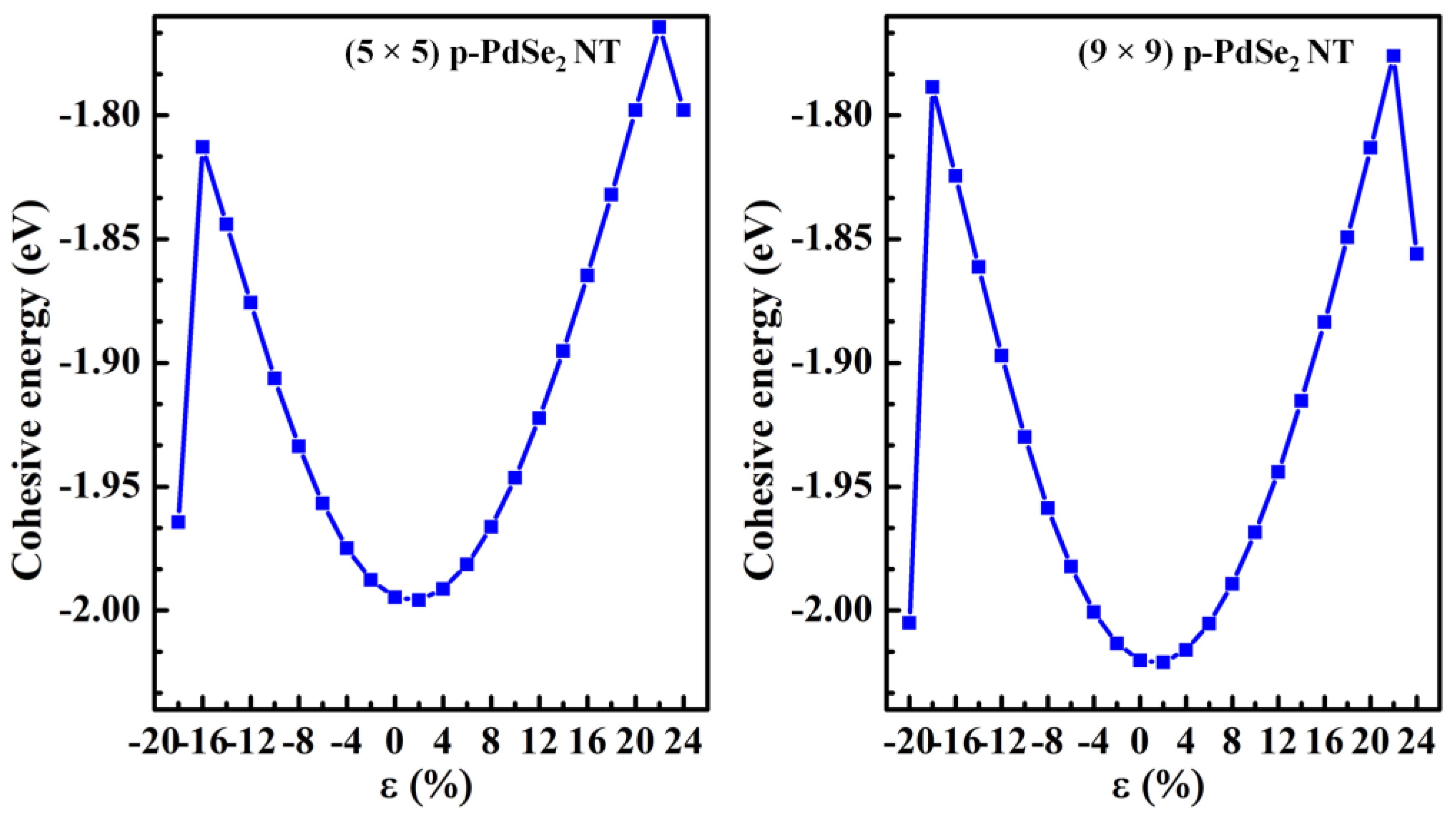
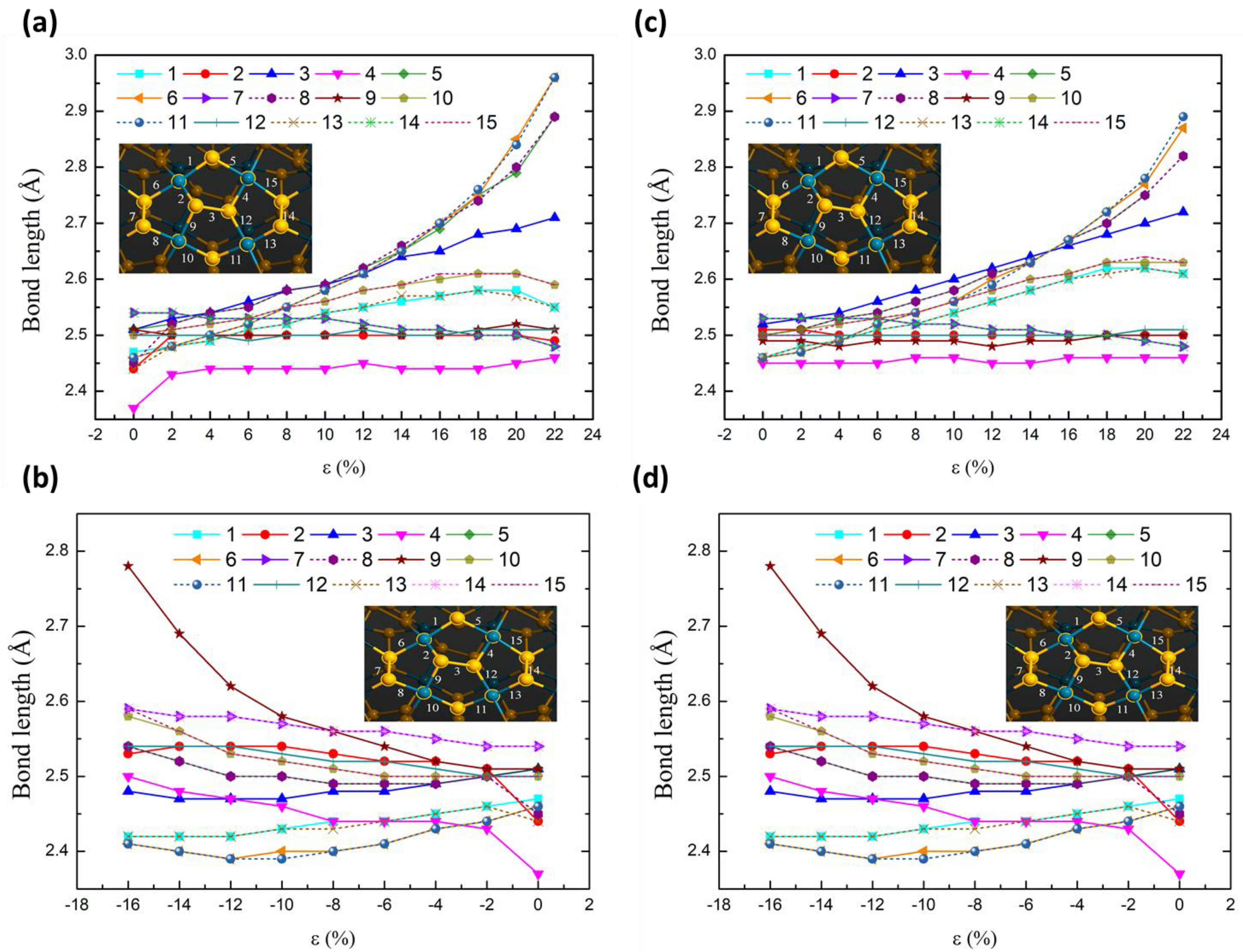
3.2.1. Structure and Energetic Stability
3.2.2. Electronic Properties
3.3. Electron Transport Properties of Pentagonal PdSe2 Nanotubes
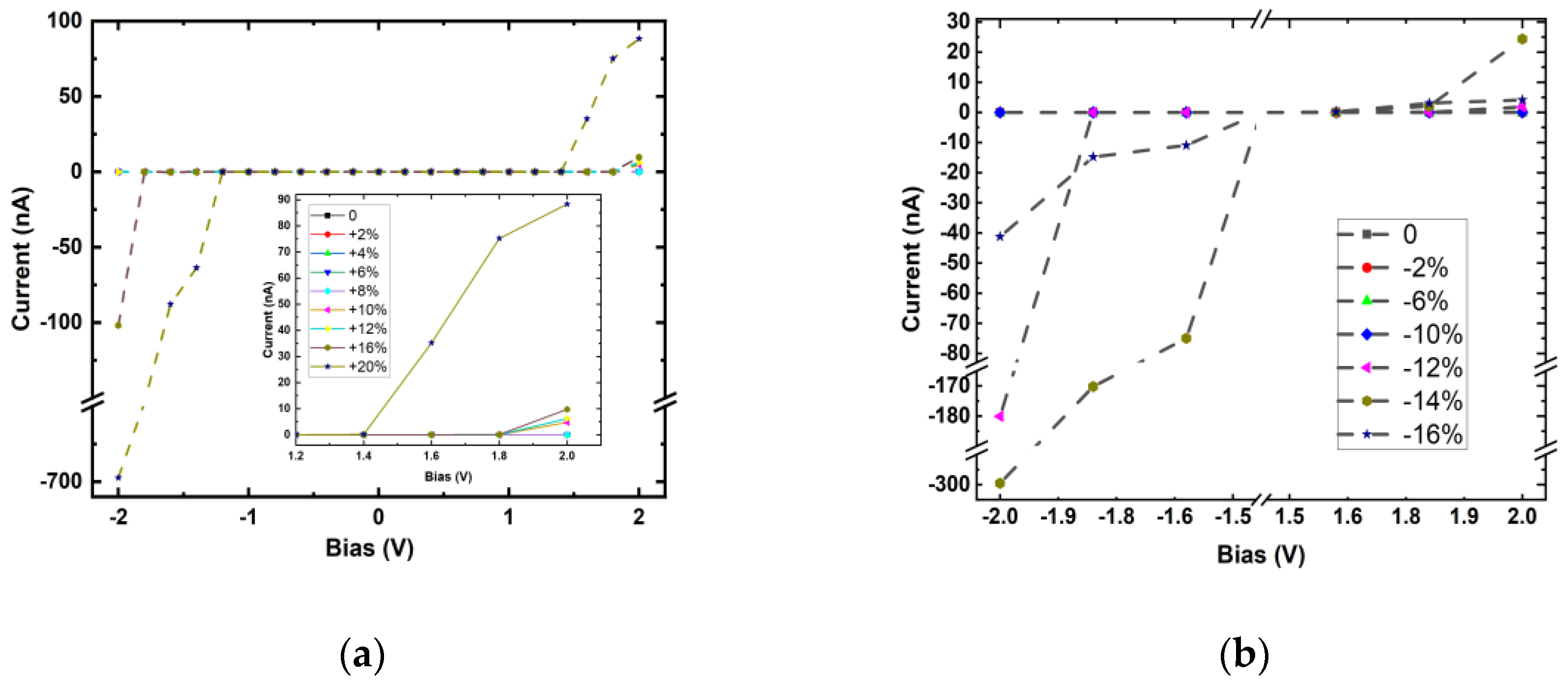
3.3.1. Strain Effect
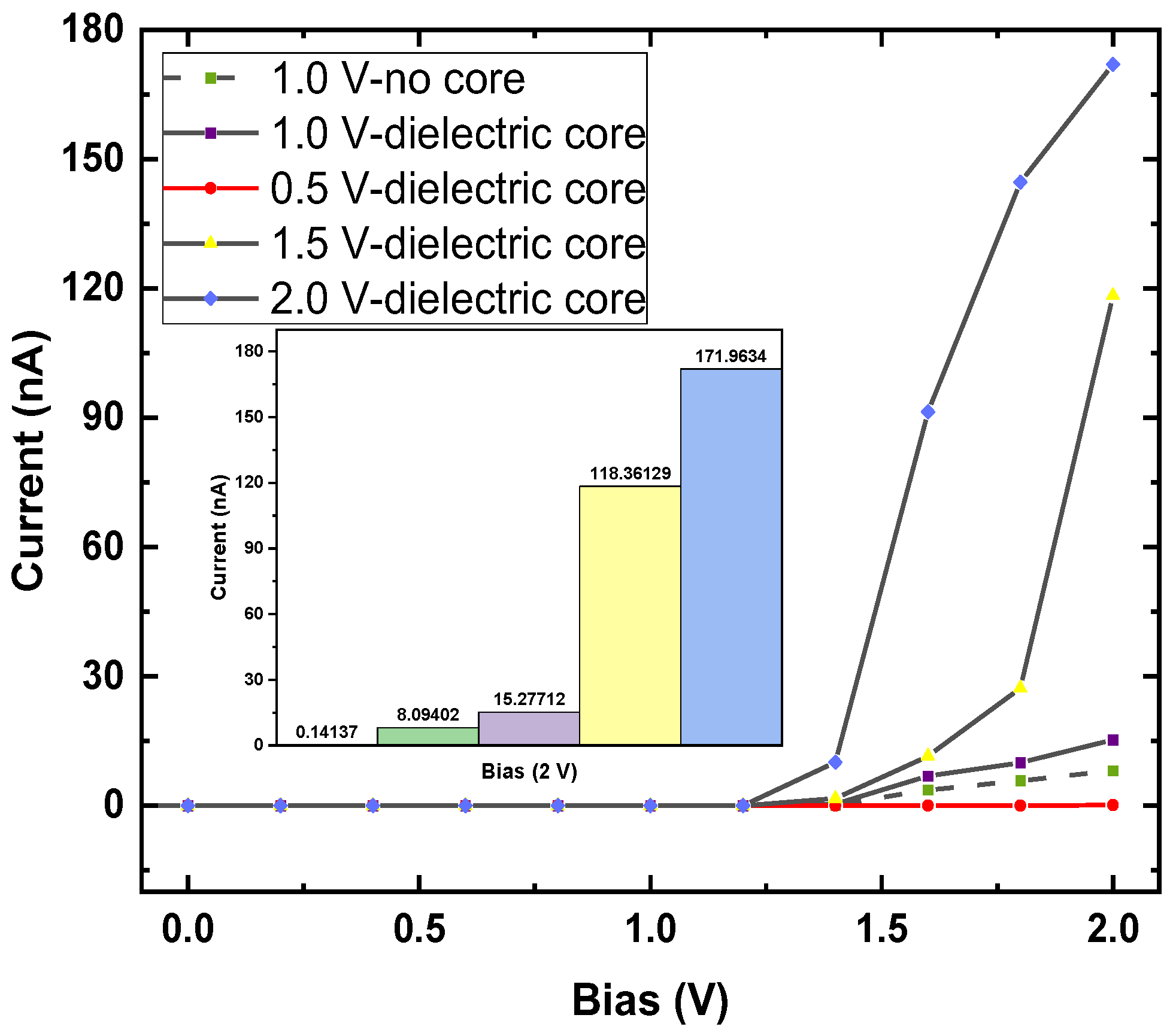
3.3.2. Field Effect
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pang, X.; He, Y.; Jung, J.; Lin, Z. 1D nanocrystals with precisely controlled dimensions, compositions, and architectures. Science 2016, 353, 1268–1272. [Google Scholar] [CrossRef]
- Abuzaid, H.; Williams, N.X.; Franklin, A.D. How good are 2D transistors? An application-specific benchmarking study. Appl. Phys. Lett. 2021, 118, 030501. [Google Scholar] [CrossRef]
- Duan, R.; He, Y.; Zhu, C.; Wang, X.; Zhu, C.; Zhao, X.; Liu, Z. 2D Cairo Pentagonal PdPS: Air-Stable Anisotropic Ternary Semiconductor with High Optoelectronic Performance. Adv. Funct. Mater. 2022, 32, 2113255. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Q. Pentagon-based 2D materials: Classification, properties and applications. Phys. Rep. 2022, 964, 1–42. [Google Scholar] [CrossRef]
- Jing, Y.; Ma, Y.; Wang, Y.; Li, Y.; Heine, T. Ultrathin layers of PdPX (X = S, Se): Two dimensional semiconductors for photocatalytic water splitting. Chem.-A Eur. J. 2017, 23, 13612–13616. [Google Scholar] [CrossRef] [PubMed]
- Lan, Y.S.; Chen, X.R.; Hu, C.E.; Cheng, Y.; Chen, Q.F. Penta-PdX2 (X = S, Se, Te) monolayers: Promising anisotropic thermoelectric materials. J. Mater. Chem. A 2019, 7, 11134–11142. [Google Scholar] [CrossRef]
- Tao, W.L.; Zhao, Y.Q.; Zeng, Z.Y.; Chen, X.R.; Geng, H.Y. Anisotropic thermoelectric materials: Pentagonal PTM2 (M = S, Se, Te). ACS Appl. Mater. Interfaces 2021, 13, 8700–8709. [Google Scholar] [CrossRef]
- Chen, L.; Yang, M.; Kong, F.; Du, W.; Guo, J.; Shu, H. Penta-BCN monolayer with high specific capacity and mobility as a compelling anode material for rechargeable batteries. Phys. Chem. Chem. Phys. 2021, 23, 17693–17702. [Google Scholar] [CrossRef]
- Debbichi, M.; Mallah, A.; Dhaou, M.H.; Lebègue, S. First-Principles Study of Monolayer penta-CoS2 as a Promising Anode Material for Li/Na-ion Batteries. Phys. Rev. Appl. 2021, 16, 024016. [Google Scholar] [CrossRef]
- Goktas, N.I.; Wilson, P.; Ghukasyan, A.; Wagner, D.; McNamee, S.; LaPierre, R.R. Nanowires for energy: A review. Appl. Phys. Rev. 2018, 5, 041305. [Google Scholar] [CrossRef]
- Wang, N.; Cai, Y.; Zhang, R.Q. Growth of nanowires. Mater. Sci. Eng. R Rep. 2008, 60, 1–51. [Google Scholar] [CrossRef]
- Tien, N.T.; Thao, P.T.B.; Thuan, L.V.P.; Chuong, D.H. First-principles study of electronic and optical properties of defective sawtooth penta-graphene nanoribbons. Comput. Mater. Sci. 2022, 203, 111065. [Google Scholar] [CrossRef]
- Tien, N.T.; Thao, P.T.B.; Phuc, V.T.; Ahuja, R. Influence of edge termination on the electronic and transport properties of sawtooth penta-graphene nanoribbons. J. Phys. Chem. Solids 2020, 146, 109528. [Google Scholar] [CrossRef]
- Mi, T.Y.; Huy, H.A.; Tien, N.T. A comparison study of the structural, electronic and electronic transport properties of nanoribbons based on Penta-graphene, Penta-P2C and Penta-SiC2. Mater. Today Commun. 2022, 32, 103912. [Google Scholar] [CrossRef]
- Quijano-Briones, J.J.; Fernández-Escamilla, H.N.; Tlahuice-Flores, A. Chiral penta-graphene nanotubes: Structure, bonding and electronic properties. Comput. Theor. Chem. 2017, 1108, 70–75. [Google Scholar] [CrossRef]
- De Sousa, J.M.; Aguiar, A.L.; Girao, E.C.; Fonseca, A.F.; Coluci, V.R.; Galvao, D.S. Mechanical properties of single-walled penta-graphene-based nanotubes: A DFT and classical molecular dynamics study. Chem. Phys. 2021, 547, 111187. [Google Scholar] [CrossRef]
- Palacios, L.R.G.; Bracamonte, A.G. Development of nano-and microdevices for the next generation of biotechnology, wearables and miniaturized instrumentation. RSC Adv. 2022, 12, 12806–12822. [Google Scholar] [CrossRef]
- Byakodi, M.; Shrikrishna, N.S.; Sharma, R.; Bhansali, S.; Mishra, Y.; Kaushik, A.; Gandhi, S. Emerging 0D, 1D, 2D, and 3D nanostructures for efficient point-of-care biosensing. Biosens. Bioelectron. X 2022, 12, 100284. [Google Scholar] [CrossRef]
- Viršek, M.; Jesih, A.; Milošević, I.; Damnjanović, M.; Remškar, M. Raman scattering of the MoS2 and WS2 single nanotubes. Surf. Sci. 2007, 601, 2868–2872. [Google Scholar] [CrossRef]
- Milošević, I.; Nikolić, B.; Dobardžić, E.; Damnjanović, M.; Popov, I.; Seifert, G. Electronic properties and optical spectra of MoS2 and WS2 nanotubes. Phys. Rev. B 2007, 76, 233414. [Google Scholar] [CrossRef]
- Di Bartolomeo, A. Emerging 2D materials and their van der Waals heterostructures. Nanomaterials 2020, 10, 579. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, G.D.; Oyedele, A.D.; Haglund, A.; Ko, W.; Liang, L.; Puretzky, A.A.; Li, A.P. Atomically precise PdSe2 pentagonal nanoribbons. ACS Nano 2020, 14, 1951–1957. [Google Scholar] [CrossRef]
- Tien, N.T.; Thao, P.T.B.; Khanh, N.D. Structural, magneto-electronic, and electric transport properties of pentagonal PdSe2 nanoribbons: A first-principles study. Surf. Sci. 2023, 728, 122206. [Google Scholar] [CrossRef]
- Ouyang, Y.; Yoon, Y.; Fodor, J.K.; Guo, J. Comparison of performance limits for carbon nanoribbon and carbon nanotube transistors. Appl. Phys. Lett. 2006, 89, 203107. [Google Scholar] [CrossRef]
- Kim, W.Y.; Choi, Y.C.; Kim, K.S. Understanding structures and electronic/spintronic properties of single molecules, nanowires, nanotubes, and nanoribbons towards the design of nanodevices. J. Mater. Chem. 2008, 18, 4510–4521. [Google Scholar] [CrossRef]
- Gardea, F.; Lagoudas, D.C. Characterization of electrical and thermal properties of carbon nanotube/epoxy composites. Compos. Part B Eng. 2014, 56, 611–620. [Google Scholar] [CrossRef]
- Zhang, X.; Cui, H.; Gui, Y.; Tang, J. Mechanism and application of carbon nanotube sensors in SF6 decomposed production detection: A review. Nanoscale Res. Lett. 2017, 12, 1–12. [Google Scholar] [CrossRef]
- Javey, A.; Guo, J.; Wang, Q.; Lundstrom, M.; Dai, H. Ballistic carbon nanotube field-effect transistors. Nature 2003, 424, 654–657. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Stokbro, K. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter 2019, 32, 015901. [Google Scholar] [CrossRef] [PubMed]
- Stokbro, K.; Petersen, D.E.; Smidstrup, S.; Blom, A.; Ipsen, M.; Kaasbjerg, K. Semiempirical model for nanoscale device simulations. Phys. Rev. B 2010, 82, 075420. [Google Scholar] [CrossRef]
- Haug, H.; Jauho, A.P. Quantum Kinetics in Transport and Optics of Semiconductors; Springer: Berlin/Heidelberg, Germany, 2008; Volume 2. [Google Scholar]
- Wang, Z.; Cao, X.; Qiao, C.; Zhang, R.J.; Zheng, Y.X.; Chen, L.Y.; Su, W.S. Novel penta-graphene nanotubes: Strain-induced structural and semiconductor–metal transitions. Nanoscale 2017, 9, 19310–19317. [Google Scholar] [CrossRef] [PubMed]
- Oyedele, A.D.; Yang, S.; Feng, T.; Haglund, A.V.; Gu, Y.; Puretzky, A.A.; Xiao, K. Defect-mediated phase transformation in anisotropic two-dimensional PdSe2 crystals for seamless electrical contacts. J. Am. Chem. Soc. 2019, 141, 8928–8936. [Google Scholar] [CrossRef]
- Kuklin, A.V.; Ågren, H.; Avramov, P.V. Structural stability of single layer PdSe2 with pentagonal puckered morphology and its nanotubes. Phys. Chem. Chem. Phys. 2020, 22, 8289–8295. [Google Scholar] [CrossRef]
- Raval, D.; Gupta, S.K.; Gajjar, P.N.; Ahuja, R. Strain modulating electronic band gaps and SQ efficiencies of semiconductor 2D PdQ2 (Q = S, Se) monolayer. Sci. Rep. 2022, 12, 2964. [Google Scholar] [CrossRef]
- Tai, Y.; Xia, X.; Xie, M.; Guo, X.; Xu, L.; Huang, Y.; Zhang, S. Electronic Structure and Sensing Performance of NO2 on 2D PdSe2 Doped with B, N, Al, and P Atoms: A First-Principles Study. J. Electron. Mater. 2023, 52, 1258–1265. [Google Scholar] [CrossRef]
- Wang, H.; Ding, N.; Jiang, T.; Zhang, F.; Zhao, X.; Liu, W.; Zaïri, F. Investigation on electronic and mechanical properties of penta-graphene nanotubes. J. Mater. Sci. 2020, 55, 14336–14344. [Google Scholar] [CrossRef]
- Ryu, G.H.; Zhu, T.; Chen, J.; Sinha, S.; Shautsova, V.; Grossman, J.C.; Warner, J.H. Striated 2D lattice with sub-nm 1D etch channels by controlled thermally induced phase transformations of PdSe2. Adv. Mater. 2019, 31, 1904251. [Google Scholar] [CrossRef]
- Zhang, G.; Amani, M.; Chaturvedi, A.; Tan, C.; Bullock, J.; Song, X.; Javey, A. Optical and electrical properties of two-dimensional palladium diselenide. Appl. Phys. Lett. 2019, 114, 253102. [Google Scholar] [CrossRef]
- Qin, D.; Yan, P.; Ding, G.; Ge, X.; Song, H.; Gao, G. Monolayer PdSe2: A promising two-dimensional thermoelectric material. Sci. Rep. 2018, 8, 2764. [Google Scholar] [CrossRef]
- Lu, P.; Wu, X.; Guo, W.; Zeng, X.C. Strain-dependent electronic and magnetic properties of MoS2 monolayer, bilayer, nanoribbons and nanotubes. Phys. Chem. Chem. Phys. 2012, 14, 13035–13040. [Google Scholar] [CrossRef] [PubMed]
- Van On, V.; Thanh, L.N.; Tien, N.T. The electronic properties and electron transport of sawtooth penta-graphene nanoribbon under uniaxial strain: Ab-initio study. Philos. Mag. 2020, 100, 1834–1848. [Google Scholar] [CrossRef]
- Blundo, E.; Felici, M.; Yildirim, T.; Pettinari, G.; Tedeschi, D.; Miriametro, A.; Polimeni, A. Evidence of the direct-to-indirect band gap transition in strained two-dimensional WS2, MoS2, and WSe2. Phys. Rev. Res. 2020, 2, 012024. [Google Scholar] [CrossRef]
- Qu, T.Y.; Sun, Y.; Chen, M.L.; Liu, Z.B.; Zhu, Q.B.; Wang, B.W.; Sun, D.M. A flexible carbon nanotube sen-memory device. Adv. Mater. 2020, 32, 1907288. [Google Scholar] [CrossRef] [PubMed]
- Loh, O.Y.; Espinosa, H.D. Nanoelectromechanical contact switches. Nat. Nanotechnol. 2012, 7, 283–295. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.E.; Zhang, Y.; Dubonos, S.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Martel, R.; Schmidt, T.; Shea, H.R.; Hertel, T.; Avouris, P. Single-and multi-wall carbon nanotube field-effect transistors. Appl. Phys. Lett. 1998, 73, 2447–2449. [Google Scholar] [CrossRef]
- Ortiz-Conde, A.; Sánchez, F.G.; Liou, J.J.; Cerdeira, A.; Estrada, M.; Yue, Y. A review of recent MOSFET threshold voltage extraction methods. Microelectron. Reliab. 2002, 42, 583–596. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, X.; Raju, S.; Lin, Z.; Villaroman, D.; Huang, B.; Chai, Y. Low voltage and high ON/OFF ratio field-effect transistors based on CVD MoS2 and ultra-high-k gate dielectric PZT. Nanoscale 2015, 7, 8695–8700. [Google Scholar] [CrossRef]

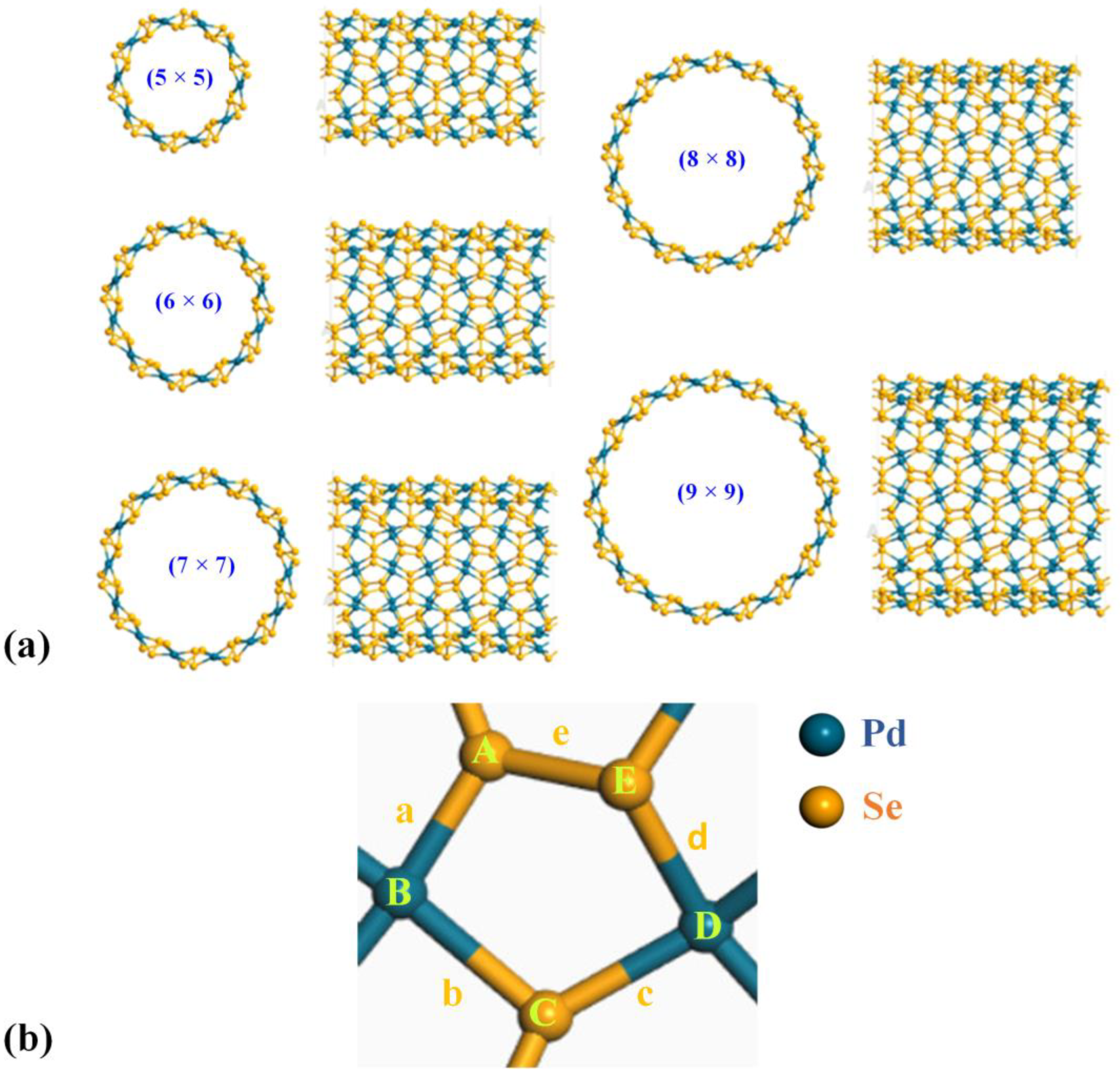


| (5 × 5) | (6 × 6) | (7 × 7) | (8 × 8) | (9 × 9) |
|---|---|---|---|---|
| −1.995 eV/atom | −2.006 eV/atom | −2.013 eV/atom | −2.017 eV/atom | −2.020 eV/atom |
| (n × n) | a | b | c | d | e | A | B | C | D | E |
|---|---|---|---|---|---|---|---|---|---|---|
| (5 × 5) | 2.51 | 2.50 | 2.51 | 2.50 | 2.46 | 92.72 | 98.72 | 111.88 | 77.32 | 104.74 |
| (6 × 6) | 2.50 | 2.50 | 2.51 | 2.50 | 2.46 | 93.60 | 98.35 | 112.06 | 78.59 | 103.21 |
| (7 × 7) | 2.50 | 2.50 | 2.51 | 2.50 | 2.46 | 94.23 | 98.05 | 112.25 | 79.43 | 102.16 |
| (8 × 8) | 2.49 | 2.50 | 2.52 | 2.50 | 2.46 | 94.70 | 97.96 | 112.33 | 80.14 | 101.56 |
| (9 × 9) | 2.49 | 2.50 | 2.52 | 2.50 | 2.46 | 95.23 | 97.86 | 112.34 | 80.84 | 100.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tien, N.T.; Thao, P.T.B.; Dang, N.H.; Khanh, N.D.; Dien, V.K. Insights into Structural, Electronic, and Transport Properties of Pentagonal PdSe2 Nanotubes Using First-Principles Calculations. Nanomaterials 2023, 13, 1728. https://doi.org/10.3390/nano13111728
Tien NT, Thao PTB, Dang NH, Khanh ND, Dien VK. Insights into Structural, Electronic, and Transport Properties of Pentagonal PdSe2 Nanotubes Using First-Principles Calculations. Nanomaterials. 2023; 13(11):1728. https://doi.org/10.3390/nano13111728
Chicago/Turabian StyleTien, Nguyen Thanh, Pham Thi Bich Thao, Nguyen Hai Dang, Nguyen Duy Khanh, and Vo Khuong Dien. 2023. "Insights into Structural, Electronic, and Transport Properties of Pentagonal PdSe2 Nanotubes Using First-Principles Calculations" Nanomaterials 13, no. 11: 1728. https://doi.org/10.3390/nano13111728
APA StyleTien, N. T., Thao, P. T. B., Dang, N. H., Khanh, N. D., & Dien, V. K. (2023). Insights into Structural, Electronic, and Transport Properties of Pentagonal PdSe2 Nanotubes Using First-Principles Calculations. Nanomaterials, 13(11), 1728. https://doi.org/10.3390/nano13111728







