Transport Characteristics of Silicon Multi-Quantum-Dot Transistor Analyzed by Means of Experimental Parametrization Based on Single-Hole Tunneling Model
Abstract
:1. Introduction
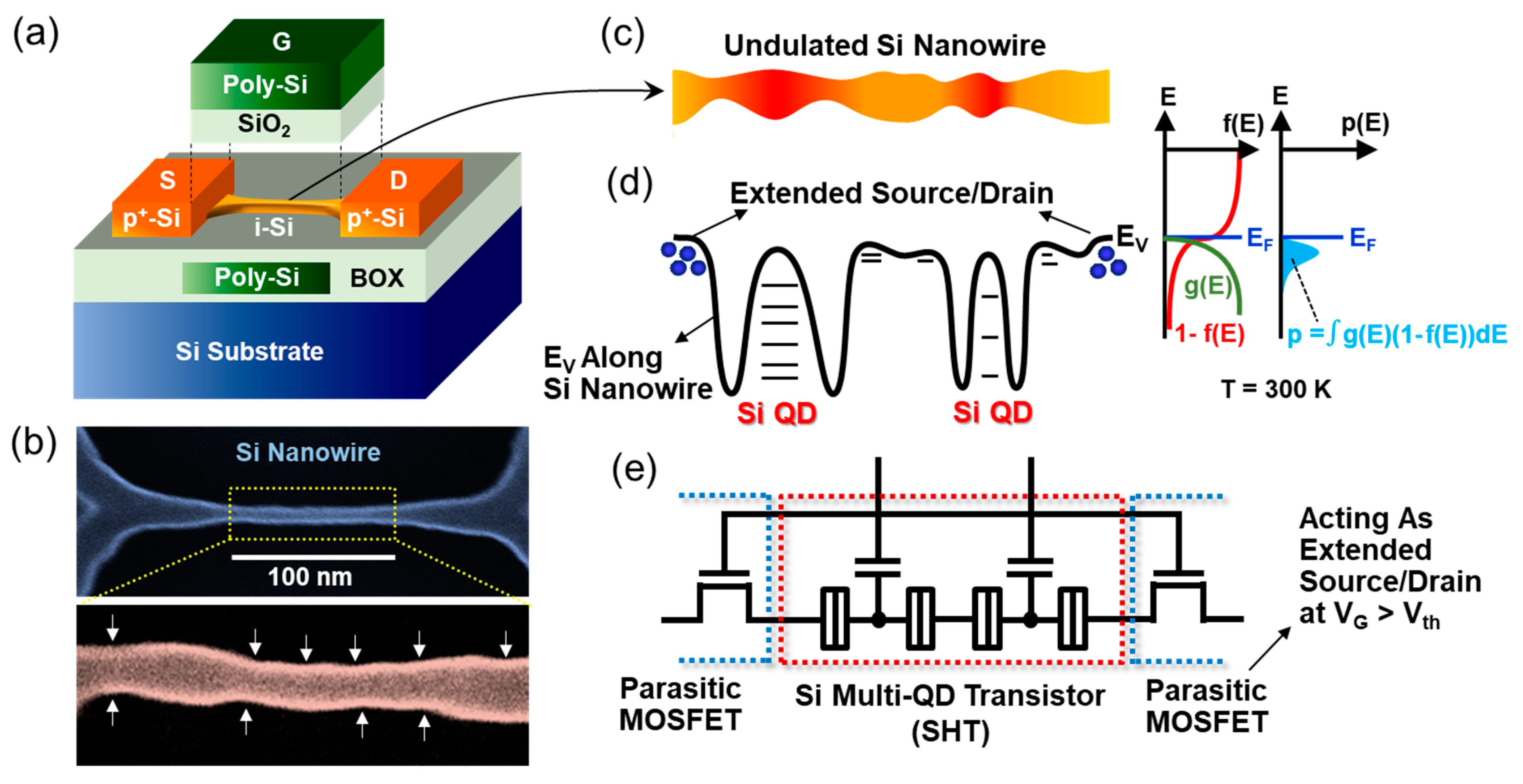
2. Experimental Section
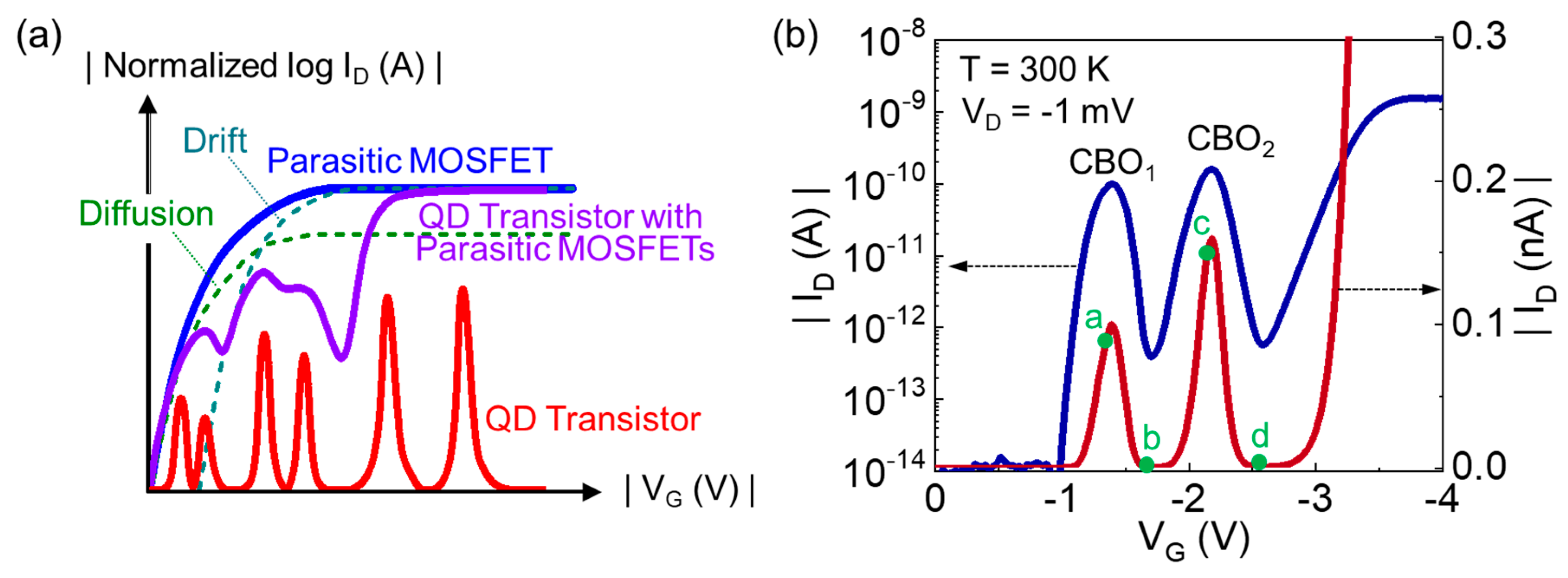
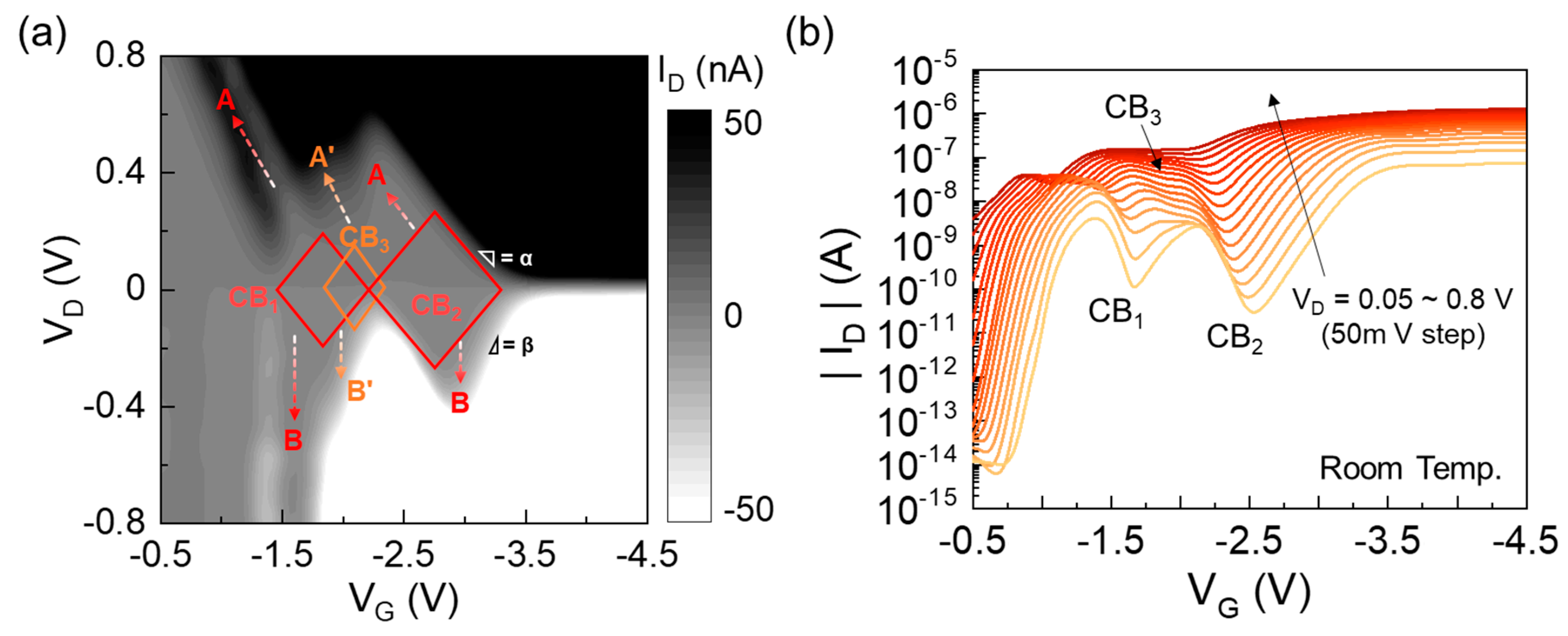
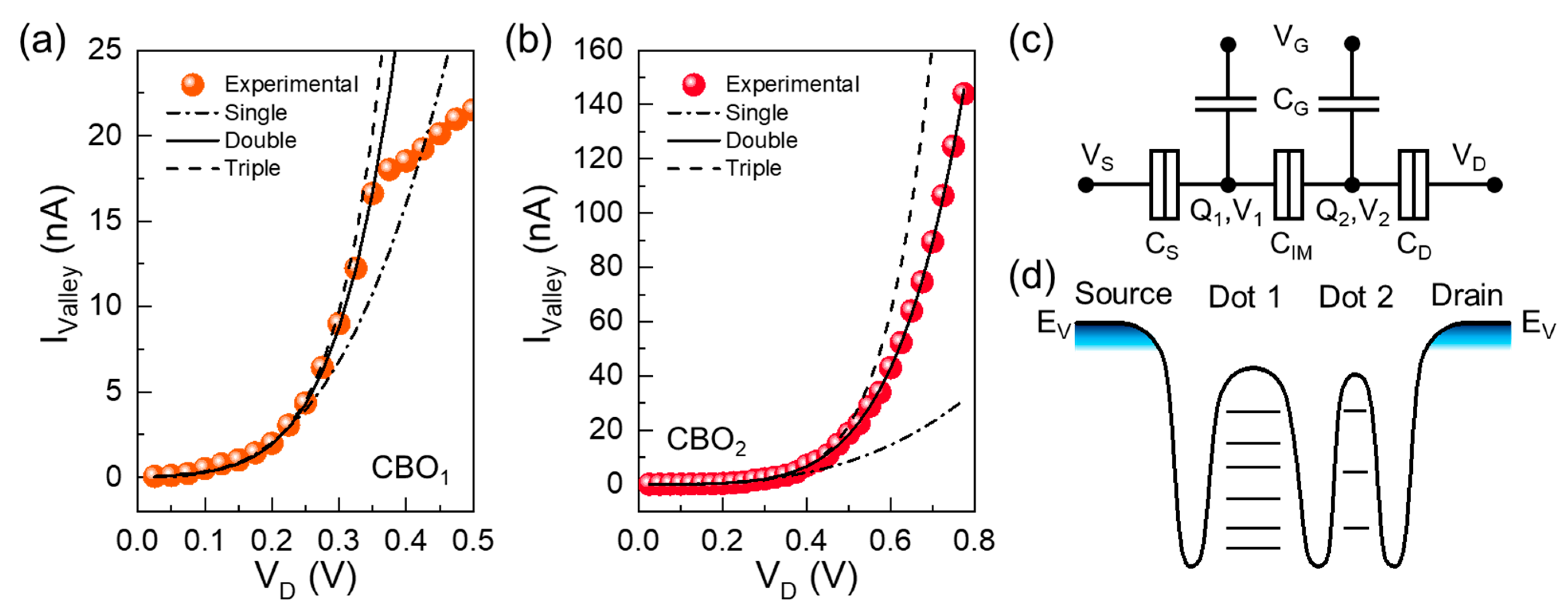
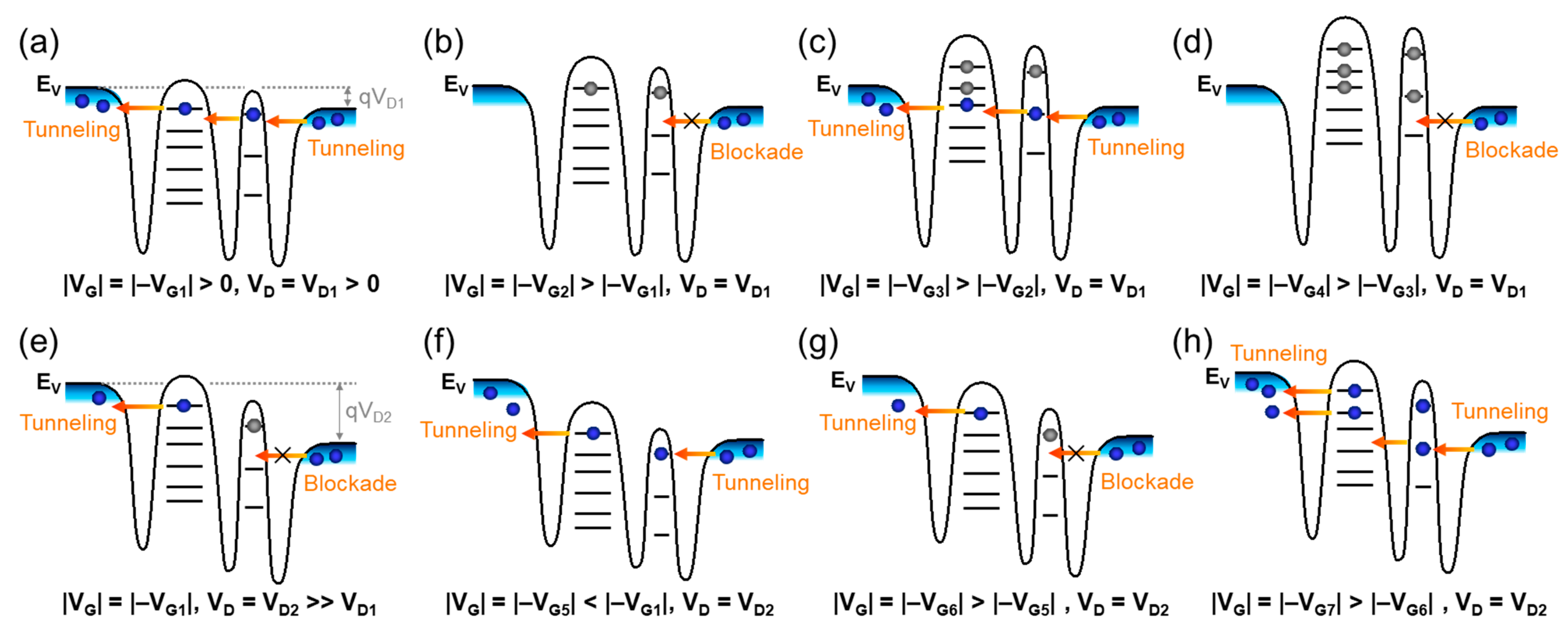
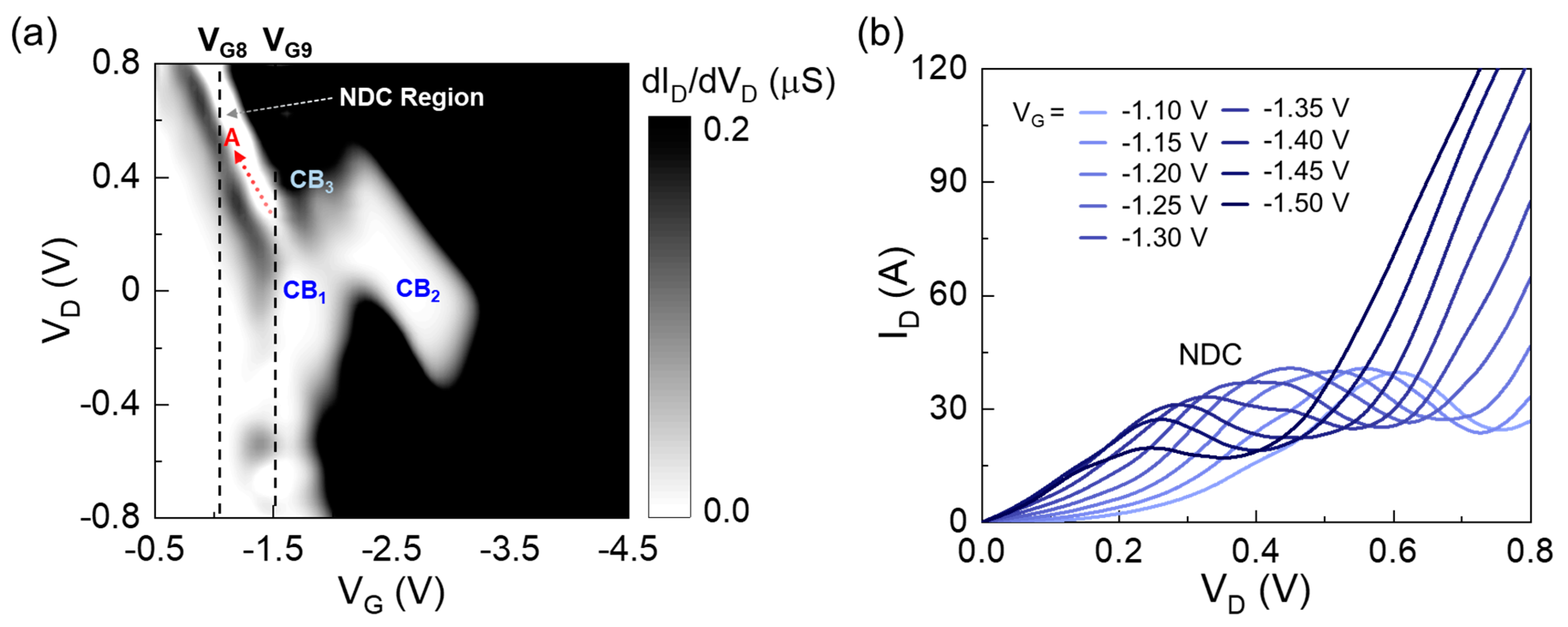
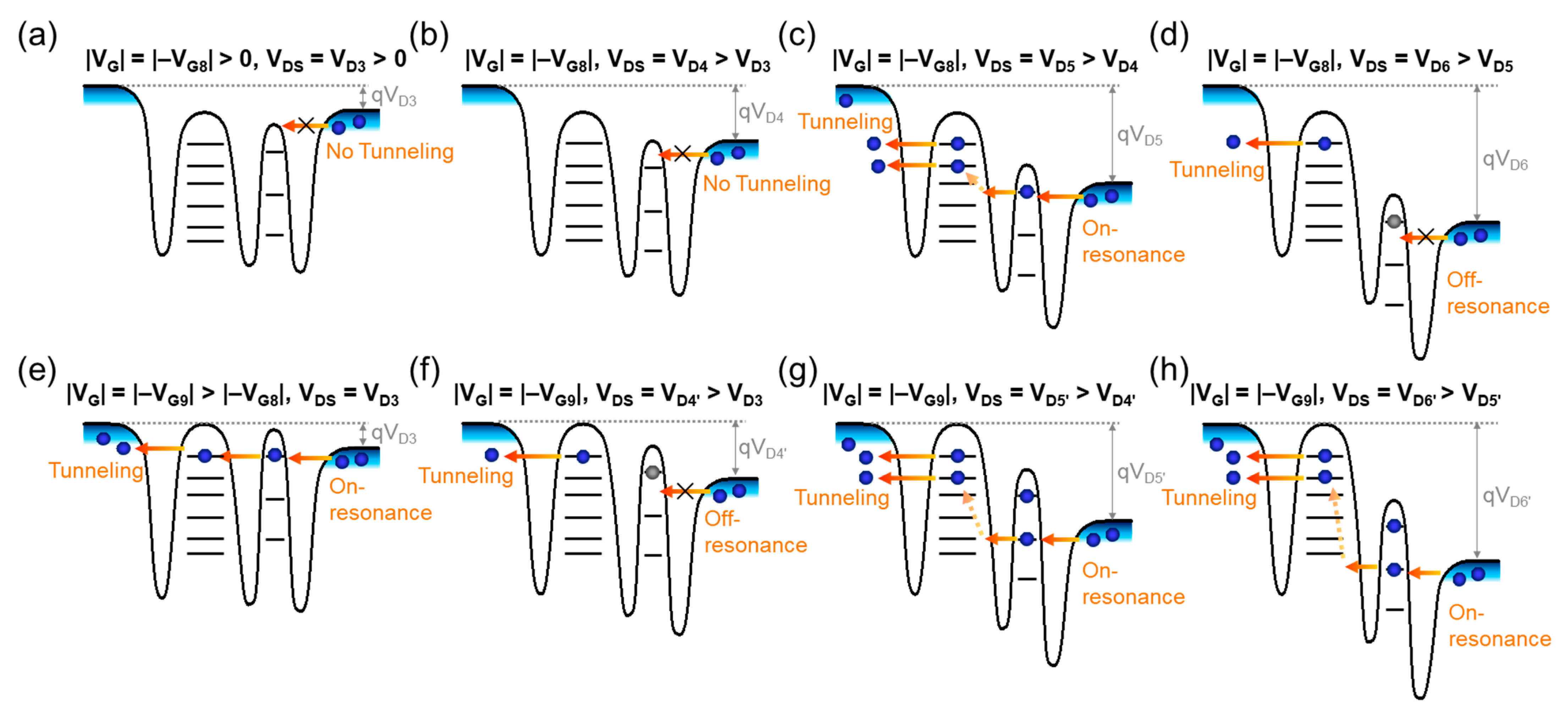
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Patra, B.; Incandela, R.M.; van Dijk, J.P.G.; Homulle, H.A.R.; Song, L.; Shahmohammadi, M.; Staszewski, R.B.; Vladimirescu, A.; Babaie, M.; Sebastiano, F.; et al. Cryo-CMOS Circuits and Systems for Quantum Computing Applications. IEEE J. Solid State Circuits 2018, 53, 309–321. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Zalba, M.F.; de Franceschi, S.; Charbon, E.; Meunier, T.; Vinet, M.; Dzurak, A.S. Scaling silicon-based quantum computing using CMOS technology. Nat. Electron. 2021, 4, 872–884. [Google Scholar] [CrossRef]
- Veldhorst, M.; Eenink, H.G.J.; Yang, C.H.; Dzurak, A.S. Silicon CMOS architecture for a spin-based quantum computer. Nat. Commun. 2017, 8, 1766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, X.; Patra, B.; van Dijk, J.P.G.; Samkharadze, N.; Subramanian, S.; Corna, A.; Paquelet Wuetz, B.; Jeon, C.; Sheikh, F.; Juarez-Hernandez, E.; et al. CMOS-based cryogenic control of silicon quantum circuits. Nature 2021, 593, 205–210. [Google Scholar] [CrossRef] [PubMed]
- Mills, A.R.; Zajac, D.M.; Gullans, M.J.; Schupp, F.J.; Hazard, T.M.; Petta, J.R. Shuttling a single charge across a one-dimensional array of silicon quantum dots. Nat. Commun. 2019, 10, 1063. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lee, Y.; Song, E.B.; Wang, K.L.; Hiramoto, T. Gate-Tunable Selective Operation of Single Electron/Hole Transistor Modes in a Silicon Single Quantum Dot at Room Temperature. Appl. Phys. Lett. 2013, 102, 083504. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y.; Kim, C. Extraordinary Transport Characteristics and Multivalue Logic Functions in a Silicon-Based Negative-Differential Transconductance Device. Sci. Rep. 2017, 7, 11065. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.; Lee, J.W.; Lee, S.; Hiramoto, T.; Wang, K.L. Reconfigurable Multivalue Logic Functions of a Silicon Ellipsoidal Quantum-Dot Transistor Operating at Room Temperature. ACS Nano 2021, 15, 18483–18493. [Google Scholar] [CrossRef]
- Kim, C.; Lee, Y.; Lee, S. Systematic Modulation of Negative-Differential Transconductance Effects for Gated p+-i-n+ Silicon Ultra-Thin Body Transistor. J. Appl. Phys. 2017, 121, 124504. [Google Scholar] [CrossRef]
- Kobayashi, M.; Hiramoto, T. Large Coulomb-Blockade Oscillations and Negative Differential Conductance in Silicon Single-Electron Transistors with [100]- and [110]-Directed Channels at Room Temperature. Jpn. J. Appl. Phys. 2007, 46, 24–27. [Google Scholar] [CrossRef]
- Kobayashi, M.; Hiramoto, T. Experimental Study on Quantum Confinement Effects in Silicon Nanowire Metal-Oxide-Semiconductor Field-Effect Transistors and Single-Electron Transistors. J. Appl. Phys. 2008, 103, 053709. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Im, H.; Hiramoto, T. Multiple Logic Functions from Extended Blockade Region in a Silicon Quantum-Dot Transistor. J. Appl. Phys. 2015, 117, 064501. [Google Scholar] [CrossRef]
- Andreev, M.; Seo, S.; Jung, K.-S.; Park, J.-H. Looking Beyond 0 and 1: Principles and Technology of Multi-Valued Logic Devices. Adv. Mater. 2022, 34, 2108830. [Google Scholar] [CrossRef] [PubMed]
- Nishiguchi, K.; Ono, Y.; Fujiwara, A.; Inokawa, H.; Takahashi, Y. Stochastic Data Processing Circuit Based on Single Electrons Using Nanoscale Field-Effect Transistors. Appl. Phys. Lett. 2008, 92, 062105. [Google Scholar] [CrossRef]
- Nishiguchi, K.; Fujiwara, A. Single-electron circuit for stochastic data processing using nano-MOSFETs. In Proceedings of the 2007 IEEE International Electron Devices Meeting, Washington, DC, USA, 10–12 December 2007; pp. 791–794. [Google Scholar]
- Mitic, M.; Cassidy, M.C.; Petersson, K.D.; Starrett, R.P.; Gauja, E.; Brenner, R.; Clark, R.G.; Dzurak, A.S.; Yang, C.; Jamieson, D.N. Demonstration of a Silicon-Based Quantum Cellular Automata Cell. Appl. Phys. Lett. 2006, 89, 013503. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Hiramoto, T. Transport Behaviors and Mechanisms in Cuspidal Blockade Region for Silicon Single-Hole Transistor. Curr. Appl. Phys. 2014, 14, 428–432. [Google Scholar] [CrossRef]
- Fujiwara, A.; Takahashi, Y.; Murase, K. Observation of Single Electron-Hole Recombination and Photon-Pumped Current in an Asymmetric Si Single-Electron Transistor. Phys. Rev. Lett. 1997, 78, 1532–1535. [Google Scholar] [CrossRef]
- Kobayashi, M.; Saitoh, M.; Hiramoto, T. Large Temperature Dependence of Coulomb Blockade Oscillations in Room-Temperature-Operating Silicon Single-Hole Transistor. Jpn. J. Appl. Phys. 2006, 45, 6157–6161. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y.; Song, E.B.; Hiramoto, T. Observation of Single Electron Transport via Multiple Quantum States of a Silicon Quantum Dot at Room Temperature. Nano Lett. 2014, 14, 71–77. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.H.; Son, H.S.; Lee, S. Reduced Electron Temperature in Silicon Multi-Quantum-Dot Single-Electron Tunneling Devices. Nanomaterials 2022, 12, 603. [Google Scholar] [CrossRef]
- Geerligs, L.J.; Averin, D.V.; Mooij, J.E. Observation of macroscopic quantum tunneling through the Coulomb energy barrier. Phys. Rev. Lett. 1990, 65, 3037–3040. [Google Scholar] [CrossRef] [Green Version]
- Miyaji, K.; Saitoh, M.; Hiramoto, T. Compact Analytical Model for Room-Temperature-Operating Silicon Single-Electron Transistors with Discrete Quantum Energy Levels. IEEE Trans. Nanotechnol. 2006, 5, 167–173. [Google Scholar] [CrossRef]
- Likharev, K.K. Single-electron devices and their applications. Proc. IEEE 1999, 87, 606–632. [Google Scholar] [CrossRef] [Green Version]
- Leobandung, E.; Guo, L.; Wang, Y.; Chou, S.Y. Observation of quantum effects and Coulomb blockade in silicon quantum-dot transistors at temperatures over 100 K. Appl. Phys. Lett. 1995, 67, 938–940. [Google Scholar] [CrossRef] [Green Version]
- Yasuo, T.; Yukinori, O.; Akira, F.; Hiroshi, I. Silicon single-electron devices. J. Phys. Condens. Matter 2002, 14, R995. [Google Scholar]
- Lim, W.H.; Zwanenburg, F.A.; Huebl, H.; Möttönen, M.; Chan, K.W.; Morello, A.; Dzurak, A.S. Observation of the single-electron regime in a highly tunable silicon quantum dot. Appl. Phys. Lett. 2009, 95, 242102. [Google Scholar] [CrossRef] [Green Version]
- Rossi, A.; Ferrus, T.; Lin, W.; Kodera, T.; Williams, D.A.; Oda, S. Detection of variable tunneling rates in silicon quantum dots. Appl. Phys. Lett. 2011, 98, 133506. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lee, Y.; Song, E.B.; Hiramoto, T. Modulation of Peak-to-Valley Current Ratio of Coulomb Blockade Oscillations in Si Single Hole Transistors. Appl. Phys. Lett. 2013, 103, 103502. [Google Scholar] [CrossRef]
- Wolf, C.R.; Thonke, K.; Sauer, R. Single-electron transistors based on self-assembled silicon-on-insulator quantum dots. Appl. Phys. Lett. 2010, 96, 142108. [Google Scholar] [CrossRef]
- Cheam, D.D.; Karre, P.S.K.; Palard, M.; Bergstrom, P.L. Mass Production of Room Temperature Single Electron Transistors using Step & Flash Imprint Lithography and Lift-Off Technique. In Proceedings of the 2008 8th IEEE Conference on Nanotechnology, Arlington, TX, USA, 18–21 August 2008; pp. 175–178. [Google Scholar]
- Fu, Y.; Dutta, A.; Willander, M.; Oda, S. Carrier conduction in a Si-nanocrystal-based single-electron transistor-I. Effect of gate bias. Superlattices Microstruct. 2000, 28, 177–187. [Google Scholar] [CrossRef]
- Saitoh, M.; Majima, H.; Hiramoto, T. Tunneling Barrier Structures in Room-Temperature Operating Silicon Single-Electron and Single-Hole Transistors. Jpn. J. Appl. Phys. 2003, 42, 2426. [Google Scholar] [CrossRef]
- Ishikuro, H.; Hiramoto, T. On the origin of tunneling barriers in silicon single electron and single hole transistors. Appl. Phys. Lett. 1999, 74, 1126–1128. [Google Scholar] [CrossRef]
- Uematsu, M.; Kageshima, H.; Shiraishi, K.; Nagase, M.; Horiguchi, S.; Takahashi, Y. Two-dimensional simulation of pattern-dependent oxidation of silicon nanostructures on silicon-on-insulator substrates. Solid State Electron. 2004, 48, 1073–1078. [Google Scholar] [CrossRef]
- Ono, Y.; Takahashi, Y.; Yamazaki, K.; Nagase, M.; Namatsu, H.; Kurihara, K.; Murase, K. Fabrication method for IC-oriented Si single-electron transistors. IEEE Trans. Electron Devices 2000, 47, 147–153. [Google Scholar] [CrossRef]
- Horiguchi, S.; Nagase, M.; Shiraishi, K.; Kageshima, H.; Takahashi, Y.; Murase, K. Mechanism of Potential Profile Formation in Silicon Single-Electron Transistors Fabricated Using Pattern-Dependent Oxidation. Jpn. J. Appl. Phys. 2001, 40, L29. [Google Scholar] [CrossRef]
- Nagase, M.; Horiguchi, S.; Fujiwara, A.; Ono, Y.; Yamazaki, K.; Namatsu, H.; Takahashi, Y. Single-electron devices formed by pattern-dependent oxidation: Microscopic structural evaluation. Appl. Surf. Sci. 2002, 190, 144–150. [Google Scholar] [CrossRef]
- Fujiwara, A.; Inokawa, H.; Yamazaki, K.; Namatsu, H.; Takahashi, Y.; Zimmerman, N.M.; Martin, S.B. Single electron tunneling transistor with tunable barriers using silicon nanowire metal-oxide-semiconductor field-effect transistor. Appl. Phys. Lett. 2006, 88, 053121. [Google Scholar] [CrossRef] [Green Version]
- Lai, N.S.; Lim, W.H.; Yang, C.H.; Zwanenburg, F.A.; Coish, W.A.; Qassemi, F.; Morello, A.; Dzurak, A.S. Pauli Spin Blockade in a Highly Tunable Silicon Double Quantum Dot. Sci. Rep. 2011, 1, 110. [Google Scholar] [CrossRef] [Green Version]
- Simmel, F.; Abusch-Magder, D.; Wharam, D.A.; Kastner, M.A.; Kotthaus, J.P. Statistics of the Coulomb-blockade peak spacings of a silicon quantum dot. Phys. Rev. B 1999, 59, R10441–R10444. [Google Scholar] [CrossRef] [Green Version]
- Hiramoto, T. Five Nanometre CMOS Technology. Nat. Electron. 2019, 2, 557–558. [Google Scholar] [CrossRef]
- Li, L.; Liu, X.; Pal, S.; Wang, S.; Ober, C.K.; Giannelis, E.P. Extreme Ultraviolet Resist Materials for Sub-7 nm Patterning. Chem. Soc. Rev. 2017, 46, 4855–4866. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Zhao, J.; Guo, J.; Wu, R.; Liu, W.; Chen, Y.; Du, G.; Duan, H. Sub-5 nm Lithography with Single GeV Heavy Ions Using Inorganic Resist. Nano Lett. 2021, 21, 2390–2396. [Google Scholar] [CrossRef] [PubMed]
- Gotszalk, T.; Jóźwiak, G.; Radojewski, J.; Fröhlich, T.; Füssl, R.; Manske, E.; Holz, M.; Ivanov, T.; Ahmad, A.; Rangelow, I.W. Tip-Based Nano-Manufacturing and -Metrology. J. Vac. Sci. Technol. B 2019, 37, 030803. [Google Scholar] [CrossRef]
- Kwak, J.; Mishra, A.K.; Lee, J.; Lee, K.S.; Choi, C.; Maiti, S.; Kim, M.; Kim, J.K. Fabrication of Sub-3 nm Feature Size Based on Block Copolymer Self-Assembly for Next-Generation Nanolithography. Macromolecules 2017, 50, 6813–6818. [Google Scholar] [CrossRef]
- Shin, M.; Lee, S.; Klimeck, G. Computational Study on the Performance of Si Nanowire pMOSFETs Based on the k·p Method. IEEE Trans. Electron Devices 2010, 57, 2274–2283. [Google Scholar] [CrossRef]
- Yan, J.-A.; Yang, L.; Chou, M.Y. Size and orientation dependence in the electronic properties of silicon nanowires. Phys. Rev. B 2007, 76, 115319. [Google Scholar] [CrossRef]
- Neophytou, N.; Paul, A.; Lundstrom, M.S.; Klimeck, G. Bandstructure Effects in Silicon Nanowire Electron Transport. IEEE Trans. Electron Dev. 2008, 55, 1286–1297. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, Y.; Fujiwara, A.; Ono, Y.; Murase, K. Silicon single-electron devices and their applications. In Proceedings of the 30th IEEE International Symposium on Multiple-Valued Logic (ISMVL 2000), Portland, OR, USA, 25 May 2000; pp. 411–420. [Google Scholar]
- Lee, S.; Hiramoto, T. Strong Dependence of Tunneling Transport Properties on Overdriving Voltage for Room-Temperature-Operating Single Electron/Hole Transistors Formed with Ultranarrow [100] Silicon Nanowire Channel. Appl. Phys. Lett. 2008, 93, 043508. [Google Scholar] [CrossRef]
- Saitoh, M.; Hiramoto, T. Extension of Coulomb blockade region by quantum confinement in the ultrasmall silicon dot in a single-hole transistor at room temperature. Appl. Phys. Lett. 2004, 84, 3172–3174. [Google Scholar] [CrossRef]
- Lee, S.; Miyaji, K.; Kobayashi, M.; Hiramoto, T. Extremely High Flexibilities of Coulomb Blockade and Negative Differential Conductance Oscillations in Room-Temperature-Operating Silicon Single Hole Transistor. Appl. Phys. Lett. 2008, 92, 073502. [Google Scholar] [CrossRef]
- Hiramoto, T.; Ishikuro, H.; Fujii, T.; Hashiguchi, G.; Ikoma, T. Room Temperature Coulomb Blockade and Low Temperature Hopping Transport in a Multiple-Dot-Channel Metal-Oxide-Semiconductor Field-Effect-Transistor. Jpn. J. Appl. Phys. 1997, 36, 4139–4142. [Google Scholar] [CrossRef]
- Ohkura, K.; Kitade, T.; Nakajima, A. Cotunneling Current in Si Single-Electron Transistor Based on Multiple Islands. Appl. Phys. Lett. 2006, 89, 183520. [Google Scholar] [CrossRef] [Green Version]
- Averin, D.V.; Nazarov, Y.V. Virtual Electron Diffusion During Quantum Tunneling of the Electric Charge. Phys. Rev. Lett. 1990, 65, 2446–2449. [Google Scholar] [CrossRef] [PubMed]
- van der Wiel, W.G.; De Franceschi, S.; Elzerman, J.M.; Fujisawa, T.; Tarucha, S.; Kouwenhoven, L.P. Electron transport through double quantum dots. Rev. Mod. Phys. 2002, 75, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lee, Y.; Song, E.B.; Hiramoto, T. The Characteristic of Elongated Coulomb-Blockade Regions in a Si Quantum-Dot Device Coupled via Asymmetric Tunnel Barriers. J. Appl. Phys. 2013, 114, 164513. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Jun, H.; Park, S.; Kim, D.Y.; Lee, S. Transport Characteristics of Silicon Multi-Quantum-Dot Transistor Analyzed by Means of Experimental Parametrization Based on Single-Hole Tunneling Model. Nanomaterials 2023, 13, 1809. https://doi.org/10.3390/nano13111809
Lee Y, Jun H, Park S, Kim DY, Lee S. Transport Characteristics of Silicon Multi-Quantum-Dot Transistor Analyzed by Means of Experimental Parametrization Based on Single-Hole Tunneling Model. Nanomaterials. 2023; 13(11):1809. https://doi.org/10.3390/nano13111809
Chicago/Turabian StyleLee, Youngmin, Hyewon Jun, Seoyeon Park, Deuk Young Kim, and Sejoon Lee. 2023. "Transport Characteristics of Silicon Multi-Quantum-Dot Transistor Analyzed by Means of Experimental Parametrization Based on Single-Hole Tunneling Model" Nanomaterials 13, no. 11: 1809. https://doi.org/10.3390/nano13111809
APA StyleLee, Y., Jun, H., Park, S., Kim, D. Y., & Lee, S. (2023). Transport Characteristics of Silicon Multi-Quantum-Dot Transistor Analyzed by Means of Experimental Parametrization Based on Single-Hole Tunneling Model. Nanomaterials, 13(11), 1809. https://doi.org/10.3390/nano13111809






