Anti-Stokes Photoluminescence in Halide Perovskite Nanocrystals: From Understanding the Mechanism towards Application in Fully Solid-State Optical Cooling
Abstract
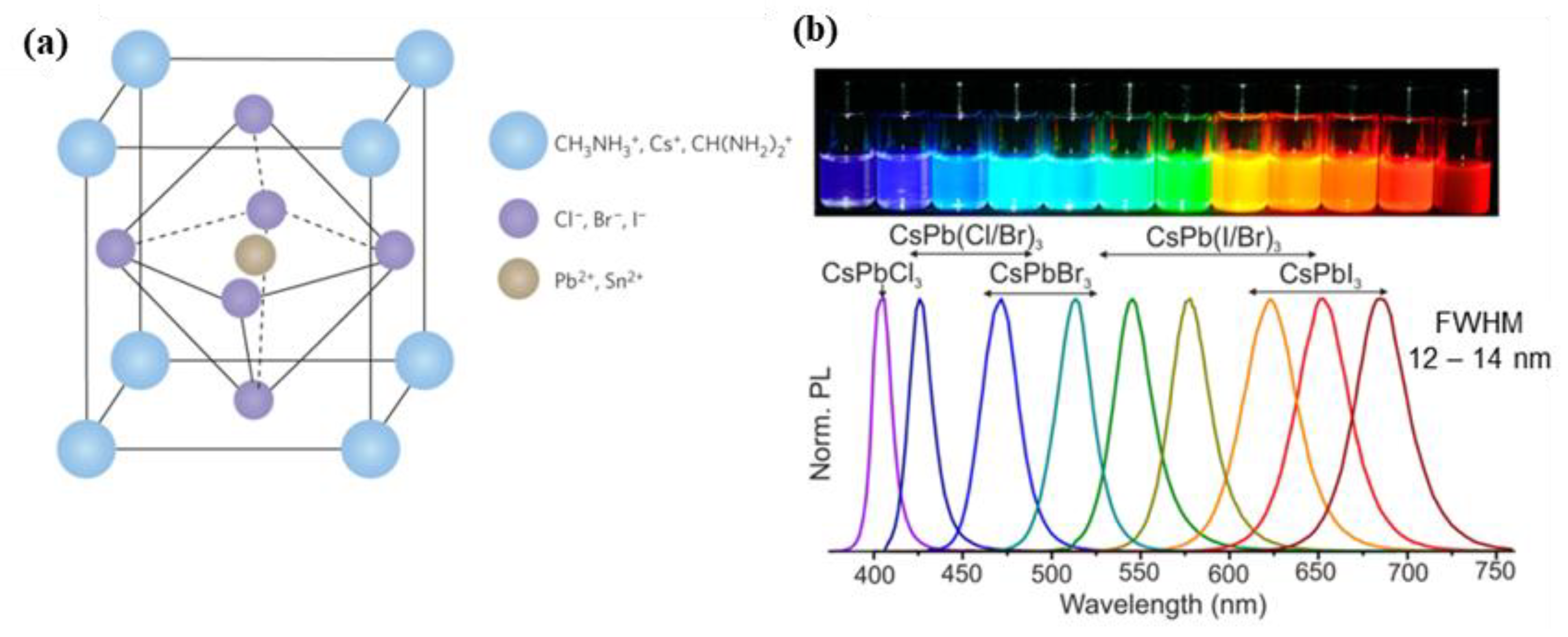
:1. Introduction
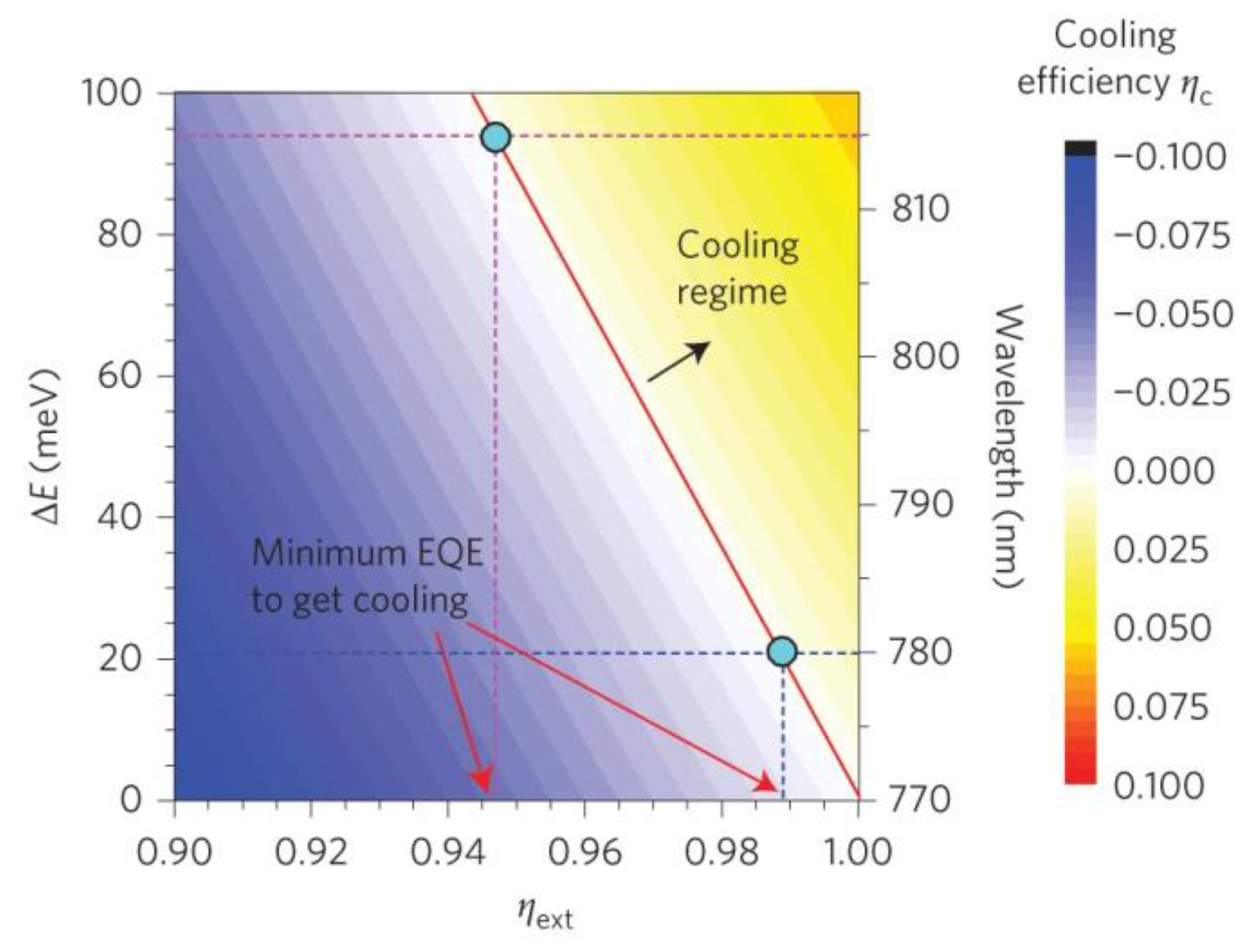
2. The Concept of Optical Refrigeration
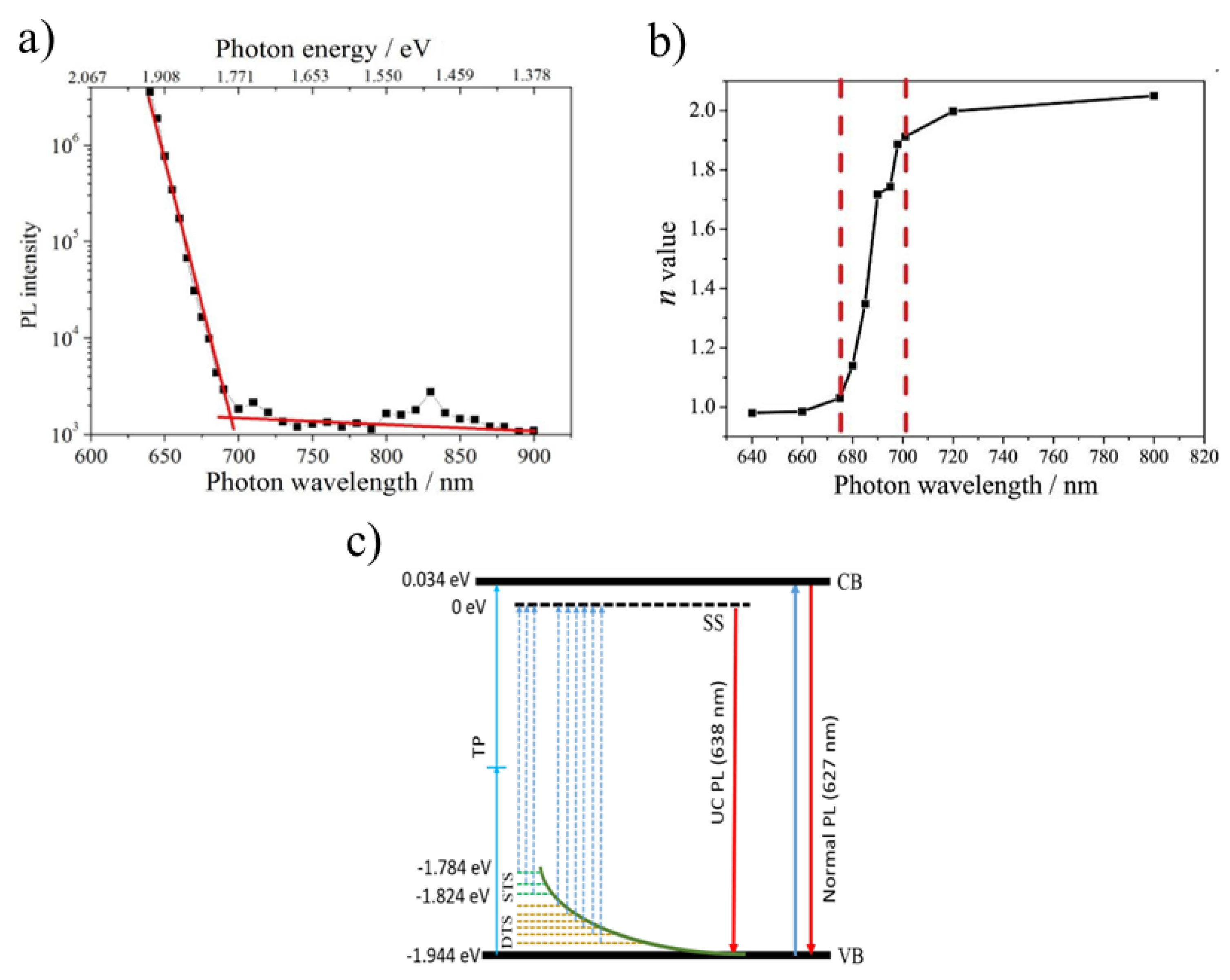
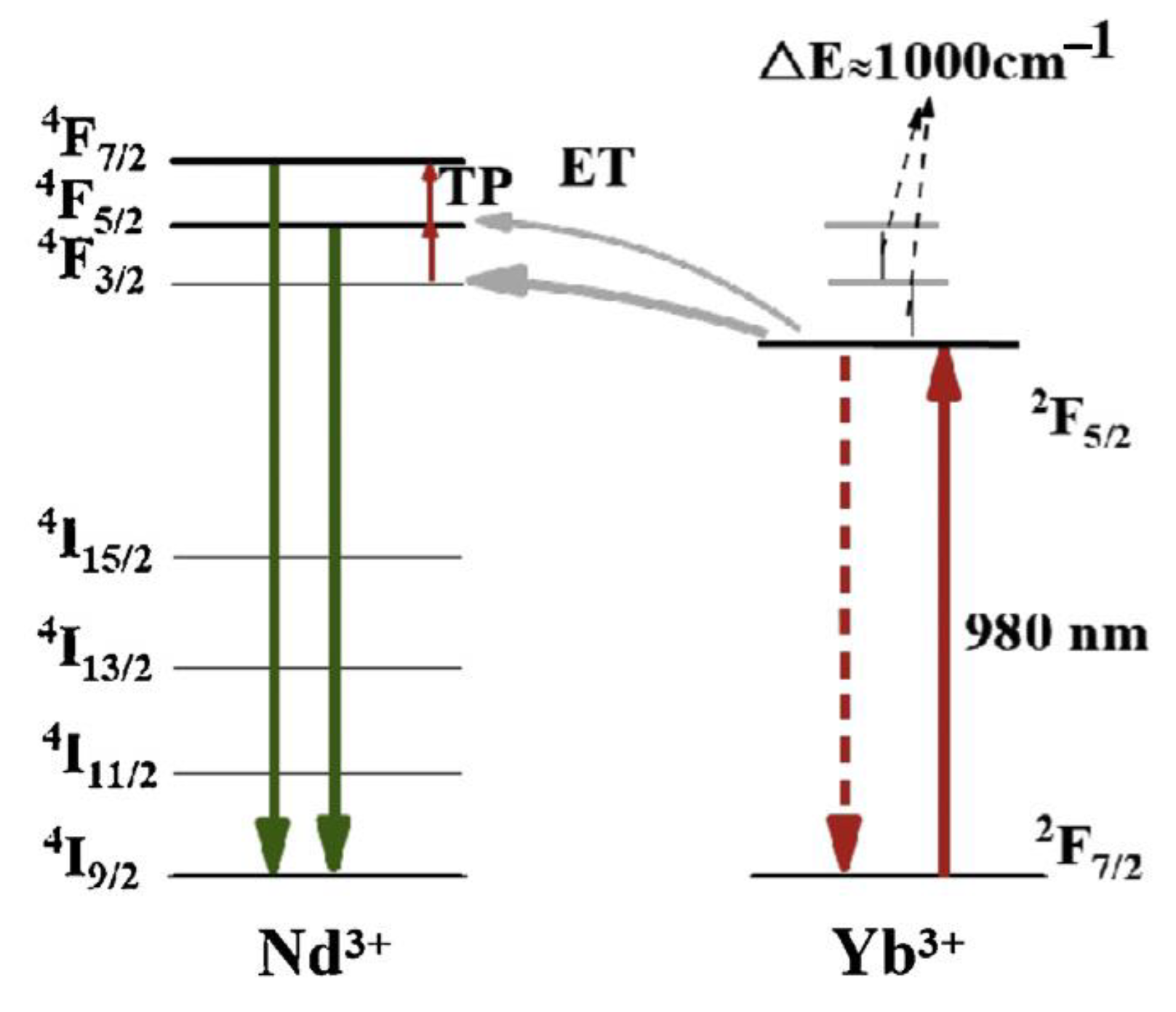
3. Up-Conversion Mechanisms
4. The Role of Electron–Phonon Interaction
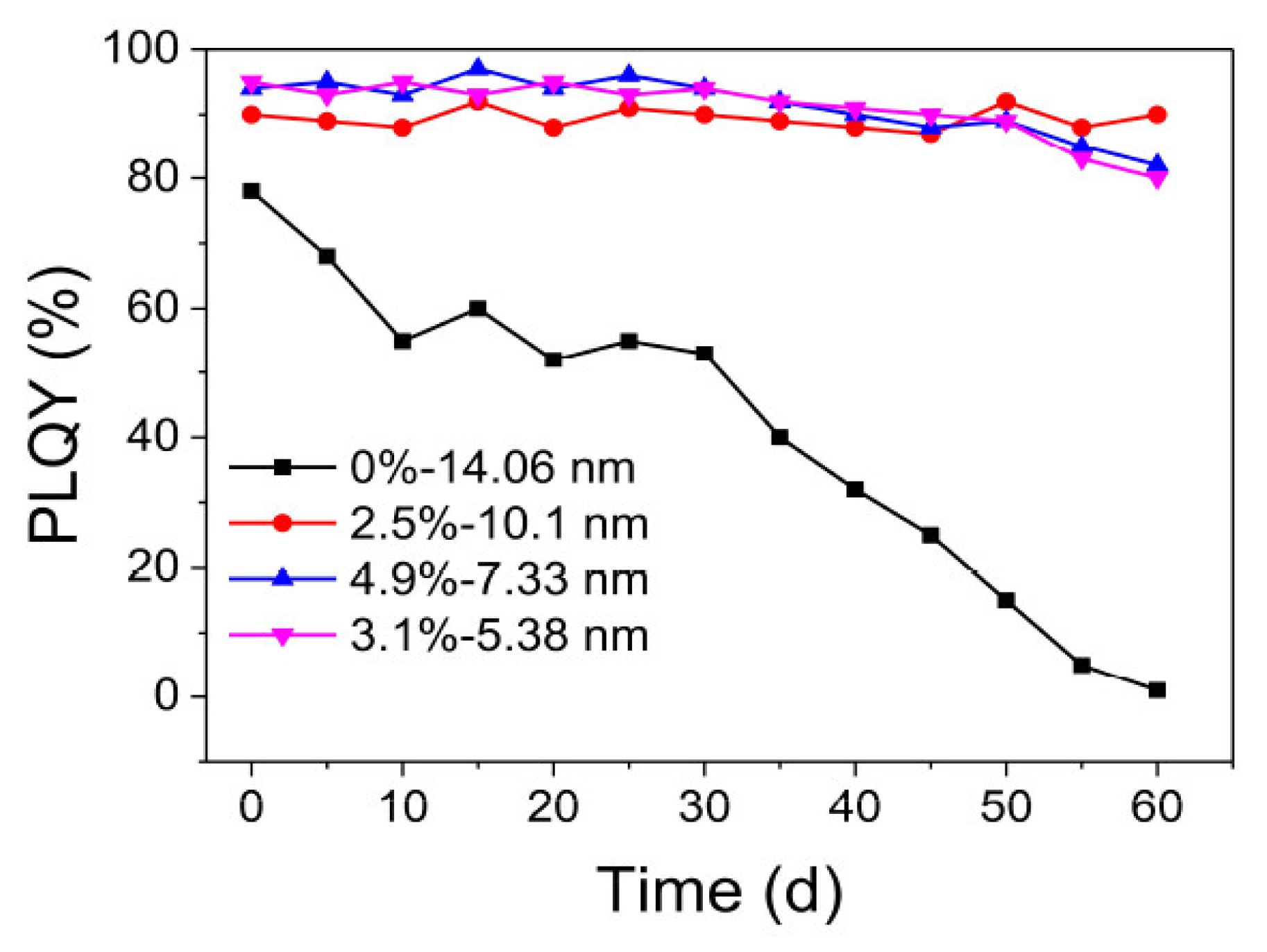
5. PL Efficiency Enhancement
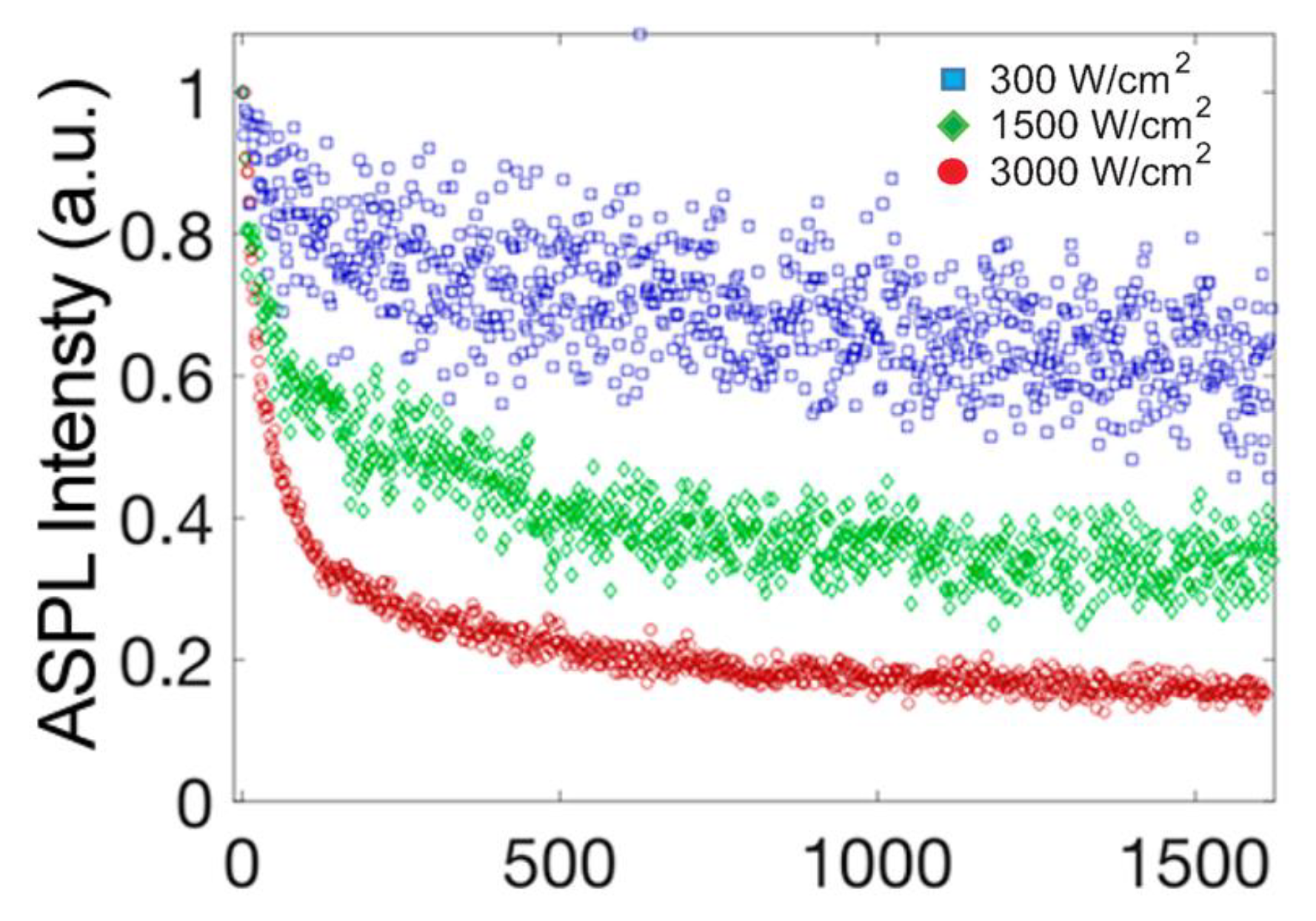
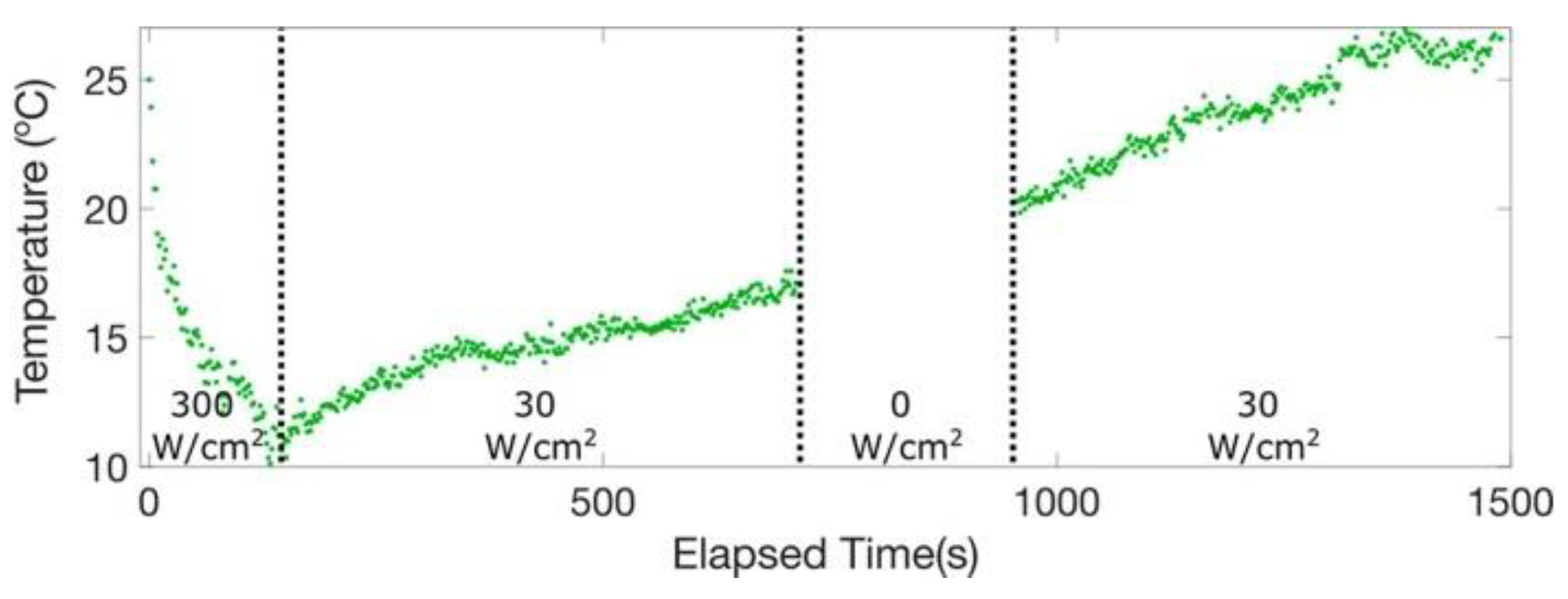
6. Optical Cooling Implementation
7. Perspectives and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, Y.H.; Cho, H.; Lee, T.W. Metal halide perovskite light emitters. Proc. Nat. Acad. Sci. USA 2016, 113, 11694–11702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brenner, T.M.; Egger, D.A.; Kronik, L.; Hodes, G.; Cahen, D. Hybrid organic—Inorganic perovskites: Low-cost semiconductors with intriguing charge-transport properties. Nat. Rev. Mater. 2016, 1, 15007. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Tan, Z.K.; Moghaddam, R.S.; Lai, M.L.; Docampo, P.; Higler, R.; Deschler, F.; Price, M.; Sadhanala, A.; Pazos, L.M.; Credgington, D.; et al. Bright light-emitting diodes based on organometal halide perovskite. Nat. Nanotechnol. 2014, 9, 687–692. [Google Scholar] [CrossRef]
- Sadhanala, A.; Ahmad, S.; Zhao, B.; Giesbrecht, N.; Pearce, P.M.; Deschler, F.; Hoye, R.L.Z.; Gödel, K.C.; Bein, T.; Docampo, P.; et al. Blue-green color tunable solution processable organolead chloride–bromide mixed halide perovskites for optoelectronic applications. Nano Lett. 2015, 15, 6095–6101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, L.; Tavakoli, M.M.; Zhang, D.; Zhang, Q.; Waleed, A.; Xiao, Y.; Tsui, K.-H.; Lin, Y.; Liao, L.; Wang, J.; et al. 3D Arrays of 1024-pixel image sensors based on lead halide perovskite nanowires. Adv. Mat. 2016, 28, 9713–9721. [Google Scholar] [CrossRef] [PubMed]
- Protesescu, L.; Yakunin, S.; Bodnarchuk, M.I.; Krieg, F.; Caputo, R.; Hendon, C.H.; Yang, R.X.; Walsh, A.; Kovalenko, M.V. Nanocrystals of cesium lead halide perovskites (CsPbX3, X = Cl, Br, and I): Novel optoelectronic materials showing bright emission with wide color gamut. Nano Lett. 2015, 15, 3692–3696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sutherland, B.R.; Sargent, E.H. Perovskite photonic sources. Nat. Photon. 2016, 10, 295–302. [Google Scholar] [CrossRef]
- Brown, A.A.; Damodaran, B.; Jiang, L.; Tey, J.N.; Pu, S.H.; Mathews, N.; Mhaisalkar, S.G. Lead halide perovskite nanocrystals: Room temperature syntheses toward commercial viability. Adv. Energy Mater. 2020, 10, 2001349. [Google Scholar] [CrossRef]
- Deng, W.; Fang, H.; Jin, X.; Zhang, X.; Zhang, X.; Jie, J. Organic–inorganic hybrid perovskite quantum dots for light-emitting diodes. J. Mater. Chem. C 2018, 6, 4831–4841. [Google Scholar] [CrossRef]
- Ou, Q.; Bao, X.; Zhang, Y.; Shao, H.; Xing, G.; Li, X.; Shao, L.; Bao, Q. Band structure engineering in metal halide perovskite nanostructures for optoelectronic applications. Nano Mater. Sci. 2019, 1, 268–287. [Google Scholar] [CrossRef]
- Wright, A.D.; Verdi, C.; Milot, R.L.; Eperon, G.E.; Pérez-Osorio, M.A.; Snaith, H.J.; Giustino, F.; Johnston, M.B.; Herz, L.M. Electron–phonon coupling in hybrid lead halide perovskites. Nat. Commun. 2016, 7, 11755. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Yu, M.; Zhao, M.; Song, J.; Qu, J. Low temperature synthesis of high-quality all-inorganic cesium lead halide perovskite nanocrystals in open air and their upconversion luminescence. J. Alloys Compd. 2018, 730, 62–70. [Google Scholar] [CrossRef]
- Pringsheim, P. Zwei bemerkungen über den unterschied von lumineszenz-und temperaturstrahlung. Z. Phys. 1929, 57, 739–746. [Google Scholar] [CrossRef]
- Rakovich, Y.P.; Donegan, J.F.; Vasilevskiy, M.I.; Rogach, A.L. Anti-Stokes cooling in semiconductor nanocrystal quantum dots: A feasibility study. Phys. Status Solidi (a) 2009, 206, 2497–2509. [Google Scholar] [CrossRef] [Green Version]
- Epstein, R.I.; Buchwald, M.I.; Edwards, B.C.; Gosnell, T.R.; Mungan, C.E. Observation of laser-induced fluorescent cooling of a solid. Nature 1995, 377, 500–503. [Google Scholar] [CrossRef]
- Melgaard, S.D.; Albrecht, A.R.; Hehlen, M.P.; Sheik-Bahae, M. Solid-state optical refrigeration to sub-100 Kelvin regime. Sci. Rep. 2016, 6, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Seletskiy, D.V.; Epstein, R.; Sheik-Bahae, M. Laser cooling in solids: Advances and prospects. Rep. Prog. Phys. 2016, 79, 096401. [Google Scholar] [CrossRef]
- Gosnell, T.R. Laser cooling of a solid by 65 K starting from room temperature. Opt. Lett. 1999, 24, 1041–1043. [Google Scholar] [CrossRef] [PubMed]
- Seletskiy, D.V.; Melgaard, S.D.; Bigotta, S.; Di Lieto, A.; Tonelli, M.; Sheik-Bahae, M. Laser cooling of solids to cryogenic temperatures. Nat. Photogr. 2010, 4, 161–164. [Google Scholar] [CrossRef]
- Clark, J.L.; Miller, P.F.; Rumbles, G. Red edge photophysics of ethanolic rhodamine 101 and the observation of laser cooling in the condensed phase. J. Phys. Chem. A 1998, 102, 4428–4437. [Google Scholar] [CrossRef]
- Dimitriev, O.; Fedoryak, A.; Slominskii, Y.; Smirnova, A.; Yoshida, T. Phonon-assisted anti-Stokes luminescence of tricarbocyanine near-infrared dye. J. Chem. Phys. Lett. 2020, 738, 136905. [Google Scholar] [CrossRef]
- Gauck, H.; Gfroerer, T.H.; Renn, M.J.; Cornell, E.A.; Bertness, K.A. External radiative quantum efficiency of 96% from a GaAs/GaInP heterostructure. Appl. Phys. A 1997, 64, 143–147. [Google Scholar] [CrossRef]
- Finkeissen, E.; Potemski, M.; Wyder, P.; Vina, L.; Weimann, G. Cooling of a semiconductor by luminescence upconversion. Appl. Phys. Lett. 1999, 75, 1258–1260. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Epstein, R.I. Optical refrigeration. Nat. Photogr. 2007, 1, 693–699. [Google Scholar] [CrossRef]
- Oraevsky, A.N. Cooling of semiconductors by laser radiation. Quantum Electron. 1996, 26, 1018. [Google Scholar] [CrossRef]
- Rivlin, L.A.; Zadernovsky, A.A. Laser cooling of semiconductors. Opt. Commun. 1997, 139, 219–222. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Epstein, R.I. Can laser light cool semiconductors? Phys. Rev. Lett. 2004, 92, 247403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rupper, G.; Kwong, N.H.; Binder, R. Theory of semiconductor laser cooling at low temperatures. Phys. Status Solidi (c) 2006, 3, 2489–2493. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Chen, R.; Xiong, Q. Laser cooling of a semiconductor by 40 kelvin. Nature 2013, 493, 504–508. [Google Scholar] [CrossRef]
- Akizuki, N.; Aota, S.; Mouri, S.; Matsuda, K.; Miyauchi, Y. Efficient near-infrared upconversion photoluminescence in carbon nanotubes. Nat. Commun. 2015, 6, 8920. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Yu, W.W.; Zhang, J.; Aldana, J.; Peng, X.; Xiao, M. Photoluminescence upconversion in colloidal CdTe quantum dots. Phys. Rev. B 2003, 68, 125318. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Joly, A.G.; McCready, D.E. Upconversion luminescence from CdSe nanoparticles. J. Chem. Phys. 2005, 122, 224708. [Google Scholar] [CrossRef]
- Deutsch, Z.; Neeman, L.; Oron, D. Luminescence upconversion in colloidal double quantum dots. Nat. Nanotechnol. 2013, 8, 649–653. [Google Scholar] [CrossRef]
- Kojima, K.; Ikemura, K.; Matsumori, K.; Yamada, Y.; Kanemitsu, Y.; Chichibu, S.F. Internal quantum efficiency of radiation in a bulk CH3NH3PbBr3 perovskite crystal quantified by using the omnidirectional photoluminescence spectroscopy. APL Mater. 2019, 7, 071116. [Google Scholar] [CrossRef] [Green Version]
- Ha, S.T.; Shen, C.; Zhang, J.; Xiong, Q. Laser cooling of organic–inorganic lead halide perovskites. Nat. Photon. 2016, 10, 115–121. [Google Scholar] [CrossRef]
- Roman, B.J.; Villegas, N.M.; Lytle, K.; Sheldon, M. Optically cooling cesium lead tribromide nanocrystals. Nano Lett. 2020, 20, 8874–8879. [Google Scholar] [CrossRef] [PubMed]
- Yamada, T.; Aharen, T.; Kanemitsu, Y. Up-converted photoluminescence from CH3NH3PbI3 perovskite semiconductors: Implications for laser cooling. Phys. Rev. Mater. 2019, 3, 024601. [Google Scholar] [CrossRef] [Green Version]
- Prochazkova, A.J.; Mayr, F.; Gugujonovic, K.; Hailegnaw, B.; Krajcovic, J.; Salinas, Y.; Scharber, M.C. Anti-Stokes photoluminescence study on a methylammonium lead bromide nanoparticle film. Nanoscale 2020, 12, 16556–16561. [Google Scholar] [CrossRef]
- Sekerbayev, K.S.; Mussabek, G.K.; Pokryshkin, N.S.; Yakunin, V.G.; Taurbayev, Y.T.; Shabdan, Y.; Utegulov, Z.N.; Chirvony, V.S.; Timoshenko, V.Y. Effect of nanocrystal size on Anti-Stokes photoluminescence in lead perovskites. JETP Lett. 2021, 114, 447–450. [Google Scholar] [CrossRef]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef] [Green Version]
- Xing, G.; Mathews, N.; Sun, S.; Lim, S.S.; Lam, Y.M.; Grätzel, M.; Mhaisalkar, S.; Sum, T.C. Long-range balanced electron-and hole-transport lengths in organic-inorganic CH3NH3PbI3. Science 2013, 342, 344–347. [Google Scholar] [CrossRef]
- De Wolf, S.; Holovsky, J.; Moon, S.J.; Loper, P.; Niesen, B.; Ledinsky, M.; Haug, F.-J.; Yum, J.-H.; Ballif, C. Organometallic halide perovskites: Sharp optical absorption edge and its relation to photovoltaic performance. J. Phys. Chem. Lett. 2014, 5, 1035–1039. [Google Scholar] [CrossRef]
- Yamada, Y.; Nakamura, T.; Endo, M.; Wakamiya, A.; Kanemitsu, Y. Photocarrier recombination dynamics in perovskite CH3NH3PbI3 for solar cell applications. J. Am. Chem. Soc. 2014, 136, 11610–11613. [Google Scholar] [CrossRef]
- Kimura, T.; Matsumori, K.; Oto, K.; Kanemitsu, Y.; Yamada, Y. Observation of high carrier mobility in CH3NH3PbBr3 single crystals by AC photo-Hall measurements. Appl. Phys. Express 2021, 14, 041009. [Google Scholar] [CrossRef]
- Kurilovich, A.A.; Mantsevich, V.N.; Mardoukhi, Y.; Stevenson, K.J.; Chechkin, A.V.; Palyulin, V.V. Non-Markovian diffusion of excitons in layered perovskites and transition metal dichalcogenides. Phys. Chem. Chem. Phys. 2022, 24, 13941–13950. [Google Scholar] [CrossRef]
- Yamada, Y.; Yamada, T.; Phuong, L.Q.; Maruyama, N.; Nishimura, H.; Wakamiya, A.; Murata, Y.; Kanemitsu, Y. Dynamic optical properties of CH3NH3PbI3 single crystals as revealed by one-and two-photon excited photoluminescence measurements. J. Am. Chem. Soc. 2015, 137, 10456–10459. [Google Scholar] [CrossRef] [PubMed]
- Pazos-Outón, L.M.; Szumilo, M.; Lamboll, R.; Richter, J.M.; Crespo-Quesada, M.; Abdi-Jalebi, M.; Beeson, H.J.; Vrućinić Harry, J.; Alsari, M.; Snaith, J.H.; et al. Photon recycling in lead iodide perovskite solar cells. Science 2016, 351, 1430–1433. [Google Scholar] [CrossRef] [PubMed]
- Sekiguchi, F.; Hirori, H.; Yumoto, G.; Shimazaki, A.; Nakamura, T.; Wakamiya, A.; Kanemitsu, Y. Enhancing the hot-phonon bottleneck effect in a metal halide perovskite by terahertz phonon excitation. Phys. Rev. Lett. 2021, 126, 077401. [Google Scholar] [CrossRef]
- Yamada, Y.; Mino, H.; Kawahara, T.; Oto, K.; Suzuura, H.; Kanemitsu, Y. Polaron masses in CH3NH3PbX3 perovskites determined by Landau level spectroscopy in low magnetic fields. Phys. Rev. Lett. 2021, 126, 237401. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Kanemitsu, Y. Electron-phonon interactions in halide perovskites. NPG Asia Mater. 2022, 14, 48. [Google Scholar] [CrossRef]
- Kajino, Y.; Otake, S.; Yamada, T.; Kojima, K.; Nakamura, T.; Wakamiya, A.; Kanemitsu, Y.; Yamada, Y. Anti-Stokes photoluminescence from CsPbBr3 nanostructures embedded in a Cs4PbBr6 crystal. Phys. Rev. Mater. 2022, 6, L043001. [Google Scholar] [CrossRef]
- Granados del Águila, A.; Do, T.T.H.; Xing, J.; Jee, W.J.; Khurgin, J.B.; Xiong, Q. Efficient upconversion photoluminescence in all-inorganic lead halide perovskite nanocrystals. Nano Res. 2020, 13, 1962–1969. [Google Scholar] [CrossRef]
- Cai, P.; Huang, Y.; Seo, H.J. Anti-Stokes ultraviolet luminescence and exciton detrapping in the two-dimensional perovskite (C6H5C2H4NH3)2PbCl4. J. Phys. Chem. Lett. 2019, 10, 4095–4102. [Google Scholar] [CrossRef]
- Ye, S.; Zhao, M.; Yu, M.; Zhu, M.; Yan, W.; Song, J.; Qu, J. Mechanistic investigation of upconversion photoluminescence in all-inorganic perovskite CsPbBrI2 nanocrystals. J. Phys. Chem. C 2018, 122, 3152–3156. [Google Scholar] [CrossRef]
- Li, J.; Gan, L.; Fang, Z.; He, H.; Ye, Z. Bright tail states in blue-emitting ultrasmall perovskite quantum dots. J. Phys. Chem. Lett. 2017, 8, 6002–6008. [Google Scholar] [CrossRef]
- Roman, B.J.; Sheldon, M. The role of mid-gap states in all-inorganic CsPbBr3 nanoparticle one photon upconversion. Chem. Commun. 2018, 54, 6851–6854. [Google Scholar] [CrossRef]
- Ma, X.; Pan, F.; Li, H.; Shen, P.; Ma, C.; Zhang, L.; Niu, H.; Zhu, Y.; Xu, S.; Ye, H. Mechanism of single-photon upconversion photoluminescence in all-inorganic perovskite nanocrystals: The role of self-trapped excitons. J. Phys. Chem. Lett. 2019, 10, 5989–5996. [Google Scholar] [CrossRef]
- Song, Z.; Zhao, J.; Liu, Q. Luminescent perovskites: Recent advances in theory and experiments. Inorg. Chem. Front. 2019, 6, 2969–3011. [Google Scholar] [CrossRef]
- Zhang, W.; Ye, Y.; Liu, C.; Wang, J.; Ruan, J.; Zhao, X.; Han, J. Two-step anti-Stokes photoluminescence of CsPbX3 nanocrystals. Adv. Opt. Mater. 2021, 9, 2001885. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, Y.; Wang, C.; Bai, G.; Shen, Y.; Jiang, Z.; Xu, S.; Chen, L. Near-infrared anti-Stokes luminescence from neodymium doped perovskite calcium titanate particles for optical temperature sensors. Sens. Actuators A Phys. 2021, 326, 112741. [Google Scholar] [CrossRef]
- Cavalcante, L.S.; Marques, V.S.; Sczancoski, J.C.; Escote, M.T.; Joya, M.R.; Varela, J.A.; Santos, M.R.M.C.; Pizani, P.S.; Longo, E. Synthesis, structural refinement and optical behavior of CaTiO3 powders: A comparative study of processing in different furnaces. Chem. Eng. J. 2008, 143, 299–307. [Google Scholar] [CrossRef]
- Sekerbayev, K.; Taurbayev, Y.; Mussabek, G.; Baktygerey, S.; Pokryshkin, N.S.; Yakunin, V.G.; Utegulov, Z.; Timoshenko, V.Y. Size-dependent phonon-assisted anti-Stokes photoluminescence in nanocrystals of organometal perovskites. Nanomaterials 2022, 12, 3184. [Google Scholar] [CrossRef]
- Li, M.; Fu, J.; Xu, Q.; Sum, T.C. Slow hot-carrier cooling in halide perovskites: Prospects for hot-carrier solar cells. Adv. Mater. 2019, 31, 1802486. [Google Scholar] [CrossRef]
- Nagai, M.; Tomioka, T.; Ashida, M.; Hoyano, M.; Akashi, R.; Yamada, Y.; Tomoko, A.; Kanemitsu, Y. Longitudinal optical phonons modified by organic molecular cation motions in organic-inorganic hybrid perovskites. Phys. Rev. Lett. 2018, 121, 145506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frost, J.M. Calculating polaron mobility in halide perovskites. Phys. Rev. B 2017, 96, 195202. [Google Scholar] [CrossRef] [Green Version]
- Fröhlich, H. Electrons in lattice fields. Adv. Phys. 1954, 3, 325–361. [Google Scholar] [CrossRef]
- Franchini, C.; Reticcioli, M.; Setvin, M.; Diebold, U. Polarons in materials. Nat. Rev. Mater. 2021, 6, 560–586. [Google Scholar] [CrossRef]
- Kovalev, D.; Heckler, H.; Polisski, G.; Koch, F. Optical properties of Si nanocrystals. Phys. Status Solidi (b) 1999, 215, 871–932. [Google Scholar] [CrossRef]
- Gualdrón-Reyes, A.F.; Masi, S.; Mora-Seró, I. Progress in halide-perovskite nanocrystals with near-unity photoluminescence quantum yield. Trends Chem. 2021, 3, 499–511. [Google Scholar] [CrossRef]
- Li, F.; Liu, Y.; Wang, H.; Zhan, Q.; Liu, Q.; Xia, Z. Postsynthetic surface trap removal of CsPbX3 (X = Cl, Br, or I) quantum dots via a ZnX2/hexane solution toward an enhanced luminescence quantum yield. Chem. Mater. 2018, 30, 8546–8554. [Google Scholar] [CrossRef]
- Yao, J.S.; Zhang, J.C.; Wang, L.; Wang, K.H.; Ru, X.C.; Yang, J.N.; Wang, J.-J.; Chen, X.; Song, Y.-H.; Yin, Y.-C.; et al. Suppressing Auger recombination in cesium lead bromide perovskite nanocrystal film for bright light-emitting diodes. J. Phys. Chem. Lett. 2020, 11, 9371–9378. [Google Scholar] [CrossRef]
- Jang, H.M.; Kim, J.S.; Heo, J.M.; Lee, T.W. Enhancing photoluminescence quantum efficiency of metal halide perovskites by examining luminescence-limiting factors. APL Mater. 2020, 8, 020904. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.H.; Kim, J.S.; Lee, T.W. Strategies to improve luminescence efficiency of metal-halide perovskites and light-emitting diodes. Adv. Mater. 2019, 31, 1804595. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.H.; Wolf, C.; Kim, Y.T.; Cho, H.; Kwon, W.; Do, S.; Sadhanala, A.; Park, C.G.; Rhee, S.-W.; Im, S.H.; et al. Highly efficient light-emitting diodes of colloidal metal–halide perovskite nanocrystals beyond quantum size. ACS Nano 2017, 11, 6586–6593. [Google Scholar] [CrossRef] [PubMed]
- Seth, S.; Ahmed, T.; De, A.; Samanta, A. Tackling the defects, stability, and photoluminescence of CsPbX3 perovskite nanocrystals. ACS Energy Lett. 2019, 4, 1610–1618. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Zhang, Y.; Zhang, X.; Shen, X.; Zhuang, X.; Lu, P.; Yu, W.W.; Kershaw, S.V.; Rogach, A.L. Cesium lead chloride/bromide perovskite quantum dots with strong blue emission realized via a nitrate-induced selective surface defect elimination process. J. Phys. Chem. Lett. 2018, 10, 90–96. [Google Scholar] [CrossRef]
- Cho, H.; Jeong, S.H.; Park, M.H.; Kim, Y.H.; Wolf, C.; Lee, C.L.; Lee, T.W. Overcoming the electroluminescence efficiency limitations of perovskite light-emitting diodes. Science 2015, 350, 1222–1225. [Google Scholar] [CrossRef]
- Koscher, B.A.; Swabeck, J.K.; Bronstein, N.D.; Alivisatos, A.P. Essentially trap-free CsPbBr3 colloidal nanocrystals by postsynthetic thiocyanate surface treatment. J. Am. Chem. Soc. 2017, 139, 6566–6569. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Zhang, Y.; Ding, C.; Kobayashi, S.; Izuishi, T.; Nakazawa, N.; Toyoda, T.; Ohta, T.; Hayase, S.; Minemoto, T.; et al. Highly luminescent phase-stable CsPbI3 perovskite quantum dots achieving near 100% absolute photoluminescence quantum yield. ACS Nano 2017, 11, 10373–10383. [Google Scholar] [CrossRef]
- Ji, S.; Yuan, X.; Cao, S.; Ji, W.; Zhang, H.; Wang, Y.; Li, H.; Zhao, J.; Zou, B. Near-unity red Mn2+ photoluminescence quantum yield of doped CsPbCl3 nanocrystals with Cd incorporation. J. Phys. Chem. Lett. 2020, 11, 2142–2149. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.S.; Ge, J.; Wang, K.H.; Zhang, G.; Zhu, B.S.; Chen, C.; Zhang, Q.; Luo, Y.; Yu, S.-H.; Yao, H.B. Few-nanometer-sized α-CsPbI3 quantum dots enabled by strontium substitution and iodide passivation for efficient red-light emitting diodes. J. Am. Chem. Soc. 2019, 141, 2069–2079. [Google Scholar] [CrossRef]
- Yong, Z.J.; Guo, S.Q.; Ma, J.P.; Zhang, J.Y.; Li, Z.Y.; Chen, Y.M.; Zhang, B.-B.; Zhou, Y.; Shu, J.; Gu, J.-L.; et al. Doping-enhanced short-range order of perovskite nanocrystals for near-unity violet luminescence quantum yield. J. Am. Chem. Soc. 2018, 140, 9942–9951. [Google Scholar] [CrossRef] [Green Version]
- Milstein, T.J.; Kroupa, D.M.; Gamelin, D.R. Picosecond quantum cutting generates photoluminescence quantum yields over 100% in ytterbium-doped CsPbCl3 nanocrystals. Nano Lett. 2018, 18, 3792–3799. [Google Scholar] [CrossRef] [PubMed]
- Di Stasio, F.; Ramiro, I.; Bi, Y.; Christodoulou, S.; Stavrinadis, A.; Konstantatos, G. High-efficiency light-emitting diodes based on formamidinium lead bromide nanocrystals and solution processed transport layers. Chem. Mater. 2018, 30, 6231–6235. [Google Scholar] [CrossRef] [Green Version]
- Di Stasio, F.; Christodoulou, S.; Huo, N.; Konstantatos, G. Near-unity photoluminescence quantum yield in CsPbBr3 nanocrystal solid-state films via postsynthesis treatment with lead bromide. Chem. Mater. 2017, 29, 7663–7667. [Google Scholar] [CrossRef]
- Kumar, S.; Jagielski, J.; Kallikounis, N.; Kim, Y.H.; Wolf, C.; Jenny, F.; Tian, T.; Hofer, C.J.; Chiu, Y.-C.; Stark, W.J.; et al. Ultrapure green light-emitting diodes using two-dimensional formamidinium perovskites: Achieving recommendation 2020 color coordinates. Nano Lett. 2017, 17, 5277–5284. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.; Liao, Q.; Xu, Z.; Li, H.; Zheng, L.; Fu, H. Embedding perovskite nanocrystals into a polymer matrix for tunable luminescence probes in cell imaging. Adv. Funct. Mater. 2017, 27, 1604382. [Google Scholar] [CrossRef]
- Liang, X.; Chen, M.; Wang, Q.; Guo, S.; Yang, H. Ethanol-precipitable, silica-passivated perovskite nanocrystals incorporated into polystyrene microspheres for long-term storage and reusage. Angew. Chem. 2019, 131, 2825–2829. [Google Scholar] [CrossRef]
- Bodnarchuk, M.I.; Boehme, S.C.; Ten Brinck, S.; Bernasconi, C.; Shynkarenko, Y.; Krieg, F.; Widmer, R.; Aeschlimann, B.; Günther, D.; Kovalenko, M.V.; et al. Rationalizing and controlling the surface structure and electronic passivation of cesium lead halide nanocrystals. ACS Energy Lett. 2018, 4, 63–74. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, Y.; Lu, M.; Zhang, X.; Sun, C.; Zhang, T.; Sun, C.; Zhang, T.; Colvinc, V.L.; William, W.Y. Surface ligand modification of cesium lead bromide nanocrystals for improved light-emitting performance. Nanoscale 2018, 10, 4173–4178. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Luan, W.; Liu, M.; Turyanska, L. DDAB-assisted synthesis of iodine-rich CsPbI3 perovskite nanocrystals with improved stability in multiple environments. J. Mater. Chem. C 2020, 8, 2381–2387. [Google Scholar] [CrossRef]
- Tonkaev, P.; Zograf, G.; Makarov, S. Optical cooling of lead halide perovskite nanoparticles enhanced by Mie resonances. Nanoscale 2019, 11, 17800–17806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imangholi, B.; Hasselbeck, M.P.; Bender, D.A.; Wang, C.; Sheik-Bahae, M.; Epstein, R.I.; Kurtz, S. Differential luminescence thermometry in semiconductor laser cooling. In Physics and Simulation of Optoelectronic Devices XIV; SPIE: Bellingham, MA, USA, 2006; Volume 6115, pp. 215–220. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pokryshkin, N.S.; Mantsevich, V.N.; Timoshenko, V.Y. Anti-Stokes Photoluminescence in Halide Perovskite Nanocrystals: From Understanding the Mechanism towards Application in Fully Solid-State Optical Cooling. Nanomaterials 2023, 13, 1833. https://doi.org/10.3390/nano13121833
Pokryshkin NS, Mantsevich VN, Timoshenko VY. Anti-Stokes Photoluminescence in Halide Perovskite Nanocrystals: From Understanding the Mechanism towards Application in Fully Solid-State Optical Cooling. Nanomaterials. 2023; 13(12):1833. https://doi.org/10.3390/nano13121833
Chicago/Turabian StylePokryshkin, Nikolay S., Vladimir N. Mantsevich, and Victor Y. Timoshenko. 2023. "Anti-Stokes Photoluminescence in Halide Perovskite Nanocrystals: From Understanding the Mechanism towards Application in Fully Solid-State Optical Cooling" Nanomaterials 13, no. 12: 1833. https://doi.org/10.3390/nano13121833
APA StylePokryshkin, N. S., Mantsevich, V. N., & Timoshenko, V. Y. (2023). Anti-Stokes Photoluminescence in Halide Perovskite Nanocrystals: From Understanding the Mechanism towards Application in Fully Solid-State Optical Cooling. Nanomaterials, 13(12), 1833. https://doi.org/10.3390/nano13121833







