Elimination of Chirality in Three-Dimensionally Confined Open-Access Microcavities
Abstract
:1. Introduction
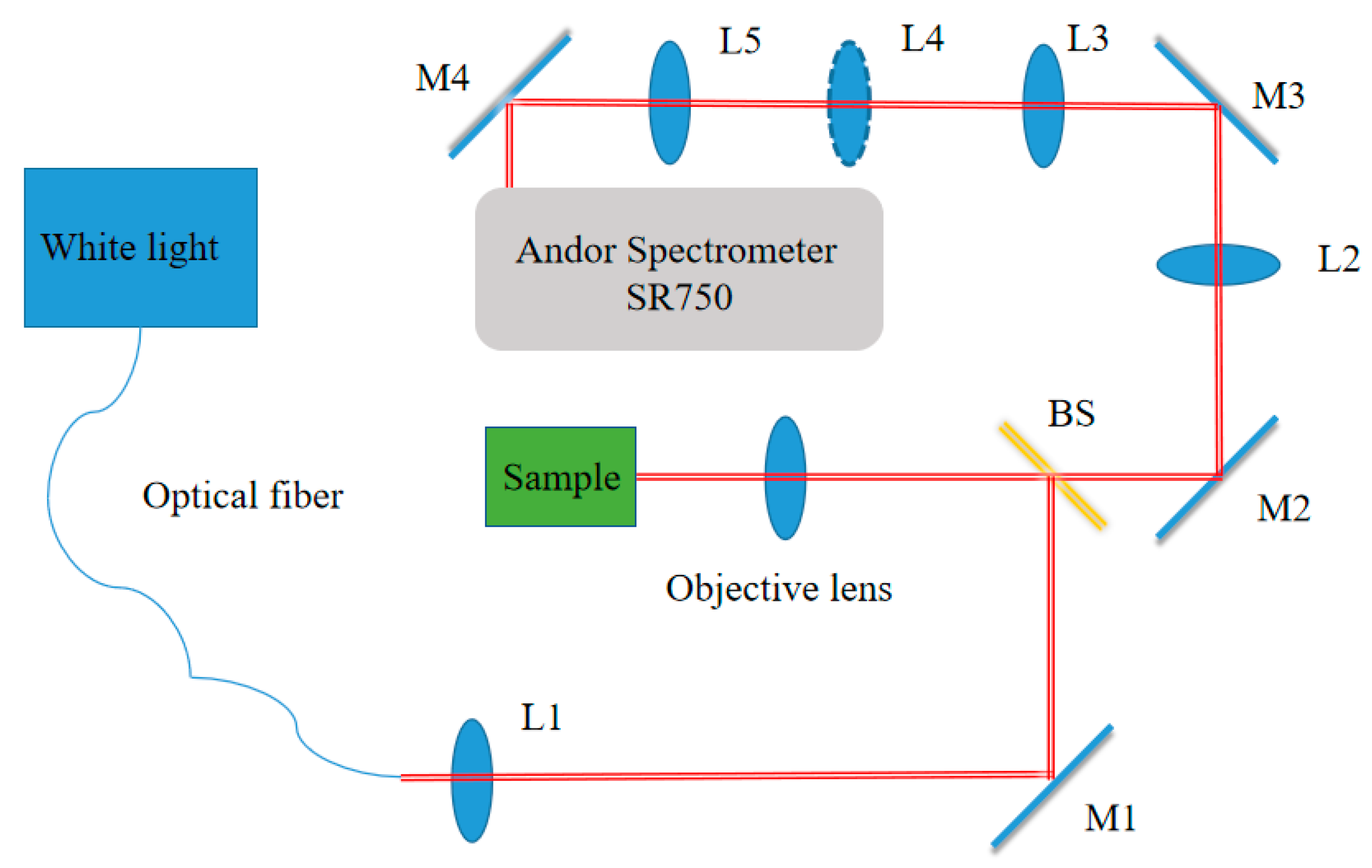
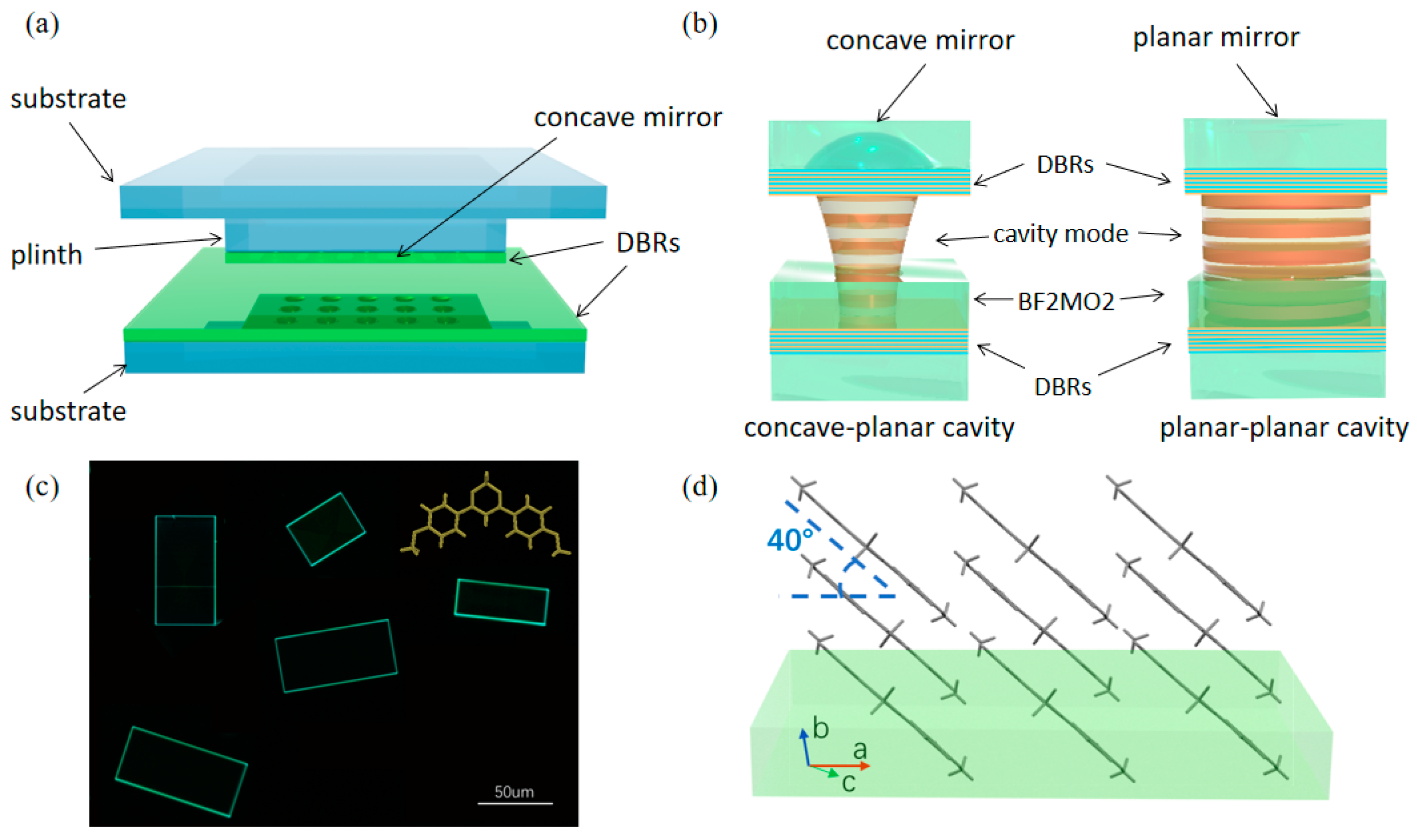
2. Materials and Methods
3. The Behavior of Free Cavity Photons
4. The Behavior of the Confined Cavity Photons: Theory
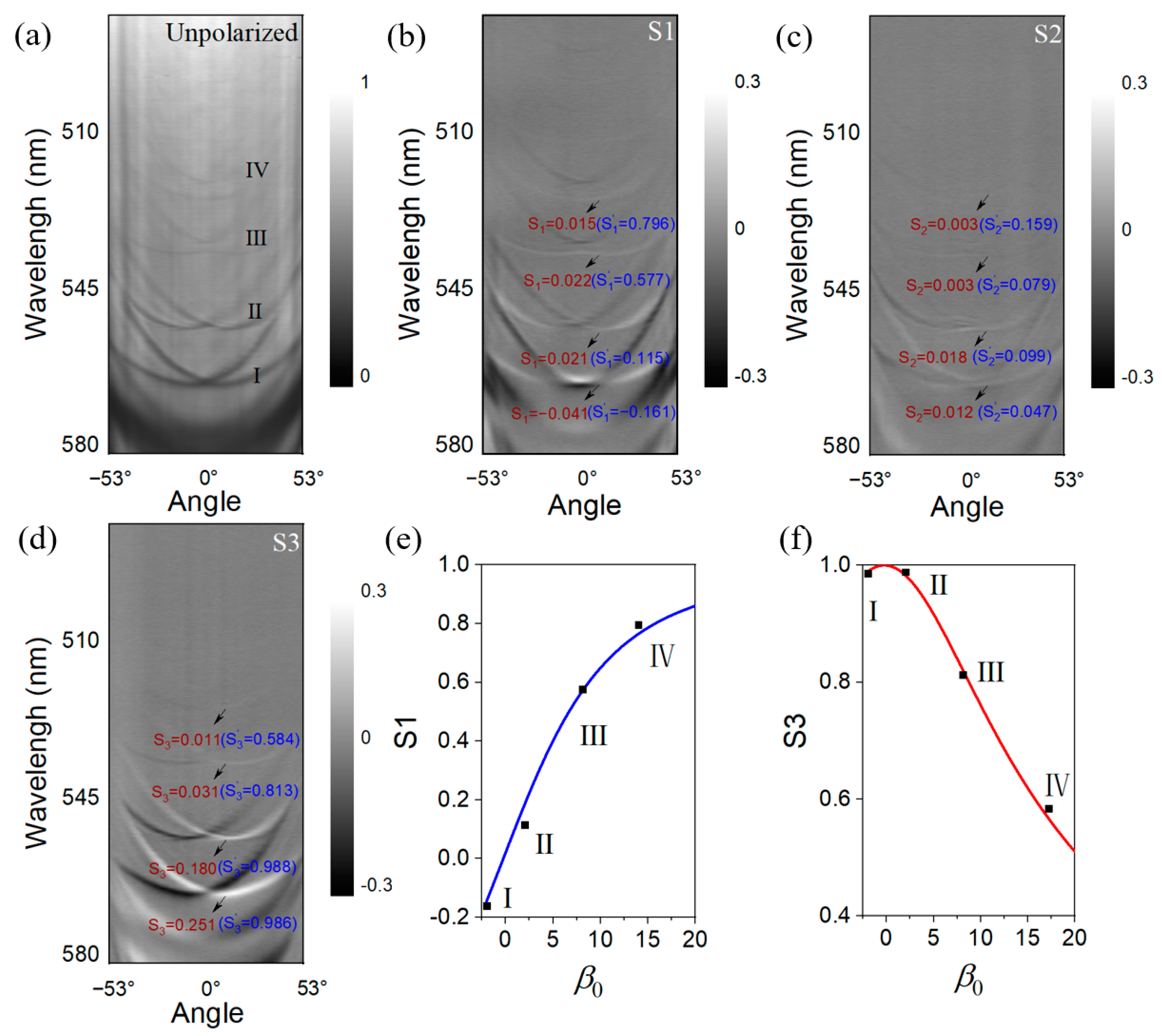
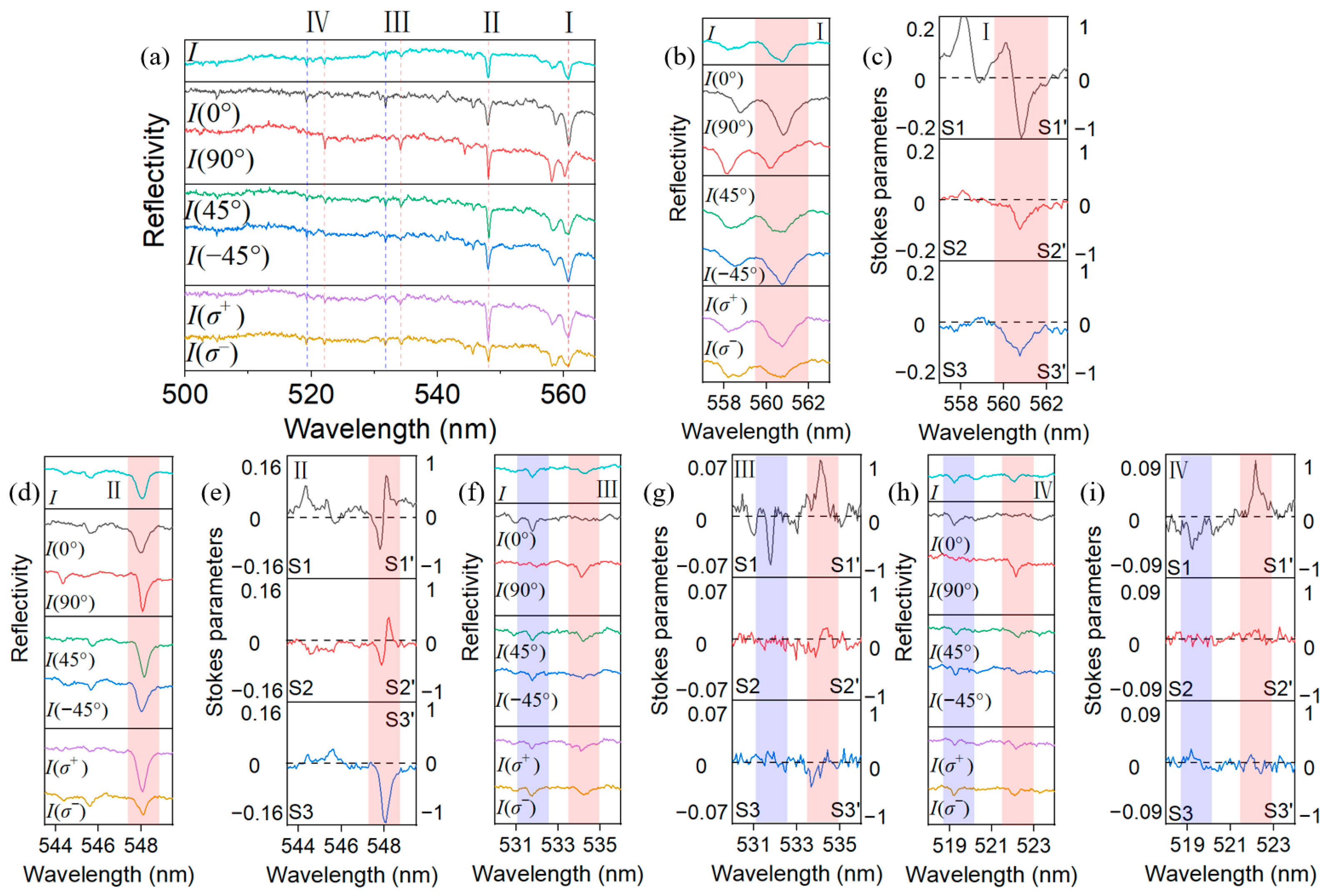
5. The Behavior of the Confined Cavity Photons: Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Lin, S.; Hong, J.; Chen, Z.; Chen, Y.; Zhou, X. Optimal weak measurement in the photonic spin Hall effect for arbitrary linear polarization incidence. Opt. Express 2022, 30, 4096–4105. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Zheng, H.; Zhong, Y.; Yu, J.; Chen, Z. Wave-Vector-Varying Pancharatnam-Berry Phase Photonic Spin Hall Effect. Phys. Rev. Lett. 2021, 126, 083901. [Google Scholar] [CrossRef]
- Shitrit, N.; Yulevich, I.; Maguid, E.; Ozeri, D.; Veksler, D.; Kleiner, V.; Hasman, E. Spin-Optical Metamaterial Route to Spin-Controlled Photonics. Science 2013, 340, 724–726. [Google Scholar] [CrossRef] [PubMed]
- Hallett, D.; Foster, A.P.; Whittaker, D.; Skolnick, M.S.; Wilson, L.R. Engineering Chiral Light-Matter Interactions in a Waveguide-Coupled Nanocavity. ACS Photonics 2022, 9, 706–713. [Google Scholar] [CrossRef]
- Klembt, S.; Harder, T.H.; Egorov, O.A.; Winkler, K.; Ge, R.; Bandres, M.A.; Emmerling, M.; Worschech, L.; Liew, T.C.H.; Segev, M.; et al. Exciton-polariton topological insulator. Nature 2018, 562, 552–556. [Google Scholar] [CrossRef] [Green Version]
- León-González, J.C.; Toscano-Negrette, R.G.; Morales, A.L.; Vinasco, J.A.; Yücel, M.B.; Sari, H.; Kasapoglu, E.; Sakiroglu, S.; Mora-Ramos, M.E.; Restrepo, R.L.; et al. Spin–Orbit and Zeeman Effects on the Electronic Properties of Single Quantum Rings: Applied Magnetic Field and Topological Defects. Nanomaterials 2023, 13, 1461. [Google Scholar] [CrossRef]
- Liu, C.; Wang, S.; Zhang, S.; Cai, Q.; Wang, P.; Tian, C.; Zhou, L.; Wu, Y.; Tao, Z. Active spintronic-metasurface terahertz emitters with tunable chirality. Adv. Photonics 2021, 3, 056002. [Google Scholar] [CrossRef]
- Wang, M.; Hu, G.; Chand, S.; Cotrufo, M.; Abate, Y.; Watanabe, K.; Taniguchi, T.; Grosso, G.; Qiu, C.-W.; Alù, A. Spin-orbit-locked hyperbolic polariton vortices carrying reconfigurable topological charges. eLight 2022, 2, 12. [Google Scholar] [CrossRef]
- Ciattoni, A.; Conti, C.; Zayats, A.V.; Marini, A. Electric Control of Spin-Orbit Coupling in Graphene-Based Nanostructures with Broken Rotational Symmetry. Laser Photonics Rev. 2020, 14, 2000214. [Google Scholar] [CrossRef]
- Lei, X.; Du, L.; Yuan, X.; Zayats, A.V. Optical spin-orbit coupling in the presence of magnetization: Photonic skyrmion interaction with magnetic domains. Nanophotonics 2021, 10, 3667–3675. [Google Scholar] [CrossRef]
- Pan, D.; Wei, H.; Gao, L.; Xu, H. Strong Spin-Orbit Interaction of Light in Plasmonic Nanostructures and Nanocircuits. Phys. Rev. Lett. 2016, 117, 166803. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Hu, H.; Pan, D.; Zhang, S.; Xu, H. Selectively Depopulating Valley-Polarized Excitons in Monolayer MoS2 by Local Chirality in Single Plasmonic Nanocavity. Nano Lett. 2020, 20, 4953–4959. [Google Scholar] [CrossRef]
- Solnyshkov, D.; Malpuech, G. Chirality in photonic systems. Comptes Rendus Phys. 2016, 17, 920–933. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Su, R.; Zhao, J.; Fieramosca, A.; Wu, J.; Li, T.; Zhang, Q.; Li, F.; Chen, Z.; Liew, T.; et al. Microcavity exciton polaritons at room temperature. Photonics Insights 2022, 1, R04. [Google Scholar] [CrossRef]
- Sanvitto, D.; Kéna-Cohen, S. The road towards polaritonic devices. Nat. Mater. 2016, 15, 1061–1073. [Google Scholar] [CrossRef]
- Kavokin, A.; Malpuech, G.; Glazov, M. Optical spin hall effect. Phys. Rev. Lett. 2005, 95, 136601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leyder, C.; Romanelli, M.; Karr, J.P.; Giacobino, E.; Liew, T.C.H.; Glazov, M.M.; Kavokin, A.V.; Malpuech, G.; Bramati, A. Observation of the optical spin Hall effect. Nat. Phys. 2007, 3, 628–631. [Google Scholar] [CrossRef]
- Hivet, R.; Flayac, H.; Solnyshkov, D.D.; Tanese, D.; Boulier, T.; Andreoli, D.; Giacobino, E.; Bloch, J.; Bramati, A.; Malpuech, G.; et al. Half-solitons in a polariton quantum fluid behave like magnetic monopoles. Nat. Phys. 2012, 8, 724–728. [Google Scholar] [CrossRef] [Green Version]
- Manni, F.; Leger, Y.; Rubo, Y.G.; Andre, R.; Deveaud, B. Hyperbolic spin vortices and textures in exciton-polariton condensates. Nat. Commun. 2013, 4, 2590. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.; Liao, Q.; Li, F.; Li, Y.; Bleu, O.; Malpuech, G.; Yao, J.; Fu, H.; Solnyshkov, D. Nontrivial band geometry in an optically active system. Nat. Commun. 2021, 12, 689. [Google Scholar] [CrossRef]
- Whittaker, C.E.; Dowling, T.; Nalitov, A.V.; Yulin, A.V.; Royall, B.; Clarke, E.; Skolnick, M.S.; Shelykh, I.A.; Krizhanovskii, D.N. Optical analogue of Dresselhaus spin-orbit interaction in photonic graphene. Nat. Photonics 2020, 15, 193–196. [Google Scholar] [CrossRef]
- Rechcińska, K.; Król, M.; Mazur, R.; Morawiak, P.; Mirek, R.; Łempicka, K.; Bardyszewski, W.; Matuszewski, M.; Kula, P.; Piecek, W.; et al. Engineering spin-orbit synthetic Hamiltonians in liquid-crystal optical cavities. Science 2019, 366, 727–730. [Google Scholar] [CrossRef] [Green Version]
- Gianfrate, A.; Bleu, O.; Dominici, L.; Ardizzone, V.; De Giorgi, M.; Ballarini, D.; Lerario, G.; West, K.W.; Pfeiffer, L.N.; Solnyshkov, D.D.; et al. Measurement of the quantum geometric tensor and of the anomalous Hall drift. Nature 2020, 578, 381–385. [Google Scholar] [CrossRef] [Green Version]
- Polimeno, L.; Lerario, G.; De Giorgi, M.; De Marco, L.; Dominici, L.; Todisco, F.; Coriolano, A.; Ardizzone, V.; Pugliese, M.; Prontera, C.T.; et al. Tuning of the Berry curvature in 2D perovskite polaritons. Nat. Nanotechnol. 2021, 16, 1349–1354. [Google Scholar] [CrossRef]
- Long, T.; Ma, X.; Ren, J.; Li, F.; Liao, Q.; Schumacher, S.; Malpuech, G.; Solnyshkov, D.; Fu, H. Helical Polariton Lasing from Topological Valleys in an Organic Crystalline Microcavity. Adv. Sci. 2022, 9, 2203588. [Google Scholar] [CrossRef] [PubMed]
- Richter, S.; Zirnstein, H.G.; Zuniga-Perez, J.; Kruger, E.; Deparis, C.; Trefflich, L.; Sturm, C.; Rosenow, B.; Grundmann, M.; Schmidt-Grund, R. Voigt Exceptional Points in an Anisotropic ZnO-Based Planar Microcavity: Square-Root Topology, Polarization Vortices, and Circularity. Phys. Rev. Lett. 2019, 123, 227401. [Google Scholar] [CrossRef] [PubMed]
- Liao, Q.; Leblanc, C.; Ren, J.; Li, F.; Li, Y.; Solnyshkov, D.; Malpuech, G.; Yao, J.; Fu, H. Experimental Measurement of the Divergent Quantum Metric of an Exceptional Point. Phys. Rev. Lett. 2021, 127, 107402. [Google Scholar] [CrossRef]
- Li, Y.; Ma, X.; Zhai, X.; Gao, M.; Dai, H.; Schumacher, S.; Gao, T. Manipulating polariton condensates by Rashba-Dresselhaus coupling at room temperature. Nat. Commun. 2022, 13, 3785. [Google Scholar] [CrossRef] [PubMed]
- Dufferwiel, S.; Li, F.; Cancellieri, E.; Giriunas, L.; Trichet, A.A.; Whittaker, D.M.; Walker, P.M.; Fras, F.; Clarke, E.; Smith, J.M.; et al. Spin Textures of Exciton-Polaritons in a Tunable Microcavity with Large TE-TM Splitting. Phys. Rev. Lett. 2015, 115, 246401. [Google Scholar] [CrossRef] [Green Version]
- Sala, V.G.; Solnyshkov, D.D.; Carusotto, I.; Jacqmin, T.; Lemaître, A.; Terças, H.; Nalitov, A.; Abbarchi, M.; Galopin, E.; Sagnes, I.; et al. Spin-Orbit Coupling for Photons and Polaritons in Microstructures. Phys. Rev. X 2015, 5, 011034. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Li, Y.; Cai, Y.; Li, P.; Tang, H.; Zhang, Y. Tunable Open-Access Microcavities for Solid-State Quantum Photonics and Polaritonics. Adv. Quantum Technol. 2019, 2, 1970061. [Google Scholar] [CrossRef]
- Ren, J.; Liao, Q.; Huang, H.; Li, Y.; Gao, T.; Ma, X.; Schumacher, S.; Yao, J.; Bai, S.; Fu, H. Efficient Bosonic Condensation of Exciton Polaritons in an H-Aggregate Organic Single-Crystal Microcavity. Nano Lett. 2020, 20, 7550–7557. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Liao, Q.; Ma, X.; Schumacher, S.; Yao, J.; Fu, H. Realization of Exciton-Mediated Optical Spin-Orbit Interaction in Organic Microcrystalline Resonators. Laser Photonics Rev. 2021, 16, 2100252. [Google Scholar] [CrossRef]
- Niesner, D.; Wilhelm, M.; Levchuk, I.; Osvet, A.; Shrestha, S.; Batentschuk, M.; Brabec, C.; Fauster, T. Giant Rashba Splitting in CH3NH3PbBr3 Organic-Inorganic Perovskite. Phys. Rev. Lett. 2016, 117, 126401. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, Y.; Luo, X.; Guo, C.; Qin, Y.; Fu, H.; Zhang, Y.; Yun, F.; Liao, Q.; Li, F. Elimination of Chirality in Three-Dimensionally Confined Open-Access Microcavities. Nanomaterials 2023, 13, 1868. https://doi.org/10.3390/nano13121868
Li Y, Li Y, Luo X, Guo C, Qin Y, Fu H, Zhang Y, Yun F, Liao Q, Li F. Elimination of Chirality in Three-Dimensionally Confined Open-Access Microcavities. Nanomaterials. 2023; 13(12):1868. https://doi.org/10.3390/nano13121868
Chicago/Turabian StyleLi, Yiming, Yuan Li, Xiaoxuan Luo, Chaowei Guo, Yuanbin Qin, Hongbing Fu, Yanpeng Zhang, Feng Yun, Qing Liao, and Feng Li. 2023. "Elimination of Chirality in Three-Dimensionally Confined Open-Access Microcavities" Nanomaterials 13, no. 12: 1868. https://doi.org/10.3390/nano13121868
APA StyleLi, Y., Li, Y., Luo, X., Guo, C., Qin, Y., Fu, H., Zhang, Y., Yun, F., Liao, Q., & Li, F. (2023). Elimination of Chirality in Three-Dimensionally Confined Open-Access Microcavities. Nanomaterials, 13(12), 1868. https://doi.org/10.3390/nano13121868







