Switchable and Tunable Terahertz Metamaterial Based on Vanadium Dioxide and Photosensitive Silicon
Abstract
1. Introduction
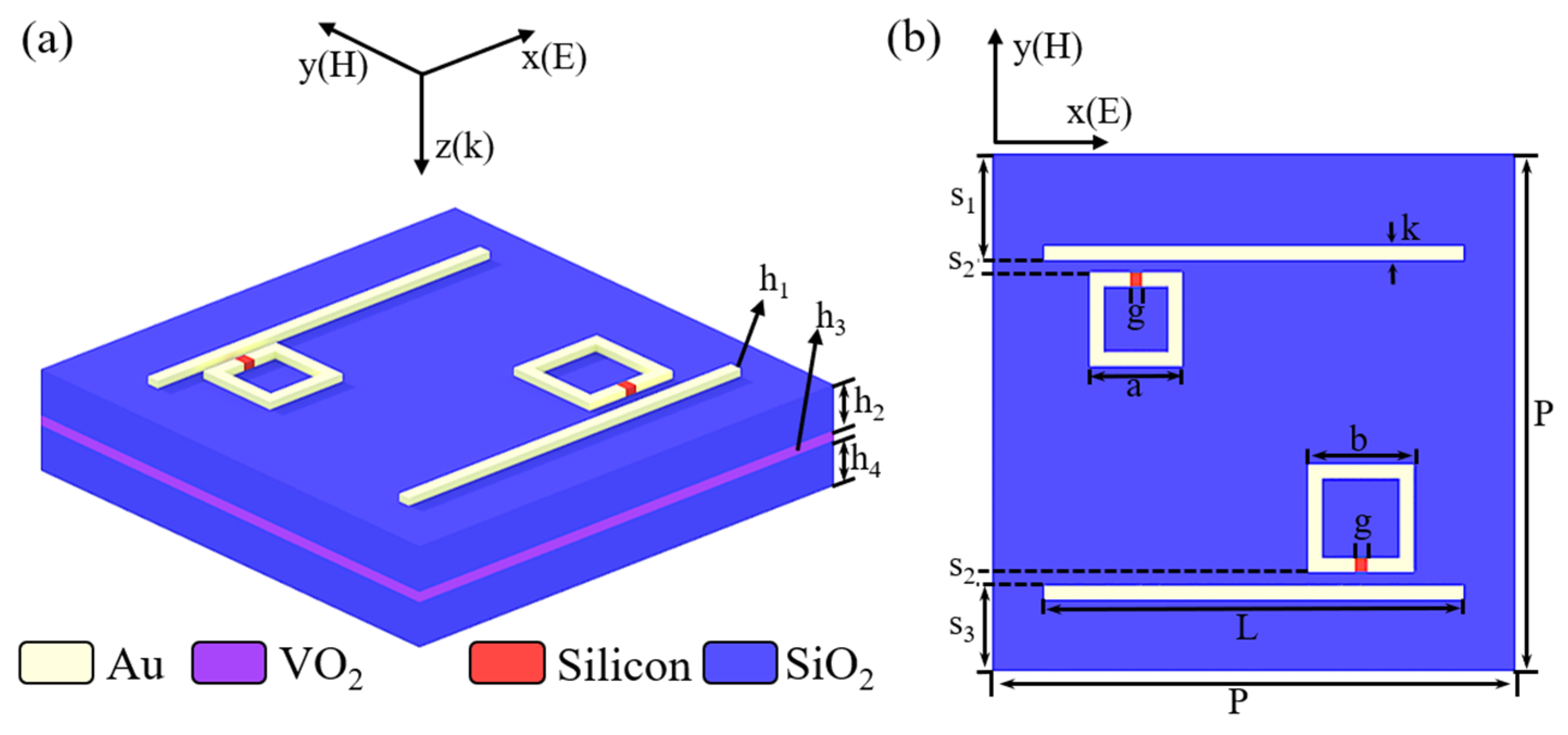
2. Materials and Methods
3. Results and Discussion
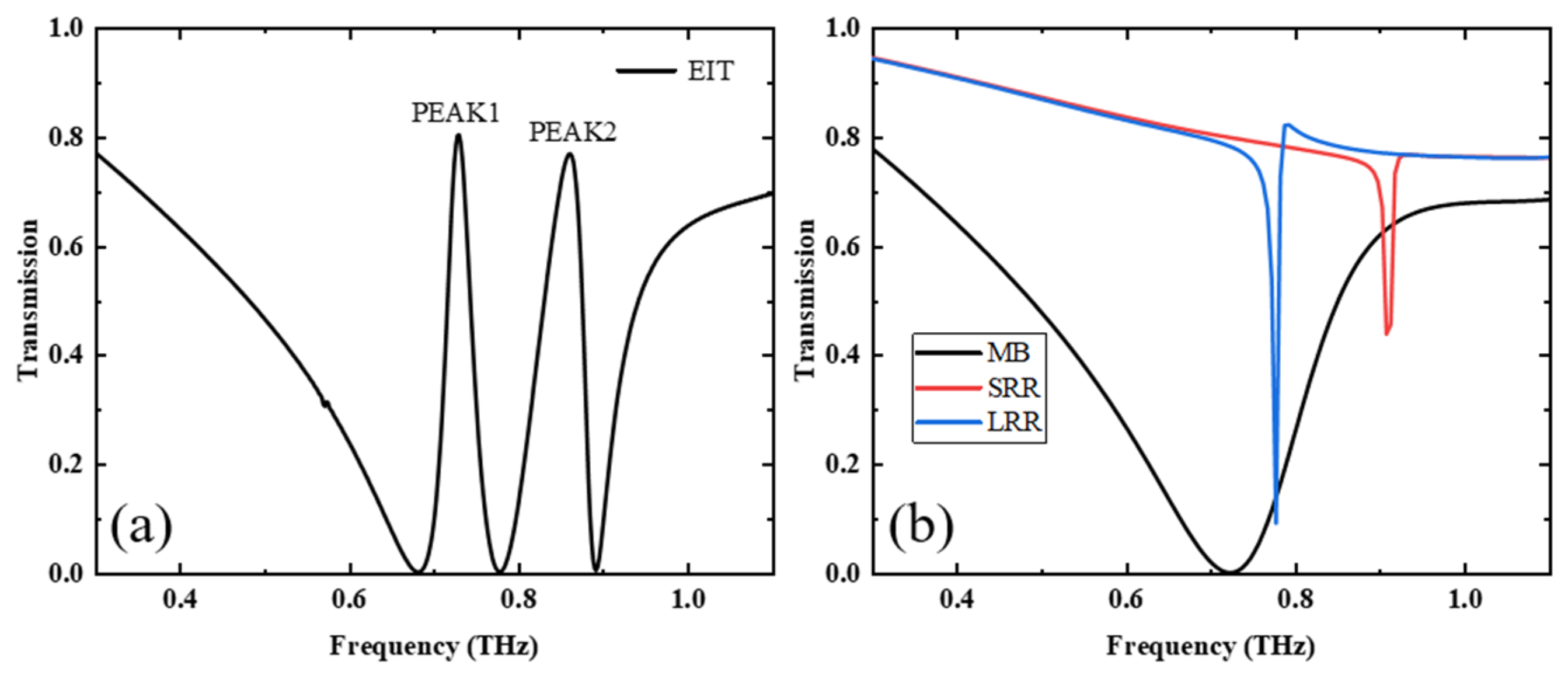
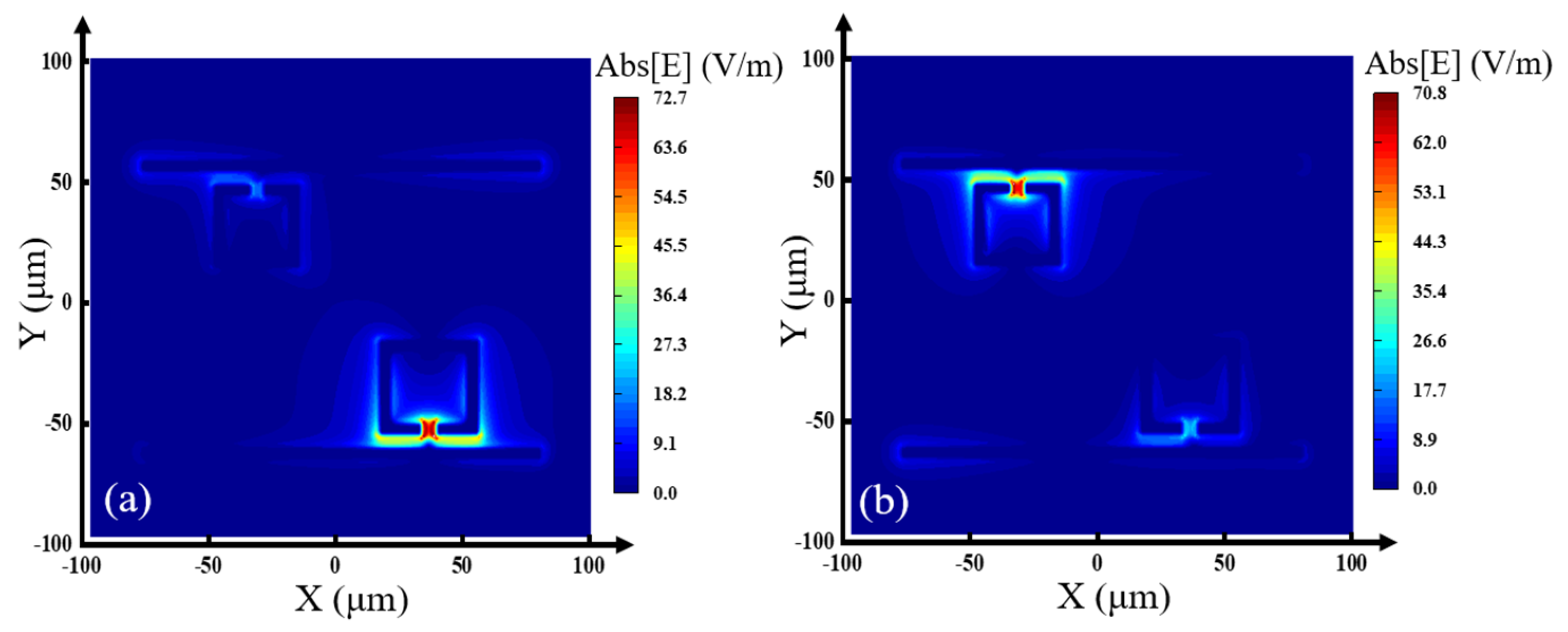
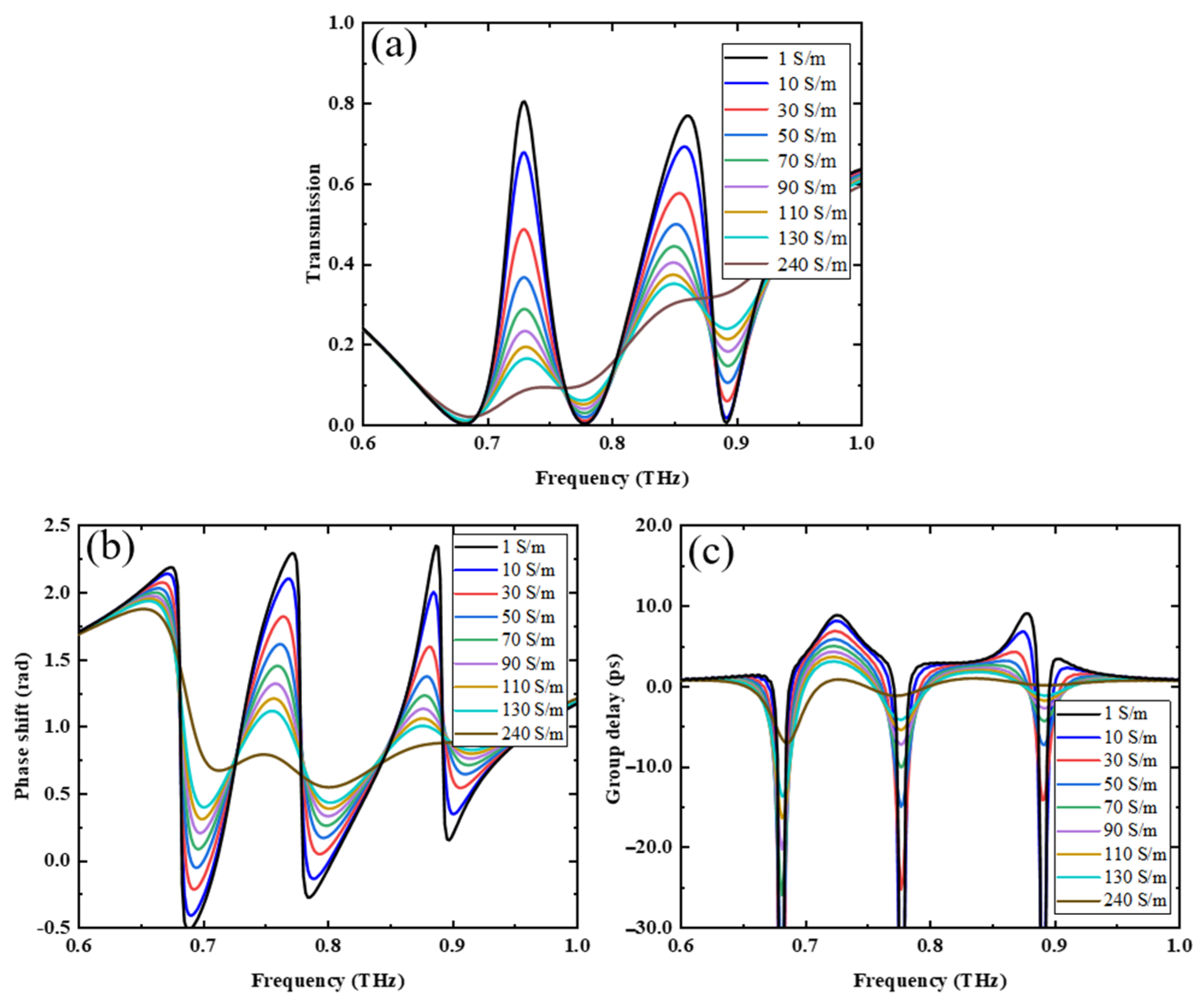
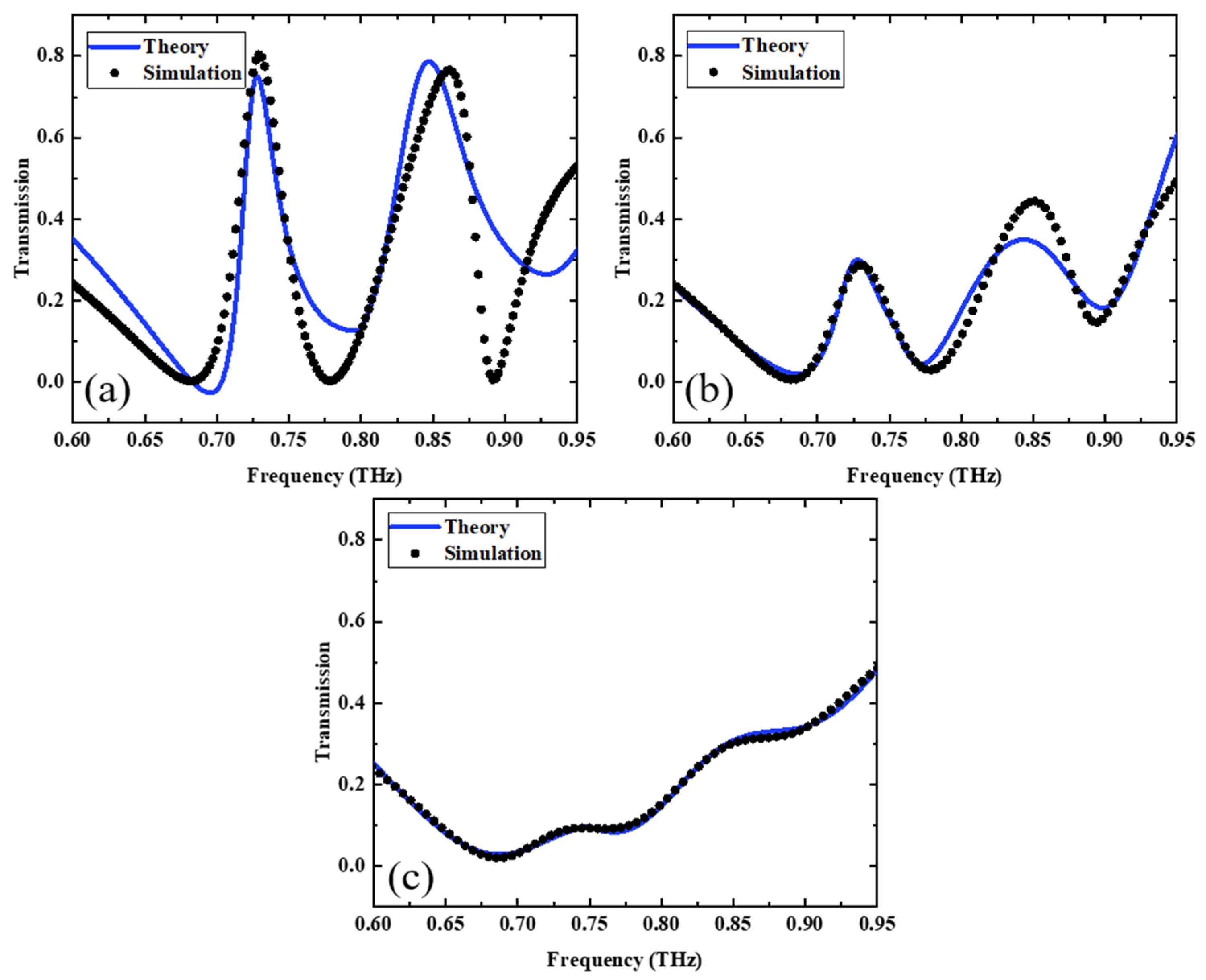
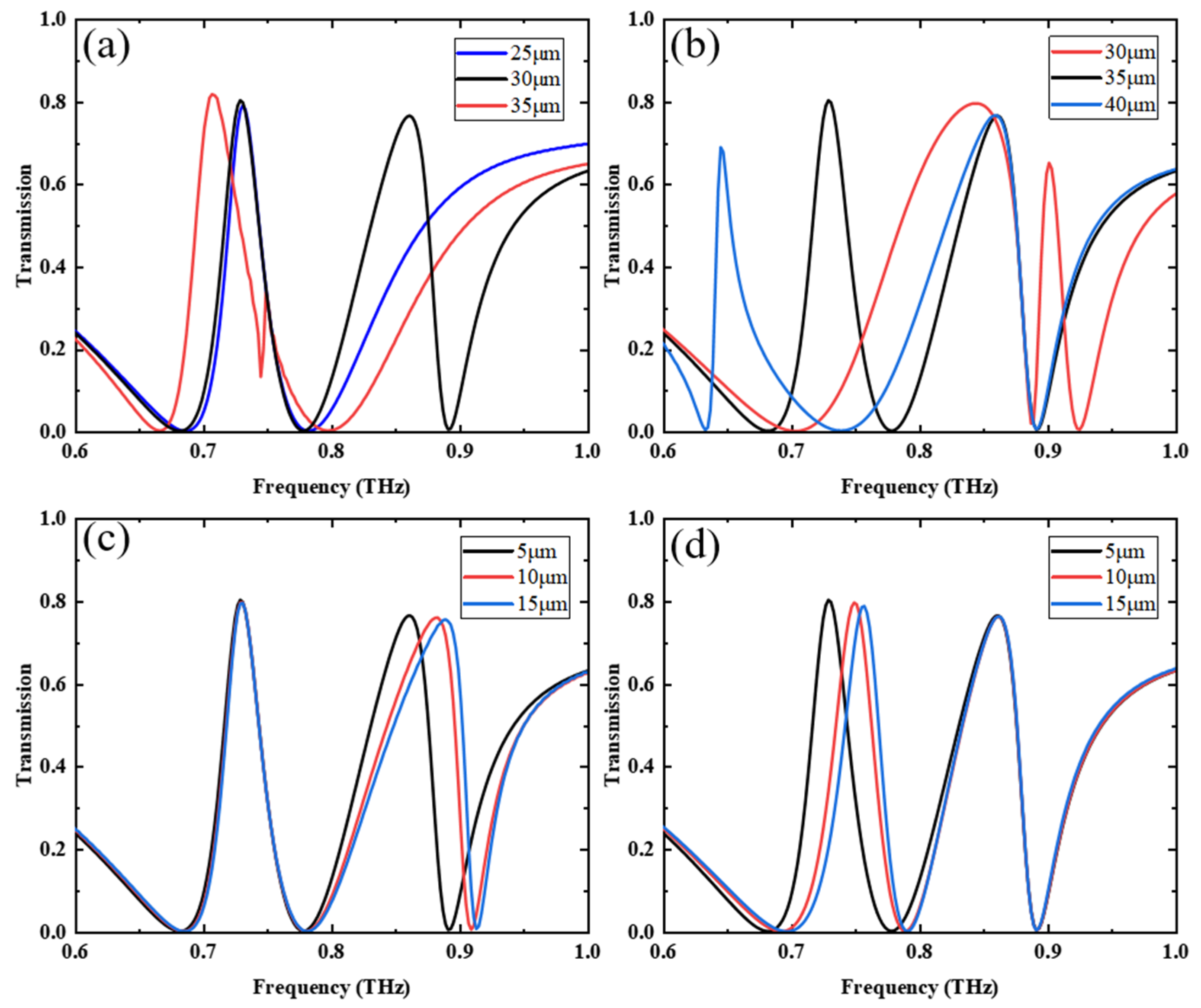
3.1. Electromagnetically Induced Transparency
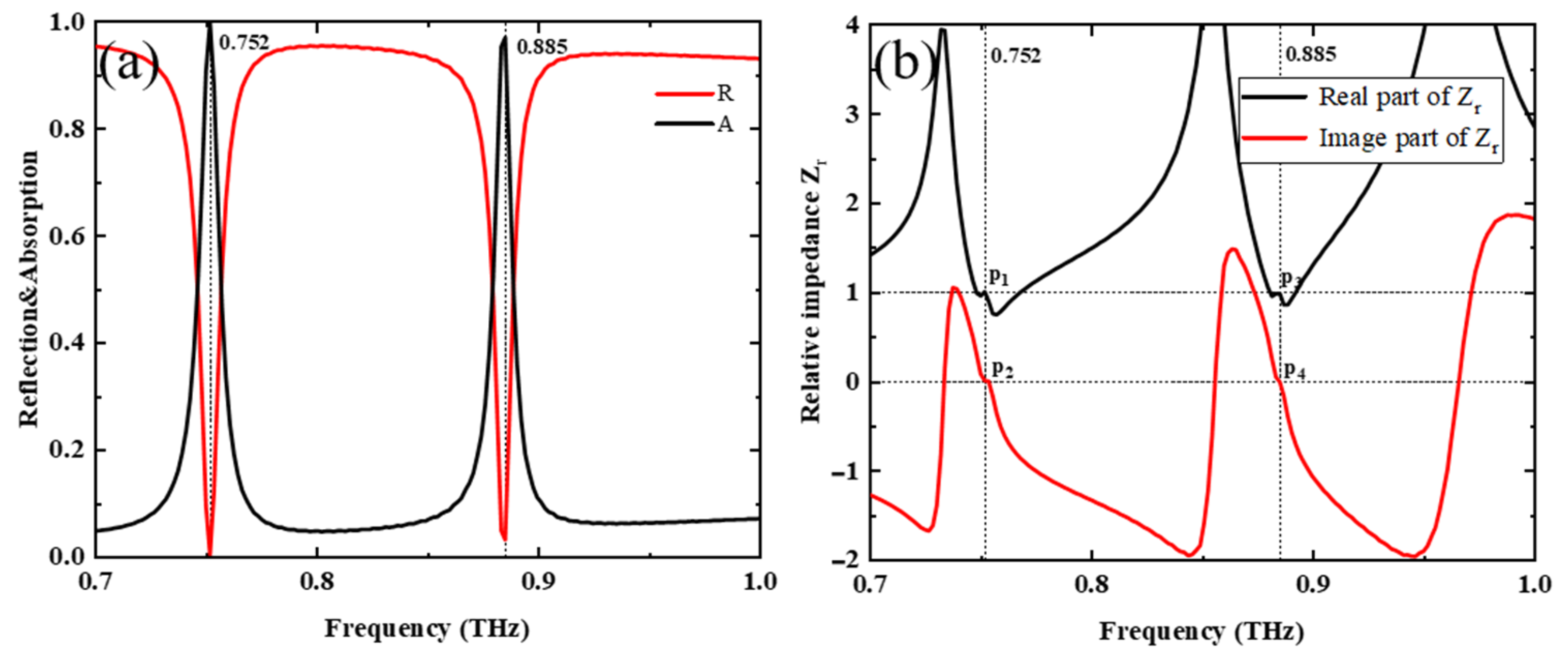
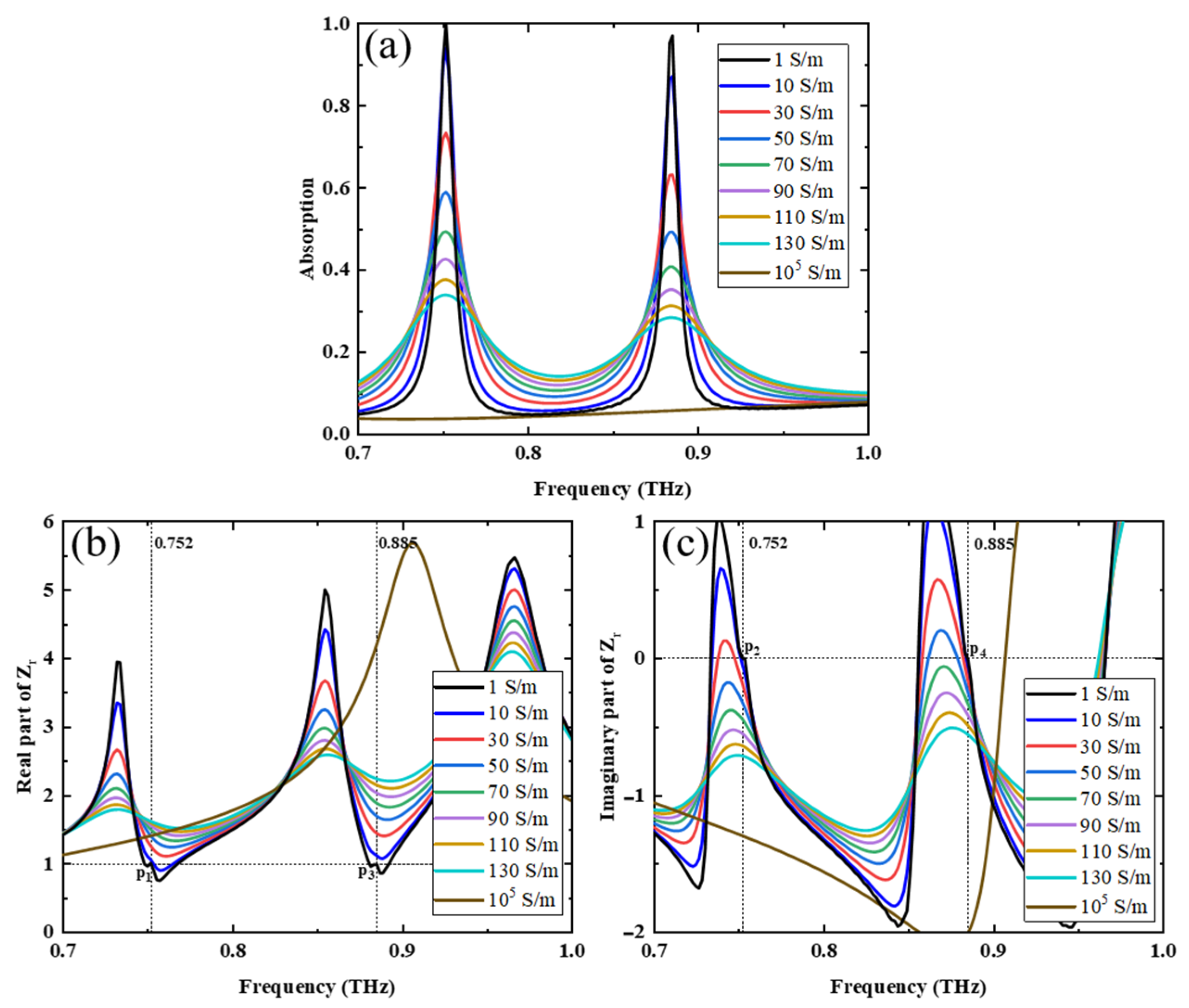
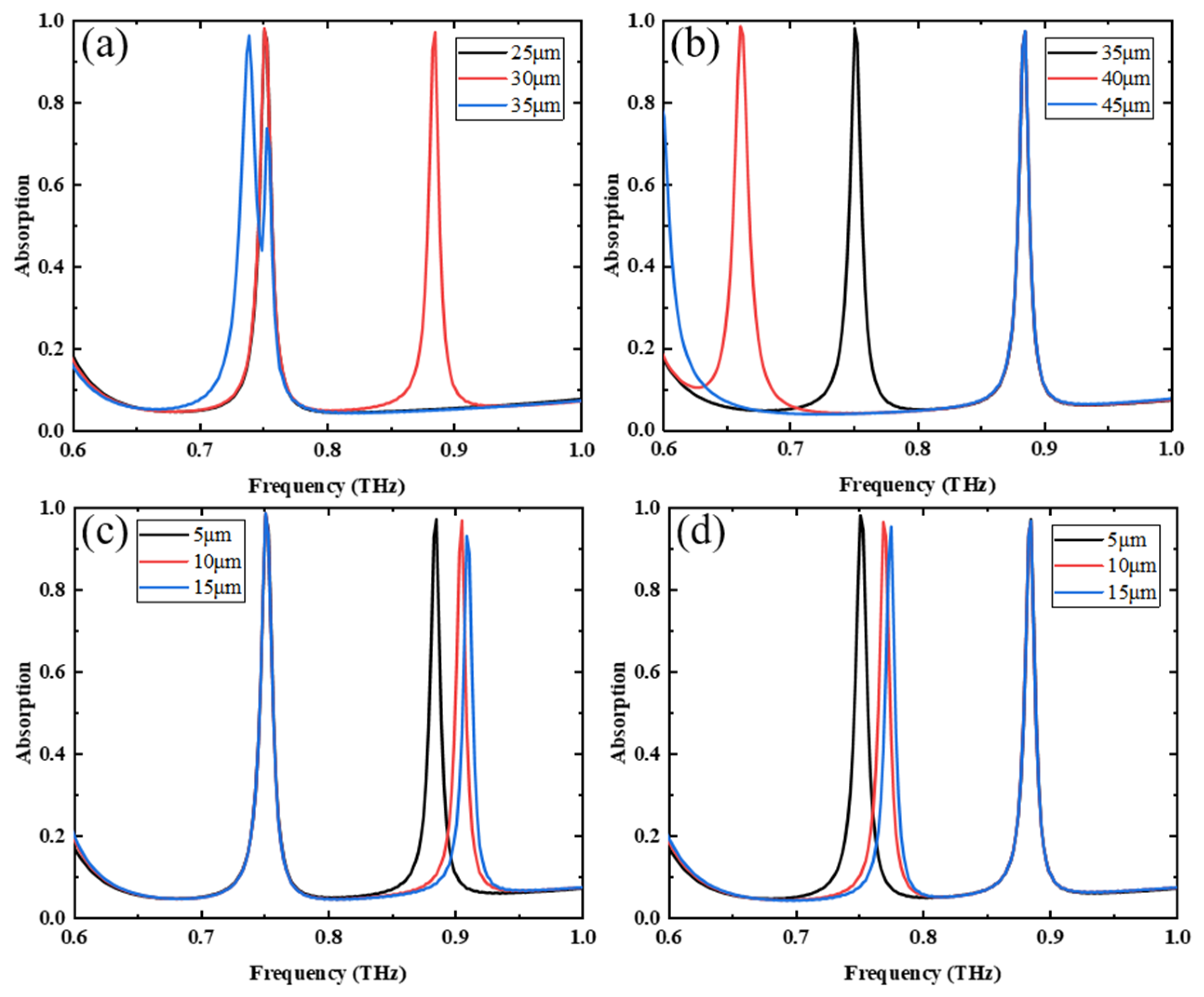
3.2. Absorption
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Otter, W.J.; Lucyszyn, S. Hybrid 3-D-Printing Technology for Tunable THz Applications. Proc. IEEE 2017, 105, 756–767. [Google Scholar] [CrossRef]
- Wang, J.; Tian, H.; Wang, Y.; Li, X.Y.; Cao, Y.J.; Li, L.; Liu, J.L.; Zhou, Z.X. Liquid crystal terahertz modulator with plasmon-induced transparency metamaterial. Opt. Express 2018, 26, 5769–5776. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.J.; Hong, H.C.; Lin, H.J.; Shen, L.G.; Yu, H.Y.; Ma, G.C.; Chen, J.R.; Liao, B.Q. Mechanistic insights into alginate fouling caused by calcium ions based on terahertz time-domain spectra analyses and DFT calculations. Water Res. 2018, 129, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub-diffraction-limited optical imaging with a silver superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef]
- Zheludev, N.I. The Road Ahead for Metamaterials. Science 2010, 328, 582–583. [Google Scholar] [CrossRef]
- Iyer, A.; Kremer, P.; Eleftheriades, G. Experimental and theoretical verification of focusing in a large, periodically loaded transmission line negative refractive index metamaterial. Opt. Express 2003, 11, 696–708. [Google Scholar] [CrossRef]
- Barzegar-Parizi, S.; Ebrahimi, A. Ultrathin, polarization-insensitive multi-band absorbers based on graphene metasurface with THz sensing application. J. Opt. Soc. Am. B Opt. Phys. 2020, 37, 2372–2381. [Google Scholar] [CrossRef]
- Wang, G.; Wu, T.; Jia, Y.; Gao, Y.; Gao, Y.C. Switchable Terahertz Absorber from Single Broadband to Dual Broadband Based on Graphene and Vanadium Dioxide. Nanomaterials 2022, 12, 2172. [Google Scholar] [CrossRef]
- Tao, H.; Landy, N.I.; Bingham, C.M.; Zhang, X.; Averitt, R.D.; Padilla, W.J. A metamaterial absorber for the terahertz regime: Design, fabrication and characterization. Opt. Express 2008, 16, 7181–7188. [Google Scholar] [CrossRef]
- Li, J.S.; Li, X.J. Switchable tri-function terahertz metasurface based on polarization vanadium dioxide and photosensitive silicon. Opt. Express 2022, 30, 12823–12834. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.Y.; Sui, J.Y.; Zhang, H.F. Switchable ultra-broadband absorption and polarization conversion metastructure controlled by light. Opt. Express 2022, 30, 34172–34187. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Langguth, L.; Weiss, T.; Kastel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 2009, 8, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Shao, Y.B.; Buyingaridi; Ma, S.; Gao, Y.C. Terahertz hybrid metal-graphene metamaterials with tunable dual-band electromagnetically induced transparency. Optik 2021, 240, 166784. [Google Scholar] [CrossRef]
- Wang, T.L.; Li, T.T.; Yao, H.Y.; Lu, Y.Y.; Yan, X.; Cao, M.Y.; Liang, L.J.; Yang, M.S.; Yao, J.Q. High-sensitivity modulation of electromagnetically induced transparency analog in a THz asymmetric metasurface integrating perovskite and graphene. Photonics Res. 2022, 10, 2317–2327. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.Y.; Liu, M.D.; Zhao, Y.K.; Liu, S.D.; Zhang, Y.P. Tunable multiple plasmon-induced transparency in three-dimensional Dirac semimetal metamaterials. Opt. Commun. 2018, 423, 57–62. [Google Scholar] [CrossRef]
- Jiang, Y.; Ning, H.Y.; Tian, C.G.; Jiang, B.J.; Li, Q.; Yan, H.J.; Zhang, X.L.; Wang, J.Q.; Jing, L.Q.; Fu, H.G. Single-crystal TiO2 nanorods assembly for efficient and stable cocatalyst-free photocatalytic hydrogen evolution. Appl. Catal. B Environ. 2018, 229, 1–7. [Google Scholar] [CrossRef]
- Zhao, J.X.; Song, J.L.; Zhou, Y.; Zhao, R.L.; Zhou, J.H. Tunable multiple plasmon-induced transparency in a simple terahertz Dirac semimetal based metamaterial. Opt. Mater. Express 2019, 9, 3325–3332. [Google Scholar] [CrossRef]
- Wu, T.; Wang, G.; Jia, Y.; Shao, Y.B.; Gao, Y.; Gao, Y.C. Multi-control plasmon-induced transparency via graphene and bulk Dirac semimetal. Diam. Relat. Mater. 2022, 129, 109369. [Google Scholar] [CrossRef]
- Alves, F.; Kearney, B.; Grbovic, D.; Karunasiri, G. Narrowband terahertz emitters using metamaterial films. Opt. Express 2012, 20, 21025–21032. [Google Scholar] [CrossRef]
- Jeong, Y.G.; Han, S.; Rhie, J.; Kyoung, J.S.; Choi, J.W.; Park, N.; Hong, S.; Kim, B.J.; Kim, H.T.; Kim, D.S. A Vanadium Dioxide Metamaterial Disengaged from Insulator-toMetal Transition. Nano Lett. 2015, 15, 6318–6323. [Google Scholar] [CrossRef] [PubMed]
- Dicken, M.J.; Aydin, K.; Pryce, I.M.; Sweatlock, L.A.; Boyd, E.M.; Walavalkar, S.; Ma, J.; Atwater, H.A. Frequency tunable near-infrared metamaterials based on VO2 phase transition. Opt. Express 2009, 17, 18330–18339. [Google Scholar] [CrossRef]
- Kats, M.A.; Sharma, D.; Lin, J.; Genevet, P.; Blanchard, R.; Yang, Z.; Qazilbash, M.M.; Basov, D.N.; Ramanathan, S.; Capasso, F. Ultra-thin perfect absorber employing a tunable phase change material. Appl. Phys. Lett. 2012, 101, 221101. [Google Scholar] [CrossRef]
- Wen, Q.Y.; Zhang, H.W.; Yang, Q.H.; Xie, Y.S.; Chen, K.; Liu, Y.L. Terahertz metamaterials with VO2 cut-wires for thermal tunability. Appl. Phys. Lett. 2010, 97, 021111. [Google Scholar] [CrossRef]
- Shen, N.H.; Massaouti, M.; Gokkavas, M.; Manceau, J.M.; Ozbay, E.; Kafesaki, M.; Koschny, T.; Tzortzakis, S.; Soukoulis, C.M. Optically Implemented Broadband Blueshift Switch in the Terahertz Regime. Phys. Rev. Lett. 2011, 106, 037403. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.Q.; Singh, R.; Liu, X.J.; Zhang, X.Q.; Ma, Y.F.; Zhang, S.; Maier, S.A.; Tian, Z.; Azad, A.K.; Chen, H.T.; et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat. Commun. 2012, 3, 1151. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, P.; Xu, X.F. Study on a terahertz modulator based on metamaterial with photoinduced vanadium dioxide film. J. Mod. Opt. 2016, 63, 1073–1077. [Google Scholar] [CrossRef]
- Liu, C.X.; Liu, P.G.; Yang, C.; Lin, Y.; Zha, S. Dynamic electromagnetically induced transparency based on a metal-graphene hybrid metamaterial. Opt. Mater. Express 2018, 8, 1132–1142. [Google Scholar] [CrossRef]
- Zheng, D.Y.; Lin, Y.S. Tunable Dual-Split-Disk Resonator with Electromagnetically Induced Transparency Characteristic. Adv. Mater. Technol. 2020, 5, 2000584. [Google Scholar] [CrossRef]
- Fang, Z.Y.; Pan, C.D.; Xue, Y.X.; Wu, B.T.; Wu, E. Switching electromagnetically induced transparency in all-dielectric Si metamaterials with orthogonal double bright modes. J. Opt. 2021, 23, 085101. [Google Scholar] [CrossRef]
- Liu, W.W.; Song, Z.Y. Terahertz absorption modulator with largely tunable bandwidth and intensity. Carbon 2021, 174, 617–624. [Google Scholar] [CrossRef]
- Ren, K.; He, Y.M.; Ren, X.B.; Zhang, Y.; Han, Q.; Wang, L.D.; Xu, M.J. Dynamically tunable multi-channel and polarization-independent electromagnetically induced transparency in terahertz metasurfaces. J. Phys. D Appl. Phys. 2020, 53, 135107. [Google Scholar] [CrossRef]
- Song, Z.Y.; Deng, Y.D.; Zhou, Y.G.; Liu, Z.Y. Terahertz toroidal metamaterial with tunable properties. Opt. Express 2019, 27, 5792–5797. [Google Scholar] [CrossRef]
- Ding, F.; Zhong, S.M.; Bozhevolnyi, S.I. Vanadium Dioxide Integrated Metasurfaces with Switchable Functionalities at Terahertz Frequencies. Adv. Opt. Mater. 2018, 6, 1701204. [Google Scholar] [CrossRef]
- Liu, M.K.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.B.; Keiser, G.R.; Sternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.W.; et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 2012, 487, 345–348. [Google Scholar] [CrossRef]
- Wang, S.X.; Kang, L.; Werner, D.H. Hybrid Resonators and Highly Tunable Terahertz Metamaterials Enabled by Vanadium Dioxide (VO2). Sci. Rep. 2017, 7, 4326. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Zhao, Y.; Holtz, M.; Fan, Z.Y.; Bernussi, A.A. Effect of substrate orientation on terahertz optical transmission through VO2 thin films and application to functional antireflection coatings. J. Opt. Soc. Am. B Opt. Phys. 2012, 29, 2373–2378. [Google Scholar] [CrossRef]
- Kim, S.J.; Lee, D.; Chae, J.Y.; Ko, B.; Lee, H.; Paik, T.; Hong, S.H. Reconfigurable, vivid reflective colors based on solution-processed Fabry-Perot absorber using thermochromic vanadium dioxide. Appl. Surf. Sci. 2021, 565, 150610. [Google Scholar] [CrossRef]
- Tai, Y.H.; Tu, C.C.; Yuan, Y.C.; Chang, Y.J.; Wang, P.C.; Kuo, Y.W. The Photosensitive Mechanism of Gap-Type Amorphous Silicon TFT. IEEE Trans. Electron Devices 2021, 68, 6177–6181. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Gong, R.Z.; Zhao, J.C. A photoexcited switchable perfect metamaterial absorber/reflector with polarization-independent and wide-angle for terahertz waves. Opt. Mater. 2016, 62, 28–33. [Google Scholar] [CrossRef]
- Xu, J.; Tang, J.; Cheng, Y.; Chen, M.; Wang, H.X.; Xiong, J.F.; Wang, T.R.; Wang, S.Z.; Zhang, Y.D.; Wen, H.; et al. Multifunctional analysis and verification of lightning-type electromagnetic metasurfaces. Opt. Express 2022, 30, 17008–17025. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Xu, K.-D. Switchable and tunable bifunctional THz metamaterial absorber. J. Opt. Soc. Am. B Opt. Phys. 2022, 39, A52–A60. [Google Scholar] [CrossRef]
- Liu, T.T.; Wang, H.X.; Liu, Y.; Xiao, L.S.; Yi, Z.; Zhou, C.B.; Xiao, S.Y. Active manipulation of electromagnetically induced transparency in a terahertz hybrid metamaterial. Opt. Commun. 2018, 426, 629–634. [Google Scholar] [CrossRef]
- Yahiaoui, R.; Manjappa, M.; Srivastava, Y.K.; Singh, R. Active control and switching of broadband electromagnetically induced transparency in symmetric metadevices. Appl. Phys. Lett. 2017, 111, 17008. [Google Scholar] [CrossRef]
- Qiu, Y.; Yan, D.X.; Feng, Q.Y.; Li, X.J.; Zhang, L.; Qiu, G.H.; Li, J.N. Vanadium dioxide-assisted switchable multifunctional metamaterial structure. Opt. Express 2022, 30, 26544–26556. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71, 036617. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, Q.P.; Cai, H.L.; Lin, X.X.; Lu, Y.L. A broadband and switchable VO2-based perfect absorber at the THz frequency. Opt. Commun. 2018, 426, 443–449. [Google Scholar] [CrossRef]
- Costa, F.; Genovesi, S.; Monorchio, A.; Manara, G. A Circuit-Based Model for the Interpretation of Perfect Metamaterial Absorbers. IEEE Trans. Antennas Propag. 2013, 61, 1201–1209. [Google Scholar] [CrossRef]
- Li, H.; Xu, W.H.; Cui, Q.; Wang, Y.; Yu, J. Theoretical design of a reconfigurable broadband integrated metamaterial terahertz device. Opt. Express 2020, 28, 40060–40074. [Google Scholar] [CrossRef]
- Wu, T.; Wang, G.; Jia, Y.; Shao, Y.B.; Chen, C.; Han, J.; Gao, Y.; Gao, Y.C. Dual-Spectral Plasmon-Induced Transparent Terahertz Metamaterial with Independently Tunable Amplitude and Frequency. Nanomaterials 2021, 11, 2876. [Google Scholar] [CrossRef]
- Ren, K.; Zhang, Y.; Ren, X.B.; He, Y.M.; Han, Q. Polarization-sensitive and active controllable electromagnetically induced transparency in U-shaped terahertz metamaterials. Front. Optoelectron. 2021, 14, 221–228. [Google Scholar] [CrossRef] [PubMed]


| Reference | Adjustable Material | Maximum Modulation Depth through the Peak (EIT) | Maximum Modulation Depth of Peak Absorption | Maximum Group Delay (ps) |
|---|---|---|---|---|
| [28] | Graphene | 81% | none | 3.6 |
| [29] | None | 75.58% | none | none |
| [49] | VO2 and graphene | 70% | 90% | none |
| [27] | VO2 | None | 78% | none |
| [50] | STO and graphene | 82.46% | none | 1.47 |
| [51] | Silicon | 61.8% | none | none |
| This work | Silicon and VO2 | 90.05% | 96.39% | 9.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, G.; Liu, J.; Zuo, S.; Li, M.; Yang, S.; Jia, Y.; Gao, Y. Switchable and Tunable Terahertz Metamaterial Based on Vanadium Dioxide and Photosensitive Silicon. Nanomaterials 2023, 13, 2144. https://doi.org/10.3390/nano13142144
Zhang X, Wang G, Liu J, Zuo S, Li M, Yang S, Jia Y, Gao Y. Switchable and Tunable Terahertz Metamaterial Based on Vanadium Dioxide and Photosensitive Silicon. Nanomaterials. 2023; 13(14):2144. https://doi.org/10.3390/nano13142144
Chicago/Turabian StyleZhang, Xin, Guan Wang, Jia Liu, Shiyi Zuo, Meichen Li, Shuang Yang, Yang Jia, and Yachen Gao. 2023. "Switchable and Tunable Terahertz Metamaterial Based on Vanadium Dioxide and Photosensitive Silicon" Nanomaterials 13, no. 14: 2144. https://doi.org/10.3390/nano13142144
APA StyleZhang, X., Wang, G., Liu, J., Zuo, S., Li, M., Yang, S., Jia, Y., & Gao, Y. (2023). Switchable and Tunable Terahertz Metamaterial Based on Vanadium Dioxide and Photosensitive Silicon. Nanomaterials, 13(14), 2144. https://doi.org/10.3390/nano13142144






