Water–Aluminum Interaction as Driving Force of Linde Type A Aluminophosphate Hydration
Abstract
:1. Introduction
2. Materials and Methods
2.1. First-Principles Calculations
2.1.1. Vibrational Density of States
2.1.2. Atomic Point Charges
2.1.3. Ab Initio Molecular Dynamics
2.2. Classical Molecular Dynamics Simulations
2.2.1. Initial Structure Preparation
2.2.2. Force-Field Validation
2.2.3. X-ray Structure Factors
2.2.4. Translational and Orientational Diffusion
2.2.5. Bulk Water as a Reference
3. Results and Discussion
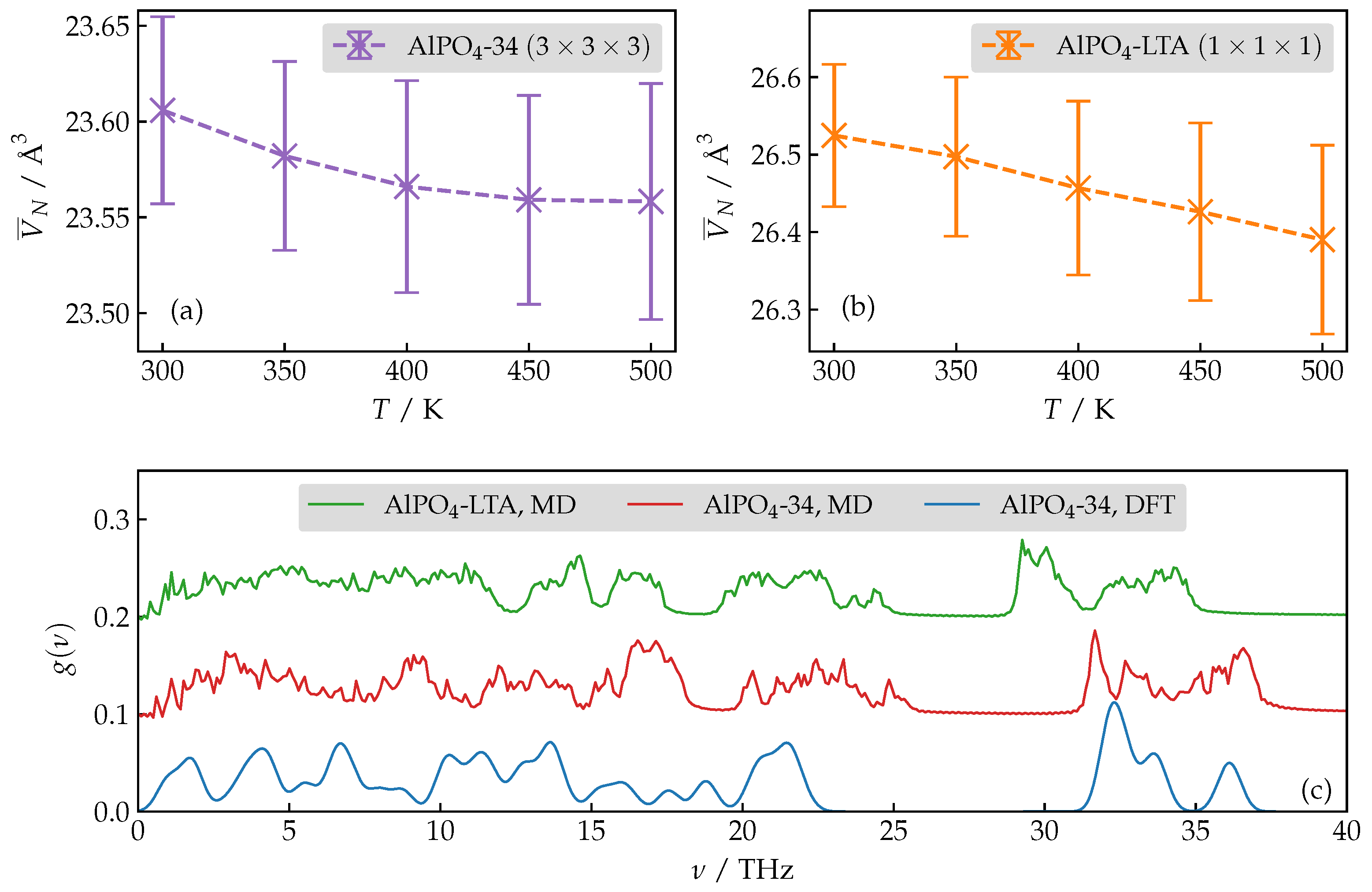
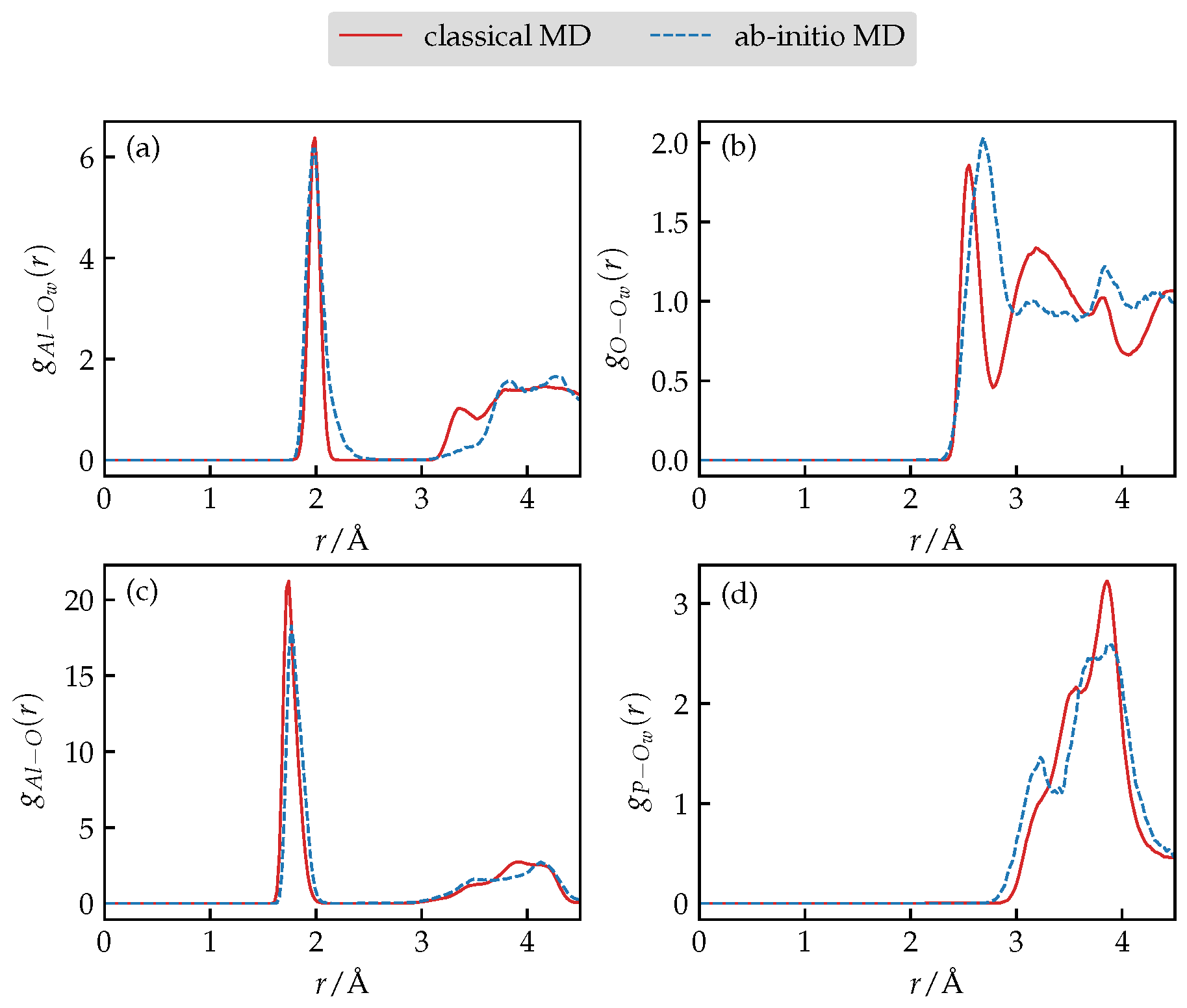
3.1. Force-Field Validation
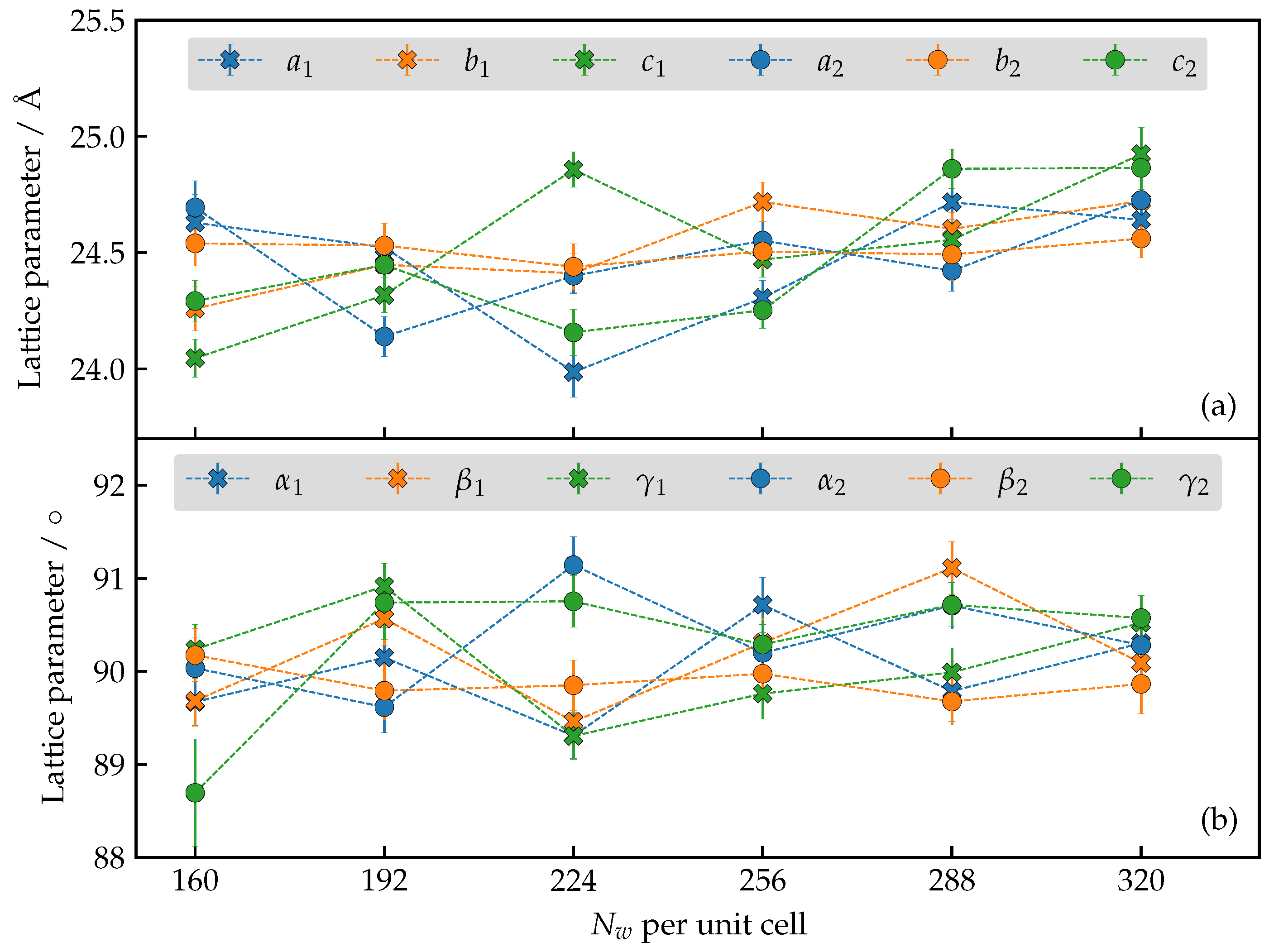
3.2. Force-Field Optimization
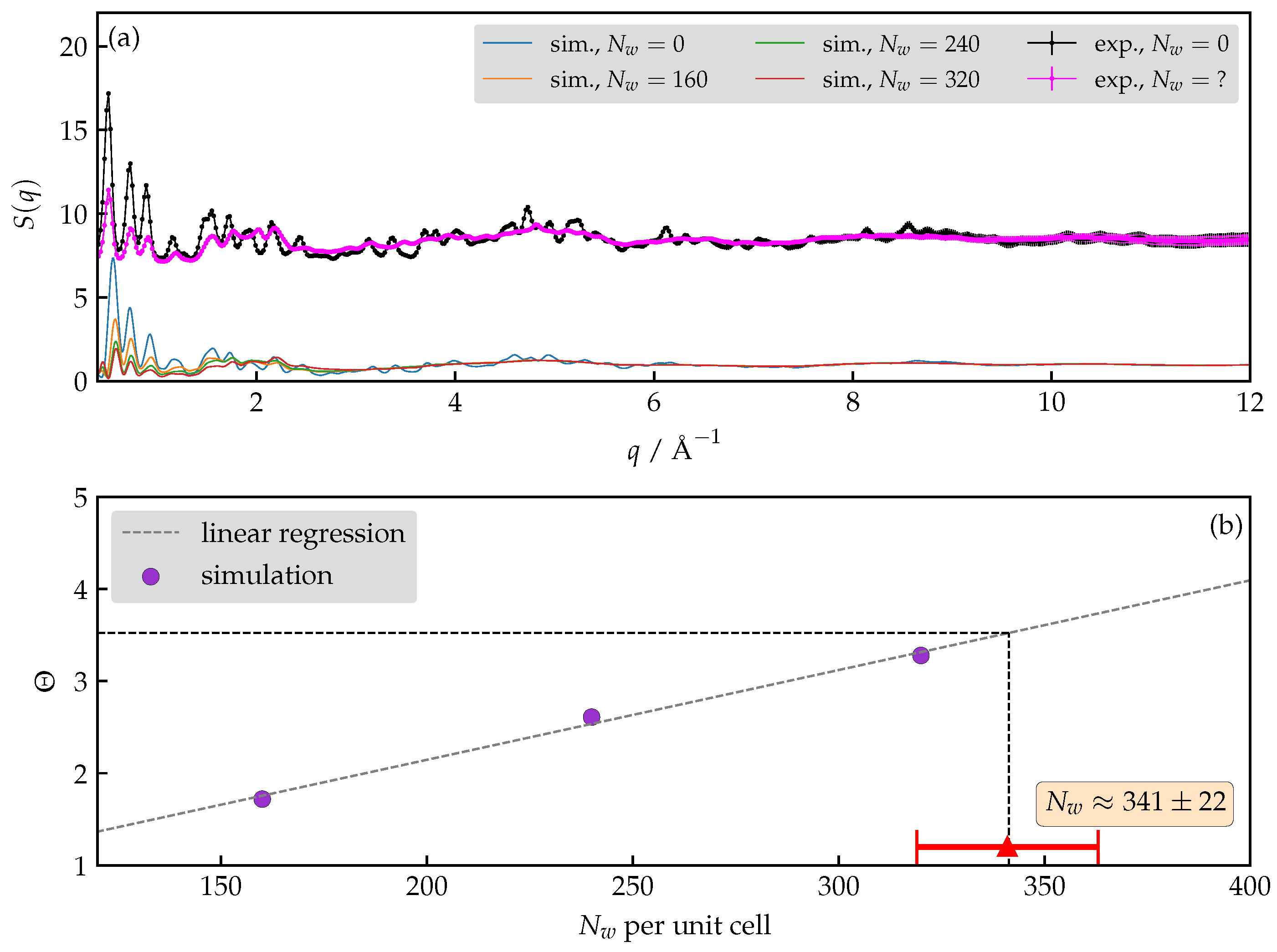
3.3. How Many Water Molecules Are Present in the Unit Cell of the Hydrated AlPO4-LTA?
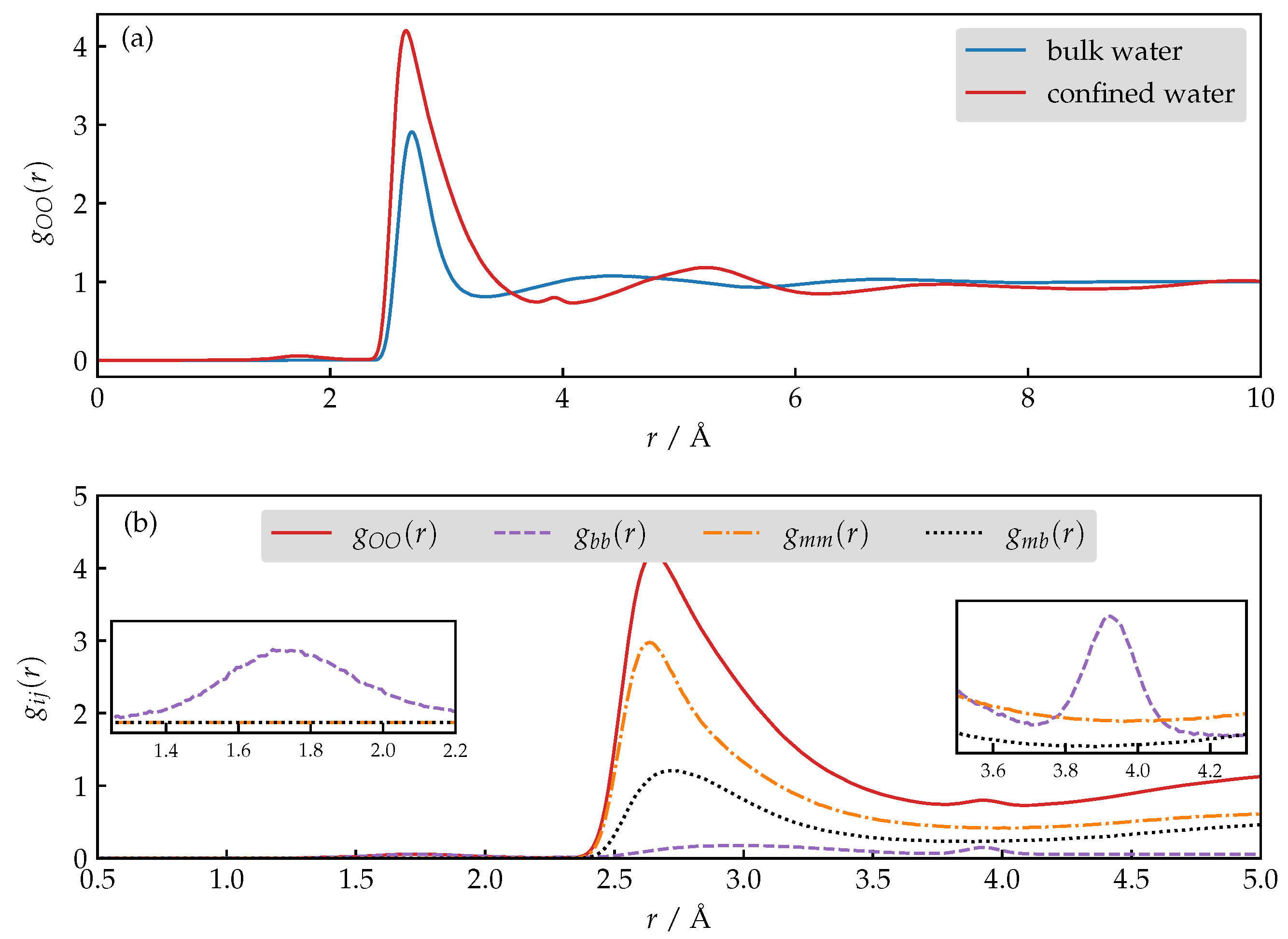
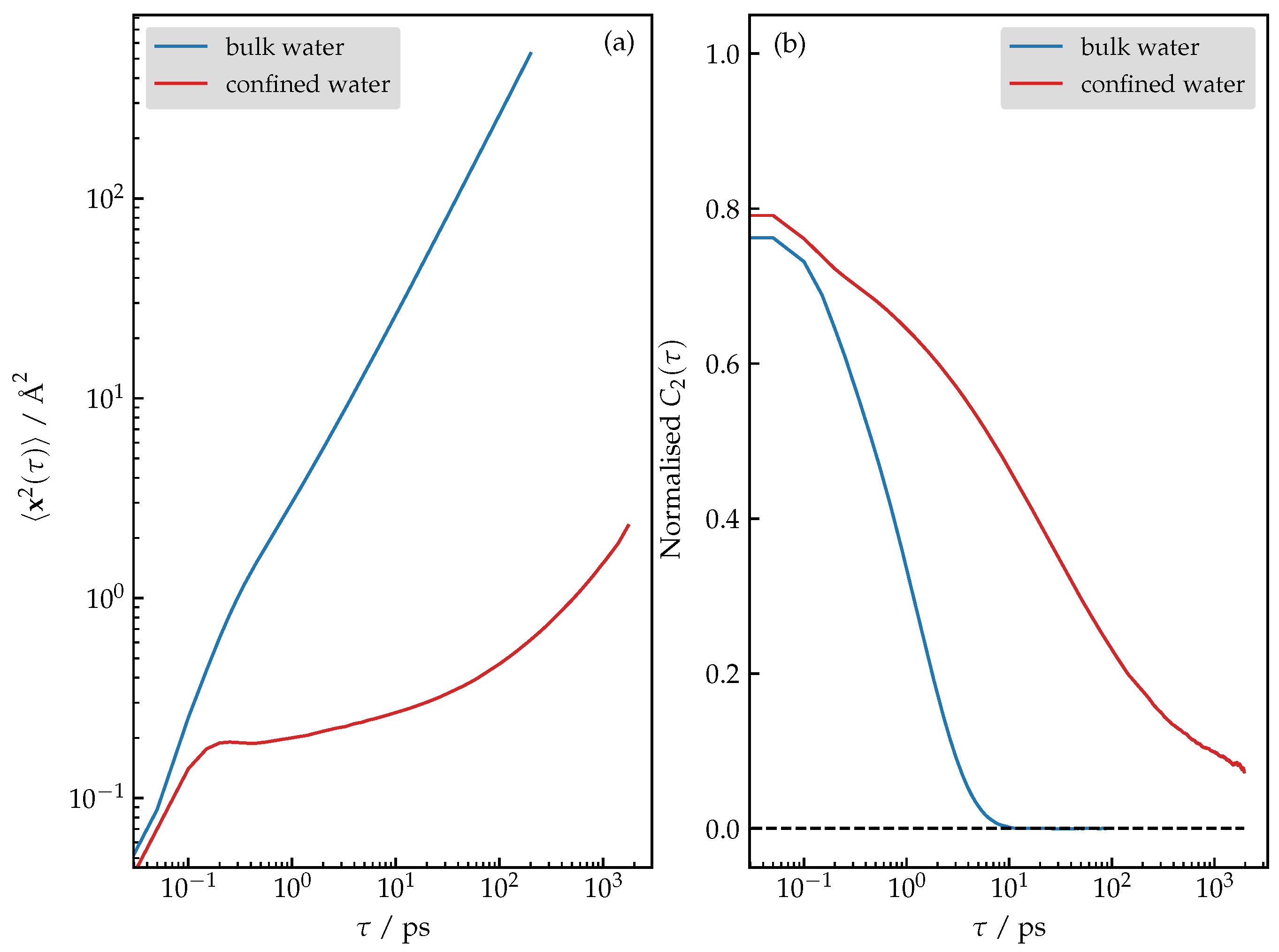
3.4. Structure and Dynamics of Water under Confinement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIM | Atoms in molecules |
| BKS | Beest, Kramer, van Santen |
| DFT | Density functional theory |
| DOS | Density of states |
| LTA | Linde type A |
| LAMMPS | Large atomic/molecular massively parallel simulator |
| LJ | Lennard–Jones |
| MD | Molecular dynamics |
| MIL | Materials Institute Lavoisier |
| MOF | Metal–organic framework |
| NMR | Nuclear magnetic resonance |
| PAW | Projector augmented wave |
| PBE | Perdew, Burke, Erzernhof |
| TIP3P-Ew | Transferable interatomic potential, 3 point, Ewald |
| VASP | Vienna ab initio simulation package |
| XRD | X-ray diffraction |
References
- Ahmad, T.; Zhang, D. A critical review of comparative global historical energy consumption and future demand: The story told so far. Energy Rep. 2020, 6, 1973–1991. [Google Scholar] [CrossRef]
- Mitali, J.; Dhinakaran, S.; Mohamad, A. Energy storage systems: A review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Jänchen, J.; Ackermann, D.; Stach, H.; Brösicke, W. Studies of the water adsorption on Zeolites and modified mesoporous materials for seasonal storage of solar heat. Sol. Energy 2004, 76, 339–344. [Google Scholar] [CrossRef]
- Henninger, S.; Schmidt, F.; Henning, H.M. Water adsorption characteristics of novel materials for heat transformation applications. Appl. Therm. Eng. 2010, 30, 1692–1702. [Google Scholar] [CrossRef]
- Tatsidjodoung, P.; Le Pierrès, N.; Luo, L. A review of potential materials for thermal energy storage in building applications. Renew. Sustain. Energy Rev. 2013, 18, 327–349. [Google Scholar] [CrossRef]
- Pastore, H.; Coluccia, S.; Marchese, L. POROUS ALUMINOPHOSPHATES: From Molecular Sieves to Designed Acid Catalysts. Annu. Rev. Mater. Res. 2005, 35, 351–395. [Google Scholar] [CrossRef]
- Yu, J.; Xu, R. Rich structure chemistry in the aluminophosphate family. Acc. Chem. Res. 2003, 36, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Varlec, J.; Krajnc, A.; Mazaj, M.; Ristić, A.; Vanatalu, K.; Oss, A.; Samoson, A.; Kaučič, V.; Mali, G. Dehydration of AlPO4-34 studied by variable-temperature NMR, XRD and first-principles calculations. New J. Chem. 2016, 40, 4178–4186. [Google Scholar] [CrossRef]
- Buchholz, A.; Wang, W.; Arnold, A.; Xu, M.; Hunger, M. Successive steps of hydration and dehydration of silicoaluminophosphates H-SAPO-34 and H-SAPO-37 investigated by in situ CF MAS NMR spectroscopy. Microporous Mesoporous Mater. 2003, 57, 157–168. [Google Scholar] [CrossRef]
- Ristić, A.; Logar, N.Z.; Henninger, S.K.; Kaučič, V. The Performance of Small-Pore Microporous Aluminophosphates in Low-Temperature Solar Energy Storage: The Structure–Property Relationship. Adv. Funct. Mater. 2012, 22, 1952–1957. [Google Scholar] [CrossRef]
- Krajnc, A.; Varlec, J.; Mazaj, M.; Ristić, A.; Logar, N.Z.; Mali, G. Superior Performance of Microporous Aluminophosphate with LTA Topology in Solar-Energy Storage and Heat Reallocation. Adv. Energy Mater. 2017, 7, 1601815. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, J.; Xu, M.; Huang, C.; Wang, R.; Li, T.; Huai, X. Ultralow-temperature-driven water-based sorption refrigeration enabled by low-cost zeolite-like porous aluminophosphate. Nat. Commun. 2022, 13, 193. [Google Scholar] [CrossRef]
- Pillai, R.S.; Jasra, R.V. Computational Study for Water Sorption in AlPO4-5 and AlPO4-11 Molecular Sieves. Langmuir 2010, 26, 1755–1764. [Google Scholar] [CrossRef] [PubMed]
- Basina, G.; Aishamia, D.; Polychronopoulou, K.; Tzitzios, V.; Balasubramanian, V.; Dawaymeh, F.; Karanikolos, G.N.; Al Wahedi, Y. Hierarchical AlPO4-5 and SAPO-5 microporous molecular sieves with mesoporous connectivity for water sorption applications. Surf. Coat. Technol. 2018, 353, 378–386. [Google Scholar] [CrossRef]
- Newalkar, B.; Jasra, R.; Kamath, V.; Bhat, S. Sorption of water in aluminophosphate molecular sieve AlPO4-5. Microporous Mesoporous Mater. 1998, 20, 129–137. [Google Scholar] [CrossRef]
- Duer, M.; HE, H.; Kolodziejski, W.; Klinowski, J. Dynamics of Water in the Aluminophosphate Molecular-Sieve VPI-5—A H-2 NMR-Study. J. Phys. Chem. 1994, 98, 1198–1204. [Google Scholar] [CrossRef]
- van Heyden, H.; Munz, G.; Schnabel, L.; Schmidt, F.; Mintova, S.; Bein, T. Kinetics of water adsorption in microporous aluminophosphate layers for regenerative heat exchangers. Appl. Therm. Eng. 2009, 29, 1514–1522. [Google Scholar] [CrossRef]
- Volavšek, J.; Pliekhov, O.; Pliekhova, O.; Mali, G.; Zabukovec Logar, N. Study of Water Adsorption on EDTA-Modified LTA Zeolites. Nanomaterials 2022, 12, 1352. [Google Scholar] [CrossRef]
- Shi, C.; Wang, J.; Li, L.; Li, Y. High-throughput Screening of Aluminophosphate Zeolites for Adsorption Heat Pump Applications. Res. Chin. Univ. 2022, 38, 161–166. [Google Scholar] [CrossRef]
- Fischer, M. Interaction of water with (silico)aluminophosphate zeotypes: A comparative investigation using dispersion-corrected DFT. Phys. Chem. Chem. Phys. 2016, 18, 15738–15750. [Google Scholar] [CrossRef]
- Fischer, M.; Angel, R.J. Accurate structures and energetics of neutral-framework zeotypes from dispersion-corrected DFT calculations. J. Chem. Phys. 2017, 146, 174111. [Google Scholar] [CrossRef]
- Fischer, M. First-Principles Study of AlPO4-H3, a Hydrated Aluminophosphate Zeotype Containing Two Different Types of Adsorbed Water Molecules. Molecules 2019, 24, 922. [Google Scholar] [CrossRef] [PubMed]
- Fischer, M. Revisiting the Structure of Calcined and Hydrated AlPO-11 with DFT-Based Molecular Dynamics Simulations. ChemPhysChem 2021, 22, 2063–2077. [Google Scholar] [CrossRef] [PubMed]
- Slavova, S.O.; Sizova, A.A.; Sizov, V.V. Molecular dynamics simulation of carbon dioxide diffusion in NaA zeolite: Assessment of surface effects and evaluation of bulk-like properties. Phys. Chem. Chem. Phys. 2020, 22, 22529–22536. [Google Scholar] [CrossRef] [PubMed]
- Alabarse, F.G.; Haines, J.; Cambon, O.; Levelut, C.; Bourgogne, D.; Haidoux, A.; Granier, D.; Coasne, B. Freezing of Water Confined at the Nanoscale. Phys. Rev. Lett. 2012, 109, 035701. [Google Scholar] [CrossRef] [PubMed]
- Coulomb, J.P.; Floquet, N.; Andre, G. Structural and dynamic properties of confined ethane in AlPO4-5 model microporous aluminophosphate: Does the predicted quasi-(1D) phase transition exist? Microporous Mesoporous Mater. 2011, 141, 43–48. [Google Scholar] [CrossRef]
- Praprotnik, M.; Hocevar, S.; Hodoscek, M.; Penca, M.; Janezic, D. New all-atom force field for molecular dynamics simulation of an AlPO4-34 molecular sieve. J. Comput. Chem. 2008, 29, 122–129. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phy. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Wood, D.M.; Zunger, A. A new method for diagonalising large matrices. J. Phys. A Math. Gen. 1985, 18, 1343. [Google Scholar] [CrossRef]
- Pulay, P. Convergence acceleration of iterative sequences. The case of scf iteration. Chem. Phys. Lett. 1980, 73, 393–398. [Google Scholar] [CrossRef]
- Leach, A. Molecular Modelling: Principles and Applications; Pearson Education; Longman: New York, NY, USA, 1996. [Google Scholar]
- Bader, R.; Bader, R. Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nosé–Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- van Beest, B.W.H.; Kramer, G.J.; van Santen, R.A. Force fields for silicas and aluminophosphates based on ab initio calculations. Phys. Rev. Lett. 1990, 64, 1955–1958. [Google Scholar] [CrossRef] [PubMed]
- Price, D.J.; Brooks, C.L., III. A modified TIP3P water potential for simulation with Ewald summation. J. Chem. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef] [PubMed]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comp. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Koh, C.; Montanari, T.; Nooney, R.; Tahir, S.; Westacott, R. Experimental and computer simulation studies of the removal of carbon dioxide from mixtures with methane using AlPO4-5 and MCM-41. Langmuir 1999, 15, 6043–6049. [Google Scholar] [CrossRef]
- Kolokathis, P.D.; Nonnen, T.; Füldner, G.; Papadopoulos, G.K. Identification of hydrated phases in ALPO4-5, and explanation of their effect on the water sorption and dynamics. Microporous Mesoporous Mater. 2022, 329, 111501. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tuckerman, M.E.; Tobias, D.J.; Klein, M.L. Explicit reversible integrators for extended systems dynamics. Mol. Phys. 1996, 87, 1117–1157. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Brown, P.J.; Fox, A.G.; Maslen, E.N.; O’Keefe, M.A.; Willis, B.T.M. International Tables for Crystallography; International Uninon of Crystallography: Chester, UK, 2006; Volume C, Chapter 6.1; pp. 554–595. [Google Scholar]
- Amri, M.; Walton, R.I. Negative Thermal Expansion in the Aluminum and Gallium Phosphate Zeotypes with CHA and AEI Structure types. Chem. Mater. 2009, 21, 3380–3390. [Google Scholar] [CrossRef]

| Interacting Pair | / eV | / Å |
|---|---|---|
| Al— | 0.0098423 | 3.798 |
| P— | 0.0076489 | 3.242 |
| O— | 0.0023926 | 3.453 |
| Lattice Parameter | Simulation | Experiment | Relative Error in % |
|---|---|---|---|
| a / Å | 18.82 ± 0.07 | 18.052 | 4.2 |
| b / Å | 18.93 ± 0.05 | 18.676 | 1.4 |
| c / Å | 19.69 ± 0.07 | 19.016 | 3.5 |
| / ∘ | 96.3 ± 0.4 | 95.1 | 1.3 |
| / ∘ | 102.5 ± 0.5 | 104.1 | 1.5 |
| / ∘ | 96.5 ± 0.4 | 96.6 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hubman, A.; Volavšek, J.; Urbič, T.; Zabukovec Logar, N.; Merzel, F. Water–Aluminum Interaction as Driving Force of Linde Type A Aluminophosphate Hydration. Nanomaterials 2023, 13, 2387. https://doi.org/10.3390/nano13172387
Hubman A, Volavšek J, Urbič T, Zabukovec Logar N, Merzel F. Water–Aluminum Interaction as Driving Force of Linde Type A Aluminophosphate Hydration. Nanomaterials. 2023; 13(17):2387. https://doi.org/10.3390/nano13172387
Chicago/Turabian StyleHubman, Anže, Janez Volavšek, Tomaž Urbič, Nataša Zabukovec Logar, and Franci Merzel. 2023. "Water–Aluminum Interaction as Driving Force of Linde Type A Aluminophosphate Hydration" Nanomaterials 13, no. 17: 2387. https://doi.org/10.3390/nano13172387
APA StyleHubman, A., Volavšek, J., Urbič, T., Zabukovec Logar, N., & Merzel, F. (2023). Water–Aluminum Interaction as Driving Force of Linde Type A Aluminophosphate Hydration. Nanomaterials, 13(17), 2387. https://doi.org/10.3390/nano13172387








