From Forces to Assemblies: van der Waals Forces-Driven Assemblies in Anisotropic Quasi-2D Graphene and Quasi-1D Nanocellulose Heterointerfaces towards Quasi-3D Nanoarchitecture
Abstract
:1. Introduction
2. vdW-Driven Assembly
3. vdW-Driven Functionalization
4. vdW-Driven Transition
4.1. Load Transfer (LT) Mechanism
4.2. Charge Transfer (CT) Mechanism
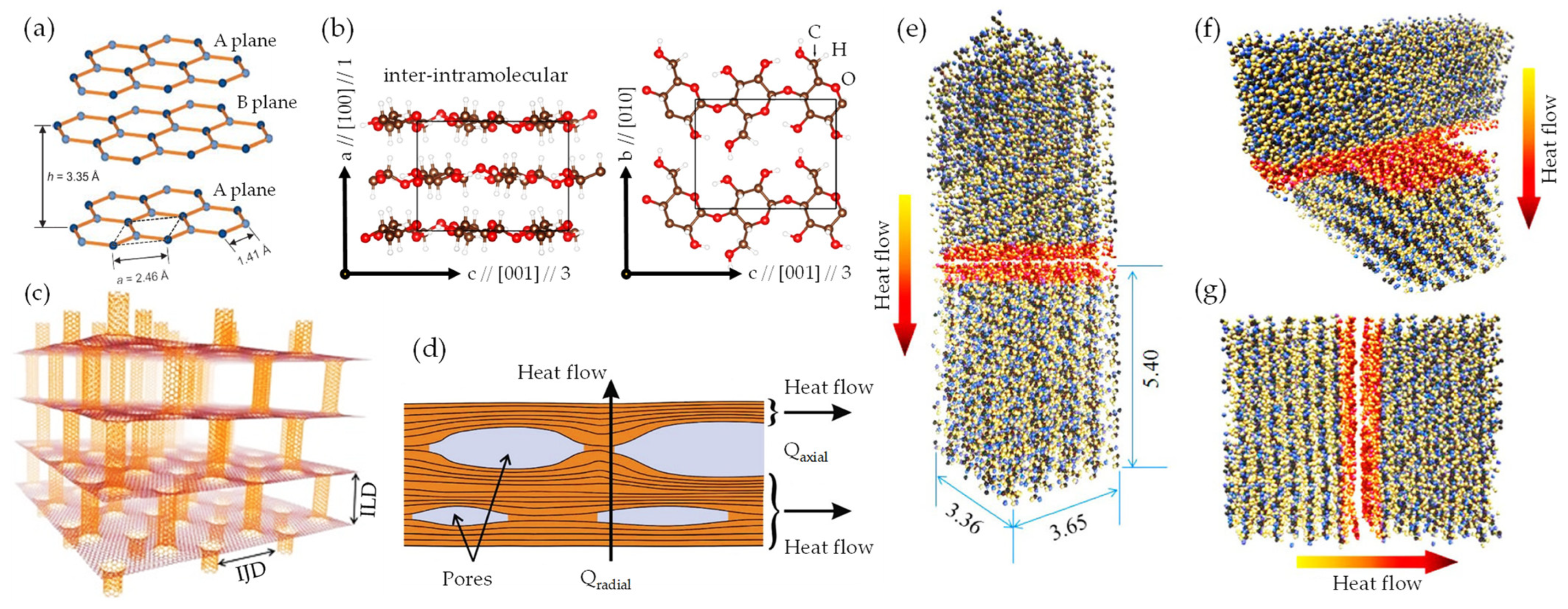
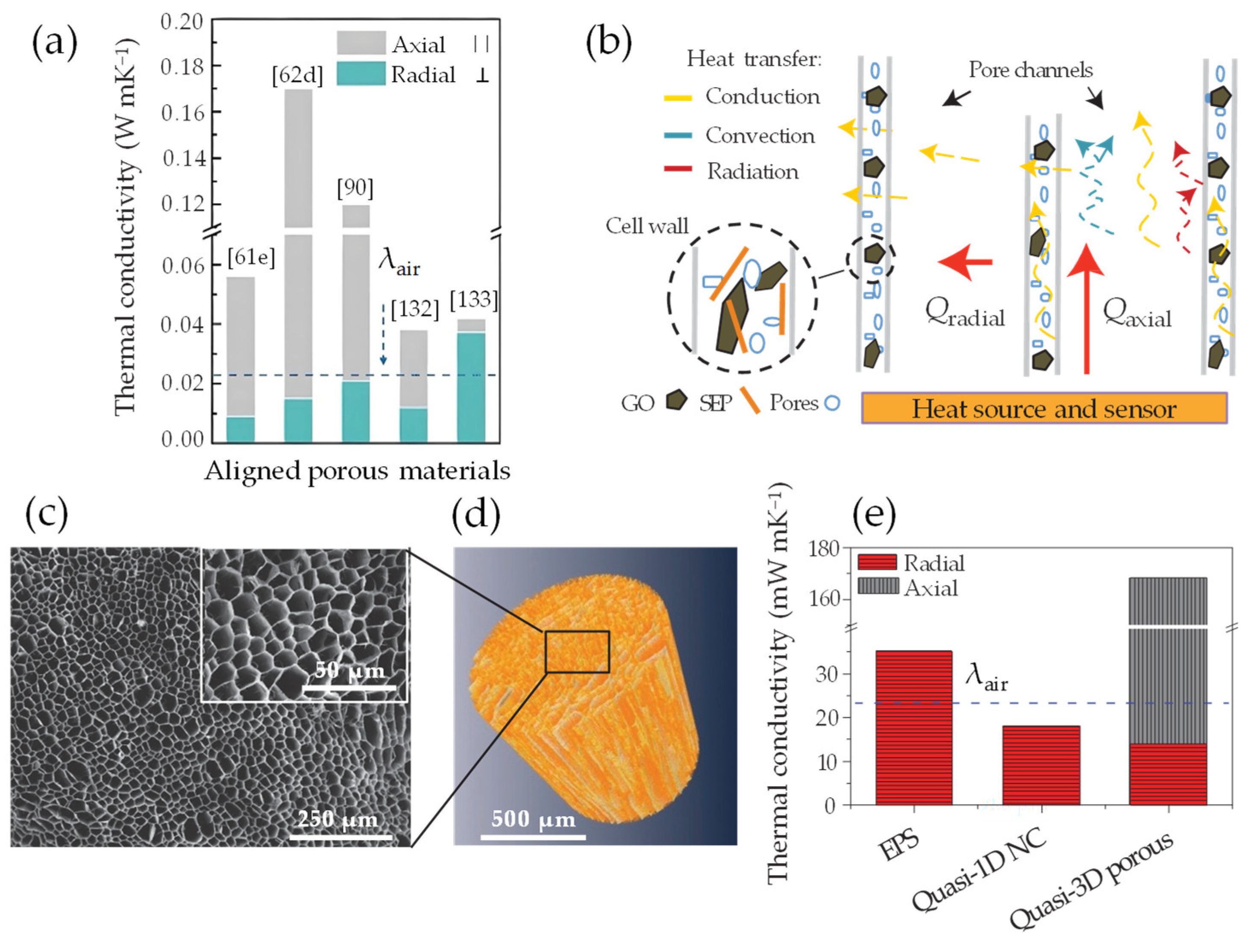
4.3. Heat Transfer (HT) Mechanism
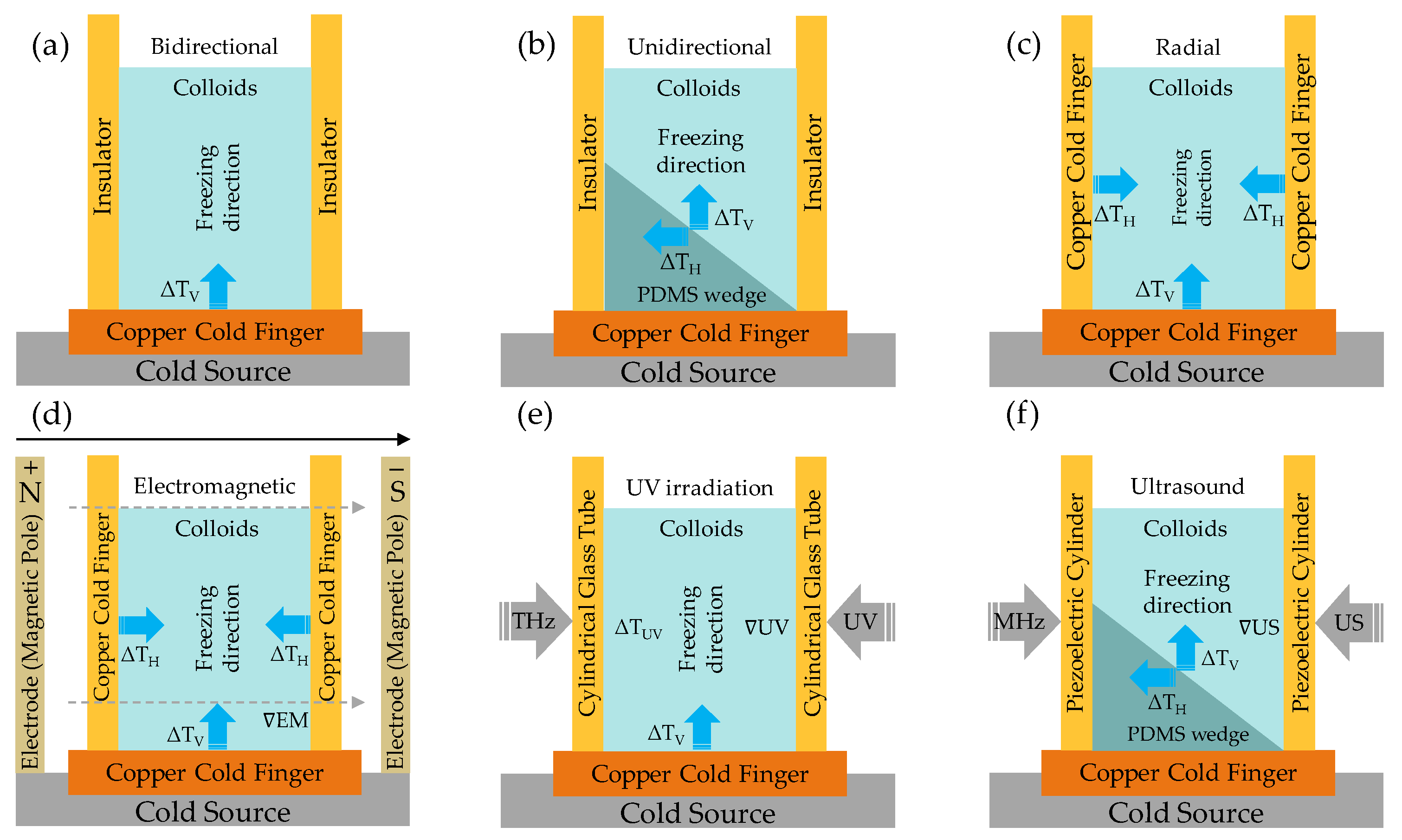
5. vdW-Driven Alignment
5.1. In Situ Alignment Induced
5.2. Ex Situ Alignment Induced
6. Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, N.; Salehiyan, R.; Chauke, V.; Joseph Botlhoko, O.; Setshedi, K.; Scriba, M.; Masukume, M.; Sinha Ray, S. Top-down synthesis of graphene: A comprehensive review. FlatChem 2021, 27, 100224. [Google Scholar] [CrossRef]
- Gong, S.; Ni, H.; Jiang, L.; Cheng, Q. Learning from nature: Constructing high performance graphene-based nanocomposites. Mater. Today 2017, 20, 210–219. [Google Scholar] [CrossRef]
- Compton, O.C.; Nguyen, S.T. Graphene Oxide, Highly Reduced Graphene Oxide, and Graphene: Versatile Building Blocks for Carbon-Based Materials. Small 2010, 6, 711–723. [Google Scholar] [CrossRef]
- Brisebois, P.P.; Siaj, M. Harvesting graphene oxide—Years 1859 to 2019: A review of its structure, synthesis, properties and exfoliation. J. Mater. Chem. C 2020, 8, 1517–1547. [Google Scholar] [CrossRef]
- Foster, E.J.; Moon, R.J.; Agarwal, U.P.; Bortner, M.J.; Bras, J.; Camarero-Espinosa, S.; Chan, K.J.; Clift, M.J.D.; Cranston, E.D.; Eichhorn, S.J.; et al. Current characterization methods for cellulose nanomaterials. Chem. Soc. Rev. 2018, 47, 2609–2679. [Google Scholar] [CrossRef]
- De France, K.; Zeng, Z.; Wu, T.; Nyström, G. Functional Materials from Nanocellulose: Utilizing Structure–Property Relationships in Bottom-Up Fabrication. Adv. Mater. 2020, 33, 2000657. [Google Scholar] [CrossRef]
- Kontturi, E.; Laaksonen, P.; Linder, M.B.; Nonappa; Gröschel, A.H.; Rojas, O.J.; Ikkala, O. Advanced Materials through Assembly of Nanocelluloses. Adv. Mater. 2018, 30, 1703779. [Google Scholar] [CrossRef]
- Trache, D.; Tarchoun, A.F.; Derradji, M.; Hamidon, T.S.; Masruchin, N.; Brosse, N.; Hussin, M.H. Nanocellulose: From fundamentals to advanced applications. Front. Chem. 2020, 8, 392. [Google Scholar] [CrossRef]
- O’Sullivan, A.C. Cellulose: The structure slowly unravels. Cellulose 1997, 4, 173–207. [Google Scholar] [CrossRef]
- Habibi, Y.; Lucia, L.A.; Rojas, O.J. Cellulose Nanocrystals: Chemistry, Self-Assembly, and Applications. Chem. Rev. 2010, 110, 3479–3500. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Brakat, A.; Zhu, H. Nanocellulose-Graphene Derivative Hybrids: Advanced Structure-Based Functionality from Top-down Synthesis to Bottom-up Assembly. ACS Appl. Bio Mater. 2021, 4, 7366–7401. [Google Scholar] [CrossRef]
- Chen, C.; Kuang, Y.; Zhu, S.; Burgert, I.; Keplinger, T.; Gong, A.; Li, T.; Berglund, L.; Eichhorn, S.J.; Hu, L. Structure–property–function relationships of natural and engineered wood. Nat. Rev. Mater. 2020, 5, 642–666. [Google Scholar] [CrossRef]
- Fengel, D. Ideas on the ultrastructural organization of the cell wall components. J. Polym. Sci. Part C Polym. Symp. 1971, 36, 383–392. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, N.; Cui, Y.; Gao, W.; Zhao, Q.; Gao, C.; Bai, H.; Xie, T. Biomimetic Architectured Graphene Aerogel with Exceptional Strength and Resilience. ACS Nano 2017, 11, 6817–6824. [Google Scholar] [CrossRef]
- Pan, Z.Z.; Nishihara, H.; Iwamura, S.; Sekiguchi, T.; Sato, A.; Isogai, A.; Kang, F.; Kyotani, T.; Yang, Q.H. Cellulose Nanofiber as a Distinct Structure-Directing Agent for Xylem-like Microhoneycomb Monoliths by Unidirectional Freeze-Drying. ACS Nano 2016, 10, 10689–10697. [Google Scholar] [CrossRef]
- Qiu, L.; Liu, J.Z.; Chang, S.L.Y.; Wu, Y.; Li, D. Biomimetic superelastic graphene-based cellular monoliths. Nat. Commun. 2012, 3, 1241. [Google Scholar] [CrossRef]
- Shao, G.; Hanaor, D.A.H.; Shen, X.; Gurlo, A. Freeze Casting: From Low-Dimensional Building Blocks to Aligned Porous Structures—A Review of Novel Materials, Methods, and Applications. Adv. Mater. 2020, 32, 1907176. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Z.; Zhuo, H.; Zhong, L.; Peng, X.; Sun, R.C. Advanced Compressible and Elastic 3D Monoliths beyond Hydrogels. Adv. Funct. Mater. 2019, 29, 1904472. [Google Scholar] [CrossRef]
- Chen, C.; Song, J.; Zhu, S.; Li, Y.; Kuang, Y.; Wan, J.; Kirsch, D.; Xu, L.; Wang, Y.; Gao, T.; et al. Scalable and Sustainable Approach toward Highly Compressible, Anisotropic, Lamellar Carbon Sponge. Chem 2018, 4, 544–554. [Google Scholar] [CrossRef]
- Luo, S.; Samad, Y.A.; Chan, V.; Liao, K. Cellular Graphene: Fabrication, Mechanical Properties, and Strain-Sensing Applications. Matter 2019, 1, 1148–1202. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Wang, B.; Huang, M.; Wang, B.; Jiang, Y.; Ruoff, R.S. Freeze-Casting Produces a Graphene Oxide Aerogel with a Radial and Centrosymmetric Structure. ACS Nano 2018, 12, 5816–5825. [Google Scholar] [CrossRef] [PubMed]
- Wicklein, B.; Kocjan, A.; Salazar-Alvarez, G.; Carosio, F.; Camino, G.; Antonietti, M.; Bergström, L. Thermally insulating and fire-retardant lightweight anisotropic foams based on nanocellulose and graphene oxide. Nat. Nanotechnol. 2015, 10, 277–283. [Google Scholar] [CrossRef]
- Yao, Q.; Fan, B.; Xiong, Y.; Jin, C.; Sun, Q.; Sheng, C. 3D assembly based on 2D structure of Cellulose Nanofibril/Graphene Oxide Hybrid Aerogel for Adsorptive Removal of Antibiotics in Water. Sci. Rep. 2017, 7, 45914. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Fang, S.; Hu, Y.H. 3D Graphene Materials: From Understanding to Design and Synthesis Control. Chem. Rev. 2020, 120, 10336–10453. [Google Scholar] [CrossRef]
- Brakat, A.; Zhu, H. Nanocellulose-Graphene Hybrids: Advanced Functional Materials as Multifunctional Sensing Platform. Nano-Micro Lett. 2021, 13, 94. [Google Scholar] [CrossRef]
- Chen, Y.; Pötschke, P.; Pionteck, J.; Voit, B.; Qi, H. Smart cellulose/graphene composites fabricated by in situ chemical reduction of graphene oxide for multiple sensing applications. J. Mater. Chem. A 2018, 6, 7777–7785. [Google Scholar] [CrossRef]
- Sadasivuni, K.K.; Kafy, A.; Zhai, L.; Ko, H.U.; Mun, S.; Kim, J. Transparent and Flexible Cellulose Nanocrystal/Reduced Graphene Oxide Film for Proximity Sensing. Small 2015, 11, 994–1002. [Google Scholar] [CrossRef]
- Zhou, K.; Chen, C.; Lei, M.; Gao, Q.; Nie, S.; Liu, X.; Wang, S. Reduced graphene oxide-based highly sensitive pressure sensor for wearable electronics via an ordered structure and enhanced interlayer interaction mechanism. RSC Adv. 2020, 10, 2150–2159. [Google Scholar] [CrossRef]
- Zhuo, H.; Hu, Y.; Tong, X.; Chen, Z.; Zhong, L.; Lai, H.; Liu, L.; Jing, S.; Liu, Q.; Liu, C.; et al. A Supercompressible, Elastic, and Bendable Carbon Aerogel with Ultrasensitive Detection Limits for Compression Strain, Pressure, and Bending Angle. Adv. Mater. 2018, 30, 1706705. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.H.; Naficy, S.; Chandrawati, R.; Dehghani, F. Nanocellulose for Sensing Applications. Adv. Mater. Interfaces 2019, 6, 1900424. [Google Scholar] [CrossRef]
- Kafy, A.; Akther, A.; Shishir, M.I.R.; Kim, H.C.; Yun, Y.; Kim, J. Cellulose nanocrystal/graphene oxide composite film as humidity sensor. Sens. Actuators A Phys. 2016, 247, 221–226. [Google Scholar] [CrossRef]
- Sadasivuni, K.K.; Kafy, A.; Kim, H.C.; Ko, H.U.; Mun, S.; Kim, J. Reduced graphene oxide filled cellulose films for flexible temperature sensor application. Synth. Met. 2015, 206, 154–161. [Google Scholar] [CrossRef]
- Kafy, A.; Sadasivuni, K.K.; Akther, A.; Min, S.K.; Kim, J. Cellulose/graphene nanocomposite as multifunctional electronic and solvent sensor material. Mater. Lett. 2015, 159, 20–23. [Google Scholar] [CrossRef]
- Dai, L.; Wang, Y.; Zou, X.; Chen, Z.; Liu, H.; Ni, Y. Ultrasensitive Physical, Bio, and Chemical Sensors Derived from 1-, 2-, and 3-D Nanocellulosic Materials. Small 2020, 16, 1906567. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, J.; Gao, Z.; Li, B.; Xiong, C. Carbonized Cellulose Nanofibril/Graphene Oxide Composite Aerogels for High-Performance Supercapacitors. ACS Appl. Energy Mater. 2020, 3, 1145–1151. [Google Scholar] [CrossRef]
- Kuzmenko, V.; Wang, N.; Haque, M.; Naboka, O.; Flygare, M.; Svensson, K.; Gatenholm, P.; Liu, J.; Enoksson, P. Cellulose-derived carbon nanofibers/graphene composite electrodes for powerful compact supercapacitors. RSC Adv. 2017, 7, 45968–45977. [Google Scholar] [CrossRef]
- Song, N.; Jiao, D.; Cui, S.; Hou, X.; Ding, P.; Shi, L. Highly Anisotropic Thermal Conductivity of Layer-by-Layer Assembled Nanofibrillated Cellulose/Graphene Nanosheets Hybrid Films for Thermal Management. ACS Appl. Mater. Interfaces 2017, 9, 2924–2932. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, Y.; Liu, T.; Huang, R.; Chai, S.; Chen, F.; Fu, Q. Completely Green Approach for the Preparation of Strong and Highly Conductive Graphene Composite Film by Using Nanocellulose as Dispersing Agent and Mechanical Compression. ACS Sustain. Chem. Eng. 2017, 5, 9102–9113. [Google Scholar] [CrossRef]
- Ahmed, A.; Adak, B.; Bansala, T.; Mukhopadhyay, S. Green Solvent Processed Cellulose/Graphene Oxide Nanocomposite Films with Superior Mechanical, Thermal, and Ultraviolet Shielding Properties. ACS Appl. Mater. Interfaces 2020, 12, 1687–1697. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wu, Z.Y.; Liang, H.W.; Chen, J.F.; Yu, S.H. Ultralight Multifunctional Carbon-Based Aerogels by Combining Graphene Oxide and Bacterial Cellulose. Small 2017, 13, 1700453. [Google Scholar] [CrossRef] [PubMed]
- Mi, H.-Y.; Jing, X.; Politowicz, A.L.; Chen, E.; Huang, H.X.; Turng, L.S. Highly compressible ultra-light anisotropic cellulose/graphene aerogel fabricated by bidirectional freeze drying for selective oil absorption. Carbon 2018, 132, 199–209. [Google Scholar] [CrossRef]
- Fang, Q.; Zhou, X.; Deng, W.; Zheng, Z.; Liu, Z. Freestanding bacterial cellulose-graphene oxide composite membranes with high mechanical strength for selective ion permeation. Sci. Rep. 2016, 6, 33185. [Google Scholar] [CrossRef]
- Valencia, L.; Monti, S.; Kumar, S.; Zhu, C.; Liu, P.; Yu, S.; Mathew, A.P. Nanocellulose/graphene oxide layered membranes: Elucidating their behaviour during filtration of water and metal ions in real time. Nanoscale 2019, 11, 22413–22422. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J. The hierarchical structure and mechanics of plant materials. J. R. Soc. Interface 2012, 9, 2749–2766. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, H.; Shen, F.; Wan, J.; Lacey, S.; Fang, Z.; Dai, H.; Hu, L. Nanocellulose as green dispersant for two-dimensional energy materials. Nano Energy 2015, 13, 346–354. [Google Scholar] [CrossRef]
- Kim, J.; Cote, L.J.; Kim, F.; Yuan, W.; Shull, K.R.; Huang, J. Graphene Oxide Sheets at Interfaces. J. Am. Chem. Soc. 2010, 132, 8180–8186. [Google Scholar] [CrossRef]
- Silvestre, G.H.; Pinto, L.O.; Bernardes, J.S.; Miwa, R.H.; Fazzio, A. Disassembly of TEMPO-Oxidized Cellulose Fibers: Intersheet and Interchain Interactions in the Isolation of Nanofibers and Unitary Chains. J. Phys. Chem. B 2021, 125, 3717–3724. [Google Scholar] [CrossRef]
- Zhan, J.; Lei, Z.; Zhang, Y. Non-covalent interactions of graphene surface: Mechanisms and applications. Chem 2022, 8, 947–979. [Google Scholar] [CrossRef]
- Silvestre, G.H.; de Lima, F.C.; Bernardes, J.S.; Fazzio, A.; Miwa, R.H. Nanoscale structural and electronic properties of cellulose/graphene interfaces. Phys. Chem. Chem. Phys. 2023, 25, 1161–1168. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Li, L.; Lee, W.B.; Ng, M.C. Structure of graphene and its disorders: A review. Sci. Technol. Adv. Mater. 2018, 19, 613–648. [Google Scholar] [CrossRef] [PubMed]
- Shih, C.J. Understanding and Engineering Molecular Interactions and Electronic Transport at 2D Materials Interfaces. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Pérez, E.M.; Martín, N. π–π interactions in carbon nanostructures. Chem. Soc. Rev. 2015, 44, 6425–6433. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Pérez, L.; Herranz, M.a.Á.; Martín, N. The chemistry of pristine graphene. Chem. Commun. 2013, 49, 3721–3735. [Google Scholar] [CrossRef]
- Thakur, V.; Guleria, A.; Kumar, S.; Sharma, S.; Singh, K. Recent advances in nanocellulose processing, functionalization and applications: A review. Mater. Adv. 2021, 2, 1872–1895. [Google Scholar] [CrossRef]
- Lee, H.; Son, N.; Jeong, H.Y.; Kim, T.G.; Bang, G.S.; Kim, J.Y.; Shim, G.W.; Goddeti, K.C.; Kim, J.H.; Kim, N.; et al. Friction and conductance imaging of sp2- and sp3-hybridized subdomains on single-layer graphene oxide. Nanoscale 2016, 8, 4063–4069. [Google Scholar] [CrossRef]
- Robertson, J.; O’Reilly, E.P. Electronic and atomic structure of amorphous carbon. Phys. Rev. B 1987, 35, 2946–2957. [Google Scholar] [CrossRef]
- Eda, G.; Mattevi, C.; Yamaguchi, H.; Kim, H.; Chhowalla, M. Insulator to Semimetal Transition in Graphene Oxide. J. Phys. Chem. C 2009, 113, 15768–15771. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Elsevier: Waltham, MA, USA, 2011; pp. 1–674. [Google Scholar]
- Stone, A. The Theory of Intermolecular Forces, 2nd ed.; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Lev, P.P. General theory of van der Waals’ forces. Sov. Phys. Uspekhi 1961, 4, 153. [Google Scholar] [CrossRef]
- Notley, S.M.; Pettersson, B.; Wågberg, L. Direct Measurement of Attractive van der Waals’ Forces between Regenerated Cellulose Surfaces in an Aqueous Environment. J. Am. Chem. Soc. 2004, 126, 13930–13931. [Google Scholar] [CrossRef]
- Chandler, D.; Weeks, J.D.; Andersen, H.C. Van der Waals Picture of Liquids, Solids, and Phase Transformations. Science 1983, 220, 787–794. [Google Scholar] [CrossRef] [PubMed]
- Georgakilas, V.; Otyepka, M.; Bourlinos, A.B.; Chandra, V.; Kim, N.; Kemp, K.C.; Hobza, P.; Zboril, R.; Kim, K.S. Functionalization of Graphene: Covalent and Non-Covalent Approaches, Derivatives and Applications. Chem. Rev. 2012, 112, 6156–6214. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, M.C. Hydrogen bonding and other non-covalent interactions at the surfaces of cellulose microfibrils. Cellulose 2023, 30, 667–687. [Google Scholar] [CrossRef]
- Georgakilas, V.; Tiwari, J.N.; Kemp, K.C.; Perman, J.A.; Bourlinos, A.B.; Kim, K.S.; Zboril, R. Noncovalent Functionalization of Graphene and Graphene Oxide for Energy Materials, Biosensing, Catalytic, and Biomedical Applications. Chem. Rev. 2016, 116, 5464–5519. [Google Scholar] [CrossRef] [PubMed]
- Ariga, K.; Malgras, V.; Ji, Q.; Zakaria, M.B.; Yamauchi, Y. Coordination nanoarchitectonics at interfaces between supramolecular and materials chemistry. Coord. Chem. Rev. 2016, 320, 139–152. [Google Scholar] [CrossRef]
- Ariga, K. Nanoarchitectonics: What’s coming next after nanotechnology? Nanoscale Horiz. 2021, 6, 364–378. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, T.; Shen, Z.; Liu, M. Chiral Nanoarchitectonics: Towards the Design, Self-Assembly, and Function of Nanoscale Chiral Twists and Helices. Adv. Mater. 2016, 28, 1044–1059. [Google Scholar] [CrossRef]
- Ariga, K.; Matsumoto, M.; Mori, T.; Shrestha, L.K. Materials nanoarchitectonics at two-dimensional liquid interfaces. Beilstein J. Nanotechnol. 2019, 10, 1559–1587. [Google Scholar] [CrossRef]
- Maji, S.; Shrestha, L.K.; Ariga, K. Nanoarchitectonics for Nanocarbon Assembly and Composite. J. Inorg. Organomet. Polym. Mater. 2020, 30, 42–55. [Google Scholar] [CrossRef]
- Giese, M.; Spengler, M. Cellulose nanocrystals in nanoarchitectonics—Towards photonic functional materials. Mol. Syst. Des. Eng. 2019, 4, 29–48. [Google Scholar] [CrossRef]
- Pan, H.; Zhu, S.; Mao, L. Graphene Nanoarchitectonics: Approaching the Excellent Properties of Graphene from Microscale to Macroscale. J. Inorg. Organomet. Polym. Mater. 2015, 25, 179–188. [Google Scholar] [CrossRef]
- Verma, C.; Ebenso, E.E. Ionic liquid-mediated functionalization of graphene-based materials for versatile applications: A review. Graphene Technol. 2019, 4, 1–15. [Google Scholar] [CrossRef]
- Aldroubi, S.; Brun, N.; Bou Malham, I.; Mehdi, A. When graphene meets ionic liquids: A good match for the design of functional materials. Nanoscale 2021, 13, 2750–2779. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Chen, Z.L. Research progress on dissolution and functional modification of cellulose in ionic liquids. J. Mol. Liq. 2008, 142, 1–5. [Google Scholar] [CrossRef]
- Richardson, J.J.; Björnmalm, M.; Caruso, F. Technology-driven layer-by-layer assembly of nanofilms. Science 2015, 348, aaa2491. [Google Scholar] [CrossRef]
- Alqus, R.; Eichhorn, S.J.; Bryce, R.A. Molecular Dynamics of Cellulose Amphiphilicity at the Graphene–Water Interface. Biomacromolecules 2015, 16, 1771–1783. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Hsieh, Y.L. Aqueous exfoliated graphene by amphiphilic nanocellulose and its application in moisture-responsive foldable actuators. Nanoscale 2019, 11, 11719–11729. [Google Scholar] [CrossRef]
- Ling, S.; Kaplan, D.L.; Buehler, M.J. Nanofibrils in nature and materials engineering. Nat. Rev. Mater. 2018, 3, 18016. [Google Scholar] [CrossRef]
- Xiong, R.; Grant, A.M.; Ma, R.; Zhang, S.; Tsukruk, V.V. Naturally-derived biopolymer nanocomposites: Interfacial design, properties and emerging applications. Mater. Sci. Eng. R Rep. 2018, 125, 1–41. [Google Scholar] [CrossRef]
- Moon, R.J.; Martini, A.; Nairn, J.; Simonsen, J.; Youngblood, J. Cellulose nanomaterials review: Structure, properties and nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. [Google Scholar] [CrossRef]
- Merindol, R.; Diabang, S.; Mujica, R.; Le Houerou, V.; Roland, T.; Gauthier, C.; Decher, G.; Felix, O. Assembly of Anisotropic Nanocellulose Films Stronger than the Original Tree. ACS Nano 2020, 14, 16525–16534. [Google Scholar] [CrossRef] [PubMed]
- Jahandideh, H.; Macairan, J.R.; Bahmani, A.; Lapointe, M.; Tufenkji, N. Fabrication of graphene-based porous materials: Traditional and emerging approaches. Chem. Sci. 2022, 13, 8924–8941. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Meng, L.; Niu, L.; Lu, Q. Simultaneous Reduction and Surface Functionalization of Graphene Oxide by Natural Cellulose with the Assistance of the Ionic Liquid. J. Phys. Chem. C 2012, 116, 16294–16299. [Google Scholar] [CrossRef]
- Amieva, E.J.C.; Lópe-Barroso, J.; Martínez-Hernández, A.L.; Velasco-Santos, C. Graphene-based Materials Functionalization with Natural Polymeric Biomolecules. Recent Adv. Graphene Res. 2016, 1, 257–298. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, Y.; Li, P.; Gao, C. Strong, Conductive, Lightweight, Neat Graphene Aerogel Fibers with Aligned Pores. ACS Nano 2012, 6, 7103–7113. [Google Scholar] [CrossRef]
- Xiong, R.; Hu, K.; Grant, A.M.; Ma, R.; Xu, W.; Lu, C.; Zhang, X.; Tsukruk, V.V. Ultrarobust Transparent Cellulose Nanocrystal-Graphene Membranes with High Electrical Conductivity. Adv. Mater. 2016, 28, 1501–1509. [Google Scholar] [CrossRef]
- Zhang, K.; Ketterle, L.; Järvinen, T.; Lorite, G.S.; Hong, S.; Liimatainen, H. Self-assembly of graphene oxide and cellulose nanocrystals into continuous filament via interfacial nanoparticle complexation. Mater. Des. 2020, 193, 108791. [Google Scholar] [CrossRef]
- Kovtun, A.; Candini, A.; Vianelli, A.; Boschi, A.; Dell’Elce, S.; Gobbi, M.; Kim, K.H.; Lara Avila, S.; Samorì, P.; Affronte, M.; et al. Multiscale Charge Transport in van der Waals Thin Films: Reduced Graphene Oxide as a Case Study. ACS Nano 2021, 15, 2654–2667. [Google Scholar] [CrossRef]
- Xiong, R.; Kim, H.S.; Zhang, L.; Korolovych, V.F.; Zhang, S.; Yingling, Y.G.; Tsukruk, V.V. Wrapping Nanocellulose Nets around Graphene Oxide Sheets. Angew. Chem. Int. Ed. 2018, 57, 8508–8513. [Google Scholar] [CrossRef]
- Haidari, M.M.; Kim, H.; Kim, J.H.; Park, M.; Lee, H.; Choi, J.S. Doping effect in graphene-graphene oxide interlayer. Sci. Rep. 2020, 10, 8258. [Google Scholar] [CrossRef]
- Rahman, R.; Foster, J.T.; Haque, A. Molecular Dynamics Simulation and Characterization of Graphene–Cellulose Nanocomposites. J. Phys. Chem. A 2013, 117, 5344–5353. [Google Scholar] [CrossRef] [PubMed]
- Mianehrow, H.; Berglund, L.A.; Wohlert, J. Interface effects from moisture in nanocomposites of 2D graphene oxide in cellulose nanofiber (CNF) matrix—A molecular dynamics study. J. Mater. Chem. A 2022, 10, 2122–2132. [Google Scholar] [CrossRef]
- Hou, Y.; Guan, Q.F.; Xia, J.; Ling, Z.C.; He, Z.; Han, Z.M.; Yang, H.B.; Gu, P.; Zhu, Y.; Yu, S.H.; et al. Strengthening and Toughening Hierarchical Nanocellulose via Humidity-Mediated Interface. ACS Nano 2021, 15, 1310–1320. [Google Scholar] [CrossRef] [PubMed]
- Mao, Q.; Yang, L.; Geng, X.; Chen, L.; Sapkota, B.; Zhao, H.; Zhu, H. Interface Strain Induced Hydrophobic Facet Suppression in Cellulose Nanocomposite Embedded with Highly Oxidized Monolayer Graphene Oxide. Adv. Mater. Interfaces 2017, 4, 1700995. [Google Scholar] [CrossRef]
- He, Z.; Zhu, Y.; Wu, H. Multiscale mechanics of noncovalent interface in graphene oxide layered nanocomposites. Theor. Appl. Mech. Lett. 2022, 12, 100304. [Google Scholar] [CrossRef]
- Zhang, C.; Keten, S.; Derome, D.; Carmeliet, J. Hydrogen bonds dominated frictional stick-slip of cellulose nanocrystals. Carbohydr. Polym. 2021, 258, 117682. [Google Scholar] [CrossRef]
- Çınar, M.N.; Antidormi, A.; Nguyen, V.H.; Kovtun, A.; Lara-Avila, S.; Liscio, A.; Charlier, J.C.; Roche, S.; Sevinçli, H. Toward Optimized Charge Transport in Multilayer Reduced Graphene Oxides. Nano Lett. 2022, 22, 2202–2208. [Google Scholar] [CrossRef]
- Rahman, R.; Haque, A. Molecular Dynamic Simulation of Graphene Reinforced Nanocomposites for Evaluating Elastic Constants. Procedia Eng. 2013, 56, 789–794. [Google Scholar] [CrossRef]
- Iwamoto, S.; Kai, W.; Isogai, A.; Iwata, T. Elastic Modulus of Single Cellulose Microfibrils from Tunicate Measured by Atomic Force Microscopy. Biomacromolecules 2009, 10, 2571–2576. [Google Scholar] [CrossRef]
- Joung, D.; Khondaker, S.I. Efros-Shklovskii variable-range hopping in reduced graphene oxide sheets of varying carbon sp2 fraction. Phys. Rev. B 2012, 86, 235423. [Google Scholar] [CrossRef]
- Gómez-Navarro, C.; Weitz, R.T.; Bittner, A.M.; Scolari, M.; Mews, A.; Burghard, M.; Kern, K. Electronic Transport Properties of Individual Chemically Reduced Graphene Oxide Sheets. Nano Lett. 2007, 7, 3499–3503. [Google Scholar] [CrossRef]
- Jiao, D.; Song, N.; Ding, P.; Shi, L. Enhanced thermal conductivity in oriented cellulose nanofibril/graphene composites via interfacial engineering. Compos. Commun. 2022, 31, 101101. [Google Scholar] [CrossRef]
- Cui, S.; Song, N.; Shi, L.; Ding, P. Enhanced Thermal Conductivity of Bioinspired Nanofibrillated Cellulose Hybrid Films Based on Graphene Sheets and Nanodiamonds. ACS Sustain. Chem. Eng. 2020, 8, 6363–6370. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Apostolopoulou-Kalkavoura, V.; Munier, P.; Bergström, L. Thermally Insulating Nanocellulose-Based Materials. Adv. Mater. 2021, 33, 2001839. [Google Scholar] [CrossRef]
- Yu, Z.L.; Yang, N.; Zhou, L.C.; Ma, Z.Y.; Zhu, Y.-B.; Lu, Y.Y.; Qin, B.; Xing, W.Y.; Ma, T.; Li, S.C.; et al. Bioinspired polymeric woods. Sci. Adv. 2018, 4, eaat7223. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Chen, C.; Yang, Z.; Kuang, Y.; Li, T.; Li, Y.; Huang, H.; Kierzewski, I.; Liu, B.; He, S.; et al. Highly Compressible, Anisotropic Aerogel with Aligned Cellulose Nanofibers. ACS Nano 2018, 12, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Song, J.; Zhao, X.; Yang, Z.; Pastel, G.; Xu, S.; Jia, C.; Dai, J.; Chen, C.; Gong, A.; et al. Anisotropic, lightweight, strong, and super thermally insulating nanowood with naturally aligned nanocellulose. Sci. Adv. 2018, 4, eaar3724. [Google Scholar] [CrossRef]
- Pop, E.; Varshney, V.; Roy, A.K. Thermal properties of graphene: Fundamentals and applications. MRS Bull. 2012, 37, 1273–1281. [Google Scholar] [CrossRef]
- Xu, L.; Tetreault, A.R.; Khaligh, H.H.; Goldthorpe, I.A.; Wettig, S.D.; Pope, M.A. Continuous Langmuir–Blodgett Deposition and Transfer by Controlled Edge-to-Edge Assembly of Floating 2D Materials. Langmuir 2019, 35, 51–59. [Google Scholar] [CrossRef]
- Jaafar, M.M.; Ciniciato, G.P.M.K.; Ibrahim, S.A.; Phang, S.M.; Yunus, K.; Fisher, A.C.; Iwamoto, M.; Vengadesh, P. Preparation of a Three-Dimensional Reduced Graphene Oxide Film by Using the Langmuir–Blodgett Method. Langmuir 2015, 31, 10426–10434. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, O.N., Jr.; Caseli, L.; Ariga, K. The Past and the Future of Langmuir and Langmuir–Blodgett Films. Chem. Rev. 2022, 122, 6459–6513. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Peng, S.; Wang, C.H. Multifunctional Polymer Nanocomposites Reinforced by Aligned Carbon Nanomaterials. Polymers 2018, 10, 542. [Google Scholar] [CrossRef] [PubMed]
- Porter, M.M.; Yeh, M.; Strawson, J.; Goehring, T.; Lujan, S.; Siripasopsotorn, P.; Meyers, M.A.; McKittrick, J. Magnetic freeze casting inspired by nature. Mater. Sci. Eng. A 2012, 556, 741–750. [Google Scholar] [CrossRef]
- Ogden, T.A.; Prisbrey, M.; Nelson, I.; Raeymaekers, B.; Naleway, S.E. Ultrasound freeze casting: Fabricating bioinspired porous scaffolds through combining freeze casting and ultrasound directed self-assembly. Mater. Des. 2019, 164, 107561. [Google Scholar] [CrossRef]
- Barrow, M.; Zhang, H. Aligned porous stimuli-responsive hydrogels via directional freezing and frozen UV initiated polymerization. Soft Matter 2013, 9, 2723–2729. [Google Scholar] [CrossRef]
- Niksiar, P.; Su, F.Y.; Frank, M.B.; Ogden, T.A.; Naleway, S.E.; Meyers, M.A.; McKittrick, J.; Porter, M.M. External Field Assisted Freeze Casting. Ceramics 2019, 2, 208–234. [Google Scholar] [CrossRef]
- Giese, M.; Blusch, L.K.; Khan, M.K.; MacLachlan, M.J. Functional Materials from Cellulose-Derived Liquid-Crystal Templates. Angew. Chem. Int. Ed. 2015, 54, 2888–2910. [Google Scholar] [CrossRef]
- Tran, A.; Boott, C.E.; MacLachlan, M.J. Understanding the Self-Assembly of Cellulose Nanocrystals—Toward Chiral Photonic Materials. Adv. Mater. 2020, 32, 1905876. [Google Scholar] [CrossRef]
- Gray, D.G.; Mu, X. Chiral Nematic Structure of Cellulose Nanocrystal Suspensions and Films; Polarized Light and Atomic Force Microscopy. Materials 2015, 8, 7873–7888. [Google Scholar] [CrossRef]
- Kim, J.E.; Han, T.H.; Lee, S.H.; Kim, J.Y.; Ahn, C.W.; Yun, J.M.; Kim, S.O. Graphene Oxide Liquid Crystals. Angew. Chem. Int. Ed. 2011, 50, 3043–3047. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Gao, C. Graphene chiral liquid crystals and macroscopic assembled fibres. Nat. Commun. 2011, 2, 571. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Zhu, C.; Lu, T.; Lin, J.; Ma, J.; Zhang, D.; Zhu, S. A chiral smectic structure assembled from nanosheets and nanorods. Chem. Commun. 2017, 53, 1868–1871. [Google Scholar] [CrossRef] [PubMed]
- Kelly, J.A.; Giese, M.; Shopsowitz, K.E.; Hamad, W.Y.; MacLachlan, M.J. The Development of Chiral Nematic Mesoporous Materials. Acc. Chem. Res. 2014, 47, 1088–1096. [Google Scholar] [CrossRef]
- Ohshima, H. The Derjaguin–Landau–Verwey–Overbeek (DLVO) Theory of Colloid Stability. In Electrical Phenomena at Interfaces and Biointerfaces; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 27–34. [Google Scholar] [CrossRef]
- Tadros, T. General Principles of Colloid Stability and the Role of Surface Forces. In Colloid Stability; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010; pp. 1–22. [Google Scholar] [CrossRef]
- Daintith, J. A Dictionary of Chemistry; Oxford University Press: Oxford, UK, 2008. [Google Scholar] [CrossRef]
- Cote, L.J.; Kim, F.; Huang, J. Langmuir−Blodgett Assembly of Graphite Oxide Single Layers. J. Am. Chem. Soc. 2009, 131, 1043–1049. [Google Scholar] [CrossRef]
- Hamley, I.W. Colloids in Introduction to Soft Matter; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 111–159. [Google Scholar] [CrossRef]
- Ye, W.; Li, X.; Zhu, H.; Wang, X.; Wang, S.; Wang, H.; Sun, R. Green fabrication of cellulose/graphene composite in ionic liquid and its electrochemical and photothermal properties. Chem. Eng. J. 2016, 299, 45–55. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, J.; Yu, J.; Zhang, X.; He, J.; Zhang, J. Application of ionic liquids for dissolving cellulose and fabricating cellulose-based materials: State of the art and future trends. Mater. Chem. Front. 2017, 1, 1273–1290. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Y.; Yang, F.; Dong, H.; Bian, Y.; Jia, H.; Xie, X.; Zhang, J. Using Cellulose Nanocrystal as Adjuvant to Improve the Dispersion Ability of Multilayer Graphene in Aqueous Suspension. Front. Bioeng. Biotechnol. 2021, 9, 638744. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Zheng, W.; Zhu, J. Regenerated cellulose/graphene nanocomposite films prepared in DMAC/LiCl solution. Carbohydr. Polym. 2012, 88, 26–30. [Google Scholar] [CrossRef]
- Kafy, A.; Sadasivuni, K.K.; Kim, H.C.; Akther, A.; Kim, J. Designing flexible energy and memory storage materials using cellulose modified graphene oxide nanocomposites. Phys. Chem. Chem. Phys. 2015, 17, 5923–5931. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, Y.; Duan, X. Van der Waals integration before and beyond two-dimensional materials. Nature 2019, 567, 323–333. [Google Scholar] [CrossRef] [PubMed]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 2011, 83, 195131. [Google Scholar] [CrossRef]
- Thonhauser, T.; Cooper, V.R.; Li, S.; Puzder, A.; Hyldgaard, P.; Langreth, D.C. Van der Waals density functional: Self-consistent potential and the nature of the van der Waals bond. Phys. Rev. B 2007, 76, 125112. [Google Scholar] [CrossRef]
- Nayani, K.; Kim, Y.K.; Abbott, N.L. Chiral interactions in liquid crystals. Nat. Mater. 2018, 17, 14–15. [Google Scholar] [CrossRef] [PubMed]
- Schipper, P.E.; Harrowell, P.R. A Van der Waals model of chiral mixtures using a chiral Lennard-Jones potential. Applications to the Pasteur Experiment and phenomena in chiral solvents. J. Am. Chem. Soc. 1983, 105, 723–730. [Google Scholar] [CrossRef]
- Börjesson, M.; Westman, G. Crystalline nanocellulose—Preparation, modification, and properties. Cellul. Fundam. Asp. Curr. Trends 2015, 7, 159–191. [Google Scholar] [CrossRef]
- Belli, S.; Dussi, S.; Dijkstra, M.; van Roij, R. Density functional theory for chiral nematic liquid crystals. Phys. Rev. E 2014, 90, 020503. [Google Scholar] [CrossRef]
- Diaz, J.A.; Ye, Z.; Wu, X.; Moore, A.L.; Moon, R.J.; Martini, A.; Boday, D.J.; Youngblood, J.P. Thermal Conductivity in Nanostructured Films: From Single Cellulose Nanocrystals to Bulk Films. Biomacromolecules 2014, 15, 4096–4101. [Google Scholar] [CrossRef]
- Nigmatullin, R.; Lovitt, R.; Wright, C.; Linder, M.; Nakari-Setälä, T.; Gama, M. Atomic force microscopy study of cellulose surface interaction controlled by cellulose binding domains. Colloids Surf. B Biointerfaces 2004, 35, 125–135. [Google Scholar] [CrossRef]
- Whitby, R.L.D.; Gun’ko, V.M.; Korobeinyk, A.; Busquets, R.; Cundy, A.B.; László, K.; Skubiszewska-Zięba, J.; Leboda, R.; Tombácz, E.; Toth, I.Y.; et al. Driving Forces of Conformational Changes in Single-Layer Graphene Oxide. ACS Nano 2012, 6, 3967–3973. [Google Scholar] [CrossRef]
- Whitby, R.L.D. Chemical Control of Graphene Architecture: Tailoring Shape and Properties. ACS Nano 2014, 8, 9733–9754. [Google Scholar] [CrossRef]
- Wohlert, M.; Benselfelt, T.; Wågberg, L.; Furó, I.; Berglund, L.A.; Wohlert, J. Cellulose and the role of hydrogen bonds: Not in charge of everything. Cellulose 2022, 29, 1–23. [Google Scholar] [CrossRef]
- Jariwala, D.; Marks, T.J.; Hersam, M.C. Mixed-dimensional van der Waals heterostructures. Nat. Mater. 2017, 16, 170–181. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Weiss, N.O.; Duan, X.; Cheng, H.C.; Huang, Y.; Duan, X. Van der Waals heterostructures and devices. Nat. Rev. Mater. 2016, 1, 16042. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, D.; Cui, T.; Li, D. Stability of hydrogen-terminated graphene edges. Phys. Chem. Chem. Phys. 2021, 23, 13261–13266. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Ning, W.; Zhang, J.; Qiao, X.; Zhang, J.; He, J.; Liu, C.Y. Stable dispersions of reduced graphene oxide in ionic liquids. J. Mater. Chem. 2010, 20, 5401–5403. [Google Scholar] [CrossRef]
- Tang, L.; Li, X.; Du, D.; He, C. Fabrication of multilayer films from regenerated cellulose and graphene oxide through layer-by-layer assembly. Prog. Nat. Sci. Mater. Int. 2012, 22, 341–346. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Chen, Y.; Duan, Y.; Zhang, J. Green Fabrication of Regenerated Cellulose/Graphene Films with Simultaneous Improvement of Strength and Toughness by Tailoring the Nanofiber Diameter. ACS Sustain. Chem. Eng. 2018, 6, 1271–1278. [Google Scholar] [CrossRef]
- Xu, M.; Huang, Q.; Wang, X.; Sun, R. Highly tough cellulose/graphene composite hydrogels prepared from ionic liquids. Ind. Crops Prod. 2015, 70, 56–63. [Google Scholar] [CrossRef]
- Maio, A.; Pibiri, I.; Morreale, M.; Mantia, F.P.L.; Scaffaro, R. An Overview of Functionalized Graphene Nanomaterials for Advanced Applications. Nanomaterials 2021, 11, 1717. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Piner, R.D.; Kohlhaas, K.A.; Kleinhammes, A.; Jia, Y.; Wu, Y.; Nguyen, S.T.; Ruoff, R.S. Synthesis of graphene-based nanosheets via chemical reduction of exfoliated graphite oxide. Carbon 2007, 45, 1558–1565. [Google Scholar] [CrossRef]
- Khosroshahi, Z.; Kharaziha, M.; Karimzadeh, F.; Allafchian, A. Green reduction of graphene oxide by ascorbic acid. AIP Conf. Proc. 2018, 1920, 020009. [Google Scholar] [CrossRef]
- Chen, J.; Li, H.; Zhang, L.; Du, C.; Fang, T.; Hu, J. Direct Reduction of Graphene Oxide/Nanofibrillated Cellulose Composite Film and its Electrical Conductivity Research. Sci. Rep. 2020, 10, 3124. [Google Scholar] [CrossRef] [PubMed]
- Renteria, J.D.; Ramirez, S.; Malekpour, H.; Alonso, B.; Centeno, A.; Zurutuza, A.; Cocemasov, A.I.; Nika, D.L.; Balandin, A.A. Strongly Anisotropic Thermal Conductivity of Free-Standing Reduced Graphene Oxide Films Annealed at High Temperature. Adv. Funct. Mater. 2015, 25, 4664–4672. [Google Scholar] [CrossRef]
- Pottathara, Y.B.; Thomas, S.; Kalarikkal, N.; Griesser, T.; Grohens, Y.; Bobnar, V.; Finšgar, M.; Kokol, V.; Kargl, R. UV-Induced reduction of graphene oxide in cellulose nanofibril composites. New J. Chem. 2019, 43, 681–688. [Google Scholar] [CrossRef]
- Li, J.; Tang, J.; Yuan, J.; Zhang, K.; Shao, Q.; Sun, Y.; Qin, L.C. Interactions between Graphene and Ionic Liquid Electrolyte in Supercapacitors. Electrochim. Acta 2016, 197, 84–91. [Google Scholar] [CrossRef]
- Voiry, D.; Yang, J.; Kupferberg, J.; Fullon, R.; Lee, C.; Jeong, H.Y.; Shin, H.S.; Chhowalla, M. High-quality graphene via microwave reduction of solution-exfoliated graphene oxide. Science 2016, 353, 1413–1416. [Google Scholar] [CrossRef]
- Shin, H.J.; Kim, K.K.; Benayad, A.; Yoon, S.M.; Park, H.K.; Jung, I.S.; Jin, M.H.; Jeong, H.K.; Kim, J.M.; Choi, J.Y.; et al. Efficient Reduction of Graphite Oxide by Sodium Borohydride and Its Effect on Electrical Conductance. Adv. Funct. Mater. 2009, 19, 1987–1992. [Google Scholar] [CrossRef]
- Tung, V.C.; Allen, M.J.; Yang, Y.; Kaner, R.B. High-throughput solution processing of large-scale graphene. Nat. Nanotechnol. 2009, 4, 25–29. [Google Scholar] [CrossRef]
- Nguyen Dang, L.; Seppälä, J. Electrically conductive nanocellulose/graphene composites exhibiting improved mechanical properties in high-moisture condition. Cellulose 2015, 22, 1799–1812. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Qi, H. Novel Functional Materials Based on Cellulose, 1st ed.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Yu, L.; Chen, G.Z. Ionic Liquid-Based Electrolytes for Supercapacitor and Supercapattery. Front. Chem. 2019, 7, 272. [Google Scholar] [CrossRef] [PubMed]
- Jónsson, E. Ionic liquids as electrolytes for energy storage applications—A modelling perspective. Energy Storage Mater. 2020, 25, 827–835. [Google Scholar] [CrossRef]
- Vijayakumar, M.; Schwenzer, B.; Shutthanandan, V.; Hu, J.; Liu, J.; Aksay, I.A. Elucidating graphene–ionic liquid interfacial region: A combined experimental and computational study. Nano Energy 2014, 3, 152–158. [Google Scholar] [CrossRef]
- Chen, K.; Chen, L.; Chen, Y.; Bai, H.; Li, L. Three-dimensional porous graphene-based composite materials: Electrochemical synthesis and application. J. Mater. Chem. 2012, 22, 20968–20976. [Google Scholar] [CrossRef]
- Chen, C.; Hu, L. Nanocellulose toward Advanced Energy Storage Devices: Structure and Electrochemistry. Acc. Chem. Res. 2018, 51, 3154–3165. [Google Scholar] [CrossRef]
- Dey, R.S.; Chi, Q. Architecture and Applications of Functional Three-Dimensional Graphene Networks. In Graphene Materials; Scrivener Publishing: Beverly, MA, USA, 2015; pp. 67–99. [Google Scholar] [CrossRef]
- Wang, M.; Duan, X.; Xu, Y.; Duan, X. Functional Three-Dimensional Graphene/Polymer Composites. ACS Nano 2016, 10, 7231–7247. [Google Scholar] [CrossRef]
- Ahmed, A.; Adak, B.; Faruk, M.O.; Mukhopadhyay, S. Nanocellulose Coupled 2D Graphene Nanostructures: Emerging Paradigm for Sustainable Functional Applications. Ind. Eng. Chem. Res. 2021, 60, 10882–10916. [Google Scholar] [CrossRef]
- DelRio, F.W.; de Boer, M.P.; Knapp, J.A.; David Reedy, E.; Clews, P.J.; Dunn, M.L. The role of van der Waals forces in adhesion of micromachined surfaces. Nat. Mater. 2005, 4, 629–634. [Google Scholar] [CrossRef]
- Sinko, R.; Qin, X.; Keten, S. Interfacial mechanics of cellulose nanocrystals. MRS Bull. 2015, 40, 340–348. [Google Scholar] [CrossRef]
- Kim, J.; Cote, L.J.; Huang, J. Two Dimensional Soft Material: New Faces of Graphene Oxide. Acc. Chem. Res. 2012, 45, 1356–1364. [Google Scholar] [CrossRef] [PubMed]
- Kim, F.; Cote, L.J.; Huang, J. Graphene Oxide: Surface Activity and Two-Dimensional Assembly. Adv. Mater. 2010, 22, 1954–1958. [Google Scholar] [CrossRef] [PubMed]
- Awasthi, A.P.; Lagoudas, D.C.; Hammerand, D.C. Modeling of graphene–polymer interfacial mechanical behavior using molecular dynamics. Model. Simul. Mater. Sci. Eng. 2009, 17, 015002. [Google Scholar] [CrossRef]
- Lagerwall, J.P.F.; Schütz, C.; Salajkova, M.; Noh, J.; Hyun Park, J.; Scalia, G.; Bergström, L. Cellulose nanocrystal-based materials: From liquid crystal self-assembly and glass formation to multifunctional thin films. NPG Asia Mater. 2014, 6, e80. [Google Scholar] [CrossRef]
- Kim, H.S.; Oweida, T.J.; Yingling, Y.G. Interfacial stability of graphene-based surfaces in water and organic solvents. J. Mater. Sci. 2018, 53, 5766–5776. [Google Scholar] [CrossRef]
- Malho, J.M.; Laaksonen, P.; Walther, A.; Ikkala, O.; Linder, M.B. Facile Method for Stiff, Tough, and Strong Nanocomposites by Direct Exfoliation of Multilayered Graphene into Native Nanocellulose Matrix. Biomacromolecules 2012, 13, 1093–1099. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, X.; Shen, Y.; Yoshino, K.; Feng, W. A mechanically strong, flexible and conductive film based on bacterial cellulose/graphene nanocomposite. Carbohydr. Polym. 2012, 87, 644–649. [Google Scholar] [CrossRef]
- Larkin, A.I.; Khmel’nitskii, D.E. Activation conductivity in disordered systems with large localization length. Sov. J. Exp. Theor. Phys. 1982, 56, 647. [Google Scholar]
- Koga, H.; Nagashima, K.; Suematsu, K.; Takahashi, T.; Zhu, L.; Fukushima, D.; Huang, Y.; Nakagawa, R.; Liu, J.; Uetani, K.; et al. Nanocellulose Paper Semiconductor with a 3D Network Structure and Its Nano–Micro–Macro Trans-Scale Design. ACS Nano 2022, 16, 8630–8640. [Google Scholar] [CrossRef]
- Eda, G.; Lin, Y.Y.; Mattevi, C.; Yamaguchi, H.; Chen, H.A.; Chen, I.S.; Chen, C.W.; Chhowalla, M. Blue Photoluminescence from Chemically Derived Graphene Oxide. Adv. Mater. 2010, 22, 505–509. [Google Scholar] [CrossRef]
- Singh, V.; Joung, D.; Zhai, L.; Das, S.; Khondaker, S.I.; Seal, S. Graphene based materials: Past, present and future. Prog. Mater. Sci. 2011, 56, 1178–1271. [Google Scholar] [CrossRef]
- Pei, S.; Zhao, J.; Du, J.; Ren, W.; Cheng, H.M. Direct reduction of graphene oxide films into highly conductive and flexible graphene films by hydrohalic acids. Carbon 2010, 48, 4466–4474. [Google Scholar] [CrossRef]
- Fernández-Merino, M.J.; Guardia, L.; Paredes, J.I.; Villar-Rodil, S.; Solís-Fernández, P.; Martínez-Alonso, A.; Tascón, J.M.D. Vitamin C Is an Ideal Substitute for Hydrazine in the Reduction of Graphene Oxide Suspensions. J. Phys. Chem. C 2010, 114, 6426–6432. [Google Scholar] [CrossRef]
- Liu, L.; Ryu, S.; Tomasik, M.R.; Stolyarova, E.; Jung, N.; Hybertsen, M.S.; Steigerwald, M.L.; Brus, L.E.; Flynn, G.W. Graphene Oxidation: Thickness-Dependent Etching and Strong Chemical Doping. Nano Lett. 2008, 8, 1965–1970. [Google Scholar] [CrossRef] [PubMed]
- Sheng, P. Fluctuation-induced tunneling conduction in disordered materials. Phys. Rev. B 1980, 21, 2180–2195. [Google Scholar] [CrossRef]
- Heeger, A.J. The Critical Regime of the Metal-Insulator Transition in Conducting Polymers: Experimental Studies. Phys. Scr. 2002, 2002, 30. [Google Scholar] [CrossRef]
- Epstein, A.J.; Lee, W.P.; Prigodin, V.N. Low-dimensional variable range hopping in conducting polymers. Synth. Met. 2001, 117, 9–13. [Google Scholar] [CrossRef]
- Fogler, M.M.; Teber, S.; Shklovskii, B.I. Variable-range hopping in quasi-one-dimensional electron crystals. Phys. Rev. B 2004, 69, 035413. [Google Scholar] [CrossRef]
- Rao, F.B.; Almumen, H.; Fan, Z.; Li, W.; Dong, L.X. Inter-sheet-effect-inspired graphene sensors: Design, fabrication and characterization. Nanotechnology 2012, 23, 105501. [Google Scholar] [CrossRef] [PubMed]
- Prasher, R. Thermal Interface Materials: Historical Perspective, Status, and Future Directions. Proc. IEEE 2006, 94, 1571–1586. [Google Scholar] [CrossRef]
- Balandin, A.A.; Nika, D.L. Phononics in low-dimensional materials. Mater. Today 2012, 15, 266–275. [Google Scholar] [CrossRef]
- Ma, H.; Babaei, H.; Tian, Z. The importance of van der Waals interactions to thermal transport in Graphene-C60 heterostructures. Carbon 2019, 148, 196–203. [Google Scholar] [CrossRef]
- Dri, F.L.; Shang, S.; Hector, L.G.; Saxe, P.; Liu, Z.K.; Moon, R.J.; Zavattieri, P.D. Anisotropy and temperature dependence of structural, thermodynamic, and elastic properties of crystalline cellulose Iβ: A first-principles investigation. Model. Simul. Mater. Sci. Eng. 2014, 22, 085012. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Froudakis, G.; Farmer, B.L. Modeling of Thermal Transport in Pillared-Graphene Architectures. ACS Nano 2010, 4, 1153–1161. [Google Scholar] [CrossRef]
- Kreith, F.; Black, W.Z. Basic Heat Transfer; Harper & Row: New York, NY, USA, 1980. [Google Scholar]
- Dai, W.; Hanaor, D.; Gan, Y. The effects of packing structure on the effective thermal conductivity of granular media: A grain scale investigation. Int. J. Therm. Sci. 2019, 142, 266–279. [Google Scholar] [CrossRef]
- Alam, M.; Singh, H.; Limbachiya, M.C. Vacuum Insulation Panels (VIPs) for building construction industry—A review of the contemporary developments and future directions. Appl. Energy 2011, 88, 3592–3602. [Google Scholar] [CrossRef]
- Jelle, B.P. Traditional, state-of-the-art and future thermal building insulation materials and solutions—Properties, requirements and possibilities. Energy Build. 2011, 43, 2549–2563. [Google Scholar] [CrossRef]
- María Mercedes, V.; Teresa, A.; David, L.D.; Beatriz, M.G.; María Dolores, M. Langmuir-Blodgett Methodology: A Versatile Technique to Build 2D Material Films. In Two-Dimensional Materials; Pramoda Kumar, N., Ed.; IntechOpen: Rijeka, Croatia, 2016; p. 2. [Google Scholar] [CrossRef]
- de Oliveira, R.F.; de Barros, A.; Ferreira, M. 4—Nanostructured Films: Langmuir–Blodgett (LB) and Layer-by-Layer (LbL) Techniques. In Nanostructures; Da Róz, A.L., Ferreira, M., de Lima Leite, F., Oliveira, O.N., Eds.; William Andrew Publishing: Norwich, NY, USA, 2017; pp. 105–123. [Google Scholar] [CrossRef]
- Li, P.; Sirviö, J.A.; Asante, B.; Liimatainen, H. Recyclable deep eutectic solvent for the production of cationic nanocelluloses. Carbohydr. Polym. 2018, 199, 219–227. [Google Scholar] [CrossRef]
- Zhang, K.; Liimatainen, H. Hierarchical Assembly of Nanocellulose-Based Filaments by Interfacial Complexation. Small 2018, 14, 1801937. [Google Scholar] [CrossRef]
- Abbasi Moud, A. Chiral Liquid Crystalline Properties of Cellulose Nanocrystals: Fundamentals and Applications. ACS Omega 2022, 7, 30673–30699. [Google Scholar] [CrossRef]
- Kolacz, J. Energy Minimization in Nematic Liquid Crystal Systems Driven by Geometric Confinement and Temperature Gradients with Applications in Colloidal Systems. Ph.D. Thesis, Kent State University, Kent, OH, USA, 2015. [Google Scholar]
- Peng, Z.; Lin, Q.; Tai, Y.A.; Wang, Y. Applications of Cellulose Nanomaterials in Stimuli-Responsive Optics. J. Agric. Food Chem. 2020, 68, 12940–12955. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Martinez, A.; Senyuk, B.; Tasinkevych, M.; Smalyukh, I.I. Chiral liquid crystal colloids. Nat. Mater. 2018, 17, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Deville, S. Ice-templating, freeze casting: Beyond materials processing. J. Mater. Res. 2013, 28, 2202–2219. [Google Scholar] [CrossRef]
- Wegst, U.G.K.; Schecter, M.; Donius, A.E.; Hunger, P.M. Biomaterials by freeze casting. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 2099–2121. [Google Scholar] [CrossRef]
- Rempel, A.W.; Worster, M.G. The interaction between a particle and an advancing solidification front. J. Cryst. Growth 1999, 205, 427–440. [Google Scholar] [CrossRef]
- Bai, H.; Chen, Y.; Delattre, B.; Tomsia, A.P.; Ritchie, R.O. Bioinspired large-scale aligned porous materials assembled with dual temperature gradients. Sci. Adv. 2015, 1, e1500849. [Google Scholar] [CrossRef] [PubMed]
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef]
- Tang, Y.; Miao, Q.; Qiu, S.; Zhao, K.; Hu, L. Novel freeze-casting fabrication of aligned lamellar porous alumina with a centrosymmetric structure. J. Eur. Ceram. Soc. 2014, 34, 4077–4082. [Google Scholar] [CrossRef]
- Zhu, X.; Yang, C.; Wu, P.; Ma, Z.; Shang, Y.; Bai, G.; Liu, X.; Chang, G.; Li, N.; Dai, J.; et al. Precise control of versatile microstructure and properties of graphene aerogel via freezing manipulation. Nanoscale 2020, 12, 4882–4894. [Google Scholar] [CrossRef]
- Jiménez-Saelices, C.; Seantier, B.; Cathala, B.; Grohens, Y. Effect of freeze-drying parameters on the microstructure and thermal insulating properties of nanofibrillated cellulose aerogels. J. Sol-Gel Sci. Technol. 2017, 84, 475–485. [Google Scholar] [CrossRef]
- Porter, M.M.; Niksiar, P.; McKittrick, J. Microstructural Control of Colloidal-Based Ceramics by Directional Solidification Under Weak Magnetic Fields. J. Am. Ceram. Soc. 2016, 99, 1917–1926. [Google Scholar] [CrossRef]
- Jia, L.; Chen, Y.; Lei, S.; Mo, S.; Luo, X.; Shao, X. External electromagnetic field-aided freezing of CMC-modified graphene/water nanofluid. Appl. Energy 2016, 162, 1670–1677. [Google Scholar] [CrossRef]
- Zhao, G.; Zhu, H. Cation–π Interactions in Graphene-Containing Systems for Water Treatment and Beyond. Adv. Mater. 2020, 32, 1905756. [Google Scholar] [CrossRef] [PubMed]
- Chiou, Y.C.; Olukan, T.A.; Almahri, M.A.; Apostoleris, H.; Chiu, C.H.; Lai, C.Y.; Lu, J.Y.; Santos, S.; Almansouri, I.; Chiesa, M. Direct Measurement of the Magnitude of the van der Waals Interaction of Single and Multilayer Graphene. Langmuir 2018, 34, 12335–12343. [Google Scholar] [CrossRef]
- Muruganathan, M.; Sun, J.; Imamura, T.; Mizuta, H. Electrically Tunable van der Waals Interaction in Graphene–Molecule Complex. Nano Lett. 2015, 15, 8176–8180. [Google Scholar] [CrossRef]
- Ebner, A.D.; Ritter, J.A.; Ploehn, H.J. Magnetic Hetero-flocculation of Paramagnetic Colloidal Particles. J. Colloid Interface Sci. 2000, 225, 39–46. [Google Scholar] [CrossRef]
- Tang, Y.; Qiu, S.; Miao, Q.; Wu, C. Fabrication of lamellar porous alumina with axisymmetric structure by directional solidification with applied electric and magnetic fields. J. Eur. Ceram. Soc. 2016, 36, 1233–1240. [Google Scholar] [CrossRef]
- Yang, M.; Yuan, Z.; Liu, J.; Fang, Z.; Fang, L.; Yu, D.; Li, Q. Photoresponsive Actuators Built from Carbon-Based Soft Materials. Adv. Opt. Mater. 2019, 7, 1900069. [Google Scholar] [CrossRef]
- Poothanari, M.A.; Schreier, A.; Missoum, K.; Bras, J.; Leterrier, Y. Photocured Nanocellulose Composites: Recent Advances. ACS Sustain. Chem. Eng. 2022, 10, 3131–3149. [Google Scholar] [CrossRef]
- Yu, X.; Cheng, H.; Zhang, M.; Zhao, Y.; Qu, L.; Shi, G. Graphene-based smart materials. Nat. Rev. Mater. 2017, 2, 17046. [Google Scholar] [CrossRef]
- Han, D.D.; Zhang, Y.L.; Liu, Y.; Liu, Y.Q.; Jiang, H.B.; Han, B.; Fu, X.Y.; Ding, H.; Xu, H.L.; Sun, H.B. Bioinspired Graphene Actuators Prepared by Unilateral UV Irradiation of Graphene Oxide Papers. Adv. Funct. Mater. 2015, 25, 4548–4557. [Google Scholar] [CrossRef]
- Chen, Z.; Li, J.; Zheng, Y. Heat-Mediated Optical Manipulation. Chem. Rev. 2022, 122, 3122–3179. [Google Scholar] [CrossRef] [PubMed]
- Quan, L.; Wang, C.; Xu, Y.; Qiu, J.; Zhang, H.; Cunning, B.; Huang, M.; Wei, H.; Seong, W.K.; Seo, J.; et al. Electromagnetic properties of graphene aerogels made by freeze-casting. Chem. Eng. J. 2022, 428, 131337. [Google Scholar] [CrossRef]
- Munch, E.; Launey, M.E.; Alsem, D.H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Tough, Bio-Inspired Hybrid Materials. Science 2008, 322, 1516–1520. [Google Scholar] [CrossRef]
- Guan, H.; Cheng, Z.; Wang, X. Highly Compressible Wood Sponges with a Spring-like Lamellar Structure as Effective and Reusable Oil Absorbents. ACS Nano 2018, 12, 10365–10373. [Google Scholar] [CrossRef] [PubMed]
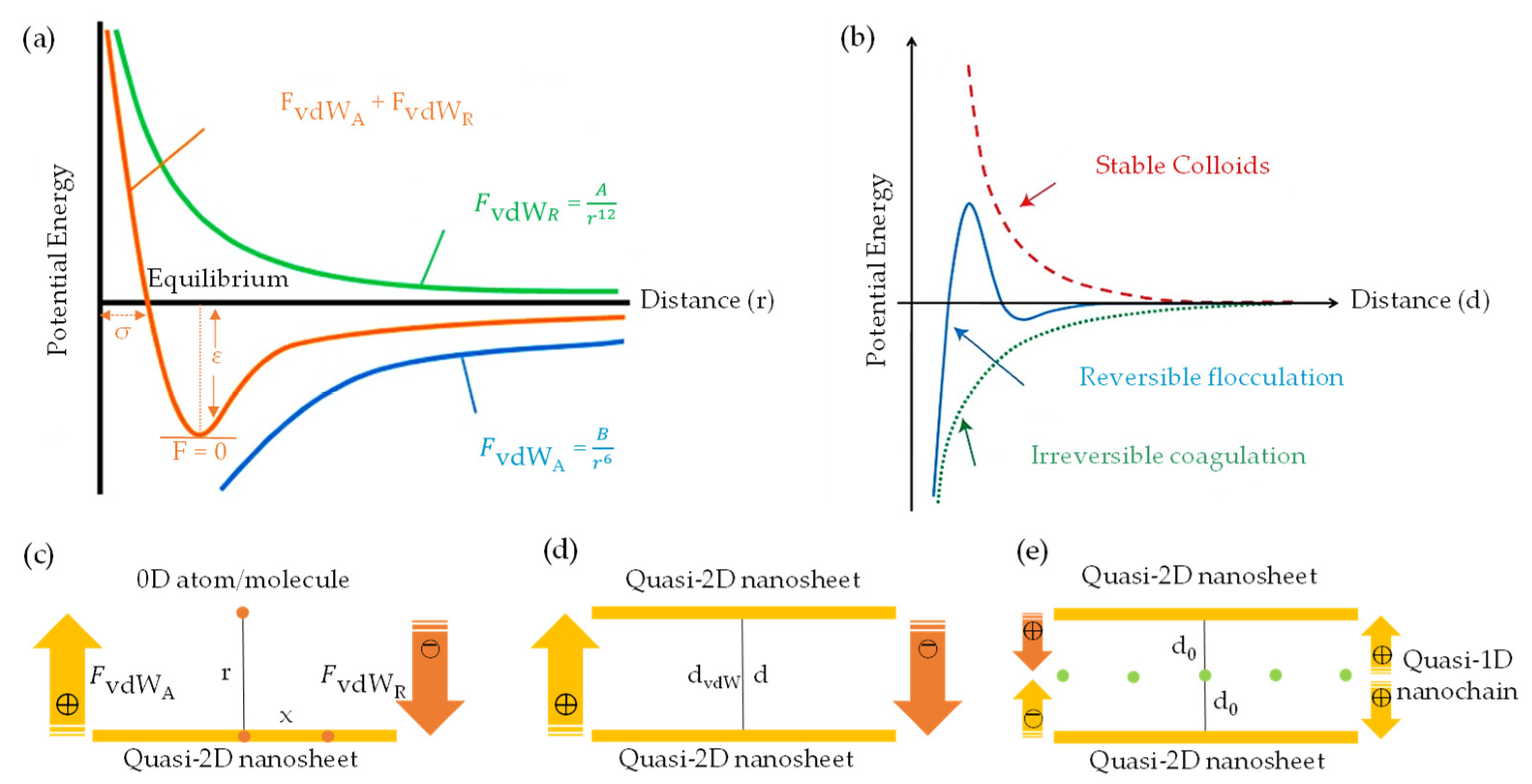
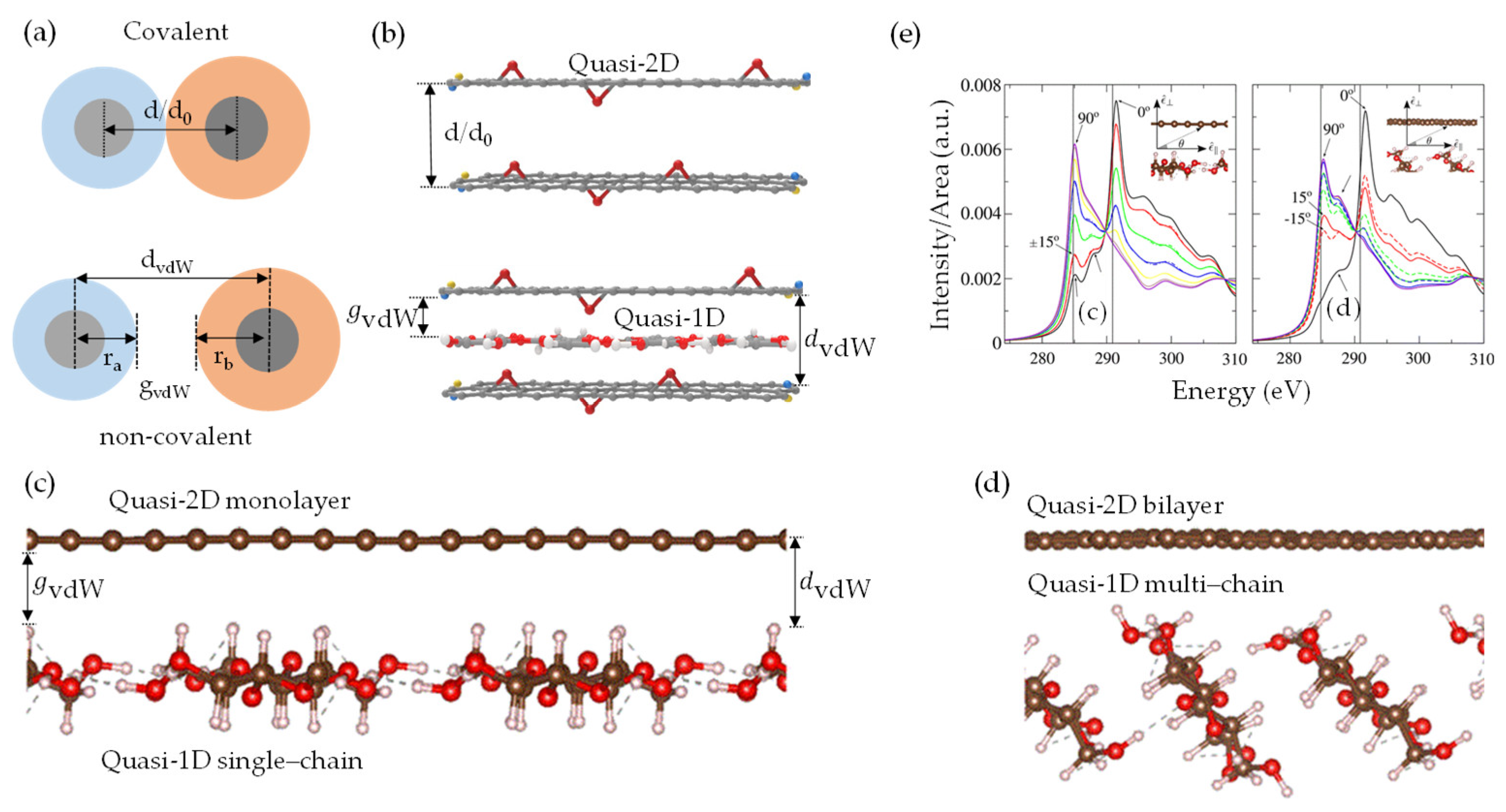

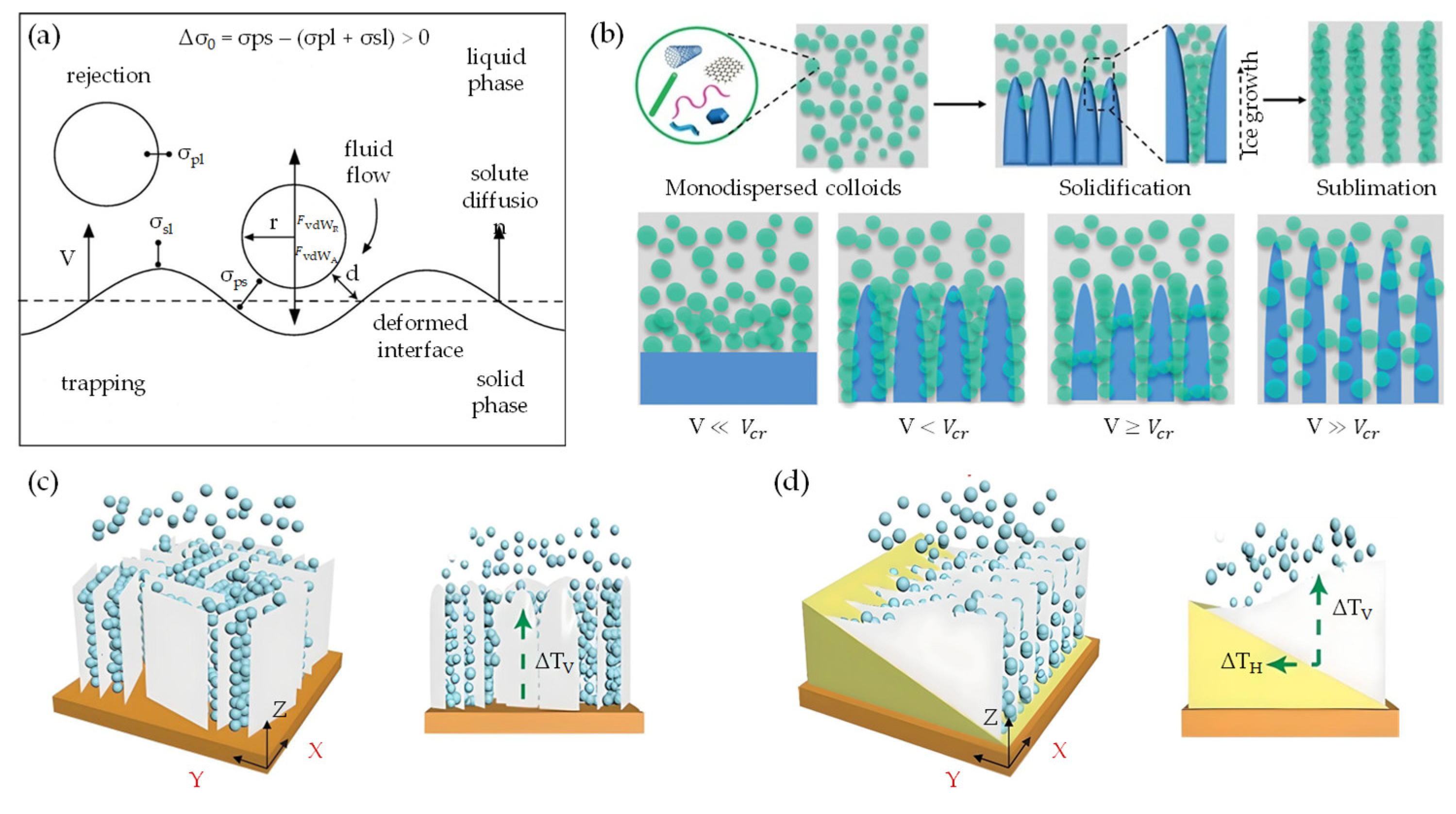
 ), hydrogen bonds (
), hydrogen bonds ( ), and π-conjugated molecules (
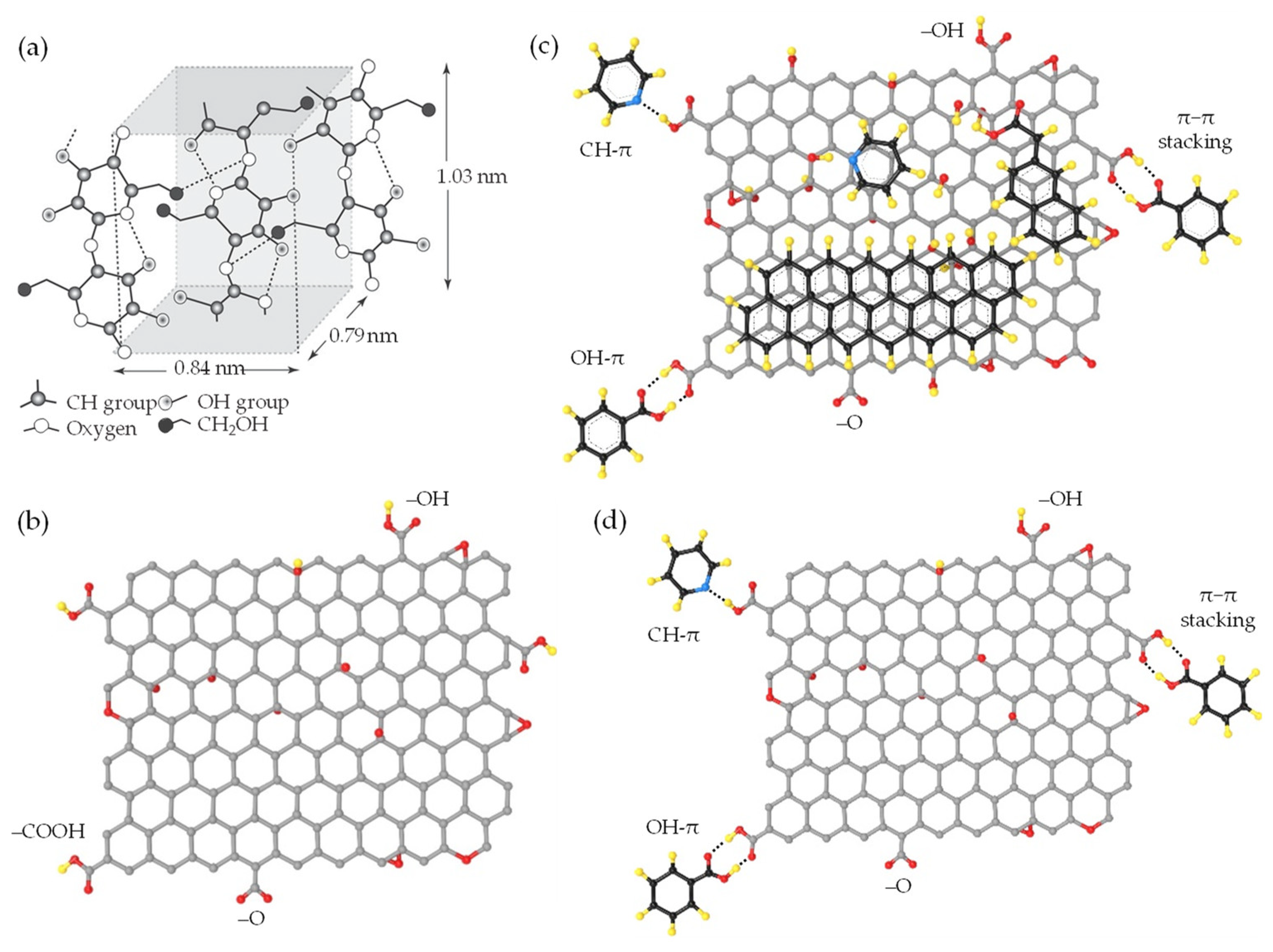
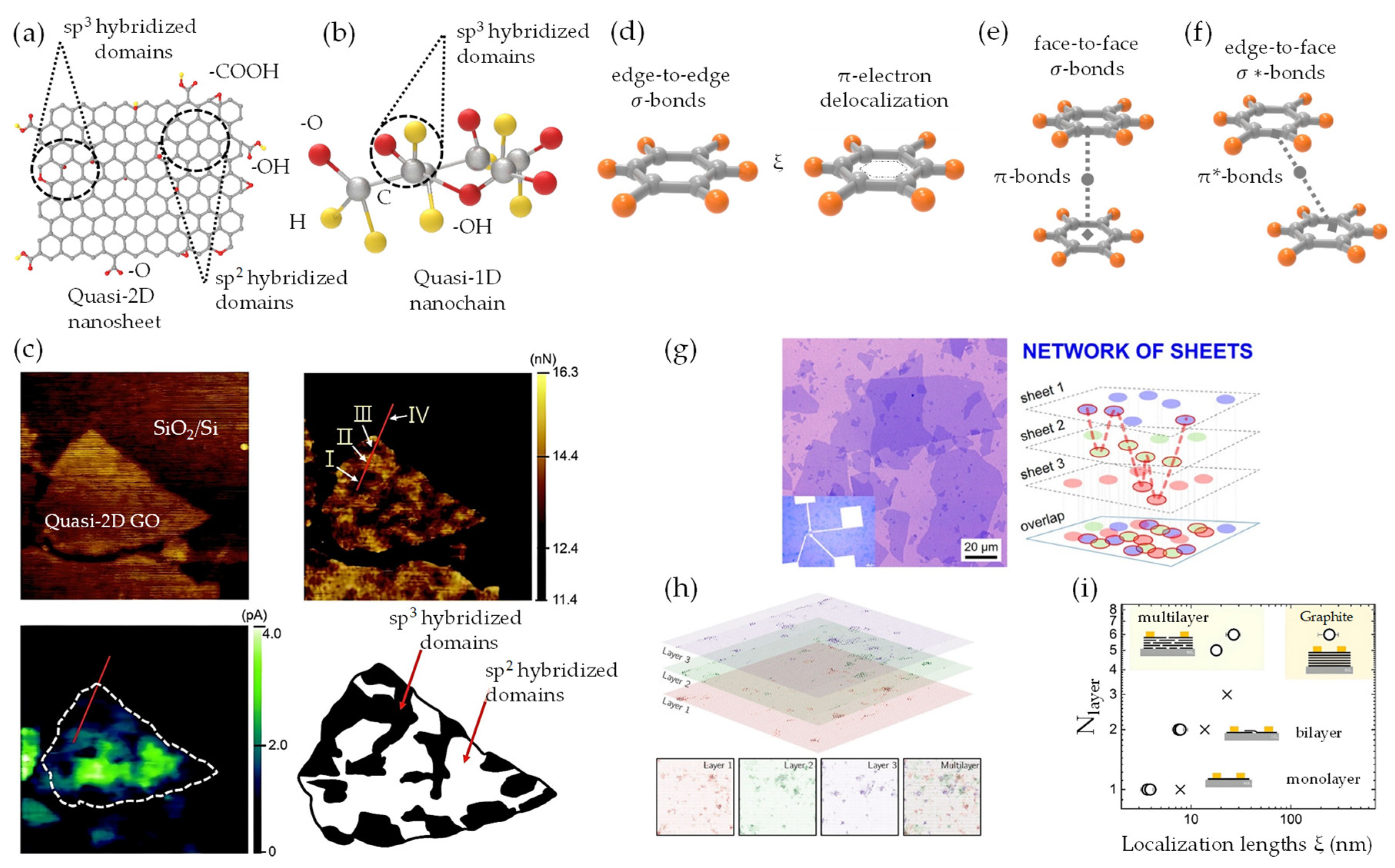
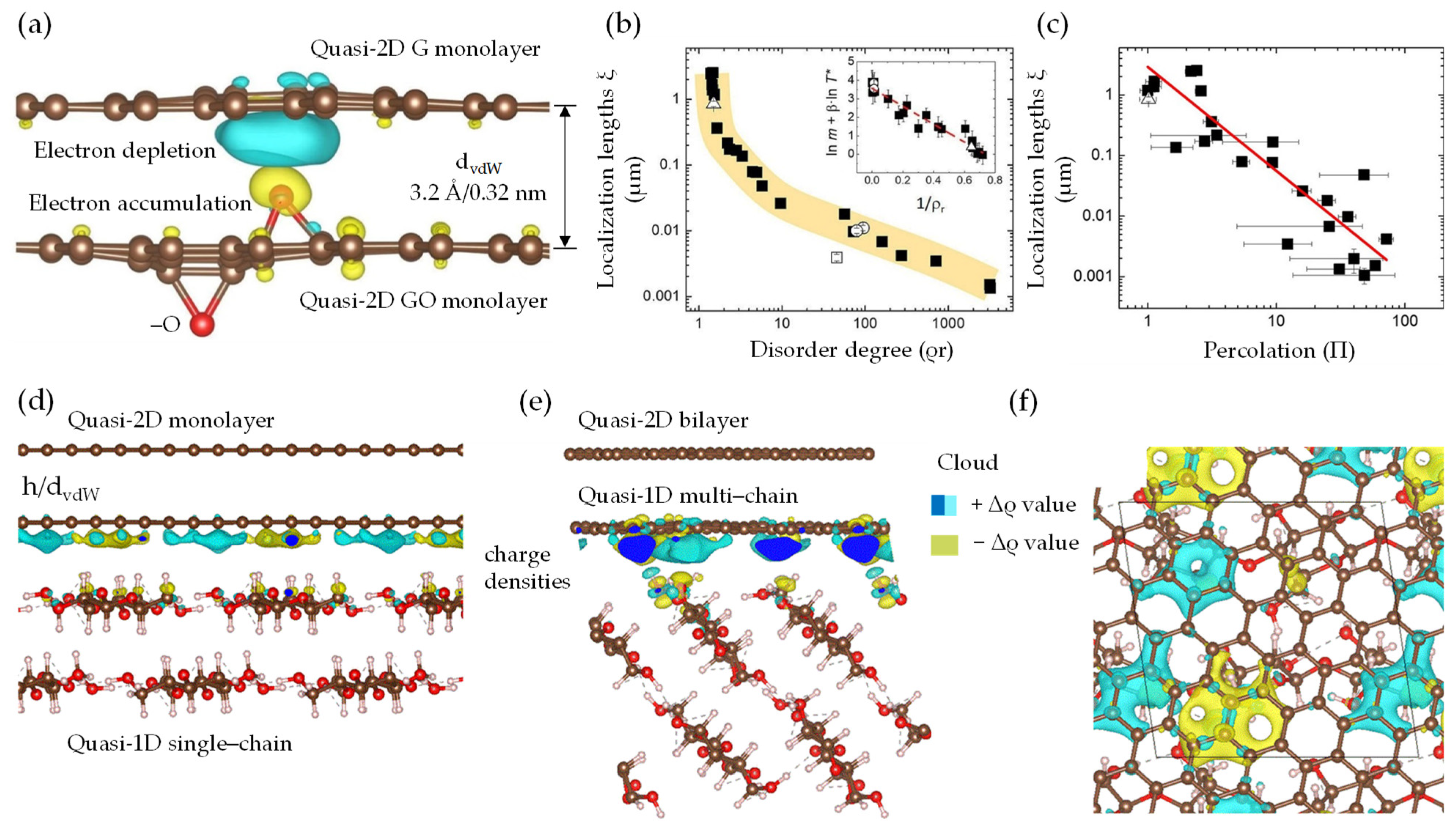
), and π-conjugated molecules ( ); (c,d) quasi-2D/1D vdW heterointerfaces and proposed weak-synergy interactions driven by vdW forces.
); (c,d) quasi-2D/1D vdW heterointerfaces and proposed weak-synergy interactions driven by vdW forces.
 ), hydrogen bonds (
), hydrogen bonds ( ), and π-conjugated molecules (
), and π-conjugated molecules ( ); (c,d) quasi-2D/1D vdW heterointerfaces and proposed weak-synergy interactions driven by vdW forces.
); (c,d) quasi-2D/1D vdW heterointerfaces and proposed weak-synergy interactions driven by vdW forces.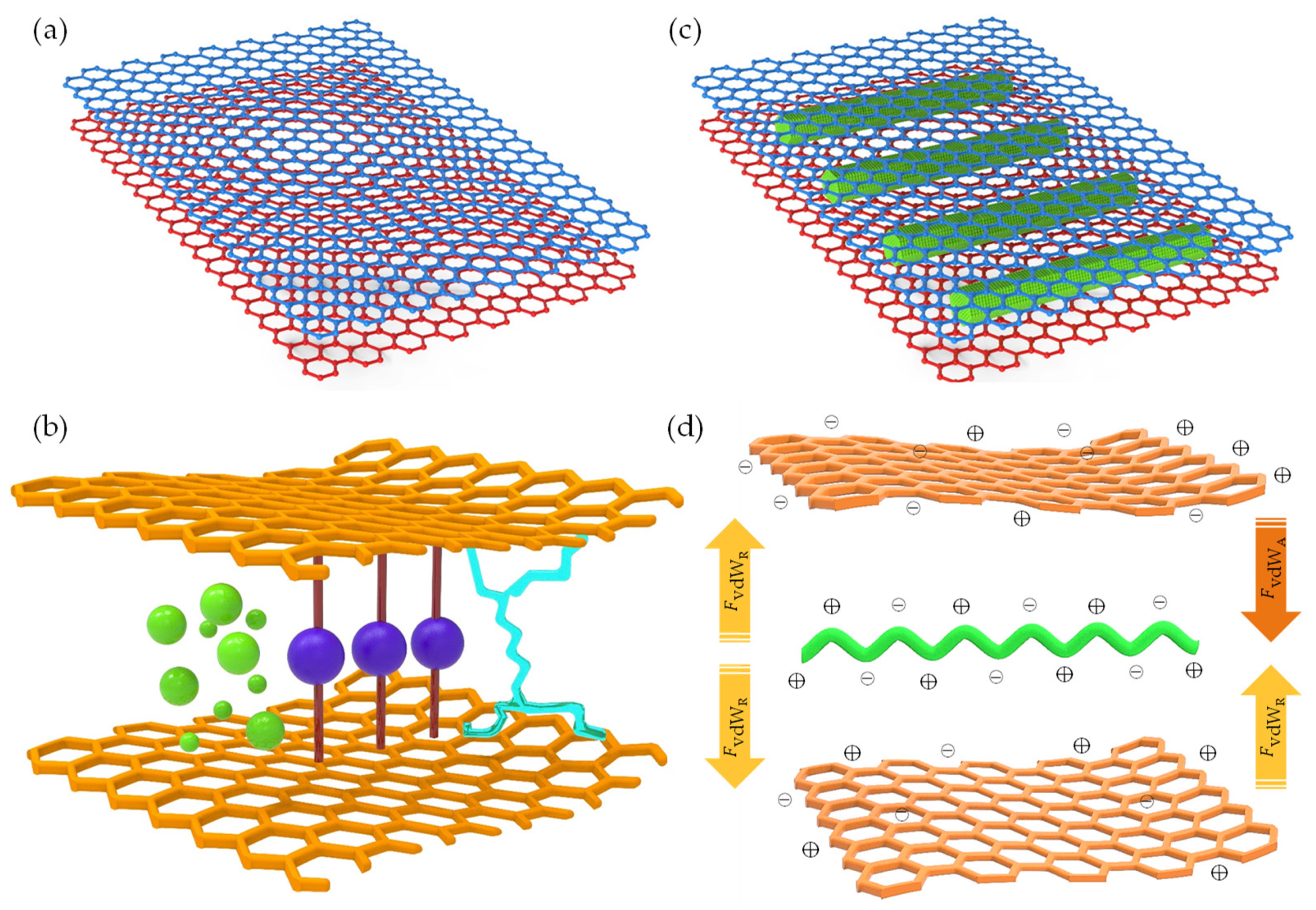





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brakat, A.; Zhu, H. From Forces to Assemblies: van der Waals Forces-Driven Assemblies in Anisotropic Quasi-2D Graphene and Quasi-1D Nanocellulose Heterointerfaces towards Quasi-3D Nanoarchitecture. Nanomaterials 2023, 13, 2399. https://doi.org/10.3390/nano13172399
Brakat A, Zhu H. From Forces to Assemblies: van der Waals Forces-Driven Assemblies in Anisotropic Quasi-2D Graphene and Quasi-1D Nanocellulose Heterointerfaces towards Quasi-3D Nanoarchitecture. Nanomaterials. 2023; 13(17):2399. https://doi.org/10.3390/nano13172399
Chicago/Turabian StyleBrakat, Abdelrahman, and Hongwei Zhu. 2023. "From Forces to Assemblies: van der Waals Forces-Driven Assemblies in Anisotropic Quasi-2D Graphene and Quasi-1D Nanocellulose Heterointerfaces towards Quasi-3D Nanoarchitecture" Nanomaterials 13, no. 17: 2399. https://doi.org/10.3390/nano13172399
APA StyleBrakat, A., & Zhu, H. (2023). From Forces to Assemblies: van der Waals Forces-Driven Assemblies in Anisotropic Quasi-2D Graphene and Quasi-1D Nanocellulose Heterointerfaces towards Quasi-3D Nanoarchitecture. Nanomaterials, 13(17), 2399. https://doi.org/10.3390/nano13172399






