Possibility of Exciton Bose–Einstein Condensation in CdSe Nanoplatelets
Abstract
:1. Introduction
2. Theory
2.1. Exciton Subsystem in CdSe NPL in the Ideal Bose Gas Approximation
2.2. Degenerate Exciton Subsystem in CdSe NPL in the Presence of Screening
2.3. The Degenerate Exciton Subsystem in CdSe NPL in the Approximation of a Weakly Nonideal Bose Gas
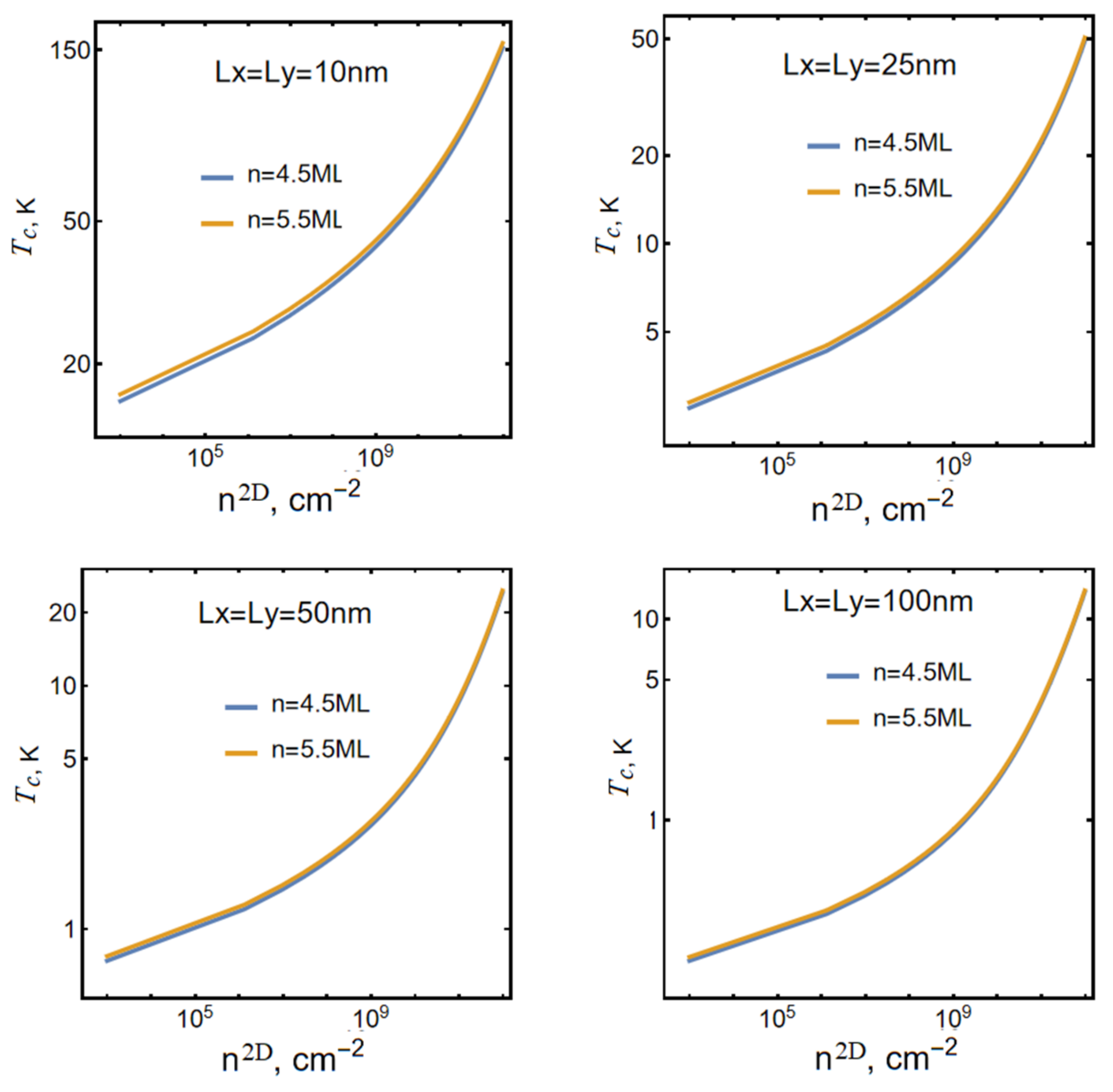
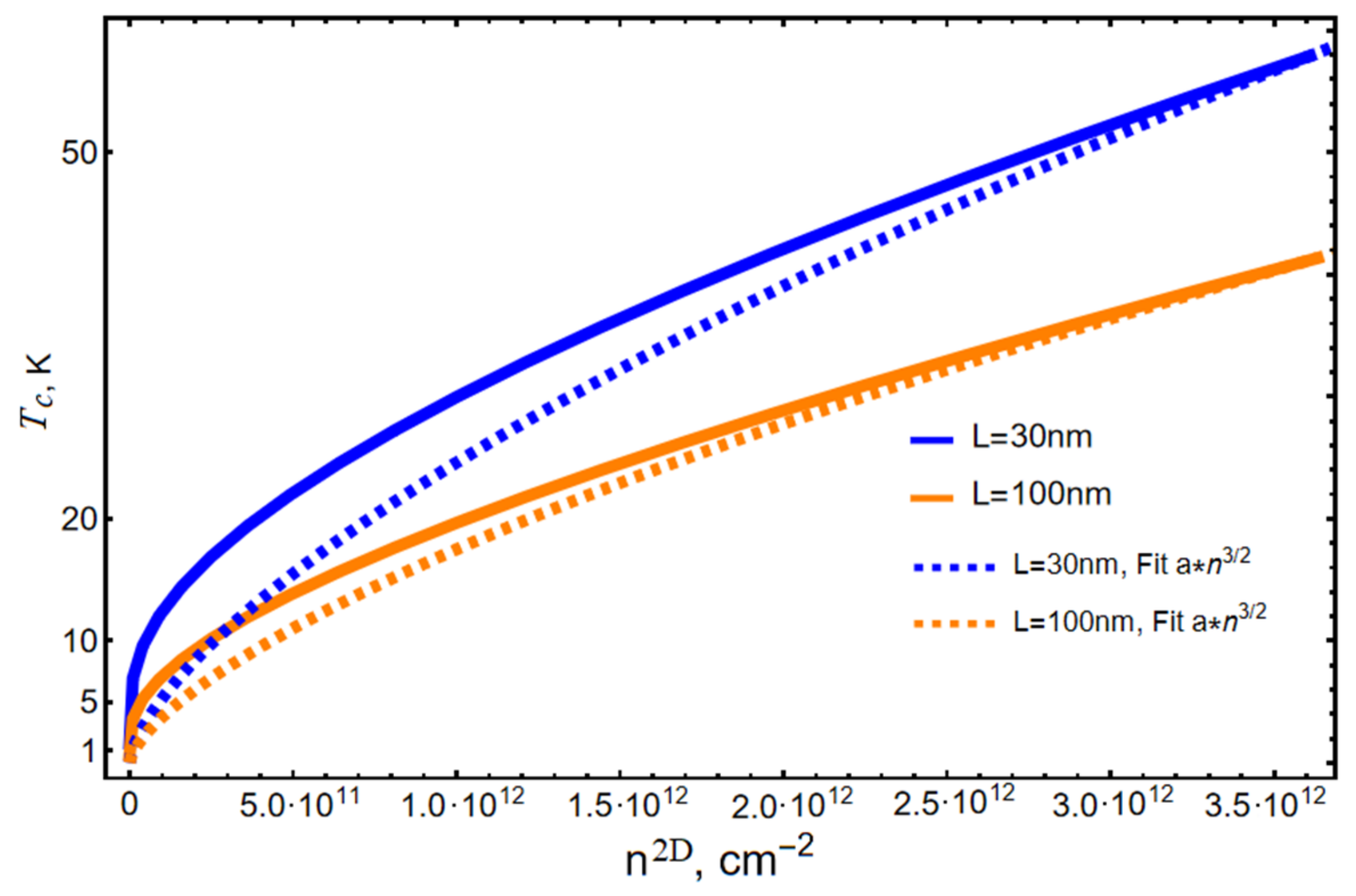
3. Results and Discussions
4. Conclusions
- If the conditions when the exciton subsystem can be described in terms of its properties within the ideal Bose gas model are realized, BEC of excitons is possible in the CdSe NPL;
- BEC critical temperature is determined by the geometric dimensions of the sample and increases with decreasing system dimensions along the plane of the NPL; as the longitudinal dimensions of the sample tend to infinity, the BEC temperature tends to zero;
- At high levels of excitation, when the exciton subsystem and the subsystems of unbound electrons and holes coexist in the CdSe NPL, excitons experience a screening effect from free carriers, as a result of which the temperature of the BEC of excitons increases;
- BEC temperature in the presence of screening is determined by the density of excitons and non-transfer charge carriers, which is ultimately determined by the density of optical pumping;
- The spectrum of elementary excitations of the exciton condensate is determined by the two-dimensional density of excitons and the potential of exciton–exciton interaction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Diagonalization of Hamiltonian (27)
References
- Ithurria, S.; Tessier, M.D.; Mahler, B.; Lobo, R.; Dubertret, B.; Efros, A.L. Colloidal nanoplatelets with two-dimensional electronic structure. Nat. Mater. 2011, 10, 936–941. [Google Scholar] [CrossRef] [PubMed]
- Ithurria, S.; Bousquet, G.; Dubertret, B. Continuous Transition from 3D to 1D Confinement Observed during the Formation of CdSe Nanoplatelets. J. Am. Chem. Soc. 2011, 133, 3070–3077. [Google Scholar] [CrossRef] [PubMed]
- Tessier, M.D.; Javaux, C.; Maksimovic, I.; Loriette, V.; Dubertret, B. Spectroscopy of Single CdSe Nanoplatelets. ACS Nano 2012, 6, 6751–6758. [Google Scholar] [CrossRef] [PubMed]
- Bouet, C.; Tessier, M.D.; Ithurria, S.; Mahler, B.; Nadal, B.; Dubertret, B. Flat Colloidal Semiconductor Nanoplatelets. Chem. Mater. 2013, 25, 1262–1271. [Google Scholar] [CrossRef]
- Lhuillier, E.; Pedetti, S.; Ithurria, S.; Nadal, B.; Heuclin, H.; Dubertret, B. 2D Colloidal Metal Chalcogenides Semiconductors: Synthesis, Spectroscopy, and Applications. Acc. Chem. Res. 2015, 48, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Rabouw, F.T.; van der Bok, J.C.; Spinicelli, P.; Mahler, B.; Nasilowski, M.; Pedetti, S.; Dubertret, B.; Vanmaekelbergh, D. Temporary Charge Carrier Separation Dominates the Photoluminescence Decay Dynamics of Colloidal CdSe Nanoplatelets. Nano Lett. 2016, 16, 2047–2053. [Google Scholar] [CrossRef] [PubMed]
- Nasilowski, M.; Mahler, B.; Lhuillier, E.; Ithurria, S.; Dubertret, B. Two-Dimensional Colloidal Nanocrystals. Chem. Rev. 2016, 116, 10934–10982. [Google Scholar] [CrossRef]
- Ott, F.D.; Riedinger, A.; Ochsenbein, D.R.; Knüsel, P.N.; Erwin, S.C.; Mazzotti, M.; Norris, D.J. Ripening of Semiconductor Nanoplatelets. Nano Lett. 2017, 17, 6870–6877. [Google Scholar] [CrossRef]
- Kechkeche, D.; Cao, E.; Grazon, C.; Caschera, F.; Noireaux, V.; Niel, M.-L.B.; Dubertret, B. Semiconductor Nanoplatelets: A New Class of Ultrabright Fluorescent Probes for Cytometric and Imaging Applications. ACS Appl. Mater. Interfaces 2018, 10, 24739–24749. [Google Scholar] [CrossRef]
- Singh, S.; Tomar, R.; Brinck, S.T.; De Roo, J.; Geiregat, P.; Martins, J.C.; Infante, I.; Hens, Z. Colloidal CdSe Nanoplatelets, A Model for Surface Chemistry/Optoelectronic Property Relations in Semiconductor Nanocrystals. J. Am. Chem. Soc. 2018, 140, 13292–13300. [Google Scholar] [CrossRef]
- Galle, T.; Kazes, M.; Hübner, R.; Lox, J.; Khoshkhoo, M.S.; Sonntag, L.; Tietze, R.; Sayevich, V.; Oron, D.; Koitzsch, A.; et al. Colloidal Mercury-Doped CdSe Nanoplatelets with Dual Fluorescence. Chem. Mater. 2019, 31, 5065–5074. [Google Scholar] [CrossRef]
- Sharma, M.; Delikanli, S.; Demir, H.V. Two-Dimensional CdSe-Based Nanoplatelets: Their Heterostructures, Doping, Photophysical Properties, and Applications. Proc. IEEE 2020, 108, 655–675. [Google Scholar] [CrossRef]
- Das, T.K.; Ganguly, S. Revolutionizing Food Safety with Quantum Dot–Polymer Nanocomposites: From Monitoring to Sensing Applications. Foods 2023, 12, 2195. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Ganguly, S.; Banerjee, S.; Das, N.C. Graphene based emergent nanolights: A short review on the synthesis, properties and application. Res. Chem. Intermed. 2019, 45, 3823–3853. [Google Scholar] [CrossRef]
- Xu, Q.; Niu, Y.; Li, J.; Yang, Z.; Gao, J.; Ding, L.; Ni, H.; Zhu, P.; Liu, Y.; Tang, Y.; et al. Recent progress of quantum dots for energy storage applications. Carbon Neutrality 2022, 1, 13. [Google Scholar] [CrossRef]
- Talapin, D.V.; Lee, J.-S.; Kovalenko, M.V.; Shevchenko, E.V. Prospects of Colloidal Nanocrystals for Electronic and Optoelectronic Applications. Chem. Rev. 2009, 110, 389–458. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, C.; Pang, G.; Sun, X.; Chen, R. Effect of Lateral Size and Surface Passivation on the Near-Band-Edge Excitonic Emission from Quasi-Two-Dimensional CdSe Nanoplatelets. ACS Appl. Mater. Interfaces 2019, 11, 41821–41827. [Google Scholar] [CrossRef]
- Specht, J.F.; Scott, R.; Castro, M.C.; Christodoulou, S.; Bertrand, G.H.V.; Prudnikau, A.V.; Antanovich, A.; Siebbeles, L.D.A.; Owschimikow, N.; Moreels, I.; et al. Size-dependent exciton substructure in CdSe nanoplatelets and its relation to photoluminescence dynamics. Nanoscale 2019, 11, 12230–12241. [Google Scholar] [CrossRef]
- Yu, R. Optical properties and applications of two-dimensional CdSe nanoplatelets. InfoMat 2020, 2, 905–927. [Google Scholar] [CrossRef]
- Dutta, A.; Medda, A.; Patra, A. Recent Advances and Perspectives on Colloidal Semiconductor Nanoplatelets for Optoelectronic Applications. J. Phys. Chem. C 2021, 125, 20–30. [Google Scholar] [CrossRef]
- Cu, J. Colloidal Semiconductor Nanocrystals for Optoelectronic Applications: Photodetectors and Light Emitting Diodes. Ph.D. Thesis, Sorbonne University, Paris, France, 29 April 2021; 132p. [Google Scholar]
- Dutta, A.; Medda, A.; Ghosh, S.; Sain, S.; Patra, A. 2D CdSe/CdS Core–Shell Nanoplatelets for High-Performance Photodetectors. ACS Appl. Nano Mater. 2022, 5, 11679–11688. [Google Scholar] [CrossRef]
- Dutta, A.; Almutairi, A.S.; Joseph, J.P.; Baev, A.; Petrou, A.; Zeng, H.; Prasad, P.N. Exploring magneto-optic properties of colloidal two-dimensional copper-doped CdSe nanoplatelets. Nanophotonics 2022, 11, 5143–5152. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, F.; Huang, P.; Wu, R.; Gu, W.; Wei, J.; Liu, F.; Li, H. Light-Emitting Diodes Based on Two-Dimensional Nanoplatelets. Energy Mater. Adv. 2022, 2022, 9857943. [Google Scholar] [CrossRef]
- Kurilovich, A.; Mantsevich, V.N.; Stevenson, K.J.; Chechkin, A.V.; Palyulin, V.V. Complex diffusion-based kinetics of photoluminescence in semiconductor nanoplatelets. Phys. Chem. Chem. Phys. 2020, 22, 24686–24696. [Google Scholar] [CrossRef]
- Halim, H.; Simon, J.; Lieberwirth, I.; Mailänder, V.; Koynov, K.; Riedinger, A. Water-dispersed semiconductor nanoplatelets with high fluorescence brightness, chemical and colloidal stability. J. Mater. Chem. B 2020, 8, 146–154. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Chen, D.; Sun, C.; Ren, Y.; Jiang, J.; Wang, L.; Li, Z.; Peng, X. Engineering of Exciton Spatial Distribution in CdSe Nanoplatelets. Nano Lett. 2021, 21, 5201–5208. [Google Scholar] [CrossRef]
- Akhmetowa, A.; Daurenbekov, D.; Kainabay, A.; Nurakhmetov, K.T.; Eliseev, A. Colloidal synthesis of CdTe nanoplatelets using various cadmium precursors. Opt. Mater. 2022, 131, 112606. [Google Scholar] [CrossRef]
- Izquierdo, E.; Robin, A.; Keuleyan, S.; Lequeux, N.; Lhuillier, E.; Ithurria, S. Strongly Confined HgTe 2D Nanoplatelets as Narrow Near-Infrared Emitters. J. Am. Chem. Soc. 2016, 138, 10496–10501. [Google Scholar] [CrossRef]
- Martinez, B.; Livache, C.; Goubet, N.; Izquierdo, E.; Silly, M.; Ithurria, S.; Lhuillier, E. Optoelectronics Using 2D Colloidal Nanocrystals from Wide Band Gap to Narrow Band Gap Materials. Phys. Status Solidi C 2017, 14, 1700138. [Google Scholar]
- Moghaddam, N.; Gréboval, C.; Qu, J.; Chu, A.; Rastogi, P.; Livache, C.; Khalili, A.; Xu, X.Z.; Baptiste, B.; Klotz, S.; et al. The Strong Confinement Regime in HgTe Two-Dimensional Nanoplatelets. J. Phys. Chem. C 2020, 124, 23460–23468. [Google Scholar] [CrossRef]
- Vázquez, F.M.; Yu, Q.; Klepzig, L.F.; Siebbeles, L.D.A.; Crisp, R.W.; Lauth, J. Probing Excitons in Ultrathin PbS Nanoplatelets with Enhanced Near-Infrared Emission. J. Phys. Chem. Lett. 2021, 12, 680–685. [Google Scholar] [CrossRef] [PubMed]
- Klepzig, L.F.; Biesterfeld, L.; Romain, M.; Niebur, A.; Schlosser, A.; Hübner, J.; Lauth, J. Colloidal 2D PbSe nanoplatelets with efficient emission reaching the telecom O.-, E- and S-band. Nanoscale Adv. 2022, 4, 590–599. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liang, G.; Wu, K. Long-lived Single Excitons, Trions, and Biexcitons in CdSe/CdTe Type-Ⅱ Colloidal Quantum Wells. Chin. J. Chem. Phys. 2017, 30, 649–656. [Google Scholar] [CrossRef]
- Benjamin, E.; Yallapragada, V.; Amgar, D.; Yang, G.; Tenne, R.; Oron, D. Temperature Dependence of Excitonic and Biexcitonic Decay Ratesin Colloidal Nanoplatelets by Time-Gated Photon Correlation. J. Phys. Chem. Lett. 2020, 11, 6513–6518. [Google Scholar] [CrossRef] [PubMed]
- Peng, L.; Cho, W.; Zhang, X.; Talapin, D.; Ma, X. Observation of biexciton emission from single semiconductor nanoplatelets. Phys. Rev. Mater. 2021, 5, 051601. [Google Scholar] [CrossRef]
- Geiregat, P.; Rodá, C.; Tanghe, I.; Singh, S.; di Giacomo, A.; Lebrun, D.; Grimaldi, G.; Maes, J.D.; Van Thourhout, I.; Moreels, A.; et al. Localization-limited exciton oscillator strength in colloidal CdSe nanoplatelets revealed by the optically induced stark effect. Light Sci. Appl. 2021, 10, 112. [Google Scholar] [CrossRef]
- Baghdasaryan, D.A.; Harutyunyan, V.A.; Hayrapetyan, D.B.; Kazaryan, E.M.; Baskoutas, S.; Sarkisyan, H.A. Exciton States and Optical Absorption in CdSe and PbS Nanoplatelets. Nanomaterials 2022, 12, 3690. [Google Scholar] [CrossRef]
- Smirnov, A.; Golinskaya, A.; Mantsevich, V.; Kozlova, M.V.; Ezhova, K.V.; Saidzhonov, B.M.; Vasiliev, R.B.; Dneprovskii, V. Optical gain appearance in the CdSe/CdS nanoplatelets colloidal solution. Results Phys. 2022, 32, 105120. [Google Scholar] [CrossRef]
- Tomar, R.; Kulkarni, A.; Chen, K.; Singh, S.; van Thourhout, D.; Hodgkiss, J.M.; Siebbeles, L.D.A.; Hens, Z.; Geiregat, P. Charge Carrier Cooling Bottleneck Opens Up Nonexcitonic Gain Mechanisms in Colloidal CdSe Quantum Wells. J. Phys. Chem. C 2019, 123, 9640–9650. [Google Scholar] [CrossRef]
- Flórez, G.; Kulkarni, F.; Siebbeles, A.; Stoof, H.T.C. Explaining observed stability of excitons in highly excited CdSe nanoplatelets. Phys. Rev. B 2019, 100, 245302. [Google Scholar] [CrossRef]
- Moskalenko, S.A.; Snoke, D.W. Bose-Einstein Condensation of Excitons and Biexcitons; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Glazov, M.; Suris, R. Collective states of excitons in semiconductors. Phys. Uspekhi 2020, 63, 1051–1071. [Google Scholar] [CrossRef]
- Morita, Y.; Yoshioka, K.; Kuwata-Gonokami, M. Observation of Bose-Einstein condensates of excitons in a bulk semiconductor. Nat. Commun. 2022, 13, 5388. [Google Scholar] [CrossRef] [PubMed]
- Lifshitz, E.; Pitaevskii, L. Statistical Physics: Theory of the Condensed State (Pt 2); Revised Edition; Butterworth-Heinemann: Oxford, UK, 1995; 387p. [Google Scholar]
- Haroutyunian, V.; Kazarian, E. An investigation of the possibility of Bose condensation of excitons in semiconducting films. Thin Solid Films 1984, 115, 245–251. [Google Scholar] [CrossRef]
- Haroutyunian, V.; Haroutyunian, S.; Kazarian, E. Possibility of Bose condensation of excitons in a size-quantized semiconductor disc. Thin Solid Films 1989, 170, 321–326. [Google Scholar] [CrossRef]
- Ketterle, W.; van Druten, N.J. Bose-Einstein condensation of a finite number of particles trapped in one or three dimensions. Phys. Rev. A 1996, 54, 656–660. [Google Scholar] [CrossRef]
- Jan, J.; Lee, Y. Bose-Einstein condensation of excitons in two dimensions. Phys. Rev. B 1998, 58, 1714. [Google Scholar] [CrossRef]
- Butov, L.V.; Lai, C.W.; Ivanov, A.L.; Gossard, A.C.; Chemla, D.S. Towards Bose–Einstein condensation of excitons in potential traps. Nature 2002, 417, 47–52. [Google Scholar] [CrossRef]
- Moskalenko, S.; Liberman, M.; Snoke, D.; Boţan, V.; Johansson, B. Bose–Einstein condensation of excitons in ideal two-dimensional system in a strong magnetic field. Phys. E Low-Dimens. Syst. Nanostruct. 2003, 19, 278–288. [Google Scholar] [CrossRef]
- Fletcher, R. Bose-Einstein Condensation and Superfluidity in Two Dimensions. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2015; 180p. [Google Scholar]
- Corman, L. The Two-Dimensional Bose Gas in Box Potentials. Ph.D. Thesis, PSL Research University, Paris, France, 2017; 216p. [Google Scholar]
- Glazov, M.M.; Suris, R.A. Exciton Condensation in a Two-Dimensional System with Disorder. J. Exp. Theor. Phys. 2018, 126, 833–841. [Google Scholar] [CrossRef]
- Xie, M. Bose–Einstein condensation in two-dimensional traps. J. Stat. Mech. Theory Exp. 2019, 2019, 043104. [Google Scholar] [CrossRef]
- Wang, Z.; Rhodes, D.; Watanabe, K.; Taniguchi, T.; Hone, J.; Shan, J.; Mak, K. Evidence of high-temperature exciton condensation in two-dimensional atomic double layers. Nature 2019, 574, 76–80. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Luo, N.; Duan, W.; Zou, X. High-Temperature Excitonic Bose–Einstein Condensate in Centrosymmetric Two-Dimensional Semiconductors. J. Phys. Chem. Lett. 2021, 12, 5479–5485. [Google Scholar] [CrossRef] [PubMed]
- Haroutunian, V.A.; Kazarian, E.M. Feasibility of the Bose Condensation of Excitons in a Quantizing Semiconductor Sphere. Phys. Status Solidi B 1986, 136, K105–K108. [Google Scholar] [CrossRef]
- Harutyunyan, V. Bose condensation in a system of particles with discrete energy spectrum. Изв. АНАрм.ССР Серияфизика 1990, 25, 87–93. [Google Scholar]
- Portnoi, M. Scattering of Two-Dimensional Particles by A Short-Range Potential. Pisma V Zhurnal Tekhnicheskoi Fiz. 1988, 14, 1252–1256. [Google Scholar]
- Landau, L.; Lifshitz, E. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Kubo, R.; McQuarrie, D.A. Statistical Mechanics; Elsevier: Amsterdam, The Netherlands, 1965. [Google Scholar]


| NPL Size (nm) | NPL Layers | meV | meV | meV | ||
|---|---|---|---|---|---|---|
| 3.5 | 0.119 | 0.733 | 0.365 | 720 | 312.8 | |
| 3.5 | 0.119 | 0.733 | 4.06 | 720 | 312.7 |
| 3.5 | 10 | 1.29 × 1013 | 1.493 | 0.444 | 279.42 |
| 3.5 | 25 | 1.28 × 1013 | 1.493 | 0.413 | 129.39 |
| 3.5 | 50 | 1.28 × 1013 | 1.493 | 0.408 | 83.661 |
| 3.5 | 100 | 1.28 × 1013 | 1.493 | 0.407 | 59.470 |
| 4.5 | 10 | 9.09 × 1012 | 1.775 | 0.323 | 270.4 |
| 4.5 | 25 | 9.07 × 1012 | 1.777 | 0.288 | 107.71 |
| 4.5 | 50 | 9.07 × 1012 | 1.777 | 0.283 | 67.135 |
| 4.5 | 100 | 9.07 × 1012 | 1.777 | 0.282 | 46.43 |
| 5.5 | 10 | 6.94 × 1012 | 2.031 | 0.250 | 240.3 |
| 5.5 | 25 | 6.87 × 1012 | 2.041 | 0.211 | 94.43 |
| 5.5 | 50 | 6.87 × 1012 | 2.041 | 0.206 | 56.99 |
| 5.5 | 100 | 6.87 × 1012 | 2.041 | 0.204 | 38.46 |
| 7.5 | 10 | 5.21 × 1012 | 2.344 | 0.159 | 201.11 |
| 7.5 | 25 | 5.04 × 1012 | 2.383 | 0.117 | 80.05 |
| 7.5 | 50 | 5.04 × 1012 | 2.383 | 0.111 | 46.80 |
| 7.5 | 100 | 5.04 × 1012 | 2.383 | 0.110 | 30.81 |
| 4.5 | 10 | 1.42 × 1013 | 1.421501 | 0.579351 | 397.067 |
| 4.5 | 25 | 1.42 × 1013 | 1.421582 | 0.555023 | 195.512 |
| 4.5 | 50 | 1.42 × 1013 | 1.42158 | 0.551548 | 128.855 |
| 4.5 | 100 | 1.42 × 1013 | 1.421583 | 0.550679 | 91.6116 |
| 5.5 | 10 | 1.11 × 1013 | 1.606809 | 0.451801 | 365.676 |
| 5.5 | 25 | 1.11 × 1013 | 1.607317 | 0.425445 | 172.604 |
| 5.5 | 50 | 1.11 × 1013 | 1.607319 | 0.42168 | 110.4491 |
| 5.5 | 100 | 1.11 × 1013 | 1.607322 | 0.420739 | 88.255 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baghdasaryan, D.A.; Harutyunyan, V.A.; Kazaryan, E.M.; Sarkisyan, H.A.; Petrosyan, L.S.; Shahbazyan, T.V. Possibility of Exciton Bose–Einstein Condensation in CdSe Nanoplatelets. Nanomaterials 2023, 13, 2734. https://doi.org/10.3390/nano13192734
Baghdasaryan DA, Harutyunyan VA, Kazaryan EM, Sarkisyan HA, Petrosyan LS, Shahbazyan TV. Possibility of Exciton Bose–Einstein Condensation in CdSe Nanoplatelets. Nanomaterials. 2023; 13(19):2734. https://doi.org/10.3390/nano13192734
Chicago/Turabian StyleBaghdasaryan, Davit A., Volodya A. Harutyunyan, Eduard M. Kazaryan, Hayk A. Sarkisyan, Lyudvig S. Petrosyan, and Tigran V. Shahbazyan. 2023. "Possibility of Exciton Bose–Einstein Condensation in CdSe Nanoplatelets" Nanomaterials 13, no. 19: 2734. https://doi.org/10.3390/nano13192734





