Lasing Emission from Soft Photonic Crystals for Pressure and Position Sensing
Abstract
:1. Introduction
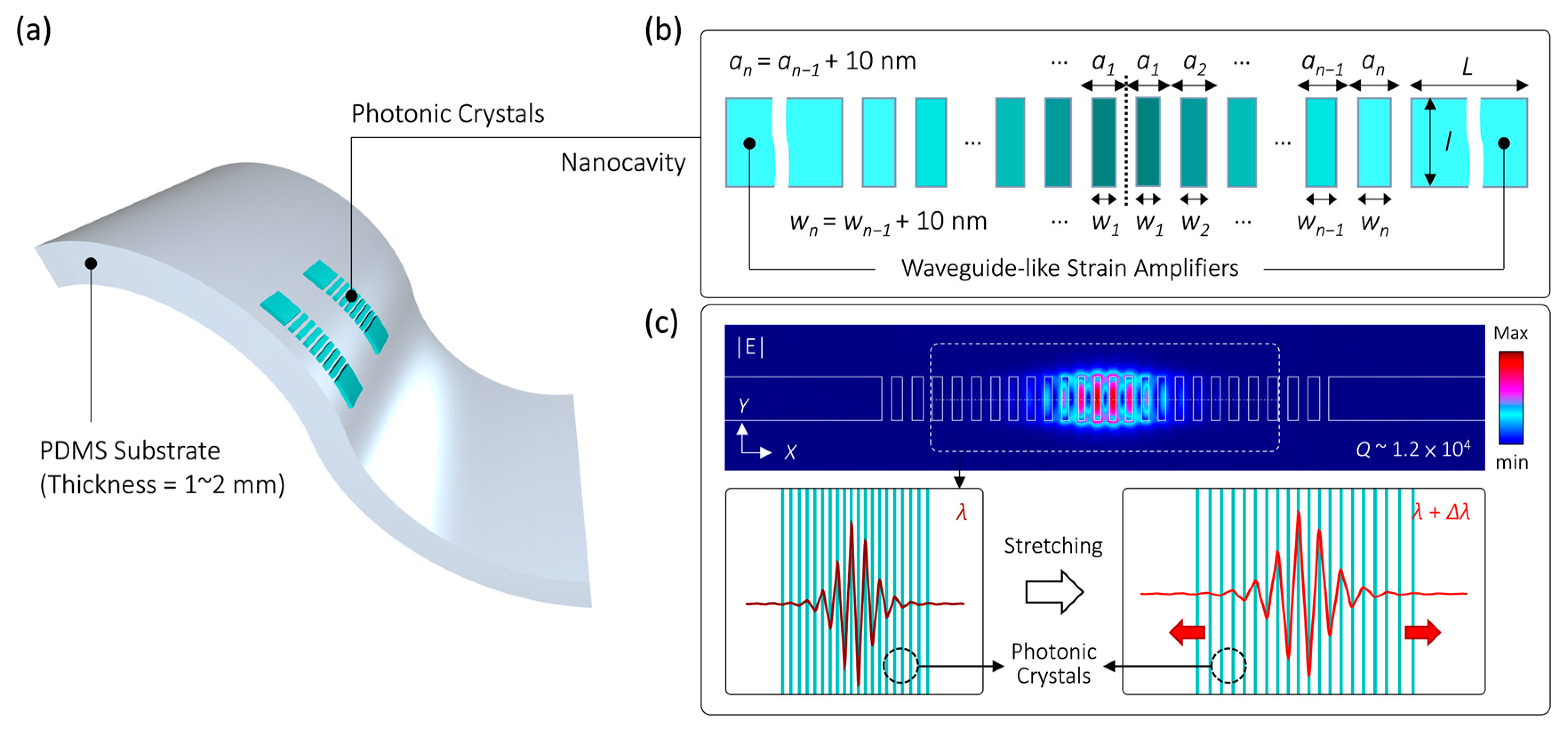
2. Design of PhC Nanocavity Sensitive to Deformation
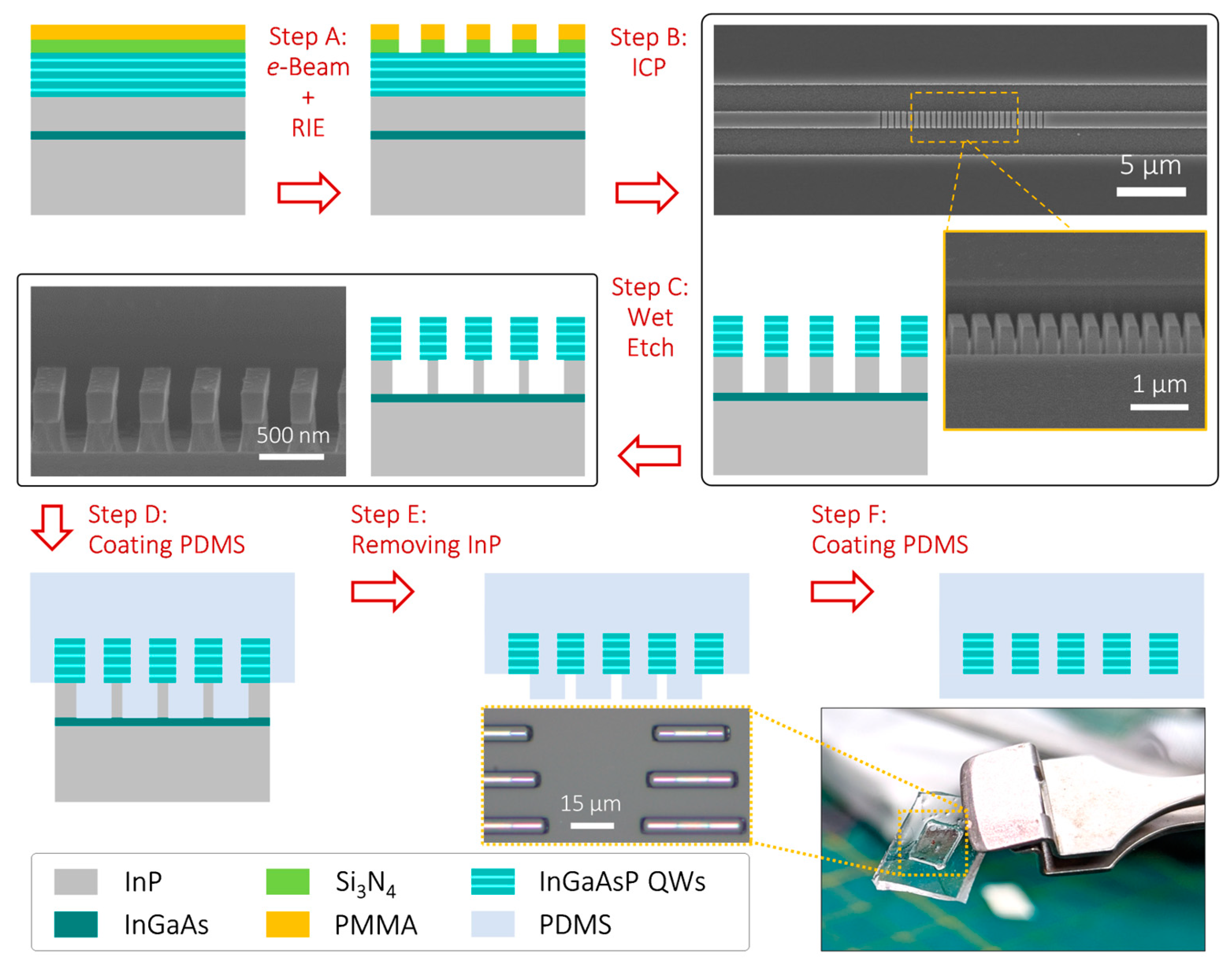
3. Manufacturing Process
4. Measurement Results and Discussions
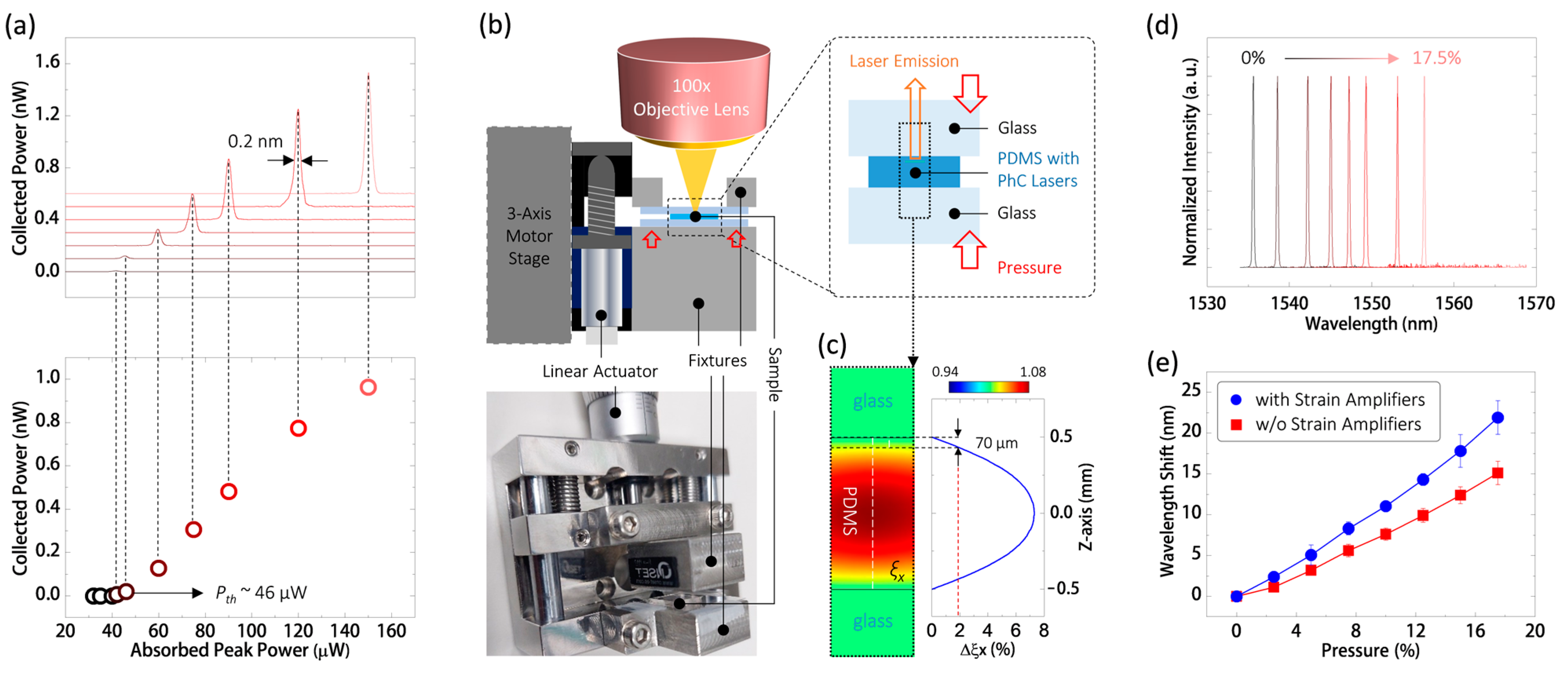
4.1. Laser Emission from PhC Nanocavity and Its Wavelength Response to Uniform Pressure
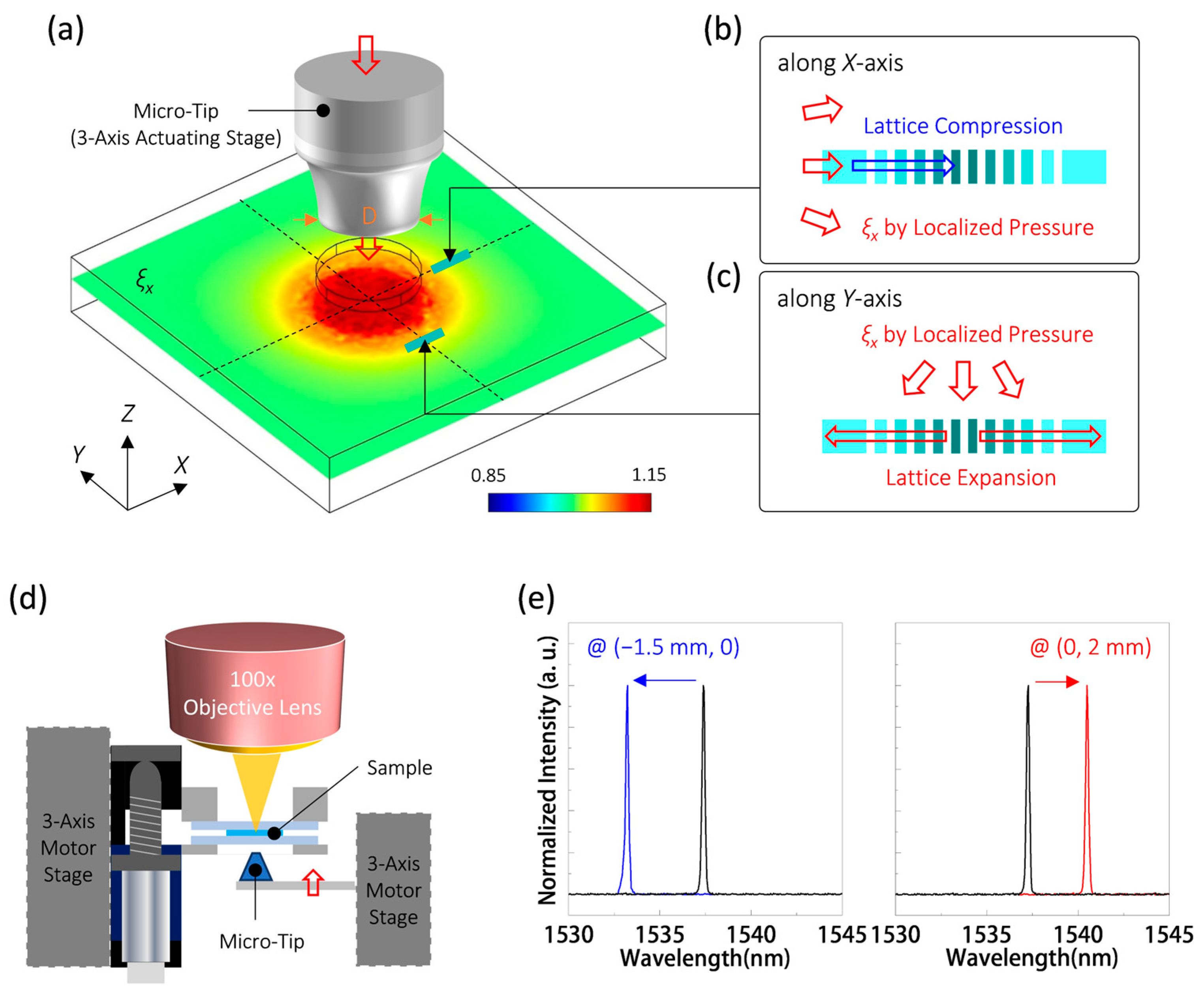
4.2. Wavelength Response to Localized Pressure for Position Sensing
4.3. Waveguide-like Strain Amplifier for Leading out the Sensing Signal
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geiger, S.; Michon, J.; Liu, S.; Qin, J.; Ni, J.; Hu, J.; Gu, T.; Lu, N. Flexible and stretchable photonics: The next stretch of opportunities. ACS Photonics 2020, 7, 2618–2635. [Google Scholar] [CrossRef]
- Clough, J.M.; Weder, C.; Schrettl, S. Mechanochromism in structurally colored polymeric materials. Macromol. Rapid Commun. 2021, 42, 2000528. [Google Scholar] [CrossRef] [PubMed]
- Pujol-Vila, F.; Güell-Grau, P.; Nogués, J.; Alvarez, M.; Sepúlveda, B. Soft optomechanical systems for sensing, modulation, and actuation. Adv. Funct. Mater. 2023, 33, 2213109. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Q.; Zheng, X. Flexible mechanochromic photonic crystals: Routes to visual sensors and their mechanical properties. J. Mater. Chem. C 2018, 6, 3182–3199. [Google Scholar] [CrossRef]
- Peng, W.; Wu, H. Flexible and stretchable photonic sensors based on modulation of light transmission. Adv. Opt. Mater. 2019, 7, 1900329. [Google Scholar] [CrossRef]
- Inci, E.; Topcu, G.; Guner, T.; Demirkurt, M.; Demir, M.M. Recent developments of colorimetric mechanical sensors based on polymer composites. J. Mater. Chem. C 2020, 8, 12036–12053. [Google Scholar] [CrossRef]
- Bae, S.I.; Lee, Y.; Seo, Y.H.; Jeong, K.H. Antireflective structures on highly flexible and large area elastomer membrane for tunable liquid-filled endoscopic lens. Nanoscale 2019, 11, 856–861. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, R.; Butt, H. Strain-multiplex metalens array for tunable focusing and imaging. Adv. Sci. 2021, 8, 2003394. [Google Scholar] [CrossRef]
- Yu, J.; Liu, Z.; Wang, M.; Wang, C.; Chen, G.; Cui, Z.; Wang, T.; Yang, H.; Wang, X.; Chen, X. Strain-enabled phase transition of periodic metasurfaces. Adv. Mater. 2022, 34, 2102560. [Google Scholar] [CrossRef] [PubMed]
- Leo, S.Y.; Zhang, W.; Zhang, Y.; Ni, Y.; Jiang, H.; Jones, C.; Jiang, P.; Basile, V.; Taylor, C. Chromogenic photonic crystal sensors enabled by multistimuli-responsive shape memory polymers. Small 2018, 14, 1703515. [Google Scholar] [CrossRef]
- Peng, J.; Jeong, H.H.; Smith, M.; Chikkaraddy, R.; Lin, Q.; Liang, H.L.; Volder, M.F.L.; Vignolini, S.; Kar-Narayan, S.; Baumberg, J.J. Fully printed flexible plasmonic metafilms with directional color dynamics. Adv. Sci. 2021, 8, 2002419. [Google Scholar] [CrossRef]
- Lio, G.E.; Palermo, G.; Caputo, R.; Luca, A. Opto-mechanical control of flexible plasmonic materials. J. Appl. Phys. 2019, 125, 082533. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, C.; Wang, J.; Luo, X.; Xie, L.; Zhan, S.; Kim, J.; Wang, X.; Liu, X.; Ying, Y. Wearable plasmonic-metasurface sensor for noninvasive and universal molecular fingerprint detection on biointerfaces. Sci. Adv. 2021, 7, eabe4553. [Google Scholar] [CrossRef]
- Peng, C.Y.; Hsu, C.W.; Li, C.W.; Wang, P.L.; Jeng, C.C.; Chang, C.C.; Wang, G.J. Flexible photonic crystal material for multiple anticounterfeiting applications. ACS Appl. Mater. Interfaces 2018, 10, 9858–9864. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Feng, L.; Liang, Y.; Xu, T. An ultra-flexible plasmonic metamaterial film for efficient omnidirectional and broadband optical absorption. Nanoscale 2019, 11, 437–443. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Lai, X.; Li, C.; Song, Y. Recent advantages of colloidal photonic crystals and their applications for luminescence enhancement. Mater. Today Nano 2019, 6, 100039. [Google Scholar] [CrossRef]
- Güell-Grau, P.; Pi, F.; Villa, R.; Eskilson, O.; Aili, D.; Nogués, J.; Sepúlveda, B.; Alvarez, M. Elastic plasmonic-enhanced fabry–pérot cavities with ultrasensitive stretching tunability. Adv. Mater. 2022, 34, 2106731. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.X.; Jin, F.; Dong, X.Z.; Liu, J.; Zheng, M.L. Switchable lasers via solvent stimulus-responsive photonic crystals. J. Mater. Chem. C 2022, 10, 15075–15083. [Google Scholar] [CrossRef]
- Yu, C.L.; Kim, H.; Leon, N.; Frank, I.W.; Robinson, J.T.; McCutcheon, M.; Liu, M.; Lukin, M.D.; Loncar, M.; Park, H. Stretchable photonic crystal cavity with wide frequency tunability. Nano Lett. 2013, 13, 248–252. [Google Scholar] [CrossRef]
- Choi, J.H.; No, Y.S.; So, J.P.; Lee, J.M.; Kim, K.H.; Hwang, M.S.; Kwo, S.H.; Park, H.G. A high-resolution strain-gauge nanolaser. Nat. Commun. 2016, 7, 11569. [Google Scholar] [CrossRef]
- Gan, X.; Clevenson, H.; Englund, D. Polymer photonic crystal nanocavity for precision strain sensing. ACS Photonics 2017, 4, 1591–1594. [Google Scholar] [CrossRef]
- Lu, T.W.; Wu, C.C.; Lee, P.T. 1D photonic crystal strain sensors. ACS Photonics 2018, 5, 2767–2772. [Google Scholar] [CrossRef]
- Wu, C.S.; Tsai, P.Y.; Wang, T.Y.; Lin, E.L.; Huang, Y.C.; Chiang, Y.W. Flexible or robust amorphous photonic crystals from network-forming block copolymers for sensing solvent vapors. Anal. Chem. 2018, 90, 4847–4855. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Kurashina, Y.; Onoe, H. Eye-recognizable and repeatable biochemical flexible sensors using low angle-dependent photonic colloidal crystal hydrogel microbeads. Sci. Rep. 2019, 9, 17059. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Chen, C. Hydrogel-based colloidal photonic crystal devices for glucose sensing. Polymers 2020, 12, 625. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Zhou, B.; Zong, R.; Pan, L.; Li, X.; Yu, X.; Yang, C.; Kong, L.; Dai, Q. Stretchable and highly sensitive optical strain sensors for human-activity monitoring and healthcare. ACS Appl. Mater. Interfaces 2019, 11, 33589–33598. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Chen, J.; Xu, B.B.; Huang, Y. Flexible plasmonic biosensors for healthcare monitoring: Progress and prospects. ACS Nano 2021, 15, 18822–18847. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Zhang, M.K.; Lu, Y.F.; Li, J.J.; Ge, S.J.; Gu, Z.Z. Dual-mode wearable strain sensor based on graphene/colloidal crystal films for simultaneously detection of subtle and large human motions. Adv. Mater. Technol. 2020, 5, 1901056. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.; Wang, J.; Mbol, N.M.; Meng, Z.; Wang, X.; Xue, M. A biocompatible, self-adhesive, and stretchable photonic crystal sensor for underwater motion detection. J. Mater. Chem. C 2022, 10, 9025–9034. [Google Scholar] [CrossRef]
- Escudero, P.; Yeste, J.; Pascual-Izarra, C.; Villa, R.; Alvarez, M. Color tunable pressure sensors based on polymer nanostructured membranes for optofluidic applications. Sci. Rep. 2019, 9, 3259. [Google Scholar] [CrossRef]
- Shin, J.; Liu, Z.; Bai, W.; Liu, Y.; Yan, Y.; Xue, Y.; Kandela, I.; Pezhouh, M.; MacEwan, M.R.; Huang, Y.; et al. Bioresorbable optical sensor systems for monitoring of intracranial pressure and temperature. Sci. Adv. 2019, 5, eaaw1. [Google Scholar] [CrossRef] [PubMed]
- Maeng, B.; Chang, H.K.; Park, J. Photonic crystal-based smart contact lens for continuous intraocular pressure monitoring. Lab Chip 2020, 20, 1740–1750. [Google Scholar] [CrossRef] [PubMed]
- Quan, Y.J.; Kim, Y.G.; Kim, M.S.; Min, S.H.; Ahn, S.H. Stretchable biaxial and shear strain sensors using diffractive structural colors. ACS Nano 2020, 14, 5392–5399. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Kong, D.; Ebendorff-Heidepriem, H. Flexible plasmonic tapes with nanohole and nanoparticle arrays for refractometric and strain sensing. ACS Appl. Nano Mater. 2020, 3, 8242–8246. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, Z.; Zheng, X.; Zhang, Y.; Wang, Q. Large-strain and full-color change photonic crystal films used as mechanochromic strain sensors. J. Mater. Sci. 2021, 32, 15586–15593. [Google Scholar] [CrossRef]
- Lu, T.W.; Wang, L.C.; Lai, C.H.; Lee, P.T. Enhancing wavelength tunability of photonic crystal nanolasers by waveguide-like strain shapers. J. Lightwave Technol. 2020, 38, 6605–6611. [Google Scholar] [CrossRef]
- Notomi, M.; Kuramochi, E.; Taniyama, H. Ultrahigh-Q nanocavity with 1D photonic gap. Opt. Express 2008, 16, 11095–11102. [Google Scholar] [CrossRef]
- Hu, S.M. Film-edge-induced stress in substrates. J. Appl. Phys. 1979, 50, 4661. [Google Scholar] [CrossRef]
- Chen, W.; Liu, W.; Jiang, Y.; Zhang, M.; Song, N.; Greybush, N.J.; Guo, J.; Estep, A.K.; Turner, K.T.; Agarwal, R.; et al. Ultrasensitive, mechanically responsive optical metasurfaces via strain amplification. ACS Nano 2018, 12, 10683–10692. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, T.-W.; Wang, Z.-Y.; Lin, K.-M.; Lee, P.-T. Lasing Emission from Soft Photonic Crystals for Pressure and Position Sensing. Nanomaterials 2023, 13, 2956. https://doi.org/10.3390/nano13222956
Lu T-W, Wang Z-Y, Lin K-M, Lee P-T. Lasing Emission from Soft Photonic Crystals for Pressure and Position Sensing. Nanomaterials. 2023; 13(22):2956. https://doi.org/10.3390/nano13222956
Chicago/Turabian StyleLu, Tsan-Wen, Zhen-Yu Wang, Kuang-Ming Lin, and Po-Tsung Lee. 2023. "Lasing Emission from Soft Photonic Crystals for Pressure and Position Sensing" Nanomaterials 13, no. 22: 2956. https://doi.org/10.3390/nano13222956
APA StyleLu, T.-W., Wang, Z.-Y., Lin, K.-M., & Lee, P.-T. (2023). Lasing Emission from Soft Photonic Crystals for Pressure and Position Sensing. Nanomaterials, 13(22), 2956. https://doi.org/10.3390/nano13222956





