Nontraditional Movement Behavior of Skyrmion in a Circular-Ring Nanotrack
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rossler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915. [Google Scholar] [CrossRef]
- Kravchuk, V.P.; Rossler, U.K.; Volkov, O.M.; Sheka, D.D.; van den Brink, J.; Makarov, D.; Fuchs, H.; Fangohr, H.; Gaididei, Y. Topologically stable magnetization states on a spherical shell: Curvature-stabilized skyrmions. Phys. Rev. B 2016, 94, 144402. [Google Scholar] [CrossRef]
- Castillo-Sepúlveda, S.; Vélez, J.A.; Corona, R.M.; Carvalho-Santos, V.L.; Laroze, D.; Altbir, D. Skyrmion dynamics in a double-disk geometry under an electric current. Nanomaterials 2022, 12, 3086. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899. [Google Scholar] [CrossRef]
- Parkin, S.S.; Hayashi, M.; Thomas, L. Magnetic domain-wall racetrack memory. Science 2008, 320, 190. [Google Scholar] [CrossRef]
- Woo, S.; Litzius, K.; Kruger, B.; Im, M.Y.; Caretta, L.; Richter, K.; Mann, M.; Krone, A.; Reeve, R.M.; Weigand, M.; et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 2016, 15, 501. [Google Scholar] [CrossRef]
- Boulle, O.; Vogel, J.; Yang, H.; Pizzini, S.; de Souza Chaves, D.; Locatelli, A.; Mentes, T.O.; Sala, A.; Buda-Prejbeanu, L.D.; Klein, O.; et al. Room-temperature chiral magnetic skyrmions in ultrathin magnetic nanostructures. Nat. Nanotechnol. 2016, 11, 449. [Google Scholar] [CrossRef]
- Yu, G.; Upadhyaya, P.; Li, X.; Li, W.; Kim, S.K.; Fan, Y.; Wong, K.L.; Tserkovnyak, Y.; Amiri, P.K.; Wang, K.L. Room-temperature creation and spin-orbit torque manipulation of skyrmions in thin films with engineered asymmetry. Nano Lett. 2016, 16, 1981. [Google Scholar] [CrossRef]
- Yu, G.; Jenkins, A.; Ma, X.; Razavi, S.A.; He, C.; Yin, G.; Shao, Q.; He, Q.L.; Wu, H.; Li, W.; et al. Room-temperature skyrmions in an antiferromagnet-based heterostructure. Nano Lett. 2018, 18, 980. [Google Scholar] [CrossRef]
- Jonietz, F.; Mühlbauer, S.; Pfleiderer, C.; Neubauer, A.; Munzer, W.; Bauer, A.; Adams, T.; Georgii, R.; Boni, P.; Duine, R.A.; et al. Spin transfer torques in MnSi at ultralow current densities. Science 2010, 330, 1648. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Zhang, W.Z.; Nagai, T.; Hara, T.; Kimoto, K.; Matsui, Y.; Onose, Y.; Tokura, Y. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 2012, 3, 988. [Google Scholar] [CrossRef]
- Lin, J.-Q.; Chen, J.-P.; Tan, Z.-Y.; Chen, Y.; Chen, Z.-F.; Li, W.-A.; Gao, X.-S.; Liu, J.-M. Manipulation of skyrmion motion dynamics for logical device application mediated by inhomogeneous magnetic anisotropy. Nanomaterials 2022, 12, 278. [Google Scholar] [CrossRef]
- Chen, G. Skyrmion Hall effect. Nat. Phys. 2017, 13, 112. [Google Scholar] [CrossRef]
- Göbel, B.; Mertig, I. Skyrmion ratchet propagation: Utilizing the skyrmion Hall effect in AC racetrack storage devices. Sci. Rep. 2021, 11, 3020. [Google Scholar] [CrossRef]
- Vizarim, N.P.; Reichhardt, C.; Venegas, P.A.; Reichhardt, C.J.O. Guided skyrmion motion along pinning array interfaces. J. Magn. Magn. Mater. 2021, 528, 167710. [Google Scholar] [CrossRef]
- Shigenaga, T.; Leonov, A.O. Harnessing skyrmion Hall effect by thickness gradients in wedge-shaped samples of cubic helimagnets. Nanomaterials 2023, 13, 2073. [Google Scholar] [CrossRef]
- Guo, J.; Hou, Y.; Zhang, X.; Pong, P.W.T.; Zhou, Y. Elimination of the skyrmion Hall effect by tuning perpendicular magnetic anisotropy and spin polarization angle. Phys. Lett. A 2022, 456, 128497. [Google Scholar] [CrossRef]
- Hong, I.S.; Lee, K.J. Magnetic skyrmion field-effect transistors. Appl. Phys. Lett. 2019, 115, 072406. [Google Scholar] [CrossRef]
- Zhou, L.; Qin, R.; Zheng, Y.-Q.; Wang, Y. Skyrmion Hall effect with spatially modulated Dzyaloshinskii–Moriya interaction. Front. Phys. 2019, 14, 536021. [Google Scholar] [CrossRef]
- Tan, A.K.C.; Ho, P.; Lourembam, J.; Huang, L.; Tan, H.K.; Reichhardt, C.J.O.; Reichhardt, C.; Soumyanarayanan, A. Visualizing the strongly reshaped skyrmion Hall effect in multilayer wire devices. Nat. Commun. 2021, 12, 4252. [Google Scholar] [CrossRef]
- Souza, J.C.B.; Vizarim, N.P.; Reichhardt, C.J.O.; Reichhardt, C.; Venegas, P.A. Skyrmion ratchet in funnel geometries. Phys. Rev. B 2021, 104, 054434. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, X.; Zhao, G.; Xiang, G. A skyrmion diode based on skyrmion Hall effect. IEEE Trans. Electron. Devices 2022, 69, 1293. [Google Scholar] [CrossRef]
- Song, C.; Zhao, L.; Liu, J.; Jiang, W. Experimental realization of a skyrmion circulator. Nano Lett. 2022, 22, 9638. [Google Scholar] [CrossRef]
- Bellizotti Souza, J.C.; Vizarim, N.P.; Reichhardt, C.J.O.; Reichhardt, C.; Venegas, P.A. Magnus induced diode effect for skyrmions in channels with periodic potentials. J. Phys. Condens. Matter 2022, 35, 015804. [Google Scholar] [CrossRef]
- Whang, H.S.; Choe, S.B. Spin-Hall-effect-modulation skyrmion oscillator. Sci. Rep. 2020, 10, 11977. [Google Scholar] [CrossRef]
- Wang, J.; Xia, J.; Zhang, X.; Zheng, X.; Li, G.; Chen, L.; Zhou, Y.; Wu, J.; Yin, H.; Chantrell, R.; et al. Magnetic skyrmionium diode with a magnetic anisotropy voltage gating. Appl. Phys. Lett. 2020, 117, 202401. [Google Scholar] [CrossRef]
- Bellizotti Souza, J.C.; Vizarim, N.P.; Reichhardt, C.J.O.; Reichhardt, C.; Venegas, P.A. Clogging, diode and collective effects of skyrmions in funnel geometries. New J. Phys. 2022, 24, 103030. [Google Scholar] [CrossRef]
- Castell-Queralt, J.; González-Gómez, L.; Del-Valle, N.; Sanchez, A.; Navau, C. Accelerating, guiding, and compressing skyrmions by defect rails. Nanoscale 2019, 11, 12589. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Zhu, D.Q.; Kang, W.; Zhang, Y.G.; Zhao, W.S. Stochastic computing implemented by skyrmionic logic devices. Phys. Rev. Appl. 2020, 13, 054049. [Google Scholar] [CrossRef]
- Paikaray, B.; Kuchibhotla, M.; Haldar, A.; Murapaka, C. Skyrmion based majority logic gate by voltage controlled magnetic anisotropy in a nanomagnetic device. Nanotechnology 2023, 34, 225202. [Google Scholar] [CrossRef] [PubMed]
- Shu, Y.; Li, Q.; Xia, J.; Lai, P.; Hou, Z.; Zhao, Y.; Zhang, D.; Zhou, Y.; Liu, X.; Zhao, G. Realization of the skyrmionic logic gates and diodes in the same racetrack with enhanced and modified edges. Appl. Phys. Lett. 2022, 121, 042402. [Google Scholar] [CrossRef]
- Yoo, M.-W.; Cros, V.; Kim, J.-V. Current-driven skyrmion expulsion from magnetic nanostrips. Phys. Rev. B 2017, 95, 184423. [Google Scholar] [CrossRef]
- Jung, D.-H.; Han, H.-S.; Kim, N.; Kim, G.; Jeong, S.; Lee, S.; Kang, M.; Im, M.-Y.; Lee, K.-S. Magnetic skyrmion diode: Unidirectional skyrmion motion via symmetry breaking of potential energy barriers. Phys. Rev. B 2021, 104, L060408. [Google Scholar] [CrossRef]
- Leonov, A.O.; Loudon, J.C.; Bogdanov, A.N. Spintronics via non-axisymmetric chiral skyrmions. Appl. Phys. Lett. 2016, 109, 172404. [Google Scholar] [CrossRef]
- Leonov, A.O.; Mostovoy, M. Edge states and skyrmion dynamics in nanostripes of frustrated magnets. Nat. Commun. 2017, 8, 14394. [Google Scholar] [CrossRef]
- Al Saidi, W.; Sbiaa, R.; Bhatti, S.; Piramanayagam, S.N.; Al Risi, S. Dynamics of interacting skyrmions in magnetic nano-track. J. Phys. D Appl. Phys. 2023, 56, 355001. [Google Scholar] [CrossRef]
- Morshed, M.G.; Vakili, H.; Ghosh, A.W. Positional stability of skyrmions in a racetrack memory with notched geometry. Phys. Rev. Appl. 2022, 17, 064019. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, G.P.; Fangohr, H.; Liu, J.P.; Xia, W.X.; Xia, J.; Morvan, F.J. Skyrmion-skyrmion and skyrmion-edge repulsions in skyrmion-based racetrack memory. Sci. Rep. 2015, 5, 7643. [Google Scholar] [CrossRef]
- Gaididei, Y.; Kravchuk, V.P.; Sheka, D.D. Curvature effects in thin magnetic shells. Phys. Rev. Lett. 2014, 112, 257203. [Google Scholar] [CrossRef] [PubMed]
- Streubel, R.; Fischer, P.; Kronast, F.; Kravchuk, V.P.; Sheka, D.D.; Gaididei, Y.; Schmidt, O.G.; Makarov, D. Magnetism in curved geometries. J. Phys. D Appl. Phys. 2016, 49, 363001. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP. Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Leliaert, J.; Dvornik, M.; Mulkers, J.; De Clercq, J.; Milošević, M.V.; Van Waeyenberge, B. Fast micromagnetic simulations on GPU—Recent advances made with MuMax3. J. Phys. D Appl. Phys. 2018, 51, 123002. [Google Scholar] [CrossRef]
- Leonov, A.O.; Monchesky, T.L.; Romming, N.; Kubetzka, A.; Bogdanov, A.N.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. New J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- Je, S.G.; Thian, D.; Chen, X.; Huang, L.; Jung, D.H.; Chao, W.; Lee, K.S.; Hong, J.I.; Soumyanarayanan, A.; Im, M.Y. Targeted writing and deleting of magnetic skyrmions in two-terminal nanowire devices. Nano Lett. 2021, 21, 1253. [Google Scholar] [CrossRef]
- Ma, C.; Zhang, X.; Xia, J.; Ezawa, M.; Jiang, W.; Ono, T.; Piramanayagam, S.N.; Morisako, A.; Zhou, Y.; Liu, X. Electric field-Iinduced creation and directional motion of domain walls and skyrmion bubbles. Nano Lett. 2018, 19, 353. [Google Scholar] [CrossRef]
- Zhang, X.C.; Xia, J.; Zhao, G.P.; Liu, X.X.; Zhou, Y. Magnetic skyrmion transport in a nanotrack with spatially varying damping and non-adiabatic torque. IEEE Trans. Magn. 2017, 53, 1500206. [Google Scholar] [CrossRef]
- Metlov, K.L. Topological memory with multiply-connected planar magnetic nanoelements. JETP Lett. 2023, 118, 105. [Google Scholar] [CrossRef]
- Chen, X.; Kang, W.; Zhu, D.; Zhang, X.; Lei, N.; Zhang, Y.; Zhou, Y.; Zhao, W. Skyrmion dynamics in width-varying nanotracks and implications for skyrmionic applications. Appl. Phys. Lett. 2017, 111, 202406. [Google Scholar] [CrossRef]
- Gorshkov, I.O.; Gorev, R.V.; Sapozhnikov, M.V.; Udalov, O.G. DMI-gradient-driven skyrmion motion. ACS Appl. Electron. Mater. 2022, 4, 3205. [Google Scholar] [CrossRef]
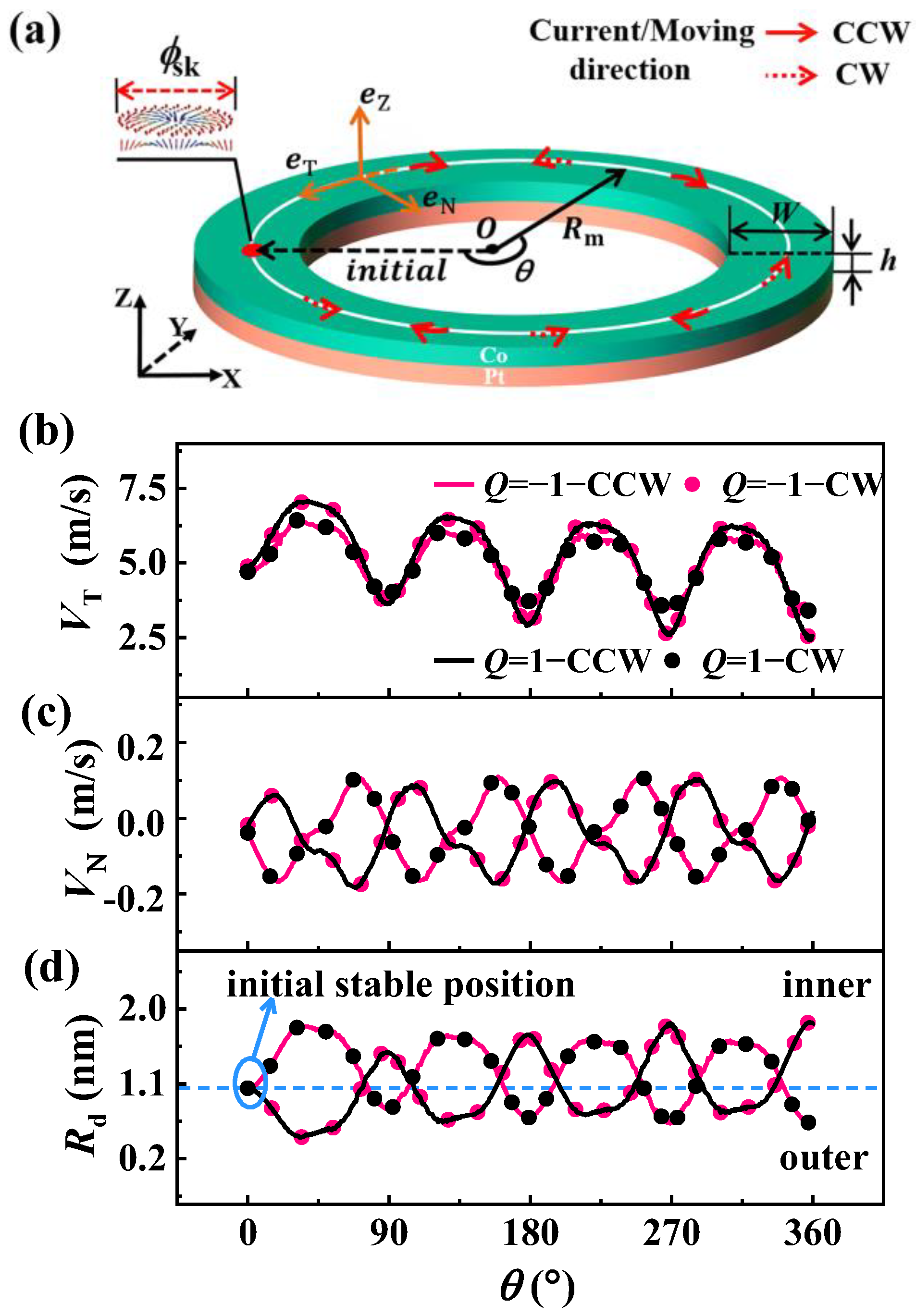
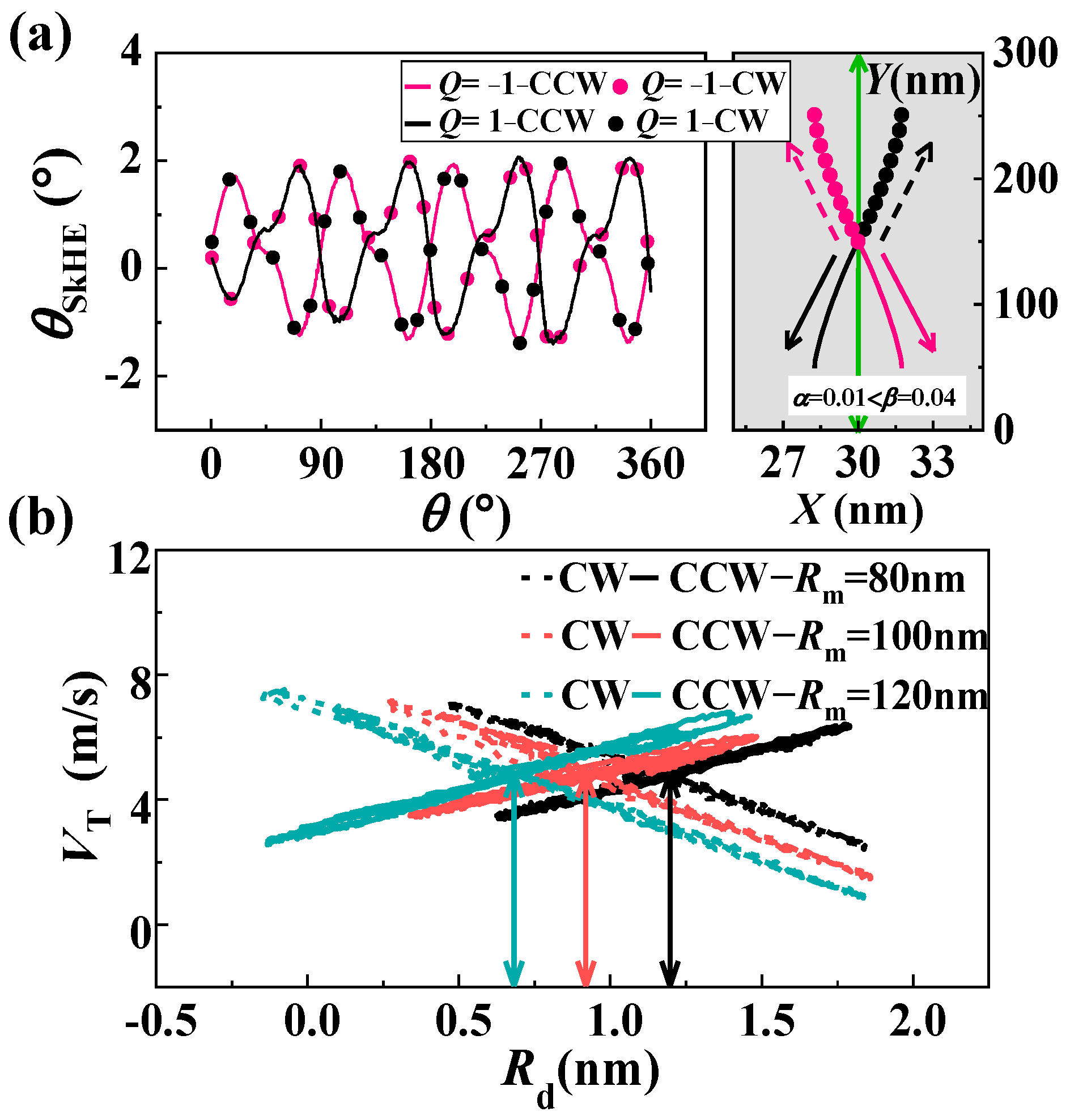
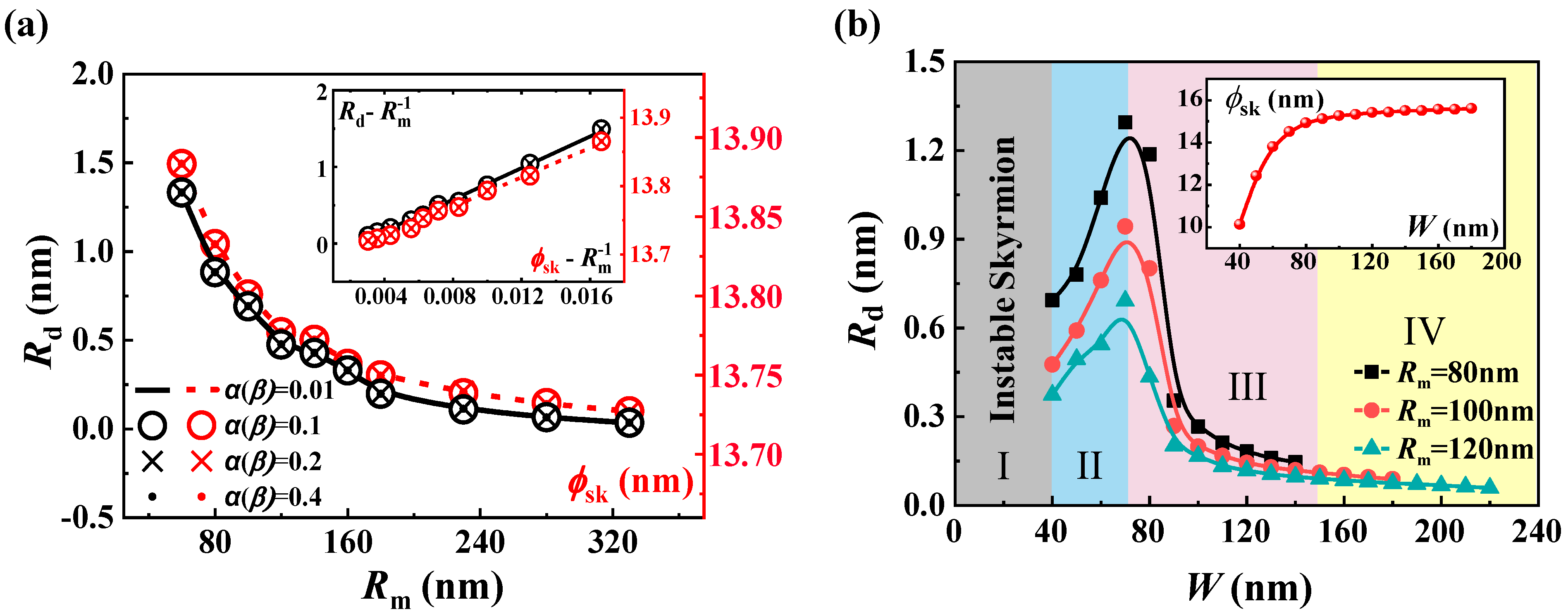
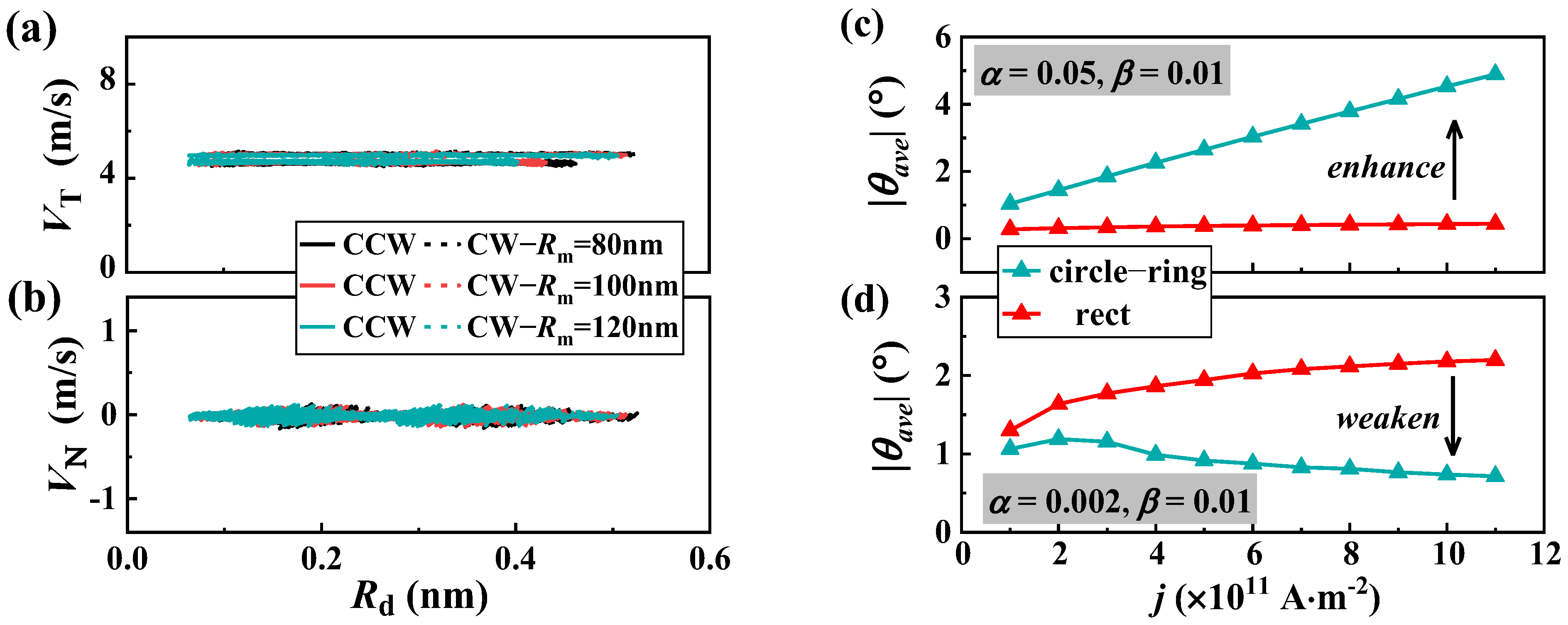
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, N.; Zhang, X.; Hu, Y.; Liu, Y. Nontraditional Movement Behavior of Skyrmion in a Circular-Ring Nanotrack. Nanomaterials 2023, 13, 2977. https://doi.org/10.3390/nano13222977
Cai N, Zhang X, Hu Y, Liu Y. Nontraditional Movement Behavior of Skyrmion in a Circular-Ring Nanotrack. Nanomaterials. 2023; 13(22):2977. https://doi.org/10.3390/nano13222977
Chicago/Turabian StyleCai, Na, Xin Zhang, Yong Hu, and Yan Liu. 2023. "Nontraditional Movement Behavior of Skyrmion in a Circular-Ring Nanotrack" Nanomaterials 13, no. 22: 2977. https://doi.org/10.3390/nano13222977
APA StyleCai, N., Zhang, X., Hu, Y., & Liu, Y. (2023). Nontraditional Movement Behavior of Skyrmion in a Circular-Ring Nanotrack. Nanomaterials, 13(22), 2977. https://doi.org/10.3390/nano13222977






