The Effect of Fabrication Error on the Performance of Mid-Infrared Metalens with Large Field-of-View
Abstract
:1. Introduction
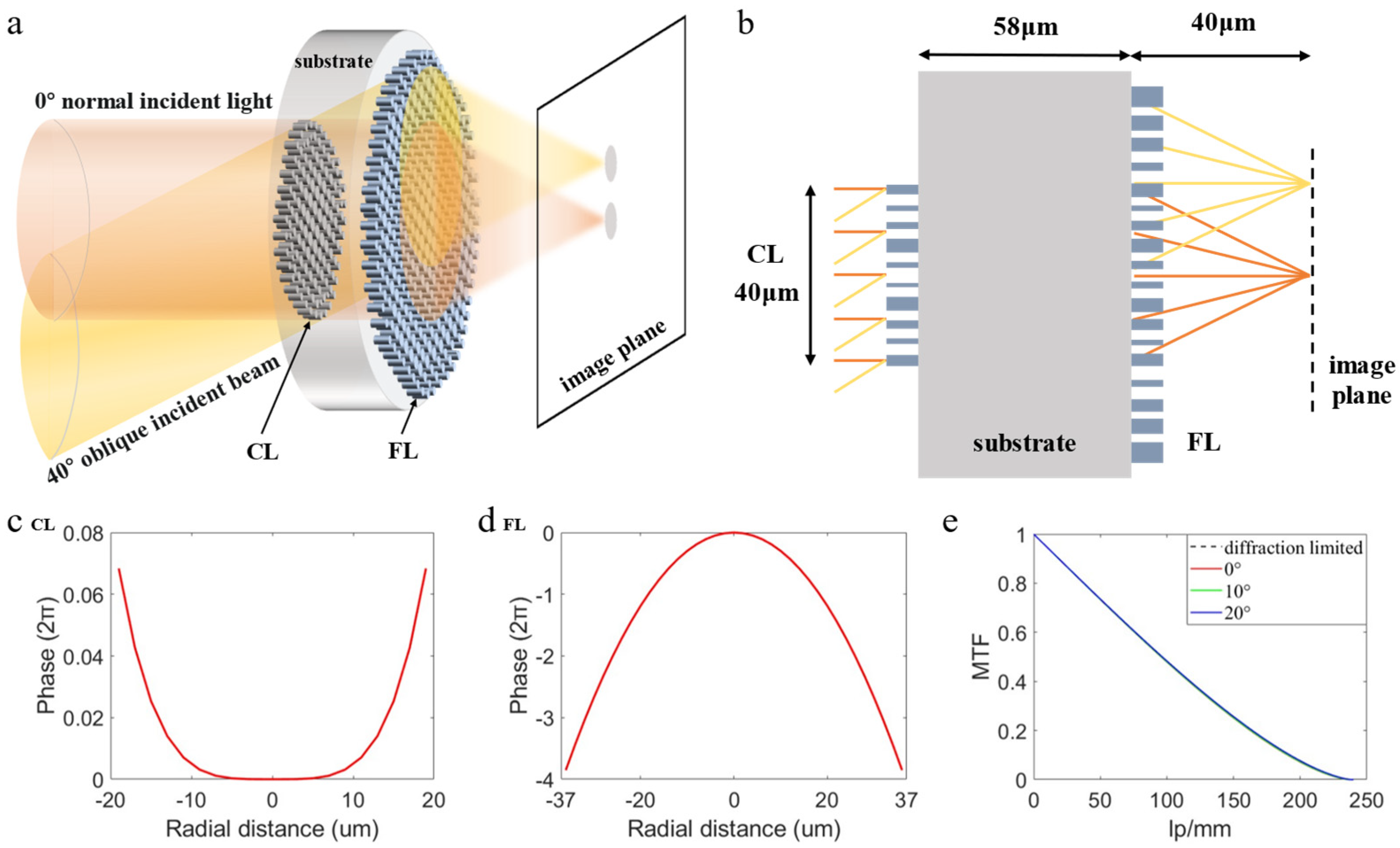
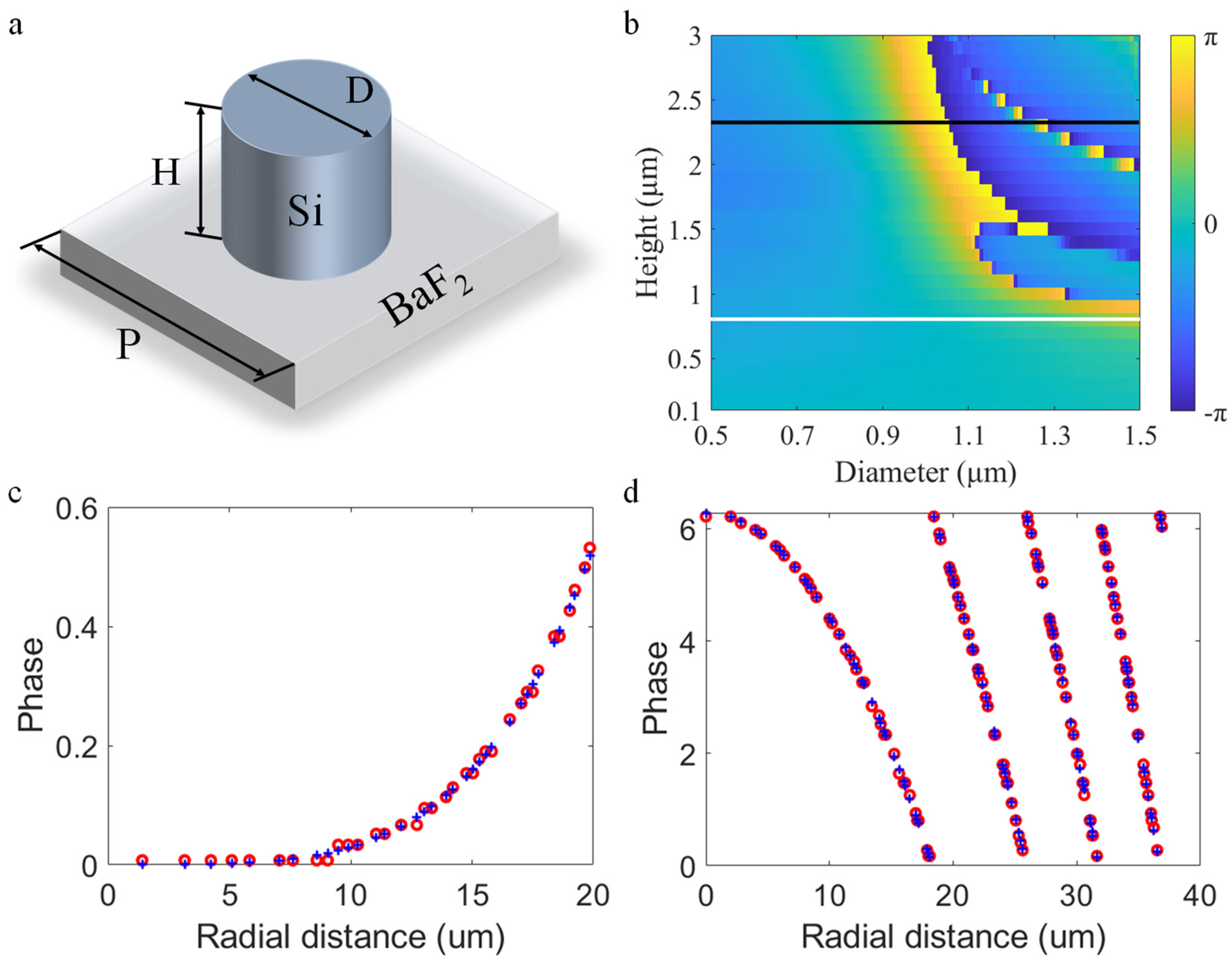
2. Principle and Design Method
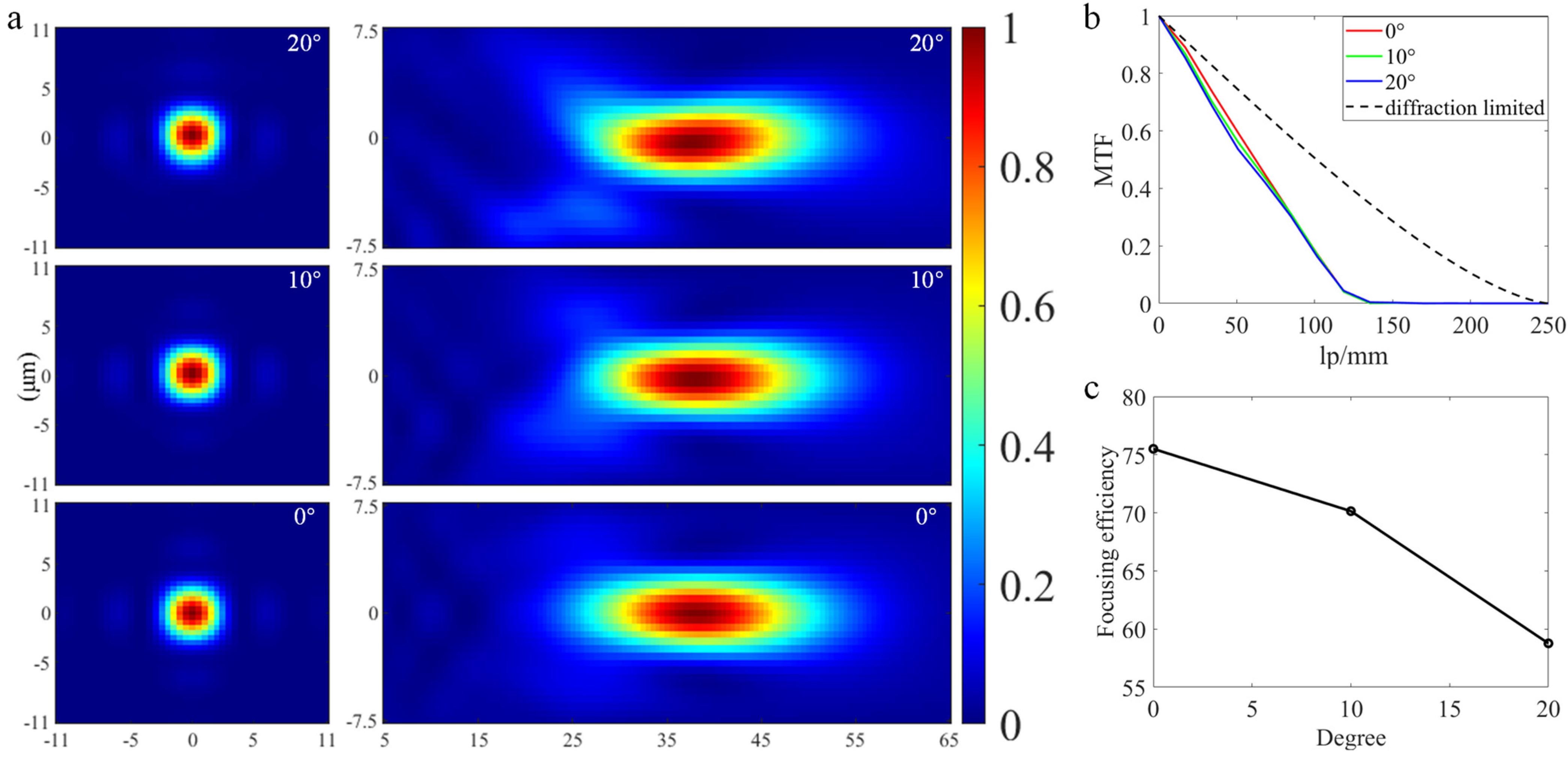
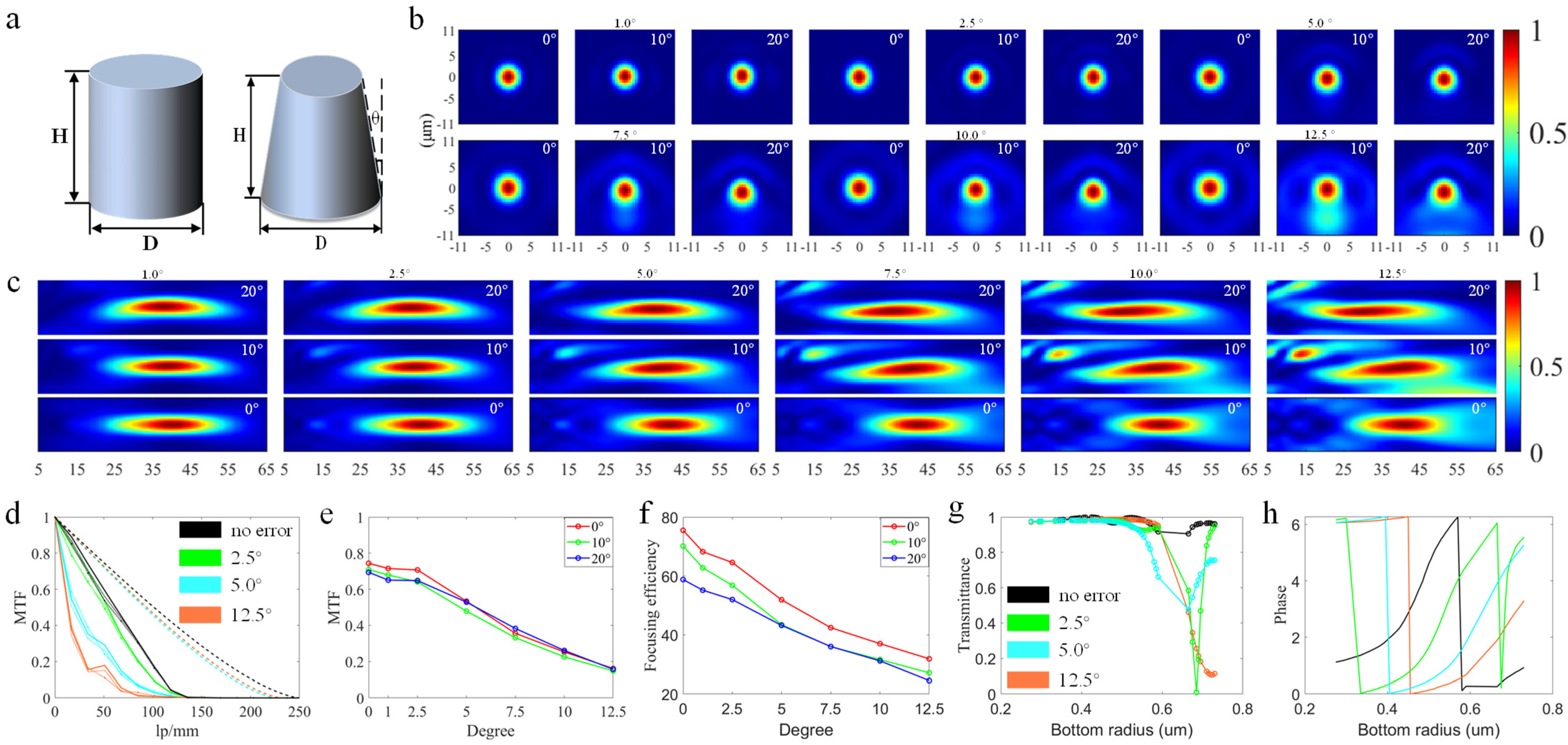
3. Error Analysis and Simulation Results
3.1. Critical Dimension (CD) Bias Error
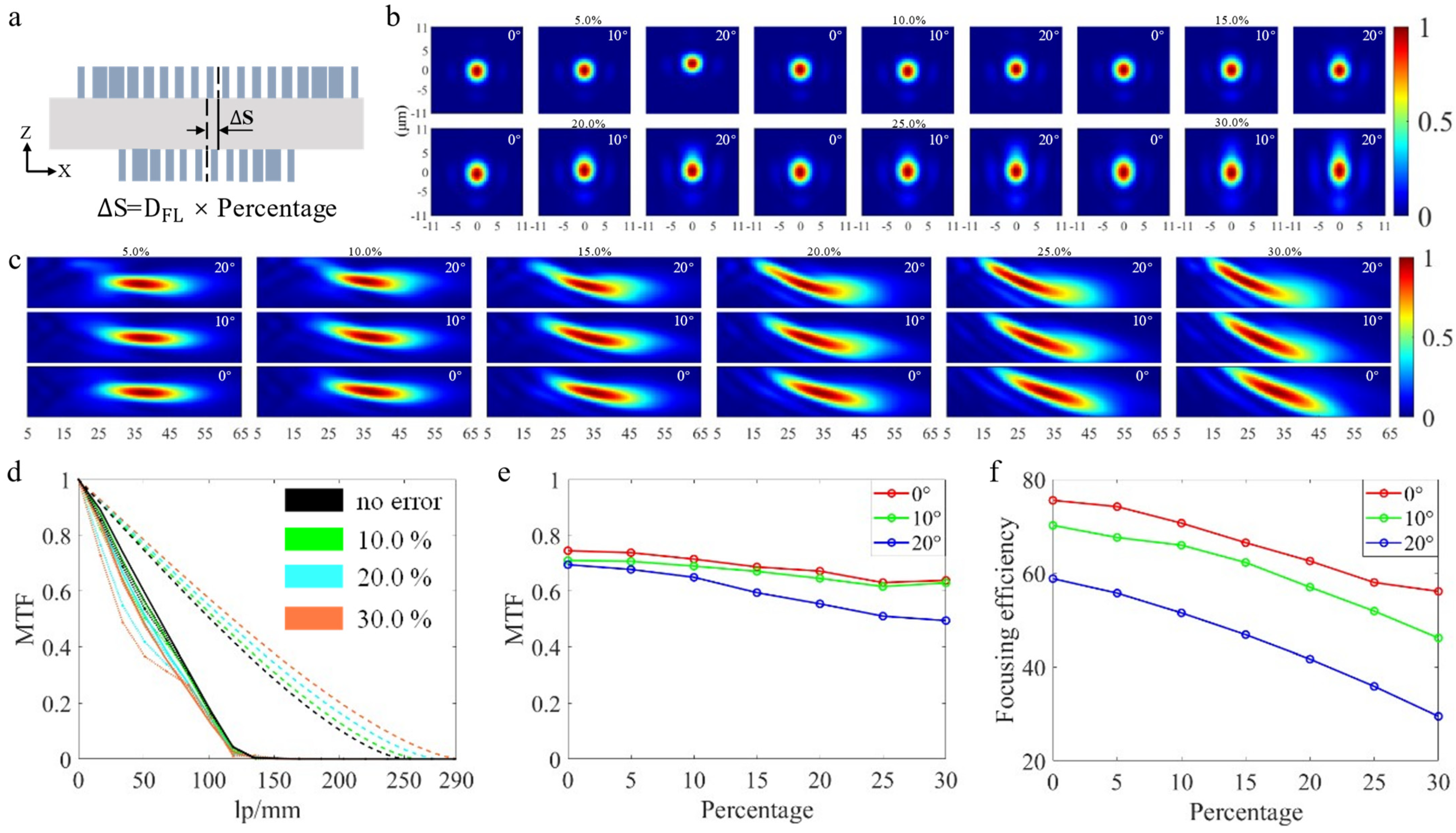
3.2. Inclined Sidewall Error
3.3. Interlayer Alignment Error
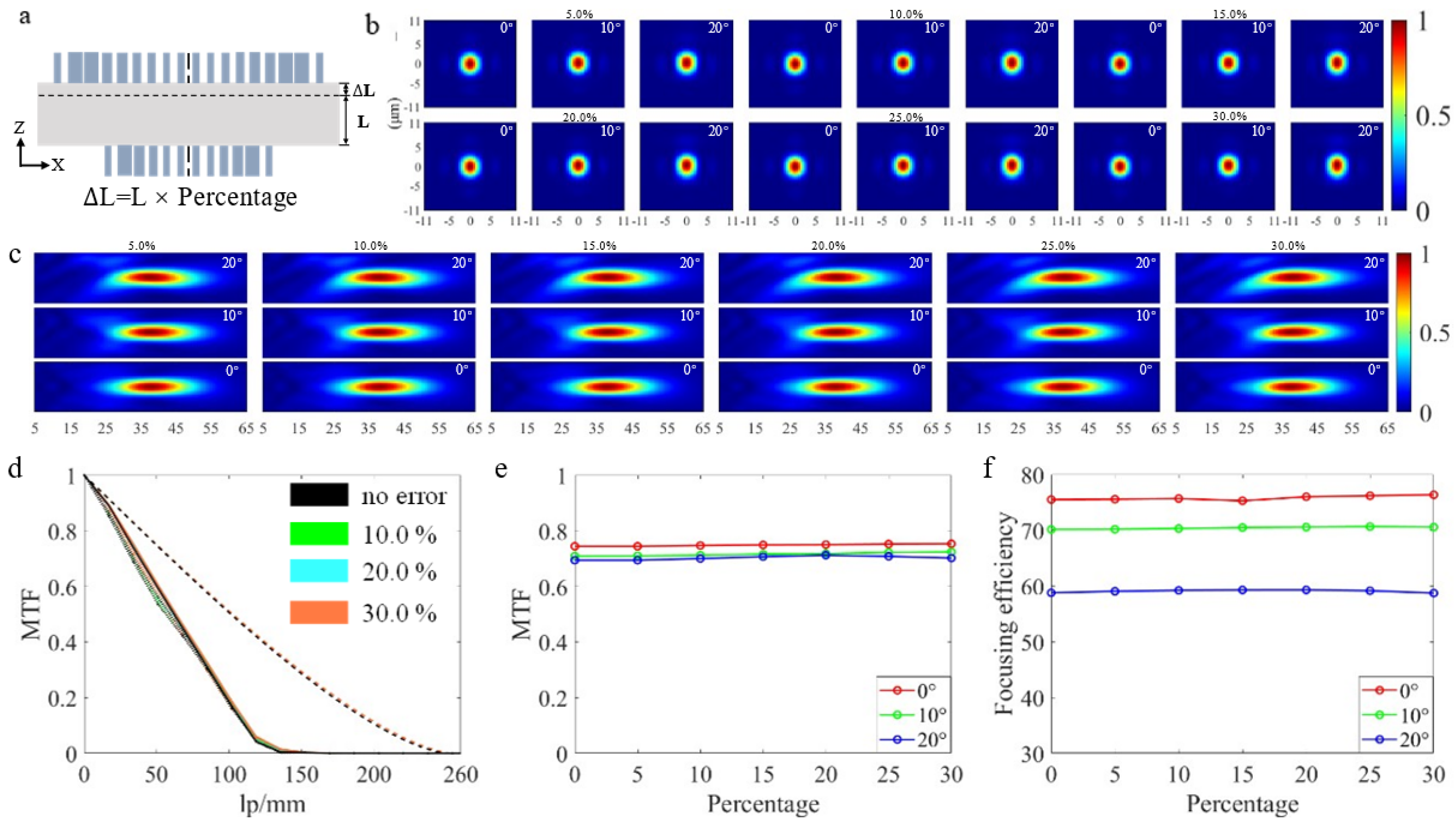
3.4. Spacer Thickness Error
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, C.L.; Mohseni, H. Emerging technologies for high performance infrared detectors. Nanophotonics 2018, 7, 169–197. [Google Scholar] [CrossRef] [Green Version]
- Ring, E.F.J.; Ammer, k. The technique of infrared imaging in medicine. Thermol. Intl. 2000, 7, 7–14. [Google Scholar]
- Zou, Y.; Chakravarty, S.; Chung, C.J.; Xu, X.C.; Chen, R.T. Mid-infrared silicon photonic waveguides and devices [Invited]. Photon. Res. 2018, 6, 254–276. [Google Scholar] [CrossRef]
- Aieta, F.; Aieta, F.; Genevet, P.; Kats, M.A.; Yu, N.; Blanchard, R.; Gaburro, Z.; Capasso, F. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 2012, 12, 4932–4936. [Google Scholar] [CrossRef]
- Aieta, F.; Genevet, P.; Kats, M.; Capasso, F. Aberrations of flat lenses and aplanatic metasurfaces. Opt. Express. 2013, 21, 31530–31539. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [Green Version]
- Kamalia, S.M.; Arbabia, E.; Arbabi, A.; Faraon, A. A review of dielectric optical metasurfaces for wavefront control. Nanophotonics 2018, 7, 1041–1068. [Google Scholar] [CrossRef]
- Hu, Y.Q.; Wang, X.D.; Luo, X.H.; Ou, X.N.; Li, L.; Chen, Y.Q.; Yang, P.; Wang, S.; Duan, H.G. All-dielectric metasurfaces for polarization manipulation: Principles and emerging applications. Nanophotonics 2020, 9, 3755–3780. [Google Scholar] [CrossRef]
- Luo, X.H.; Hu, Y.Q.; Li, X.; Jiang, Y.T.; Wang, Y.S.; Dai, P.; Liu, Q.; Shu, Z.W.; Duan, H.G. Integrated metasurfaces with microprints and helicity-multiplexed holograms for real-time optical encryption. Adv. Opt. Mater. 2020, 8, 1902020. [Google Scholar] [CrossRef]
- Feng, B.; Chen, Y.F.; Sun, D.; Yang, Z.Y.; Yang, B.; Li, X.; Li, T. Precision integration of grating-based polarizers onto focal plane arrays of near-infrared photovoltaic detectors for enhanced contrast polarimetric imaging. Int. J. Extrem. Manuf. 2021, 3, 035201. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.Q.; Jiang, Y.T.; Zhang, Y.; Lai, J.J.; He, P.; Ou, X.N.; Li, L.; Duan, H.G. Ultra-broadband dispersion-manipulated dielectric metalenses by nonlinear dispersive phase compensation. arXiv 2021, arXiv:2112.14127. [Google Scholar]
- Pan, M.Y.; Fu, Y.F.; Zheng, M.J.; Chen, H.; Zang, Y.J.; Duan, H.G.; Li, Q.; Qiu, M.; Hu, Y.Q. Dielectric metalens for miniaturized imaging systems: Progress and challenges. Light Sci. Appl. 2022, 11, 195. [Google Scholar] [CrossRef] [PubMed]
- Groever, B.; Chen, W.T.; Capasso, F. Meta-lens doublet in the visible region. Nano Lett. 2017, 17, 4902–4907. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Arbabi, E.; Kamali, S.M.; Horie, Y.; Han, S.; Faraon, A. Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations. Nat. Commun. 2016, 7, 13682. [Google Scholar] [CrossRef]
- Shalaginov, M.Y.; An, S.; Yang, F.; Su, P.; Lyzwa, D.; Agarwal, A.M.; Zhang, H.; Hu, J.; Gu, T. Single-element diffraction-limited fisheye metalens. Nano Lett. 2020, 20, 7429–7437. [Google Scholar] [CrossRef]
- Engelberg, J.; Zhou, C.; Mazurski, N.; Bar-David, J.; Kristensen, A.; Levy, U. Near-IR wide-field-of-view Huygens metalens for outdoor imaging applications. Nanophotonics 2020, 9, 361–370. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; He, W.L.; Xin, L.; Yang, Z.M.; Liu, Z.J. Imaging performance of a mid-infrared metalens with a machining error. Appl. Opt. 2022, 61, 60. [Google Scholar] [CrossRef]
- Jenkins, R.P.; Campbell, S.D.; Werner, D.H. Establishing exhaustive metasurface robustness against fabrication uncertainties through deep learning. Nanophotonics 2021, 10, 4497–4509. [Google Scholar] [CrossRef]
- Yoon, G.; Kim, I.; Rho, J. Challenges in fabrication towards realization of practical metamaterials. Microelectron. Eng. 2016, 163, 7–20. [Google Scholar] [CrossRef]
- Hu, Y.Q.; Li, X.; Wang, X.D.; Lai, J.J.; Duan, H.G. Progress of micro-nano fabrication technologies for optical metasurfaces. Infrared Laser Eng. 2020, 49, 20201035. [Google Scholar]
- Li, P.; Chen, S.Y.; Dai, H.F.; Yang, Z.M.; Chen, Z.Q.; Wang, Y.S.; Chen, Y.Q.; Peng, W.Q.; Shan, W.B.; Duan, H.G. Recent advances in focused ion beam nanofabrication for nanostructures and devices: Fundamentals and applications. Nanoscale 2021, 13, 1529–1565. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Y.; Jiao, Y.L.; Li, C.Z.; Chen, C.; Li, J.W. Bioinspired micro/nanostructured surfaces prepared by femtosecond laser direct writing for multi-functional applications. Int. J. Extrem. Manuf. 2020, 2, 032002. [Google Scholar] [CrossRef]
- Mack, C.A. Analytical expression for the standing wave intensity in photoresist. Appl. Opt. 1986, 25, 1958. [Google Scholar] [CrossRef] [PubMed]
- Du, J.L.; Gao, F.H.; Guo, Y.K.; Du, C.L.; Qiu, C.K.; Cui, Z. Precompensation approach for improving the quality of laser direct writing patterns by a modified proximity function. Opt. Eng. 2000, 39, 771–775. [Google Scholar] [CrossRef]
- Linfoot, E.H.; Wolf, E. On the corrector plates of Schmidt cameras. J. Opt. Soc. Am. A 1949, 39, 752. [Google Scholar] [CrossRef]
- Buralli, D.A.; Morris, G.M. Design of a wide field diffractive landscape lens. Appl. Opt. 1989, 28, 3950–3959. [Google Scholar] [CrossRef] [Green Version]
- Toba, H.; Takagi, H.; Ohashi, M.; Otaki, K.; Takigawa, Y. Influence on wide-angle doublet metalenses due to different types of all-dielectric metasurfaces. Appl. Opt. 2022, 61, 597–606. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Ball, A.; Bagheri, M.; Faraon, A. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat. Commun. 2015, 6, 7069. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-insensitive metalenses at visible wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef]
- Boreman, G.D. Modulation Transfer Function in Optical and Electro-Optical Systems; SPIE: Bellingham, WA, USA, 2001. [Google Scholar]
- Zhao, M.X.; Chen, M.K.; Zhuang, Z.P.; Zhang, Y.W.; Chen, A.; Chen, Q.M.; Liu, W.Z.; Wang, J.J.; Chen, Z.M.; Wang, B.; et al. Phase characterisation of metalenses. Light Sci. Appl. 2021, 10, 52. [Google Scholar] [CrossRef] [PubMed]
- Sökmen, Ü.; Stranz, A.; Fündling, S.; Wehmann, H.-H.; Bandalo, V.; Bora, A.; Tornow, M.; Waag, A.; Peiner, E. Capabilities of ICP-RIE cryogenic dry etching of silicon: Review of exemplary microstructures. J. Micromech. Microeng. 2009, 19, 105005. [Google Scholar] [CrossRef]
- Gao, F.; Ylinen, S.; Kainlauri, M.; Kapulainen, M. Smooth silicon sidewall etching for waveguide structures using a modified Bosch process. J. Micro-Nanolith MEM. 2014, 13, 013010. [Google Scholar] [CrossRef]
- Marty, F.; Rousseau, L.; Saadany, B.; Mercier, B.; Français, O.; Mita, Y.; Bourouina, T. Advanced etching of silicon based on deep reactive ion etching for silicon high aspect ratio microstructures and three-dimensional micro- and nanostructures. Microelectron. J. 2005, 36, 673–677. [Google Scholar] [CrossRef]
- Fu, J.Y.; Li, J.J.; Yu, J.H.; Liu, R.W.; Li, J.F.; Wang, W.B.; Wang, W.W.; Chen, D.P. Improving sidewall roughness by combined RIE-Bosch process. Mat. Sci. Semicon. Proc. 2018, 83, 186–191. [Google Scholar] [CrossRef]
- Ohara, J.; Takeuchi, Y.; Sato, K. Improvement of high aspect ratio Si etching by optimized oxygen plasma irradiation inserted DRIE. J. Micromech. Microeng. 2009, 19, 095022. [Google Scholar] [CrossRef]
- Meng, L.K.; Yan, J. Effect of process parameters on sidewall damage in deep silicon etch. J. Micromech. Microeng. 2015, 25, 035024. [Google Scholar] [CrossRef]
- Lee, S.H.; Chen, K.N.; Lu, J.J.Q. Wafer-to-wafer alignment for three-dimensional integration: A Review. J. Microelectromech. S 2011, 20, 885–898. [Google Scholar] [CrossRef]
- Zhou, L.; Tian, Y.B.; Huang, H.; Sato, H.; Shimizu, J. A study on the diamond grinding of ultra-thin silicon wafers. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 66–75. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, A.; Li, J.; Jia, H.; Duan, H.; Hu, Y. The Effect of Fabrication Error on the Performance of Mid-Infrared Metalens with Large Field-of-View. Nanomaterials 2023, 13, 440. https://doi.org/10.3390/nano13030440
Li A, Li J, Jia H, Duan H, Hu Y. The Effect of Fabrication Error on the Performance of Mid-Infrared Metalens with Large Field-of-View. Nanomaterials. 2023; 13(3):440. https://doi.org/10.3390/nano13030440
Chicago/Turabian StyleLi, Aoling, Jianhua Li, Honghui Jia, Huigao Duan, and Yueqiang Hu. 2023. "The Effect of Fabrication Error on the Performance of Mid-Infrared Metalens with Large Field-of-View" Nanomaterials 13, no. 3: 440. https://doi.org/10.3390/nano13030440
APA StyleLi, A., Li, J., Jia, H., Duan, H., & Hu, Y. (2023). The Effect of Fabrication Error on the Performance of Mid-Infrared Metalens with Large Field-of-View. Nanomaterials, 13(3), 440. https://doi.org/10.3390/nano13030440





