Application of Population Balance Models in Particle-Stabilized Dispersions
Abstract
:1. Introduction
1.1. Population Balance Equations
1.2. Desorption Energy and Particle Coverage Degree
- (a)
- particle/drop collision efficiency, which depends on the film drainage process,
- (b)
- initial attachment efficiency, which considers the impact of the three-phase contact line formation,
- (c)
- particle attachment efficiency, which describes the ability of the particles to remain attached at the interface,
- (d)
- the drop coverage efficiency, which defines the system’s ability to prevent coalescence as a function of particle coverage.
2. Materials and Methods
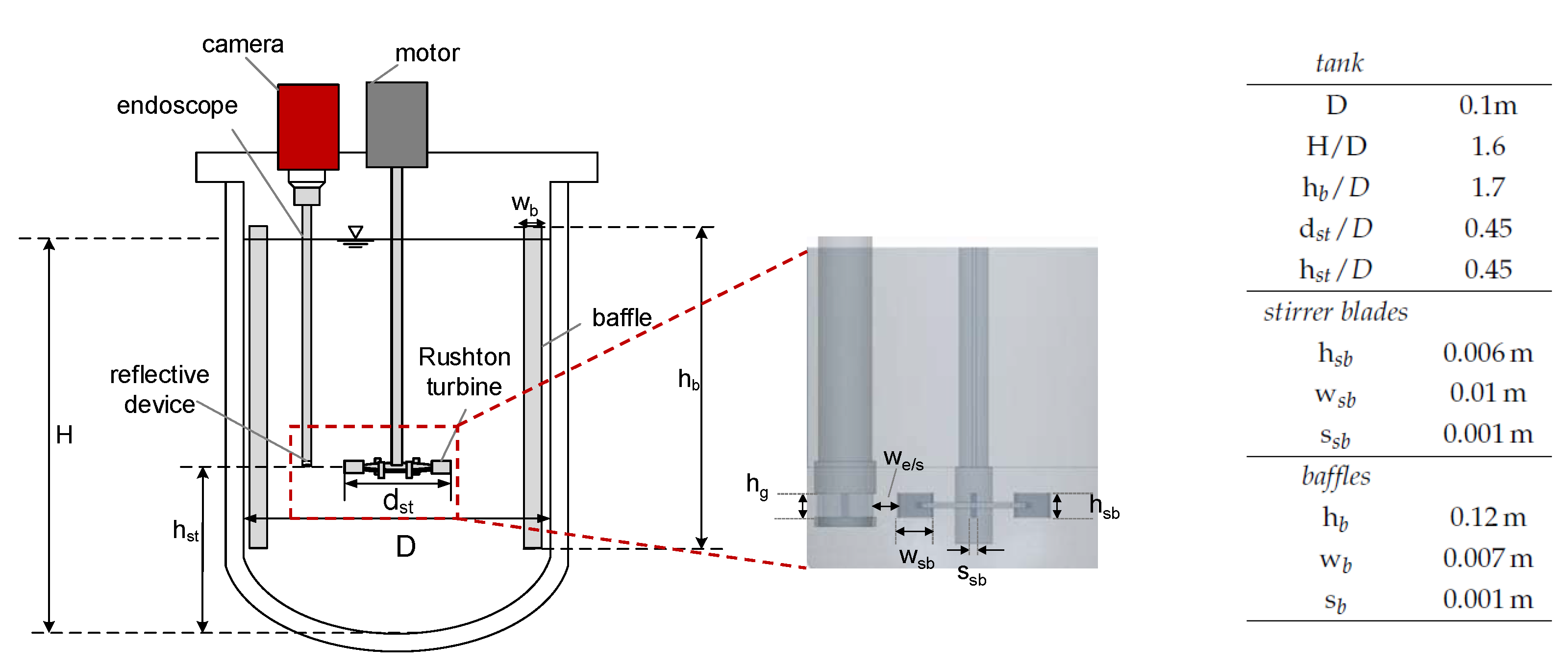
2.1. Experimental Investigations Stirred Tank
2.2. Numerical Investigations
3. Results and Discussion
3.1. Experimental Results
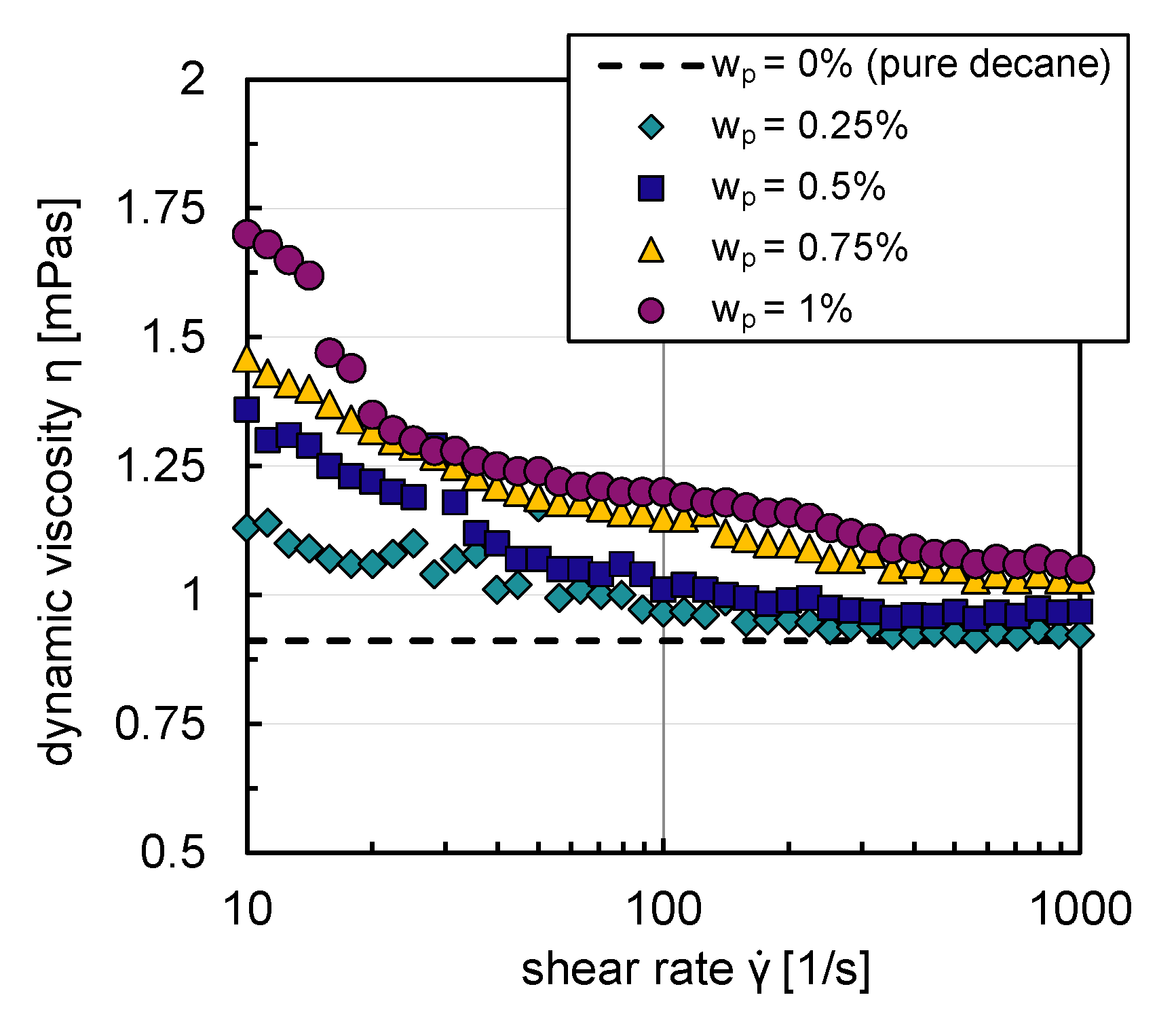
3.1.1. Impact of Nanoparticles on Physical Properties
3.1.2. Experimental Drop Size Distributions
3.2. Numerical Results
3.2.1. Parameter Estimation
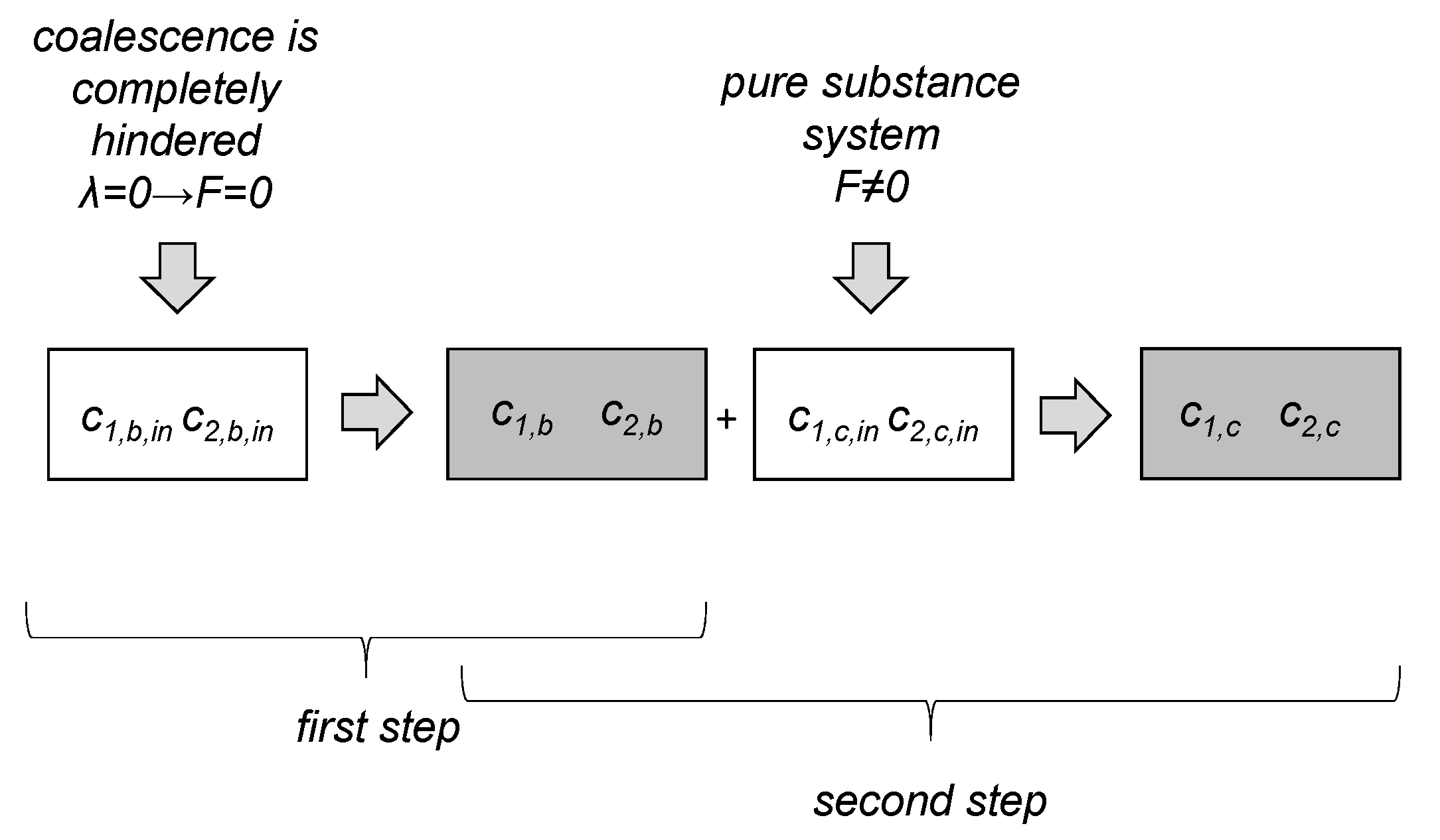
3.2.2. Development of Modified Coalescence Efficiency Model
3.3. Comparison of Simulated and Experimental Results
3.3.1. Comparison of Simulated and Experimental Transient Sauter Mean Diameters
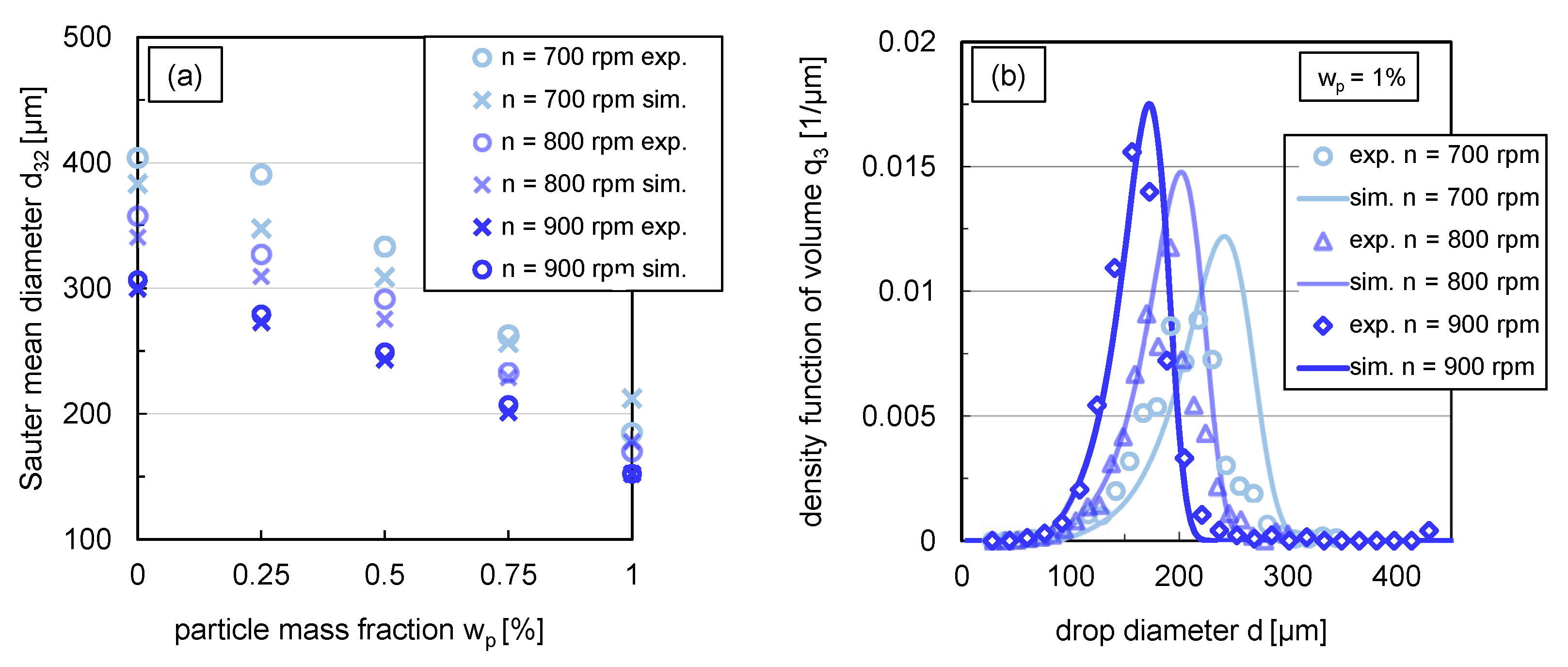
3.3.2. Simulated and Experimental Sauter Mean Diameters and DSDs in Steady State
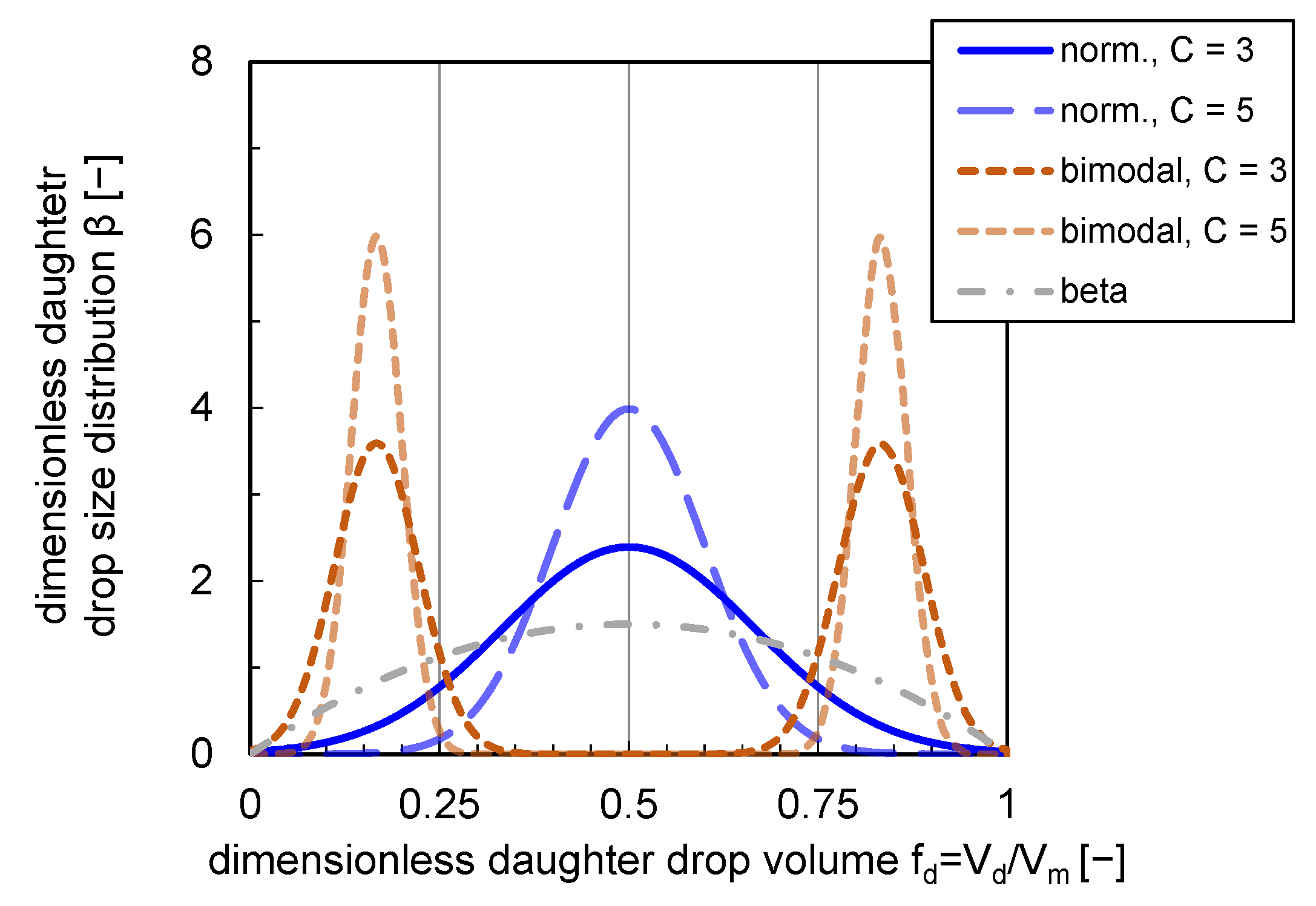
3.3.3. Daughter Drop Size Distribution
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| C&T | work from Coulaloglou and Tavlarides [8] | |
| DSD | drop size distribution | |
| DDSD | daughter drop size distribution | |
| PBE | population balance equation | |
| RRMSD | relative root-mean-square deviation | |
| TEM | transmission electron microscopy | |
| w/o | water-in-oil | |
| 2D | two-dimensional | |
| Symbols Used | ||
| A | area | |
| a | [-] | constant in beta distribution |
| birthrate in PBE | ||
| b | [-] | constant in beta distribution |
| C | [-] | measure of the width of the normal distribution |
| c | [-] | fitparameter in PBE submodels |
| [-] | dimensionless damping factor in coalescence efficiency | |
| fitparameter in the energybarrier modell | ||
| d | drop diameter (d and d are used to differentiate between drops) | |
| Sauter mean diameter | ||
| death rate in PBE | ||
| D | tank diameter | |
| E | energy | |
| F | coalescence rate | |
| f | density function of number | |
| [-] | ratio of daughter drop volume to mother drop volume | |
| g | breakage rate | |
| h | height | |
| H | height | |
| n | stirring speed | |
| [-] | number of particles in the system | |
| [-] | desorbed number of particles | |
| P | power | |
| q | density function | |
| Q | [-] | cumulative function |
| r | radius | |
| s | strength | |
| t | time | |
| T | temperature | |
| V | volume | |
| w | [-] | mass fraction |
| w | wide | |
| Greek Symbols | ||
| [-] | daughter drop size distribution | |
| dynamic viscosity | ||
| mass specific energy dissipation rate | ||
| [-] | voidage | |
| [-] | coalescence efficiency | |
| electrical conductivity | ||
| [-] | number of daughter drops | |
| [-] | dispersed-phase volume fraction | |
| density | ||
| interfacial tension | ||
| shear rate | ||
| standard deviation | ||
| mean value | ||
| contact angle | ||
| [-] | interface coverage degree by particles | |
| coalescence frequency | ||
| zeta potential | ||
| Subscripts | ||
| adsorption | ||
| b | breakage | |
| b | baffle | |
| c | continous phase | |
| c | coalescence | |
| covered | ||
| d | dispersed phase | |
| d | desorbed | |
| d | daughter | |
| desorption | ||
| effective | ||
| experimental | ||
| between endoscope and stirrer | ||
| g | gap | |
| initial | ||
| m | mother | |
| maximum | ||
| minimum | ||
| nanoparticle | ||
| o | organic phase | |
| oil/water interface | ||
| p | particle | |
| stirrer blades | ||
| simulated | ||
| stirrer | ||
| in steady-state | ||
| total | ||
| 3 | volume-based |
References
- Chevalier, Y.; Bolzinger, M.-A. Emulsions stabilized with solid nanoparticles: Pickering emulsions. Colloids Surfaces A Physicochem. Eng. Asp. 2013, 439, 23–34. [Google Scholar] [CrossRef]
- Tsabet, È.; Fradette, L. Effect of the properties of oil, particles, and water on the production of Pickering emulsions. Chem. Eng. Res. Des. 2015, 97, 9–17. [Google Scholar] [CrossRef]
- Stock, S.; Jakob, F.; Röhl, S.; Gräff, K.; Kühnhammer, M.; Hondow, N.; Micklethwaite, S.; Kraume, M.; von Klitzing, R. Exploring water in oil emulsions simultaneously stabilized by solid hydrophobic silica nanospheres and hydrophilic soft PNIPAM microgel. Soft Matter. 2021, 24, 4443. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Ao, F.; Ge, X.; Shen, W. Food-grade Pickering emulsions: Preparation, stabilization and applications. Molecules 2020, 25, 3202. [Google Scholar] [CrossRef]
- von Klitzing, R.; Stehl, D.; Pogrzeba, T.; Schomäcker, R.; Minullina, R.; Panchal, A.; Konnova, S.; Fakhrullin, R.; Koetz, J.; Möhwald, H.; et al. Halloysites Stabilized Emulsions for Hydroformylation of Long Chain Olefins. Adv. Mater. Interfaces 2017, 4, 1600435. [Google Scholar] [CrossRef]
- Kempin, M.V.; Stock, S.; von Klitzing, R.; Kraume, M.; Drews, A. Influence of particle type and concentration on the ultrafiltration behavior of nanoparticle stabilized Pickering emulsions and suspensions. Sep. Purif. Technol. 2020, 252, 117457. [Google Scholar] [CrossRef]
- Tsabet, È.; Fradette, L. Semiempirical approach for predicting the mean size of solid-stabilized emulsions. Ind. Eng. Chem. Res. 2015, 54, 11661–11677. [Google Scholar] [CrossRef]
- Coulaloglou, C.; Tavlarides, L. Description of interaction processes in agitated liquid-liquid dispersions. Chem. Eng. Sci. 1977, 32, 1289–1297. [Google Scholar] [CrossRef]
- Maaß, S.; Paul, N.; Kraume, M. Influence of the dispersed phase fraction on experimental and predicted drop size distributions in breakage dominated stirred systems. Chem. Eng. Sci. 2012, 76, 140–153. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review on mechanisms and models for the coalescence process of fluid particles. Chem. Eng. Sci. 2010, 65, 2851–2864. [Google Scholar] [CrossRef]
- Ribeiro, M.M.; Regueiras, P.F.; Guimarães, M.M.L.; Madureira, C.M.N.; Cruz_Pinto, J.J.C. Optimization of breakage and coalescence model parameters in a steady-state batch agitated dispersion. Ind. Eng. Chem. Res. 2011, 50, 2182–2191. [Google Scholar] [CrossRef]
- Tsouris, C.; Tavlarides, L.L. Breakage and coalescence models for drops in turbulent dispersions. AIChE J. 1994, 40, 395–406. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar]
- Hesketh, R.P.; Etchells, A.W.; Russell, T.W.F. Experimental observations of bubble breakage in turbulent flow. Ind. Eng. Chem. Res. 1991, 30, 835–841. [Google Scholar] [CrossRef]
- Maass, S.; Buscher, S.; Hermann, S.; Kraume, M. Analysis of particle strain in stirred bioreactors by drop breakage investigations. Biotechnol. J. 2011, 6, 979–992. [Google Scholar] [CrossRef]
- Alopaeus, V.; Koskinen, J.; Keskinen, K.I. Simulation of the population balances for liquid–liquid systems in a nonideal stirred tank. Part 1—Description and qualitative validation of the model. Chem. Eng. Sci. 1999, 54, 5887–5899. [Google Scholar] [CrossRef]
- Lee, C.H.; Erickson, L.E.; Glasgow, L.A. Bubble break up and coalescence in turbulent gas-liquid dispersions. Chem. Eng. Commun. 1987, 59, 65–84. [Google Scholar] [CrossRef]
- Kamp, J.; Villwock, J.; Kraume, M. Drop coalescence in technical liquid/liquid applications: A review on experimental techniques and modeling approaches. Rev. Chem. Eng. 2017, 33, 1–47. [Google Scholar] [CrossRef]
- Sovová, H. Breakage and coalescence of drops in a batch stirred vessel—II comparison of model and experiments. Chem. Eng. Sci. 1981, 36, 1567–1573. [Google Scholar] [CrossRef]
- Lehr, F.; Millies, M.; Mewes, D. Bubble-Size distributions and flow fields in bubble columns. AIChE J. 2002, 48, 2426–2443. [Google Scholar] [CrossRef]
- Ozan, S.C.; Solsvik, J.; Jakobsen, H.A. A bubble coalescence kernel combining the characteristics of the film drainage, energy, and critical velocity models. Chem. Eng. Sci. 2023, 269, 118458. [Google Scholar] [CrossRef]
- Pearce, A.K.; Wilks, T.R.; Arno, M.C.; O’Reilly, R.K. Synthesis and applications of anisotropic nanoparticles with precisely defined dimensions. Nat. Rev. Chem. 2021, 5, 21–45. [Google Scholar] [CrossRef]
- Vassaux, S.; Savary, G.; Le Pluart, L.; Grisel, M. On the key role of process parameters to control stability and properties of Pickering emulsions stabilized by montmorillonite. Colloids Surfaces A Physicochem. Eng. Asp. 2019, 583, 123952. [Google Scholar] [CrossRef]
- Binks, B.; Horozov, T. (Eds.) Colloidal Particles at Liquid Interfaces; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Arditty, S.; Whitby, C.P.; Binks, B.P.; Schmitt, V.; Leal-Calderon, F. Some general features of limited coalescence in solid-stabilized emulsions. Eur. Phys. J. E Soft Matter 2003, 11, 273–281. [Google Scholar] [CrossRef]
- Stock, S.; Schlander, A.; Kempin, M.; Geisler, R.; Stehl, D.; Spanheimer, K.; Hondow, N.; Micklethwaite, S.; Weber, A.; Schomäcker, R.; et al. The quantitative impact of fluid vs. solid interfaces on the catalytic performance of pickering emulsions. Phys. Chem. Chem. Phys. 2021, 23, 2355–2367. [Google Scholar] [CrossRef]
- Deshmukh, O.S.; van den Ende, D.; Stuart, M.C.; Mugele, F.; Duits, M.H.G. Hard and soft colloids at fluid interfaces: Adsorption, interactions, assembly & rheology. Adv. Colloid Interface Sci. 2015, 222, 215–227. [Google Scholar] [CrossRef]
- Hohl, L.; Röhl, S.; Stehl, D.; von Klitzing, R.; Kraume, M. Influence of nanoparticles and drop size distributions on the rheology of w/o Pickering emulsions. Chem. Ing. Tech. 2016, 88, 1815–1826. [Google Scholar] [CrossRef]
- Mondragon, R.; Julia, J.E.; Barba, A.; Jarque, J.C. Characterization of silica–water nanofluids dispersed with an ultrasound probe: A study of their physical properties and stability. Powder Technol. 2012, 224, 138–146. [Google Scholar] [CrossRef]
- Ye, X.; Kandlikar, S.G.; Li, C. Viscosity of nanofluids containing anisotropic particles: A critical review and a comprehensive model. Eur. Phys. J. E Soft Matter 2019, 42, 159. [Google Scholar] [CrossRef]
- Röhl, S.; Hohl, L.; Kempin, M.; Enders, F.; Jurtz, N.; Kraume, M. Influence of different Silica nanoparticles on drop size distributions in agitated liquid–liquid systems. Chem. Ing. Tech. 2019, 91, 1640–1655. [Google Scholar] [CrossRef]
- Chesters, A. The modelling of coalescence processes in fluid-liquid dispersions: A review of current understanding. Chem. Eng. Res. Des. 1991, 69, 259–270. [Google Scholar]
- Maindarkar, S.N.; Hoogland, H.; Henson, M.A. Predicting the combined effects of oil and surfactant concentrations on the drop size distributions of homogenized emulsions. Colloids Surfaces A Physicochem. Eng. Asp. 2015, 467, 18–30. [Google Scholar] [CrossRef]
- Alopaeus, V. Modeling surfactant and drop size dynamics in polydisperse liquid-liquid systems with population balances. Chem. Eng. Sci. 2022, 248, 117269. [Google Scholar] [CrossRef]
- Binks, B.P. Particles as surfactants—Similarities and differences. Curr. Opin. Colloid Interface Sci. 2002, 7, 21–41. [Google Scholar] [CrossRef]
- Calabrese, R.V.; Chang, T.; Dang, P.T. Drop breakup in turbulent stirred tank contactors—Part 1—Effect of dispersed-phase viscosity. AiChe J. 1986, 32, 657–666. [Google Scholar] [CrossRef]
- Maaß, S.; Wollny, S.; Voigt, A.; Kraume, M. Experimental comparison of measurement techniques for drop size distributions in liquid/liquid dispersions. Exp. Fluids 2011, 50, 259–269. [Google Scholar] [CrossRef]
- Emmerich, J.; Tang, Q.; Wang, Y.; Neubauer, P.; Junne, S.; Maaß, S. Optical inline analysis and monitoring of particle size and shape distributions for multiple applications: Scientific and industrial relevance. Chin. J. Chem. Eng. 2019, 27, 257–277. [Google Scholar] [CrossRef]
- Wulkow, M.; Gerstlauer, A.; Nieken, U. Modeling and simulation of crystallization processes using parsival. Chem. Eng. Sci. 2001, 56, 2575–2588. [Google Scholar] [CrossRef]
- Petzold, M.; Röhl, S.; Hohl, L.; Stehl, D.; Lehmann, M.; von Klitzing, R.; Kraume, M. Mass transfer and drop size distributions in reactive nanoparticle-stabilized multiphase systems. Chem. Ing. Tech. 2017, 89, 1561–1573. [Google Scholar] [CrossRef]
- Vignati, E.; Piazza, R.; Lockhart, T.P. Pickering Emulsions: Interfacial Tension, Colloidal Layer Morphology, and Trapped-Particle Motion. Langmuir 2003, 19, 6650–6656. [Google Scholar] [CrossRef]






| initial values | ||||
| fitted values |
| Particle Mass Fraction [%] | 0 | 0.25 | 0.5 | 0.75 | 1 | Total |
|---|---|---|---|---|---|---|
| RRMSD () [%] n = 900 rpm | 2.24 | 2.31 | 2.41 | 2.96 | 0.03 | 2.23 |
| RRMSD () [%] n = 800 rpm | 4.70 | 5.37 | 5.49 | 1.68 | 4.61 | 4.59 |
| RRMSD () [%] n = 700 rpm | 5.14 | 11.05 | 7.29 | 2.28 | 15.02 | 9.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Röhl, S.; Hohl, L.; Stock, S.; Zhan, M.; Kopf, T.; von Klitzing, R.; Kraume, M. Application of Population Balance Models in Particle-Stabilized Dispersions. Nanomaterials 2023, 13, 698. https://doi.org/10.3390/nano13040698
Röhl S, Hohl L, Stock S, Zhan M, Kopf T, von Klitzing R, Kraume M. Application of Population Balance Models in Particle-Stabilized Dispersions. Nanomaterials. 2023; 13(4):698. https://doi.org/10.3390/nano13040698
Chicago/Turabian StyleRöhl, Susanne, Lena Hohl, Sebastian Stock, Manlin Zhan, Tobias Kopf, Regine von Klitzing, and Matthias Kraume. 2023. "Application of Population Balance Models in Particle-Stabilized Dispersions" Nanomaterials 13, no. 4: 698. https://doi.org/10.3390/nano13040698
APA StyleRöhl, S., Hohl, L., Stock, S., Zhan, M., Kopf, T., von Klitzing, R., & Kraume, M. (2023). Application of Population Balance Models in Particle-Stabilized Dispersions. Nanomaterials, 13(4), 698. https://doi.org/10.3390/nano13040698







