Optical Orientation of Excitons in a Longitudinal Magnetic Field in Indirect-Band-Gap (In,Al)As/AlAs Quantum Dots with Type-I Band Alignment
Abstract
1. Introduction
2. Experimental Details
3. Experimental Results
3.1. Time-Resolved Unpolarized PL
3.2. PL under Selective Excitation at Zero Magnetic Field
3.3. Optical Orientation in Longitudinal Magnetic Field
3.4. Effect of Excitation Detection Protocol on Optical Orientation
- (i)
- The optical orientation depends on the modulation frequency of the excitation polarization.
- (ii)
- Measurement of the - and -polarized PL components in a short time window with delay after changing the excitation polarization (from to , and vice versa) allows us to reveal the lifetime and other features of the exciton spin dynamics in indirect QDs.
- (iii)
- At zero magnetic field, both the co- and counter-polarized PL component intensities have identical temporal dependence, while in a magnetic field with a strength exceeding the fluctuations of the nuclear field, the intensity of the co-polarized PL component strongly increases after the change in the excitation polarization and then decays with the increase in . However, the intensity of the counter-polarized PL component does not depend on the delay time.
- (iv)
- The decrease in co-polarized PL component intensity with delay time in a magnetic field disappears with the increase in temperature.
4. Discussion
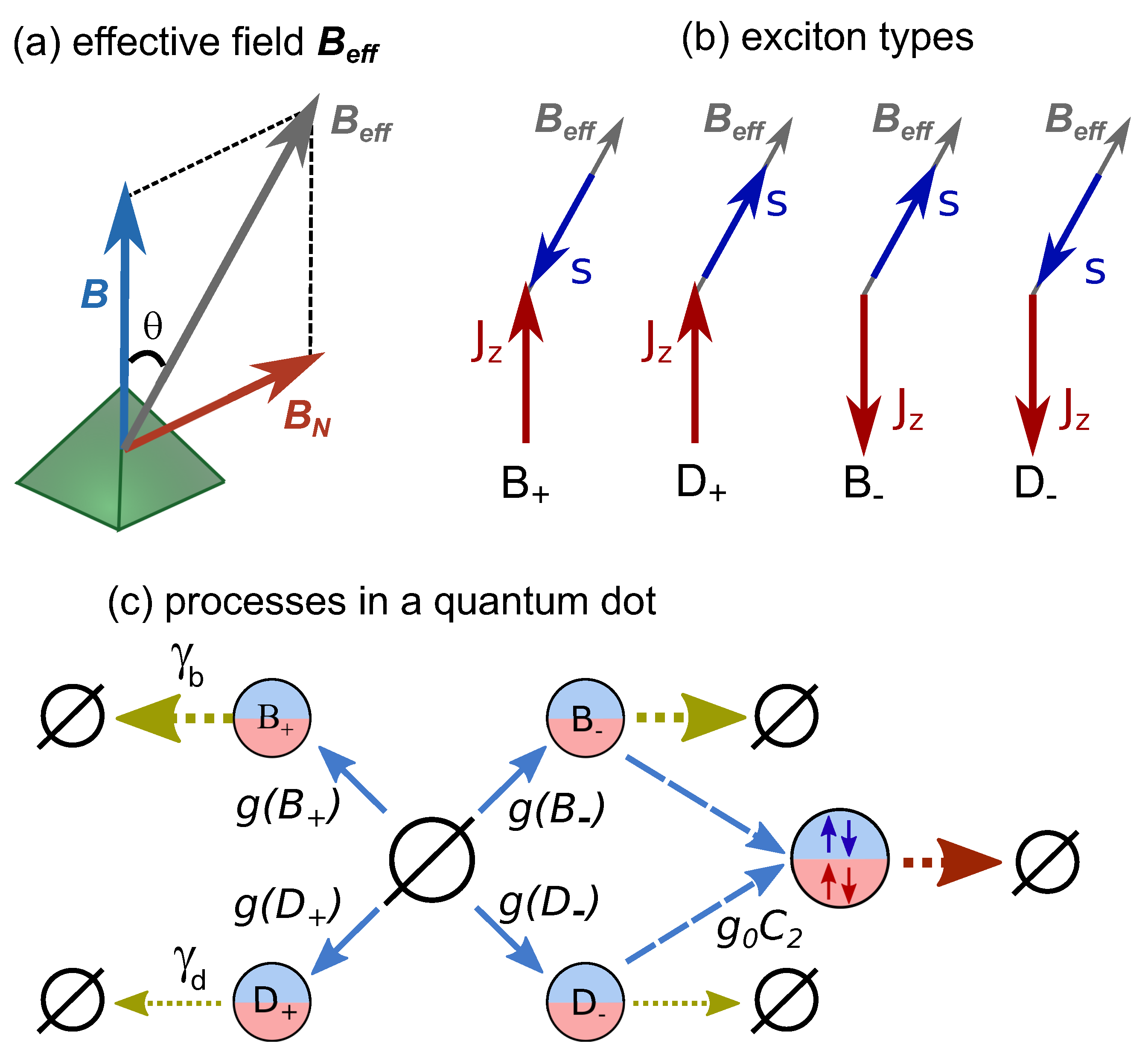
4.1. Theory of QD Blockade
4.2. Modeling of Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dyakonov, M.I. (Ed.) Spin Physics in Semiconductors; Springer: Berlin, Germany, 2008. [Google Scholar]
- Glazov, M.M. Electron and Nuclear Spin Dynamics in Semiconductor Nanostructures; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Fert, A. Nobel Lecture: Origin, development, and future of spintronics. Rev. Mod. Phys. 2008, 80, 1517. [Google Scholar] [CrossRef]
- Bader, S.D.; Parkin, S.S.P. Spintronics. Annu. Rev. Condens. Matter Phys. 2010, 1, 71–88. [Google Scholar] [CrossRef]
- Khaetskii, A.V.; Nazarov, Y.V. Spin relaxation in semiconductor quantum dots. Phys. Rev. B 2000, 61, 12639. [Google Scholar] [CrossRef]
- Kroutvar, M.; Ducommun, Y.; Heiss, D.; Bichler, M.; Schuh, D.; Abstreiter, G.; Finley, J.J. Optically programmable electron spin memory using semiconductor quantum dots. Nature 2004, 432, 81. [Google Scholar] [CrossRef]
- Meier, F.; Zakharchenja, B.P. (Eds.) Optical Orientation; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Rautert, J.; Rakhlin, M.V.; Belyaev, K.G.; Shamirzaev, T.S.; Bakarov, A.K.; Toropov, A.A.; Mukhin, I.S.; Yakovlev, D.R.; Bayer, M. Anisotropic exchange splitting of excitons affected by Γ-X mixing in (In,Al)As/AlAs quantum dots: Microphotoluminescence and macrophotoluminescence measurements. Phys. Rev. B 2019, 100, 205303. [Google Scholar] [CrossRef]
- Taylor, M.W.; Spencer, P.; Murray, R. Negative circular polarization as a universal property of quantum dots. Appl. Phys. Lett. 2015, 106, 122404. [Google Scholar] [CrossRef]
- Dunker, D.; Shamirzaev, T.S.; Debus, J.; Yakovlev, D.R.; Zhuravlev, K.S.; Bayer, M. Spin relaxation of negatively charged excitons in (In,Al)As/AlAs quantum dots with indirect band gap and type-I band alignment. Appl. Phys. Lett. 2012, 101, 142108. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Yakovlev, D.R.; Kopteva, N.E.; Kudlacik, D.; Glazov, M.M.; Krechetov, A.G.; Gutakovskii, A.K.; Bayer, M. Spin dynamics of charged excitons in ultrathin (In,Al)(Sb,As)/AlAs and Al(Sb,As)/AlAs quantum wells with an indirect band gap. Phys. Rev. B 2022, 106, 075407. [Google Scholar] [CrossRef]
- Rautert, J.; Shamirzaev, T.S.; Nekrasov, S.V.; Yakovlev, D.R.; Klenovský, P.; Kusrayev, Y.G.; Bayer, M. Optical orientation and alignment of excitons in direct and indirect band gap (In,Al)As/AlAs quantum dots with type-I alignment. Phys. Rev. B 2019, 99, 195411. [Google Scholar] [CrossRef]
- Kuznetsova, M.S.; Rautert, J.; Kavokin, K.V.; Smirnov, D.S.; Yakovlev, D.R.; Bakarov, A.K.; Gutakovskii, A.K.; Shamirzaev, T.S.; Bayer, M. Electron-nuclei interaction in the X valley of (In,Al)As/AlAs quantum dots. Phys. Rev. B 2020, 101, 075412. [Google Scholar] [CrossRef]
- Smirnov, D.S.; Shamirzaev, T.S.; Yakovlev, D.R.; Bayer, M. Dynamic Polarization of Electron Spins Interacting with Nuclei in Semiconductor Nanostructures. Phys. Rev. Lett. 2020, 125, 156801. [Google Scholar] [CrossRef] [PubMed]
- Shamirzaev, T.S.; Shumilin, A.V.; Smirnov, D.S.; Rautert, J.; Yakovlev, D.R.; Bayer, M. Dynamic polarization of electron spins in indirect band gap (In,Al)As/AlAs quantum dots in a weak magnetic field: Experiment and theory. Phys. Rev. B 2021, 104, 115405. [Google Scholar] [CrossRef]
- Shumilin, A.V. Dynamic spin polarization in organic semiconductors with intermolecular exchange interaction. Phys. Rev. B 2022, 105, 104206. [Google Scholar] [CrossRef]
- Smirnov, D.S. Dynamic valley polarization in moiré quantum dots. Phys. Rev. B 2021, 104, L241401. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, C.; Park, H.; Zhu, J.; Wang, C.; Taniguchi, T.; Watanabe, K.; Yan, J.; Xiao, D.; Gamelin, D.R.; et al. Light-induced ferromagnetism in moiré superlattices. Nature 2022, 604, 468. [Google Scholar] [CrossRef]
- Ivchenko, E.L. Magnetic circular polarization of exciton photoluminescence. Phys. Solid State 2018, 60, 1514. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Debus, J.; Yakovlev, D.R.; Glazov, M.M.; Ivchenko, E.L.; Bayer, M. Dynamics of exciton recombination in strong magnetic fields in ultrathin GaAs/AlAs quantum wells with indirect band gap and type-II band alignment. Phys. Rev. B 2016, 94, 045411. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Rautert, J.; Yakovlev, D.R.; Debus, J.; Gornov, A.Y.; Glazov, M.M.; Ivchenko, E.L.; Bayer, M. Spin dynamics and magnetic field induced polarization of excitons in ultrathin GaAs/AlAs quantum wells with indirect band gap and type-II band alignment. Phys. Rev. B 2017, 96, 035302. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Rautert, J.; Yakovlev, D.R.; Bayer, M. Exciton recombination and spin relaxation in strong magnetic fields in ultrathin (In,Al)As/AlAs quantum wells with indirect band gap and type-I band alignment. Phys. Rev. B 2021, 104, 045305. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Yakovlev, D.R.; Bakarov, A.K.; Kopteva, N.E.; Kudlacik, D.; Gutakovskii, A.K.; Bayer, M. Recombination and spin dynamics of excitons in thin (Ga,Al)(Sb,As)/AlAs quantum wells with an indirect band gap and type-I band alignment. Phys. Rev. B 2020, 102, 165423. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Nenashev, A.V.; Gutakovskii, A.K.; Kalagin, A.K.; Zhuravlev, K.S.; Larsson, M.; Holtz, P.O. Atomic and energy structure of InAs/AlAs quantum dots. Phys. Rev. B 2008, 78, 085323. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Gilinsky, A.M.; Kalagin, A.K.; Toropov, A.I.; Gutakovskii, A.K.; Zhuravlev, K.S. Strong sensitivity of photoluminescence of InAs/AlAs quantum dots to defects: Evidence for lateral inter-dot transport. Semicond. Sci. Technol. 2006, 21, 527. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Abramkin, D.S.; Dmitriev, D.V.; Gutakovskii, A.K. Nonradiative energy transfer between vertically coupled indirect and direct bandgap InAs quantum dots. Appl. Phys. Lett. 2010, 97, 263102. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.R.; Ram-Mohan, L.R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Debus, J.; Abramkin, D.S.; Dunker, D.; Yakovlev, D.R.; Dmitriev, D.V.; Gutakovskii, A.K.; Braginsky, L.S.; Zhuravlev, K.S.; Bayer, M. Exciton recombination dynamics in an ensemble of (In,Al)As/AlAs quantum dots with indirect band-gap and type-I band alignment. Phys. Rev. B 2011, 84, 155318. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Nenashev, A.V.; Zhuravlev, K.S. Coexistence of direct and indirect band structures in arrays of InAs/AlAs quantum dots. Appl. Phys. Lett. 2008, 92, 213101. [Google Scholar] [CrossRef]
- Abramkin, D.S.; Putyato, M.A.; Budennyy, S.A.; Gutakovskii, A.K.; Semyagin, B.R.; Preobrazhenskii, V.V.; Kolomys, O.F.; Strelchuk, V.V.; Shamirzaev, T.S. Atomic structure and energy spectrum of Ga(As,P)/GaP heterostructures. J. Appl. Phys. 2012, 112, 083713. [Google Scholar] [CrossRef]
- Shamirzaev, T.S. Exciton recombination and spin dynamics in indirect-gap quantum wells and quantum dots. Phys. Solid State 2018, 60, 1554. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Abramkin, D.S.; Gutakovskii, A.K.; Putyato, M.A. Novel self-assembled quantum dots in the GaSb/AlAs Heterosystem. JETP Lett. 2012, 95, 534. [Google Scholar] [CrossRef]
- Abramkin, D.S.; Rumynin, K.M.; Bakarov, A.K.; Kolotovkina, D.A.; Gutakovskii, A.K.; Shamirzaev, T.S. Quantum Dots Formed in InSb/AlAs and AlSb/AlAs Heterostructures. JETP Lett. 2016, 103, 692. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Abramkin, D.S.; Gutakovskii, A.K.; Putyato, M.A. High quality relaxed GaAs quantum dots in GaP matrix. Appl. Phys. Lett. 2010, 97, 023108. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Abramkin, D.S.; Nenashev, A.V.; Zhuravlev, K.S.; Trojanek, F.; Dzurnak, B.; Maly, P. Carrier dynamics in InAs/AlAs quantum dots: Lack in carrier transfer from wetting layer to quantum dots. Nanotechnology 2010, 21, 155703–155707. [Google Scholar] [CrossRef]
- Bayer, M.; Ortner, G.; Stern, O.; Kuther, A.; Gorbunov, A.A.; Forchel, A.; Hawrylak, P.; Fafard, S.; Hinzer, K.; Reinecke, T.L.; et al. Fine structure of neutral and charged excitons in self-assembled In(Ga)As/(Al)GaAs quantum dots. Phys. Rev. B 2002, 65, 195315. [Google Scholar] [CrossRef]
- Paillard, M.; Marie, X.; Renucci, P.; Amand, T.; Jbeli, A.; Gérard, J.M. Spin relaxation quenching in semiconductor quantum dots. Phys. Rev. Lett. 2001, 86, 1634. [Google Scholar] [CrossRef] [PubMed]
- Bir, G.L.; Pikus, G.E. Symmetry and Strain-Induced Effects in Semiconductors; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Pikus, G.E.; Bir, G.L. Exchange interaction in excitons in semiconductors. Sov. Phys. JETP 1971, 33, 108. [Google Scholar]
- Smirnov, D.S.; Zhukov, E.A.; Yakovlev, D.R.; Kirstein, E.; Bayer, M.; Greilich, A. Spin polarization recovery and Hanle effect for charge carriers interacting with nuclear spins in semiconductors. Phys. Rev. B 2020, 102, 235413. [Google Scholar] [CrossRef]
- Merkulov, I.A.; Efros, A.L.; Rosen, M. Electron spin relaxation by nuclei in semiconductor quantum dots. Phys. Rev. B 2002, 65, 205309. [Google Scholar] [CrossRef]
- Debus, J.; Shamirzaev, T.S.; Dunker, D.; Sapega, V.F.; Ivchenko, E.L.; Yakovlev, D.R.; Toropov, A.I.; Bayer, M. Spin-flip Raman scattering of the Γ-X mixed exciton in indirect band gap (In,Al)As/AlAs quantum dots. Phys. Rev. B 2014, 90, 125431. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Shamirzaev, T.S.; Yakovlev, D.R.; Gutakovskii, A.K.; Owczarczyk, S.; Bayer, M. Optically detected magnetic resonance of photoexcited electrons in (In,Al)As/AlAs quantum dots with indirect band gap and type-I band alignment. Phys. Rev. B 2018, 97, 245306. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Tolmachev, D.O.; Shamirzaev, T.S.; Yakovlev, D.R.; Slupinski, T.; Bayer, M. Optically detected magnetic resonance of indirect excitons in an ensemble of (In, Al, Ga)As/(Al, Ga)As quantum dots. Phys. Rev. B 2021, 104, 195306. [Google Scholar] [CrossRef]
- Nikolaev, I.S.; Lodahl, P.; van Driel, A.F.; Koenderink, A.F.; Vos, W.L. Strongly nonexponential time-resolved fluorescence of quantum-dot ensembles in three-dimensional photonic crystals. Phys. Rev. B 2007, 75, 115302. [Google Scholar] [CrossRef]
- Urbaszek, B.; Marie, X.; Amand, T.; Krebs, O.; Voisin, P.; Maletinsky, P.; Högele, A.; Imamoglu, A. Nuclear spin physics in quantum dots: An optical investigation. Rev. Mod. Phys. 2013, 85, 79. [Google Scholar] [CrossRef]
- Kuznetsova, M.S.; Flisinski, K.; Gerlovin, I.Y.; Petrov, M.Y.; Ignatiev, I.V.; Verbin, S.Y.; Yakovlev, D.R.; Reuter, D.; Wieck, A.D.; Bayer, M. Nuclear magnetic resonances in (In, Ga)As/GaAs quantum dots studied by resonant optical pumping. Phys. Rev. B 2014, 89, 125304. [Google Scholar] [CrossRef]
- Dyakonov, M.; Marie, X.; Amand, T.; Jeune, P.L.; Robart, D.; Brousseau, M.; Barrau, J. Coherent spin dynamics of excitons in quantum wells. Phys. Rev. B 1997, 56, 10412. [Google Scholar] [CrossRef]
- Smirnov, D.S.; Mantsevich, V.N.; Glazov, M.M. Theory of optically detected spin noise in nanosystems. Phys. Usp. 2021, 64, 923. [Google Scholar] [CrossRef]
- Avdeev, I.D.; Smirnov, D.S. Hyperfine interaction in atomically thin transition metal dichalcogenides. Nanoscale Adv. 2019, 1, 2624. [Google Scholar] [CrossRef]
- Zhukov, E.A.; Kirstein, E.; Smirnov, D.S.; Yakovlev, D.R.; Glazov, M.M.; Reuter, D.; Wieck, A.D.; Bayer, M.; Greilich, A. Spin inertia of resident and photoexcited carriers in singly charged quantum dots. Phys. Rev. B 2018, 98, 121304. [Google Scholar] [CrossRef]
- Shumilin, A.V.; Smirnov, D.S. Nuclear Spin Dynamics, Noise, Squeezing, and Entanglement in Box Model. Phys. Rev. Lett. 2021, 126, 216804. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamirzaev, T.S.; Shumilin, A.V.; Smirnov, D.S.; Kudlacik, D.; Nekrasov, S.V.; Kusrayev, Y.G.; Yakovlev, D.R.; Bayer, M. Optical Orientation of Excitons in a Longitudinal Magnetic Field in Indirect-Band-Gap (In,Al)As/AlAs Quantum Dots with Type-I Band Alignment. Nanomaterials 2023, 13, 729. https://doi.org/10.3390/nano13040729
Shamirzaev TS, Shumilin AV, Smirnov DS, Kudlacik D, Nekrasov SV, Kusrayev YG, Yakovlev DR, Bayer M. Optical Orientation of Excitons in a Longitudinal Magnetic Field in Indirect-Band-Gap (In,Al)As/AlAs Quantum Dots with Type-I Band Alignment. Nanomaterials. 2023; 13(4):729. https://doi.org/10.3390/nano13040729
Chicago/Turabian StyleShamirzaev, T. S., A. V. Shumilin, D. S. Smirnov, D. Kudlacik, S. V. Nekrasov, Yu G. Kusrayev, D. R. Yakovlev, and M. Bayer. 2023. "Optical Orientation of Excitons in a Longitudinal Magnetic Field in Indirect-Band-Gap (In,Al)As/AlAs Quantum Dots with Type-I Band Alignment" Nanomaterials 13, no. 4: 729. https://doi.org/10.3390/nano13040729
APA StyleShamirzaev, T. S., Shumilin, A. V., Smirnov, D. S., Kudlacik, D., Nekrasov, S. V., Kusrayev, Y. G., Yakovlev, D. R., & Bayer, M. (2023). Optical Orientation of Excitons in a Longitudinal Magnetic Field in Indirect-Band-Gap (In,Al)As/AlAs Quantum Dots with Type-I Band Alignment. Nanomaterials, 13(4), 729. https://doi.org/10.3390/nano13040729





