Effect of Confinement and Coulomb Interactions on the Electronic Structure of the (111) LaAlO3/SrTiO3 Interface
Abstract
1. Introduction
2. Methods and Results
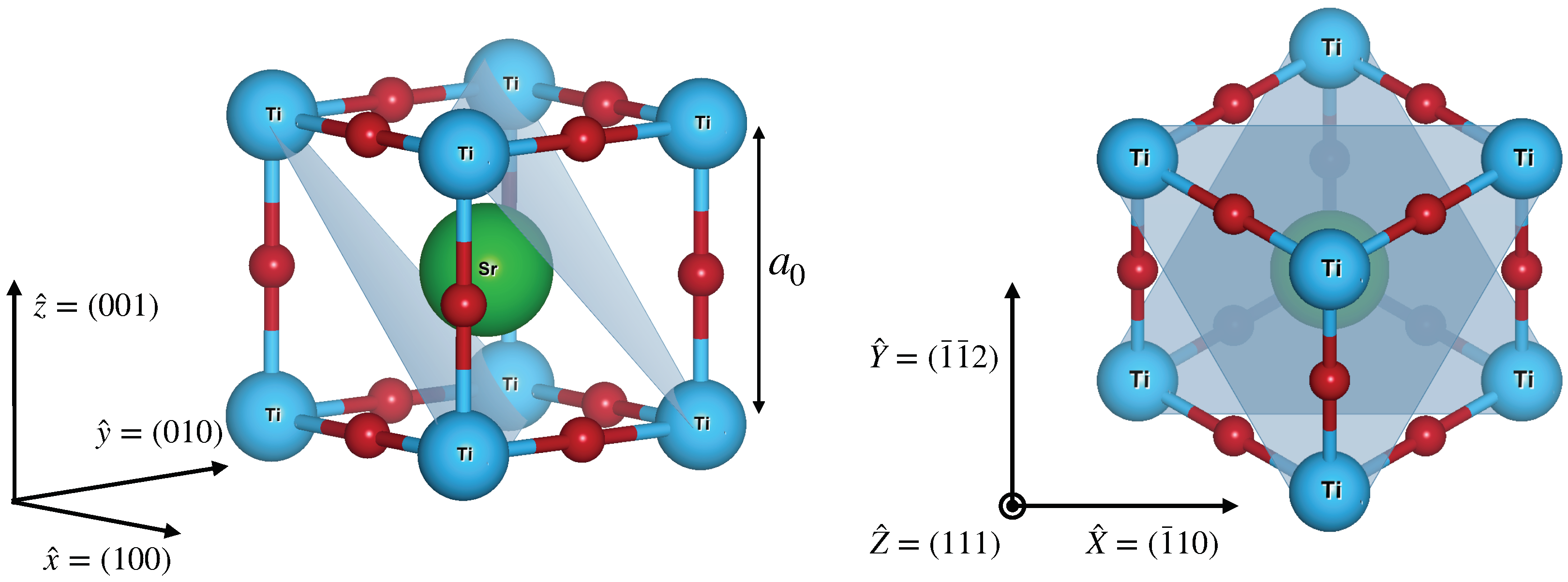
2.1. Model
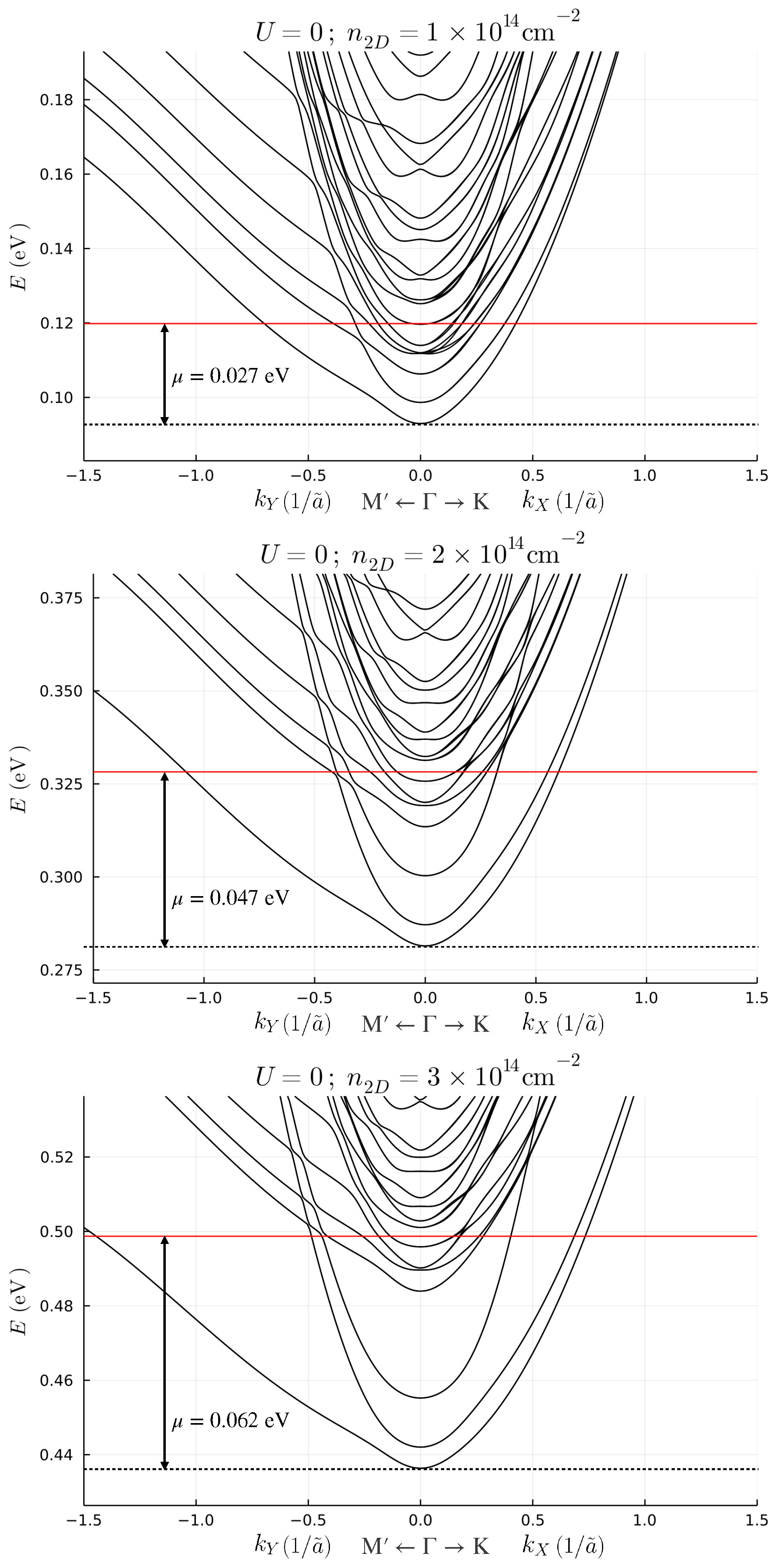
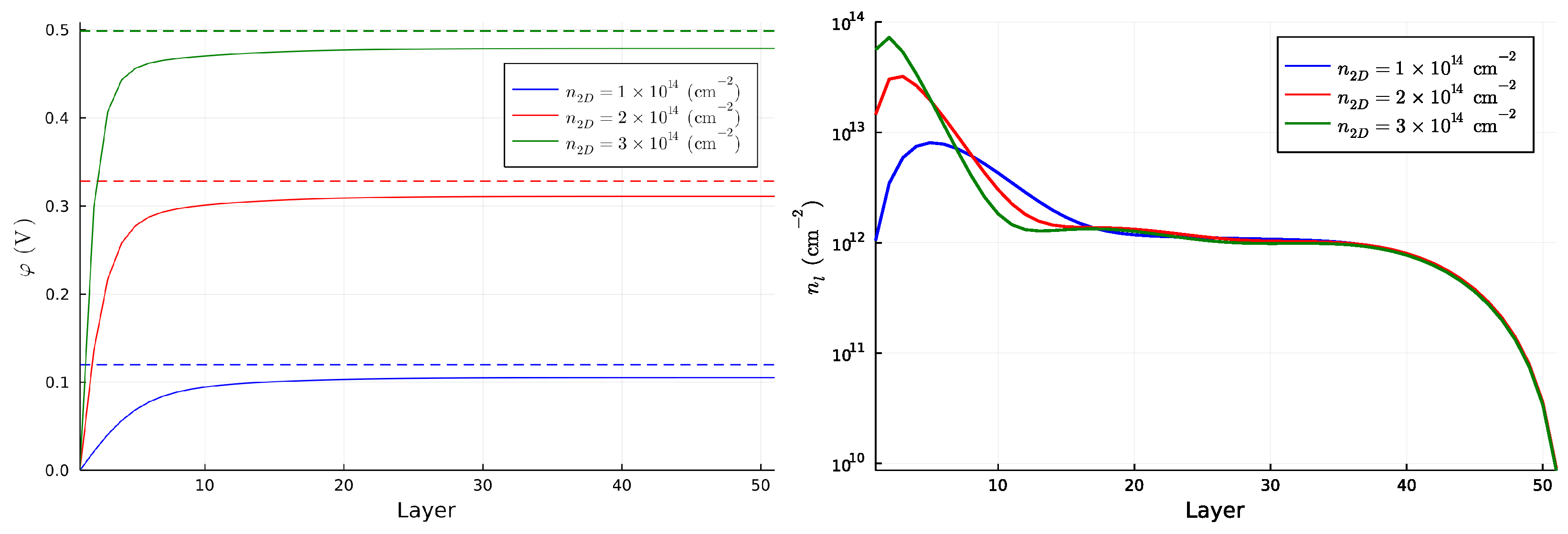
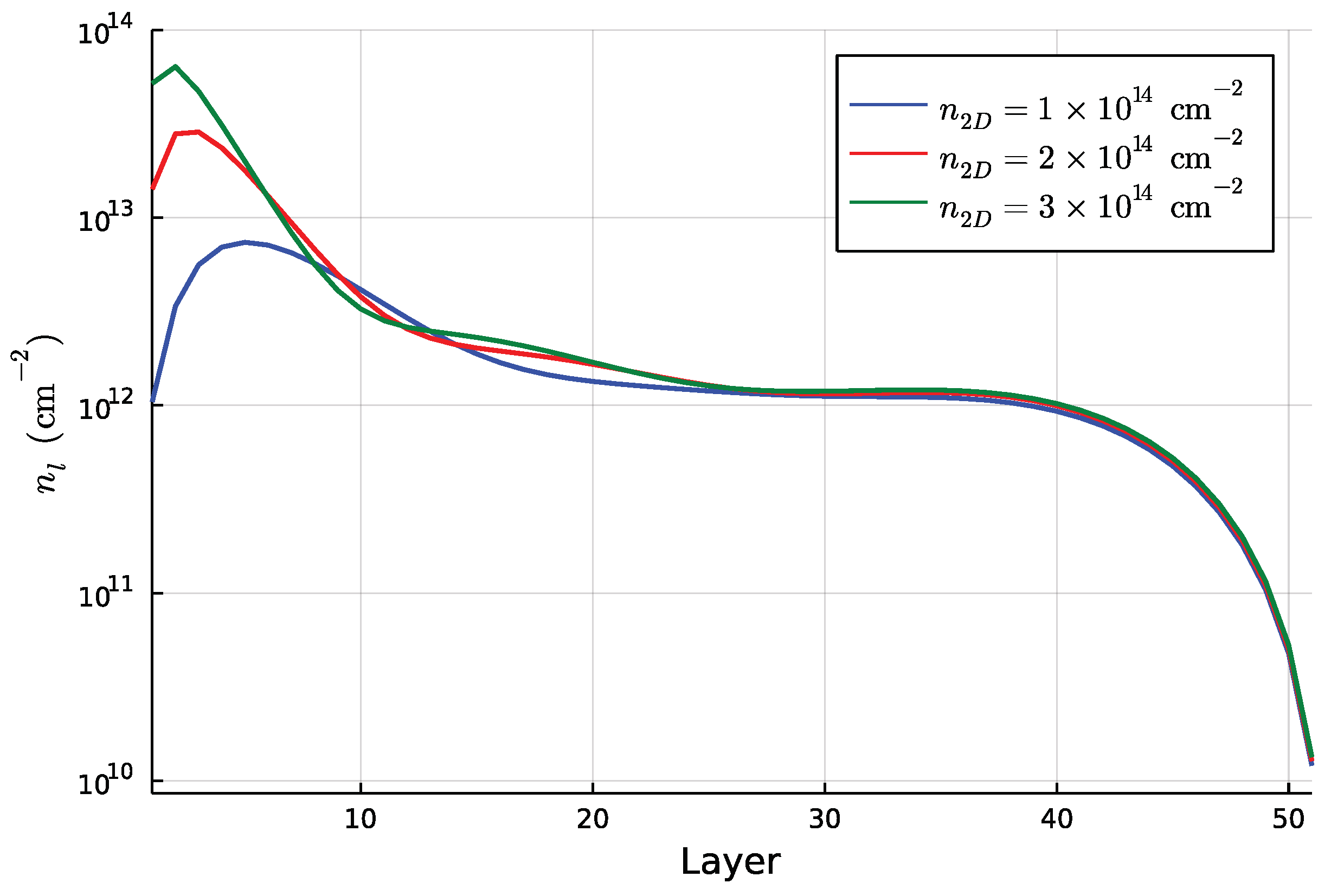
2.2. Results in the Absence of Local Hubbard Interaction Terms
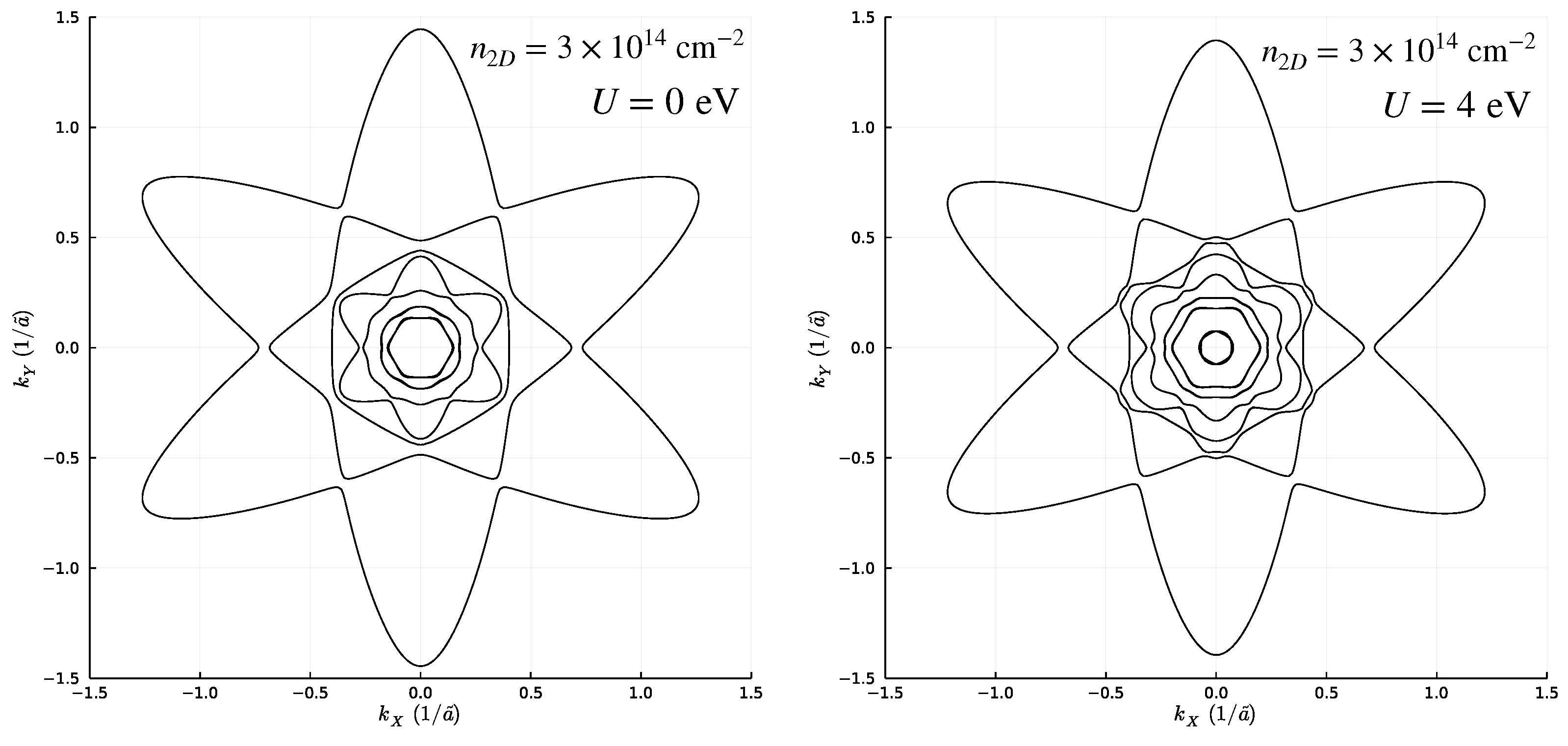
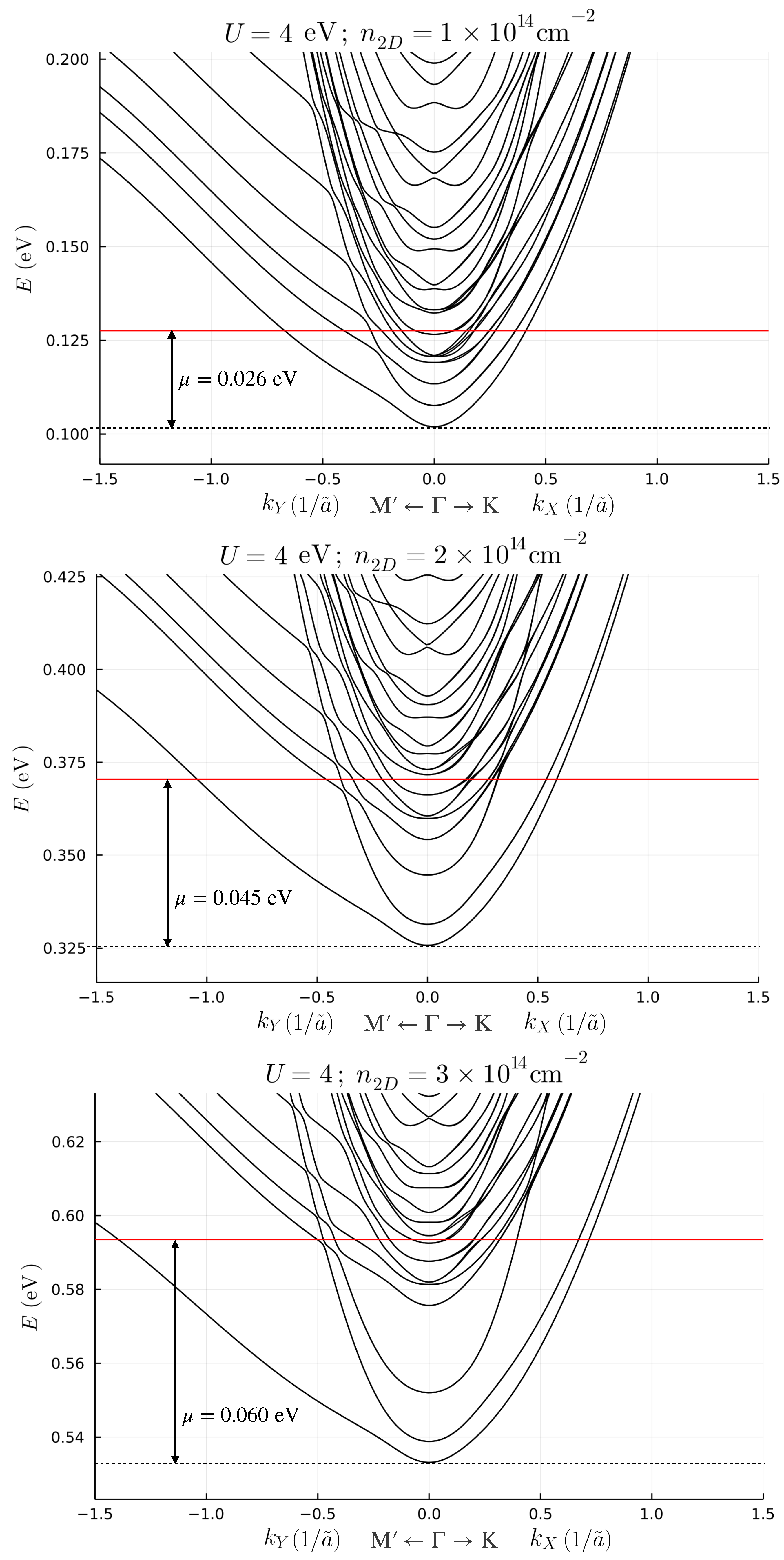
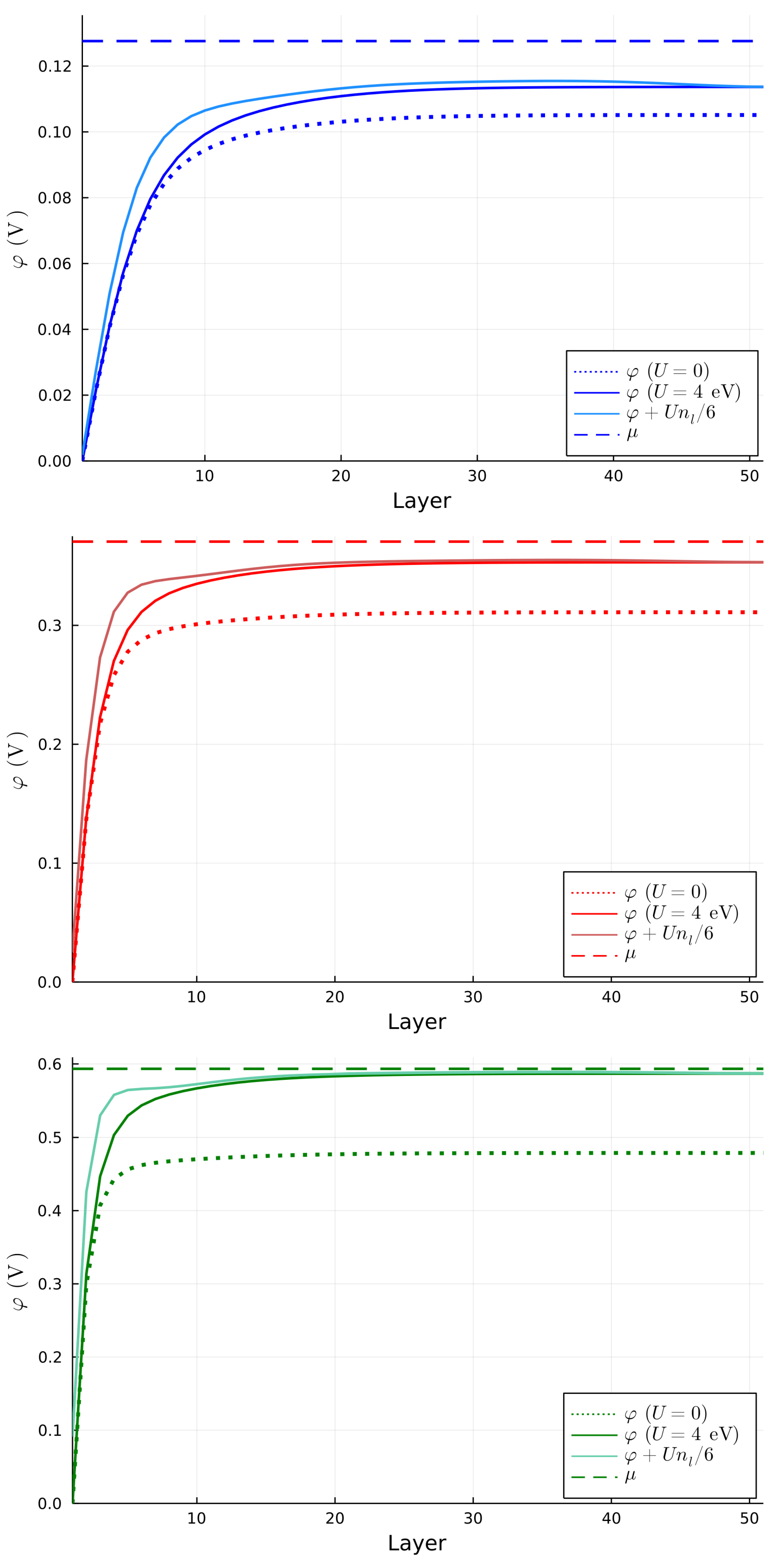
2.3. Effect of Local Hubbard Interaction Terms
3. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SOC | spin–orbit coupling |
| 2DEG | two-dimensional electronic gas |
| STO | SrTiO |
| LAO | LaAlO |
| TB | tight binding |
| FS | Fermi surface |
| ARPES | angle-resolved photoemission spectroscopy |
Appendix A. Model
Appendix A.1. Tight-Binding Supercell Hamiltonian
Appendix A.2. Poisson–Schrödinger Approximation
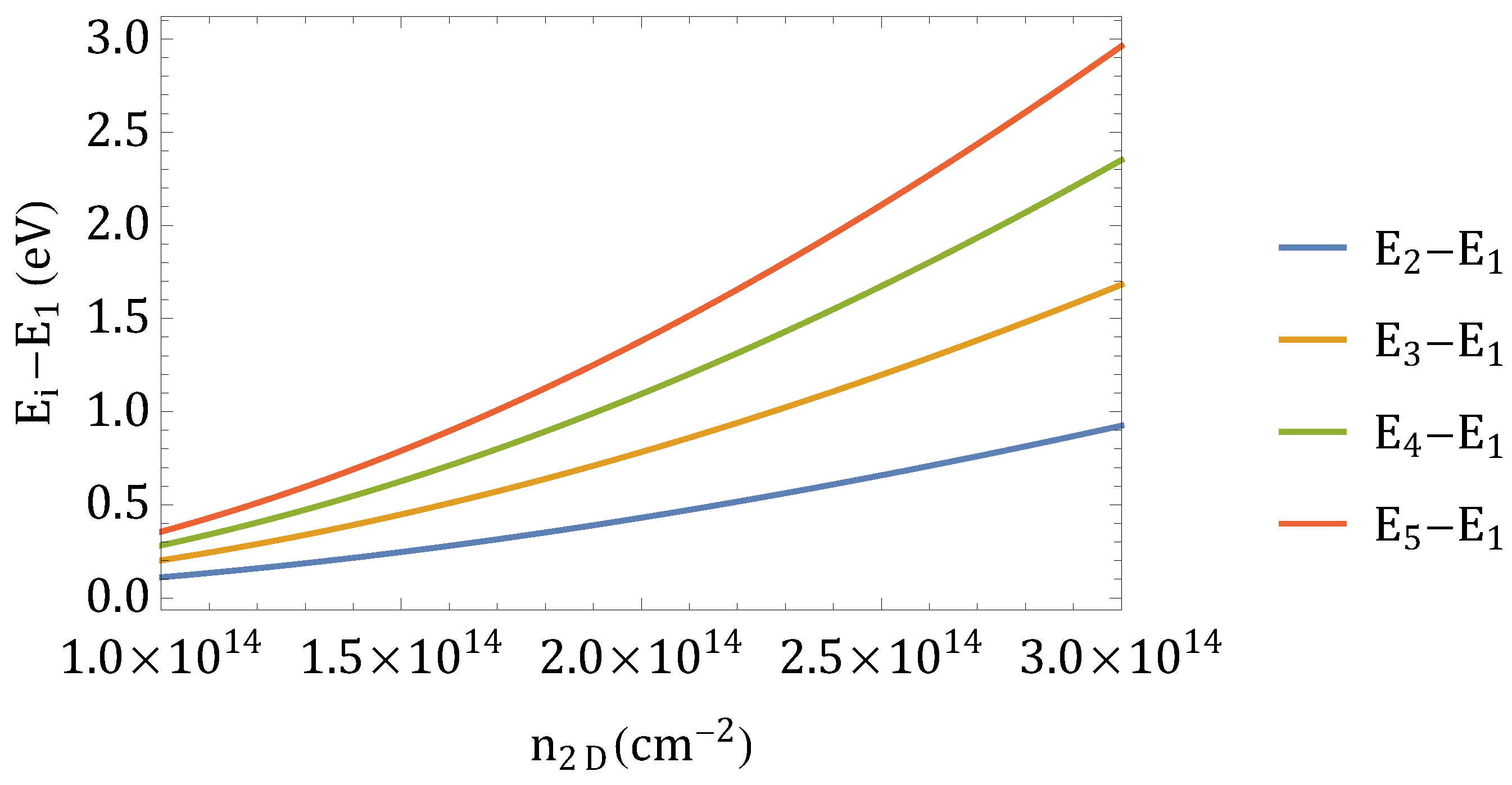
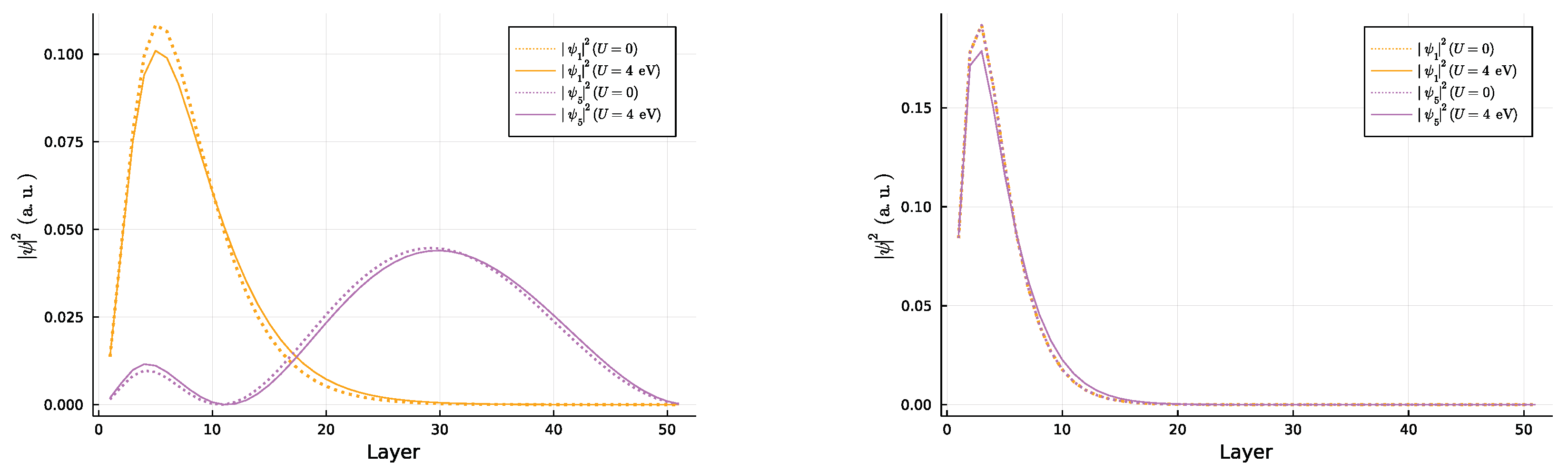
Appendix B. Sub-Set Band Behaviour
References
- Ohtomo, A.; Hwang, H. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 2004, 427, 423–426. [Google Scholar] [CrossRef]
- Caviglia, A.; Gariglio, S.; Reyren, N.; Jaccard, D.; Schneider, T.; Gabay, M.; Thiel, S.; Hammerl, G.; Mannhart, J.; Triscone, J.M. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 2008, 456, 624–627. [Google Scholar] [CrossRef]
- Reyren, N.; Thiel, S.; Caviglia, A.; Kourkoutis, L.F.; Hammerl, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Rüetschi, A.S.; Jaccard, D.; et al. Superconducting interfaces between insulating oxides. Science 2007, 317, 1196–1199. [Google Scholar] [CrossRef]
- Perroni, C.A.; Cataudella, V.; Salluzzo, M.; Cuoco, M.; Citro, R. Evolution of topological superconductivity by orbital-selective confinement in oxide nanowires. Phys. Rev. B 2019, 100, 094526. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Perroni, C.A.; Cataudella, V.; Citro, R. Unveiling signatures of topological phases in open Kitaev chains and ladders. Nanomaterials 2019, 9, 894. [Google Scholar] [CrossRef] [PubMed]
- Barthelemy, A.; Bergeal, N.; Bibes, M.; Caviglia, A.; Citro, R.; Cuoco, M.; Kalaboukhov, A.; Kalisky, B.; Perroni, C.A.; Santamaria, J.; et al. Quasi-two-dimensional electron gas at the oxide interfaces for topological quantum physics. Europhys. Lett. 2021, 133, 17001. [Google Scholar] [CrossRef]
- Davis, S.; Huang, Z.; Han, K.; Venkatesan, T.; Chandrasekhar, V. Anisotropic superconductivity and frozen electronic states at the (111) LaAlO3/SrTiO3 interface. Phys. Rev. B 2018, 98, 024504. [Google Scholar] [CrossRef]
- Monteiro, A.; Vivek, M.; Groenendijk, D.; Bruneel, P.; Leermakers, I.; Zeitler, U.; Gabay, M.; Caviglia, A. Band inversion driven by electronic correlations at the (111) LaAlO3/SrTiO3 interface. Phys. Rev. B 2019, 99, 201102. [Google Scholar] [CrossRef]
- Trama, M.; Cataudella, V.; Perroni, C.A. Strain-induced topological phase transition at (111) SrTiO3-based heterostructures. Phys. Rev. Res. 2021, 3, 043038. [Google Scholar] [CrossRef]
- Trama, M.; Cataudella, V.; Perroni, C.A.; Romeo, F.; Citro, R. Gate tunable anomalous Hall effect: Berry curvature probe at oxides interfaces. Phys. Rev. B 2022, 106, 075430. [Google Scholar] [CrossRef]
- Trama, M.; Cataudella, V.; Perroni, C.A.; Romeo, F.; Citro, R. Tunable Spin and Orbital Edelstein Effect at (111) LaAlO3/SrTiO3 Interface. Nanomaterials 2022, 12, 2494. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.M.; De La Torre, A.; Bruno, F.Y.; Tamai, A.; Kim, T.; Hoesch, M.; Shi, M.; Bahramy, M.; King, P.; Baumberger, F. Control of a two-dimensional electron gas on SrTiO3 (111) by atomic oxygen. Phys. Rev. Lett. 2014, 113, 177601. [Google Scholar] [CrossRef] [PubMed]
- King, P.; Mckeown Walker, S.; Tamai, A.; De La Torre, A.; Eknapakul, T.; Buaphet, P.; Mo, S.K.; Meevasana, W.; Bahramy, M.; Baumberger, F. Quasiparticle dynamics and spin–orbital texture of the SrTiO3 two-dimensional electron gas. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Bahramy, M.; King, P.; De La Torre, A.; Chang, J.; Shi, M.; Patthey, L.; Balakrishnan, G.; Hofmann, P.; Arita, R.; Nagaosa, N.; et al. Emergent quantum confinement at topological insulator surfaces. Nat. Commun. 2012, 3, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Reich, K.; Schecter, M.; Shklovskii, B. Accumulation, inversion, and depletion layers in SrTiO3. Phys. Rev. B 2015, 91, 115303. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Pai, Y.Y.; Tylan-Tyler, A.; Irvin, P.; Levy, J. Physics of SrTiO3-based heterostructures and nanostructures: A review. Rep. Prog. Phys. 2018, 81, 036503. [Google Scholar] [CrossRef]
- Xiao, D.; Zhu, W.; Ran, Y.; Nagaosa, N.; Okamoto, S. Interface engineering of quantum Hall effects in digital transition metal oxide heterostructures. Nat. Commun. 2011, 2, 1–8. [Google Scholar] [CrossRef]
- Bruneel, P. Electronic and Spintronic Properties of the Interfaces between Transition Metal Oxides. Ph.D. Thesis, Université Paris-Saclay, Gif-sur-Yvette, France, 2020. [Google Scholar]
- Neville, R.; Hoeneisen, B.; Mead, C. Permittivity of strontium titanate. J. Appl. Phys. 1972, 43, 2124–2131. [Google Scholar] [CrossRef]
- Dunitz, J.; Orgel, L. Electronic properties of transition-metal oxides-II: Cation distribution amongst octahedral and tetrahedral sites. J. Phys. Chem. Solids 1957, 3, 318–323. [Google Scholar] [CrossRef]
- Barrett, J.H. Dielectric Constant in Perovskite Type Crystals. Phys. Rev. 1952, 86, 118–120. [Google Scholar] [CrossRef]
- Delugas, P.; Filippetti, A.; Fiorentini, V.; Bilc, D.I.; Fontaine, D.; Ghosez, P. Spontaneous 2-dimensional carrier confinement at the n-type SrTiO3/LaAlO3 interface. Phys. Rev. Lett. 2011, 106, 166807. [Google Scholar] [CrossRef] [PubMed]
- Khomskii, D. Transition Metal Compounds; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- De Luca, G.; Di Capua, R.; Di Gennaro, E.; Sambri, A.; Granozio, F.M.; Ghiringhelli, G.; Betto, D.; Piamonteze, C.; Brookes, N.; Salluzzo, M. Symmetry breaking at the (111) interfaces of SrTiO3 hosting a two-dimensional electron system. Phys. Rev. B 2018, 98, 115143. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trama, M.; Cataudella, V.; Perroni, C.A.; Romeo, F.; Citro, R. Effect of Confinement and Coulomb Interactions on the Electronic Structure of the (111) LaAlO3/SrTiO3 Interface. Nanomaterials 2023, 13, 819. https://doi.org/10.3390/nano13050819
Trama M, Cataudella V, Perroni CA, Romeo F, Citro R. Effect of Confinement and Coulomb Interactions on the Electronic Structure of the (111) LaAlO3/SrTiO3 Interface. Nanomaterials. 2023; 13(5):819. https://doi.org/10.3390/nano13050819
Chicago/Turabian StyleTrama, Mattia, Vittorio Cataudella, Carmine Antonio Perroni, Francesco Romeo, and Roberta Citro. 2023. "Effect of Confinement and Coulomb Interactions on the Electronic Structure of the (111) LaAlO3/SrTiO3 Interface" Nanomaterials 13, no. 5: 819. https://doi.org/10.3390/nano13050819
APA StyleTrama, M., Cataudella, V., Perroni, C. A., Romeo, F., & Citro, R. (2023). Effect of Confinement and Coulomb Interactions on the Electronic Structure of the (111) LaAlO3/SrTiO3 Interface. Nanomaterials, 13(5), 819. https://doi.org/10.3390/nano13050819






