Probing the Boundary between Classical and Quantum Mechanics by Analyzing the Energy Dependence of Single-Electron Scattering Events at the Nanoscale
Abstract
:1. Introduction
2. Materials and Methods
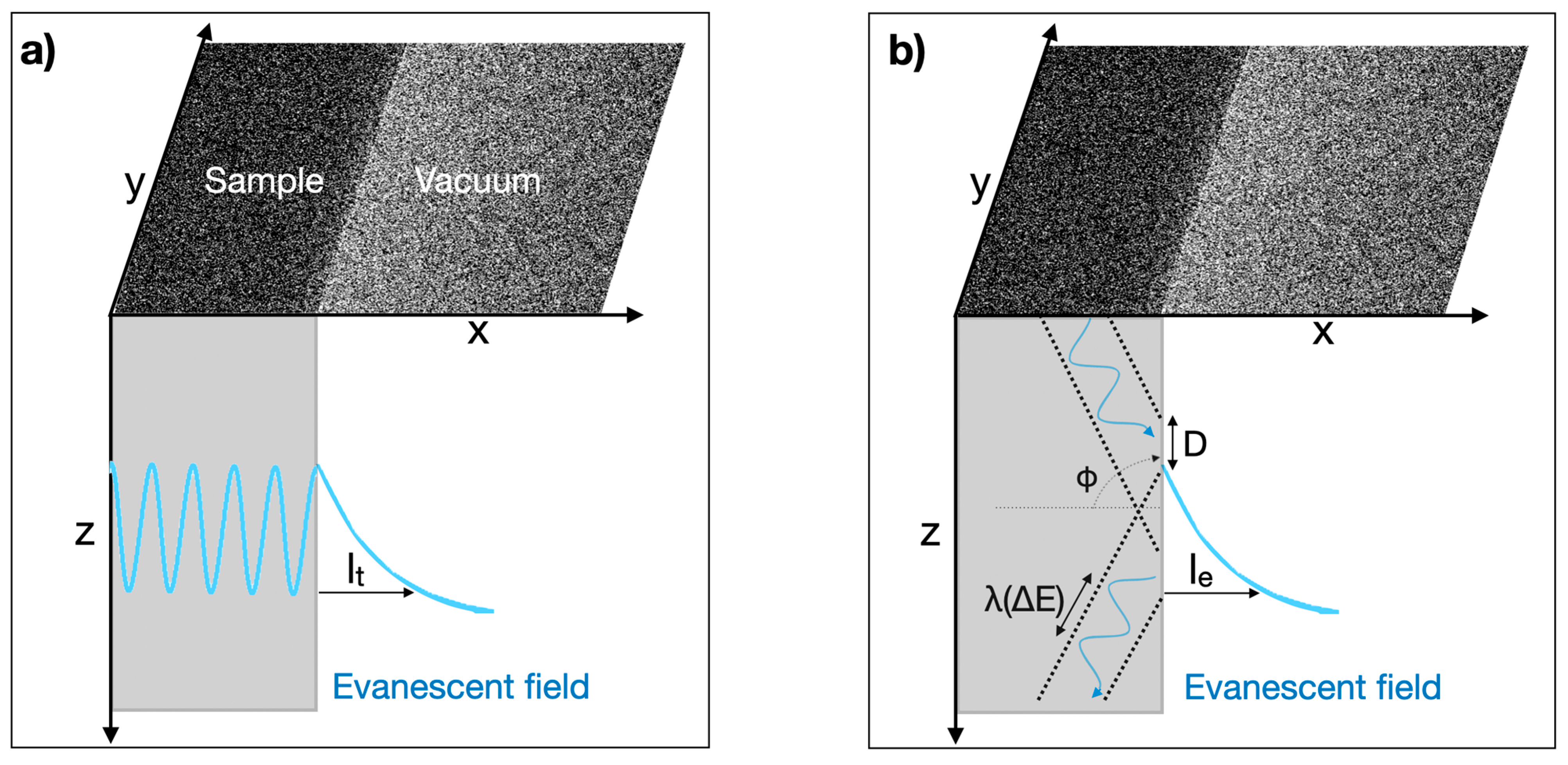
2.1. Measurement Principle
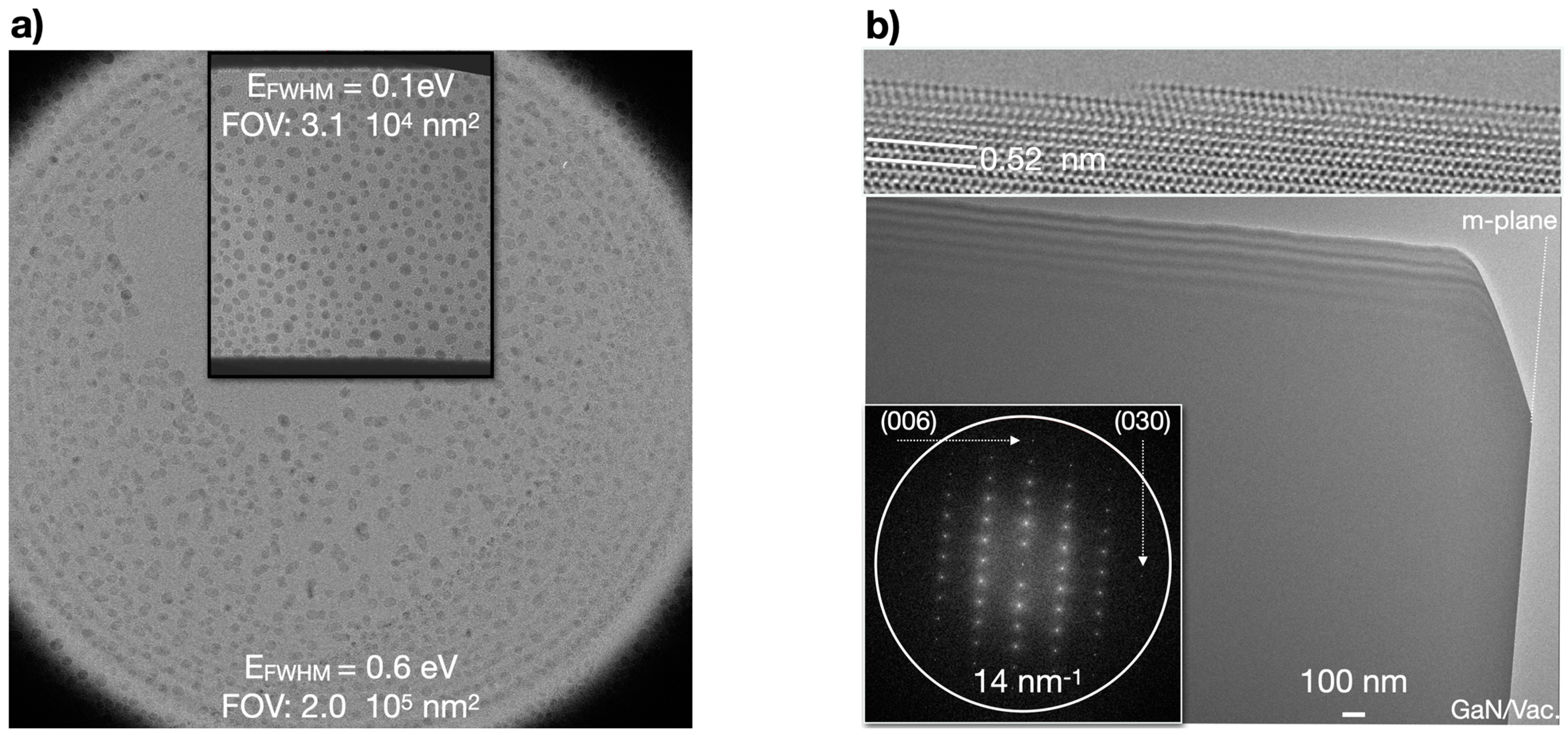
2.2. Aberration-Corrected, Energy-Filtered Amplitude Imaging with Single-Electron Detection
2.3. Materials and Methods
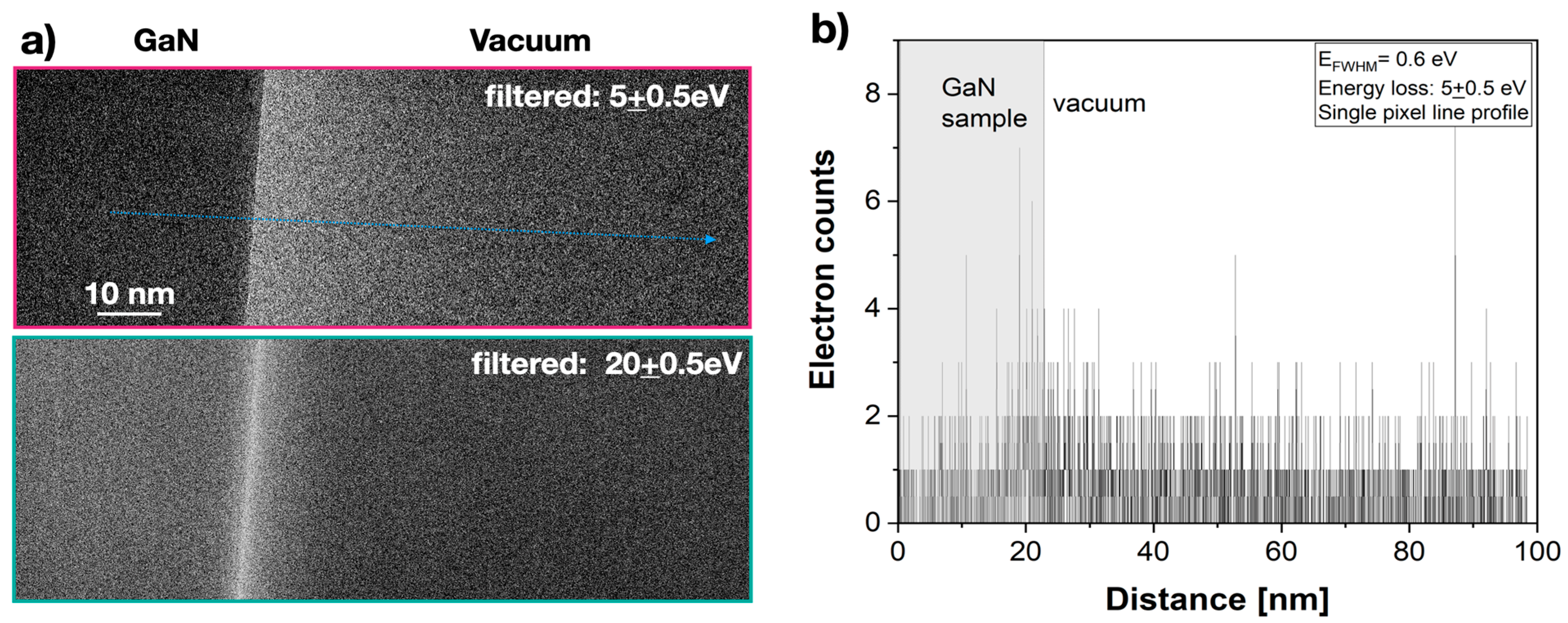
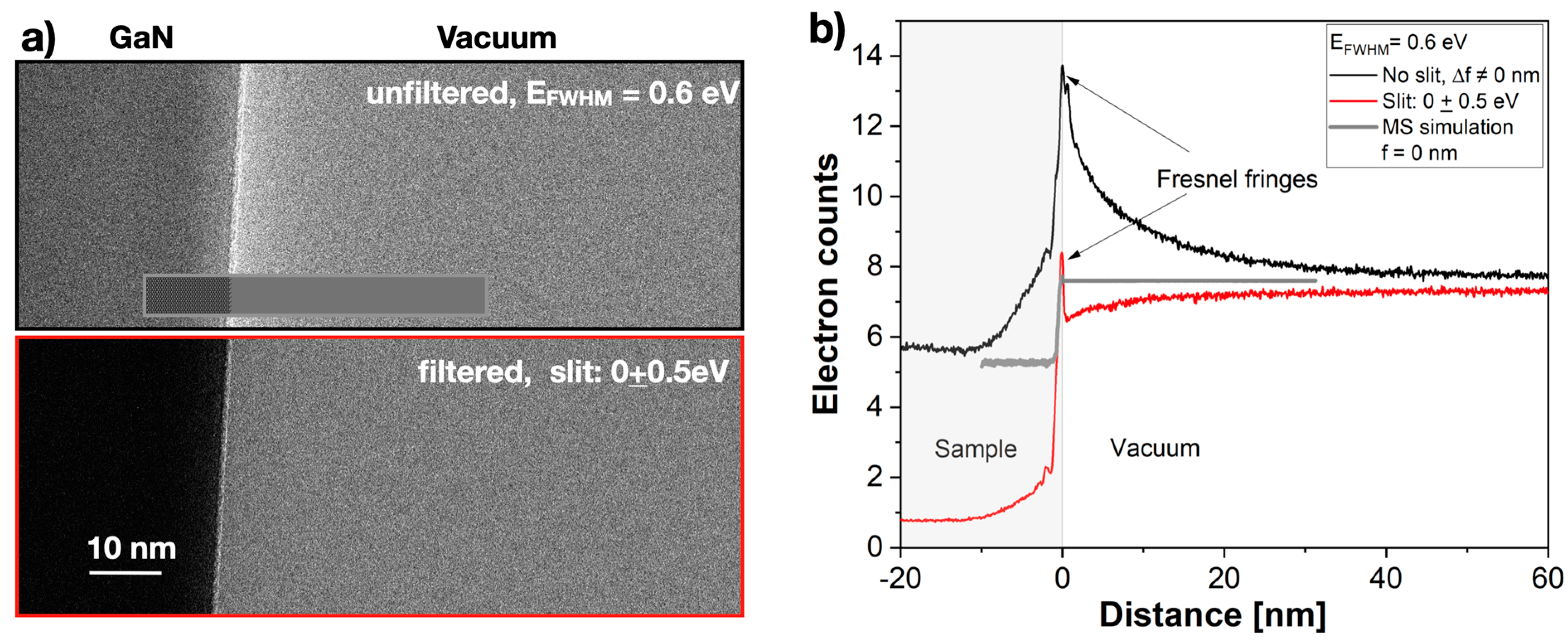
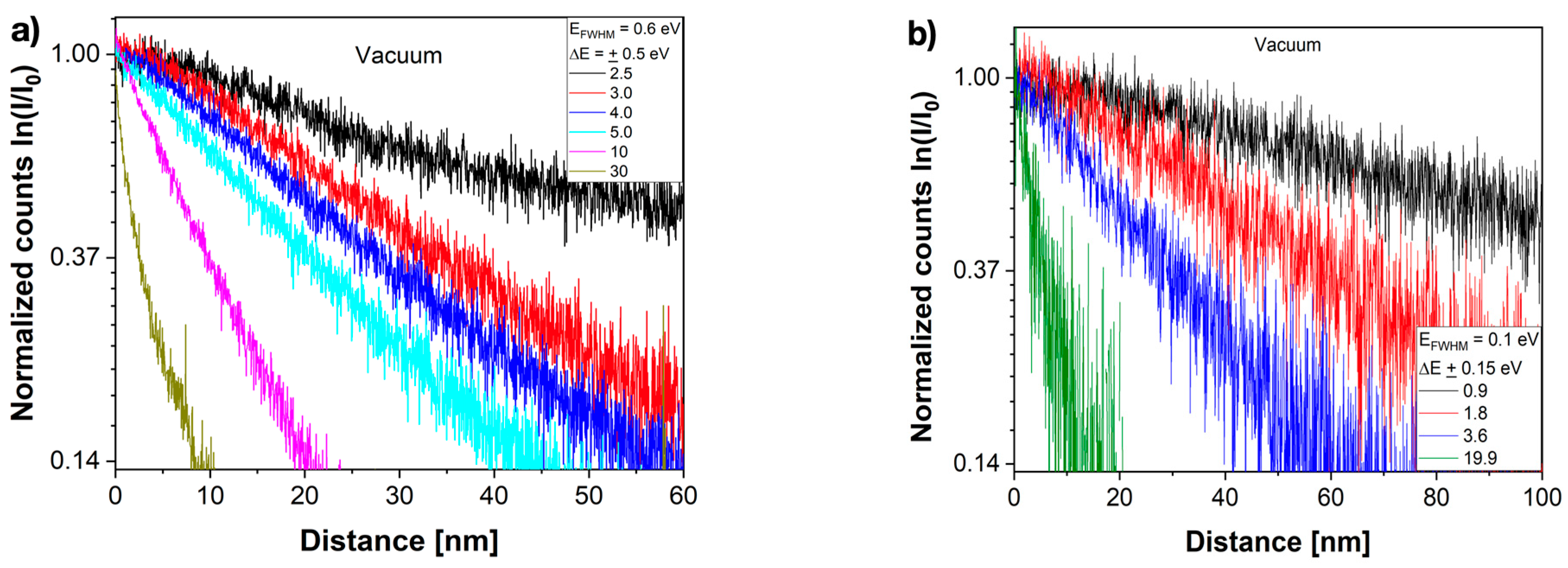
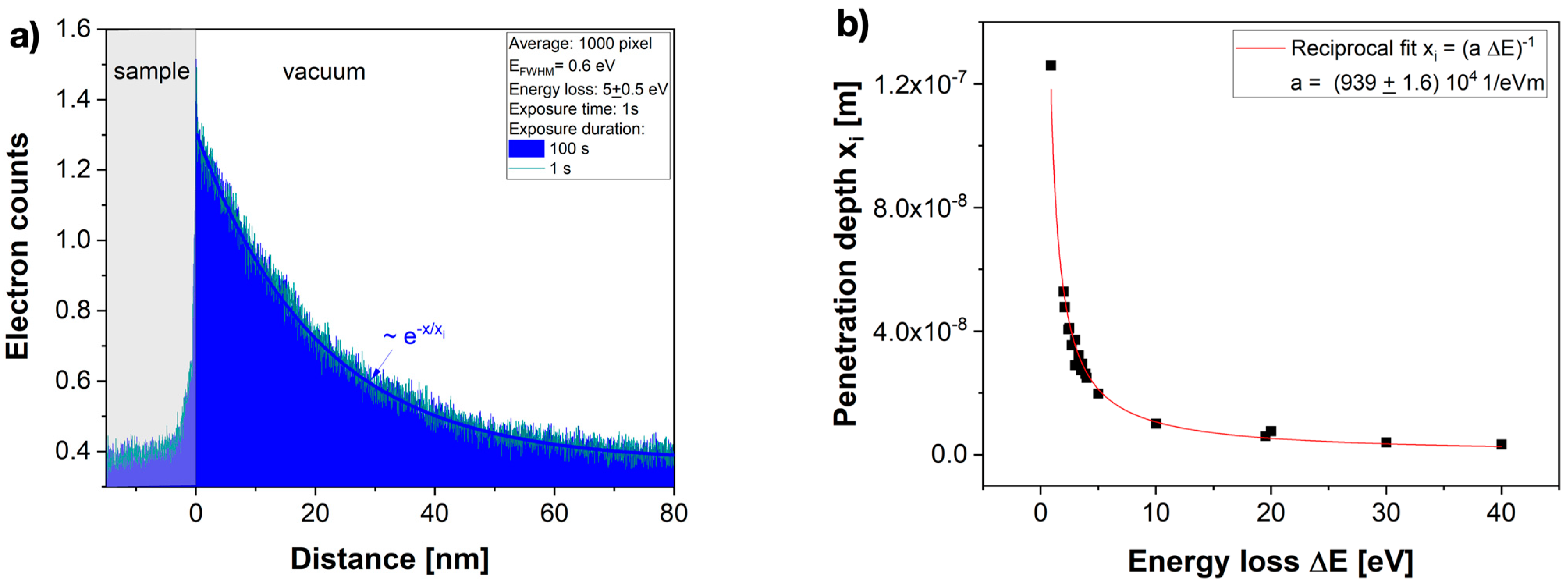
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carter, C.B.; Williams, D.B. (Eds.) Transmission Electron Microscopy, Diffraction, Imaging, Spectroscopy; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Erni, R.; Rossell, M.D.; Kisielowski, C.; Dahmen, U. Atomic-Resolution Imaging with a Sub-50-pm Electron Probe. Phys. Rev. Lett. 2009, 102, 096101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cowley, J.M.; Moodie, A.F. Scattering of electrons by atoms and crystals. I. A new theoretical approach. Acta Cryst. 1957, 10, 609–619. [Google Scholar] [CrossRef]
- Lobato, I.; Van Dyck, D. MULTEM: A new multislice program to perform accurate and fast electron diffraction and imaging simulations using Graphics Processing Units with CUDA. Ultramicroscopy 2015, 156, 9–17. [Google Scholar] [CrossRef]
- Kilaas, R. Available online: https://totalresolution.com/ (accessed on 3 March 2023).
- Zewail, A.H. Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond. J. Phys. Chem. A 2000, 104, 5660–5694. [Google Scholar] [CrossRef]
- Flannigan, D.J.; Zewail, A.H. 4D electron microscopy: Principles and applications. Acc. Chem. Res. 2012, 45, 1828–1839. [Google Scholar] [CrossRef]
- Kisielowski, C.; Specht, P.; Freitag, B.; Kieft, E.R.; Verhoeven, W.; van Rens, J.F.M.; Mutsaers, P.; Luiten, J.; Rozeveld, S.; Kang, J.; et al. Discovering Hidden Material Properties of MgCl2 at Atomic Resolution with Structured Temporal Electron Illumination of Picosecond Time Resolution. Adv. Func. Mater. 2019, 29, 1807818. [Google Scholar] [CrossRef]
- Chen, F.-R.; Van Dyck, D.; Kisielowski, C.; Lars, P.; Hansen, L.P.; Barton, B.; Helveg, S. Probing atom dynamics of excited Co-Mo-S nanocrystals in 3D. Nat. Commun. 2021, 12, 5005. [Google Scholar]
- Schattschneider, P.; Löffler, S. Entanglement and decoherence in electron microscopy. Ultramicroscopy 2018, 190, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Kruit, P.; Hobbs, R.G.; Kim, C.-S.; Yang, Y.; Manfriando, V.R.; Hammer, J.; Thomas, S.; Weber, P.; Klopfer, B.; Kohstall, C.; et al. Designs for a quantum electron microscope. Ultramicroscopy 2016, 164, 31–45. [Google Scholar] [CrossRef] [Green Version]
- Kisielowski, C.; Specht, P.; Rozeveld, S.; Kang, J.; Fielitz, A.J.; Barton, D.; Salazar, A.C.; Dubon, O.D.; Van Dyck, D.; Yancey, D.F. Modulating electron beam–sample interactions in imaging and diffraction modes by dose fractionation with low dose rates. Microsc. Microanal. 2021, 27, 1420–1430. [Google Scholar] [CrossRef]
- Bohr, N. Atomic Physics and Human Knowledge; Wiley: New York, NY, USA, 1958. [Google Scholar]
- Hopson, A. There are no particles, there are only fields. Am. J. Phys. 2013, 81, 211. [Google Scholar] [CrossRef] [Green Version]
- Van Dyck, D.; Lichte, H.; Spence, J.C.H. Inelastic scattering and holography. Ultramicroscopy 2000, 81, 187–194. [Google Scholar] [CrossRef]
- Haider, M.; Hartel, P.; Müller, H.; Uhlemann, S.; Zach, J. Information transfer in a TEM corrected for spherical and chromatic aberration. Microsc. Microanal. 2010, 16, 393–408. [Google Scholar] [CrossRef] [PubMed]
- Kisielowski, C.; Specht, P.; Rozeveld, S.; Freitag, B.; Kieft, E.R.; Kang, J.; Fielitz, A.J.; Fielitz, T.R.; Van Dyck, D.; Yancey, D.F. Exploring Functional Materials by Understanding Beam-Sample Interactions. Adv. Func. Mat. 2022, 32, 2201112. [Google Scholar] [CrossRef]
- Binning, G.; Rohrer, H.; Gerber, C.; Weibel, E. Surface studies by scanning tunneling microscopy. Phys. Rev. Lett. 1982, 49, 57–61. [Google Scholar] [CrossRef] [Green Version]
- Goos, F.; Hänchen, H. Ein neuer und fundamentaler Versuch zur Totalreflexion. Ann. Phys. 1947, 436, 333–346. [Google Scholar] [CrossRef] [Green Version]
- Salomon, L.; De Fornel, F.; Goudonne, J.P. Sample-tip coupling efficiencies of the photon-scanning tunneling microscope. J. Opt. Soc. Am. A 1991, 8, 2009–2015. [Google Scholar] [CrossRef]
- Ahmad, M.; Hench, L.L. Effect of taper geometries and launch angle on evanescent wave penetration depth in optical fibers. Biosens. Bioelectron. 2005, 20, 1312–1319. [Google Scholar] [CrossRef]
- Renard, R.H. Total Reflection: A New Evaluation of the Goos-Hänchen Shift. J. Opt. Soc. Am. 1964, 54, 1190–1197. [Google Scholar] [CrossRef]
- Gardo-Caffaro, M.A.; Gardo-Caffaro, M. Refractive index and material dispersion in relativistic electron optics. Optik 2005, 116, 551–552. [Google Scholar] [CrossRef]
- Dahmen, U.; Erni, R.; Radmilovic, V.; Kisielowski, C.; Rossell, M.-D.; Denes, P. Background, status and future of the Transmission Electron Aberration-corrected Microscope project. Philos. Transact. Royal Soc. 2009, 367, 3795–3808. [Google Scholar]
- Ritchie, R.H.; Howie, A. Electron excitation and optical potential in electron microscopy. Philos. Mag. A 1977, 36, 463–481. [Google Scholar] [CrossRef]
- Kociak, M.; Stephan, O. Mapping plasmons at the nanometer scale in an electron microscope. Chem. Soc. Rev. 2014, 43, 3865–3883. [Google Scholar] [CrossRef]
- Rez, P.; Aoki, T.; March, K.; Gur, D.; Krivanek, O.L.; Dellby, N.; Lovejoy, T.C.; Wolf, S.G.; Cohen, H. Damage-free vibrational spectroscopy of biological materials in the electron microscope. Nat. Commun. 2016, 7, 10945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hage, F.S.; Kepaptsoglou, D.M.; Ramasse, Q.M.; Allen, L.J. Phonon Spectroscopy at Atomic Resolution. Phys. Rev. Lett. 2019, 122, 016103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rezikyan, A.; Jibben, Z.J.; Rock, B.A.; Zhao, G.; Koeck, F.A.M.; Nemanich, R.F.; Treacy, M.M.J. Speckle suppression by decoherence in fluctuation electron microscopy. Microsc. Microanal. 2015, 21, 1455–1474. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, J.; Zhu, F.; Yuan, Y.; Chang, D.J.; Kim, D.S.; Pham, M.; Rana, A.; Tian, X.; Yao, Y.; et al. Determining the three-dimensional atomic structure of an amorphous solid. Nature 2021, 592, 60–64. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, Y.; Shao, Y.-T.; Holtz, M.H.; Odstrcil, M.; Guizar-Sicairos, M.; Hanke, I.; Ganschow, S.; Schlom, D.G.; Muller, D.A. Electron ptychograph achieves atomic-resolution limits set by lattice vibrations. Science 2021, 372, 826–831. [Google Scholar] [CrossRef]
- Tang, W.; Yang, T.; Cristian, A.; Morales-Rivera, C.A.; Geng, X.; Srirambhatla, V.K.; Kang, X.; Chauhan, V.P.; Hong, S.; Tu, Q.; et al. Tautomerism unveils a self-inhibition mechanism of crystallization. Nat. Commun. 2023, 14, 561. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kisielowski, C.; Specht, P.; Helveg, S.; Chen, F.-R.; Freitag, B.; Jinschek, J.; Van Dyck, D. Probing the Boundary between Classical and Quantum Mechanics by Analyzing the Energy Dependence of Single-Electron Scattering Events at the Nanoscale. Nanomaterials 2023, 13, 971. https://doi.org/10.3390/nano13060971
Kisielowski C, Specht P, Helveg S, Chen F-R, Freitag B, Jinschek J, Van Dyck D. Probing the Boundary between Classical and Quantum Mechanics by Analyzing the Energy Dependence of Single-Electron Scattering Events at the Nanoscale. Nanomaterials. 2023; 13(6):971. https://doi.org/10.3390/nano13060971
Chicago/Turabian StyleKisielowski, Christian, Petra Specht, Stig Helveg, Fu-Rong Chen, Bert Freitag, Joerg Jinschek, and Dirk Van Dyck. 2023. "Probing the Boundary between Classical and Quantum Mechanics by Analyzing the Energy Dependence of Single-Electron Scattering Events at the Nanoscale" Nanomaterials 13, no. 6: 971. https://doi.org/10.3390/nano13060971




