Next Article in Journal
Glycerol Electro-Oxidation in Alkaline Medium with Pt-Fe/C Electrocatalysts Synthesized by the Polyol Method: Increased Selectivity and Activity Provided by Less Expensive Catalysts
Next Article in Special Issue
Remanence Increase in SrFe12O19/Fe Exchange-Decoupled Hard-Soft Composite Magnets Owing to Dipolar Interactions
Previous Article in Journal
Controlled Synthesis and Enhanced Gas Sensing Performance of Zinc-Doped Indium Oxide Nanowires
Previous Article in Special Issue
Magnetoresistive Properties of Nanocomposites Based on Ferrite Nanoparticles and Polythiophene
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Nanomaterials
Volume 13
Issue 7
10.3390/nano13071172
nanomaterials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Exploring Spin-Phonon Coupling in Magnetic 2D Metal-Organic Frameworks

by
Diego López-Alcalá
,
Alberto M. Ruiz
and
José J. Baldoví
*
Instituto de Ciencia Molecular, Universitat de València, 46980 Paterna, Spain
*
Author to whom correspondence should be addressed.
Nanomaterials 2023, 13(7), 1172; https://doi.org/10.3390/nano13071172
Submission received: 10 March 2023 / Revised: 22 March 2023 / Accepted: 23 March 2023 / Published: 25 March 2023
(This article belongs to the Special Issue Hybrid Magnetic Nanomaterials)
Browse Figures
Versions Notes

Abstract

:
Layered magnetic metal-organic frameworks (MOFs) are an emerging class of materials that can combine the advantages of both MOFs and 2D magnetic crystals. The recent discovery of large coercivity and long-range magnetic ordering up to 515 K in a layered MOF of general formula MCl2(pyz)2 (M = transition metal, pyz = pyrazine) offers an exciting versatile platform to achieve high-TC magnetism at the 2D limit. In this work, we investigate the exfoliation feasibility down to the monolayer of VCl2(pyz)2 and CrCl2(pyz)2 by means of first-principles calculations. We explore their structural, electronic, magnetic and vibrational properties, as well as the effect of halide substitution. Then, we provide a full analysis of the spin-phonon coupling (SPC) in both 2D derivatives. Our calculations reveal a low SPC and thermal evolution of the magnetic exchange interactions and single-ion anisotropy mainly governed by low-frequency phonon modes. Finally, we provide chemical insights to improve the performance of these magnetic 2D MOFs based on the effective manipulation of the phonon modes that can present a major impact on their magnetic properties.

1. Introduction

Metal-Organic Frameworks (MOFs) are emerging porous materials constructed by the interconnection of metal ions and organic linkers. This structural arrangement gives rise to highly versatile coordination compounds with a large variety of astonishing features such as structural, electronic and magnetic tunability, sizable porosity and the presence of very large surfaces [1,2,3]. Thanks to these features, MOFs have applications in a diverse set of fields, for example, gas separation [4], catalysis [5], drug delivery [6] and energy storage [7,8], among others. Importantly, the chemical nature of these crystalline frameworks results in their design à la carte, thus leading to the effective tailoring of the desired properties [9]. In addition, post-synthetic modification of their crystallographic coordinates by means of chemical reactivity provides an appealing route for a detailed fine-tuning of their electronic functionalities [10,11].
A particular class that is gaining increasing interest is that of the so-called MOF magnets [12,13]. Compared to classical magnetic materials, these systems present the advantages of MOFs, which allows the regulation of their structural, electronic, or magnetic properties via chemical modifications. This opens new avenues for their application as building blocks for emergent technologies such as spintronics [14] or magnonics [15]. Specifically, MOF magnets with open-shell organic linkers have been shown to display strong magnetic coupling between magnetic moments arising from the d orbitals of metal centers and radicals. This situation leads to ultra-high operative temperatures, e.g., TC = 400 K (V(TCNE)x where x ≈ 2) [16] or, more recently, TC = 515 K in a reduced chromium derivative of a family of coordination solids of general formula MCl2(pyz)2 (M = transition metal; pyz = pyrazine) [17,18,19]. This last example represents the highest ordering temperature exhibited for any bulk octahedrally coordinated metal ion, combined with large magnetic coercivity, and opens a wide range of possibilities to achieve higher critical temperatures.
Moreover, this family of MOF magnets is composed of electrically neutral magnetic layers that are exclusively stacked by van der Waals interactions. This enables the possibility of mechanical exfoliation to a few layers [20,21,22,23], allowing the combination in an atomically-thin material the advantages of both MOFs and 2D magnetic crystals [24,25]. Furthermore, the fast development of on-surface synthetic approaches creates a promising route to achieve a scalable fabrication process [26], whereas long-range magnetic order and electronic communication between the spin carriers in the system can be favored by chemical substitution [27,28]. The survival of long-range magnetic ordering in a limited-layer magnetic material is strongly dependent on the intrinsic spin-phonon coupling (SPC), which is responsible for the magnetic fluctuations and magnon dissipation [29]. However, the investigation of the effect of spin and lattice degrees of freedom in MOF magnets is still in its infancy and deserves to be tackled [30].
Here, we present a first-principles study based on density functional theory (DFT) of the Cr and V derivatives of the family of MCl2(pyz)2 neutral 2D layered MOFs. First, we determine the feasibility of the exfoliation of these nanomaterials, as well as the effects on the electronic structure when reducing the dimensionality of the system. Then, we substitute the Cl ligands for heavier halides, exploring a promising way to tune their electronic, structural and magnetic properties by means of chemical design. Finally, we systematically investigate the lattice vibrations and corresponding spin-phonon coupling and thermal evolution of magnetic exchange and single-ion anisotropy parameters. This allows us to provide chemical insights for their further rational design to make them operative at higher temperatures.

2. Methods

We performed first-principles spin-polarized density functional theory (DFT) calculations as implemented in the QuantumEspresso package [31]. The exchange-correlation energy was described using the generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof (PBE) functional [32]. We selected standard ultra-soft solid-state pseudopotentials (USPP) from the QuantumEspresso database. The electronic wave functions were expanded with well-converged kinetic energy cut-offs for the wave functions (charge density) of 80(800) and 90(900) for V and Cr derivatives, respectively. We fully optimized both atomic positions and lattice parameters until the forces on each atom were smaller than 10−3 Ry and the energy difference between two consecutive relaxation steps was less than 10−4 Ry. To avoid unphysical interactions between images along the non-periodic directions, we added a vacuum of 18 Å in the z direction in all single-layer calculations. The Brillouin zone was sampled by a fine Γ-centered 10 × 10 × 1 (10 × 10 × 10) and 20 × 20 × 1 (20 × 20 × 20) k-point Monkhorst–Pack mesh [33] to simulate the monolayer (bulk) of the studied V and Cr-based materials, respectively. In the bulk calculations, we considered van der Waals interactions by adding dispersion corrections by means of the semi-empirical Grimme-D2 approach [34]. To properly describe the electronic structure of all the systems, we adopted a Hubbard-corrected (DFT + U) approach, where U is the on-site Coulomb repulsion, to properly describe the strong correlation of d electrons of V and Cr using the simplified version proposed by Dudarev et al. [35].
In addition, we carried out broken-symmetry and vibrational DFT calculations using the Gaussian09 package in its revision D01 [36]. For magnetic exchange calculations, we employed the TPSSh hybrid functional [37] and Def2TZVP basis set [38] in combination with the corresponding density fitting approximation. We computed J values from the total energy difference of the high-spin (HS) and low-spin (LS) cases, as established by Yamaguchi et al. [39]. The vibrational analysis was performed using the PBE0 hybrid-exchange correlation functional [40] in combination with a 6-311G basis set [41,42]. The single-ion anisotropy (D) was obtained at the NEVPT2 level [43] using the Orca package [44,45]. We used the BP86 functional [46] in all calculations. The Def2TZVP basis set [38] was used for V, Cr, and N atoms, while the Def2SVP basis set [38] was used for C and H atoms. In all calculations, we included the corresponding auxiliary basis set.

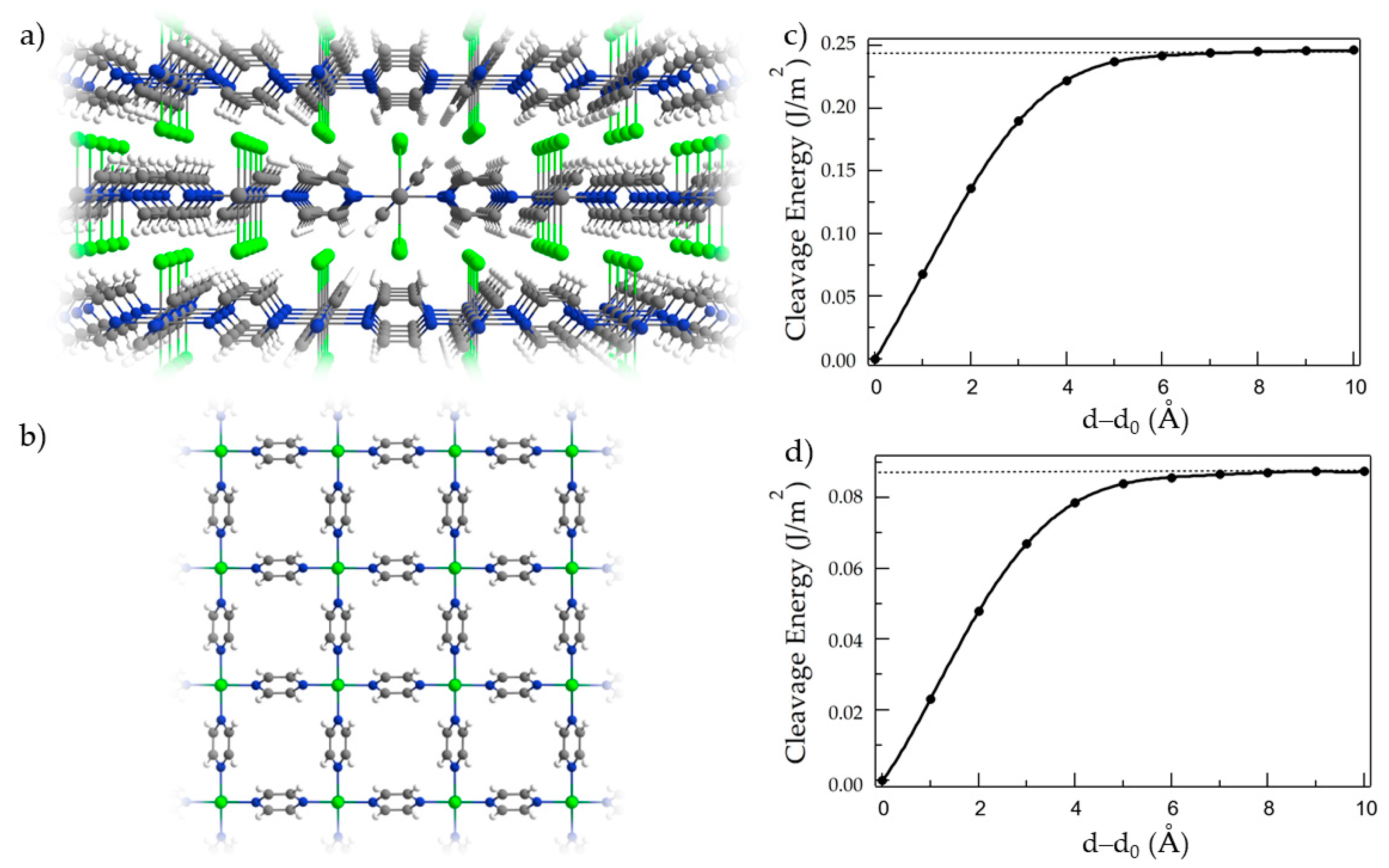
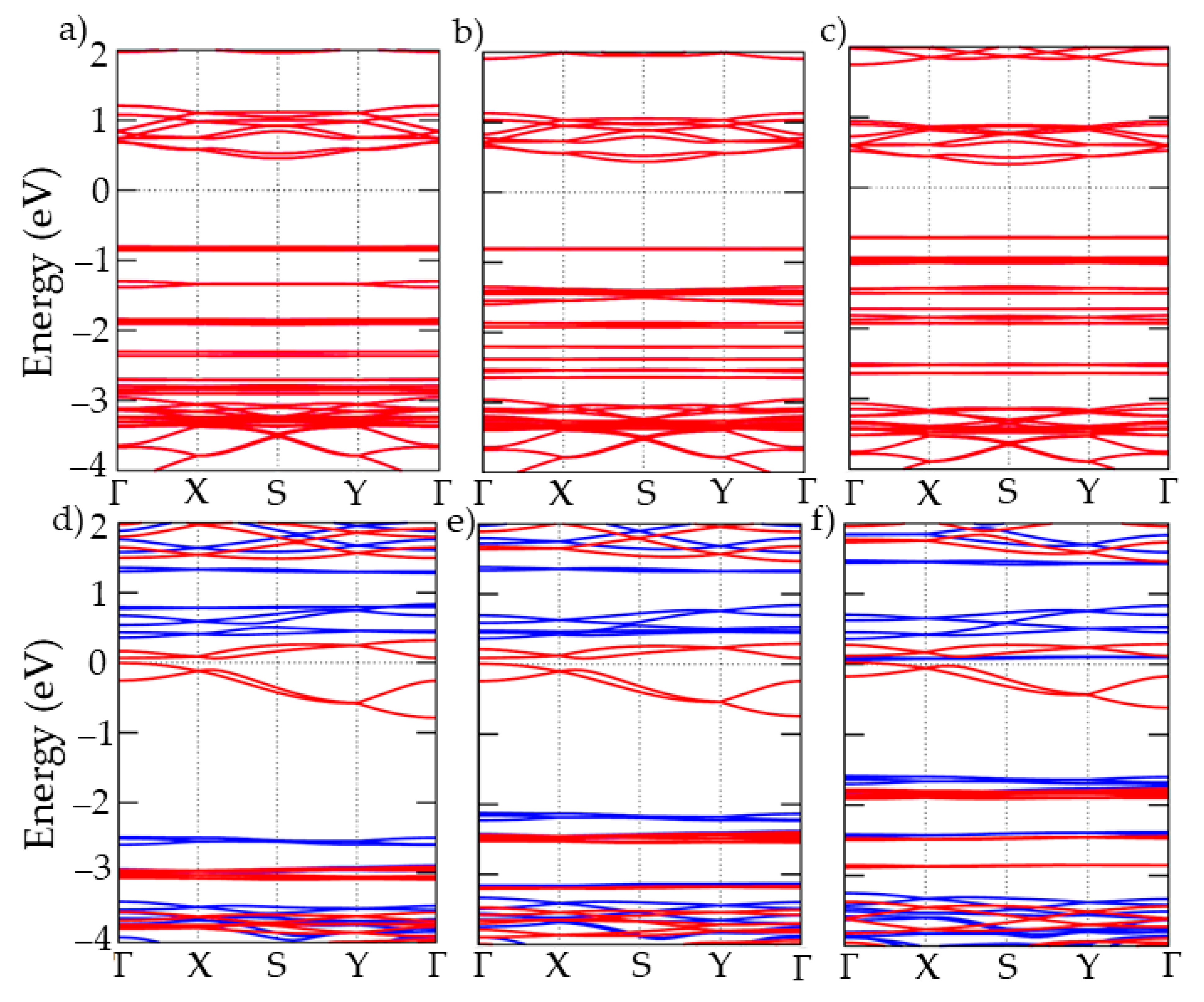
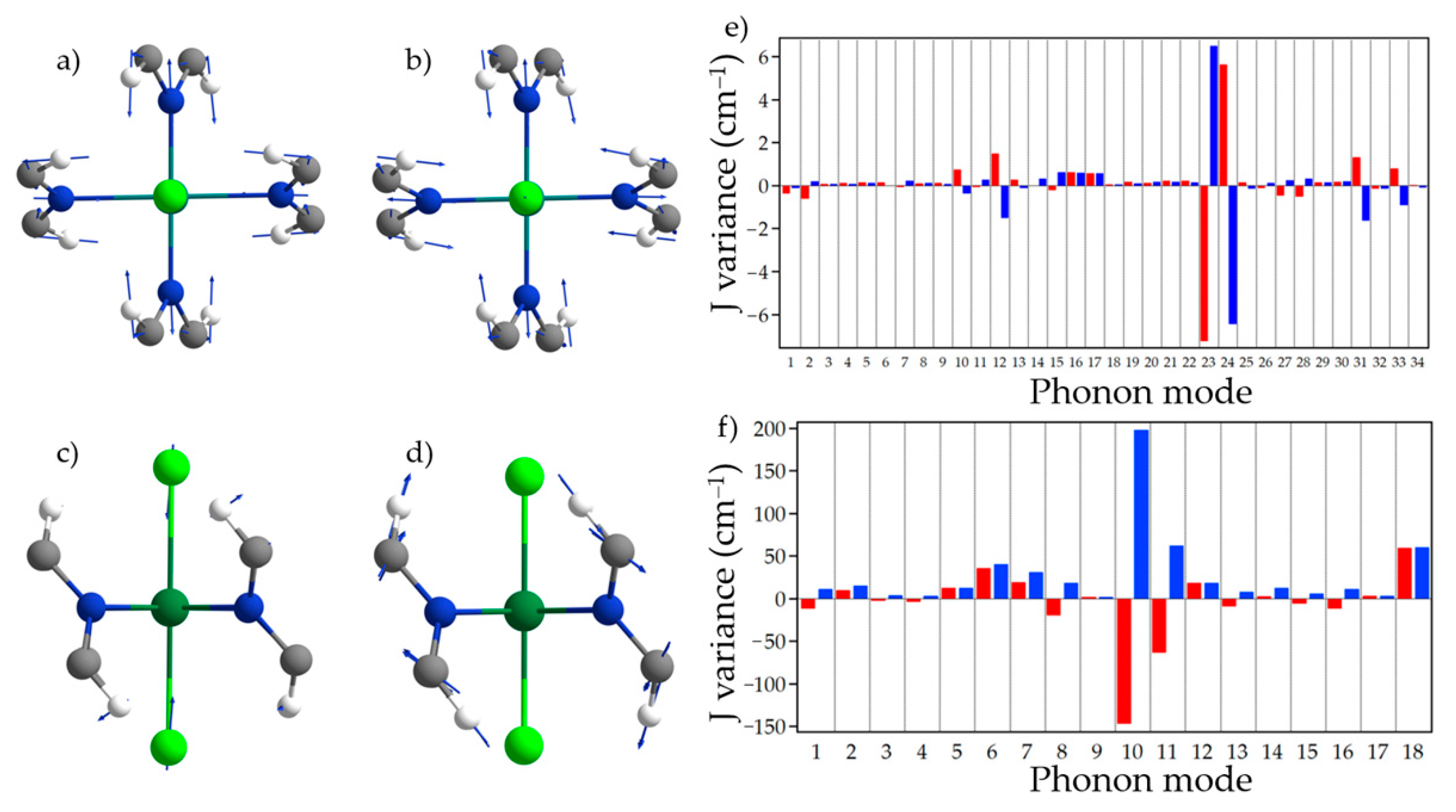
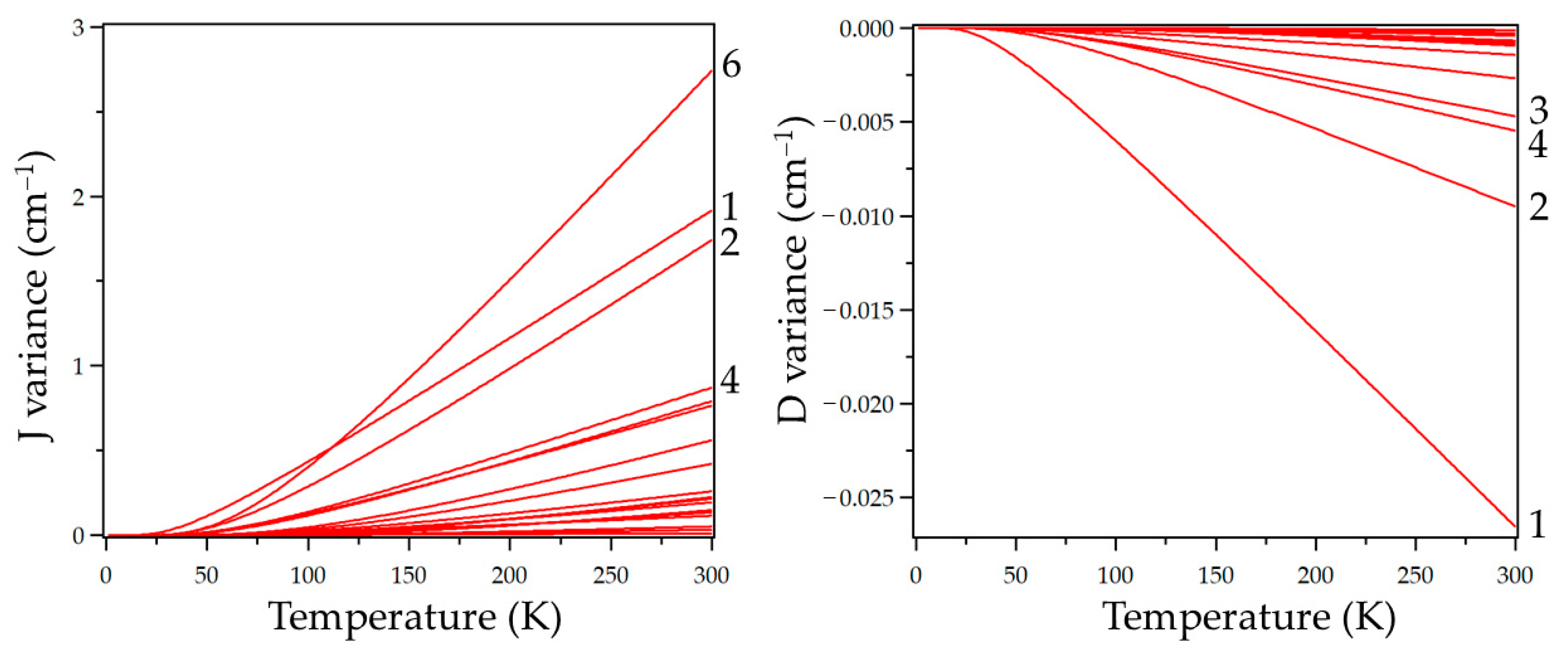
3. Results

VCl2(pyz)2 and CrCl2(pyz)2 are layered materials stacked by van der Waals interactions and crystallize in tetragonal I4/mmm and orthorhombic Immm space groups, respectively. Within each layer, VCl2(pyz)2 presents a square lattice of pyrazine-bridged metal centers with pyz rings disordered on two positions (cis- and trans-oriented) and chloride ligands aligned along the c crystallographic direction. Meanwhile, CrCl2(pyz)2 is almost isostructural with VCl2(pyz)2 but the Cr-Cr and Cr-N bond distances slightly deviate from a perfect 2D square network, as determined from synchrotron X-ray powder diffraction. For CrCl2(pyz)2, the magnetic intralayer interactions take place between the Cr(III) ions (S = 3/2) and pyrazine radical spins (S = 1/2), both coupled antiferromagnetically, which results in a net ferrimagnetic state (S = 1 per molecule) below ~55 K. In the case of VCl2(pyz)2, adjacent V(II) metallic centers are coupled antiferromagnetically—mediated by neutral pyrazine ligands—and preserve the global antiferromagnetic behavior up to ~120 K.
Recently, it has been proposed that these layered materials could be easily exfoliated down to the 2D limit due to the neutral nature of the layers [19]. In order to rationalize this possibility and provide insights for their experimental study, we perform systematic total energy calculations as a function of the interlayer distance (d) in a slab formed by two layers, where d0 is the optimized separation between layers in the bulk. This allows us to obtain the cleavage energy of both nanomaterials (Figure 1c,d). The cleavage energy is equivalent to the exfoliation energy and thus is defined as the necessary energy to separate a single layer from the bulk material. It directly reflects the strength of the interlayer interactions. As we can observe, the cleavage energy saturates at d-d0 ~7 Å, with values of ~0.25 and 0.1 J/m2 for VCl2(pyz)2 and CrCl2(pyz), respectively. This indicates that at higher interlayer distances both layers are not interacting anymore and thus the total energy of the system is the result of two independent monolayers. The obtained values are smaller than the calculated for prototypical 2D layered materials such as graphite (0.39 J/m2) or MoS2 (0.27 J/m2) [47] whereas they are similar to other magnetic 2D materials such as CrSBr (0.18 J/m2) [48] or CrI3 (0.3 J/m2) [49]. Therefore, our calculations reveal that both VCl2(pyz)2 and CrCl2(pyz) are likely to be easily exfoliated in the laboratory.
Next, we perform a full optimization of their atomic coordinates and lattice vectors by means of DFT and investigate the effect of halogen substitution in the monolayer. This is done by replacing the Cl ions with Br, thus forming VBr2(pyz)2 and CrBr2(pyz)2, and with I, which leads to VI2(pyz)2 and CrI2(pyz)2 (see Table S1). Compared with the bulk, the optimized chemical structures of single-layer VCl2(pyz)2 and CrCl2(pyz)2 reveal torsion angles of ~25–26°, which implies that the pyrazine rings are less tilted than in their bulk counterparts (~33–35°). This is because van der Waals forces play a major role in the interlayer interaction of the pyrazine rings and stabilize a more planar configuration with respect to the c-axis. The analysis of the 2D systems, when moving from Cl to Br and I, evidence an increase in the torsion angles of the pyrazine and the metal-halogen distances due to stronger repulsion interactions between the atoms. This is a consequence of the larger ionic radius. The substitution of the halide plays also an important role in the bond distance between the metal and the nitrogen of the pyrazine ring. This results in longer distances when moving from Cl (2.33 Å) to Br (2.55 Å) and I (2.77 Å) in the case of the Cr-based family. This can be explained by the higher covalent nature of the bond when moving down the periodic table.
Then, we calculate the electronic band structure by means of PBE + U along the high-symmetry points Γ-S-X-Y-Γ (Figure 2) of the Brillouin zone of the orthorhombic lattice [50]. We used U values of 5 and 4 eV for the V and Cr derivatives, respectively. These were extracted from the literature [18,19] and reproduce well the insulating and metallic nature of the VCl2(pyz)2 and CrCl2(pyz)2 bulk compounds, respectively (Figure S2). The density of states of the six investigated monolayers is reported in Figures S3–S8. In the case of the single-layer systems, the electronic band structures show direct bandgaps (at S high symmetry k-point, Figure 2) of 1.25, 1.20 and 1.02 eV for VCl2(pyz)2 (Figure 2a), VBr2(pyz)2 (Figure 2b) and VI2(pyz)2 (Figure 2c), respectively. This gives rise to insulating behavior, which is preserved either at the 2D limit or by chemical substitution. In the case of the Cr-based compounds, for CrCl2(pyz)2 (Figure 2d) and CrBr2(pyz)2 (Figure 2e), the systems turn out to be semimetallic (with the highest occupied and lowest unoccupied levels having the same spin polarization). This contrasts with the metallic nature of the CrCl2(pyz)2 bulk compound. Conversely CrI2(pyz)2 is metallic (Figure 2f) and presents two new bands above the Fermi level, which correspond to Cr d orbitals (Figure S8).
In order to explore the magnetic properties of the targeted systems, we determine the magnetic exchange interactions (J) between the magnetic centers. The J values are calculated using the Gaussian09 package on a representative fragment formed by 75 and 43 atoms for VCl2(pyz)2 and CrCl2(pyz)2 (Figure 3), respectively. This allows us to compute them using the difference in energies between the high-spin state and the broken-symmetry situation. This is a standard procedure often used in quantum chemistry to study molecular magnetic materials [51]. In the case of the VX2(pyz)2 family (X = Cl, Br, I), magnetic exchange is due to the interaction of the V centers in the system because in these compounds the pyrazine ligand is not reduced to a radical. From DFT, we calculate J = −40.57 cm−1 in the VCl2(pyz)2 system (within the −2J∑ijSiSj Hamiltonian definition). This is compatible with previously reported J values for the bulk [18,19]. The broken-symmetry configuration for two V(II) magnetic centers results in S = 3/2 − S’ = −3/2. This provides magnetic moment values of 2.84 μB and −2.84 μB for each V(II) center. As expected, one can observe that the neutral bridge pyrazine holds a negligible spin density, and thus there is superexchange coupling mediated by the pyrazine ring. This results in a moderate change of J values, as shown in Table 1, due to the slight structural changes reported in Table S1.
Conversely, in the case of the CrX2(pyz)2 family (where X = Cl, Br, I), the magnetic intralayer interactions take place between each Cr(III) metal center (S = 3/2) and the pyrazine radicals (S = 1/2). According to our calculations, this scenario gives rise to a final ferrimagnetic state with an isotropic J value of −2034.13 cm−1, which is ~50 times higher than that of CrCl2(pyz)2. We obtain spin moments of 2.75 μB on Cr(III) and −0.72 μB on the pyrazine ligands, which are in good agreement with those expected for a broken-symmetry case S = 3/2 − S’ = −1/2. The total spin density on the pyrazine radicals is mostly due to the local magnetic moments of the N atoms (−0.18 for each pyrazine) and a small contribution of the magnetic moments of C, while the local magnetic moments of Cl are almost negligible. Upon halogen substitution, the magnetic exchange coupling substantially decreases by 27.2% for CrBr2(pyz)2 and by a drastic change of 72.9% for CrI2(pyz)2 (Table 1). This is different from the VX2(pyz)2 family case because the magnetic interaction mainly takes place between the Cr(III) and the radical. Concretely, the competition between a ferrimagnetic interaction Cr(III)-radical versus a ferromagnetic one between Cr3+ ions (t2g–eg) when decreasing the ligand field from Cl-Br-I is enhanced. This combined with the small increase in the distance between the magnetic centers (See Table S1) leads to a more noticeable reduction of the J values in CrX2(pyz)2.
Halogen substitution in the first coordination sphere has a direct effect on the ligand field around the metal. Thus, we determine the single-ion anisotropy (D) of the six compounds presented in this work. For that, we use NEVPT2 as implemented in the Orca package, which is a second-order perturbation theory using a CAS-like reference wavefunction (See Methods). In the case of the CrX2(pyz)2 series, the values of the single-ion anisotropy are 0.331 (Cl), −0.242 (Br) and −0.298 (I) cm−1 (E/D values are 0.217, 0.090 and 0.299, respectively). These values follow the trend experimentally observed in similar octahedral Cr compounds, where there is a significant change in the behavior of D from Cl to Br/I, due to the higher ligand field of the former [52]. This has its origin in the fact that the diffuse electron density around the nuclei of the heavier atoms causes a less effective overlap of the orbitals involved in the halide-metal bond. For the VX2(pyz)2 family, the calculated D values are 0.140 (Cl), 0.190 (Br) and 0.228 (I) cm−1 (E/D values are 0.195, 0.195 and 0.220, respectively). As in the previous case, the observed effect of the substitution with heavier halides is to increase the value of D, due to the enhancement in SOC in the ligands.
To investigate the effect of the lattice on the spin states, we explore spin-phonon coupling (SPC) in both families. First, we calculate the phonon normal modes in Gaussian09 using periodic boundary conditions. This allows us to generate a series of distorted coordinates following each mode until the differential energy of the distorted coordinates is equal to the next normal mode (see Section S4 in the Supplementary Material). From each finite displacement—point-by-point—calculation, we evaluate the variation in J with respect to the displacement. This is indicative of how each mode is coupled to the magnetic properties. The organic-based nature of the targeted compounds results in a unit cell that contains 23 atoms and thus leads to 66 phonon normal modes. Assuming a Boltzmann distribution, we selected the ones that have a significant population below the experimental TC, i.e., ~120 K and ~55 K for VCl2(pyz)2 and CrCl2(pyz)2, respectively (see Section S3 in the Supplementary Material). For each mode, we determine the J values following the set of finite distorted coordinates. This permits us to evaluate the effect of the vibrational modes in the magnetic exchange, which is indicative of SPC (Figure 4). We can observe that some modes cause a maximum variance of ~7 (VCl2(pyz)2) and 198 cm−1 (CrCl2(pyz)2). In the case of VCl2(pyz)2, one can observe that modes 23 and 24 cause the maximum variation for both negative and positive oscillation phases. This fact is easily explained because these lattice vibration modes directly affect V-N bond elongation and compression, both in-phase (Figure 4c and Figure S46) and out-of-phase (Figure 4d and Figure S47). Hence, they change directly the distance between the V(II) magnetic centers, thus affecting directly the nature of magnetic exchange. However, the overall effect of these modes will not be very significant because the antisymmetric character of both phases acts to partially cancel the net effect on the magnetic parameters. In CrCl2(pyz)2, the most drastic effects are observed for mode 10, which reaches almost 198 cm−1 of variation. This mode consists of the in-phase movement of the pyrazines towards the closer pyrazine ring. In addition, mode 18 also gives a noticeable variation in magnetic exchange due to the movement of the Cr(III) central ions towards the vicinity of two pyrazine rings in each extreme of the harmonic oscillation. This could be exploited by means of an external activation at low temperatures of specific lattice vibration modes, thus allowing an efficient tuning of the magnetic properties of the system. In addition, the opportunity of chemical substitution opens a window to change the resonant frequency of a selected lattice vibration mode to another region. We checked this possibility by calculating the vibrational lattice modes of VI2(pyz)2. In the latter, mode 24 is red-shifted from 675 cm−1 in VCl2(pyz)2 to 640 cm−1. This is due to the ratio k/m between both systems, k being the force constant and m being the reduced mass, which decreases from 0.267 to 0.24 cm−1.
As a next step, we investigate the thermal evolution of J and D due to the temperature-dependent population of phonon modes in CrCl2(pyz)2 as a case study. We recalculate both parameters at four finite displacements of the atomic coordinates following the eigenvectors while varying Qk, where Qk is a given real value of the distortion coordinate of the vibrational mode k. Then, we estimate the second derivative of the variation in these parameters with respect to Qk (See Section S5 in the Supplementary Material). We include the effect of temperature by considering a Gran Canonical Ensemble [53]. The thermal dependence of a magnetic parameter (B) is calculated as follows:
B − T ≈ B − T = 0 + ∑ K = 1 R ℏ 4 π ∂ 2 B ∂ Q k 2 e 1 m k ν k n k
where B − T = 0 and n k are
B − T = 0 ≈ B e + ℏ 8 π ∑ K = 1 R ∂ 2 B ∂ Q k 2 e 1 m k ν k
n k = 1 e υ k / k B T − 1
B e is the magnetic parameter at the undistorted geometry; ν k is the frequency and m k is the reduced mass of the vibrational mode k.
The effect of each phonon normal mode on the thermal evolution of J and D is represented in Figure 5. We can see that J and D show the opposite behavior versus temperature. Regarding J, all phonon modes lead to an enhancement in magnetic exchange coupling. One may observe that the total effect of each mode is quite similar, except for the 6, 10 and 18 modes, which exhibit a much larger contribution (See Table S4). This explains why once mode 6 starts to be populated, its contribution becomes the most dominant. Meanwhile, modes 10 and 18 show almost a negligible contribution to the variation in J despite their enormous effect. This is a consequence of their higher activation energies, presenting a negligible effect at the selected range of temperatures. Conversely, D follows a downward trend with increasing temperature. In this case, as the individual effect of each mode is quite similar (See Table S5), the net result is governed by the vibrations that are populated at lower temperatures. These are the vibrations activated at lower frequencies, i.e., modes 1–4 (Figure 5). This validates our initial assumption, where we only consider those modes with a significant population up to the magnetic phase transition temperature. We can observe that these four vibrational modes have a prominent effect even at lower temperatures than the TC value of 55 K. This underlines the importance of the study of thermal effects on such parameters as, even at low temperatures, lattice vibrations vary in a non-negligible way key parameters that govern the magnetic behavior. Overall, our results suggest that spin-phonon coupling in this family is rather weak, as the response of the magnetic properties to the phonon displacements is mostly caused by normal modes that resonate at lower frequencies. The most interesting case is that of phonon mode 6, which dominates the thermal evolution of J above 100 K. In that mode, the halide ions are moving towards the vicinity of two pyrazine rings in each phase of the oscillation (Figure S45), causing a separation of these rings which affect directly the magnetic exchange coupling between Cr and the radical. This effect would be more pronounced at lower temperatures in the case of the CrI2(pyz)2 compound because it resonates at even lower frequencies (98.9 cm−1) in CrI2(pyz)2) compared with 140.1 cm−1 in CrCl2(pyz)2, due to the heavier mass of I. As a synthetic insight to limit the effect of this phonon mode on the magnetic behavior, we suggest the introduction of steric repulsion on the pyrazine rings, e.g., by substituting H with methyl groups. This will eventually act over the effect of mode 6 by restricting the pyrazine movement, which will lead to quenching or diminishing of spin-phonon coupling through this mode.
The high synthetic versatility of MOFs represents a good opportunity to quench/enhance lattice vibrations that affect either positively or negatively the magnetic parameters. This permits the tailoring of the magnetic behavior by designing new MOF magnets with the aim of hardening/softening specific lattice vibrations. Furthermore, the described magnetic and electronic properties of the studied compounds and the prominent new applications of the novel 2D MOFs make these MX2(pyz)2 appealing candidates in research fields such as spintronics or magnonics [14,15]. Chemically, the studied compounds have a set of similarities with the well-known V(TCNE)x magnetic material, which is achieving a remarkable performance in the field of magnonics [54]. This is because V(TCNE)x contains several magnon modes with high quality factors, such as long lifetime and low Gilbert damping arising from the small SOC of the system. In V(TCNE)x the V(II) centers are coupled with an unpaired electron lying in the C-C bond in an S = 3/2 − S’= 1/2 magnetic configuration that is quite similar to the one found in CrCl2(pyz)2. Although we expect that VCl2(pyz)2 compound will not display magnon transport due to the large distance between the V(II) magnetic centers, the magnetic exchange interaction between them could be modified by lattice-strain engineering [55], which can also be interesting for magnon straintronics applications [56]. Conversely, CrCl2(pyz)2 could be more interesting because there is antiferromagnetic coupling between Cr(III) and the delocalized radical between the pyrazine rings. So, these unpaired spins are located in a similar disposition to those of V(TCNE)x. Moreover, magnetic exchange interactions that take place in CrCl2(pyz)2 are in the same energy range as the calculated J in V(TCNE)x [57,58]. This motivates further exploration of this type of compound toward its application in magnonics, as they could represent a great opportunity to push back the frontiers of MOFs in this emerging field.

4. Conclusions

We investigated the structural, electronic and magnetic properties of two appealing magnetic MOFs, namely CrCl2(pyz)2 and VCl2(pyz)2, by means of first principles at the 2D limit. Firstly, we demonstrated the feasibility of isolating a single layer, as their simulated cleavage energies are similar to those reported for paradigmatic 2D materials. Regarding their magnetic properties, our results reveal robust intralayer magnetic exchange interactions, reaching −2034.13 and −40.57 cm−1 for the Cr and V derivatives, respectively. Then, we simulate the effect of halogen substitution by Br and I on the properties, which results in a decrease in J, due to the lengthening of the bonds in the systems, and an enhancement of single-ion anisotropy, due to the larger SOC of the heavier halides. Finally, we perform a full analysis of spin-phonon coupling in CrCl2(pyz)2 and VCl2(pyz)2 by applying a finite displacement approach. This allowed us to unveil the most coupled phonon modes and their thermal evolution. Overall, we observed modest spin-phonon coupling in this class of materials, which is consistent with their excellent magnetic performance. Our results pave the way to their improvement by effective manipulation of the phonon modes that have a major impact on the magnetic properties of this family, e.g., moving them towards other resonant frequencies where they may be easily activated or triggered by external stimuli.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano13071172/s1, Table S1: Geometrical parameters of the VX2(pyz)2 and CrX2(pyz)2 systems as described in Figure S1. Figure S1: Structural scheme followed to define the structural parameters of the described systems. Color code: M (dark green), Cl (green), C (black), N (blue) and H (pink). Figure S2: Electronic band structure of (left) CrCl2(pyz)2 and (right) VCl2(pyz)2 bulk materials. Figure S3: Calculated projected density of states (pDOS) for VCl2(pyz)2. Figure S4: Calculated projected density of states (pDOS) for VBr2(pyz)2. Figure S5: Calculated projected density of states (pDOS) for VI2(pyz)2. Figure S6: Calculated projected density of states (pDOS) for CrCl2(pyz)2. Figure S7: Calculated projected density of states (pDOS) for CrBr2(pyz)2. Figure S8: Calculated projected density of states (pDOS) for CrI2(pyz)2. Table S2: Population analysis parameter for each phonon mode in VCl2(pyz)2 at 120 K. Table S3: Population analysis parameter for each phonon mode in CrCl2(pyz)2 at 55 K. Figures S9–S26: Calculated J values as a function of the distorted geometries Qk with the fitting 2nd grade polynomial for phonon modes 1–18 at the CrCl2(pyz)2 system. Table S4: ∂ 2 J ∂ Q k 2 e calculated terms and Qk for each phonon mode in CrCl2(pyz)2 system. Figures S27–S44: Calculated D values as a function of the distorted geometries Qk with the fitting 2nd grade polynomial for phonon modes 1–18 at the CrCl2(pyz)2 system. Table S5: ∂ 2 D ∂ Q k 2 e calculated terms and Qk for each phonon mode in CrCl2(pyz)2 system. Figures S45–S47: Graphical representation of phonon modes 6,10 and 18 on CrCl2(pyz)2 (a) top view of negative phase (b) top view of positive phase (c) side view of negative phase (d) side view of positive phase.

Author Contributions

D.L.-A. performed first principles, magnetic exchange and spin-phonon calculations and wrote the first draft of the manuscript and prepared the figures, helped by A.M.R. Electronic structure calculations were performed and analyzed by A.M.R., J.J.B. conceived the work, proposed the methodology and supervised all the work and the preparation of the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the EU (Grant No. 2D-SMARTiES ERC-StG-101042680), the Plan Gent of Excellence of the Generalitat Valenciana (Grant No. CDEIGENT/2019/022), the Spanish MIU (Grant No. FPU21/04195) and the Excellence Unit María de Maeztu Grant No. CEX2019-000919-M from the Spanish MICINN.

Acknowledgments

The computations were performed on the Tirant III cluster of the Servei d’Informàtica of the University of Valencia.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Furukawa, H.; Cordova, K.E.; O’Keeffe, M.; Yaghi, O.M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341, 1230444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Lu, J.; Xu, H.; Yu, H.; Hu, X.; Xia, J.; Zhu, Y.; Wang, F.; Wu, H.-A.; Jiang, L.; Wang, H. Ultrafast Rectifying Counter-Directional Transport of Proton and Metal Ions in Metal-Organic Framework–Based Nanochannels. Sci. Adv. 2022, 8, eabl5070. [Google Scholar] [CrossRef]
  3. Huang, Z.; Xiong, C.; Ying, L.; Wang, W.; Wang, S.; Ding, J.; Lu, J. Facile Synthesis of a MOF-Derived Magnetic CoAl-LDH@chitosan Composite for Pb (II) and Cr (VI) Adsorption. Chem. Eng. J. 2022, 449, 137722. [Google Scholar] [CrossRef]
  4. Zhang, Y.; Feng, X.; Yuan, S.; Zhou, J.; Wang, B. Challenges and Recent Advances in MOF–Polymer Composite Membranes for Gas Separation. Inorg. Chem. Front. 2016, 3, 896–909. [Google Scholar] [CrossRef]
  5. Cui, W.-G.; Zhang, G.-Y.; Hu, T.-L.; Bu, X.-H. Metal-Organic Framework-Based Heterogeneous Catalysts for the Conversion of C1 Chemistry: CO, CO2 and CH4. Coord. Chem. Rev. 2019, 387, 79–120. [Google Scholar] [CrossRef]
  6. Wu, M.-X.; Yang, Y.-W. Metal-Organic Framework (MOF)-Based Drug/Cargo Delivery and Cancer Therapy. Adv. Mater. 2017, 29, 1606134. [Google Scholar] [CrossRef]
  7. Liu, C.; Bai, Y.; Li, W.; Yang, F.; Zhang, G.; Pang, H. In Situ Growth of Three-Dimensional MXene/Metal–Organic Framework Composites for High-Performance Supercapacitors. Angew. Chem. 2022, 134, e2021162. [Google Scholar]
  8. Wu, H.B.; Lou, X.W. (David) Metal-Organic Frameworks and Their Derived Materials for Electrochemical Energy Storage and Conversion: Promises and Challenges. Sci. Adv. 2017, 3, eaap9252. [Google Scholar] [CrossRef] [Green Version]
  9. Damron, J.T.; Ma, J.; Kurz, R.; Saalwächter, K.; Matzger, A.J.; Ramamoorthy, A. The Influence of Chemical Modification on Linker Rotational Dynamics in Metal–Organic Frameworks. Angew. Chem. 2018, 130, 8814–8817. [Google Scholar] [CrossRef]
  10. Tanabe, K.K.; Cohen, S.M. Postsynthetic Modification of Metal–Organic Frameworks—A Progress Report. Chem. Soc. Rev. 2011, 40, 498–519. [Google Scholar] [CrossRef] [PubMed]
  11. Mandal, S.; Natarajan, S.; Mani, P.; Pankajakshan, A. Post-Synthetic Modification of Metal–Organic Frameworks toward Applications. Adv. Funct. Mater. 2021, 31, 2006291. [Google Scholar] [CrossRef]
  12. Kurmoo, M. Magnetic Metal–Organic Frameworks. Chem. Soc. Rev. 2009, 38, 1353. [Google Scholar] [CrossRef]
  13. Thorarinsdottir, A.E.; Harris, T.D. Metal–Organic Framework Magnets. Chem. Rev. 2020, 120, 8716–8789. [Google Scholar] [CrossRef]
  14. Song, X.; Wang, X.; Li, Y.; Zheng, C.; Zhang, B.; Di, C.; Li, F.; Jin, C.; Mi, W.; Chen, L.; et al. 2D Semiconducting Metal–Organic Framework Thin Films for Organic Spin Valves. Angew. Chem. Int. Ed. 2020, 59, 1118–1123. [Google Scholar] [CrossRef]
  15. Barman, A.; Gubbiotti, G.; Ladak, S.; Adeyeye, A.O.; Krawczyk, M.; Gräfe, J.; Adelmann, C.; Cotofana, S.; Naeemi, A.; Vasyuchka, V.I.; et al. The 2021 Magnonics Roadmap. J. Phys. Condens. Matter 2021, 33, 413001. [Google Scholar] [CrossRef]
  16. Manriquez, J.M.; Yee, G.T.; McLean, R.S.; Epstein, A.J.; Miller, J.S. A Room-Temperature Molecular/Organic-Based Magnet. Science 1991, 252, 1415–1417. [Google Scholar] [CrossRef] [PubMed]
  17. Perlepe, P.; Oyarzabal, I.; Mailman, A.; Yquel, M.; Platunov, M.; Dovgaliuk, I.; Rouzières, M.; Négrier, P.; Mondieig, D.; Suturina, E.A.; et al. Metal-Organic Magnets with Large Coercivity and Ordering Temperatures up to 242 °C. Science 2020, 370, 587–592. [Google Scholar] [CrossRef] [PubMed]
  18. Perlepe, P.; Oyarzabal, I.; Voigt, L.; Kubus, M.; Woodruff, D.N.; Reyes-Lillo, S.E.; Aubrey, M.L.; Négrier, P.; Rouzières, M.; Wilhelm, F.; et al. From an Antiferromagnetic Insulator to a Strongly Correlated Metal in Square-Lattice MCl2(Pyrazine)2 Coordination Solids. Nat. Commun. 2022, 13, 5766. [Google Scholar] [CrossRef]
  19. Pedersen, K.S.; Perlepe, P.; Aubrey, M.L.; Woodruff, D.N.; Reyes-Lillo, S.E.; Reinholdt, A.; Voigt, L.; Li, Z.; Borup, K.; Rouzières, M.; et al. Formation of the Layered Conductive Magnet CrCl2(Pyrazine)2 through Redox-Active Coordination Chemistry. Nat. Chem. 2018, 10, 1056–1061. [Google Scholar] [CrossRef]
  20. Dong, R.; Han, P.; Arora, H.; Ballabio, M.; Karakus, M.; Zhang, Z.; Shekhar, C.; Adler, P.; Petkov, P.S.; Erbe, A.; et al. High-Mobility Band-like Charge Transport in a Semiconducting Two-Dimensional Metal–Organic Framework. Nat. Mater. 2018, 17, 1027–1032. [Google Scholar] [CrossRef] [PubMed]
  21. Sun, Z.; Martinez, A.; Wang, F. Optical Modulators with 2D Layered Materials. Nat. Photonics 2016, 10, 227–238. [Google Scholar] [CrossRef] [Green Version]
  22. López-Cabrelles, J.; Mañas-Valero, S.; Vitórica-Yrezábal, I.J.; Bereciartua, P.J.; Rodríguez-Velamazán, J.A.; Waerenborgh, J.C.; Vieira, B.J.C.; Davidovikj, D.; Steeneken, P.G.; van der Zant, H.S.J.; et al. Isoreticular Two-Dimensional Magnetic Coordination Polymers Prepared through Pre-Synthetic Ligand Functionalization. Nat. Chem. 2018, 10, 1001–1007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Mao, N.; Zhou, C.H.; Tong, D.S.; Yu, W.H.; Cynthia Lin, C.X. Exfoliation of Layered Double Hydroxide Solids into Functional Nanosheets. Appl. Clay Sci. 2017, 144, 60–78. [Google Scholar] [CrossRef]
  24. Liu, L.; Lu, X.-Y.; Zhang, M.-L.; Ren, Y.-X.; Wang, J.-J.; Yang, X.-G. 2D MOF Nanosheets as an Artificial Light-Harvesting System with Enhanced Photoelectric Switching Performance. Inorg. Chem. Front. 2022, 9, 2676–2682. [Google Scholar] [CrossRef]
  25. Liu, J.; Chen, Y.; Feng, X.; Dong, R. Conductive 2D Conjugated Metal–Organic Framework Thin Films: Synthesis and Functions for (Opto-)Electronics. Small Struct. 2022, 3, 2100210. [Google Scholar] [CrossRef]
  26. Zhang, R.; Liu, J.; Gao, Y.; Hua, M.; Xia, B.; Knecht, P.; Papageorgiou, A.C.; Reichert, J.; Barth, J.V.; Xu, H.; et al. On-surface Synthesis of a Semiconducting 2D Metal–Organic Framework Cu3 (C6O6) Exhibiting Dispersive Electronic Bands. Angew. Chem. 2020, 132, 2691–2695. [Google Scholar] [CrossRef]
  27. Darago, L.E.; Aubrey, M.L.; Yu, C.J.; Gonzalez, M.I.; Long, J.R. Electronic Conductivity, Ferrimagnetic Ordering, and Reductive Insertion Mediated by Organic Mixed-Valence in a Ferric Semiquinoid Metal–Organic Framework. J. Am. Chem. Soc. 2015, 137, 15703–15711. [Google Scholar] [CrossRef]
  28. Tiana, D.; Hendon, C.H.; Walsh, A. Ligand Design for Long-Range Magnetic Order in Metal–Organic Frameworks. Chem. Commun. 2014, 50, 13990–13993. [Google Scholar] [CrossRef] [Green Version]
  29. Zhang, B.H.; Hou, Y.S.; Wang, Z.; Wu, R.Q. First-Principles Studies of Spin-Phonon Coupling in Monolayer Cr2Ge2Te6. Phys. Rev. B 2019, 100, 224427. [Google Scholar] [CrossRef] [Green Version]
  30. Moseley, D.H.; Stavretis, S.E.; Thirunavukkuarasu, K.; Ozerov, M.; Cheng, Y.; Daemen, L.L.; Ludwig, J.; Lu, Z.; Smirnov, D.; Brown, C.M.; et al. Spin–Phonon Couplings in Transition Metal Complexes with Slow Magnetic Relaxation. Nat. Commun. 2018, 9, 2572. [Google Scholar] [CrossRef]
  31. Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
  32. Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef] [Green Version]
  33. Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  34. Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
  35. Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
  36. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09; Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  37. Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [Green Version]
  38. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
  39. Yamanaka, S.; Kawakami, T.; Nagao, H.; Yamaguchi, K. Effective Exchange Integrals for Open-Shell Species by Density Functional Methods. Chem. Phys. Lett. 1994, 231, 25–33. [Google Scholar] [CrossRef]
  40. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  41. Glukhovtsev, M.N.; Pross, A.; McGrath, M.P.; Radom, L. Extension of Gaussian-2 (G2) Theory to Bromine- and Iodine-containing Molecules: Use of Effective Core Potentials. J. Chem. Phys. 1995, 103, 1878–1885. [Google Scholar] [CrossRef]
  42. Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
  43. Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of n-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
  44. Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  45. Neese, F. Software Update: The ORCA Program System, Version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
  46. Perdew, J.P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
  47. Björkman, T.; Gulans, A.; Krasheninnikov, A.V.; Nieminen, R.M. Van Der Waals Bonding in Layered Compounds from Advanced Density-Functional First-Principles Calculations. Phys. Rev. Lett. 2012, 108, 235502. [Google Scholar] [CrossRef] [Green Version]
  48. Yang, K.; Wang, G.; Liu, L.; Lu, D.; Wu, H. Triaxial Magnetic Anisotropy in the Two-Dimensional Ferromagnetic Semiconductor CrSBr. Phys. Rev. B 2021, 104, 144416. [Google Scholar] [CrossRef]
  49. McGuire, M.A.; Dixit, H.; Cooper, V.R.; Sales, B.C. Coupling of Crystal Structure and Magnetism in the Layered, Ferromagnetic Insulator Cri3. Chem. Mater. 2015, 27, 612–620. [Google Scholar] [CrossRef]
  50. Setyawan, W.; Curtarolo, S. High-Throughput Electronic Band Structure Calculations: Challenges and Tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef] [Green Version]
  51. Ruiz, E.; Cano, J.; Alvarez, S.; Alemany, P. Broken Symmetry Approach to Calculation of Exchange Coupling Constants for Homobinuclear and Heterobinuclear Transition Metal Complexes. J. Comput. Chem. 1999, 20, 1391–1400. [Google Scholar] [CrossRef]
  52. Chen, L.; Stone, M.B.; Kolesnikov, A.I.; Winn, B.; Shon, W.; Dai, P.; Chung, J.H. Massless Dirac Magnons in the Two Dimensional van Der Waals Honeycomb Magnet CrCl3. 2D Mater. 2022, 9, 015006. [Google Scholar] [CrossRef]
  53. Escalera-Moreno, L.; Suaud, N.; Gaita-Ariño, A.; Coronado, E. Determining Key Local Vibrations in the Relaxation of Molecular Spin Qubits and Single-Molecule Magnets. J. Phys. Chem. Lett. 2017, 8, 1695–1700. [Google Scholar] [CrossRef] [Green Version]
  54. Liu, H.; Malissa, H.; Stolley, R.M.; Singh, J.; Groesbeck, M.; Popli, H.; Kavand, M.; Chong, S.K.; Deshpande, V.V.; Miller, J.S.; et al. Spin Wave Excitation, Detection, and Utilization in the Organic-Based Magnet, V(TCNE)x (TCNE = Tetracyanoethylene). Adv. Mater. 2020, 32, 2002663. [Google Scholar] [CrossRef] [PubMed]
  55. Ji, Q.; Kong, Y.; Wang, C.; Tan, H.; Duan, H.; Hu, W.; Li, G.; Lu, Y.; Li, N.; Wang, Y.; et al. Lattice Strain Induced by Linker Scission in Metal–Organic Framework Nanosheets for Oxygen Evolution Reaction. ACS Catal. 2020, 10, 5691–5697. [Google Scholar] [CrossRef]
  56. Esteras, D.L.; Rybakov, A.; Ruiz, A.M.; Baldoví, J.J. Magnon Straintronics in the 2D van Der Waals Ferromagnet CrSBr from First-Principles. Nano Lett. 2022, 22, 8771–8778. [Google Scholar] [CrossRef] [PubMed]
  57. Cimpoesu, F.; Frecus, B.; Oprea, C.I.; Panait, P.; Gîrţu, M.A. Disorder, Exchange and Magnetic Anisotropy in the Room-Temperature Molecular Magnet V[TCNE]x—A Theoretical Study. Comput. Mater. Sci. 2014, 91, 320–328. [Google Scholar] [CrossRef]
  58. Frecus, B.; Oprea, C.I.; Panait, P.; Ferbinteanu, M.; Cimpoesu, F.; Gîrţu, M.A. Ab Initio Study of Exchange Coupling for the Consistent Understanding of the Magnetic Ordering at Room Temperature in V[TCNE]x. Theor. Chem. Acc. 2014, 133, 1–17. [Google Scholar] [CrossRef]
Nanomaterials 13 01172 g001 550
Figure 1. (a) Lateral and (b) top view of bulk MCl2(pyz)2. Color code: M (dark green), Cl (green), C (gray), N (blue) and H (white). (c,d) Cleavage energy as a function of interlayer separation from equilibrium (d0) between two (c) VCl2(pyz)2 and (d) CrCl2(pyz)2 monolayers.
Figure 1. (a) Lateral and (b) top view of bulk MCl2(pyz)2. Color code: M (dark green), Cl (green), C (gray), N (blue) and H (white). (c,d) Cleavage energy as a function of interlayer separation from equilibrium (d0) between two (c) VCl2(pyz)2 and (d) CrCl2(pyz)2 monolayers.
Nanomaterials 13 01172 g001
Nanomaterials 13 01172 g002 550
Figure 2. Electronic band structure of (a) VCl2(pyz)2, (b) VBr2(pyz)2, (c) VI2(pyz)2, (d) CrCl2(pyz)2, (e) CrBr2(pyz)2 and (f) CrI2(pyz)2. Blue (red) color represents states with spin up (down) in the PBE + U calculations.
Figure 2. Electronic band structure of (a) VCl2(pyz)2, (b) VBr2(pyz)2, (c) VI2(pyz)2, (d) CrCl2(pyz)2, (e) CrBr2(pyz)2 and (f) CrI2(pyz)2. Blue (red) color represents states with spin up (down) in the PBE + U calculations.
Nanomaterials 13 01172 g002
Nanomaterials 13 01172 g003 550
Figure 3. DFT-calculated spin density of a representative fragment of (left) VCl2(pyz)2 and (right) CrCl2(pyz)2. The isosurface value is set to 0.004.
Figure 3. DFT-calculated spin density of a representative fragment of (left) VCl2(pyz)2 and (right) CrCl2(pyz)2. The isosurface value is set to 0.004.
Nanomaterials 13 01172 g003
Nanomaterials 13 01172 g004 550
Figure 4. (a–d) Graphical representation of phonon mode (a) 23 and (b) 24 of VCl2(pyz)2; phonon mode (c) 10 and (b) 18 of CrCl2(pyz)2. Blue arrows represent the eigenvectors of each normal mode; (e,f) Effect of the phonon distortion on the J values for (e) VCl2(pyz)2 and (f) CrCl2(pyz)2. Color code: negative (positive) phase of oscillation in blue (red).
Figure 4. (a–d) Graphical representation of phonon mode (a) 23 and (b) 24 of VCl2(pyz)2; phonon mode (c) 10 and (b) 18 of CrCl2(pyz)2. Blue arrows represent the eigenvectors of each normal mode; (e,f) Effect of the phonon distortion on the J values for (e) VCl2(pyz)2 and (f) CrCl2(pyz)2. Color code: negative (positive) phase of oscillation in blue (red).
Nanomaterials 13 01172 g004
Nanomaterials 13 01172 g005 550
Figure 5. Thermal evolution of the effect on the J (left) and D (right) caused by each phonon mode (modes with higher effect are indicated at the edge of each graph).
Figure 5. Thermal evolution of the effect on the J (left) and D (right) caused by each phonon mode (modes with higher effect are indicated at the edge of each graph).
Nanomaterials 13 01172 g005
Table
Table 1. Calculated magnetic exchange constants of each studied compound in cm−1.
Table 1. Calculated magnetic exchange constants of each studied compound in cm−1.
J (cm−1)
XVX2(pyz)2CrX2(pyz)2
Cl−40.57−2034.13
Br−37.02−1480.83
I−34.43−549.66
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

López-Alcalá, D.; Ruiz, A.M.; Baldoví, J.J. Exploring Spin-Phonon Coupling in Magnetic 2D Metal-Organic Frameworks. Nanomaterials 2023, 13, 1172. https://doi.org/10.3390/nano13071172

AMA Style

López-Alcalá D, Ruiz AM, Baldoví JJ. Exploring Spin-Phonon Coupling in Magnetic 2D Metal-Organic Frameworks. Nanomaterials. 2023; 13(7):1172. https://doi.org/10.3390/nano13071172

Chicago/Turabian Style

López-Alcalá, Diego, Alberto M. Ruiz, and José J. Baldoví. 2023. "Exploring Spin-Phonon Coupling in Magnetic 2D Metal-Organic Frameworks" Nanomaterials 13, no. 7: 1172. https://doi.org/10.3390/nano13071172

APA Style

López-Alcalá, D., Ruiz, A. M., & Baldoví, J. J. (2023). Exploring Spin-Phonon Coupling in Magnetic 2D Metal-Organic Frameworks. Nanomaterials, 13(7), 1172. https://doi.org/10.3390/nano13071172

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop