Ultrafast Dynamics of Valley-Polarized Excitons in WSe2 Monolayer Studied by Few-Cycle Laser Pulses
Abstract
:1. Introduction
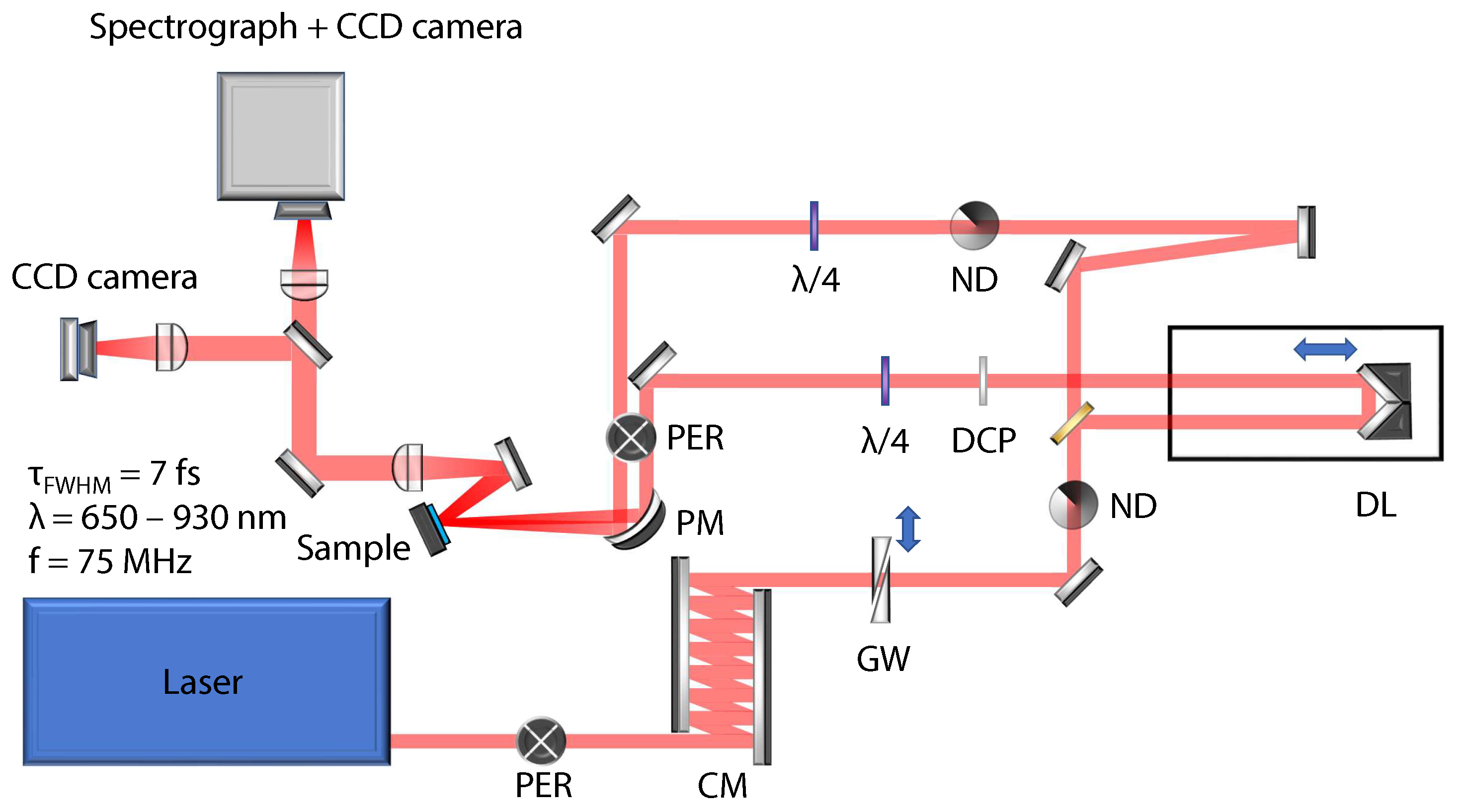
2. Materials and Methods
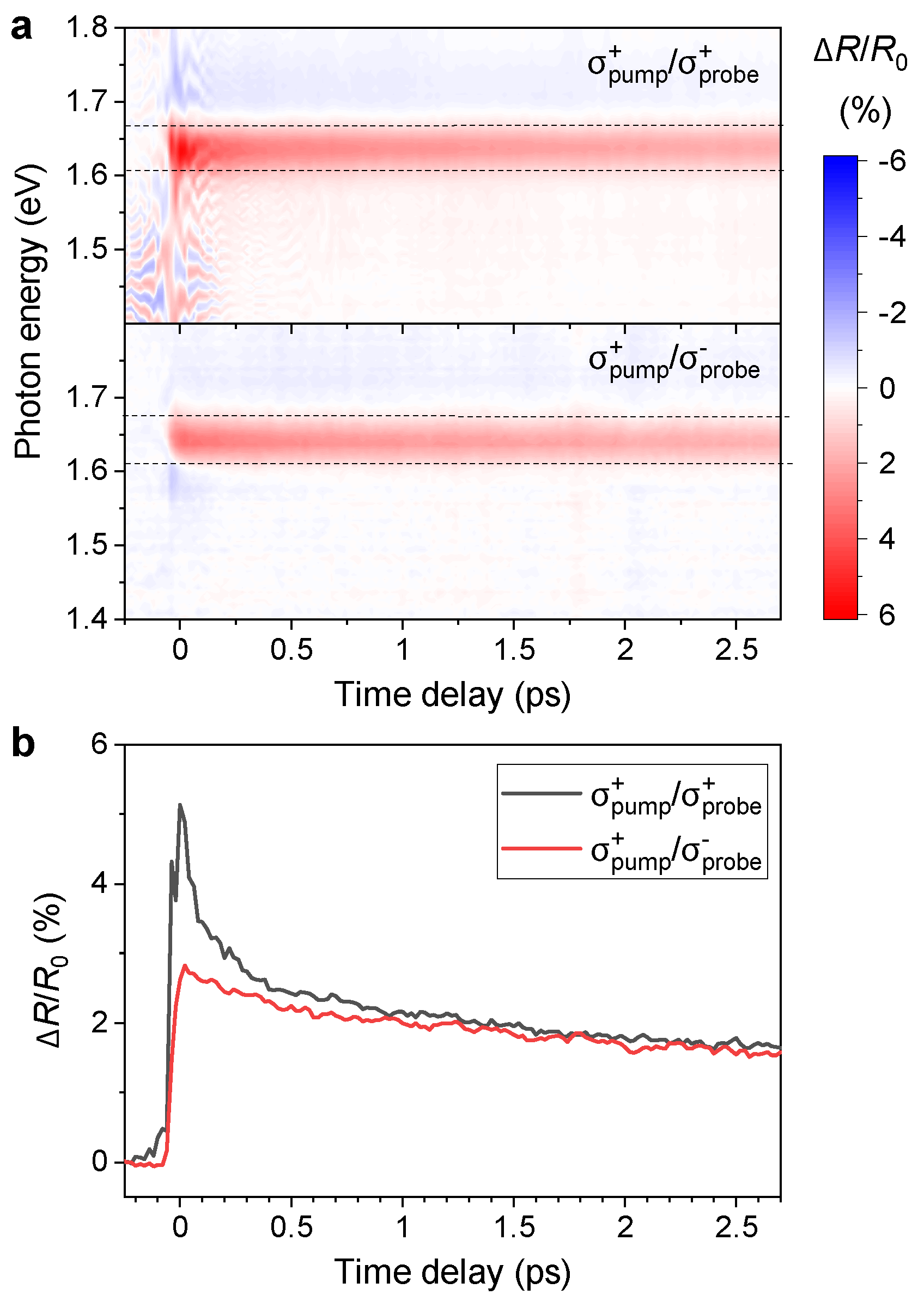
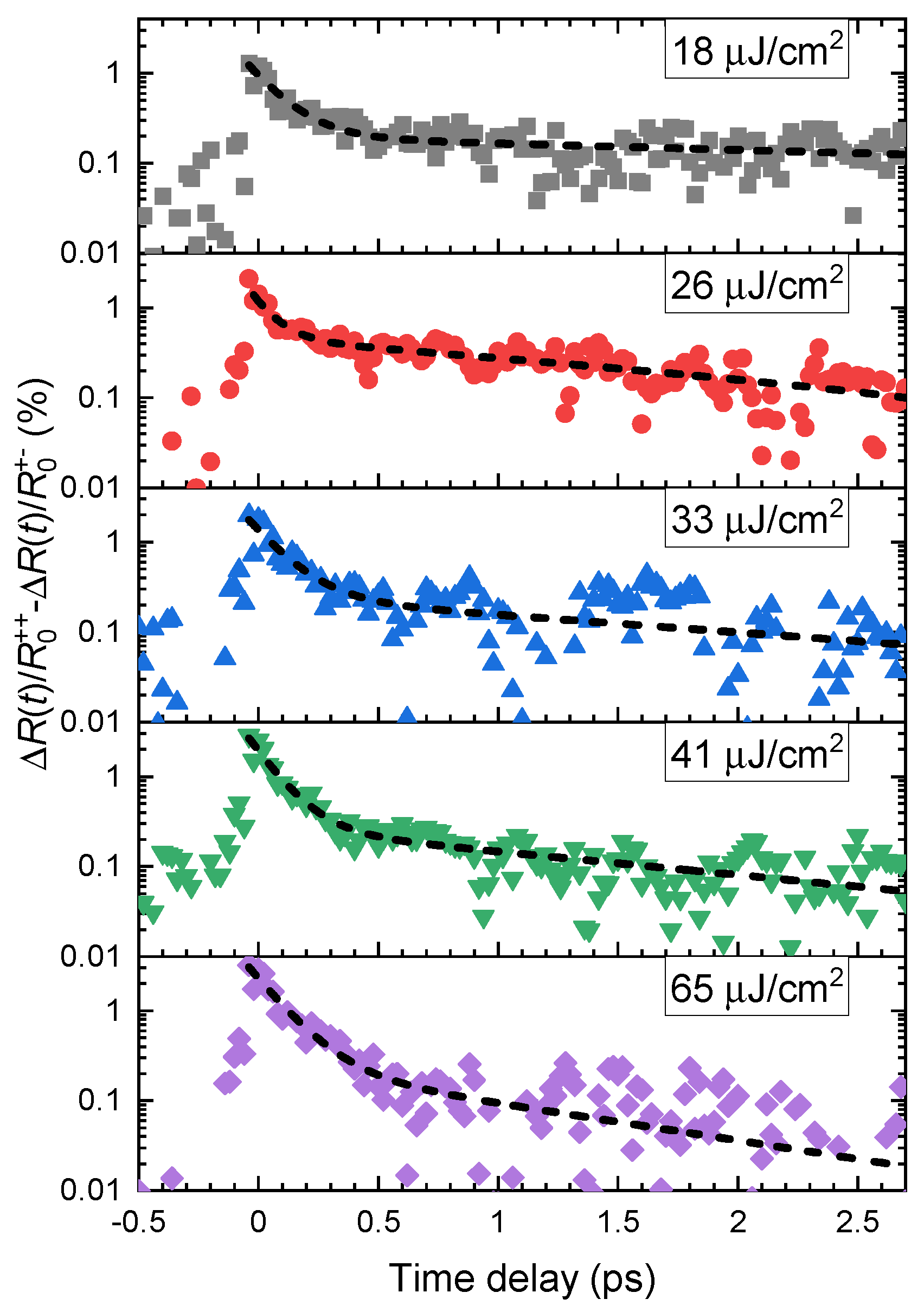
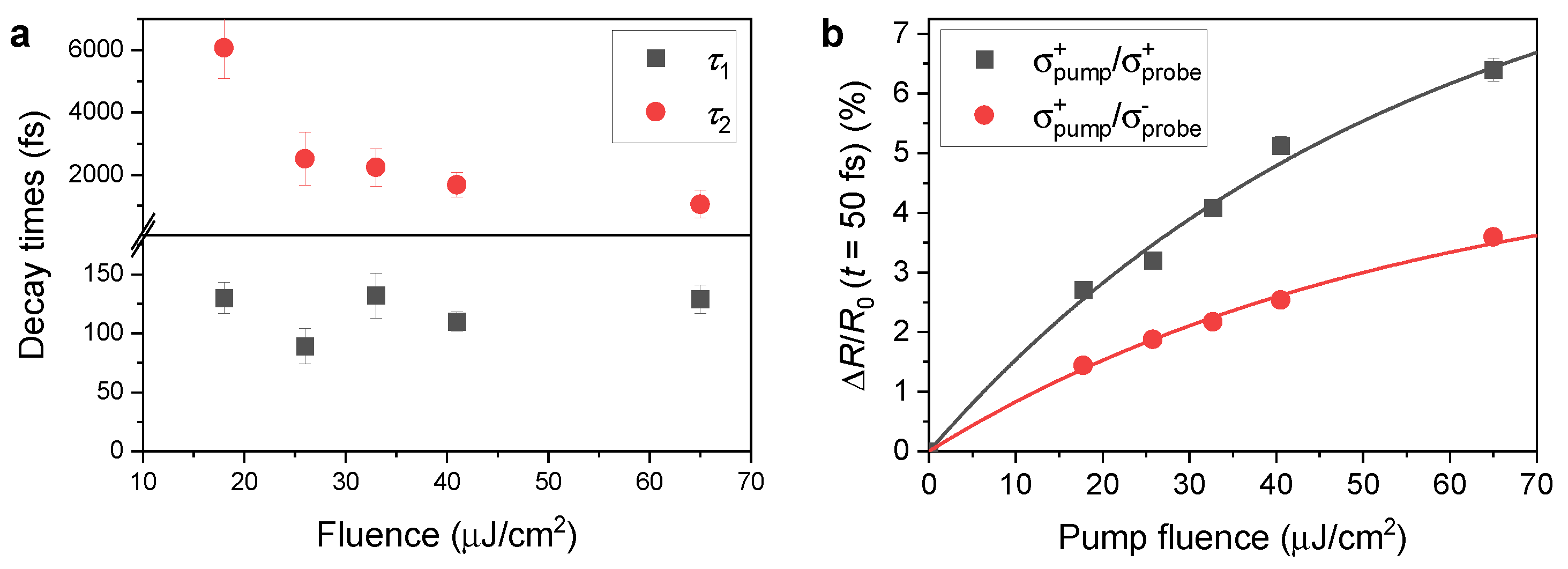
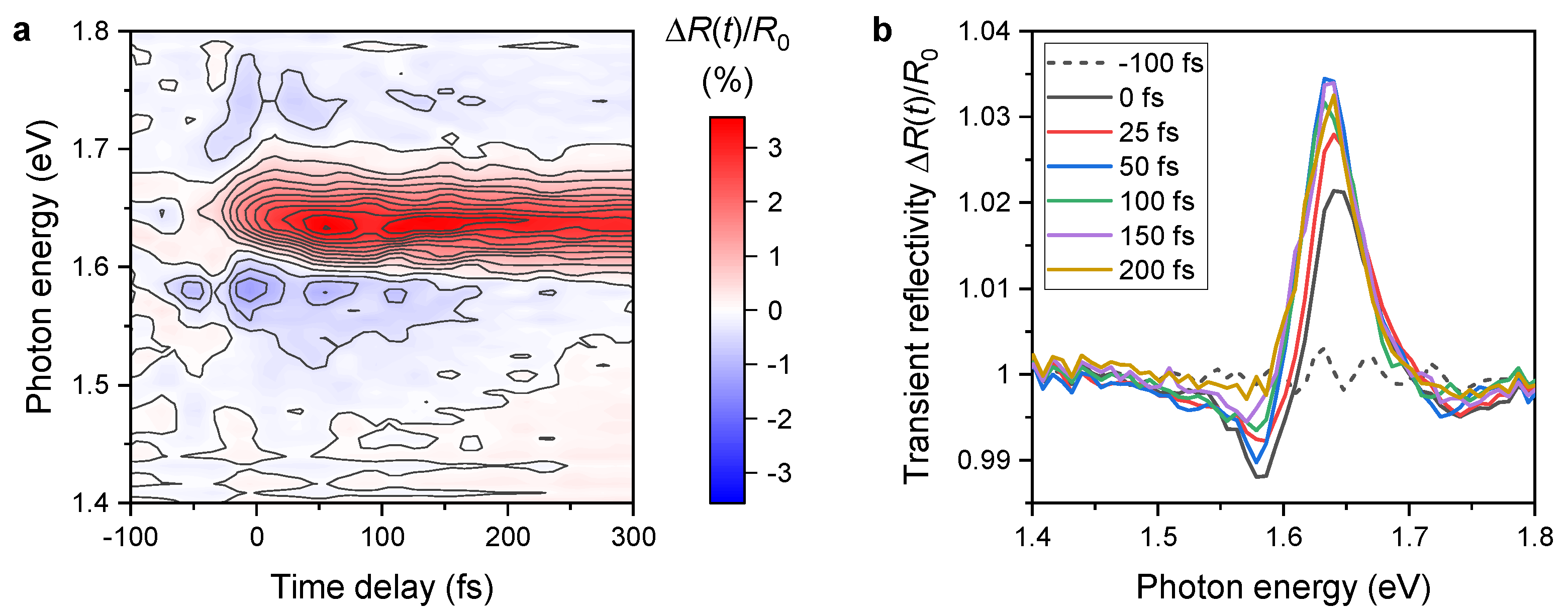
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| TMDs | Transition metal dichalcogenide monolayers |
| FWHM | Full width at half maximum |
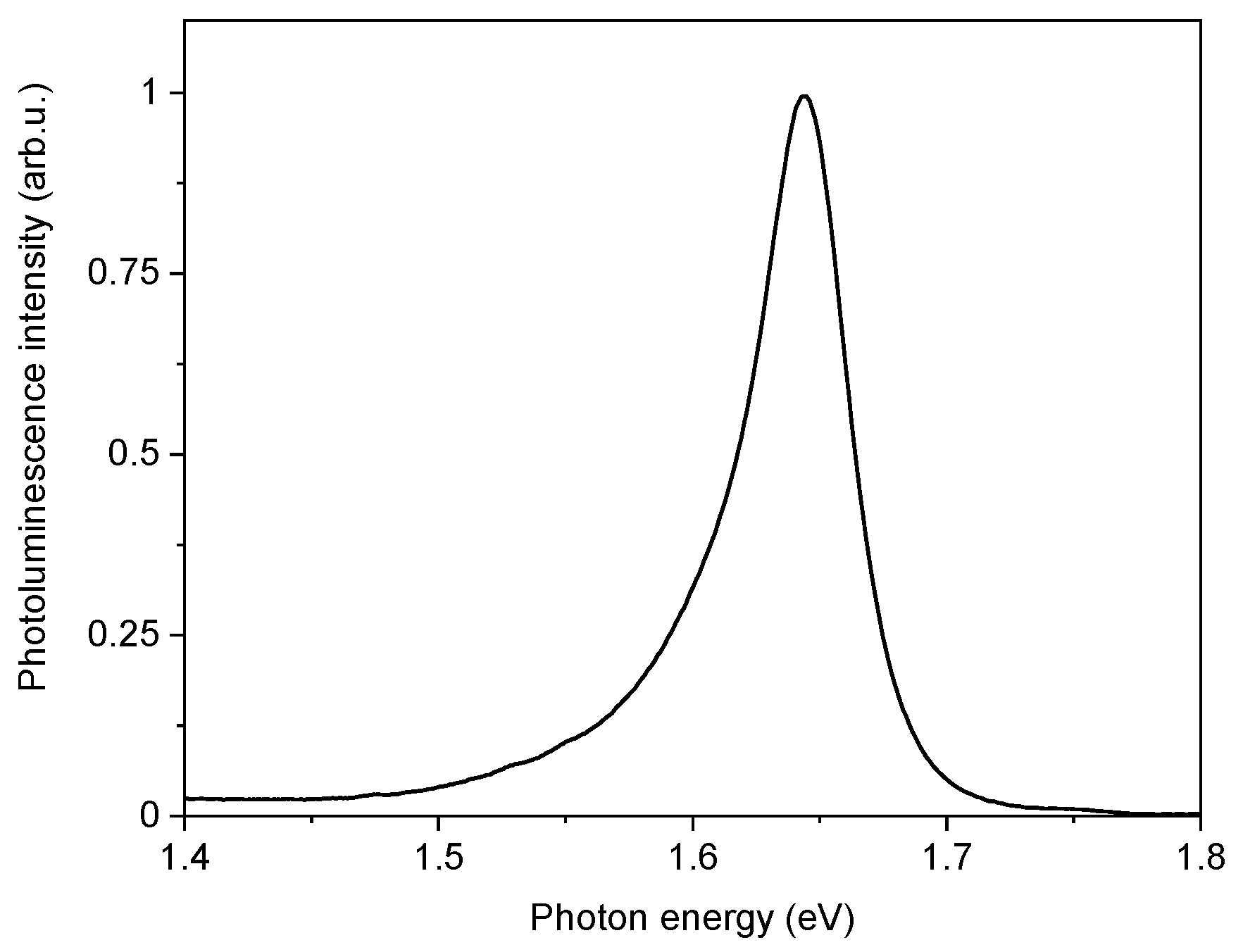
Appendix A. Photoluminescence Characterization of the WSe2 Monolayer Used in the Experiments
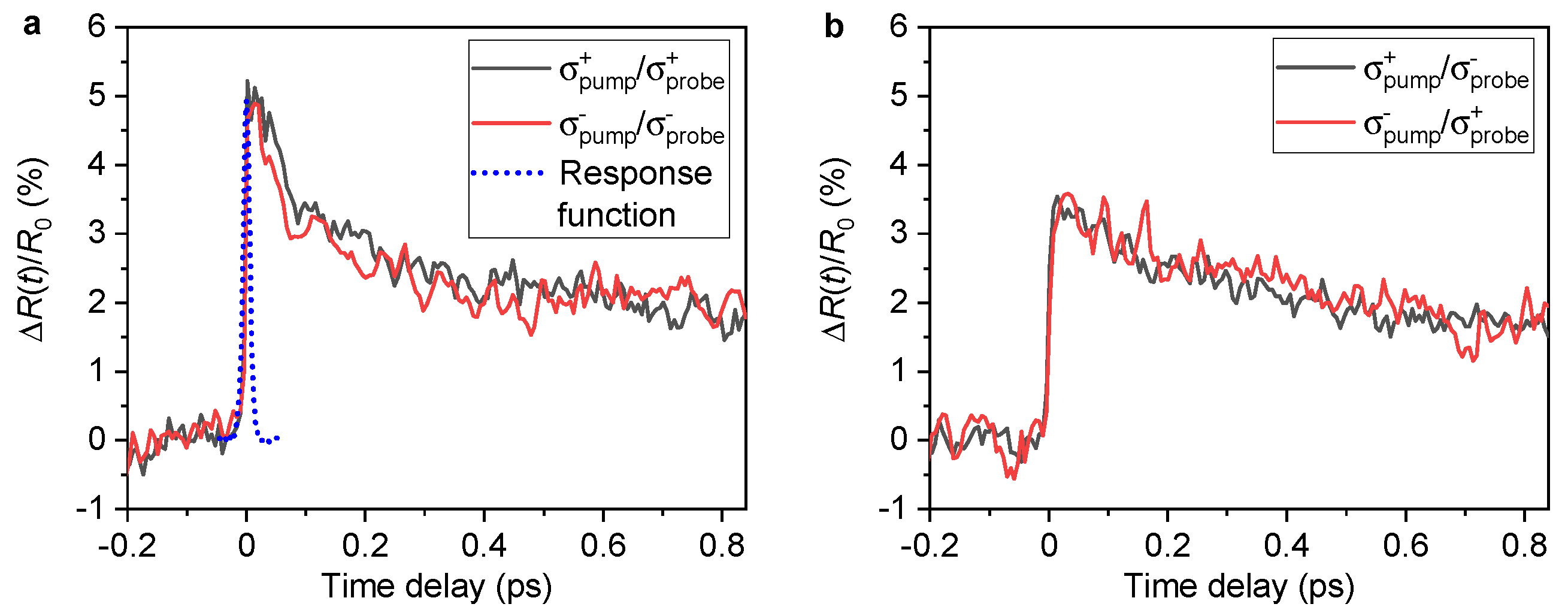
Appendix B. Verification of the Valley Selective Transient Reflectivity for Opposite Combinations of Circular Polarizations
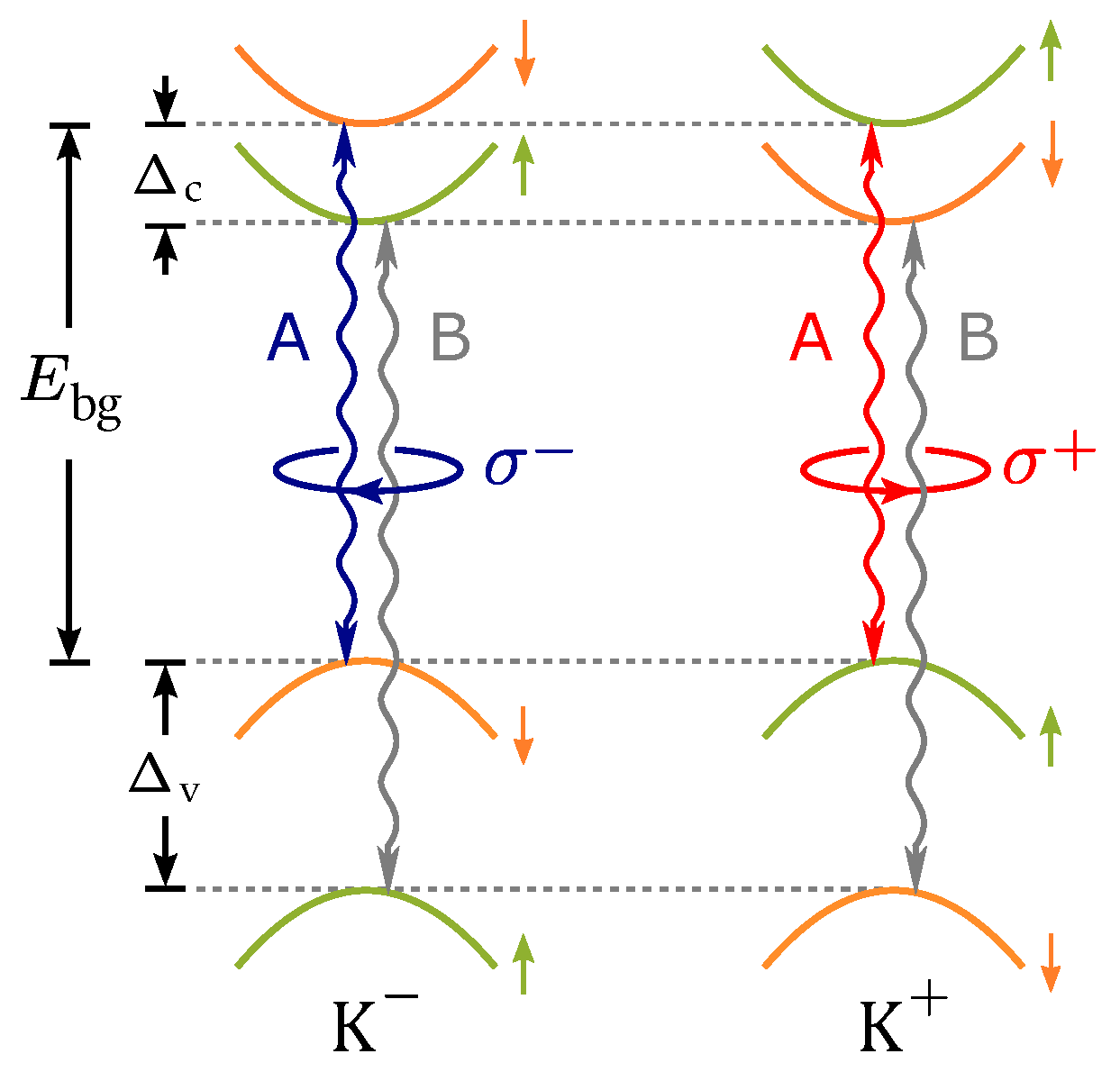
Appendix C. Band Structure of the Monolayer WSe2
References
- Xu, X.; Yao, W.; Xiao, D.; Heinz, T.F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 2014, 10, 343–350. [Google Scholar] [CrossRef]
- Xia, F.; Wang, H.; Xiao, D.; Dubey, M.; Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photonics 2014, 8, 899–907. [Google Scholar] [CrossRef] [Green Version]
- Eda, G.; Maier, S.A. Two-Dimensional Crystals: Managing Light for Optoelectronics. ACS Nano 2013, 7, 5660–5665. [Google Scholar] [CrossRef]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef]
- Molas, M.R.; Slobodeniuk, A.O.; Kazimierczuk, T.; Nogajewski, K.; Bartos, M.; Kapuściński, P.; Oreszczuk, K.; Watanabe, K.; Taniguchi, T.; Faugeras, C.; et al. Probing and Manipulating Valley Coherence of Dark Excitons in Monolayer WSe2. Phys. Rev. Lett. 2019, 123, 096803. [Google Scholar] [CrossRef] [Green Version]
- Bussolotti, F.; Kawai, H.; Ooi, Z.E.; Chellappan, V.; Thian, D.; Pang, A.L.C.; Goh, K.E.J. Roadmap on finding chiral valleys: Screening 2D materials for valleytronics. Nano Futur. 2018, 2, 032001. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, G.B.; Feng, W.; Xu, X.; Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kormányos, A.; Burkard, G.; Gmitra, M.; Fabian, J.; Zólyomi, V.; Drummond, N.D.; Fal’ko, V. k·p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2015, 2, 022001. [Google Scholar] [CrossRef]
- Koperski, M.; Molas, M.R.; Arora, A.; Nogajewski, K.; Slobodeniuk, A.O.; Faugeras, C.; Potemski, M. Optical properties of atomically thin transition metal dichalcogenides: Observations and puzzles. Nanophotonics 2017, 6, 1289–1308. [Google Scholar] [CrossRef]
- Wang, G.; Chernikov, A.; Glazov, M.M.; Heinz, T.F.; Marie, X.; Amand, T.; Urbaszek, B. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 2018, 90, 021001. [Google Scholar] [CrossRef] [Green Version]
- Yao, W.; Xiao, D.; Niu, Q. Valley-dependent optoelectronics from inversion symmetry breaking. Phys. Rev. B 2008, 77, 235406. [Google Scholar] [CrossRef] [Green Version]
- Chernikov, A.; Berkelbach, T.C.; Hill, H.M.; Rigosi, A.; Li, Y.; Aslan, B.; Reichman, D.R.; Hybertsen, M.S.; Heinz, T.F. Exciton Binding Energy and Nonhydrogenic Rydberg Series in Monolayer WS2. Phys. Rev. Lett. 2014, 113, 076802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molas, M.R.; Slobodeniuk, A.O.; Nogajewski, K.; Bartos, M.; Bala, L.; Babiński, A.; Watanabe, K.; Taniguchi, T.; Faugeras, C.; Potemski, M. Energy Spectrum of Two-Dimensional Excitons in a Nonuniform Dielectric Medium. Phys. Rev. Lett. 2019, 123, 136801. [Google Scholar] [CrossRef] [Green Version]
- Berkelbach, T.C.; Hybertsen, M.S.; Reichman, D.R. Theory of neutral and charged excitons in monolayer transition metal dichalcogenides. Phys. Rev. B 2013, 88, 045318. [Google Scholar] [CrossRef] [Green Version]
- Jones, A.M.; Yu, H.J.; Ghimire, N.J.; Wu, S.; Aivazian, G.; Ross, J.S.; Zhao, B.; Yan, J.; Mandrus, D.G.; Xiao, D.; et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 2013, 8, 634–638. [Google Scholar] [CrossRef]
- Mak, K.F.; He, K.; Shan, J.; Heinz, T. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechol. 2012, 7, 494–498. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.; Dai, J.; Yao, W.; Xiao, D.; Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechol. 2012, 7, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Glazov, M.M.; Amand, T.; Marie, X.; Lagarde, D.; Bouet, L.; Urbaszek, B. Exciton fine structure and spin decoherence in monolayers of transition metal dichalcogenides. Phys. Rev. B 2014, 89, 201302. [Google Scholar] [CrossRef] [Green Version]
- Hao, K.; Moody, G.; Wu, F.; Dass, C.K.; Xu, L.; Chen, C.H.; Sun, L.; Li, M.Y.; Li, L.J.; MacDonald, A.H.; et al. Direct measurement of exciton valley coherence in monolayer WSe2. Nat. Phys. 2016, 12, 677–682. [Google Scholar] [CrossRef] [Green Version]
- Robert, C.; Lagarde, D.; Cadiz, F.; Wang, G.; Lassagne, B.; Amand, T.; Balocchi, A.; Renucci, P.; Tongay, S.; Urbaszek, B.; et al. Exciton radiative lifetime in transition metal dichalcogenide monolayers. Phys. Rev. B 2016, 93, 205423. [Google Scholar] [CrossRef] [Green Version]
- Moody, G.; Dass, C.K.; Hao, K.; Chen, C.H.; Li, L.J.; Singh, A.; Tran, K.; Clark, G.; Xu, X.; Berghäuser, G.; et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nat. Commun. 2015, 6, 8315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palummo, M.; Bernardi, M.; Grossman, J.C. Exciton Radiative Lifetimes in Two-Dimensional Transition Metal Dichalcogenides. Nano Lett. 2015, 15, 2794–2800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poellmann, C.; Steinleitner, P.; Leierseder, U.; Nagler, P.; Plechinger, G.; Porer, M.; Bratschitsch, R.; Schüller, C.; Korn, T.; Huber, R. Resonant internal quantum transitions and femtosecond radiative decay of excitons in monolayer WSe2. Nat. Mater. 2015, 14, 889–893. [Google Scholar] [CrossRef] [PubMed]
- Jakubczyk, T.; Delmonte, V.; Koperski, M.; Nogajewski, K.; Faugeras, C.; Langbein, W.; Potemski, M.; Kasprzak, J. Radiatively Limited Dephasing and Exciton Dynamics in MoSe2 Monolayers Revealed with Four-Wave Mixing Microscopy. Nano Lett. 2016, 16, 5333–5339. [Google Scholar] [CrossRef] [Green Version]
- Yan, T.; Ye, J.; Qiao, X.; Tan, P.; Zhang, X. Exciton valley dynamics in monolayer WSe2 probed by the two-color ultrafast Kerr rotation. Phys. Chem. Chem. Phys. 2017, 19, 3176–3181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyauchi, Y.; Konabe, S.; Wang, F.; Zhang, W.; Hwang, A.; Hasegawa, Y.; Zhou, L.; Mouri, S.; Toh, M.; Eda, G.; et al. Evidence for line width and carrier screening effects on excitonic valley relaxation in 2D semiconductors. Nat. Commun. 2018, 9, 2598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castellanos-Gomez, A.; Buscema, M.; Molenaar, R.; Singh, V.; Janssen, L.; van der Zant, H.S.J.; Steele, G.A. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. 2D Mater. 2014, 1, 011002. [Google Scholar] [CrossRef]
- Budania, P.; Baine, P.T.; Montgomery, J.H.; McNeill, D.W.; Neil Mitchell, S.; Modreanu, M.; Hurley, P.K. Comparison between Scotch tape and gel-assisted mechanical exfoliation techniques for preparation of 2D transition metal dichalcogenide flakes. Micro Nano Lett. 2017, 12, 970–973. [Google Scholar] [CrossRef]
- Slobodeniuk, A.O.; Koutenský, P.; Bartoš, M.; Trojánek, F.; Malý, P.; Novotný, T.; Kozák, M. Semiconductor Bloch equation analysis of optical Stark and Bloch-Siegert shifts in monolayer WSe2 and MoS2. Phys. Rev. B 2022, 106, 235304. [Google Scholar] [CrossRef]
- Vaquero, D.; Salvador-Sánchez, J.; Clericò, V.; Diez, E.; Quereda, J. The Low-Temperature Photocurrent Spectrum of Monolayer MoSe2: Excitonic Features and Gate Voltage Dependence. Nanomaterials 2022, 12, 322. [Google Scholar] [CrossRef]
- Niu, Y.; Gonzalez-Abad, S.; Frisenda, R.; Marauhn, P.; Drüppel, M.; Gant, P.; Schmidt, R.; Taghavi, N.S.; Barcons, D.; Molina-Mendoza, A.J.; et al. Thickness-Dependent Differential Reflectance Spectra of Monolayer and Few-Layer MoS2, MoSe2, WS2 and WSe2. Nanomaterials 2018, 8, 725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tonndorf, P.; Schmidt, R.; Böttger, P.; Zhang, X.; Börner, J.; Liebig, A.; Albrecht, M.; Kloc, C.; Gordan, O.; Zahn, D.R.T.; et al. Photoluminescence emission and Raman response of monolayer MoS2, MoSe2, and WSe2. Opt. Express 2013, 21, 4908–4916. [Google Scholar] [CrossRef]
- McIntyre, J.; Aspnes, D. Differential reflection spectroscopy of very thin surface films. Surf. Sci. 1971, 24, 417–434. [Google Scholar] [CrossRef]
- Trovatello, C.; Katsch, F.; Borys, N.J.; Selig, M.; Yao, K.; Borrego-Varillas, R.; Scotognella, F.; Kriegel, I.; Yan, A.; Zettl, A.; et al. The ultrafast onset of exciton formation in 2D semiconductors. Nat. Commun. 2020, 11, 5277. [Google Scholar] [CrossRef]
- Steinleitner, P.; Merkl, P.; Nagler, P.; Mornhinweg, J.; Schüller, C.; Korn, T.; Chernikov, A.; Huber, R. Direct Observation of Ultrafast Exciton Formation in a Monolayer of WSe2. Nano Lett. 2017, 17, 1455–1460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yadav, D.; Trushin, M.; Pauly, F. Thermalization of photoexcited carriers in two-dimensional transition metal dichalcogenides and internal quantum efficiency of van der Waals heterostructures. Phys. Rev. Res. 2020, 2, 043051. [Google Scholar] [CrossRef]
- Katsch, F.; Selig, M.; Knorr, A. Exciton-Scattering-Induced Dephasing in Two-Dimensional Semiconductors. Phys. Rev. Lett. 2020, 124, 257402. [Google Scholar] [CrossRef]
- Katsch, F.; Selig, M.; Knorr, A. Theory of coherent pump–probe spectroscopy in monolayer transition metal dichalcogenides. 2D Mater. 2019, 7, 015021. [Google Scholar] [CrossRef]
- Glazov, M.M.; Ivchenko, E.L.; Wang, G.; Amand, T.; Marie, X.; Urbaszek, B.; Liu, B.L. Spin and valley dynamics of excitons in transition metal dichalcogenide monolayers. Phys. Status Solidi (B) 2015, 252, 2349–2362. [Google Scholar] [CrossRef] [Green Version]
- Danovich, M.; Zólyomi, V.; Fal’ko, V.I.; Aleiner, I.L. Auger recombination of dark excitons in WS2 and WSe2 monolayers. 2D Mater. 2016, 3, 035011. [Google Scholar] [CrossRef]
- Siday, T.; Sandner, F.; Brem, S.; Zizlsperger, M.; Perea-Causin, R.; Schiegl, F.; Nerreter, S.; Plankl, M.; Merkl, P.; Mooshammer, F.; et al. Ultrafast Nanoscopy of High-Density Exciton Phases in WSe2. Nano Lett. 2022, 22, 2561–2568. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Hong, X.; Jin, C.; Shi, S.F.; Chang, C.Y.S.; Chiu, M.H.; Li, L.J.; Wang, F. Ultrafast generation of pseudo-magnetic field for valley excitons in WSe2 monolayers. Science 2014, 346, 1205–1208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sie, E.J.; McIver, J.W.; Lee, Y.H.; Fu, L.; Kong, J.; Gedik, N. Valley-selective optical Stark effect in monolayer WS2. Nat. Mater. 2015, 14, 290–294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cunningham, P.D.; Hanbicki, A.T.; Reinecke, T.L.; McCreary, K.M.; Jonker, B.T. Resonant optical Stark effect in monolayer WS2. Nat. Commun. 2019, 10, 5539. [Google Scholar] [CrossRef] [Green Version]
- Autler, S.H.; Townes, C.H. Stark Effect in Rapidly Varying Fields. Phys. Rev. 1955, 100, 703–722. [Google Scholar] [CrossRef]
- Kuklinski, J.R.; Mukamel, S. Real versus virtual excitonic Stark effect in semiconductor quantum wells. Phys. Rev. B 1990, 42, 11938–11941. [Google Scholar] [CrossRef] [PubMed]
- Maialle, M.Z.; de Andrada e Silva, E.A.; Sham, L.J. Exciton spin dynamics in quantum wells. Phys. Rev. B 1993, 47, 15776–15788. [Google Scholar] [CrossRef] [PubMed]
- Vaquero, D.; Clericò, V.; Salvador-Sánchez, J.; Díaz, E.; Domínguez-Adame, F.; Chico, L.; Meziani, Y.M.; Diez, E.; Quereda, J. Fast response photogating in monolayer MoS2 phototransistors. Nanoscale 2021, 13, 16156–16163. [Google Scholar] [CrossRef] [PubMed]
- Rybkovskiy, D.V.; Gerber, I.C.; Durnev, M.V. Atomically inspired k·p approach and valley Zeeman effect in transition metal dichalcogenide monolayers. Phys. Rev. B 2017, 95, 155406. [Google Scholar] [CrossRef] [Green Version]
- Slobodeniuk, A.O.; Basko, D.M. Spin–flip processes and radiative decay of dark intravalley excitons in transition metal dichalcogenide monolayers. 2D Mater. 2016, 3, 035009. [Google Scholar] [CrossRef] [Green Version]
- Slobodeniuk, A.O.; Basko, D.M. Exciton-phonon relaxation bottleneck and radiative decay of thermal exciton reservoir in two-dimensional materials. Phys. Rev. B 2016, 94, 205423. [Google Scholar] [CrossRef] [Green Version]
- Koirala, S.; Mouri, S.; Miyauchi, Y.; Matsuda, K. Homogeneous linewidth broadening and exciton dephasing mechanism in MoTe2. Phys. Rev. B 2016, 93, 075411. [Google Scholar] [CrossRef] [Green Version]
- Dey, P.; Paul, J.; Wang, Z.; Stevens, C.E.; Liu, C.; Romero, A.H.; Shan, J.; Hilton, D.J.; Karaiskaj, D. Optical Coherence in Atomic-Monolayer Transition-Metal Dichalcogenides Limited by Electron-Phonon Interactions. Phys. Rev. Lett. 2016, 116, 127402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Selig, M.; Berghäuser, G.; Raja, A.; Nagler, P.; Schüller, C.; Heinz, T.F.; Korn, T.; Chernikov, A.; Malic, E.; Knorr, A. Excitonic linewidth and coherence lifetime in monolayer transition metal dichalcogenides. Nat. Commun. 2016, 7, 13279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidt, R.; Berghäuser, G.; Schneider, R.; Selig, M.; Tonndorf, P.; Malić, E.; Knorr, A.; Michaelis de Vasconcellos, S.; Bratschitsch, R. Ultrafast Coulomb-Induced Intervalley Coupling in Atomically Thin WS2. Nano Lett. 2016, 16, 2945–2950. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutenský, P.; Slobodeniuk, A.; Bartoš, M.; Trojánek, F.; Malý, P.; Kozák, M. Ultrafast Dynamics of Valley-Polarized Excitons in WSe2 Monolayer Studied by Few-Cycle Laser Pulses. Nanomaterials 2023, 13, 1207. https://doi.org/10.3390/nano13071207
Koutenský P, Slobodeniuk A, Bartoš M, Trojánek F, Malý P, Kozák M. Ultrafast Dynamics of Valley-Polarized Excitons in WSe2 Monolayer Studied by Few-Cycle Laser Pulses. Nanomaterials. 2023; 13(7):1207. https://doi.org/10.3390/nano13071207
Chicago/Turabian StyleKoutenský, Petr, Artur Slobodeniuk, Miroslav Bartoš, František Trojánek, Petr Malý, and Martin Kozák. 2023. "Ultrafast Dynamics of Valley-Polarized Excitons in WSe2 Monolayer Studied by Few-Cycle Laser Pulses" Nanomaterials 13, no. 7: 1207. https://doi.org/10.3390/nano13071207
APA StyleKoutenský, P., Slobodeniuk, A., Bartoš, M., Trojánek, F., Malý, P., & Kozák, M. (2023). Ultrafast Dynamics of Valley-Polarized Excitons in WSe2 Monolayer Studied by Few-Cycle Laser Pulses. Nanomaterials, 13(7), 1207. https://doi.org/10.3390/nano13071207