Towards Bright Single-Photon Emission in Elliptical Micropillars
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of the Structure
2.2. Optical Measurements
2.3. Numerical Calculations
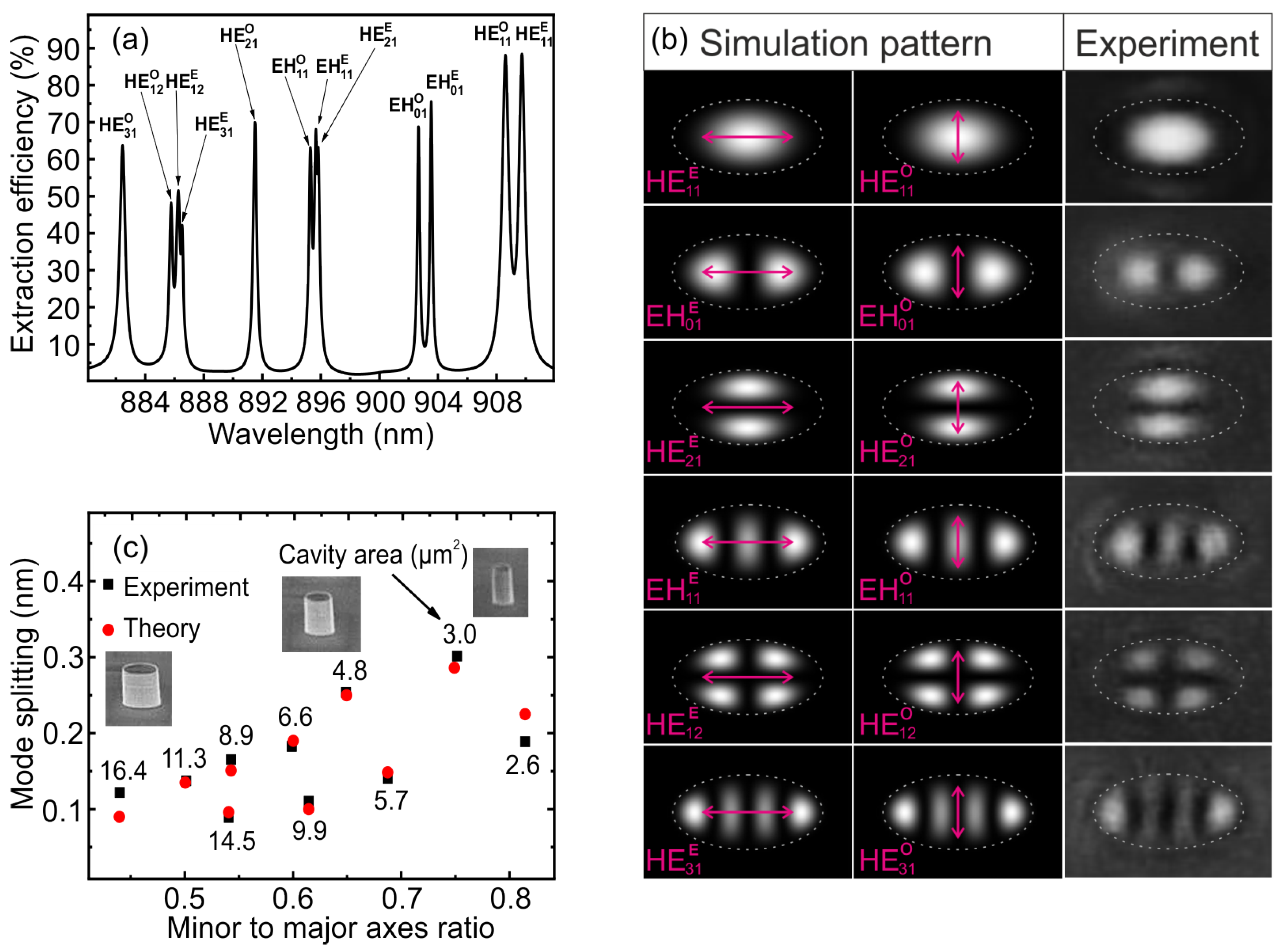
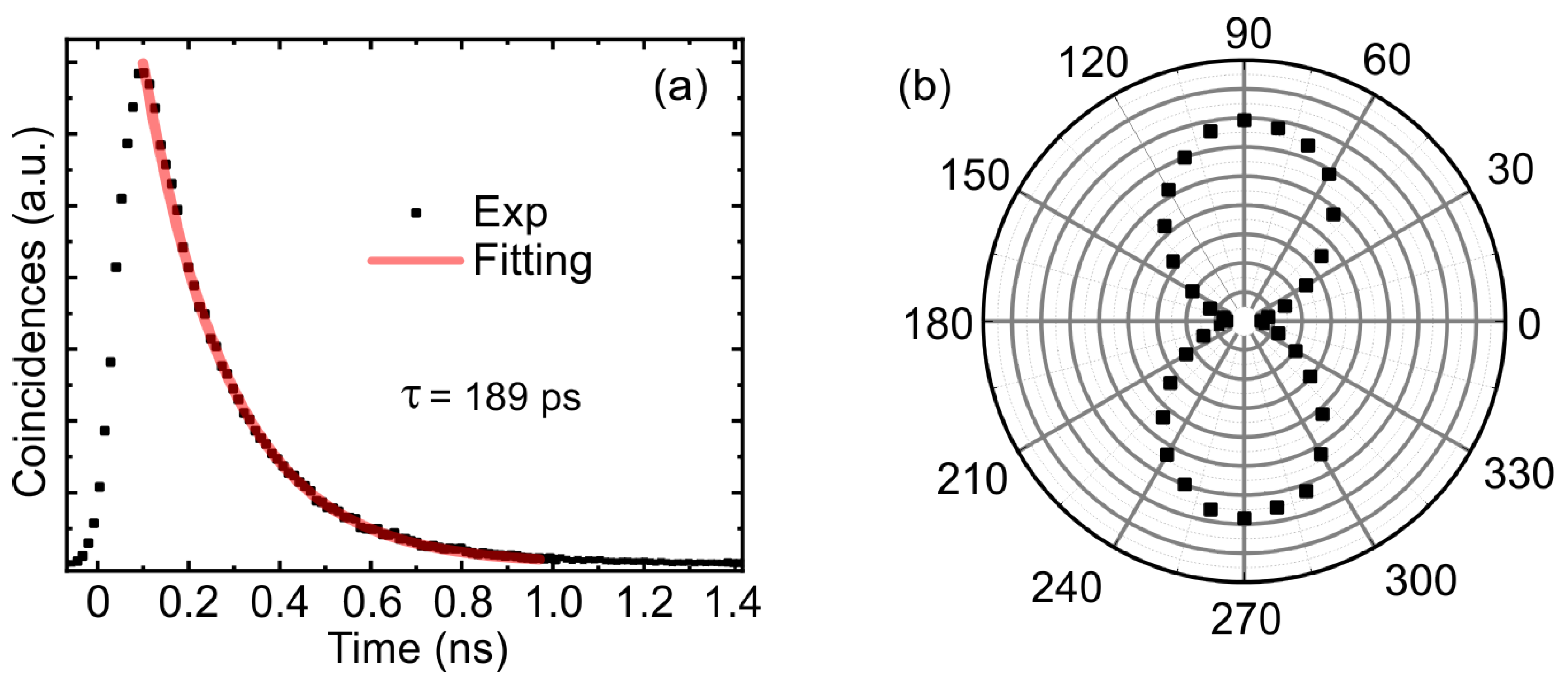
3. Results and Discussions
3.1. Optical Modes in Elliptical Microresonators
3.2. QD in Elliptical Microresonator
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef]
- Wang, H.; He, Y.-M.; Li, Y.-H.; Su, Z.E.; Li, B.; Huang, H.L.; Ding, X.; Chen, M.C.; Liu, C.; Qin, J.; et al. High-efficiency multiphoton boson sampling. Nat. Photonics 2017, 11, 361–365. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Zhao, J.; Ma, C.; Rüsing, M.; Mookherjea, S. High quality entangled photon pair generation in periodically poled thin-film lithium niobate waveguides. Phys. Rev. Lett. 2020, 124, 163603. [Google Scholar] [CrossRef]
- Ma, C.; Wang, X.; Anant, V.; Beyer, A.D.; Shaw, M.D.; Mookherjea, S. Silicon photonic entangled photon-pair and heralded single photon generation with CAR > 12000 and g2(0) < 0.006. Opt. Express 2017, 25, 32995–33006. [Google Scholar]
- Michler, P.; Kiraz, A.; Schoenfeld, W.V.; Petroff, P.M.; Zhang, L.; Hu, E.; Imamoglu, A. A quantum dot single-photon turnstile device. Science 2000, 290, 2282–2285. [Google Scholar] [CrossRef]
- He, Y.-M.; He, Y.; Wey, Y.-J.; Wu, D.; Atature, M.; Schneider, C.; Hofling, S.; Kamp, M.; Lu, C.-Y.; Pan, J.-W. On-demand semiconductor single-photon source with nearunity indistinguishability. Nat. Nanotechnol. 2013, 8, 213–217. [Google Scholar] [CrossRef]
- Beugnon, J.; Jones, M.P.; Dingjan, J.; Darquié, B.; Messin, G.; Browaeys, A.; Grangier, P. Quantum interference between two single photons emitted by independently trapped atoms. Nature 2006, 440, 779–782. [Google Scholar] [CrossRef]
- Higginbottom, D.B.; Slodička, L.; Araneda, G.; Lachman, L.; Filip, R.; Hennrich, M.; Blatt, R. Pure single photons from a trapped atom source. New J. Phys. 2016, 18, 093038. [Google Scholar] [CrossRef]
- Maunz, P.; Moehring, D.; Olmschenk, S.; Younge, K.C.; Matsukevich, D.N.; Monroe, C. Quantum interference of photon pairs from two remote trapped atomic ions. Nat. Phys. 2007, 3, 538–541. [Google Scholar] [CrossRef]
- Zhang, Q.; Dang, C.; Urabe, H.; Wang, J.; Sun, S.; Nurmikko, A. Large ordered arrays of single photon sources based on II-VI semiconductor colloidal quantum dot. Opt. Express 2008, 16, 19592. [Google Scholar] [CrossRef]
- Aharonovich, I.; Englund, D.; Toth, M. Solid-state single-photon emitters. Nat. Photonics 2016, 10, 631–641. [Google Scholar] [CrossRef]
- Bernien, H.; Childress, L.; Robledo, L.; Markham, M.; Twitchen, D.; Hanson, R. Two-photon quantum interference from separate nitrogen vacancy centers in diamond. Phys. Rev. Lett. 2012, 108, 043604. [Google Scholar] [CrossRef]
- Holmes, M.J.; Choi, K.; Kako, S.; Arita, M.; Arakawa, Y. Room-temperature triggered single photon emission from a III-nitride site-controlled nanowire quantum dot. Nano Lett. 2014, 14, 982. [Google Scholar] [CrossRef] [PubMed]
- Rakhlin, M.; Sorokin, S.; Kazanov, D.; Sedova, I.; Shubina, T.; Ivanov, S.; Mikhailovskii, V.; Toropov, A. Bright single-photon emitters with a CdSe quantum dot and multimode tapered nanoantenna for the visible spectral range. Nanomaterials 2021, 11, 916. [Google Scholar] [CrossRef] [PubMed]
- Gazzano, O.; Michaelis de Vasconcellos, S.; Arnold, C.; Nowak, A.; Galopin, E.; Sagnes, I.; Lanco, L.; Lemaître, A.; Senellart, P. Bright solid-state sources of indistinguishable single photons. Nat. Commun. 2013, 4, 1425. [Google Scholar] [CrossRef]
- Friedler, I.; Sauvan, C.; Hugonin, J.P.; Lalanne, P.; Claudon, J.; Gerard, J.-M. Solid-state single photon sources: The nanowire antenna. Opt. Express 2009, 17, 2095. [Google Scholar] [CrossRef]
- Claudon, J.; Bleuse, J.; Malik, N.S.; Bazin, M.; Jaffrennou, P.; Gregersen, N.; Sauvan, C.; Lalanne, P.; Gérard, J.-M. A highly efficient single-photon source based on a quantum dot in a photonic nanowire. Nat. Photonics 2010, 4, 174–177. [Google Scholar] [CrossRef]
- Rakhlin, M.; Klimko, G.; Sorokin, S.; Kulagina, M.; Zadiranov, Y.; Kazanov, D.; Shubina, T.; Ivanov, S.; Toropov, A. Bright single-photon sources for the telecommunication O-band based on an InAs quantum dot with (In)GaAs asymmetric barriers in a photonic nanoantenna. Nanomaterials 2022, 12, 1562. [Google Scholar] [CrossRef]
- Kuhlmann, A.; Houel, J.; Ludwig, A.; Greuter, L.; Reuter, D.; Wieck, A.D.; Poggio, M.; Warburton, R.J. Charge noise and spin noise in a semiconductor quantum device. Nat. Phys. 2013, 9, 570–575. [Google Scholar] [CrossRef]
- Purcell, E.M.; Torrey, H.C.; Pound, R.V. Resonance Absorption by Nuclear Magnetic Moments in a Solid. Phys. Rev. 1946, 69, 37. [Google Scholar] [CrossRef]
- Madsen, K.H.; Ates, S.; Liu, J.; Javadi, A.; Albrecht, S.M.; Yeo, I.; Stobbe, S.; Lodahl, P. Efficient out-coupling of high-purity single photons from a coherent quantum dot in a photonic-crystal cavity. Phys. Rev. B 2014, 90, 155303. [Google Scholar] [CrossRef]
- Arcari, M.; Söllner, I.; Javadi, A.; Albrecht, S.M.; Yeo, I.; Stobbe, S.; Lodahl, P. Near-unity coupling efficiency of a quantum emitter to a photonic crystal waveguide. Phys. Rev. Lett. 2014, 113, 093603. [Google Scholar] [CrossRef]
- Wang, H.; Hu, H.; Chung, T.-H.; Qin, J.; Yang, X.; Li, J.-P.; Liu, R.-Z.; Zhong, H.-S.; He, Y.-M.; Ding, X.; et al. On-demand demiconductor source of entangled photons which simultaneously has high fidelity, efficiency, and indistinguishability. Phys. Rev. Lett. 2019, 122, 113602. [Google Scholar] [CrossRef] [PubMed]
- Santori, C.; Fattal, D.; Vučković, J.; Solomon, G.S.; Yamamoto, Y. Indistinguishable photons from a single-photon device. Nature 2002, 419, 6907. [Google Scholar] [CrossRef]
- Ding, X.; He, Y.; Duan, Z.-C.; Gregersen, N.; Chen, M.-C.; Unsleber, S.; Maier, S.; Schneider, C.; Kamp, M.; Höfling, S.; et al. On-demand single photons with high extraction efficiency and near-unity indistinguishability from a resonantly driven quantum dot in a micropillar. Phys. Rev. Lett. 2016, 116, 020401. [Google Scholar] [CrossRef]
- Somaschi, N.; Giesz, V.; De Santis, L.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Antón, C.; Demory, J.; et al. Near-optimal single-photon sources in the solid state. Nat. Photonics 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Ollivier, H.; Maillette de Buy Wenniger, I.; Thomas, S.; Wein, S.C.; Harouri, A.; Coppola, G.; Hilaire, P.; Millet, C.; Lemaître, A.; Sagnes, I.; et al. Reproducibility of high performance quantum dot single photon sources. ACS Photonics 2020, 7, 1050–1059. [Google Scholar] [CrossRef]
- Tomm, N.; Javadi, A.; Antoniadis, N.O.; Najer, D.; Löbl, M.C.; Korsch, A.R.; Schott, R.; Valentin, S.R.; Wieck, A.D.; Ludwig, A.; et al. A bright and fast source of coherent single photons. Nat. Nanotechnol. 2021, 16, 399–403. [Google Scholar] [CrossRef]
- Rakhlin, M.V.; Galimov, A.I.; Dyakonov, I.V.; Skryabin, N.; Klimko, G.; Kulagina, M.; Zadiranov, Y.; Sorokin, S.; Sedova, I.; Guseva, Y.; et al. Demultiplexed single-photon source with a quantum dot coupled to microresonator. J. Lumin. 2023, 253, 119496. [Google Scholar] [CrossRef]
- He, Y.-M.; Wang, H.; Wang, C.; Chen, M.-C.; Ding, X.; Qin, J.; Duan, Z.-C.; Chen, S.; Li, J.-P.; Liu, R.-Z.; et al. Coherently driving a single quantum two-level system with dichromatic laser pulses. Nat. Phys. 2019, 15, 941–946. [Google Scholar] [CrossRef]
- Thomas, S.E.; Billard, M.; Coste, N.; Wein, S.C.; Priya; Ollivier, H.; Krebs, O.; Tazaïrt, L.; Harouri, A.; Lemaitre, A.; et al. Bright polarized single-photon source based on a linear dipole. Phys. Rev. Lett. 2021, 126, 233601. [Google Scholar] [CrossRef]
- Ortiz, O.; Pastier, F.; Rodriguez, A.; Priya; Lemaitre, A.; Gomez-Carbonell, C.; Sagnes, I.; Harouri, A.; Senellart, P.; Giesz, V.; et al. Fiber-integrated microcavities for efficient generation of coherent acoustic phonons. Appl. Phys. Lett. 2020, 117, 183102. [Google Scholar] [CrossRef]
- Gayral, B.; Gérard, J.M.; Legrand, B.; Costard, E.; Thierry-Mieg, V. Optical study of GaAs/AlAs pillar microcavities with elliptical cross section. Appl. Phys. Lett. 1998, 72, 1421–1423. [Google Scholar] [CrossRef]
- Unitt, D.C.; Bennett, A.J.; Atkinson, P.; Ritchie, D.A.; Shields, A.J. Polarization control of quantum dot single-photon sources via a dipole-dependent Purcell effect. Phys. Rev. B 2005, 72, 033318. [Google Scholar] [CrossRef]
- Lee, Y.; Lin, S. Polarized emission of quantum dots in microcavity and anisotropic Purcell factors. Opt. Express 2014, 22, 1512–1523. [Google Scholar] [CrossRef]
- Uğur Meriç, G.; Michael, M.; Samel, A.; Niels, G. Elliptical micropillar cavity design for highly efficient polarized emission of single photons. Appl. Phys. Lett. 2021, 118, 061101. [Google Scholar]
- Daraei, A.; Tahraoui, A.; Sanvitto, D.; Timpson, J.A.; Fry, P.W.; Hopkinson, M.; Guimarães, P.S.S.; Vinck, H.; Whittaker, D.M.; Skolnick, M.S.; et al. Control of polarized single quantum dot emission in high-quality-factor microcavity pillars. Appl. Phys. Lett. 2006, 88, 051113. [Google Scholar] [CrossRef]
- Strauf, S.; Stoltz, N.; Rakher, M.; Coldren, L.A.; Petroff, P.M.; Bouwmeester, D. High-frequency single-photon source with polarization control. Nat. Photonics 2007, 1, 704–708. [Google Scholar] [CrossRef]
- Wang, H.; He, Y.-M.; Chung, T.-H.; Hu, H.; Yu, Y.; Chen, S.; Ding, X.; Chen, M.-C.; Qin, J.; Yang, X.; et al. Towards optimal single-photon sources from polarized microcavities. Nat. Photonics 2019, 13, 770–775. [Google Scholar] [CrossRef]
- Varoutsis, S.; Laurent, S.; Sagnes, I.; Lemaître, A.; Ferlazzo, L.; Mériadec, C.; Patriarche, G.; Robert-Philip, I.; Abram, I. Reactive-ion etching of high-Q and submicron-diameter GaAs/AlAs micropillar cavities. J. Vac. Sci. Technol. 2005, 23, 2499. [Google Scholar] [CrossRef]
- Heuser, T.; Grobe, J.; Holzinger, S.; Sommer, M.; Reitzenstein, S. Development of highly homogenous quantum dot micropillar arrays for optical reservoir computing. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1900109. [Google Scholar] [CrossRef]
- Joint, F.; Abadie, C.; Vigneron, P.B.; Boulley, L.; Bayle, F.; Isac, N.; Cavanna, A.; Cambril, E.; Herth, E. GaAs manufacturing processes conditions for micro- and nanoscale devices. J. Manuf. Process. 2020, 60, 666. [Google Scholar] [CrossRef]
- Bobrov, M.A.; Blokhin, S.A.; Maleev, N.A.; Kuz’menkov, A.G.; Vasil’ev, A.P.; Guseva, Y.A.; Rakhlin, M.V.; Galimov, A.I.; Serov, Y.M.; Troshkov, S.I.; et al. Simulation and analysis of the optical characteristics of cylindrical micropillars with InAs/GaAs quantum dots. JETP Lett. 2022, 116, 613–618. [Google Scholar] [CrossRef]
- Yeh, C.; Shimabukuro, F.I. The Essence of Dielectric Waveguides; Springer: New York, NY, USA, 2010; Volume 6, pp. 179–210. [Google Scholar]
- Monmayrant, A.; Weber, S.; Chatel, B. A newcomer’s guide to ultrashort pulse shaping and characterization. J. Phys. B At. Mol. Opt. Phys 2010, 43, 103001. [Google Scholar] [CrossRef]
- Wang, G.; Fafard, S.; Leonard, D.; Bowers, J.E.; Merz, J.L.; Petroff, P.M. Time-resolved optical characterization of InGaAs/GaAs quantum dots. Appl. Phys. Lett. 1994, 64, 2815. [Google Scholar] [CrossRef]
- Barnes, W.; Björk, G.; Gérard, J.; Jonsson, P.; Wasey, J.A.E.; Worthing, P.T.; Zwiller, V. Solid-state single photon sources: Light collection strategies. Eur. Phys. J. D 2002, 18, 197–210. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galimov, A.; Bobrov, M.; Rakhlin, M.; Serov, Y.; Kazanov, D.; Veretennikov, A.; Klimko, G.; Sorokin, S.; Sedova, I.; Maleev, N.; et al. Towards Bright Single-Photon Emission in Elliptical Micropillars. Nanomaterials 2023, 13, 1572. https://doi.org/10.3390/nano13091572
Galimov A, Bobrov M, Rakhlin M, Serov Y, Kazanov D, Veretennikov A, Klimko G, Sorokin S, Sedova I, Maleev N, et al. Towards Bright Single-Photon Emission in Elliptical Micropillars. Nanomaterials. 2023; 13(9):1572. https://doi.org/10.3390/nano13091572
Chicago/Turabian StyleGalimov, Aidar, Michail Bobrov, Maxim Rakhlin, Yuriy Serov, Dmitrii Kazanov, Alexey Veretennikov, Grigory Klimko, Sergey Sorokin, Irina Sedova, Nikolai Maleev, and et al. 2023. "Towards Bright Single-Photon Emission in Elliptical Micropillars" Nanomaterials 13, no. 9: 1572. https://doi.org/10.3390/nano13091572
APA StyleGalimov, A., Bobrov, M., Rakhlin, M., Serov, Y., Kazanov, D., Veretennikov, A., Klimko, G., Sorokin, S., Sedova, I., Maleev, N., Zadiranov, Y., Kulagina, M., Guseva, Y., Berezina, D., Nikitina, E., & Toropov, A. (2023). Towards Bright Single-Photon Emission in Elliptical Micropillars. Nanomaterials, 13(9), 1572. https://doi.org/10.3390/nano13091572






