Proton Irradiation on Halide Perovskites: Numerical Calculations
Abstract
:1. Introduction
2. Theory and Calculation Details
3. Results and Discussions
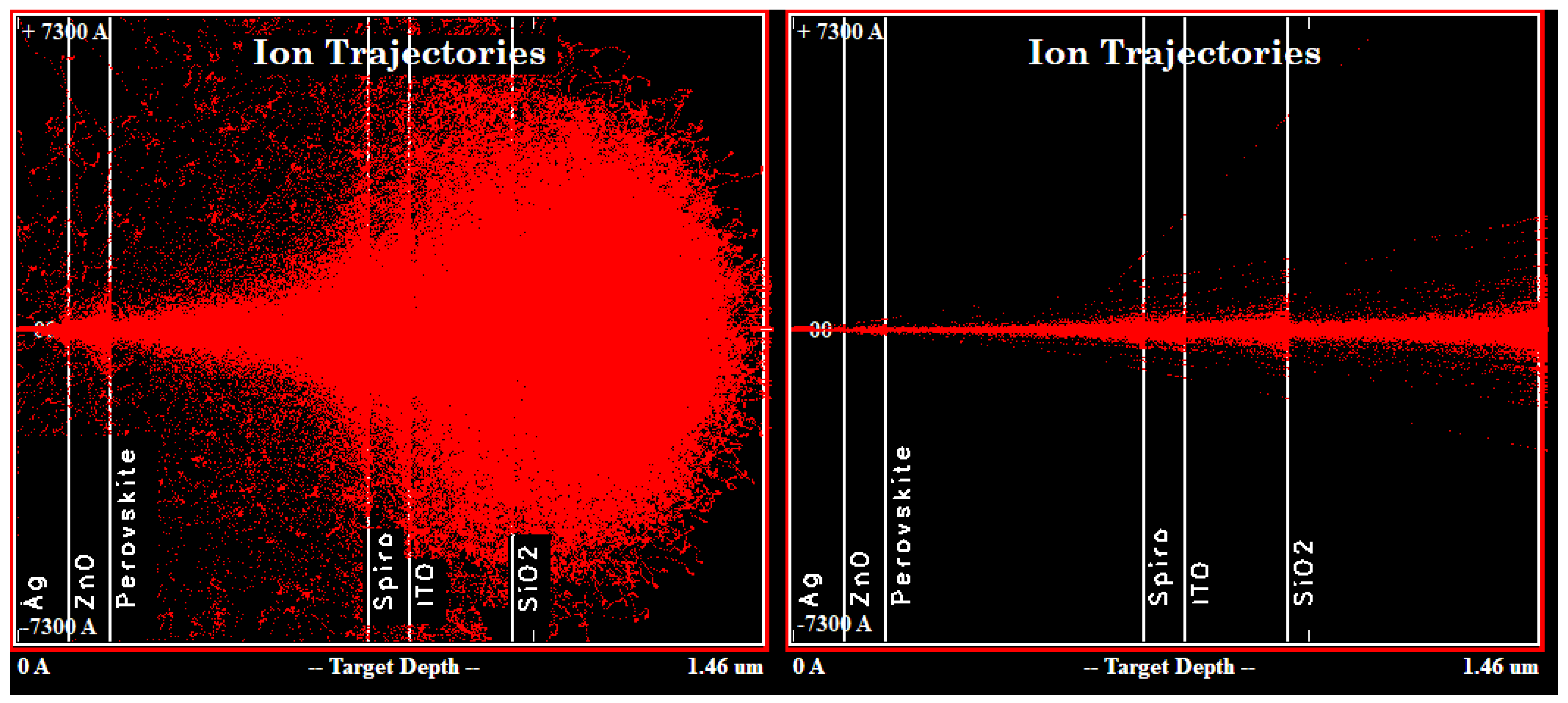
3.1. SRIM Calculations
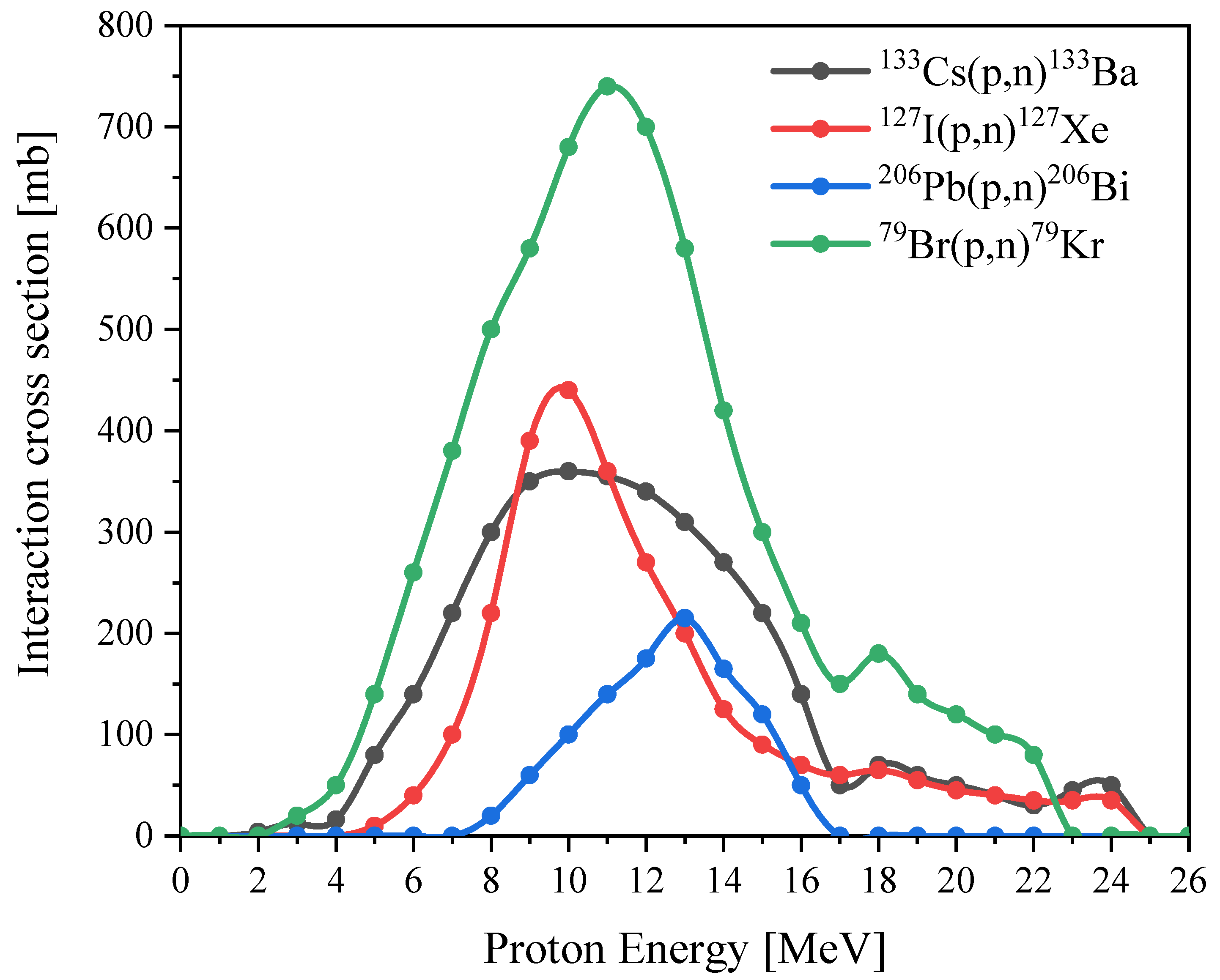
3.2. Calculation of Activation of Irradiated Materials (Inelastic Nuclear Reactions) and Specific Ionization Losses of Proton Energy in Perovskite Samples
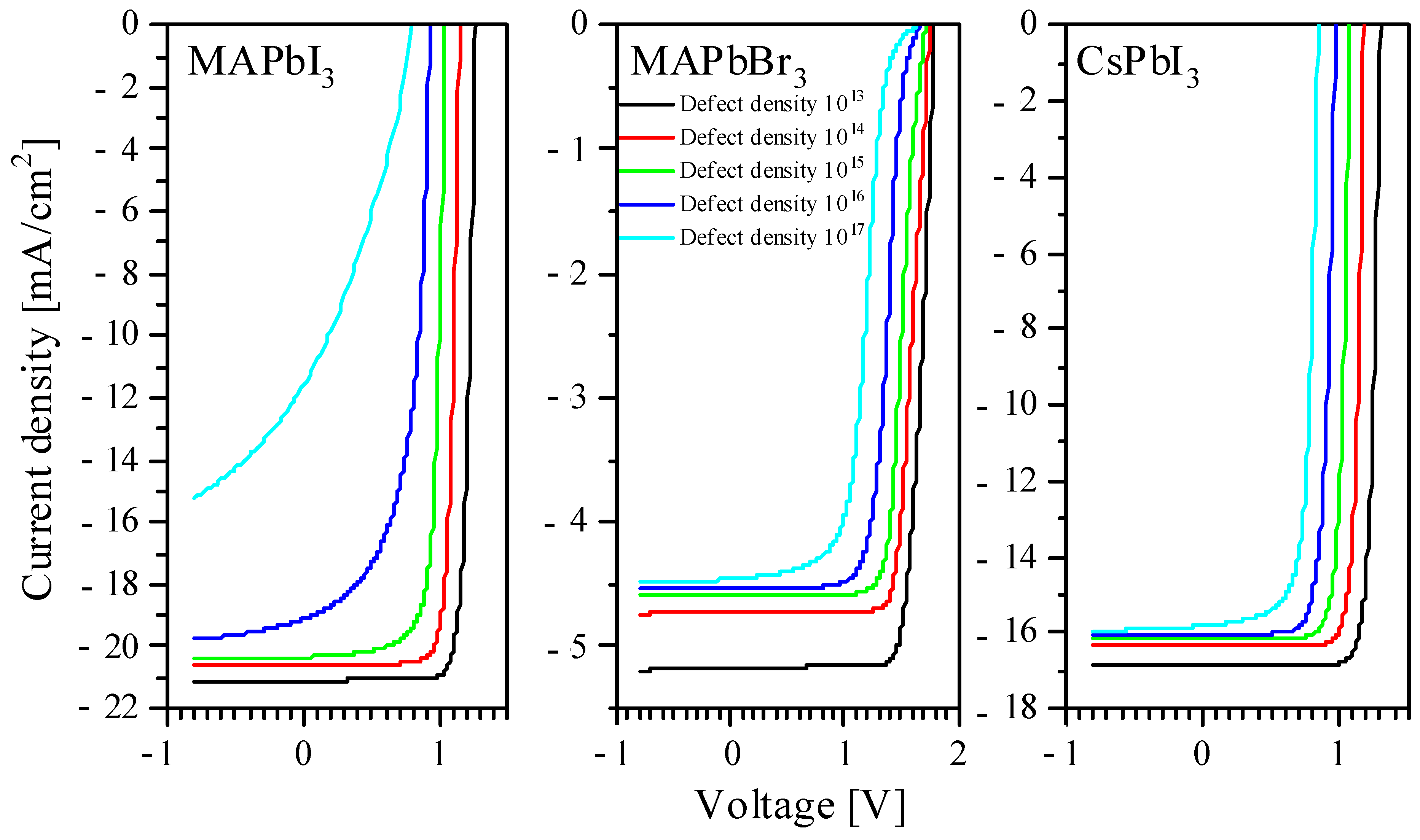
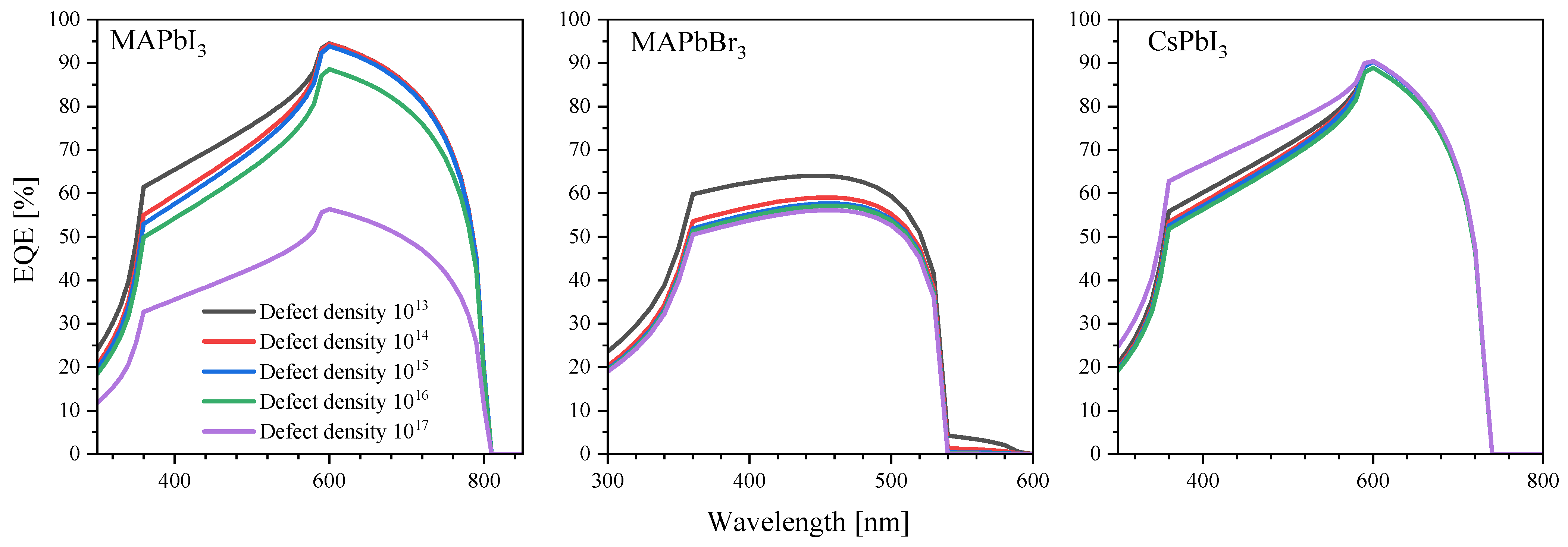
3.3. Effect of Defects on the PCE and Electrophysics Characteristics of PSC
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lang, F.; Shargaieva, O.; Brus, V.V.; Neitzert, H.C.; Rappich, J.; Nickel, N.H. Influence of Radiation on the Properties and the Stability of Hybrid Perovskites. Adv. Mater. 2018, 30, 1702905. [Google Scholar] [CrossRef] [PubMed]
- Lang, F.; Nickel, N.H.; Bundesmann, J.; Seidel, S.; Denker, A.; Albrecht, S.; Brus, V.V.; Rappich, J.; Rech, B.; Landi, G.; et al. Radiation Hardness and Self-Healing of Perovskite Solar Cells. Adv. Mater. 2016, 28, 8726–8731. [Google Scholar] [CrossRef] [PubMed]
- Afshari, H.; Chacon, S.A.; Sourabh, S.; Byers, T.A.; Whiteside, V.R.; Crawford, R.; Rout, B.; Eperon, G.E.; Sellers, I.R. Radiation Tolerance and Self-Healing in Triple Halide Perovskite Solar Cells. APL Energy 2023, 1, 026105. [Google Scholar] [CrossRef]
- Lin, L.; Jones, T.W.; Yang, T.C.-J.; Li, X.; Wu, C.; Xiao, Z.; Li, H.; Li, J.; Qian, J.; Lin, L.; et al. Hydrogen Bonding in Perovskite Solar Cells. Matter 2023. [Google Scholar] [CrossRef]
- Wang, F.; Han, Y.; Duan, D.; Ge, C.; Hu, H.; Li, G. Recent Progress of Scalable Perovskite Solar Cells and Modules. Energy Rev. 2022, 1, 100010. [Google Scholar] [CrossRef]
- Kanaya, S.; Kim, G.M.; Ikegami, M.; Miyasaka, T.; Suzuki, K.; Miyazawa, Y.; Toyota, H.; Osonoe, K.; Yamamoto, T.; Hirose, K. Proton Irradiation Tolerance of High-Efficiency Perovskite Absorbers for Space Applications. J. Phys. Chem. Lett. 2019, 10, 6990–6995. [Google Scholar] [CrossRef]
- Miyazawa, Y.; Ikegami, M.; Chen, H.-W.; Ohshima, T.; Imaizumi, M.; Hirose, K.; Miyasaka, T. Tolerance of Perovskite Solar Cell to High-Energy Particle Irradiations in Space Environment. iScience 2018, 2, 148–155. [Google Scholar] [CrossRef]
- Delmas, W.; Erickson, S.; Arteaga, J.; Woodall, M.; Scheibner, M.; Krause, T.S.; Crowley, K.; VanSant, K.T.; Luther, J.M.; Williams, J.N.; et al. Evaluation of Hybrid Perovskite Prototypes After 10-Month Space Flight on the International Space Station. Adv. Energy Mater. 2023, 13, 2203920. [Google Scholar] [CrossRef]
- Anspaugh, B.E. Proton and Electron Damage Coefficients for GaAs/Ge Solar Cells. In Proceedings of the the Conference Record of the Twenty-Second IEEE Photovoltaic Specialists Conference, Las Vegas, NV, USA, 7–11 October 1991; pp. 1593–1598. [Google Scholar]
- Kirmani, A.R.; Durant, B.K.; Grandidier, J.; Haegel, N.M.; Kelzenberg, M.D.; Lao, Y.M.; McGehee, M.D.; McMillon-Brown, L.; Ostrowski, D.P.; Peshek, T.J.; et al. Countdown to Perovskite Space Launch: Guidelines to Performing Relevant Radiation-Hardness Experiments. Joule 2022, 6, 1015–1031. [Google Scholar] [CrossRef]
- Stoller, R.E.; Toloczko, M.B.; Was, G.S.; Certain, A.G.; Dwaraknath, S.; Garner, F.A. On the Use of SRIM for Computing Radiation Damage Exposure. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2013, 310, 75–80. [Google Scholar] [CrossRef]
- Grieder, P.K.F. Cosmic Ray Properties, Relations and Definitions. In Cosmic Rays at Earth; Elsevier: Amsterdam, The Netherlands, 2001; pp. 1–53. [Google Scholar]
- Biersack, J.P.; Ziegler, J.F. The Stopping and Range of Ions in Solids. In Ion Implantation Techniques; Springer: Berlin/Heidelberg, Germany, 1982; pp. 122–156. [Google Scholar]
- Ziegler, J.F. SRIM-2003. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2004, 219–220, 1027–1036. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM–The Stopping and Range of Ions in Matter (2010). Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Burgelman, M.; Nollet, P.; Degrave, S. Modelling Polycrystalline Semiconductor Solar Cells. Thin Solid Film. 2000, 361–362, 527–532. [Google Scholar] [CrossRef]
- Roy, P.; Raoui, Y.; Khare, A. Design and Simulation of Efficient Tin Based Perovskite Solar Cells through Optimization of Selective Layers: Theoretical Insights. Opt. Mater. 2022, 125, 112057. [Google Scholar] [CrossRef]
- Hao, L.; Li, T.; Ma, X.; Wu, J.; Qiao, L.; Wu, X.; Hou, G.; Pei, H.; Wang, X.; Zhang, X. A Tin-Based Perovskite Solar Cell with an Inverted Hole-Free Transport Layer to Achieve High Energy Conversion Efficiency by SCAPS Device Simulation. Opt. Quantum Electron. 2021, 53, 524. [Google Scholar] [CrossRef]
- Sarker, S.; Islam, M.T.; Rauf, A.; Al Jame, H.; Jani, M.R.; Ahsan, S.; Islam, M.S.; Nishat, S.S.; Shorowordi, K.M.; Ahmed, S. A SCAPS Simulation Investigation of Non-Toxic MAGeI3-on-Si Tandem Solar Device Utilizing Monolithically Integrated (2-T) and Mechanically Stacked (4-T) Configurations. Sol. Energy 2021, 225, 471–485. [Google Scholar] [CrossRef]
- Roy, P.; Khare, A. Analysis of an Efficient and Eco-Friendly CsGeSnI3 Based Perovskite Solar Cell: A Theoretical Study. Mater. Today Proc. 2021, 44, 2997–3000. [Google Scholar] [CrossRef]
- Hossain, M.K.; Rubel, M.H.K.; Toki, G.F.I.; Alam, I.; Rahman, M.F.; Bencherif, H. Effect of Various Electron and Hole Transport Layers on the Performance of CsPbI 3 -Based Perovskite Solar Cells: A Numerical Investigation in DFT, SCAPS-1D, and WxAMPS Frameworks. ACS Omega 2022, 7, 43210–43230. [Google Scholar] [CrossRef]
- Dipta, S.S.; Uddin, A.; Conibeer, G. Enhanced Light Management and Optimization of Perovskite Solar Cells Incorporating Wavelength Dependent Reflectance Modeling. Heliyon 2022, 8, e11380. [Google Scholar] [CrossRef]
- Elsayed, M.R.A.; Elseman, A.M.; Abdelmageed, A.A.; Hashem, H.M.; Hassen, A. Synthesis and Numerical Simulation of Formamidinium-Based Perovskite Solar Cells: A Predictable Device Performance at NIS-Egypt. Sci. Rep. 2023, 13, 10115. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, Y.; Juarez-Perez, E.J.; Ono, L.K.; Qi, Y. Accelerated Degradation of Methylammonium Lead Iodide Perovskites Induced by Exposure to Iodine Vapour. Nat. Energy 2016, 2, 16195. [Google Scholar] [CrossRef]
- Berhe, T.A.; Su, W.-N.; Chen, C.-H.; Pan, C.-J.; Cheng, J.-H.; Chen, H.-M.; Tsai, M.-C.; Chen, L.-Y.; Dubale, A.A.; Hwang, B.-J. Organometal Halide Perovskite Solar Cells: Degradation and Stability. Energy Environ. Sci. 2016, 9, 323–356. [Google Scholar] [CrossRef]
- Zhidkov, I.S.; Yu, M.-H.; Kukharenko, A.I.; Han, P.-C.; Cholakh, S.O.; Yu, W.-Y.; Wu, K.C.-W.; Chueh, C.-C.; Kurmaev, E.Z. The Stability of Hybrid Perovskites with UiO-66 Metal–Organic Framework Additives with Heat, Light, and Humidity. Nanomaterials 2022, 12, 4349. [Google Scholar] [CrossRef] [PubMed]
- Scalon, L.; Vaynzof, Y.; Nogueira, A.F.; Oliveira, C.C. How Organic Chemistry Can Affect Perovskite Photovoltaics. Cell Rep. Phys. Sci. 2023, 4, 101358. [Google Scholar] [CrossRef]
- Kang, S.; Jeong, J.; Cho, S.; Yoon, Y.J.; Park, S.; Lim, S.; Kim, J.Y.; Ko, H. Ultrathin, Lightweight and Flexible Perovskite Solar Cells with an Excellent Power-per-Weight Performance. J. Mater. Chem. A 2019, 7, 1107–1114. [Google Scholar] [CrossRef]
- Aloy, A.S.; Kovalev, N.V.; Prokoshin, A.M.; Karpovich, N.F.; Koltsova, T.I.; Gorshkov, N.G.; Kalinin, V.A.; Blokhin, A.I.; Blokhin, P.A.; Dorofeev, A.N. Radiation Resistance of Borosilicate Glass to Beta and Gamma Radiation Evaluated Using the Accelerated Proton Method. Radioact. Waste 2021, 14, 8–18. [Google Scholar] [CrossRef]
- Ozerova, V.V.; Emelianov, N.A.; Kiryukhin, D.P.; Kushch, P.P.; Shilov, G.V.; Kichigina, G.A.; Aldoshin, S.M.; Frolova, L.A.; Troshin, P.A. Exploring the Limits: Degradation Behavior of Lead Halide Perovskite Films under Exposure to Ultrahigh Doses of γ Rays of Up to 10 MGy. J. Phys. Chem. Lett. 2023, 14, 743–749. [Google Scholar] [CrossRef]
- Teodoro, L.; Davila, A.; Elphic, R.C.; Hamilton, D.; McKay, C.; Quinn, R. Habitability and Biomarker Preservation in the Martian Near-Surface Radiation Environment. In From Habitability to Life on Mars; Elsevier: Amsterdam, The Netherlands, 2018; pp. 211–231. [Google Scholar]
- Nuclear Reaction Database (EXFOR). Available online: http://cdfe.sinp.msu.ru/exfor/index.php (accessed on 12 June 2023).
- Hajjiah, A.; Gamal, M.; Kandas, I.; Gorji, N.E.; Shehata, N. DFT and AMPS-1D Simulation Analysis of All-Perovskite Solar Cells Based on CsPbI3/FAPbI3 Bilayer Structure. Sol. Energy Mater. Sol. Cells 2022, 248, 112026. [Google Scholar] [CrossRef]

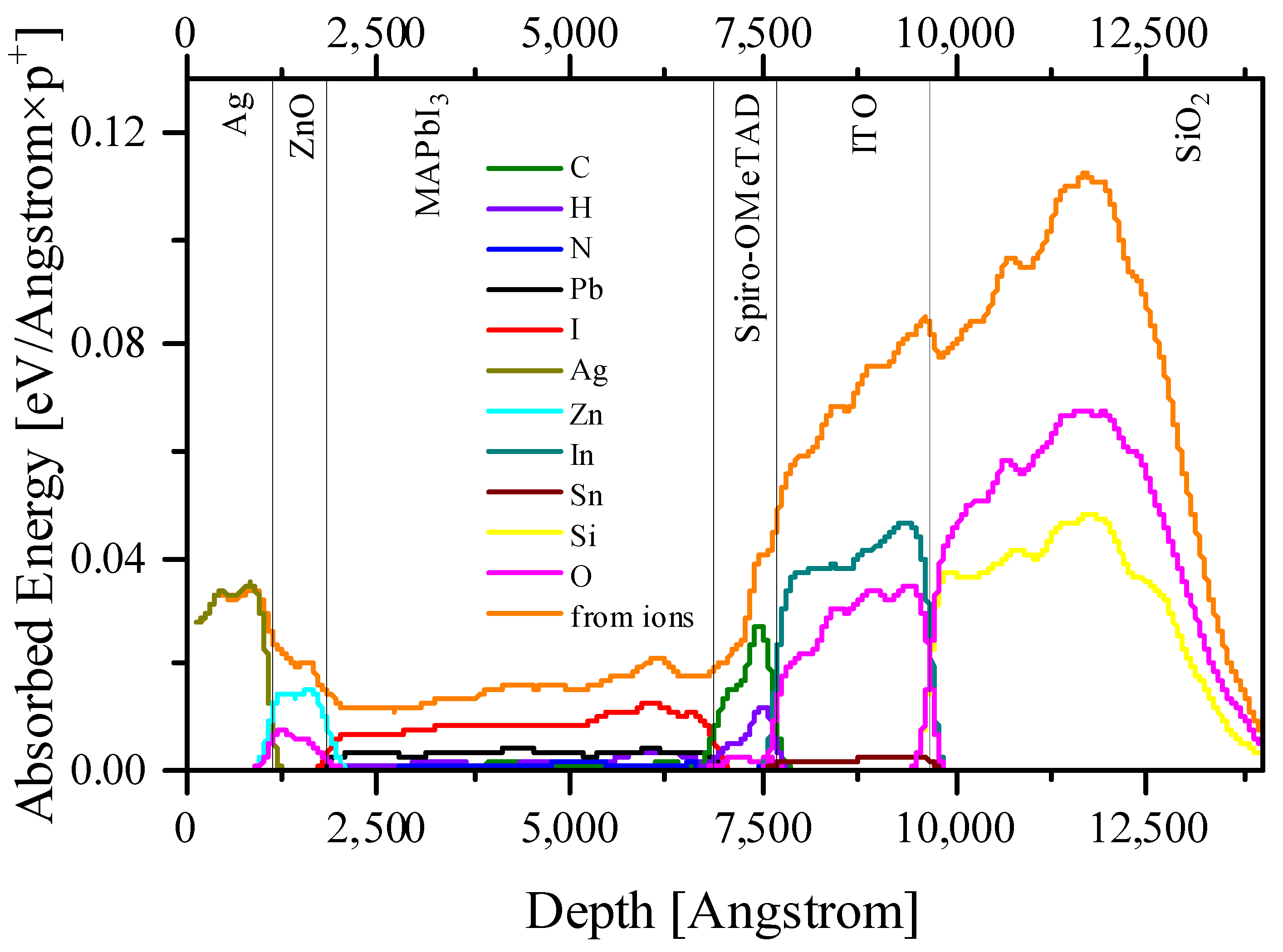
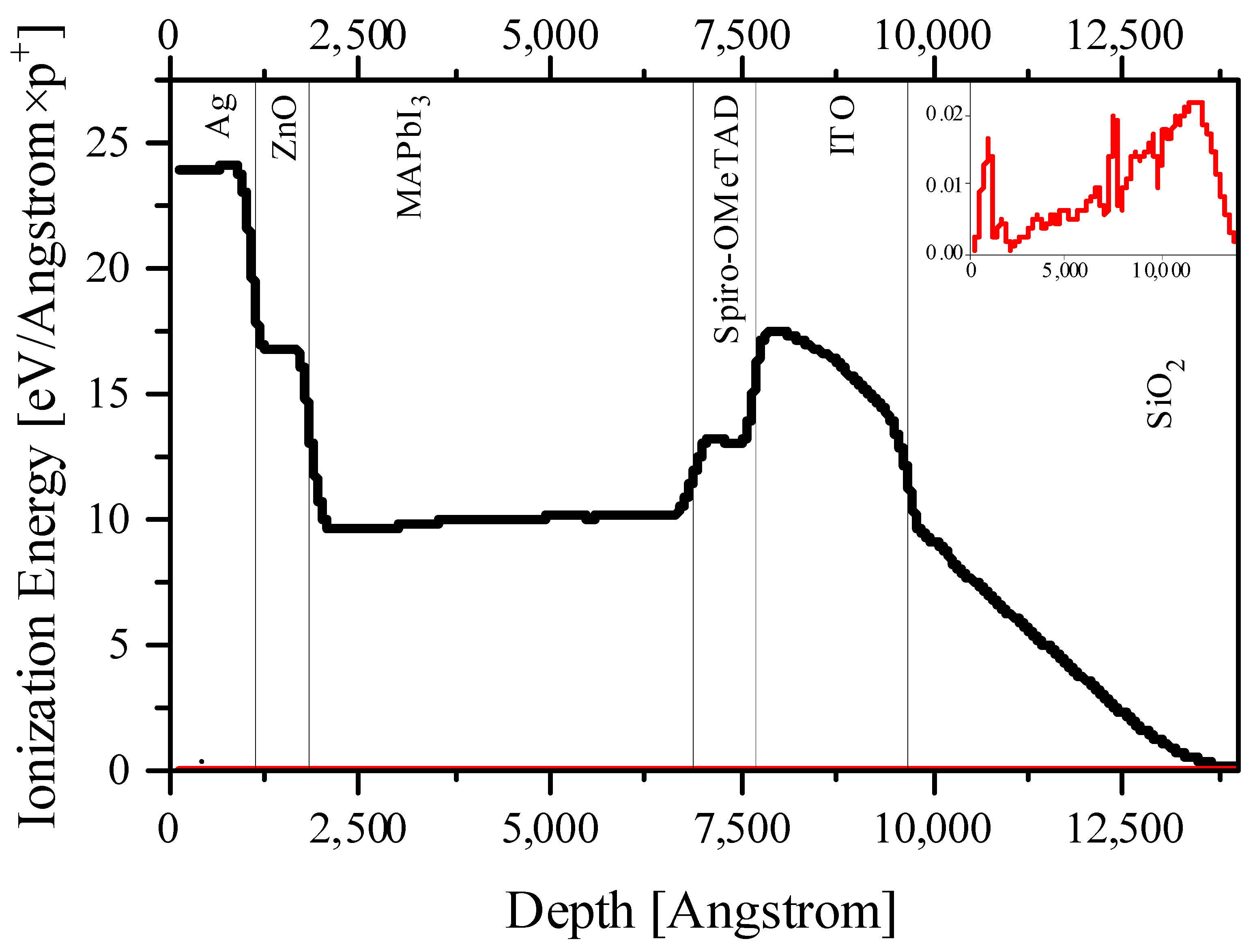
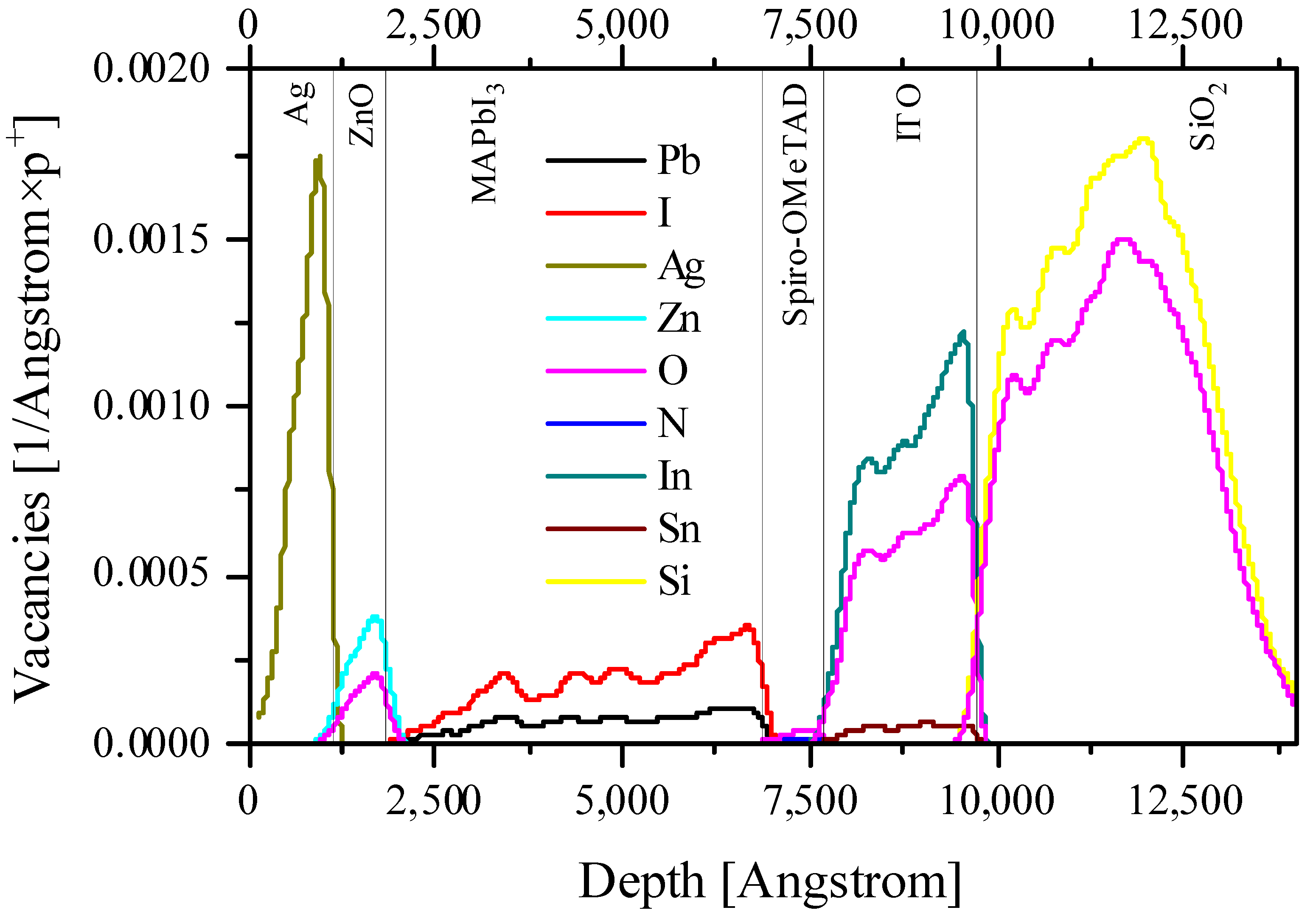
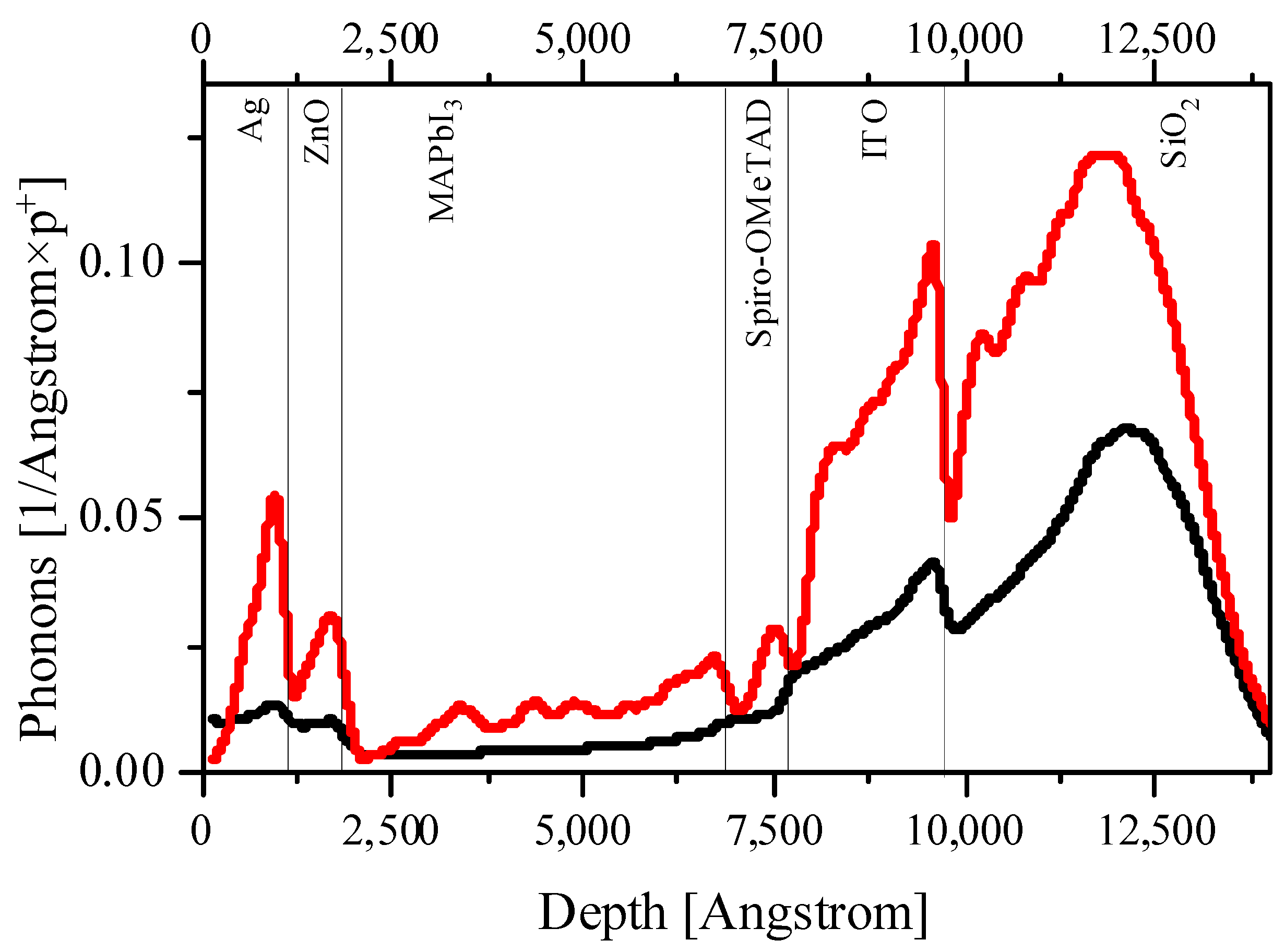
| Sample | Proton Energy, MeV | v, m/s | β | dE/dx, MeV/cm | ∆x, cm |
|---|---|---|---|---|---|
| CsPbBr3 | 16 | 5.537·107 | 0.185 | 40.481 | 0.025 |
| CsPbI3 | 16 | 5.537·107 | 0.185 | 38.539 | 0.026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasmetyeva, A.V.; Zyryanov, S.S.; Novoselov, I.E.; Kukharenko, A.I.; Makarov, E.V.; Cholakh, S.O.; Kurmaev, E.Z.; Zhidkov, I.S. Proton Irradiation on Halide Perovskites: Numerical Calculations. Nanomaterials 2024, 14, 1. https://doi.org/10.3390/nano14010001
Rasmetyeva AV, Zyryanov SS, Novoselov IE, Kukharenko AI, Makarov EV, Cholakh SO, Kurmaev EZ, Zhidkov IS. Proton Irradiation on Halide Perovskites: Numerical Calculations. Nanomaterials. 2024; 14(1):1. https://doi.org/10.3390/nano14010001
Chicago/Turabian StyleRasmetyeva, Alexandra V., Stepan S. Zyryanov, Ivan E. Novoselov, Andrey I. Kukharenko, Efrem V. Makarov, Seif O. Cholakh, Ernst Z. Kurmaev, and Ivan S. Zhidkov. 2024. "Proton Irradiation on Halide Perovskites: Numerical Calculations" Nanomaterials 14, no. 1: 1. https://doi.org/10.3390/nano14010001
APA StyleRasmetyeva, A. V., Zyryanov, S. S., Novoselov, I. E., Kukharenko, A. I., Makarov, E. V., Cholakh, S. O., Kurmaev, E. Z., & Zhidkov, I. S. (2024). Proton Irradiation on Halide Perovskites: Numerical Calculations. Nanomaterials, 14(1), 1. https://doi.org/10.3390/nano14010001









