Mechanical Alloying as a Way to Produce Metastable Single-Phase High-Entropy Alloys beyond the Stability Criteria
Abstract
:1. Introduction
2. Materials and Methods
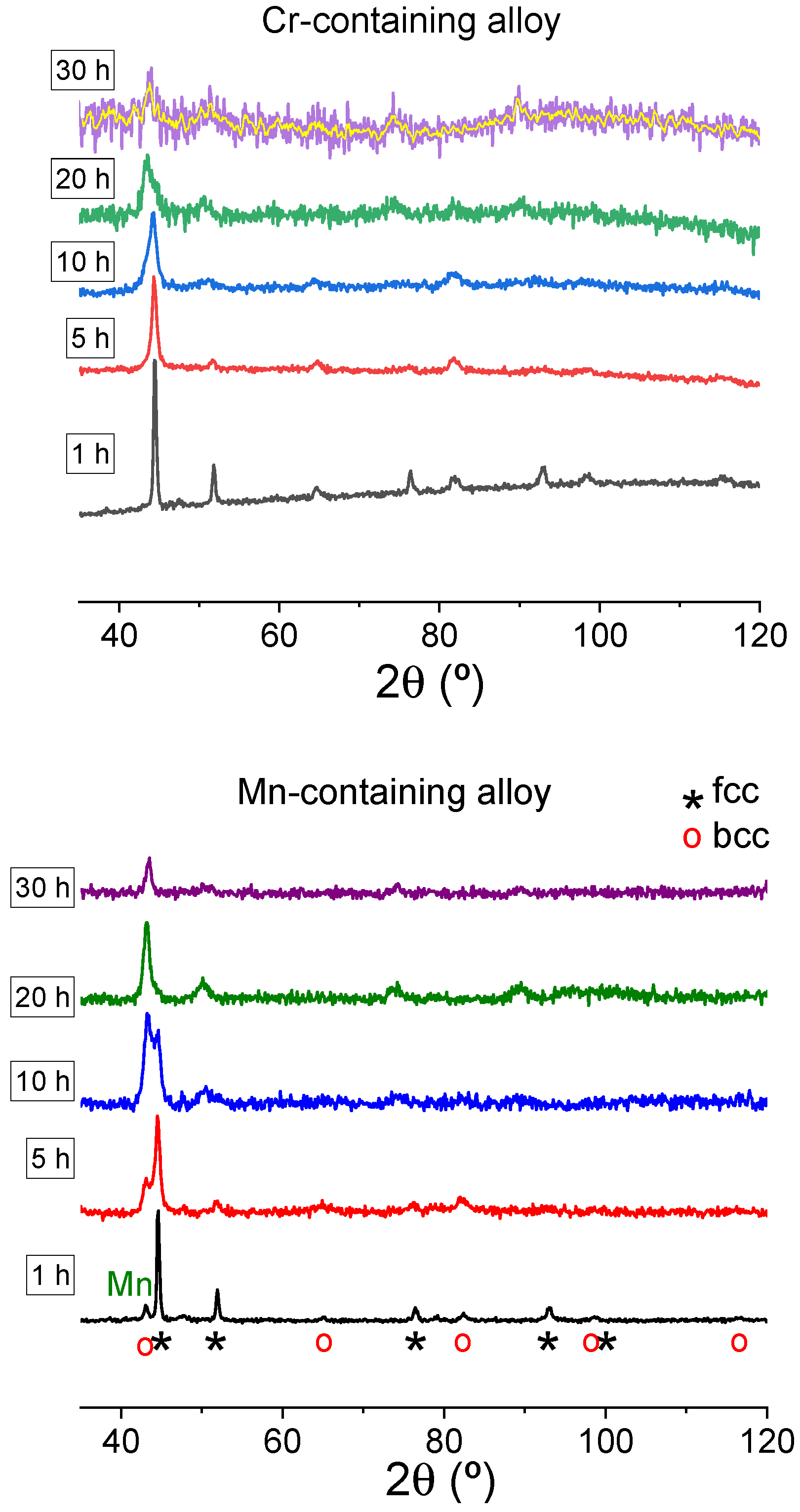
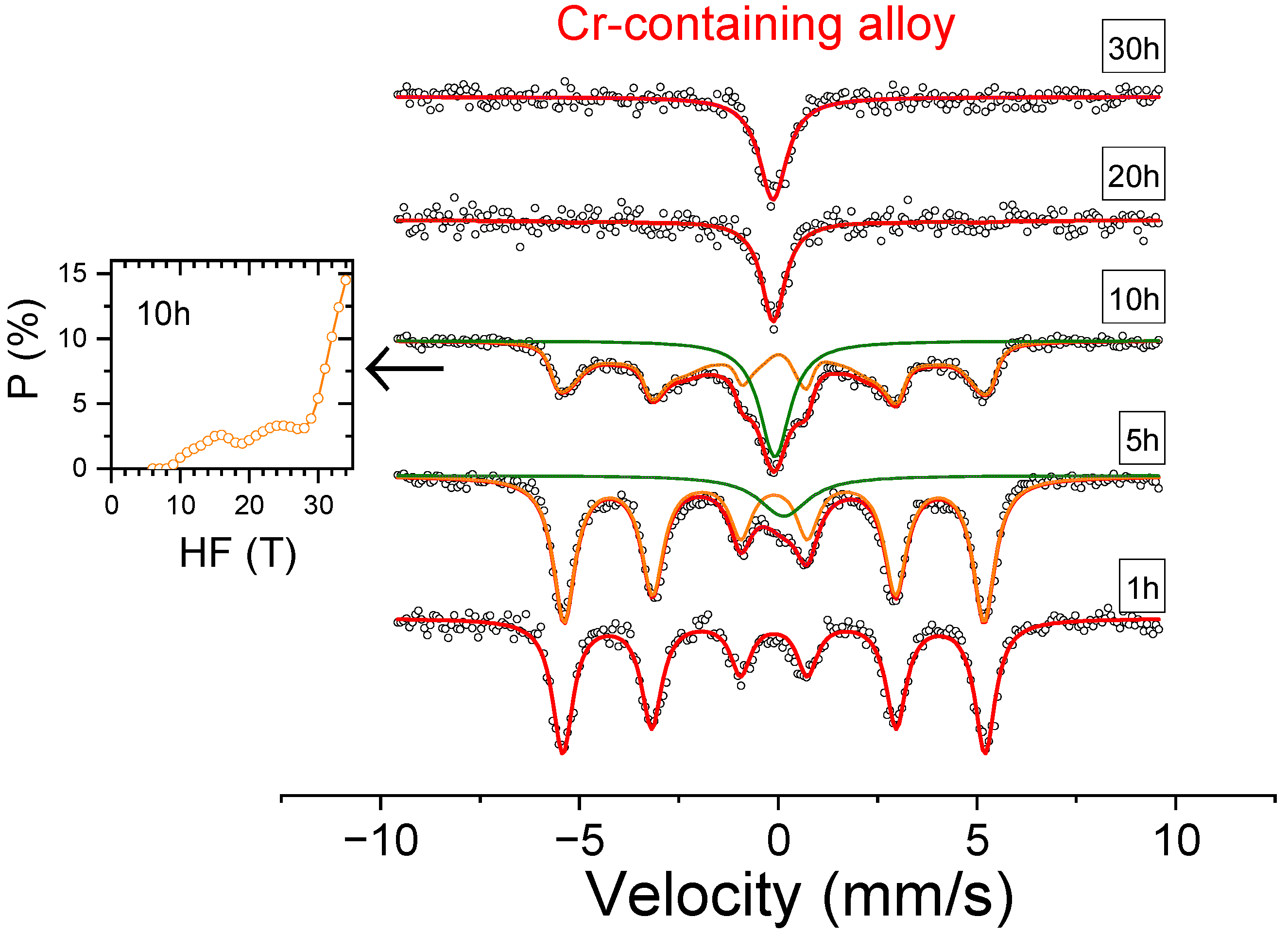
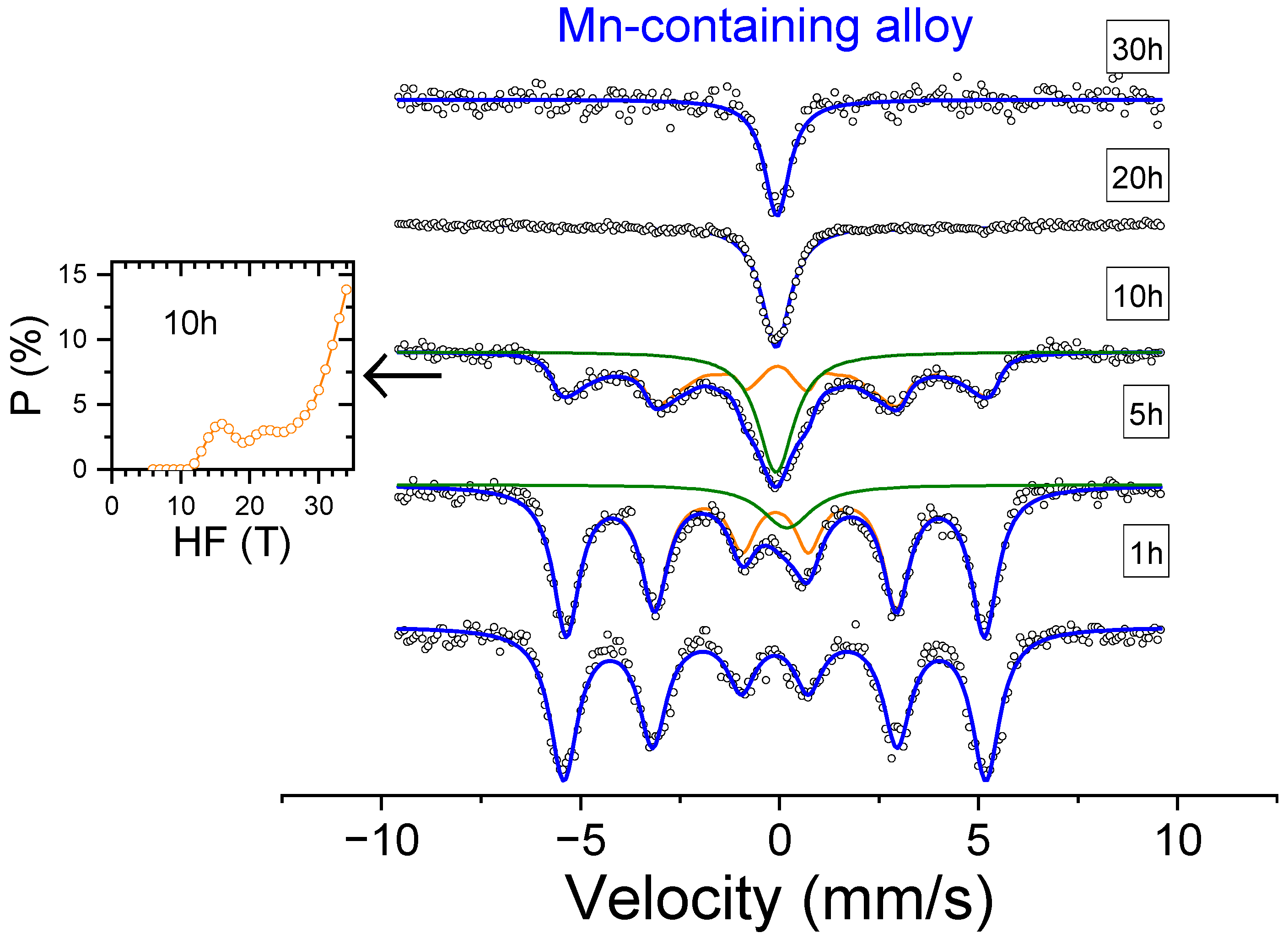
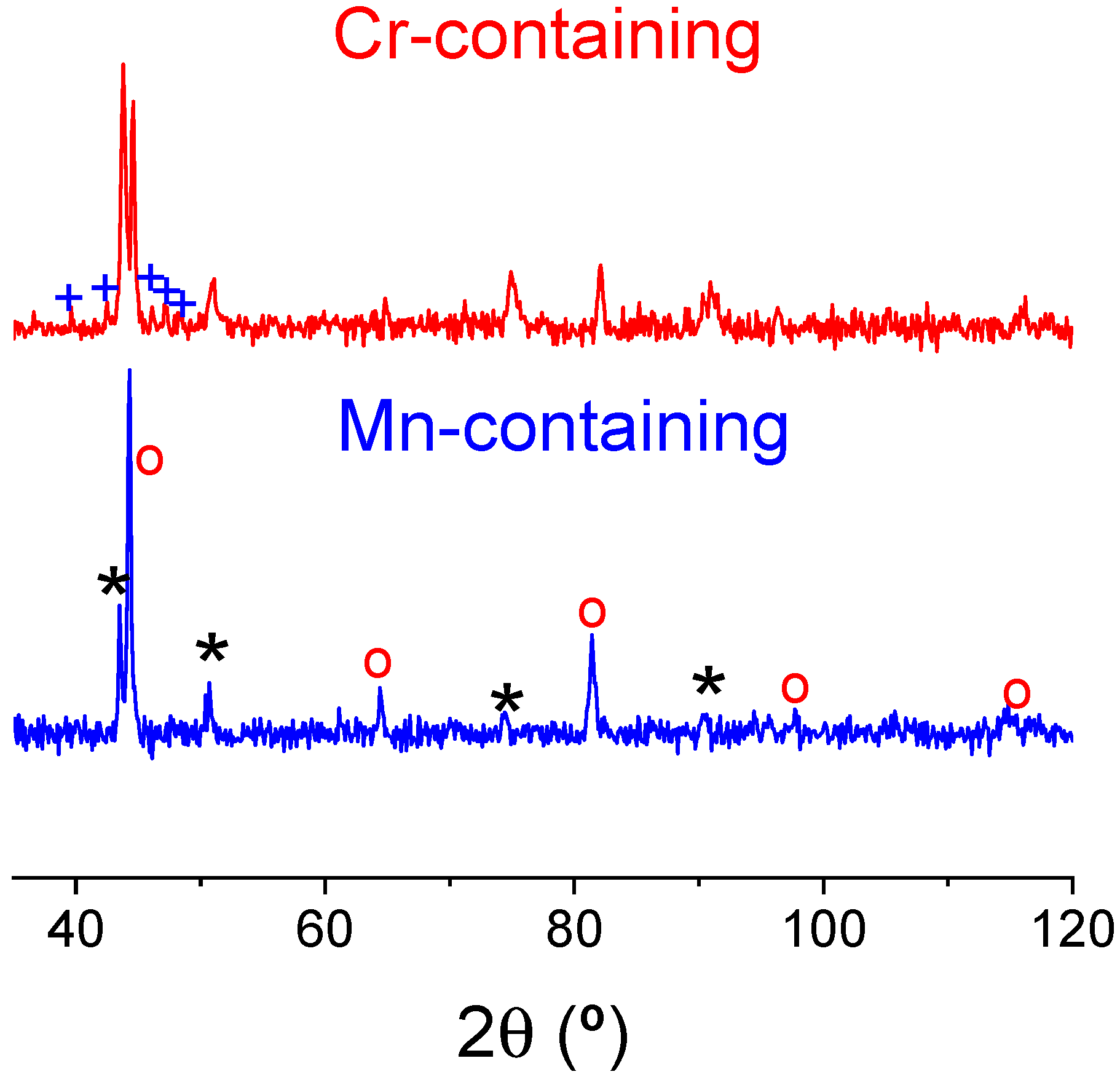
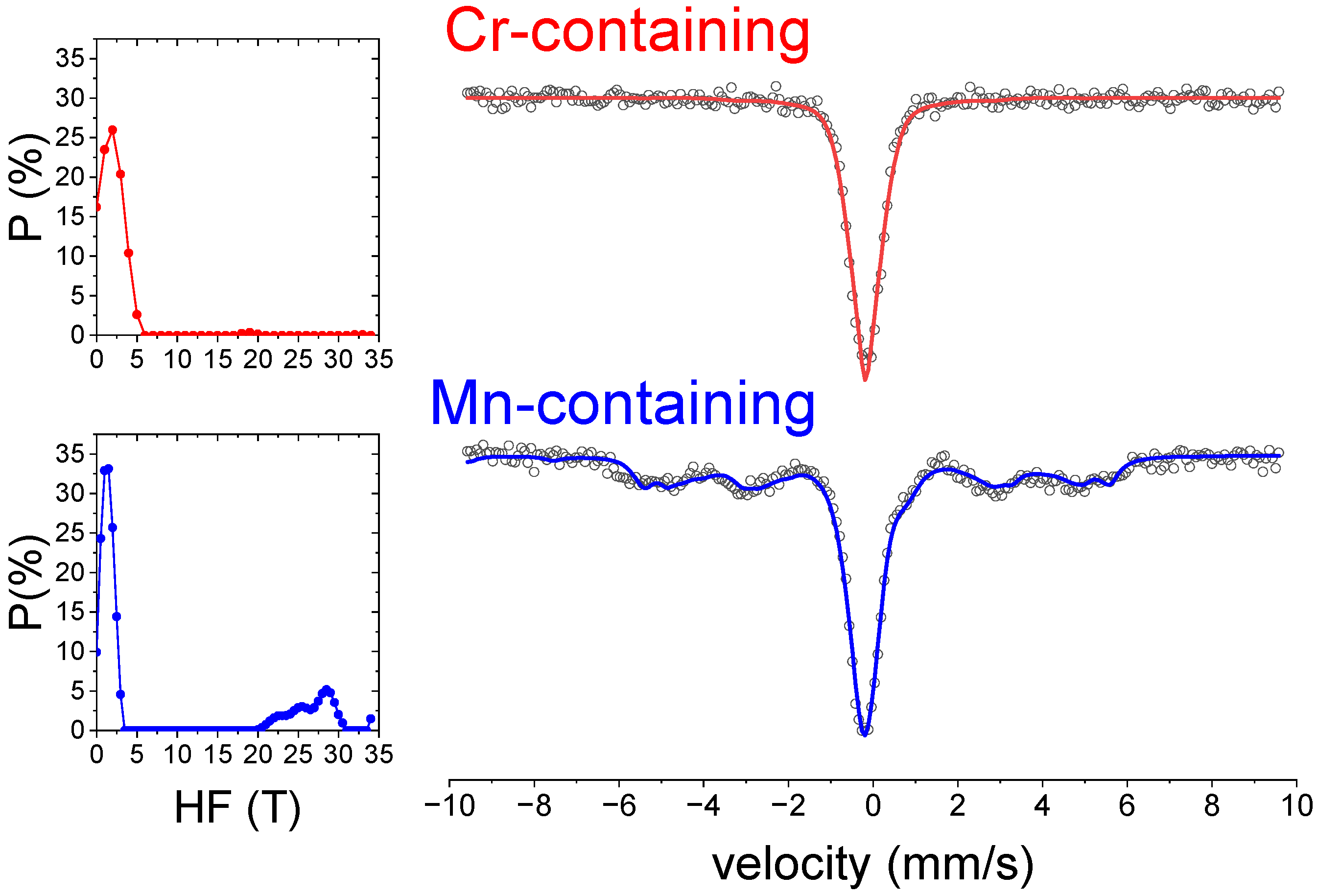
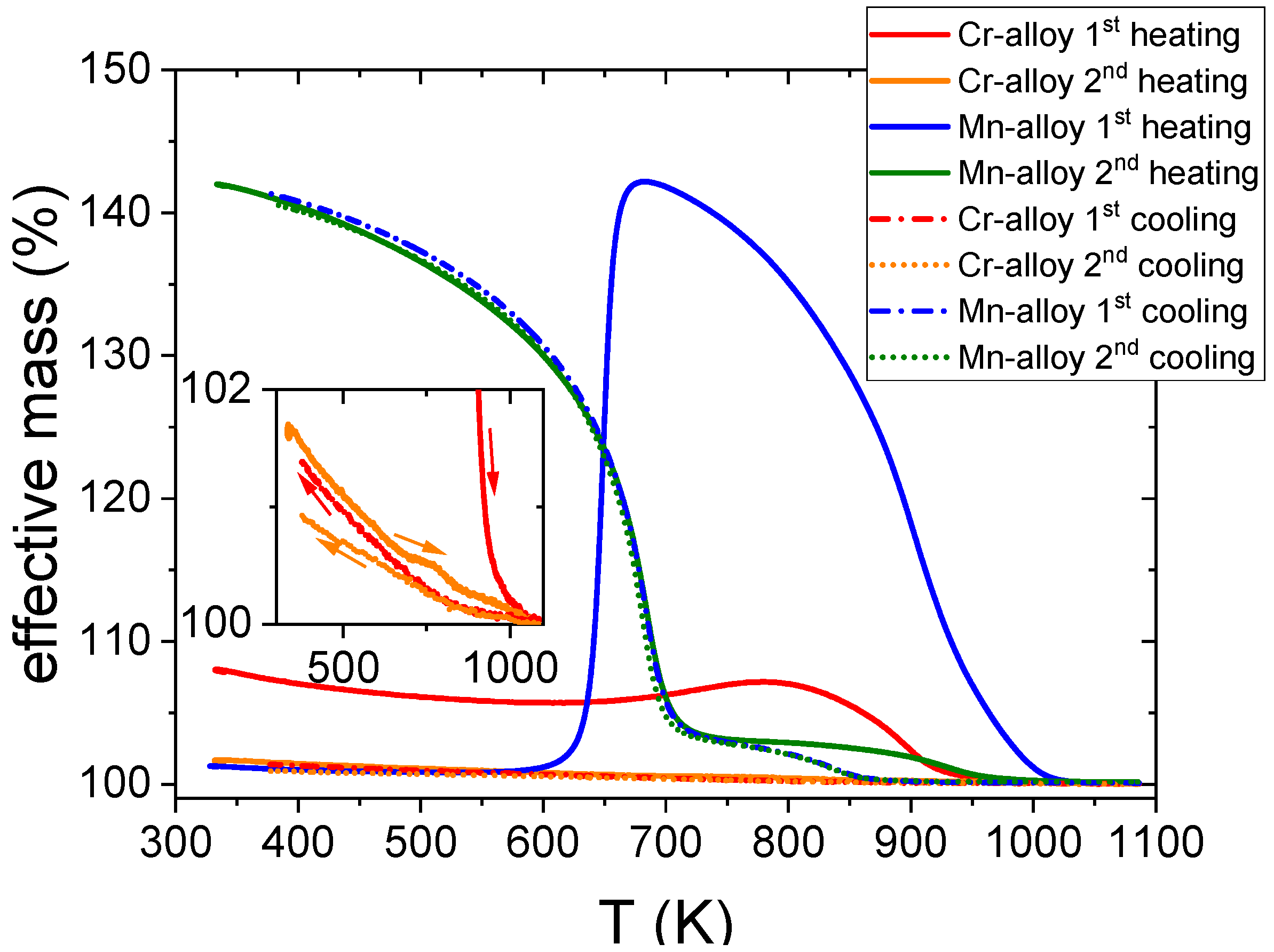
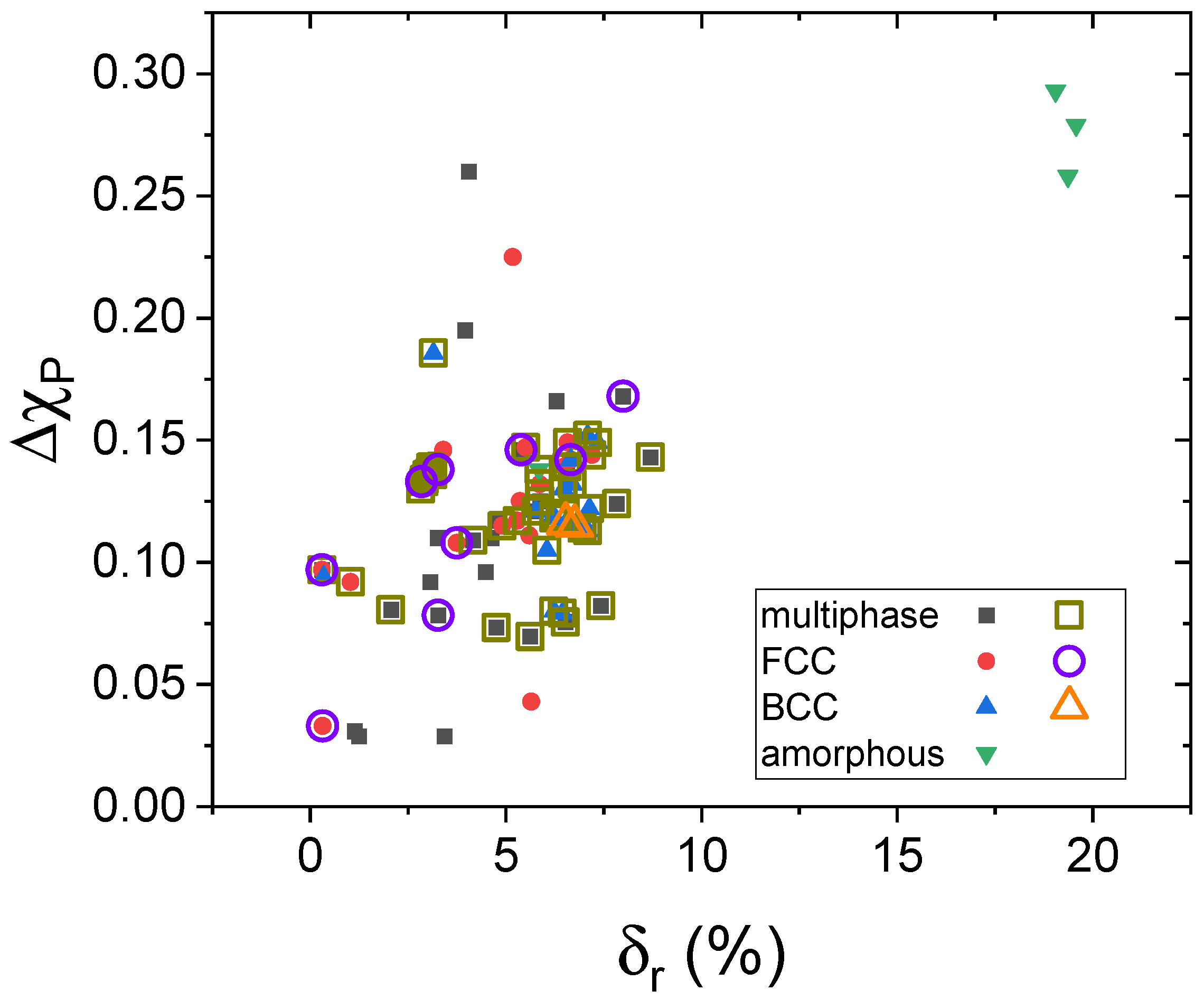
3. Results
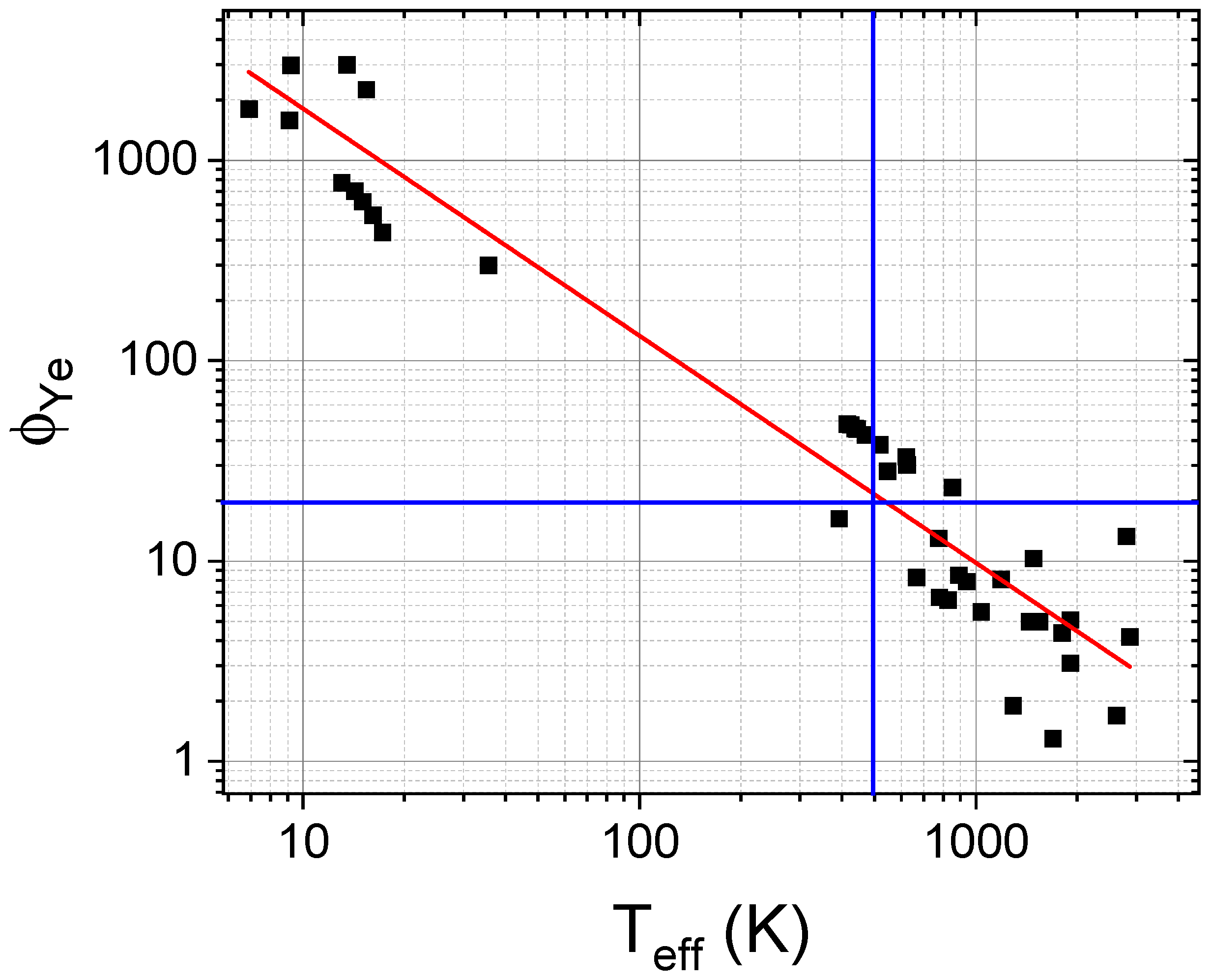
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Wei, S.; He, F.; Tasan, C.C. Metastability in high-entropy alloys: A review. J. Mater. Res. 2018, 33, 2924–2937. [Google Scholar] [CrossRef]
- Miracle, D.B.; Miller, J.D.; Senkov, O.N.; Woodward, C.; Uchic, M.D.; Tiley, J. Exploration and development of high entropy alloys for structural applications. Entropy 2014, 16, 494–525. [Google Scholar] [CrossRef]
- Miracle, D.; Senkov, O. A critical review of high entropy alloys and related concepts. Acta Mater. 2016, 122, 448–511. [Google Scholar] [CrossRef]
- Singh, A.K.; Kumar, N.; Dwivedi, A.; Subramaniam, A. A geometrical parameter for the formation of disordered solid solutions in multi-component alloys. Intermetallics 2014, 53, 112–119. [Google Scholar] [CrossRef]
- King, D.J.M.; Middleburgh, S.C.; McGregor, A.G.; Cortie, M.B. Predicting the formation and stability of single phase high-entropy alloys. Acta Mater. 2016, 104, 172–179. [Google Scholar] [CrossRef]
- Luan, H.W.; Shao, Y.; Li, J.F.; Mao, W.L.; Han, Z.D.; Shao, C.; Yao, K.F. Phase stabilities of high entropy alloys. Scr. Mater. 2020, 179, 40–44. [Google Scholar] [CrossRef]
- Nong, Z.S.; Zhu, J.C.; Cao, Y.; Yang, X.W.; Lai, Z.H.; Liu, Y. Stability and structure prediction of cubic phase in as cast high entropy alloys. Mater. Sci. Technol. 2014, 30, 363–368. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solutions in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Martin, P.; Madrid-Cortes, C.E.; Cáceres, C.; Araya, N.; Aguilar, C.; Cabrera, J.M. HEAPS: A user-friendly tool for the design and exploration of high-entropy alloys based on semiempirical parameters. Comp. Phys. Commun. 2022, 278, 108398. [Google Scholar] [CrossRef]
- Blázquez, J.S.; García-Pinto, N.; Conde, C.F. A simple phenomenological model to describe stability of homogeneous solid solutions in high entropy alloys from metallic bonding potential. Materialia 2023, 28, 101744. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College Publishing: Philadelphia, PA, USA, 1976; pp. 410–412. [Google Scholar]
- Ye, Y.F.; Wang, Q.; Lu, J.; Liu, C.T.; Yang, Y. Design of high entropy alloys: A single-parameter thermodynamic rule. Scr. Mater. 2015, 104, 53–55. [Google Scholar] [CrossRef]
- Gorban, V.F.; Krapivka, N.A.; Firstov, S.A. High-entropy alloys: Interrelations between electron concentration, phase composition, lattice parameter, and properties. Phys. Met. Metall. 2017, 118, 970–981. [Google Scholar] [CrossRef]
- Mansoori, G.A.; Carnahan, N.F.; Starling, K.E.; Leland, T.W., Jr. Equilibrium Thermodynamic Properties of the Mixture of Hard Spheres. J. Chem. Phys. 1971, 54, 1523–1525. [Google Scholar] [CrossRef]
- Duwez, P.; Willens, R.H.; Klement, W., Jr. Continuous Series of Metastable Solid Solutions in Silver-Copper Alloys. J. Appl. Phys. 1960, 31, 1136–1137. [Google Scholar] [CrossRef]
- He, J.H.; Sheng, H.W.; Lin, J.S.; Schilling, P.J.; Tittsworth, R.C.; Ma, E. Homogeneity of a Supersaturated Solid Solution. Phys. Rev. Lett. 2002, 89, 125507. [Google Scholar] [CrossRef]
- Suryanarayana, C.; Al-Aqeeli, N. Mechanically alloyed nanocomposites. Prog. Mater. Sci. 2013, 58, 383–502. [Google Scholar] [CrossRef]
- Liu, H.; Yang, D.; Jiang, Q.; Jiang, Y.; Yang, W.; Liu, L.; Zhang, L.C. Additive manufacturing of metallic glasses and high-entropy alloys: Significance, unsettled issues, and future directions. J. Mater. Sci. Technol. 2023, 140, 79–120. [Google Scholar] [CrossRef]
- Chen, X.; Kong, J.; Feng, S.; Dong, K.; Liang, Y.; Wang, Q.; Yang, Y.; Liu, X. A precipitation-strengthened high-entropy alloy prepared by selective laser melting in-situ alloying and post-heat treatment. J. Alloys Compd. 2023, 936, 168145. [Google Scholar] [CrossRef]
- Vaidya, M.; Muralikrishna, G.M.; Murty, B.S. High-entropy alloys by mechanical alloying: A review. J. Mat. Res. 2019, 34, 664. [Google Scholar] [CrossRef]
- Varalakshmi, C.; Kamaraj, M.; Murty, B.S. Synthesis and characterization of nanocrystalline AlFeTiCrZnCu high entropy solution by mechanical alloying. J. Alloys Compd. 2008, 460, 253–257. [Google Scholar] [CrossRef]
- Koch, C.C. Nanocrystalline high-entropy alloys. J. Mater. Res. 2017, 32, 3435–3444. [Google Scholar] [CrossRef]
- Torralba, J.M.; Alvaredo, P.; García-Junceda, A. High-entropy alloys fabricated via powder metallurgy. A critical Review. Powder Metall. 2019, 62, 84–114. [Google Scholar] [CrossRef]
- Suryanarayana, C. Mechanical Alloying: A critical review. Mater. Res. Lett. 2022, 10, 619–647. [Google Scholar] [CrossRef]
- Nagini, M.; Murty, B.S. Advanced High-Entropy Alloys: A Next Generation Materials. Trans. Indian Nat. Acad. Eng. 2023, 2023, 1–17. [Google Scholar] [CrossRef]
- Chou, H.P.; Chang, Y.S.; Lee, P.H.; Yeh, J.W. Microstructure, thermophysical and electrical properties in AlxCoCrFeNi (0 < x < 2 ) high-entropy alloys. Mat. Sci. Eng. B 2009, 163, 184–189. [Google Scholar] [CrossRef]
- Brand, R.A.; Lauer, J.; Herlach, D.M. The evaluation of hyperfine field distributions in overlapping and asymmetric mossbauer-spectra: A study of the amorphous alloy Pd77.5-XCu6Si16.5FeX. J. Phys. F-Metal Phys. 1983, 13, 675–683. [Google Scholar] [CrossRef]
- Rogachev, A.S.; Kovalev, D.Y.; Kochetov, N.A.; Shchukin, A.S.; Vadchenko, S.G. Evolution of crystal structure in high-entropy AlCoCrFeNi alloy: An in situ high-temperature X-ray diffraction study. J. Alloys Compd. 2021, 861, 158562. [Google Scholar] [CrossRef]
- Gao, W.; Dong, Y.; Jia, X.; Yang, L.; Li, X.; Wu, S.; Zhao, R.; Wu, H.; Li, Q.; He, A.; et al. Novel CoFeAlMn high-entropy alloys with excellent soft magnetic properties and high thermal stability. J. Mater. Sci. Tech. 2023, 153, 22–31. [Google Scholar] [CrossRef]
- Blázquez, J.S.; Ipus, J.J.; Conde, A.; Lozano-Pérez, S. Metastable soft magnetic materials produced by mechanical alloying: Analysis using an equivalent time approach. JOM 2013, 65, 870–882. [Google Scholar] [CrossRef]
- Zeng, Y.; Man, M.; Bai, K.; Zhang, Y.-W. Revealing high-fidelity phase selection rules for high entropy alloys: A combined CALPHAD and machine learning study. Mater. Des. 2021, 202, 109532. [Google Scholar] [CrossRef]
- Guo, S.; Ng, C.; Lu, J.; Liu, C.T. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, S.; Liu, C.T. Phase Selection in High-Entropy Alloys: From Nonequilibrium to Equilibrium. JOM 2014, 66, 1966–1972. [Google Scholar] [CrossRef]
- Poletti, M.G.; Battezzati, L. Electronic and thermodynamic criteria for the occurrence of high entropy alloys in metallic systems. Acta Mater. 2014, 75, 297–306. [Google Scholar] [CrossRef]
- Miedema, A.R.; Châtel, P.F.; de Boer, F.R. Cohesion in alloys. Fundamentals of a semi-empirical model. Phys. B+C 1980, 100, 1–28. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Q.; Zhou, W.; He, F.; Yu, C.; Lin, D.; Wang, J.; Liu, C.T. Quantitative determination of lattice constant in high entropy alloys. Scr. Mater. 2019, 162, 468–471. [Google Scholar] [CrossRef]
- Tsai, M.H.; Tsai, K.Y.; Tsai, C.W.; Lee, C.; Juan, C.C.; Yeh, J.W. Criterion for sigma phase formation in Cr-and V-containing high-entropy alloys. Mater. Res. Lett. 2013, 1, 207–212. [Google Scholar] [CrossRef]
- Tsai, M.H.; Chang, K.C.; Li, J.H.; Tsai, R.C.; Cheng, A.H. A second criterion for sigma phase formation in high-entropy alloys. Mater. Res. Lett. 2015, 4, 90–95. [Google Scholar] [CrossRef]
- Sang, L.; Xu, Y. Amorphous behavior of ZrxFeNiSi0.4B0.6 high entropy alloys synthesized by mechanical alloying. J. Non-Cryst. Solids 2020, 530, 119854. [Google Scholar] [CrossRef]
- Chauhan, P.; Yebaji, S.; Nadakuduru, V.N.; Shanmugasundaram, T. Development of a novel light weight Al35Cr14Mg6Ti35V10 high entropy alloy using mechanical alloying and spark plasma sintering. J. Alloys Compd. 2020, 820, 153367. [Google Scholar] [CrossRef]
- Agarwal, S.; Kumar, R. Synthesis and characterization of nanocrystalline high entropy alloy powder. Mater. Today Proc. 2021, 41, 921–924. [Google Scholar] [CrossRef]
- Rogachev, A.; Kovalev, D.; Fourmont, A.; Vadchenko, S.; Kochetov, N.; Shkodich, N.; Baras, F.; Politano, O.; Moskovskikh, D. Structural Transformations in Medium- and High-Entropy Alloy Systems in Course of High-Energy Ball Milling. Int. J. Self-Propag. High-Temp. Synth. 2022, 31, 62–68. [Google Scholar] [CrossRef]
- Rogachev, A.S.; Kochetov, N.A.; Panteleeva, A.V.; Kuskov, K.V.; Kovalev, D.Y.; Shchukin, A.S.; Vadchenko, S.G.; Scheck, Y.B. High-Energy Ball Milling and Spark Plasma Sintering of the CoCrFeNiAl High-Entropy Alloy. Metals 2020, 10, 1489. [Google Scholar] [CrossRef]
- Rogachev, A.S.; Vadchenko, S.G.; Kochetov, N.A.; Rouvimov, S.; Kovalev, D.Y.; Shchukin, A.S.; Moskovskikh, D.O.; Nepapushev, A.A.; Mukasyan, A.S. Structure and properties of equiatomic CoCrFeNiMn alloy fabricated by high-energy ball milling and spark plasma sintering. J. Alloys Compd. 2019, 805, 1237–1245. [Google Scholar] [CrossRef]
- Chen, C.L.; Suprianto. Microstructure and mechanical properties of AlCuNiFeCr high entropy alloy coatings by mechanical alloying. Surf. Coat. Tech. 2020, 386, 125443. [Google Scholar] [CrossRef]
- Shivam, V.; Shadangi, Y.; Basu, J.; Mukhopadhyay, N.K. Evolution of phases, hardness and magnetic properties of AlCoCrFeNi high entropy alloy processed by mechanical alloying. J. Alloys Compd. 2020, 832, 154826. [Google Scholar] [CrossRef]
- Zhang, Y.; Ai, Y.; Chen, W.; Ouyang, S. Preparation and microstructure and properties of AlCuFeMnTiV lightweight high entropy alloy. J. Alloys Compd. 2022, 900, 163352. [Google Scholar] [CrossRef]
- Ziaei, H.; Sadeghi, B.; Marfavi, Z.; Ebrahimzadeh, N.; Cavaliere, P. Phase evolution in mechanical alloying and spark plasma sintering of AlxCoCrCuFeNi HEAs. Mater. Sci. Technol. 2020, 36, 604–614. [Google Scholar] [CrossRef]
- Youssef, K.M.; Zaddach, A.J.; Niu, C.; Irving, D.L.; Koch, C.C. A Novel Low-Density, High-Hardness, High-entropy Alloy with Close-packed Single-phase Nanocrystalline Structures. Mater. Res. Lett. 2015, 3, 95–99. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, R.; Ren, B.; Jiang, A.; Chen, C.; Liu, J.; Zhou, Y. Mechanical Alloying Behavior and Thermal Stability of CoCrCuFeMnNix High-Entropy Alloy Powders Prepared via MA. Materials 2023, 16, 3179. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Sharma, A.; Ahn, B. Exploring strengthening mechanism of FeCoNiAl high-entropy alloy by non-metallic silicon addition produced via powder metallurgy. J. Alloys Compd. 2023, 947, 169545. [Google Scholar] [CrossRef]
- Chen, Z.; Ren, X.; Wang, P.; Hu, J.; Ge, C. Microstructure and Properties of NiCoCrAlTi High Entropy Alloy Prepared Using MA-SPS Technique. Materials 2023, 16, 2082. [Google Scholar] [CrossRef] [PubMed]
- Jahani, N.; Reihanian, M.; Gheisari, K. Alloying, phases and magnetic behaviour of mechanically alloyed FeNiMnCu-based high entropy alloys. Mater. Sci. Technol. 2023, 39, 1745–1759. [Google Scholar] [CrossRef]
- Rogachev, A.S.; Vadchenko, S.G.; Kovalev, D.Y.; Kochetov, N.A.; Zhukovskyi, M.; Orlova, T.; Mukasyan, A.S. Long term stability of a high-entropy CoCrFeNiTi alloy fabricated by mechanical alloying. J. Alloys Compd. 2023, 931, 167470. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Annasamy, M.; Cizek, P.; Kamaraj, M.; Muralikrishna, G.M.; Hodgson, P.; Fabijanic, D.; Murty, B.S. Evolution of phase constitution with mechanical alloying and spark plasma sintering of nanocrystalline AlxCoCrFeNi (x = 0, 0.3, 0.6, 1 mol) high-entropy alloys. J. Mater. Res. 2022, 37, 959–975. [Google Scholar] [CrossRef]
- Sharma, A.; Lee, H.; Ahn, B. Effect of Additive Elements (x = Cr, Mn, Zn, Sn) on the Phase Evolution and Thermodynamic Complexity of AlCuSiFe-x High Entropy Alloys Fabricated via Powder Metallurgy. Met. Mater. Int. 2022, 28, 2216–2224. [Google Scholar] [CrossRef]
- Moazzen, P.; Toroghinejad, M.R.; Zargar, T.; Cavaliere, P. Investigation of hardness, wear and magnetic properties of NiCoCrFeZrx HEA prepared through mechanical alloying and spark plasma sintering. J. Alloys Compd. 2022, 892, 161924. [Google Scholar] [CrossRef]
- Salemi, F.; Karimzadeh, F.; Abbasi, M.H. Evaluation of Thermal and Mechanical Behavior of CuNiCoZnAl High-Entropy Alloy Fabricated Using Mechanical Alloying and Spark Plasma Sintering. Metall. Mat. Trans. A 2021, 52, 1947–1962. [Google Scholar] [CrossRef]
- Jain, H.; Shadangi, Y.; Shivam, V.; Chakravarty, D.; Mukhopadhyay, N.K.; Kumar, D. Phase evolution and mechanical properties of non-equiatomic Fe–Mn–Ni–Cr–Al–Si–C high entropy steel. J. Alloys Compd. 2020, 834, 155013. [Google Scholar] [CrossRef]
- Dwivedi, A.; Koch, C.C.; Rajulapati, K.V. On the single phase fcc solid solution in nanocrystalline Cr-Nb-Ti-V-Zn high-entropy alloy. Mater. Lett. 2016, 183, 44–47. [Google Scholar] [CrossRef]
- Thangaraju, S.; Bouzy, E.; Hazotte, A. Phase Stability of a Mechanically Alloyed CoCrCuFeNi High Entropy Alloy. Adv. Eng. Mater. 2017, 19, 1700095. [Google Scholar] [CrossRef]
- Mishra, R.K.; Shahi, R.R. Phase evolution and magnetic characteristics of TiFeNiCr and TiFeNiCrM (M = Mn, Co) high entropy alloys. J. Magn. Magn. Mater. 2017, 442, 218–223. [Google Scholar] [CrossRef]
- Song, R.K.; Wei, L.J.; Yang, C.X.; Wu, S.J. Phase formation and strengthening mechanisms in a dual-phase nanocrystalline CrMnFeVTi high-entropy alloy with ultrahigh hardness. J. Alloys Compd. 2018, 744, 552–560. [Google Scholar] [CrossRef]
- Zhao, R.F.; Ren, B.; Zhang, G.P.; Liu, Z.X.; Zhang, J.J. Effect of Co content on the phase transition and magnetic properties of CoxCrCuFeMnNi high-entropy alloy powders. J. Magn. Magn. Mater. 2018, 468, 14–24. [Google Scholar] [CrossRef]
- Vaidya, M.; Karati, A.; Marshal, A.; Pradeep, K.G.; Murty, B.S. Phase evolution and stability of nanocrystalline CoCrFeNi and CoCrFeMnNi high entropy alloys. J. Alloys Compd. 2019, 770, 1004–1015. [Google Scholar] [CrossRef]
- Joy, J.; Jadhav, M.; Sahane, D.; Davis, D.; Singh, S. Elemental effect on formation of solid solution phase in CoCrFeNiX and CoCuFeNiX (X = Ti, Zn, Si, Al) high entropy alloys. Mater. Sci. Technol. 2019, 35, 1700–1707. [Google Scholar] [CrossRef]
- Dong, Q.; Li, M.; Liu, X.; Zhang, Y.; Zhang, J. Microstructure, phase stability, and mechanical properties of (AlLiMg0.5Ti1.5)100-xScx lightweight high-entropy alloys. Intermetallics 2024, 164, 108089. [Google Scholar] [CrossRef]
- Geambazu, L.E.; Talpeanu, D.; Bololoi, R.V.; Manea, C.A.; Bololoi, A.E.; Miculescu, F.; Patroi, D.; Cojocaru, V.D. Microstructural Characterization of Al0.5CrFeNiTi High Entropy Alloy Produced by Powder Metallurgy Route. Materials 2023, 16, 7038. [Google Scholar] [CrossRef]
- Alleg, S.; Bekhouche, A.; Hachache, H.; Sunol, J.J. Effect of Aluminum Addition on the Microstructure, Magnetic, and Mechanical Properties of FeCrCoNiMn High-Entropy Alloy. Crystals 2023, 13, 1483. [Google Scholar] [CrossRef]
- Bololoi, A.E.; Geambazu, L.E.; Antoniac, I.V.; Bololoi, R.V.; Manea, C.A.; Cojocaru, V.D.; Patroi, D. Solid-State Processing of CoCrMoNbTi High-Entropy Alloy for Biomedical Applications. Materials 2023, 16, 6520. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.Y.; Liu, R.; Zhang, X.Z.; Yao, M.X. Influence of Tungsten Content on Microstructural Evolution of Cobalt-Containing High-Entropy Alloy via Mechanical Alloying. Metallogr. Microstruct. Anal. 2023, 12, 760–778. [Google Scholar] [CrossRef]
- Nagarjuna, C.; Dewangan, S.K.; Lee, H.; Ahn, B. Evolution of phase stability and structural properties in CrFeNiTiV high-entropy alloy under high-temperature heat treatment conditions. Mater. Sci. Eng. A 2023, 886, 145680. [Google Scholar] [CrossRef]
- Chen, Z.P.; Ren, X.N.; Wang, P.; Wang, W.C.; Ge, C. Design and experimental investigation of the high-entropy alloys AlCrFeNiCu and AlCrFeNbMo. J. Mater. Res. Technol. 2023, 26, 3118–3135. [Google Scholar] [CrossRef]
- Boztemur, B.; Bayrak, K.G.; Gökçe, H.; Ayas, E.; Balcı-Çağıran, O.; Derin, B.; Ağaoğulları, D.; Öveçoğlu, M.L. Mechanically alloyed and spark plasma sintered WNbMoVTa refractory high entropy alloys: Effects of Cr and Al on the microstructural and mechanical properties. J. Alloys Compd. 2023, 965, 171415. [Google Scholar] [CrossRef]


| Parameter | Ref | Comment | Range for Single-Phase HEA | |
|---|---|---|---|---|
| [10] | Ratio between entropic and enthalpic contributions to mix | Ω ≥ 1.1 and ≤ 6.6% | ||
| [6] | Ratio between entropy due to mixing and elastic energy stored due to size misfit | and | ||
| [14] | Entropy ratio between mixing and excess energy due to atomic size misfit. | bcc | ||
| fcc | ||||
| [7] | is the scaled maximum among absolute values of mixing Gibbs enthalpies of the binary alloys and possible intermetallics | |||
| [12] | Effective temperature at which entropic term equals bonding energy | |||
| Parameter | Ref | Comment | Units | Cr-Alloy | Mn-Alloy |
|---|---|---|---|---|---|
| [3] | Configurational entropy. Maximum entropy, assuming complete atomic disorder | J mol−1K−1 | 13.3 | 13.3 | |
| [3] | Mixing enthalpy, assuming complete atomic disorder | kJ mol−1 | −10.9 | −12.3 | |
| [6] | Atomic size misfit: should be related to the lattice strain energy | % | 5.29 | 5.51 | |
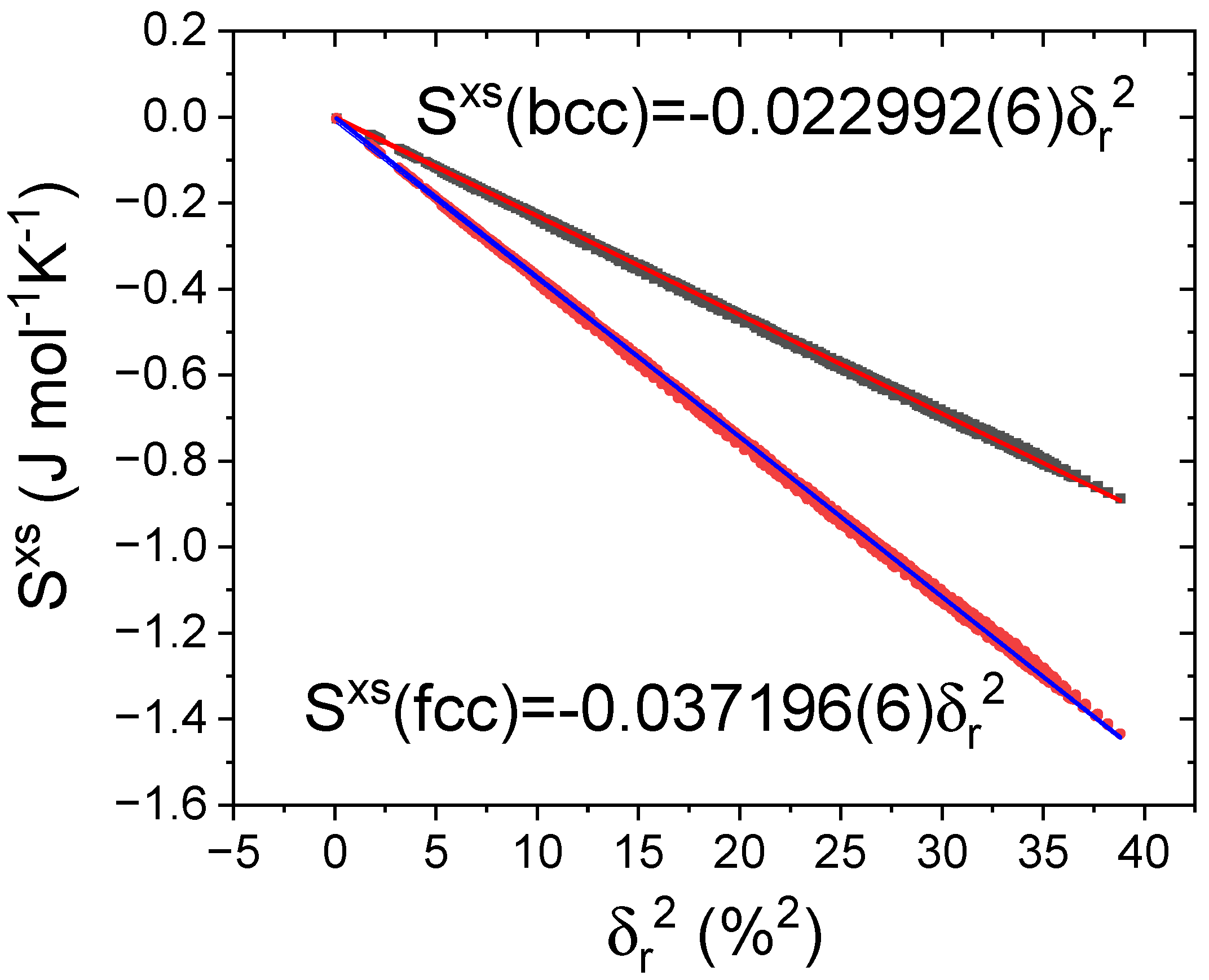
| [16] (*) | Correction to ; due to preferential location of smaller atoms close to larger ones. Linearity estimated for CoFeNiMn(x)Cr(y)Al(z) | J mol−1K−1 | −0.65 | −0.68 | |
| J mol−1K−1 | −1.06 | −1.11 | |||
| [28] | Allen electronegativity misfit | % | 5.89 | 4.91 | |
| Pauling | 6.56 | 8.34 | |||
| [33] | is the valence electron concentration number of electrons per atom in incomplete shells | 2.35 | 2.25 | ||
| [10] | Ratio between entropic and enthalpic contributions to the solid solution | 2.11 | 1.72 | ||
| [6] | Ratio between entropy due to mixing and elastic energy stored due to atomic size misfit | J mol−1K−1 | 0.476 | 0.439 | |
| [14] | Ratio between entropic term favoring solid solution and excess energy due to atomic size misfit. | 6.63 | 5.02 | ||
| [7] | corresponds to the scaled maximum absolute value among the mixing Gibbs enthalpies of the different binary alloys and the possible binary intermetallics | ~0.3 | ~0.3 | ||
| [12] | Effective temperature at which entropic term equals bonding energy | K | 775 | 1543 |
| Composition | As-Milled | Ω | Λ | /K | Annealed | Ref. | |
|---|---|---|---|---|---|---|---|
| FeCoNiMnAl0.75 | fcc | 1.7 | 0.44 | 5.0 | 1544 | fcc+bcc | This work |
| FeCoNiCrAl0.75 | fcc | 2.1 | 0.48 | 6.6 | 777 | fcc+bcc+σ | |
| ZrFeNiSi0.4B0.6 | amorphous+fcc | 0.5 | 0.03 | not reported | [41] | ||
| Zr1.5FeNiSi0.4B0.6 | amorphous+fcc | 0.4 | 0.03 | not reported | [41] | ||
| Zr2.5FeNiSi0.4B0.6 | amorphous+fcc | 0.4 | 0.03 | not reported | [41] | ||
| Al35Cr14Mg6Ti35V10 | bcc | 1.1 | 0.30 | 1.3 | 1692 | bcc(1)+bcc(2)+hcp | [42] |
| Fe30Ni30Al15Cr20Mn5 | fcc | 2.0 | 0.43 | 5.6 | 1035 | not reported | [43] |
| CoCrFeNi | fcc | 5.8 | 130 | 2988 | 9.2 | not reported | [44] |
| AlCoCrFeNi | fcc+bcc | 1.8 | 0.40 | 937 | B2+fcc | [45] | |
| CoCrFeMnNi | fcc | 5.8 | 1.25 | 28.1 | 546 | fcc | [46] |
| Al5Cu5Ni30Cr30Fe30 | bcc+fcc | 4.7 | 1.08 | 332 | not reported | [47] | |
| Al12.5Cu12.5Ni25Cr25Fe25 | fcc+bcc | 5.2 | 0.56 | 663 | not reported | [47] | |
| AlCoCrFeNi | bcc | 1.8 | 0.40 | 7.9 | 937 | B2+L12+σ | [48] |
| AlCuFeMnTiV | bcc/amorphous | 2.3 | 0.44 | 2336 | bcc+B2+fcc+hcp | [49] | |
| Al0.5CoCrCuFeNi | fcc(1)+fcc(2)+bcc | 16.4 | 0.85 | 431 | fcc(1)+fcc(2)+bcc * | [50] | |
| Al1.5CoCrCuFeNi | fcc(1)+fcc(2)+bcc | 3.3 | 0.43 | 902 | fcc(1)+fcc(2)+bcc * | [50] | |
| Al2.5CoCrCuFeNi | B2 | 2.2 | 0.34 | 8.1 | 1185 | B2+fcc * | [50] |
| Al4CoCrCuFeNi | B2 | 1.6 | 0.29 | 5.0 | 1442 | B2 * | [50] |
| Al20Li20Mg10Sc20Ti30 | fcc | 42.6 | 0.48 | 13.0 | 773 | hcp | [51] |
| CoCrCuFeMn | fcc | 5.6 | 1.35 | 30.3 | 623 | fcc(1)+fcc(2)+σ | [52] |
| CoCrCuFeMnNi0.5 | fcc | 9.9 | 1.56 | 38.2 | 517 | fcc(1)+fcc(2)+σ | [52] |
| CoCrCuFeMnNi | fcc | 17.8 | 1.66 | 42.6 | 469 | fcc(1)+fcc(2) | [52] |
| CoCrCuFeMnNi1.5 | fcc | 41.5 | 1.73 | 45.8 | 437 | fcc(1)+fcc(2) | [52] |
| CoCrCuFeMnNi2 | fcc | 100 | 1.79 | 48.3 | 414 | fcc | [52] |
| FeCoNiAl | bcc | 1.3 | 0.30 | 1.9 | 1288 | bcc+fcc | [53] |
| FeCoNiAlSi0.2 | bcc | 1.1 | 0.30 | 0.5 | -- | bcc | [53] |
| FeCoNiAlSi0.4 | bcc | 0.9 | 0.28 | −0.7 | -- | bcc | [53] |
| FeCoNiAlSi0.6 | bcc | 0.8 | 0.27 | −1.6 | -- | bcc+B2 | [53] |
| FeCoNiAlSi0.8 | bcc | 0.8 | 0.27 | −2.3 | -- | bcc+B2 | [53] |
| Ni35Co35Cr12.6Al7.5Ti5Mo1.7W1.4Nb1.0Ta0.5 | fcc+bcc | 1.8 | 0.44 | 1214 | fcc | [54] | |
| FeNiMnCu | fcc | 6.7 | 1.00 | 23.3 | 850 | not reported | [55] |
| FeNiMnCuCo | fcc | 12.4 | 1.33 | 33.2 | 620 | not reported | [55] |
| FeNiMnCuCr | fcc+bcc | 8.5 | 1.31 | 599 | not reported | [55] | |
| FeNiMnCuMo | bcc+fcc | 6.0 | 0.85 | 1687 | not reported | [55] | |
| FeNiMnCuTi | fcc+(bcc) | 2.4 | 0.34 | 2803 | not reported | [55] | |
| FeNiMnCuW | bcc+(fcc) | 4.7 | 0.82 | 2006 | not reported | [55] | |
| Co0.18Cr0.20Fe0.24Ni0.19Ti0.19 | bcc+fcc | 1.7 | 0.31 | 1853 | fcc(1)+fcc(2) * | [56] | |
| CoCrFeNi | fcc | 5.8 | 130 | 2988 | 9.2 | fcc+Cr7C3 | [57] |
| Al0.3CoCrFeNi | fcc | 3.2 | 0.91 | 16.3 | 392 | fcc+Cr7C3 | [57] |
| Al0.6CoCrFeNi | fcc | 2.4 | 0.55 | 8.3 | 665 | fcc+bcc+Cr7C3 | [57] |
| AlCoCrFeNi | bcc+fcc | 1.8 | 0.40 | 937 | fcc+bcc+Cr7C3 | [57] | |
| AlCuSiFeCr | bcc | 1.2 | 0.26 | 2.2 | -- | bcc +fcc+σ | [58] |
| AlCuSiFeMn | bcc | 0.9 | 0.25 | −0.9 | -- | bcc +fcc+μ | [58] |
| AlCuSiFeZn | bcc+fcc | 1.3 | 0.22 | -- | fcc+bcc | [58] | |
| AlCuSiFeSn | bcc+fcc | 1.8 | 0.18 | -- | Fcc * | [58] | |
| NiCoCrFe | bcc+fcc | 5.8 | 130 | 9.2 | fcc+bcc | [59] | |
| NiCoCrFeZr0.4 | bcc+fcc | 1.8 | 0.20 | 2803 | fcc | [59] | |
| CuNiCoZnAl | fcc | 2.5 | 0.39 | 6.4 | 823 | multiphase | [60] |
| Fe40Mn14Ni10Cr10Al15C1 | bcc | 1.9 | 0.25 | 5.5 | -- | fcc+B2+Cr3Si * | [61] |
| CrNbTiVZn | fcc | 7.4 | 0.42 | 10.3 | 1480 | not reported | [62] |
| CoCrCuFeNi | fcc | 7.4 | 12.6 | 300 | 35.5 | fcc(1)+fcc(2) | [63] |
| TiFeNiCr | fcc | 1.4 | 0.22 | 1.7 | 2615 | fcc(1)+fcc(2)+σ | [64] |
| TiFeNiCrMn | fcc | 2.0 | 0.31 | 4.2 | 2868 | fcc(1)+fcc(2)+σ | [64] |
| TiFeNiCrCo | fcc | 1.6 | 0.30 | 3.1 | 1907 | fcc | [64] |
| CrMnFeVTi | bcc | 5.6 | 0.37 | 13.3 | 2796 | bcc+fcc | [65] |
| Co0.5CrCuFeMnNi | fcc+bcc | 12.8 | 1.54 | 508 | fcc(1)+fcc(2) * | [66] | |
| CoCrCuFeMnNi | fcc | 17.8 | 1.66 | 42.6 | 469 | fcc(1)+fcc(2) | [66] |
| Co1.5CrCuFeMnNi | fcc | 24.6 | 1.75 | 45.6 | 443 | fcc(1)+fcc(2) | [66] |
| Co2CrCuFeMnNi | fcc | 34.3 | 1.82 | 47.9 | 424 | fcc(1)+fcc(2) | [66] |
| CoFeNi | fcc | 12.1 | 88.6 | 2257 | 15.4 | fcc+Cr7C3 | [67] |
| CoCrFeNi | fcc | 5.8 | 130 | 2988 | 9.2 | fcc+Cr7C3 | [67] |
| CoCrFeMnNi | fcc | 5.8 | 1.25 | 28.1 | 546 | fcc | [67] |
| CoCrFe | bcc | 6.6 | 78.9 | 3008 | 13.5 | not reported | [68] |
| CoCrFeNi | fcc | 5.8 | 130 | 2988 | 9.2 | not reported | [68] |
| CoCrFeNiTi | bcc | 1.6 | 0.30 | 5.1 | 1907 | not reported | [68] |
| CoCrFeNiZn | fcc+bcc | 6.8 | 0.62 | 161 | not reported | [68] | |
| CoCrFeNiSi | fcc+bcc | 0.9 | 1.42 | -- | not reported | [68] | |
| CoCrFeNiAl | bcc | 1.8 | 0.40 | 7.9 | 937 | not reported | [68] |
| CoCuFe | fcc+bcc | 1.9 | 5.96 | 65 | not reported | [68] | |
| CoCuFeNi | fcc(1)+fcc(2) | 3.8 | 8.90 | 49 | not reported | [68] | |
| CoCuFeNiTi | fcc | 2.1 | 0.32 | 4.4 | 1799 | not reported | [68] |
| CoCuFeNiZn | fcc(1)+fcc(2) | 11.2 | 0.66 | 164 | not reported | [68] | |
| CoCuFeNiSi | fcc(1)+fcc(2) | 1.3 | 1.13 | -- | not reported | [68] | |
| CoCuFeNiAl | fcc | 3.9 | 0.43 | 8.5 | 889 | not reported | [68] |
| AlLiMg0.5Ti1.5 | hcp+AlLi | 4.0 | 0.84 | 17.2 | 437 | intermetallics | [69] |
| (AlLiMg0.5Ti1.5)95Sc5 | hcp | 6.7 | 0.69 | 16.1 | 532 | intermetallics | [69] |
| (AlLiMg0.5Ti1.5)90Sc10 | hcp | 12.7 | 0.59 | 15.0 | 623 | intermetallics | [69] |
| (AlLiMg0.5Ti1.5)85Sc15 | hcp | 44.4 | 0.53 | 14.2 | 703 | intermetallics | [69] |
| (AlLiMg0.5Ti1.5)80Sc20 | hcp | 42.6 | 0.48 | 13.0 | 773 | hcp+intermet. | [69] |
| Al0.5CrFeNiTi | fcc+bcc+hcp | 1.2 | 0.24 | 2279 | fcc+bcc+2 hcp | [70] | |
| FeCoCrNiMn | fcc+bcc | 5.8 | 1.25 | 546 | fcc | [71] | |
| (FeCoCrNi)80Mn10Al10 | fcc+bcc | 2.8 | 0.65 | 800 | fcc+bcc+σ | [71] | |
| CoCrMnNbTi | bcc(1)+bcc(2)+tet | 2.2 | 0.32 | not reported | [72] | ||
| CoCrFeNiW0.2 | bcc+fcc | 7.0 | 2.95 | 433 | bcc+fcc+σ | [73] | |
| CrFeNiTiV | bcc | 2.0 | 0.32 | 6.9 | 1802 | bcc+Ni3Ti * | [74] |
| AlCrFeNiCu | bcc+fcc | 5.4 | 0.42 | 912 | B2+fcc+σ | [75] | |
| AlCrFeNbMo | bcc | 2.3 | 0.35 | 9.1 | 1587 | bcc+fcc+σ | [75] |
| WNbMoVTa | bcc+WC | 8.5 | 1.35 | bcc+others | [76] | ||
| WNbMoVTaCr | bcc+WC+NbTa | 9.0 | 0.69 | bcc+others | [76] | ||
| WNbMoVTaAl | bcc+WC+NbTa | 4.0 | 1.49 | bcc+others | [76] | ||
| WNbMoVTaCr0.5 | bcc+WC+NbTa | 9.1 | 0.87 | bcc+others | [76] | ||
| WNbMoVTaAl0.5 | bcc+WC+NbTa | 5.2 | 1.46 | bcc+others | [76] | ||
| WNbMoVTaCr0.5Al0.5 | bcc+WC+NbTa | 5.7 | 0.94 | bcc+others | [76] | ||
| WNbMoVTaCr0.5Al | bcc+WC+NbTa | 4.4 | 0.96 | bcc+others | [76] | ||
| WNbMoVTaCrAl0.5 | bcc+WC+NbTa | 5.9 | 0.73 | bcc+others | [76] | ||
| WNbMoVTaCrAl | bcc+WC+NbTa | 4.5 | 0.75 | bcc+others | [76] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santiago-Andrades, L.; Vidal-Crespo, A.; Blázquez, J.S.; Ipus, J.J.; Conde, C.F. Mechanical Alloying as a Way to Produce Metastable Single-Phase High-Entropy Alloys beyond the Stability Criteria. Nanomaterials 2024, 14, 27. https://doi.org/10.3390/nano14010027
Santiago-Andrades L, Vidal-Crespo A, Blázquez JS, Ipus JJ, Conde CF. Mechanical Alloying as a Way to Produce Metastable Single-Phase High-Entropy Alloys beyond the Stability Criteria. Nanomaterials. 2024; 14(1):27. https://doi.org/10.3390/nano14010027
Chicago/Turabian StyleSantiago-Andrades, Lucía, Antonio Vidal-Crespo, Javier S. Blázquez, Jhon J. Ipus, and Clara F. Conde. 2024. "Mechanical Alloying as a Way to Produce Metastable Single-Phase High-Entropy Alloys beyond the Stability Criteria" Nanomaterials 14, no. 1: 27. https://doi.org/10.3390/nano14010027
APA StyleSantiago-Andrades, L., Vidal-Crespo, A., Blázquez, J. S., Ipus, J. J., & Conde, C. F. (2024). Mechanical Alloying as a Way to Produce Metastable Single-Phase High-Entropy Alloys beyond the Stability Criteria. Nanomaterials, 14(1), 27. https://doi.org/10.3390/nano14010027








