Metasurface Holography with Multiplexing and Reconfigurability
Abstract
:1. Introduction
2. Single Metasurface Holography
2.1. Phase-Only Metasurface Holography
2.2. Amplitude-Only Metasurface Holography
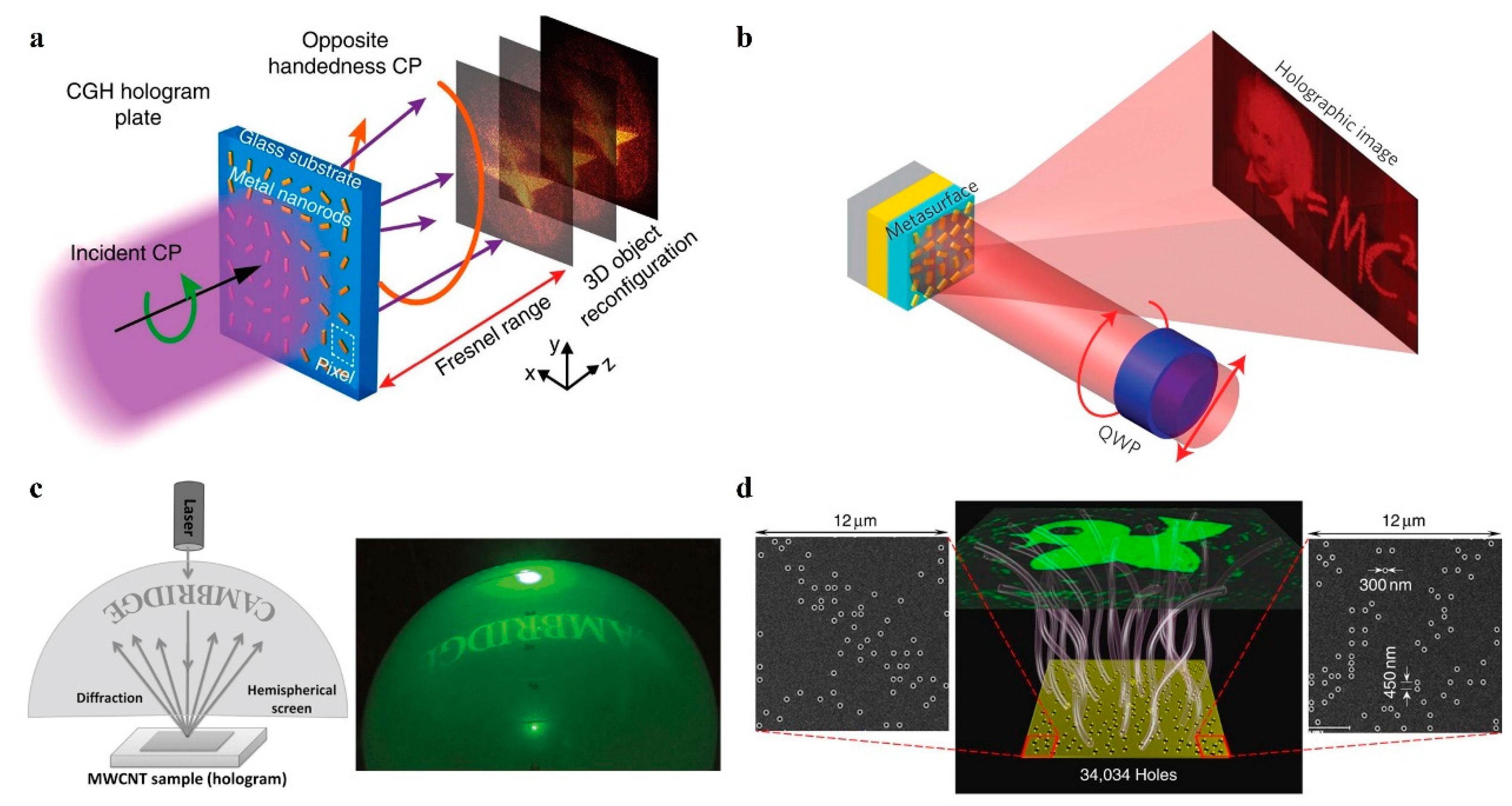
2.3. Complex Amplitude Metasurface Holography
3. Multiplexed Metasurface Holography
3.1. Orbital Angular Momentum Multiplexed Metasurface Holography
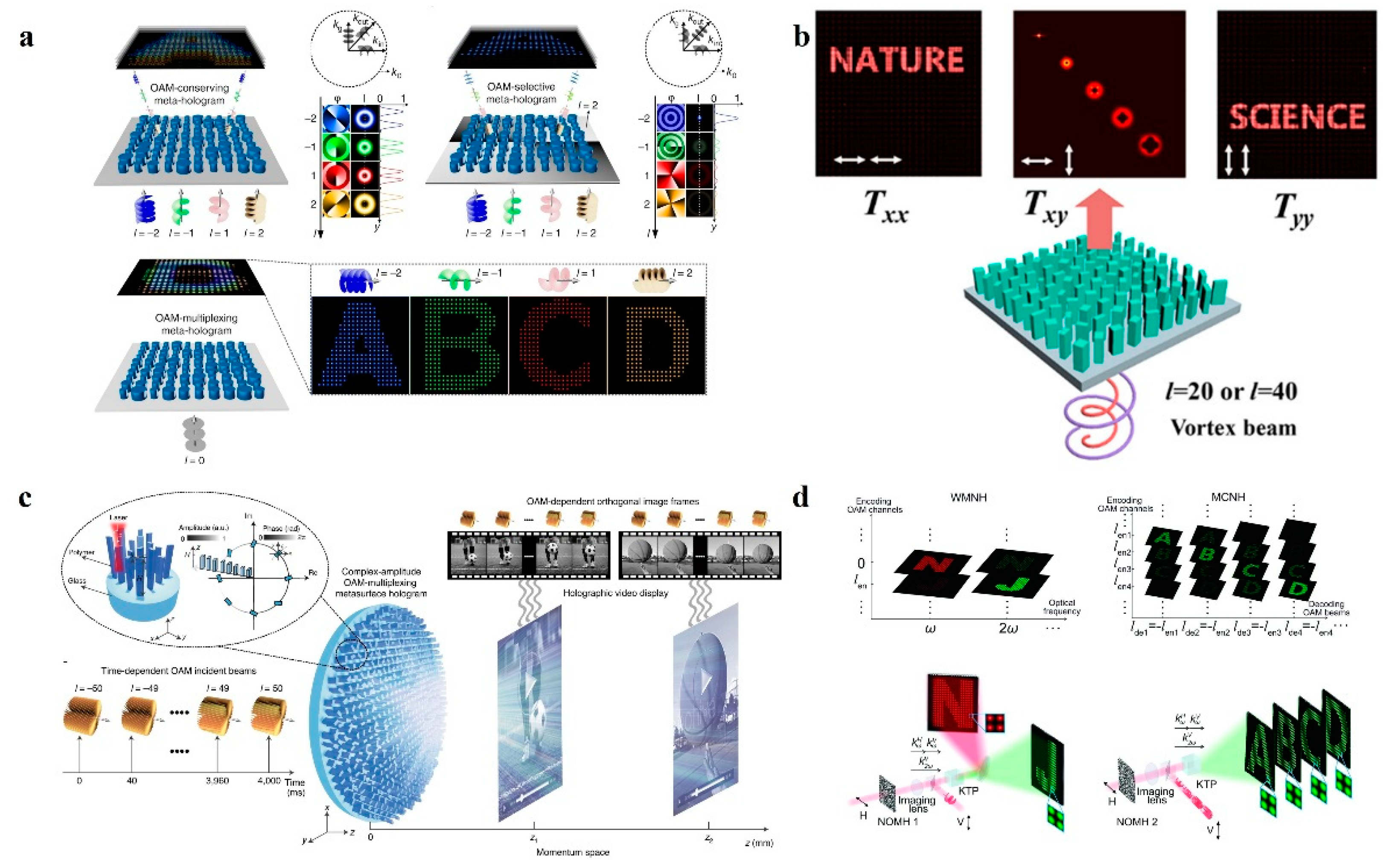
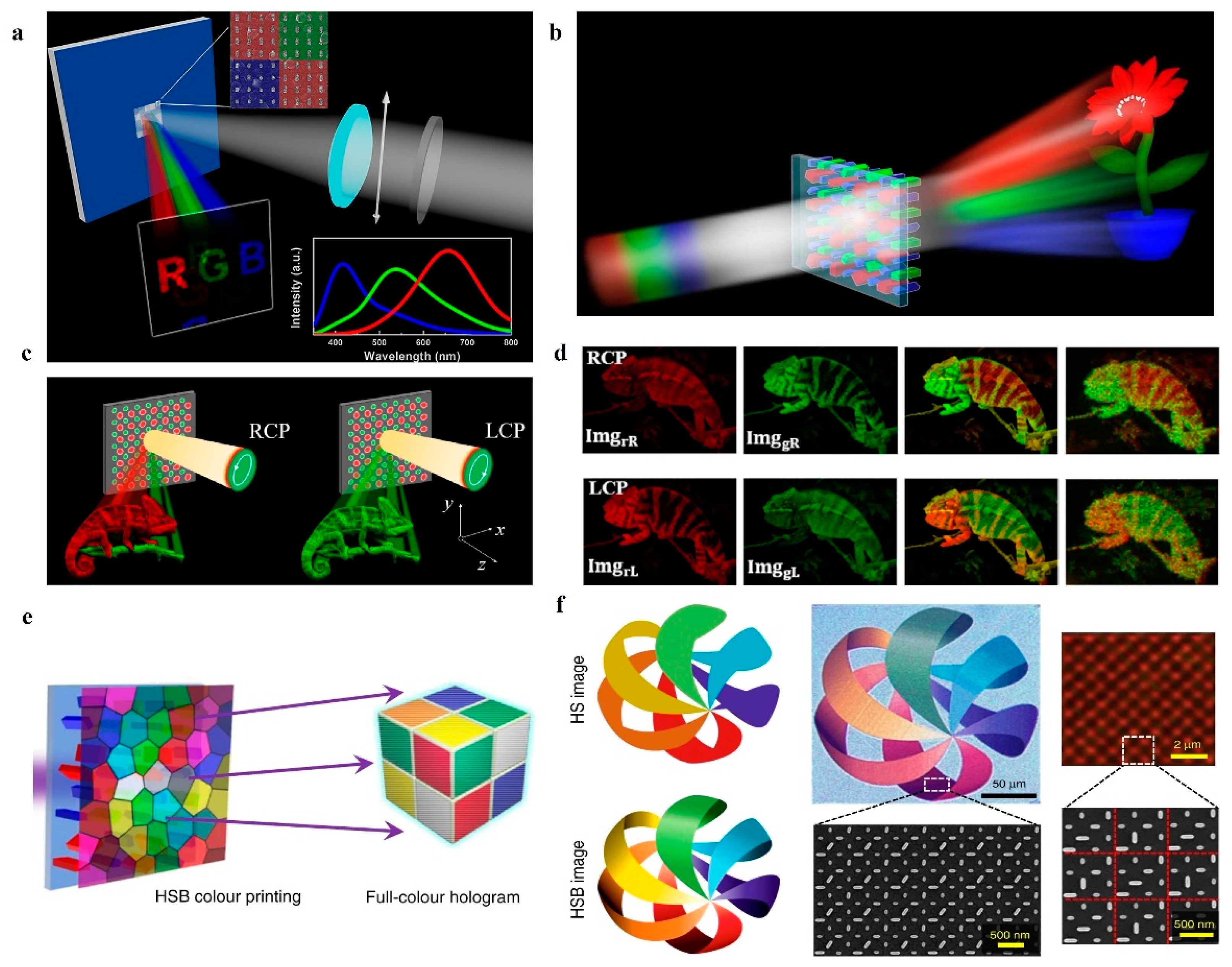
3.2. Wavelength Multiplexed (Colorful) Metasurface Holography
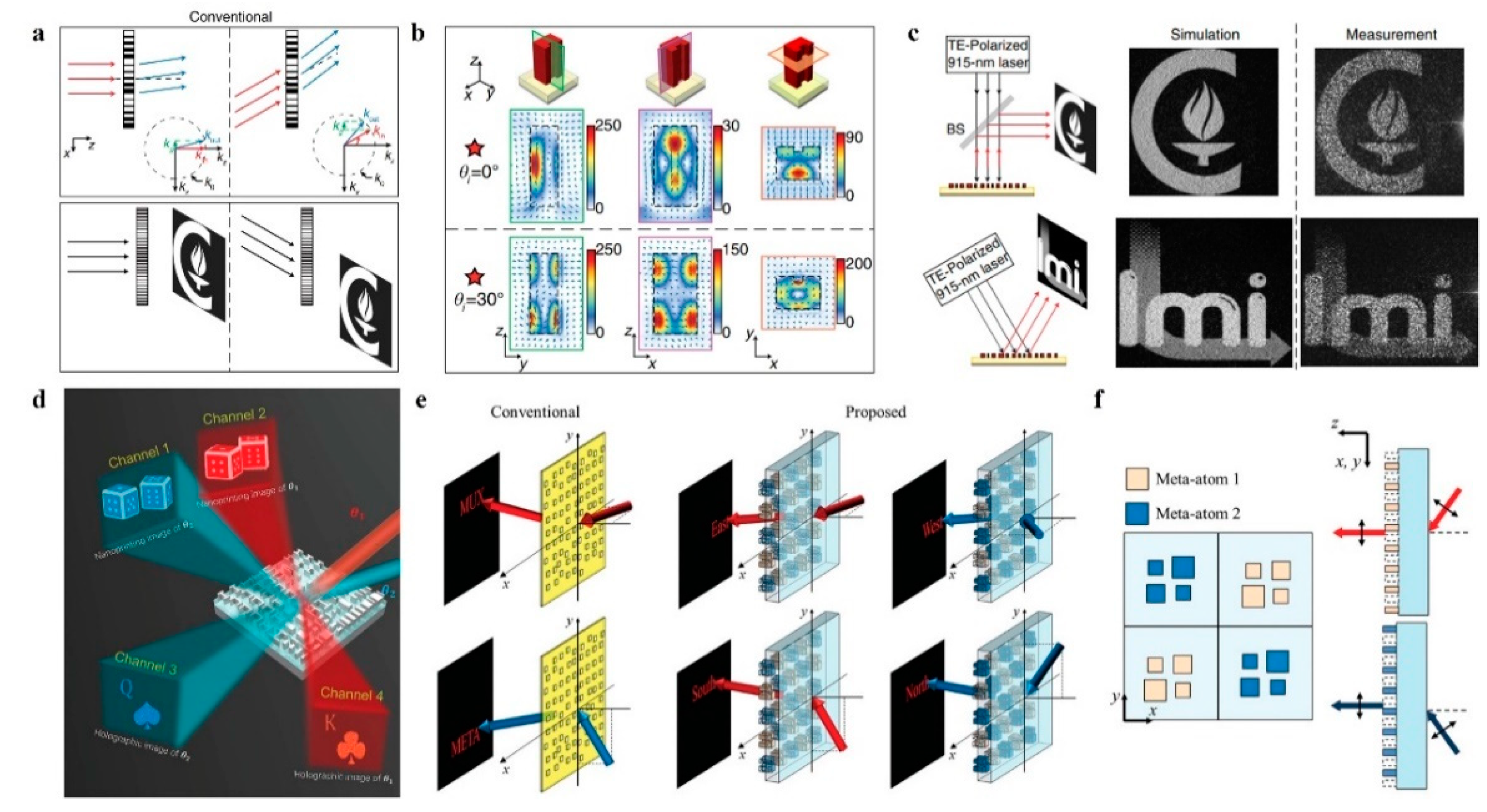
3.3. Angular Multiplexed Metasurface Holography
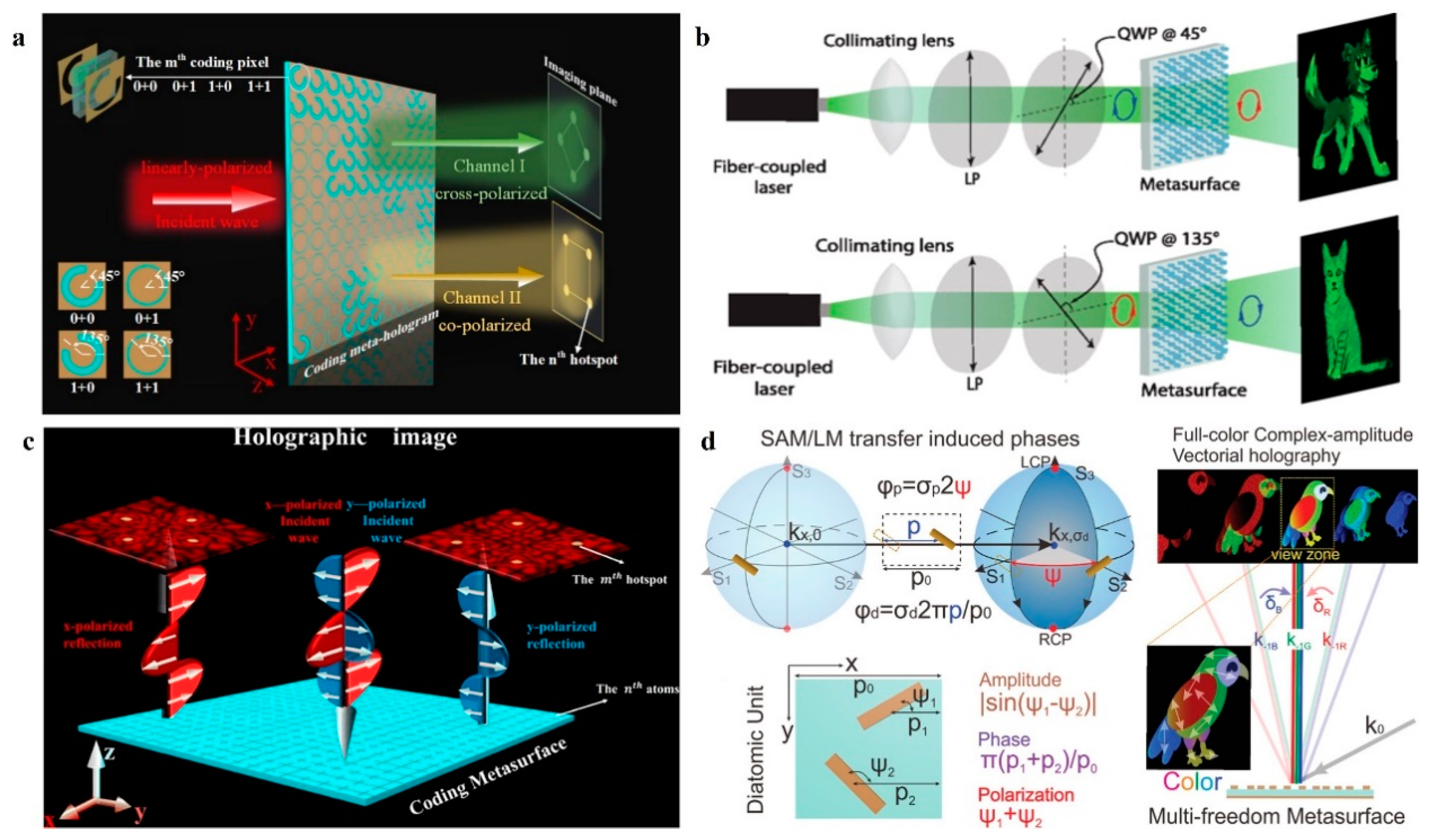
3.4. Polarization Multiplexing Metasurface Holography
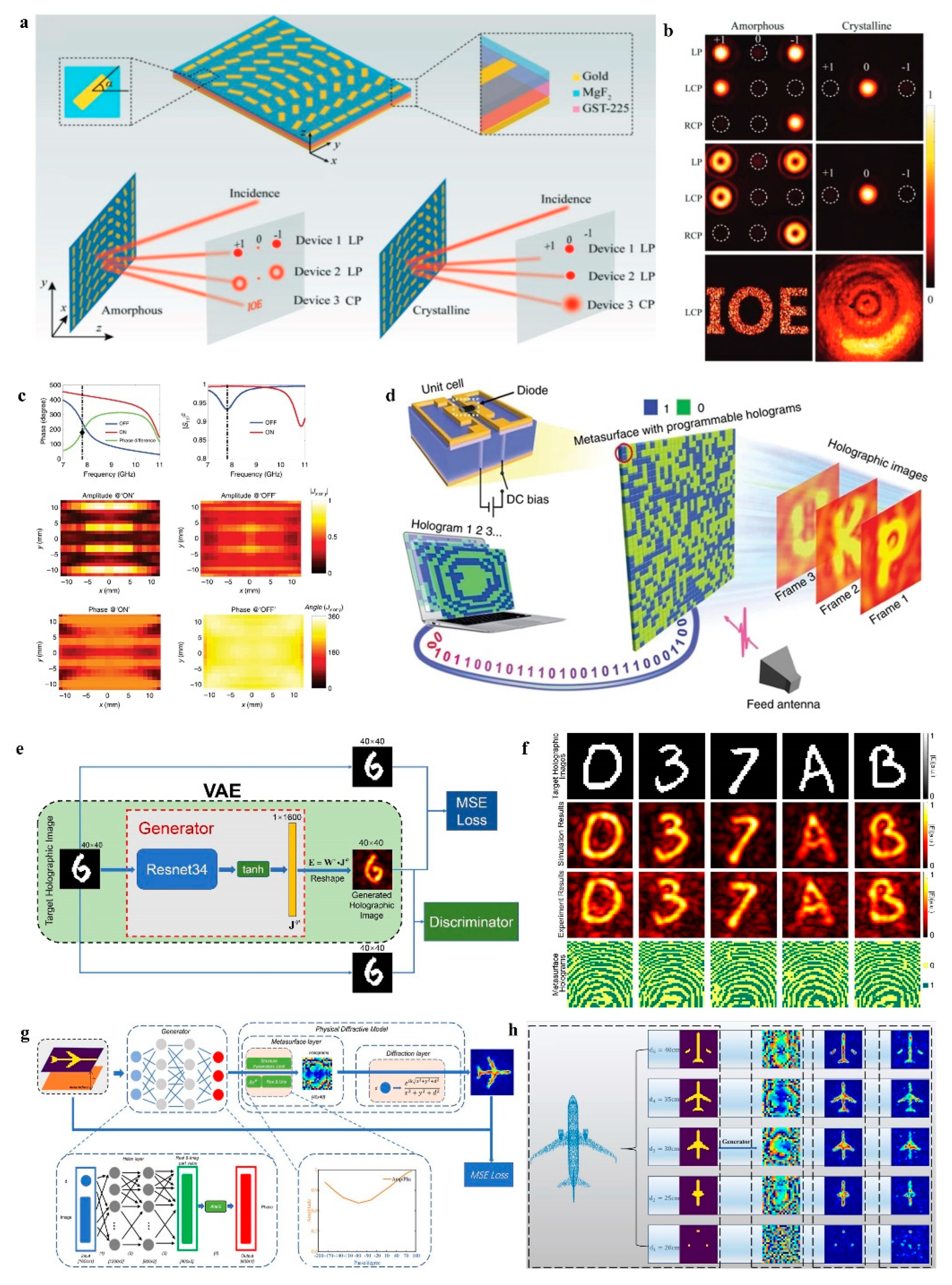
4. Reconfigurable Metasurface Holography
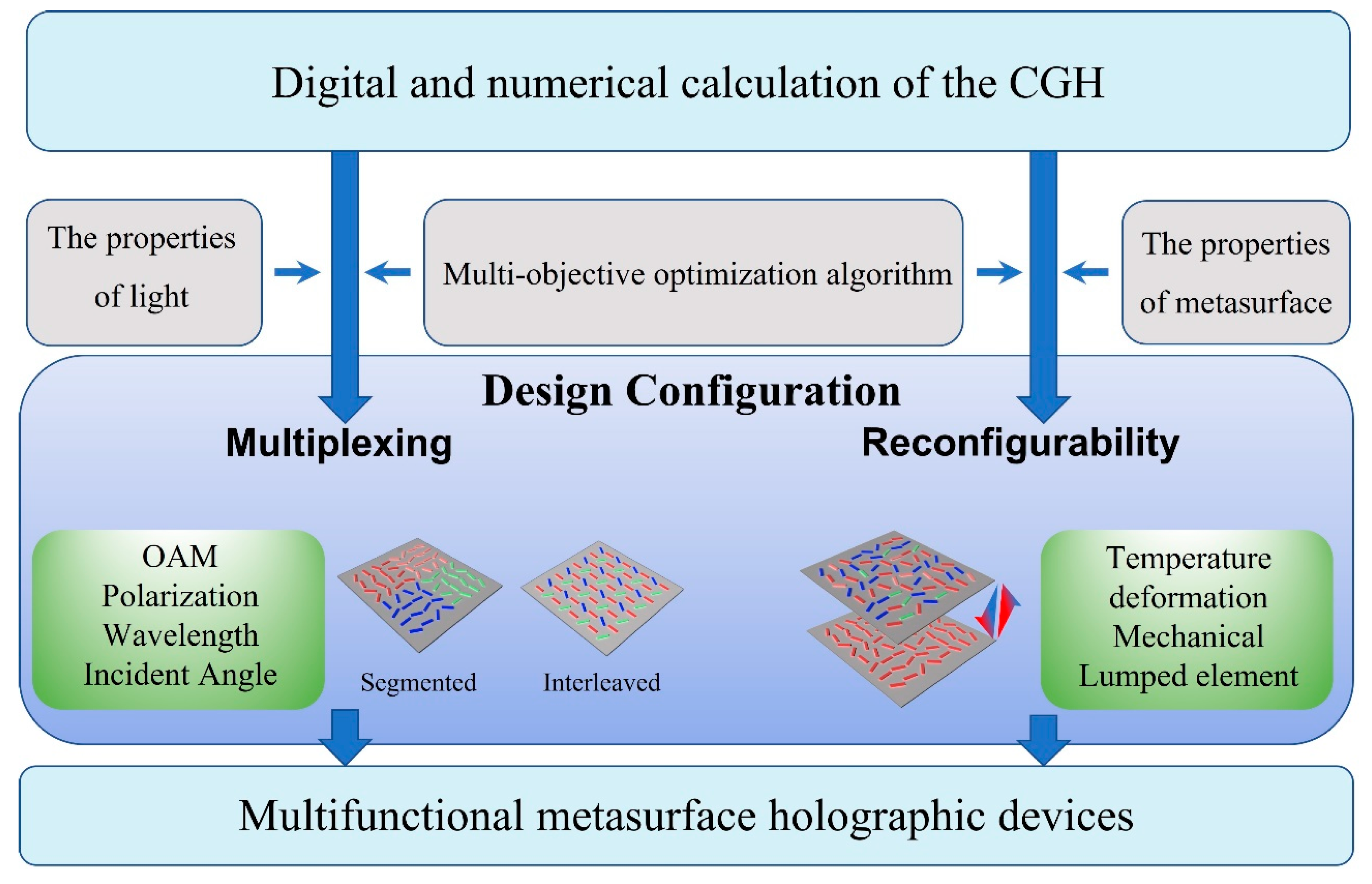
5. Discussion and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Gabor, D. A new microscopic principle. Nature 1984, 161, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Brown, B.R.; Lohmann, A.W. Complex spatial filtering with binary masks. Appl. Opt. 1966, 5, 967–969. [Google Scholar] [CrossRef] [PubMed]
- Lesem, L.B.; Hirsch, P.M.; Jordan, J.A., Jr. Scientific applications: Computer synthesis of holograms for 3-D display. Commun. ACM 1968, 11, 661–674. [Google Scholar] [CrossRef]
- Slinger, C.; Cameron, C.; Stanley, M. Computer-generated holography as a generic display technology. Computer 2005, 38, 46–53. [Google Scholar] [CrossRef]
- Mok, F.; Diep, J.; Liu, H.-K.; Psaltis, D. Real-time computer-generated hologram by means of liquid-crystal television spatial light modulator. Opt. Lett. 1986, 11, 748–750. [Google Scholar] [CrossRef] [PubMed]
- Hahn, J.; Kim, H.; Lim, Y.; Park, G.; Lee, B. Wide viewing angle dynamic holographic stereogram with a curved array of spatial light modulators. Opt. Express 2008, 16, 12372–12386. [Google Scholar] [CrossRef] [PubMed]
- Levy, U.; Kim, H.-C.; Tsai, C.-H.; Fainman, Y. Near-infrared demonstration of computer-generated holograms implemented by using subwavelength gratings with space-variant orientation. Opt. Lett. 2005, 30, 2089–2091. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, S.; Zentgraf, T. Metasurface holography: From fundamentals to applications. Nanophotonics 2018, 7, 1169–1190. [Google Scholar] [CrossRef]
- Zhao, R.; Huang, L.; Wang, Y. Recent advances in multi-dimensional metasurfaces holographic technologies. PhotoniX 2020, 1, 1–24. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Li, Z.; Cao, G.; Li, C.; Dong, S.; Deng, Y.; Liu, X.; Ho, J.S.; Qiu, C.-W. Non-hermitian electromagnetic metasurfaces at exceptional points. Prog. Electromagn. Res. 2021, 171, 1–20. [Google Scholar] [CrossRef]
- Ni, X.; Emani, N.K.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Broadband light bending with plasmonic nanoantennas. Science 2012, 335, 427. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; He, N.; Sun, Y.; Jin, Y.; He, S. Wideband high-reflection chiral dielectric metasurface. Prog. Electromagn. Res. 2021, 172, 51–60. [Google Scholar] [CrossRef]
- Cai, T.; Tang, S.; Zheng, B.; Wang, G.; Ji, W.; Qian, C.; Wang, Z.; Li, E.; Chen, H. Ultrawideband chromatic aberration-free meta-mirrors. Adv. Photon. 2020, 3, 016001. [Google Scholar] [CrossRef]
- Han, T.; Wen, K.; Xie, Z.; Yue, X. An ultra-thin wideband reflection reduction metasurface based on polarization conversion. Prog. Electromagn. Res. 2022, 173, 1–8. [Google Scholar] [CrossRef]
- Yin, X.; Ye, Z.; Rho, J.; Wang, Y.; Zhang, X. Photonic spin hall effect at metasurfaces. Science 2013, 339, 1405–1407. [Google Scholar] [CrossRef] [PubMed]
- Zhou, E.; Cheng, Y.; Chen, F.; Luo, H.; Li, X. Low-Profile high-gain wideband multi-resonance microstrip-fed slot antenna with anisotropic metasurface. Prog. Electromagn. Res. 2022, 175, 91–104. [Google Scholar] [CrossRef]
- Cai, T.; Tang, S.; Wang, G.; Xu, H.; Sun, S.; He, Q.; Zhou, L. High-performance bifunctional metasurfaces in transmission and reflection geometries. Adv. Opt. Mater. 2017, 5, 1600506. [Google Scholar] [CrossRef]
- Karimi, E.; A Schulz, S.; De Leon, I.; Qassim, H.; Upham, J.; Boyd, R.W. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface. Light. Sci. Appl. 2014, 3, 167. [Google Scholar] [CrossRef]
- Yu, S.; Li, L.; Shi, G.; Zhu, C.; Zhou, X.; Shi, Y. Design, fabrication, and measurement of reflective metasurface for orbital angular momentum vortex wave in radio frequency domain. Appl. Phys. Lett. 2016, 108, 121903. [Google Scholar] [CrossRef]
- Li, G.; Kang, M.; Chen, S.; Zhang, S.; Pun, E.Y.; Cheah, K.W.; Li, J. Spin-enabled plasmonic metasurfaces for manipulating orbital angular momentum of light. Nano Lett. 2013, 13, 4148–4151. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.F.; Huang, H. M/ Millimeter-wave wideband high efficiency circular airy OAM multibeams with multiplexing OAM modes based on transmission metasurfaces. Prog. Electromagn. Res. 2022, 173, 151–159. [Google Scholar] [CrossRef]
- Pu, M.; Li, X.; Ma, X.; Wang, Y.; Zhao, Z.; Wang, C.; Hu, C.; Gao, P.; Huang, C.; Ren, H.; et al. Catenary optics for achromatic generation of perfect optical angular momentum. Sci. Adv. 2015, 1, e1500396. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Li, Y.; Chen, L.; Jin, J.; Pu, M.; Li, X.; Gao, P.; Wang, C.; Luo, X.; Hong, M. Quasi-Talbot effect of orbital angular momentum beams for generation of optical vortex arrays by multiplexing metasurface design. Nanoscale 2017, 10, 666–671. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Jing, L.; Zheng, B.; Hao, R.; Yin, W.; Li, E.; Soukoulis, C.M.; Chen, H. Full-polarization 3D metasurface cloak with preserved amplitude and phase. Adv. Mater. 2016, 28, 6866–6871. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wang, H.; Yu, F.; Xu, Z.; Chen, H. A metasurface carpet cloak for electromagnetic, acoustic and water waves. Sci. Rep. 2016, 6, 20219. [Google Scholar] [CrossRef] [PubMed]
- Zhen, Z.; Qian, C.; Jia, Y.; Fan, Z.; Hao, R.; Cai, T.; Zheng, B.; Chen, H.; Li, E. Realizing transmitted metasurface cloak by a tandem neural network. Photon. Res. 2021, 9, B229–B235. [Google Scholar] [CrossRef]
- Wang, C.; Yang, Y.; Liu, Q.; Liang, D.; Zheng, B.; Chen, H.; Xu, Z.; Wang, H. Multi-frequency metasurface carpet cloaks. Opt. Express 2018, 26, 14123–14131. [Google Scholar] [CrossRef]
- Qian, C.; Chen, H. A perspective on the next generation of invisibility cloaks—Intelligent cloaks. Appl. Phys. Lett. 2021, 118, 180501. [Google Scholar] [CrossRef]
- Cai, T.; Zheng, B.; Lou, J.; Shen, L.; Yang, Y.; Tang, S.; Li, E.; Qian, C.; Chen, H. Experimental realization of a superdispersion-enabled ultrabroadband terahertz cloak. Adv. Mater. 2022, 34, 2205053. [Google Scholar] [CrossRef]
- Azad, A.K.; Efimov, A.V.; Ghosh, S.; Singleton, J.; Taylor, A.J.; Chen, H.-T. Ultra-thin metasurface microwave flat lens for broadband applications. Appl. Phys. Lett. 2017, 110, 224101. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Liu, Y.; Lei, Y.; Pian, S.; Wang, Z.; Ma, Y. Recent progress on achromatic metalenses. Prog. Electromagn. Res. 2022, 173, 9–23. [Google Scholar] [CrossRef]
- Li, H.; Wang, G.; Liang, J.; Gao, X.; Hou, H.; Jia, X. Single-layer focusing gradient metasurface for ultrathin planar lens antenna application. IEEE Trans. Antennas Propag. 2016, 65, 1452–1457. [Google Scholar] [CrossRef]
- Deng, F.; Guo, Z.; Ren, M.; Su, X.; Dong, L.; Liu, Y.H.; Shi, Y.L.; Chen, H. Bessel beam generated by the zero-index metalens. Prog. Electromagn. Res. 2022, 174, 89–106. [Google Scholar] [CrossRef]
- Shaltout, A.; Liu, J.; Kildishev, A.; Shalaev, V. Photonic spin Hall effect in gap–plasmon metasurfaces for on-chip chiroptical spectroscopy. Optica 2015, 2, 860–863. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, G.; Zhang, T.; Shen, F.; Meng, L.; Wang, L.; Li, F.; Zhang, Y.; Zhang, Y.; He, N.; et al. VOC detections with optical spectroscopy. Prog. Electromagn. Res. 2022, 174, 71–92. [Google Scholar] [CrossRef]
- Ni, X.; Kildishev, A.V.; Shalaev, V.M. Metasurface holograms for visible light. Nat. Commun. 2013, 4, 2807. [Google Scholar] [CrossRef]
- Kruk, S.; Hopkins, B.; Kravchenko, I.I.; Miroshnichenko, A.; Neshev, D.N.; Kivshar, Y.S. Invited Article: Broadband highly efficient dielectric metadevices for polarization control. APL Photon. 2016, 1, 030801. [Google Scholar] [CrossRef]
- Wang, B.; Dong, F.; Yang, D.; Song, Z.; Xu, L.; Chu, W.; Gong, Q.; Li, Y. Polarization-controlled color-tunable holograms with dielectric metasurfaces. Optica 2017, 4, 1368–1371. [Google Scholar] [CrossRef]
- Bao, Y.; Yu, Y.; Xu, H.; Guo, C.; Li, J.; Sun, S.; Zhou, Z.-K.; Qiu, C.-W.; Wang, X.-H. Full-colour nanoprint-hologram synchronous metasurface with arbitrary hue-saturation-brightness control. Light. Sci. Appl. 2019, 8, 95. [Google Scholar] [CrossRef]
- Liu, C.; Yu, W.M.; Ma, Q.; Li, L.; Cui, T.J. Intelligent coding metasurface holograms by physics-assisted unsupervised generative adversarial network. Photon. Res. 2021, 9, B159–B167. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, R.; Shen, L.; Zheng, B. Reconfigurable metasurface hologram of dynamic distance via deep learning. Front. Mater. 2022, 9, 907672. [Google Scholar] [CrossRef]
- Zhou, H.; Sain, B.; Wang, Y.; Schlickriede, C.; Zhao, R.; Zhang, X.; Wei, Q.; Li, X.; Huang, L.; Zentgraf, T. Polarization-encrypted orbital angular momentum multiplexed metasurface holography. ACS Nano 2020, 14, 5553–5559. [Google Scholar] [CrossRef]
- Wan, S.; Wan, C.; Dai, C.; Li, Z.; Tang, J.; Zheng, G.; Li, Z. Angular-Multiplexing Metasurface: Building Up Independent-Encoded Amplitude/Phase Dictionary for Angular Illumination. Adv. Opt. Mater. 2021, 9, 2101547. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Zentgraf, T.; Zhang, S. Dispersionless phase discontinuities for controlling light propagation. Nano Lett. 2012, 12, 5750–5755. [Google Scholar] [CrossRef]
- Kang, M.; Feng, T.; Wang, H.-T.; Li, J. Wave front engineering from an array of thin aperture antennas. Opt. Express 2012, 20, 15882–15890. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Zhang, H.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.-W.; Qiu, C.-W.; et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4, 2808. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef]
- Ghirardini, L.; Marino, G.; Gili, V.F.; Favero, I.; Rocco, D.; Carletti, L.; Locatelli, A.; De Angelis, C.; Finazzi, M.; Celebrano, M.; et al. Shaping the nonlinear emission pattern of a dielectric nanoantenna by integrated holographic gratings. Nano Lett. 2018, 18, 6750–6755. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef]
- Butt, H.; Montelongo, Y.; Butler, T.; Rajesekharan, R.; Dai, Q.; Shiva-Reddy, S.G.; Wilkinson, T.D.; Amaratunga, G.A. Carbon nanotube based high resolution holograms. Adv. Mater. 2012, 24, 331–336. [Google Scholar] [CrossRef]
- Huang, K.; Liu, H.; Garcia-Vidal, F.J.; Hong, M.; Luk’yanchuk, B.; Teng, J.; Qiu, C.-W. Ultrahigh-capacity non-periodic photon sieves operating in visible light. Nat. Commun. 2015, 6, 7059. [Google Scholar] [CrossRef]
- Walther, B.; Helgert, C.; Rockstuhl, C.; Setzpfandt, F.; Eilenberger, F.; Kley, E.-B.; Lederer, F.; Tünnermann, A.; Pertsch, T. Spatial and spectral light shaping with metamaterials. Adv. Mater. 2012, 24, 6300–6304. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Xu, Y.; Gu, J.; Li, Y.; Tian, Z.; Singh, R.; Zhang, S.; Han, J.; Zhang, W. Broadband metasurface holograms: Toward complete phase and amplitude engineering. Sci. Rep. 2016, 6, 32867. [Google Scholar] [CrossRef]
- Lee, G.Y.; Yoon, G.; Lee, S.Y.; Yun, H.; Cho, J.; Lee, K.; Kim, H.; Rho, J.; Lee, B. Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 2018, 10, 4237–4245. [Google Scholar] [CrossRef]
- Overvig, A.C.; Shrestha, S.; Malek, S.C.; Lu, M.; Stein, A.; Zheng, C.; Yu, N. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light. Sci. Appl. 2019, 8, 92. [Google Scholar] [CrossRef]
- Djordjevic, I.B. Deep-space and near-Earth optical communications by coded orbital angular momentum (OAM) modulation. Opt. Express 2011, 19, 14277–14289. [Google Scholar] [CrossRef]
- Djordjevic, I.B.; Arabaci, M. LDPC-coded orbital angular momentum (OAM) modulation for free-space optical communication. Opt. Express 2010, 18, 24722–24728. [Google Scholar] [CrossRef]
- Bowell, R.A.; Brandsema, M.J.; Narayanan, R.M.; Howell, S.W.; Dilger, J.M. Comparison of correlation performance for various measurement schemes in quantum bipartite radar and communication systems. Prog. Electromagn. Res. 2022, 174, 43–53. [Google Scholar] [CrossRef]
- Yan, L.; Gregg, P.; Karimi, E.; Rubano, A.; Marrucci, L.; Boyd, R.; Ramachandran, S. Q-plate enabled spectrally diverse orbital-angular-momentum conversion for stimulated emission depletion microscopy. Optica 2015, 2, 900–903. [Google Scholar] [CrossRef]
- Vieira, J.; Trines, R.M.G.M.; Alves, E.P.; Fonseca, R.A.; Mendonça, J.T.; Bingham, R.; Norreys, P.; Silva, L.O. Amplification and generation of ultra-intense twisted laser pulses via stimulated Raman scattering. Nat. Commun. 2016, 7, 10371. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light. Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Chenot, S.; Vézian, S.; Damilano, B.; Brändli, V.; et al. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 2986. [Google Scholar] [CrossRef]
- Blom, H.; Widengren, J. Stimulated emission depletion microscopy. Chem. Rev. 2017, 117, 7377–7427. [Google Scholar] [CrossRef]
- Tam, J.; Merino, D. Stochastic optical reconstruction microscopy (STORM) in comparison with stimulated emission depletion (STED) and other imaging methods. J. Neurochem. 2015, 135, 643–658. [Google Scholar] [CrossRef]
- Ren, H.; Fang, X.; Jang, J.; Bürger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 2020, 15, 948–955. [Google Scholar] [CrossRef]
- Fang, X.; Yang, H.; Yao, W.; Wang, T.; Zhang, Y.; Gu, M.; Xiao, M. High-dimensional orbital angular momentum multiplexing nonlinear holography. Adv. Photon. 2021, 3, 015001. [Google Scholar] [CrossRef]
- Cox, G.; Kable, E.; Jones, A.; Fraser, I.; Manconi, F.; Gorrell, M.D. 3-dimensional imaging of collagen using second harmonic generation. J. Struct. Biol. 2003, 141, 53–62. [Google Scholar] [CrossRef]
- Huang, Y.-W.; Chen, W.T.; Tsai, W.-Y.; Wu, P.C.; Wang, C.-M.; Sun, G.; Tsai, D.P. Aluminum plasmonic multicolor meta-hologram. Nano Lett. 2015, 15, 3122–3127. [Google Scholar] [CrossRef]
- Wang, B.; Dong, F.; Li, Q.-T.; Yang, D.; Sun, C.; Chen, J.; Song, Z.; Xu, L.; Chu, W.; Xiao, Y.-F.; et al. Visible-frequency dielectric metasurfaces for multiwavelength achromatic and highly dispersive holograms. Nano Lett. 2016, 16, 5235–5240. [Google Scholar] [CrossRef]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Horie, Y.; Faraji-Dana, M.; Faraon, A. Angle-multiplexed metasurfaces: Encoding independent wavefronts in a single metasurface under different illumination angles. Phys. Rev. X 2017, 7, 041056. [Google Scholar] [CrossRef]
- Durach, M.; Williamson, R.; Adams, J.; Holtz, T.; Bhatt, P.; Moreno, R.; Smith, F. On Fresnel-airy equations, fabry-perot resonances and surface electromagnetic waves in arbitrary bianisotropic metamaterials. Prog. Electromagn. Res. 2022, 173, 53–69. [Google Scholar] [CrossRef]
- Jang, J.; Lee, G.; Sung, J.; Lee, B. Independent multichannel wavefront modulation for angle multiplexed meta-holograms. Adv. Opt. Mater. 2021, 9, 2100678. [Google Scholar] [CrossRef]
- Swanson, G.J.; Veldkamp, W.B. Diffractive optical elements for use in infrared systems. Opt. Eng. 1989, 28, 605–608. [Google Scholar] [CrossRef]
- Siemion, A. The magic of optics—An overview of recent advanced terahertz diffractive optical elements. Sensors 2020, 21, 100. [Google Scholar] [CrossRef]
- Ichimura, K. Photoalignment of liquid-crystal systems. Chem. Rev. 2000, 100, 1847. [Google Scholar] [CrossRef]
- Guan, C.; Liu, J.; Ding, X.; Wang, Z.; Zhang, K.; Li, H.; Jin, M.; Burokur, S.N.; Wu, Q. Dual-polarized multiplexed meta-holograms utilizing coding metasurface. Nanophotonics 2020, 9, 3605–3613. [Google Scholar] [CrossRef]
- Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef]
- Ding, X.; Monticone, F.; Zhang, K.; Zhang, L.; Gao, D.; Burokur, S.N.; de Lustrac, A.; Wu, Q.; Qiu, C.; Alù, A. Ultrathin Pancharatnam–Berry metasurface with maximal cross-polarization efficiency. Adv. Mater. 2014, 27, 1195–1200. [Google Scholar] [CrossRef]
- Luo, W.; Sun, S.; Xu, H.-X.; He, Q.; Zhou, L. Transmissive ultrathin Pancharatnam-Berry metasurfaces with nearly 100% efficiency. Phys. Rev. Appl. 2017, 7, 044033. [Google Scholar] [CrossRef]
- Shang, G.; Li, H.; Wang, Z.; Zhang, K.; Burokur, S.N.; Liu, J.; Wu, Q.; Ding, X.; Ding, X. Coding metasurface holography with polarization-multiplexed functionality. J. Appl. Phys. 2021, 129, 035304. [Google Scholar] [CrossRef]
- Deng, Z.L.; Jin, M.; Ye, X.; Wang, S.; Shi, T.; Deng, J.; Mao, N.; Cao, Y.; Guan, B.O.; Alù, A.; et al. Full-color complex-amplitude vectorial holograms based on multi-freedom metasurfaces. Adv. Funct. Mater. 2020, 30, 1910610. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef]
- Beneck, R.J.; Das, A.; Mackertich-Sengerdy, G.; Chaky, R.J.; Wu, Y.; Soltani, S.; Werner, D. Reconfigurable Antennas: A review of recent progress and future prospects for next generation. Prog. Electromagn. Res. 2021, 171, 89–121. [Google Scholar]
- Minovich, A.E.; Miroshnichenko, A.E.; Bykov, A.Y.; Murzina, T.V.; Neshev, D.N.; Kivshar, Y.S. Functional and nonlinear optical metasurfaces. Laser Photon. Rev. 2015, 9, 195–213. [Google Scholar] [CrossRef]
- Raeis-Hosseini, N.; Rho, J. Metasurfaces based on phase-change material as a reconfigurable platform for multifunctional devices. Materials 2017, 10, 1046. [Google Scholar] [CrossRef]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
- Ding, Y.; Wei, C.; Su, H.; Sun, S.; Tang, Z.; Wang, Z.; Li, G.; Liu, D.; Gwo, S.; Dai, J.; et al. Second harmonic generation covering the entire visible range from a 2D material–plasmon hybrid metasurface. Adv. Opt. Mater. 2021, 9, 2100625. [Google Scholar] [CrossRef]
- Cui, T.J.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light: Sci. Appl. 2014, 3, 218. [Google Scholar] [CrossRef]
- Zhang, X.G.; Jiang, W.X.; Jiang, H.L.; Wang, Q.; Tian, H.W.; Bai, L.; Luo, Z.J.; Sun, S.; Luo, Y.; Qiu, C.-W.; et al. An optically driven digital metasurface for programming electromagnetic functions. Nat. Electron. 2020, 3, 165–171. [Google Scholar] [CrossRef]
- Wu, N.; Zhang, Y.; Ma, H.; Chen, H.; Qian, H. Tunable high-Q plasmonic metasurface with multiple surface lattice resonances. Prog. Electromagn. Res. 2021, 172, 23–32. [Google Scholar] [CrossRef]
- Jia, D.; Wang, Y.; Ge, Y.; Yuan, S.-Q.; Sun, H.-X. Tunable topological refractions in valley sonic crystals with triple valley hall phase transitions. Prog. Electromagn. Res. 2021, 172, 13–22. [Google Scholar] [CrossRef]
- Yamada, N. Origin, secret, and application of the ideal phase-change material GeSbTe. Phys. Status Solidi (b) 2012, 249, 1837–1842. [Google Scholar] [CrossRef]
- Zhang, M.; Pu, M.; Zhang, F.; Guo, Y.; He, Q.; Ma, X.; Huang, Y.; Li, X.; Yu, H.; Luo, X. Plasmonic metasurfaces for switchable photonic spin–orbit interactions based on phase change materials. Adv. Sci. 2018, 5, 1800835. [Google Scholar] [CrossRef]
- Rocco, D.; Zilli, A.; Ferraro, A.; Borne, A.; Vinel, V.; Leo, G.; Lemaître, A.; Zucchetti, C.; Celebrano, M.; Caputo, R.; et al. Tunable second harmonic generation by an all-dielectric diffractive metasurface embedded in liquid crystals. New J. Phys. 2022, 24, 045002. [Google Scholar] [CrossRef]
- Rocco, D.; Carletti, L.; Caputo, R.; Finazzi, M.; Celebrano, M.; De Angelis, C. Switching the second harmonic generation by a dielectric metasurface via tunable liquid crystal. Opt. Express 2020, 28, 12037–12046. [Google Scholar] [CrossRef]
- Li, L.; Cui, T.J.; Ji, W.; Liu, S.; Ding, J.; Wan, X.; Li, Y.B.; Jiang, M.; Qiu, C.-W.; Zhang, S. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef]
- Gong, D.; Ma, T.; Evans, J.; He, S. Deep neural networks for image super-resolution in optical microscopy by using modified hybrid task cascade U-net. Prog. Electromagn. Res. 2021, 171, 185–199. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, J.; Zheng, B.; Qian, C.; Cai, T.; Li, E.; Chen, H. Eye accommodation-inspired neuro-metasurface focusing. Nat. Commun. 2023, 14, 3301. [Google Scholar] [CrossRef]
- Huang, M.; Zheng, B.; Li, R.; Li, X.; Zou, Y.; Cai, T.; Chen, H. Diffraction neural network for multi-source information of arrival sensing. Laser Photon. Rev. 2023, 17, 2300202. [Google Scholar] [CrossRef]
- Bao, Y.; Yan, J.; Yang, X.; Qiu, C.-W.; Li, B. Point-source geometric metasurface holography. Nano Lett. 2020, 21, 2332–2338. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Jin, H.; Zhu, R.; Zhang, T. Metasurface Holography with Multiplexing and Reconfigurability. Nanomaterials 2024, 14, 66. https://doi.org/10.3390/nano14010066
Zou Y, Jin H, Zhu R, Zhang T. Metasurface Holography with Multiplexing and Reconfigurability. Nanomaterials. 2024; 14(1):66. https://doi.org/10.3390/nano14010066
Chicago/Turabian StyleZou, Yijun, Hui Jin, Rongrong Zhu, and Ting Zhang. 2024. "Metasurface Holography with Multiplexing and Reconfigurability" Nanomaterials 14, no. 1: 66. https://doi.org/10.3390/nano14010066




