Effect of Substitutional Metallic Impurities on the Optical Absorption Properties of TiO2
Abstract
1. Introduction
2. Theoretical Approach and Computational Details
3. Results and Discussion
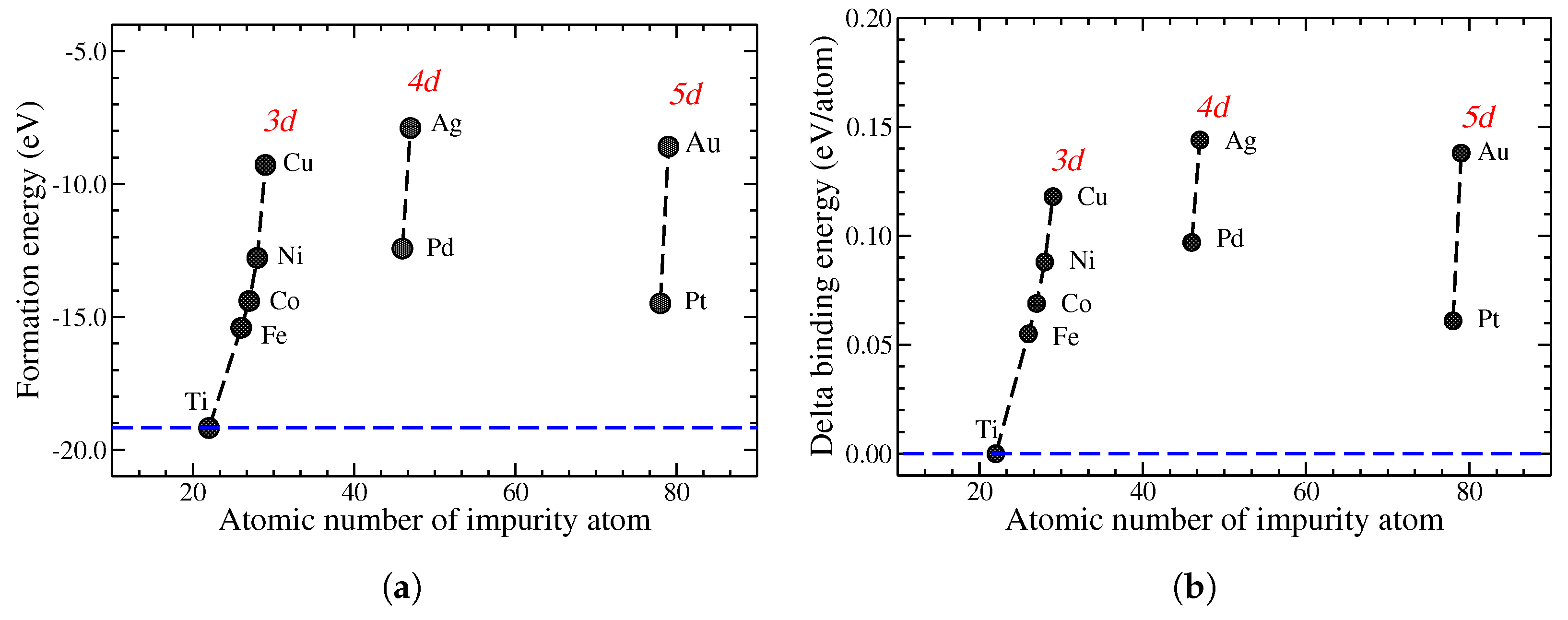
3.1. Structures and Energies
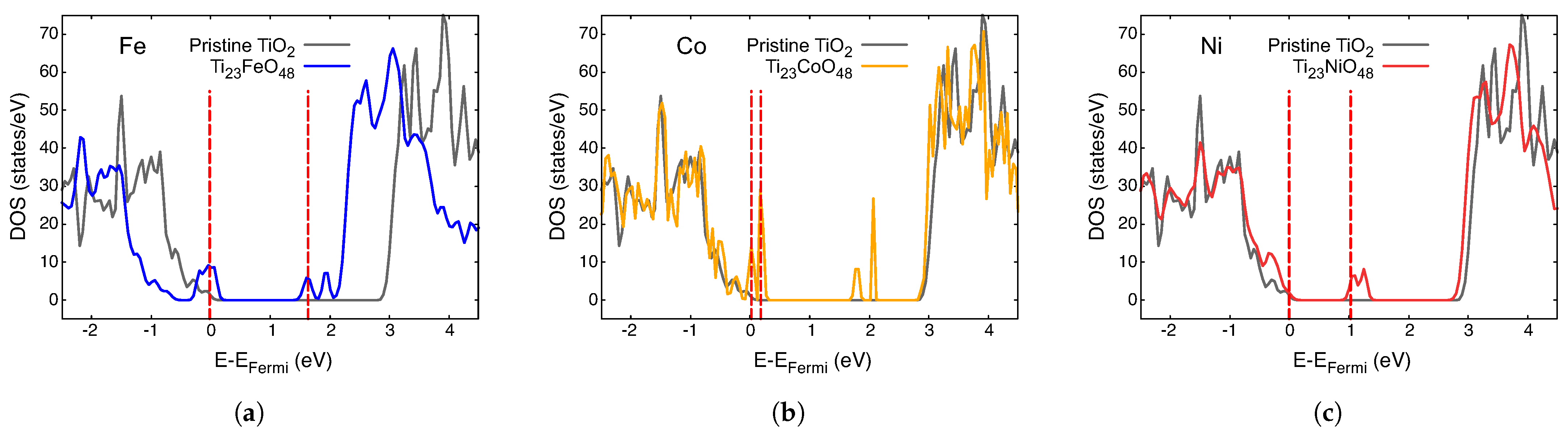
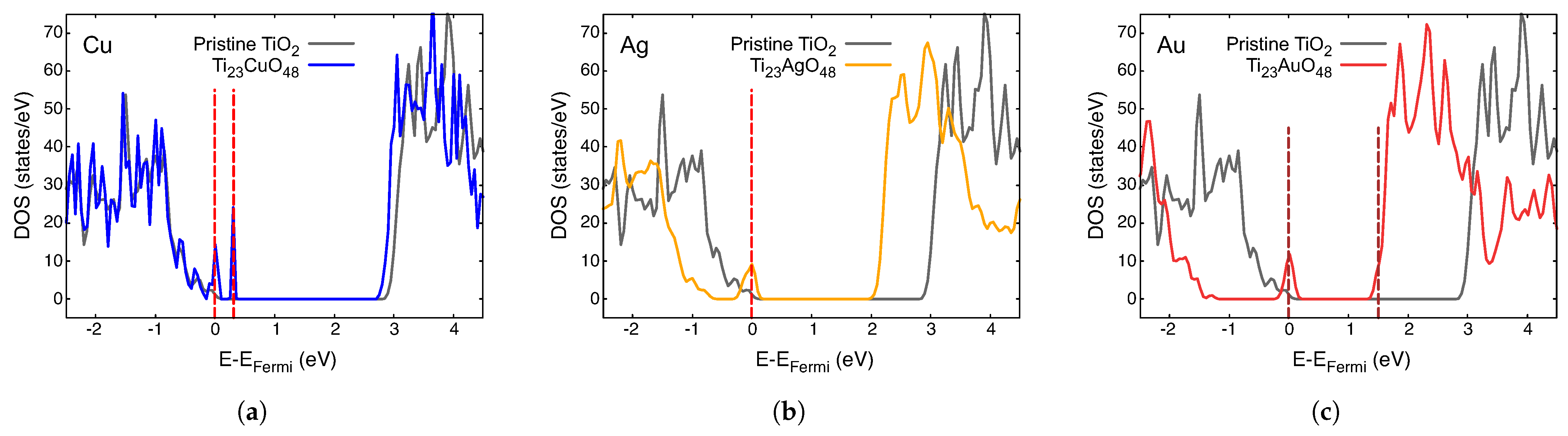
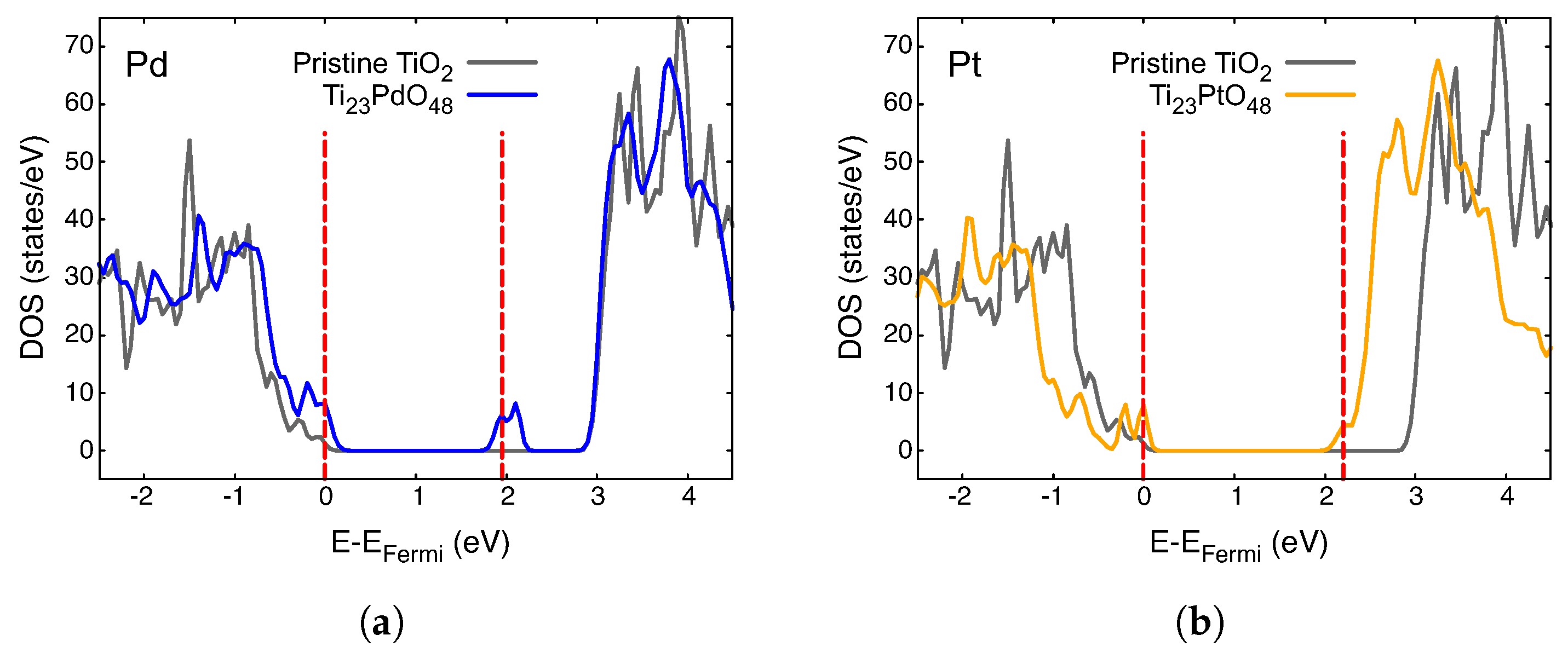
3.2. Electronic Density of States
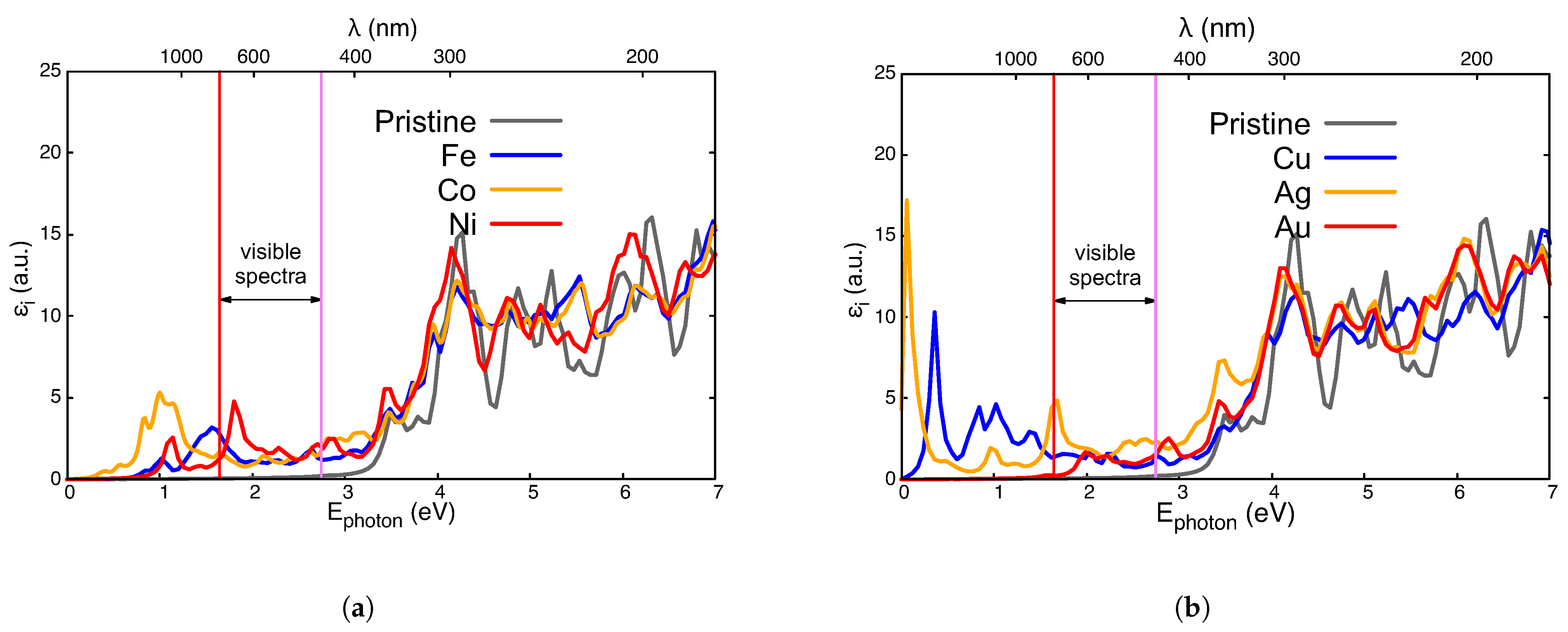
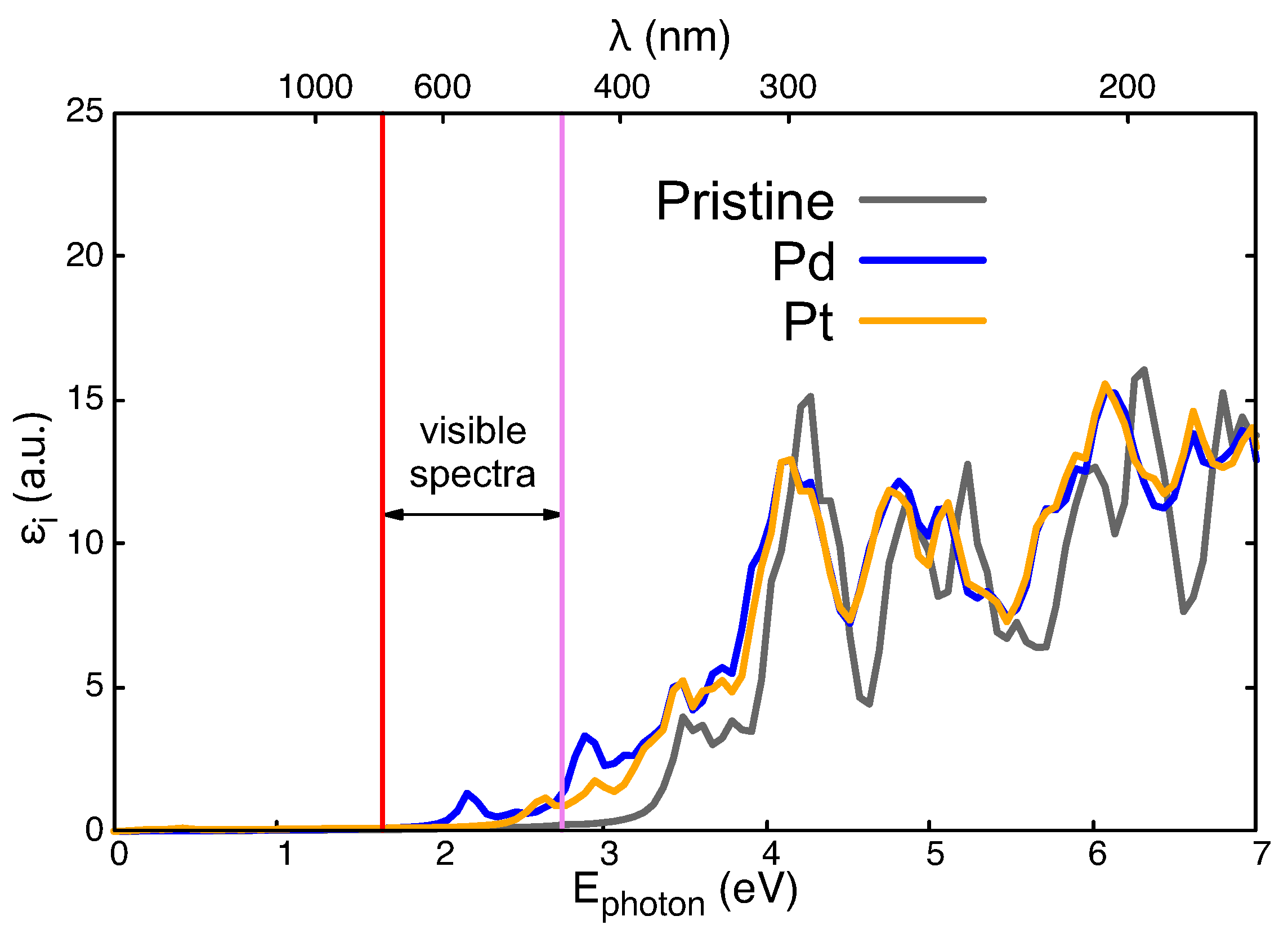
3.3. Optical Absorption Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| DOS | Density of States |
| GGA | General Gradient Approximation |
| LDA | Local Density Approximation |
| NC-PP | Norm-conserving pseudo-potentials |
| VB | Valence band |
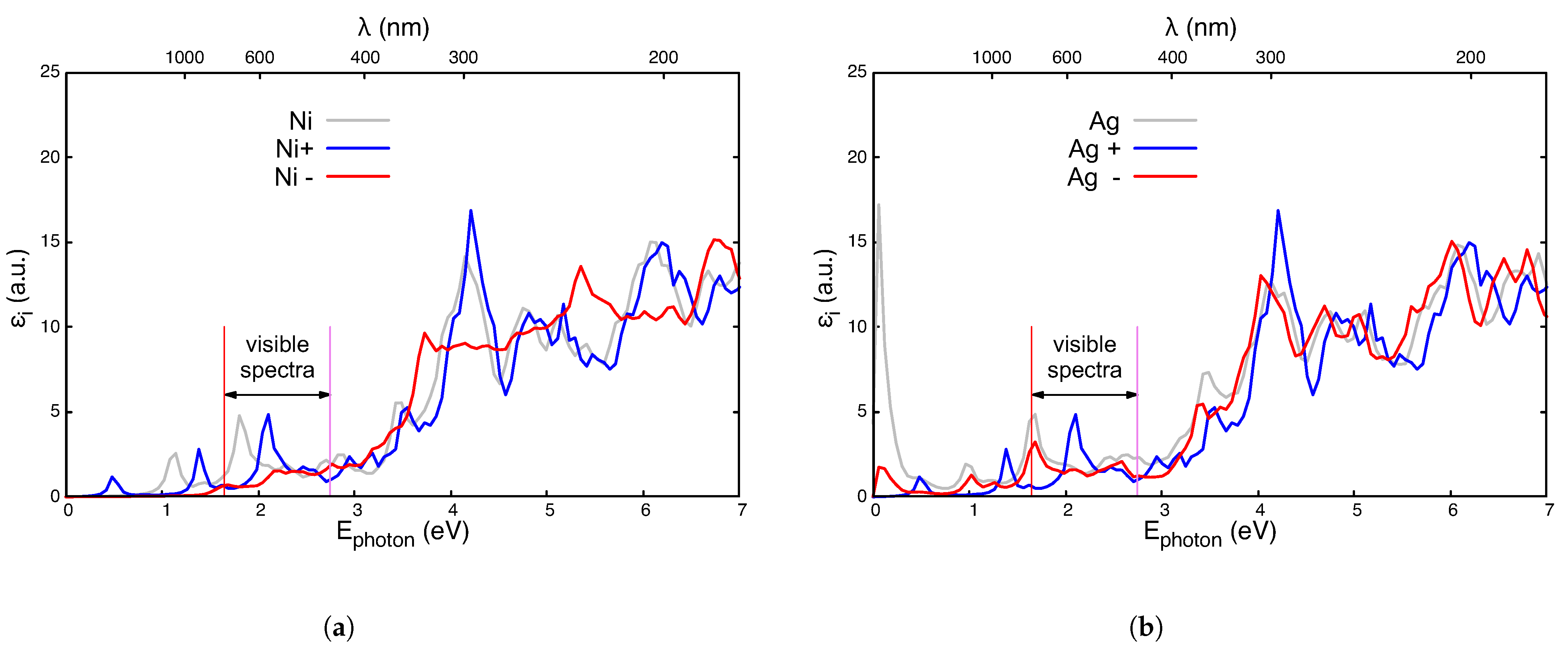
Appendix A. Effect of Charged Impurities
References
- Rajakumar, G.; Rahuman, A.A.; Roopan, S.M.; Khanna, V.G.; Elango, G.; Kamaraj, C.; Zahir, A.A.; Velayutham, K. Fungus-mediated biosynthesis and characterization of TiO2 nanoparticles and their activity against pathogenic bacteria. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2012, 91, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Daimon, T.; Hirakawa, T.; Kitazawa, M.; Suetake, J.; Nosaka, Y. Formation of singlet molecular oxygen associated with the formation of superoxide radicals in aqueous suspensions of TiO2 photocatalysts. Appl. Catal. A Gen. 2008, 340, 169–175. [Google Scholar] [CrossRef]
- Miyasaka, T. Toward Printable Sensitized Mesoscopic Solar Cells: Light-Harvesting Management with Thin TiO2 Films. J. Phys. Chem. Lett. 2011, 2, 262–269. [Google Scholar] [CrossRef]
- Dutta, P.K.; Ginwalla, A.; Hogg, B.; Patton, B.R.; Chwieroth, B.; Liang, Z.; Gouma, P.; Mills, M.; Akbar, S. Interaction of Carbon Monoxide with Anatase Surfaces at High Temperatures: Optimization of a Carbon Monoxide Sensor. J. Phys. Chem. B 1999, 103, 4412–4422. [Google Scholar] [CrossRef]
- Hou, X.; Huang, M.; Wu, X.; Liu, A. First-principles calculations on implanted TiO2 by 3d transition metal ions. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 838–842. [Google Scholar] [CrossRef]
- Abd, A.; Habubi, N.; Alkaim, A. Fe doped TiO2 thin films for Solar Cell Applications. Int. J. Adv. Sci. Technol. 2020, 29, 5428–5437. [Google Scholar]
- Yamaguchi, M.; Takamoto, T.; Khan, A.; Imaizumi, M.; Matsuda, S.; Ekins-Daukes, N.J. Super-high-efficiency multi-junction solar cells. Prog. Photovolt. Res. Appl. 2005, 13, 125–132. [Google Scholar] [CrossRef]
- Umebayashi, T.; Yamaki, T.; Itoh, H.; Asai, K. Analysis of electronic structures of 3d transition metal-doped TiO2 based on band calculations. J. Phys. Chem. Solids 2002, 63, 1909–1920. [Google Scholar] [CrossRef]
- Andersen, O.K. Linear methods in band theory. Phys. Rev. B 1975, 12, 3060–3083. [Google Scholar] [CrossRef]
- Schwarz, K.; Blaha, P. Solid state calculations using WIEN2k. Comput. Mater. Sci. 2003, 28, 259–273. [Google Scholar] [CrossRef]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- German, E.; Faccio, R.; Mombrú, A.W. A DFT+U study on structural, electronic, vibrational and thermodynamic properties of TiO2 polymorphs and hydrogen titanate: Tuning the Hubbard ’U-term’. J. Phys. Commun. 2017, 1, 055006. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, R.; Li, J.; Li, L.; Lin, S. First-principles study on transition metal-doped anatase TiO2. Nanoscale Res. Lett. 2014, 9, 46. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wu, H.C.; Li, S.H.; Lin, S.W. Effect of Fe Concentration on Fe-Doped Anatase TiO2 from GGA+U Calculations. Int. J. Photoenergy 2012, 2012, 823498. [Google Scholar] [CrossRef]
- Park, S.G.; Magyari-Köpe, B.; Nishi, Y. Electronic correlation effects in reduced rutile TiO2 within the LDA+U method. Phys. Rev. B 2010, 82, 115109. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejon, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys.-Condens. Mat. 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Kleinman, L.; Bilander, D.M. Efficacious Form for Model Pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425–1428. [Google Scholar] [CrossRef]
- Aguilera-Granja, F.; Longo, R.C.; Gallego, L.J.; Vega, A. Structural and magnetic properties of X2Y (X, Y = Fe, Co, Ni, Ru, Rh, Pd, and Pt) nanoalloys. J. Chem. Phys. 2010, 132, 184507. [Google Scholar] [CrossRef]
- Alonso-Lanza, T.; Ayuela, A.; Aguilera-Granja, F. Substitutional 4d and 5d impurities in graphene. Phys. Chem. Chem. Phys. 2016, 18, 21913–21920. [Google Scholar] [CrossRef] [PubMed]
- del Toro, R.A.; Aguilera-Granja, F.; Vogel, E. Structural and electronic properties of (TiO2)10 clusters with impurities: A density functional theory investigation. J. Phys. Chem. Solids 2019, 135, 109107. [Google Scholar] [CrossRef]
- Hou, D.L.; Meng, H.J.; Jia, L.Y.; Ye, X.J.; Zhou, H.J.; Li, X.L. Impurity concentration study on ferromagnetism in Cu-doped TiO2 thin films. Europhys. Lett. 2007, 78, 67001. [Google Scholar] [CrossRef]
- Ahmed, S.A. Structural, optical, and magnetic properties of Cu-doped TiO2 samples. Cryst. Res. Technol. 2017, 52, 1600335. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Liu, Q.L.; Dai, W.W. Structural, Electronic and Optical Properties of BiOX1 xYx (X, Y = F, Cl, Br and I) Solid Solutions from DFT Calculations. Sci. Rep. 2016, 6, 31449. [Google Scholar] [CrossRef] [PubMed]
- Kumaravel, V.; Rhatigan, S.; Mathew, S.; Michel, M.C.; Bartlett, J.; Nolan, M.; Hinder, S.J.; Gascó, A.; Ruiz-Palomar, C.; Hermosilla, D.; et al. Mo doped TiO2: Impact on oxygen vacancies, anatase phase stability and photocatalytic activity. J. Phys. Mater. 2020, 3, 025008. [Google Scholar] [CrossRef]
- Kumaravel, V.; Bianchetti, E.; Mathew, S.; Hinder, S.J.; Bartlett, J.; Di Valentin, C.; Pillai, S.C. New Insights into Crystal Defects, Oxygen Vacancies, and Phase Transition of Ir-TiO2. J. Phys. Chem. C 2021, 125, 23548–23560. [Google Scholar] [CrossRef]
- Aguilera-Granja, F.; Aguilera–del–Toro, R.; Vogel, E.; Cisternas, E. TiO2 nano-clusters adsorbed on surfaces: A density-functional-theoretic study. J. Phys. Chem. Solids 2021, 150, 109716. [Google Scholar] [CrossRef]
- Alam, M.S.; Saiduzzaman, M.; Biswas, A.; Ahmed, T.; Sultana, A.; Hossain, K.M. Tuning bandgap and enhancing optical functions of AGeF3 (A = K, Rb) under pressure for improved optoelectronic applications. Sci. Rep. 2022, 12, 8663. [Google Scholar] [CrossRef]
- Ehrenreich, H.; Cohen, M.H. Self-Consistent Field Approach to the Many-Electron Problem. Phys. Rev. 1959, 115, 786–790. [Google Scholar] [CrossRef]
- Tsafack, T.; Piccinini, E.; Lee, B.S.; Pop, E.; Rudan, M. Electronic, optical and thermal properties of the hexagonal and rocksalt-like Ge2Sb2Te5 chalcogenide from first-principle calculations. J. Appl. Phys. 2011, 110, 063716. [Google Scholar] [CrossRef]
- Eddiouane, A.; Chaib, H.; Nafidi, A.; Najjaoui, M.; Ait-Taleb, T. First principles investigation of electronic properties and high refractive index of rutile TiO2 for photovoltaic applications. AIP Conf. Proc. 2018, 2056, 020005. [Google Scholar] [CrossRef]
- Thatribud, A. Electronic and optical properties of TiO2 by first-principle calculation (DFT-GW and BSE). Mater. Res. Express 2019, 6, 095021. [Google Scholar] [CrossRef]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Kresse, G.; Janotti, A.; Van de Walle, C.G. First-principles calculations for point defects in solids. Rev. Mod. Phys. 2014, 86, 253–305. [Google Scholar] [CrossRef]
- Lyons, J.L.; Van de Walle, C.G. Computationally predicted energies and properties of defects in GaN. NPJ Comput. Mater. 2017, 3, 12. [Google Scholar] [CrossRef]
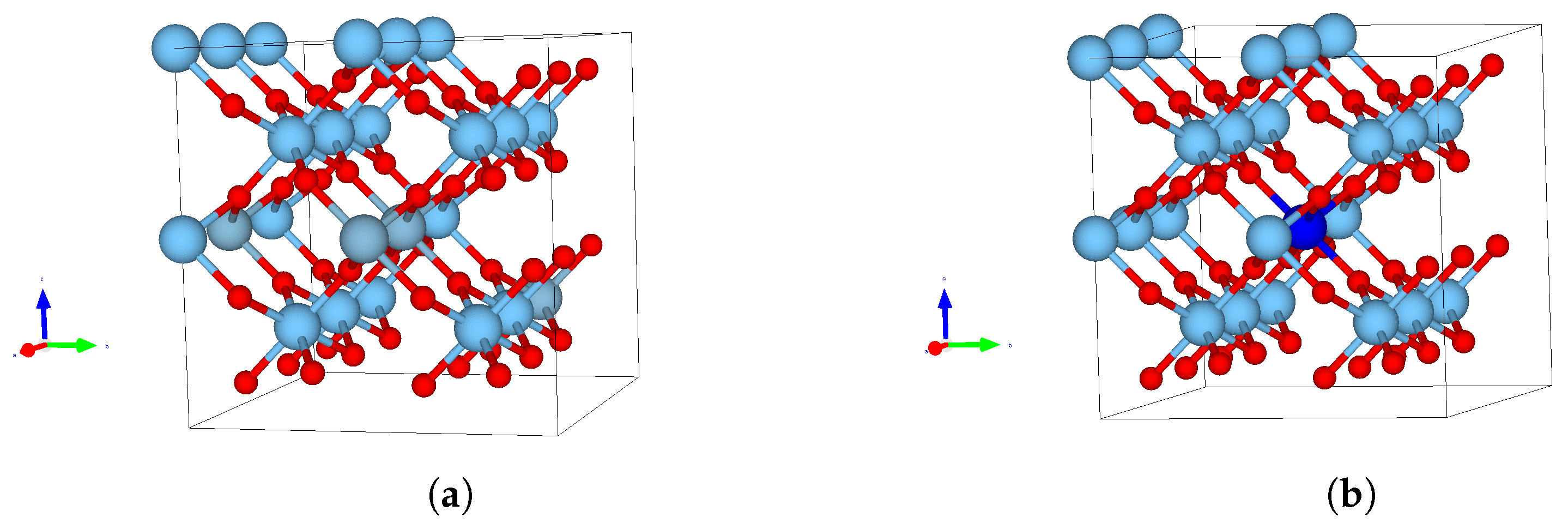
| Impurity | a | b | c | c/a | Magnetic Moment | (a) |
|---|---|---|---|---|---|---|
| Å | Å | Å | /Cell | meV | ||
| Pristine | 4.621 | 4.621 | 3.055 | 0.661 | 0.0 | - |
| Fe | 4.609 | 4.609 | 3.046 | 0.661 | 2.5 | 6.1 |
| Co | 4.602 | 4.647 | 3.046 | 0.662 | 1.0 | 1.0 |
| Ni | 4.603 | 4.602 | 3.046 | 0.662 | 0.0 | - |
| Cu | 4.605 | 4.605 | 3.058 | 0.664 | 2.0 | −9.4 |
| Pd | 4.617 | 4.617 | 3.058 | 0.662 | 0.0 | - |
| Ag | 4.626 | 4.756 | 3.063 | 0.662 | 0.0 | - |
| Pt | 4.617 | 4.617 | 3.060 | 0.663 | 0.0 | - |
| Au | 4.628 | 4.627 | 3.065 | 0.662 | 0.3 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cisternas, E.; Aguilera-del-Toro, R.; Aguilera-Granja, F.; Vogel, E.E. Effect of Substitutional Metallic Impurities on the Optical Absorption Properties of TiO2. Nanomaterials 2024, 14, 1224. https://doi.org/10.3390/nano14141224
Cisternas E, Aguilera-del-Toro R, Aguilera-Granja F, Vogel EE. Effect of Substitutional Metallic Impurities on the Optical Absorption Properties of TiO2. Nanomaterials. 2024; 14(14):1224. https://doi.org/10.3390/nano14141224
Chicago/Turabian StyleCisternas, Eduardo, Rodrigo Aguilera-del-Toro, Faustino Aguilera-Granja, and Eugenio E. Vogel. 2024. "Effect of Substitutional Metallic Impurities on the Optical Absorption Properties of TiO2" Nanomaterials 14, no. 14: 1224. https://doi.org/10.3390/nano14141224
APA StyleCisternas, E., Aguilera-del-Toro, R., Aguilera-Granja, F., & Vogel, E. E. (2024). Effect of Substitutional Metallic Impurities on the Optical Absorption Properties of TiO2. Nanomaterials, 14(14), 1224. https://doi.org/10.3390/nano14141224








