Thermophysical Profile of Industrial Graphene Water-Based Nanofluids
Abstract
:1. Introduction
2. Mateirials and Methods
2.1. Nanofluids Preparation from Enhanced Liquid-Phase Exfoliation
2.2. Characterization Methods
3. Results and Discussion
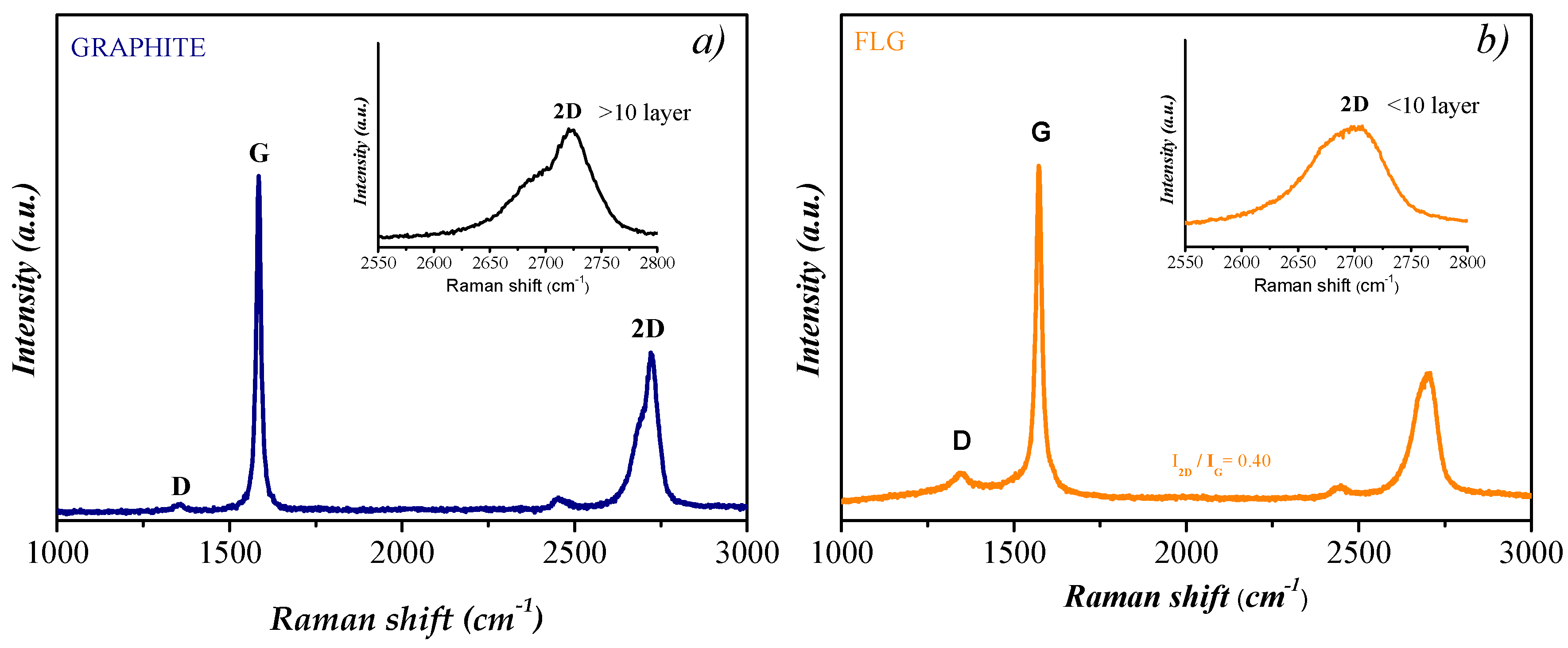
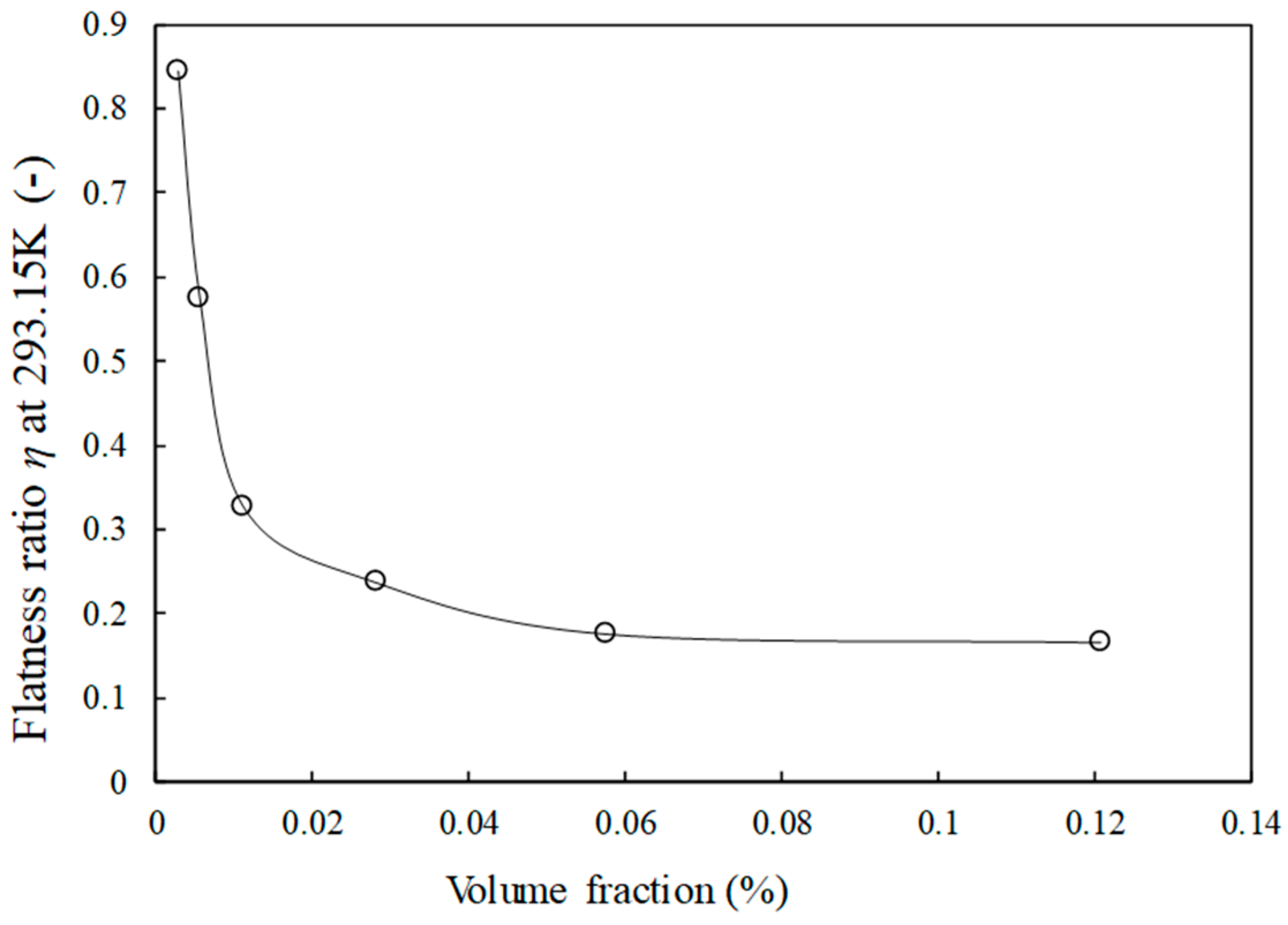
3.1. Structural Properties of Graphene Sheets
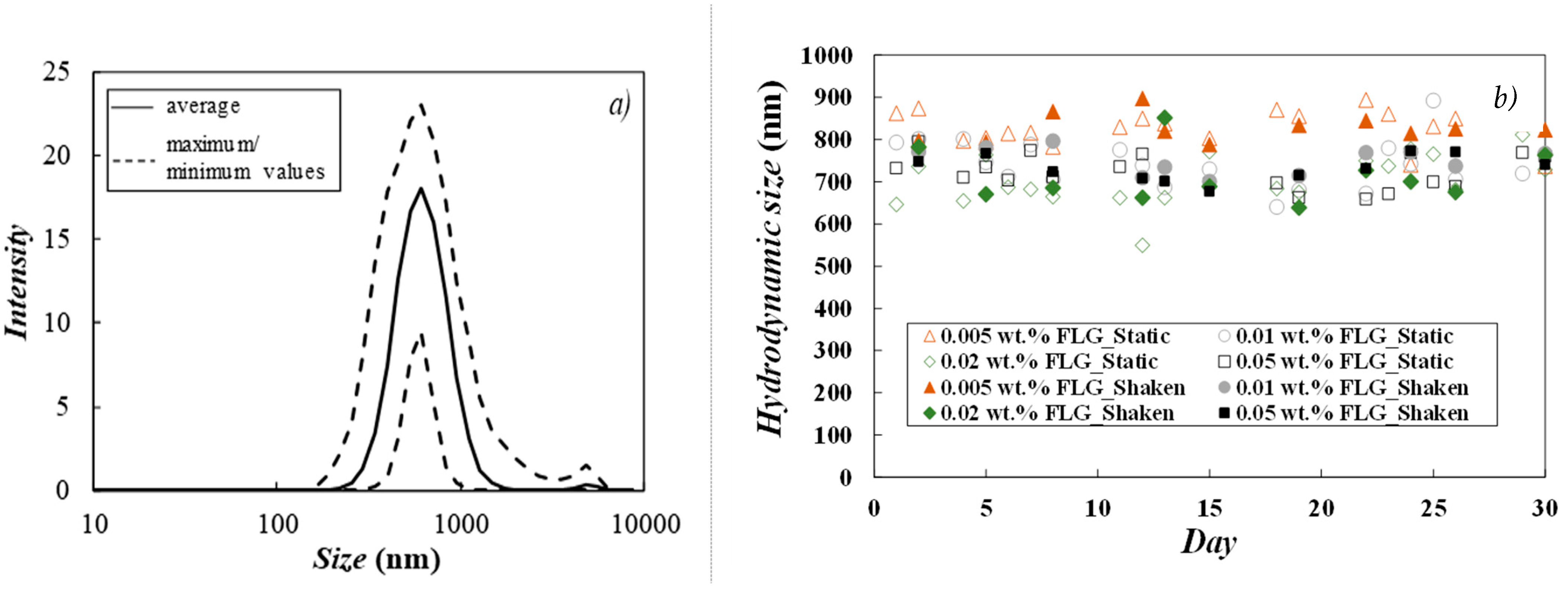
3.2. Stability Analyses
3.3. Thermophysical Profile
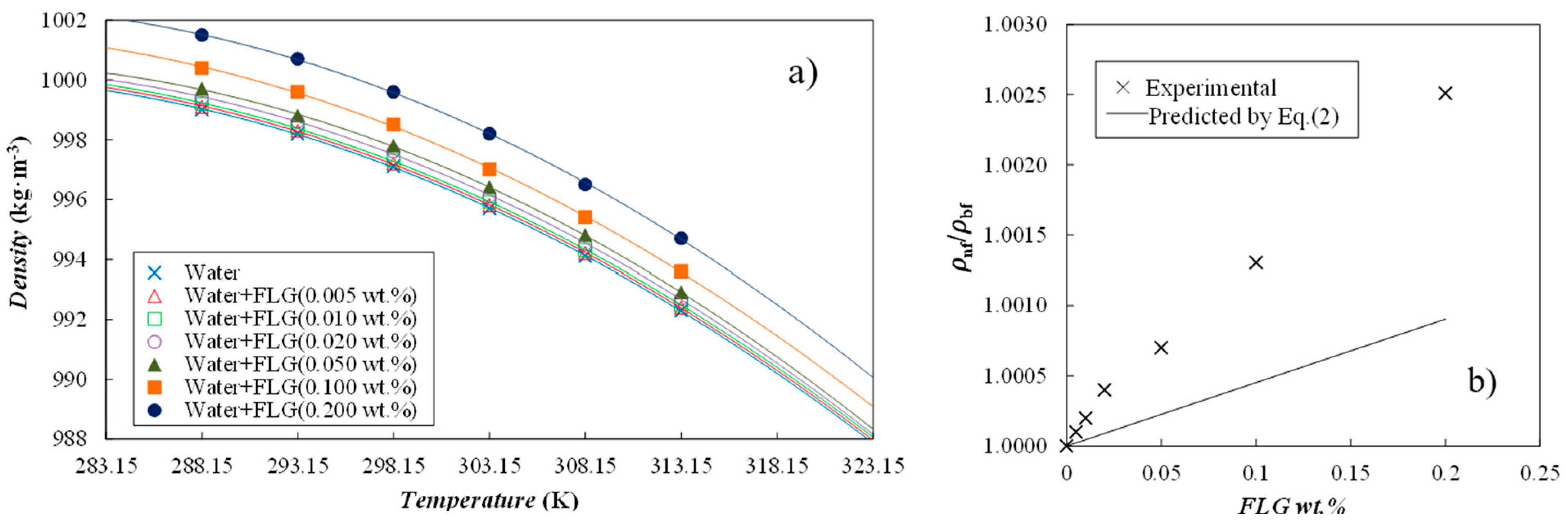
3.3.1. Density and Thermal Expansivity
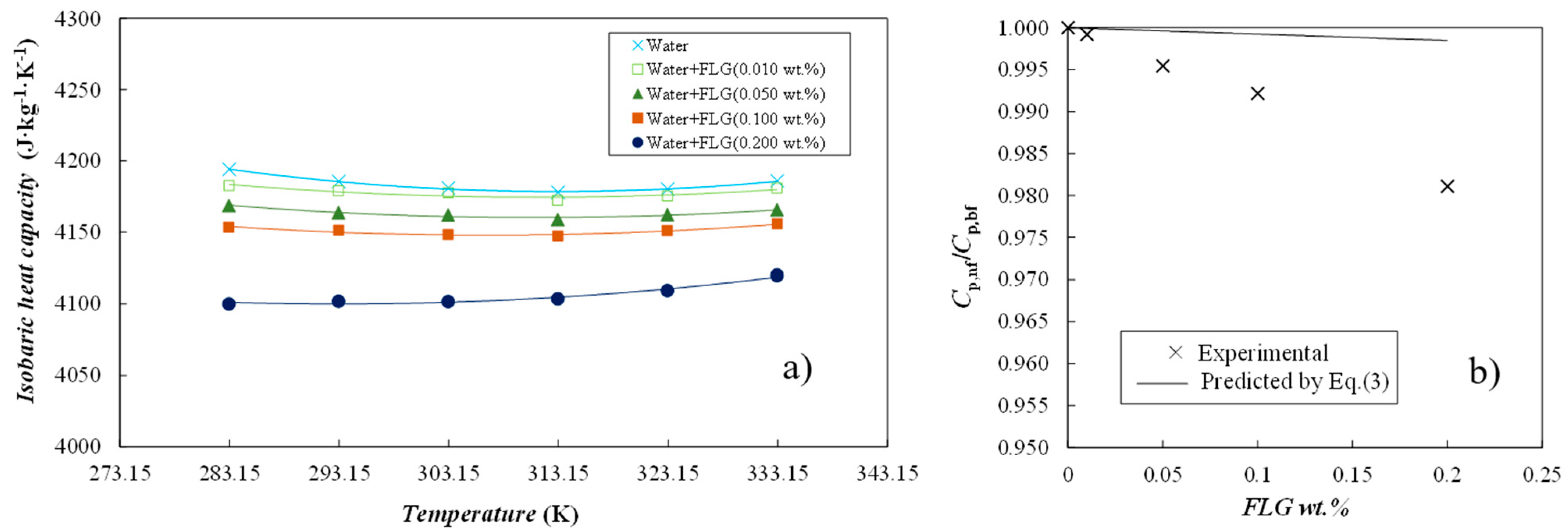
3.3.2. Isobaric Heat Capacity
3.3.3. Thermal Conductivity
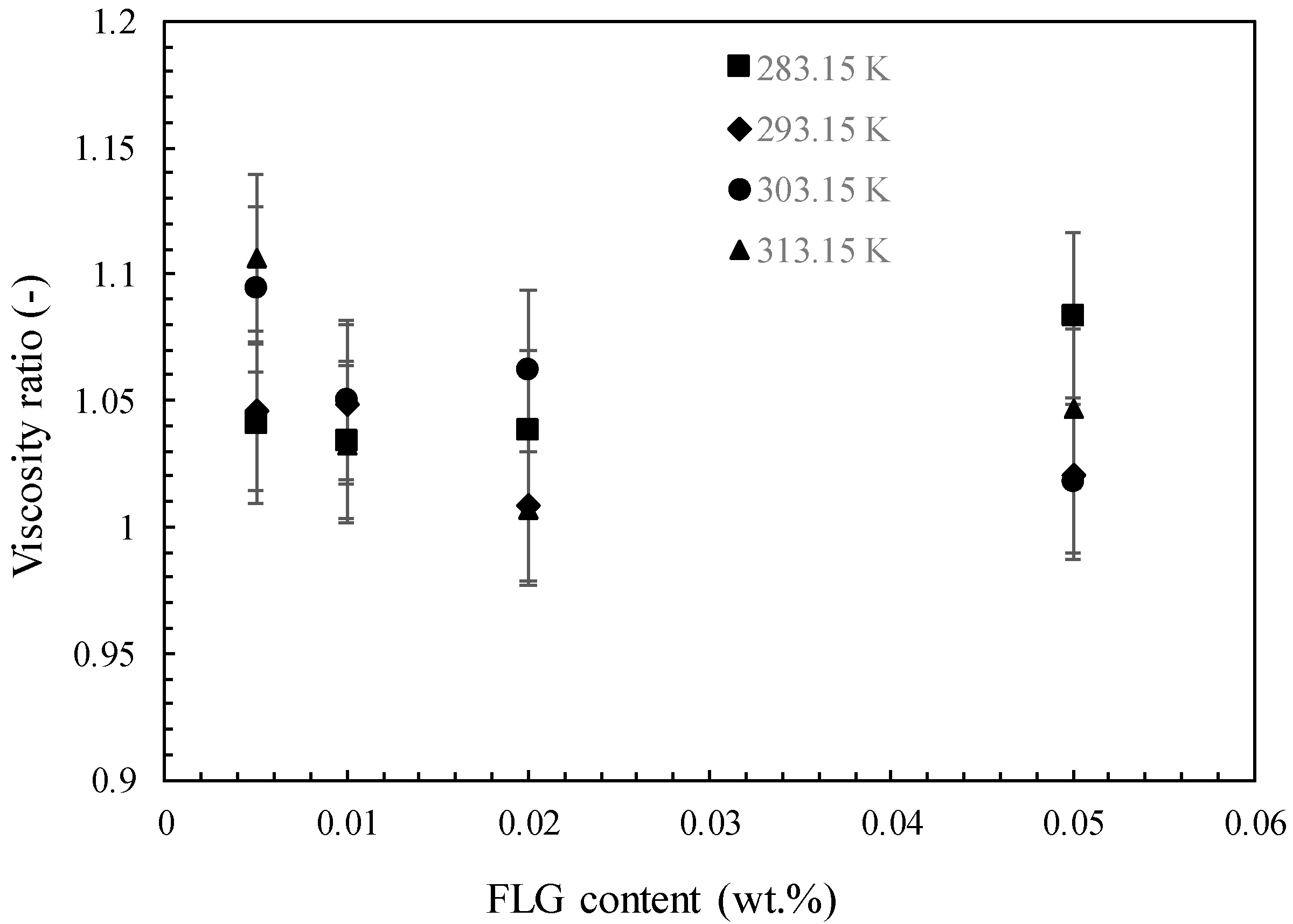
3.3.4. Dynamic Viscosity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| AAD | Average absolute deviation (%) |
| DLS | Dynamic light scattering |
| Isobaric heat capacity, (J·kg−1·K−1) | |
| DW | Deionized/Distilled water |
| FLG | Few layer graphene |
| HTF | Heat transfer fluid |
| HRTEM | High-resolution transmission electron microscopy |
| GNP | Graphene nanoplatelets |
| Thermal conductivity (W·m−1·K−1) | |
| L | Average length of graphene (μm) |
| MLG | Multilayer/thick graphene |
| PHP | Pulsed heat pipe |
| RK | Interfacial thermal resistance (m2·K·W−1) |
| SEM | Scanning electron microscopy |
| T | Temperature (K) |
| t | Graphene thickness (nm) |
| TEM | Transmission electron microscopy |
| TMDSC | Temperature-modulated differential scanning calorimetry |
| Greek letters | |
| αp | Isobaric thermal expansivity coefficient (K−1) |
| ζ | Zeta potential (mV) |
| Average flatness ratio of FLG | |
| Density (kg·m−3) | |
| Mass fraction | |
| Volume fraction | |
| Subscripts | |
| bf | Base fluid |
| nf | Nanofluid |
| np | Nanoparticles |
References
- Tam, N.T.; Phuong, N.V.; Khoi, P.H.; Minh, P.N.; Afrand, M.; Van Trinh, P.; Thang, B.H.; Zyła, G.; Estellé, P. Carbon nanomaterial-based nanofluids for direct thermal solar absorption. Nanomaterials 2020, 10, 1199. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Parvin, N.; Kumar, V.; Joo, S.W.; Park, S.-S.; Mandal, T.K. Recent advances in the characterized identification of mono-to-multi-layer graphene and its biomedical applications: A review. Electronics 2022, 11, 3345. [Google Scholar] [CrossRef]
- Hamze, S.; Cabaleiro, D.; Estellé, P. Graphene-based nanofluids: A comprehensive review about rheological behavior and dynamic viscosity. J. Mol. Liq. 2021, 325, 115207. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Graphene family nanofluids: A critical review and future research directions. Energy Convers. Manag. 2019, 196, 1222–1256. [Google Scholar] [CrossRef]
- Pavía, M.; Alajami, K.; Estellé, P.; Desforges, A.; Vigolo, B. A critical review on thermal conductivity enhancement of graphene-based nanofluids. Adv. Colloid Interface Sci. 2021, 294, 102452. [Google Scholar] [CrossRef] [PubMed]
- Hamze, S.; Berrada, N.; Cabaleiro, D.; Desforges, A.; Ghanbaja, J.; Gleize, J.; Bégin, D.; Michaux, F.; Maré, T.; Vigolo, B.; et al. Few-layer graphene-based nanofluids with enhanced thermal conductivity. Nanomaterials 2020, 10, 1258. [Google Scholar] [CrossRef]
- Le Ba, T.; Mahian, O.; Wongwises, S.; Szilágyi, I.M. Review on the recent progress in the preparation and stability of graphene-based nanofluids. J. Therm. Anal. Calorim. 2020, 142, 1145–1172. [Google Scholar] [CrossRef]
- Sadeghinezhad, E.; Akhiani, A.R.; Metselaar, H.S.C.; Latibari, S.T.; Mehrali, M.; Mehrali, M. Parametric study on the thermal performance enhancement of a thermosyphon heat pipe using covalent functionalized graphene nanofluids. Appl. Therm. Eng. 2020, 175, 115385. [Google Scholar] [CrossRef]
- Kumar, L.H.; Kazi, S.N.; Masjuki, H.H.; Zubir, M.N.M.; Jahan, A.; Bhinitha, C. Energy, exergy and economic analysis of liquid flat-plate solar collector using green covalent functionalized graphene nanoplatelets. Appl. Therm. Eng. 2021, 192, 116916. [Google Scholar] [CrossRef]
- Balaji, T.; Selvam, C.; Lal, D.M.; Harish, S. Enhanced heat transport behavior of micro channel heat sink with graphene based nanofluids. Int. Commun. Heat Mass Transf. 2020, 117, 104716. [Google Scholar] [CrossRef]
- Xu, Y.; Xue, Y.; Qi, H.; Cai, W. Experimental study on heat transfer performance of pulsating heat pipes with hybrid working fluids. Int. J. Heat Mass Transf. 2020, 157, 119727. [Google Scholar] [CrossRef]
- Alawi, O.A.; Sidik, N.A.C.; Kazi, S.N.; Najafi, G. Graphene nanoplatelets and few-layer graphene studies in thermo-physical properties and particle characterization. J. Therm. Anal. Calorim. 2019, 135, 1081–1093. [Google Scholar] [CrossRef]
- Janowska, I.; Truong-Phuoc, L.; Ba, H.; Pham-Huu, C. Nanocomposites Nanomatériau/Système Polymoléculaire Colloïdaux, et Méthodes de Préparation. WO 2018/087484 A1 [Online]. Available online: https://patents.google.com/patent/WO2018087484A1/fr (accessed on 30 July 2024).
- Cabaleiro, D.; Gracia-Fernández, C.; Lugo, L. (Solid+liquid) phase equilibria and heat capacity of (diphenyl ether+biphenyl) mixtures used as thermal energy storage materials. J. Chem. Thermodyn. 2014, 74, 43–50. [Google Scholar] [CrossRef]
- Hamze, S.; Cabaleiro, D.; Maré, T.; Vigolo, B.; Estellé, P. Shear flow behavior and dynamic viscosity of few-layer graphene nanofluids based on propylene glycol-water mixture. J. Mol. Liq. 2020, 316, 113875. [Google Scholar] [CrossRef]
- Osswald, S.; Havel, M.; Gogotsi, Y. Monitoring oxidation of multiwalled carbon nanotubes by Raman spectroscopy. J. Raman Spectrosc. 2007, 38, 728. [Google Scholar] [CrossRef]
- Chizari, K.; Janowskaa, I.; Houlléa, M.; Florea, I.; Ersenb, O.; Romeroa, T.; Bernhardt, P.; Ledouxa, M.J.; Pham-Huua, C. Tuning of nitrogen-doped carbon nanotubes as catalyst support for liquid-phase reaction. Appl. Catal. A 2010, 380, 72–80. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 2006, 97, 187401. [Google Scholar] [CrossRef]
- Chakraborty, S.; Panigrahi, P.K. Stability of nanofluid: A review. Appl. Therm. Eng. 2020, 174, 115259. [Google Scholar] [CrossRef]
- Ilyas, S.U.; Shamsuddin, R.; Xiang, T.K.; Estellé, P.; Pendyala, R. Rheological profile of graphene-based nanofluids in thermal oil with hybrid additives of carbon nanotubes and nanofibers. J. Mol. Liq. 2023, 376, 121443. [Google Scholar] [CrossRef]
- Fedele, L.; Colla, L.; Bobbo, S.; Barison, S.; Agresti, F. Experimental stability analysis of different water-based nanofluids. Nanoscale Res. Lett. 2011, 6, 300. [Google Scholar] [CrossRef]
- Ilyas, S.U.; Pendyala, R. Preparation sedimentation and agglomeration of nanofluids. Chem. Eng. Technol. 2014, 37, 2011. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST reference fluid thermodynamic and transport properties database. In NIST 23, (REFPROP), 8th ed.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007. [Google Scholar]
- Vallejo, J.P.; Pérez-Tavernier, J.; Cabaleiro, D.; Fernández-Seara, J.; Lugo, L. Potential heat transfer enhancement of functionalized graphene nanoplatelet dispersions in a propylene glycol-water mixture. Thermophysical profile. J. Chem. Thermodyn. 2018, 123, 174–184. [Google Scholar] [CrossRef]
- Hamze, S.; Cabaleiro, D.; Bégin, D.; Desforges, A.; Maré, T.; Vigolo, B.; Lugo, L.; Estellé, P. Volumetric Properties and Surface Tension of few-layer graphene nanofluids based on a commercial heat transfer fluid. Energies 2020, 13, 3462. [Google Scholar] [CrossRef]
- Picard, S.; Burns, D.T.; Roger, P. Determination of the specific heat capacity of a graphite sample using absolute and differential methods. Metrologia 2007, 44, 294–302. [Google Scholar] [CrossRef]
- Picard, S.; Burns, D.T.; Roger, P. Measurement of the Specific Heat Capacity of Graphite; (BIPM--2006-01); Bureau International des Poids et Mesures (BIPM): Paris, France, 2006. [Google Scholar]
- Marcos, M.A.; Cabaleiro, D.; Guimarey, M.J.G.; Comuñas, M.J.P.; Fedele, L.; Fernández, J.; Lugo, L. PEG 400-based phase change materials nano-enhanced with functionalized graphene nanoplatelets. Nanomaterials 2017, 8, 16. [Google Scholar] [CrossRef]
- Pop, E.; Varshney, V.; Roy, A.K. Thermal properties of graphene: Fundamentals and applications. MRS Bull. 2012, 37, 1273–1281. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701. [Google Scholar] [CrossRef]
- Żyła, G.; Vallejo, J.P.; Lugo, L. Isobaric heat capacity and density of ethylene glycol based nanofluids containing various nitride nanoparticle types: An experimental study. J. Mol. Liq. 2018, 261, 530–539. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, H.; Sasmito, A.P.; Mujumdar, A.S. Measurement and modeling of thermal conductivity of graphene nanoplatelet water and ethylene glycol base nanofluids. Int. J. Heat Mass Transf. 2018, 123, 97–109. [Google Scholar] [CrossRef]
- Maré, T.; Halelfadl, S.; Van Vaerenbergh, S.; Estellé, P. Unexpected sharp peak in thermal conductivity of carbon nanotubes water-based nanofluids. Int. Commun. Heat Mass Transf. 2015, 66, 80. [Google Scholar] [CrossRef]
- Chu, K.; Li, W.; Tang, F. Flatness-dependent thermal conductivity of graphene-based composites. Phys. Lett. A 2013, 377, 910–914. [Google Scholar] [CrossRef]
- Alexeev, D.; Chen, J.; Walther, J.H.; Giapis, K.P.; Angelikopoulos, P.; Koumoutsakos, P. Kapitza resistance between few-layer graphene and water: Liquid layering effects. Nano Lett. 2015, 15, 5744–5749. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.; Sun, Z.; Huang, P.; Li, Y.; Hu, N. Some basic aspects of polymer nanocomposites: A critical review. Nano Mater. Sci. 2019, 1, 2–30. [Google Scholar] [CrossRef]
- Androulidakis, C.; Koukaras, E.N.; Rahova, J.; Sampathkumar, K.; Parthenios, J.; Papagelis, K.; Frank, O.; Galiotis, C. Wrinkled few-layer graphene as highly efficient load bearer. ACS Appl. Mater. Interfaces 2017, 9, 26593–26601. [Google Scholar] [CrossRef]
- Sadeghinezhad, E.; Mehrali, M.; Rosen, M.A.; Akhiani, A.R.; Latibari, S.T.; Mehrali, M.; Metselaar, H.S.C. Experimental investigation of the effect of graphene nanofluids on heat pipe thermal performance. Appl. Therm. Eng. 2016, 100, 775–787. [Google Scholar] [CrossRef]
- Vakili, M.; Khosrojerdi, S.; Aghajannezhad, P.; Yahyaei, M. A hybrid artificial neural network-genetic algorithm modeling approach for viscosity estimation of graphene nanoplatelets nanofluid using experimental data. Int. Commun. Heat Mass Transf. 2017, 82, 40–48. [Google Scholar] [CrossRef]
- Yarmand, H.; Gharehkhani, S.; Shirazi, S.F.S.; Amiri, A.; Alehashem, M.S.; Dahari, M.; Kazi, S. Experimental investigation of thermo-physical properties, convective heat transfer and pressure drop of functionalized graphene nanoplatelets aqueous nanofluid in a square heated pipe. Energy Convers. Manag. 2016, 114, 38–49. [Google Scholar] [CrossRef]
- Vallejo, J.P.; Gómez-Barreiro, S.; Cabaleiro, D.; Gracia-Fernández, C.; Fernández-Seara, J.; Lugo, L. Flow behaviour of suspensions of functionalized graphene nanoplatelets in propylene glycol–water mixtures. Int. Commun. Heat Mass Transf. 2018, 91, 150–157. [Google Scholar] [CrossRef]
- Wang, Y.; Al-Saaidi, H.A.I.; Kong, M.; Alvarado, J.L. Thermophysical performance of graphene based aqueous nanofluids. Int. J. Heat Mass Transf. 2018, 119, 408–417. [Google Scholar] [CrossRef]



| FLG Concentration wt.% | ζeta Potential (mV) | ||||
|---|---|---|---|---|---|
| 1st Day | 8th Day | 16th Day | 23rd Day | 30th Day | |
| 0.005 | −35.3 ± 0.3 | −36.5 ± 0.5 | −38.4 ± 0.6 | −36.5 ± 0.7 | −34.0 ± 0.2 |
| 0.010 | −39.2 ± 1.6 | −35.3 ± 0.3 | −37.9 ± 0.8 | −37.1 ± 1.2 | −35.5 ± 1.0 |
| 0.020 | −39.6 ± 0.1 | −36.5 ± 0.3 | −37.8 ± 0.8 | −37.6 ± 1.4 | −40.4 ± 2.4 |
| 0.050 | −38.3 ± 0.4 | −39.9 ± 0.2 | −38.4 ± 1.1 | −38.3 ± 0.9 | −36.7 ± 1.3 |
| 0.100 | −39.7 ± 1.0 | −37.2 ± 1.3 | −36.1 ± 0.9 | −38.8 ± 1.1 | −37.3 ± 1.2 |
| 0.200 | −36.5 ± 0.5 | −37.4 ± 1.1 | −37.2 ± 0.4 | −35.0 ± 0.6 | −35.5 ± 0.6 |
| FLG Mass Fraction (wt.%) | ||||||
|---|---|---|---|---|---|---|
| 0.005 | 0.010 | 0.020 | 0.050 | 0.100 | 0.200 | |
| a0/(kg·m−3) | 625.6 | 625.7 | 625.8 | 600.4 | 544.9 | 628.5 |
| a1/(kg·m−3·K−1) | 2.74 | 2.74 | 2.74 | 2.91 | 3.29 | 2.73 |
| −103·a2/(kg·m−3·K−2) | 5.00 | 5.00 | 5.00 | 5.29 | 5.93 | 5.00 |
| 102·s/(kg·m−3) | 6.1 | 6.1 | 9.5 | 5.1 | 7.4 | 5.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gal, S.; Cabaleiro, D.; Hassen, W.; Nasri, A.; Lafue, Y.; Pham-Huu, C.; Ba, H.; Estellé, P. Thermophysical Profile of Industrial Graphene Water-Based Nanofluids. Nanomaterials 2024, 14, 1401. https://doi.org/10.3390/nano14171401
Gal S, Cabaleiro D, Hassen W, Nasri A, Lafue Y, Pham-Huu C, Ba H, Estellé P. Thermophysical Profile of Industrial Graphene Water-Based Nanofluids. Nanomaterials. 2024; 14(17):1401. https://doi.org/10.3390/nano14171401
Chicago/Turabian StyleGal, Soulayma, David Cabaleiro, Walid Hassen, Anaghim Nasri, Yannick Lafue, Cuong Pham-Huu, Housseinou Ba, and Patrice Estellé. 2024. "Thermophysical Profile of Industrial Graphene Water-Based Nanofluids" Nanomaterials 14, no. 17: 1401. https://doi.org/10.3390/nano14171401
APA StyleGal, S., Cabaleiro, D., Hassen, W., Nasri, A., Lafue, Y., Pham-Huu, C., Ba, H., & Estellé, P. (2024). Thermophysical Profile of Industrial Graphene Water-Based Nanofluids. Nanomaterials, 14(17), 1401. https://doi.org/10.3390/nano14171401









