Magnetization States and Coupled Spin-Wave Modes in Concentric Double Nanorings
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory for Equilibrium Configurations
2.2. Theory for Magnetization Dynamics
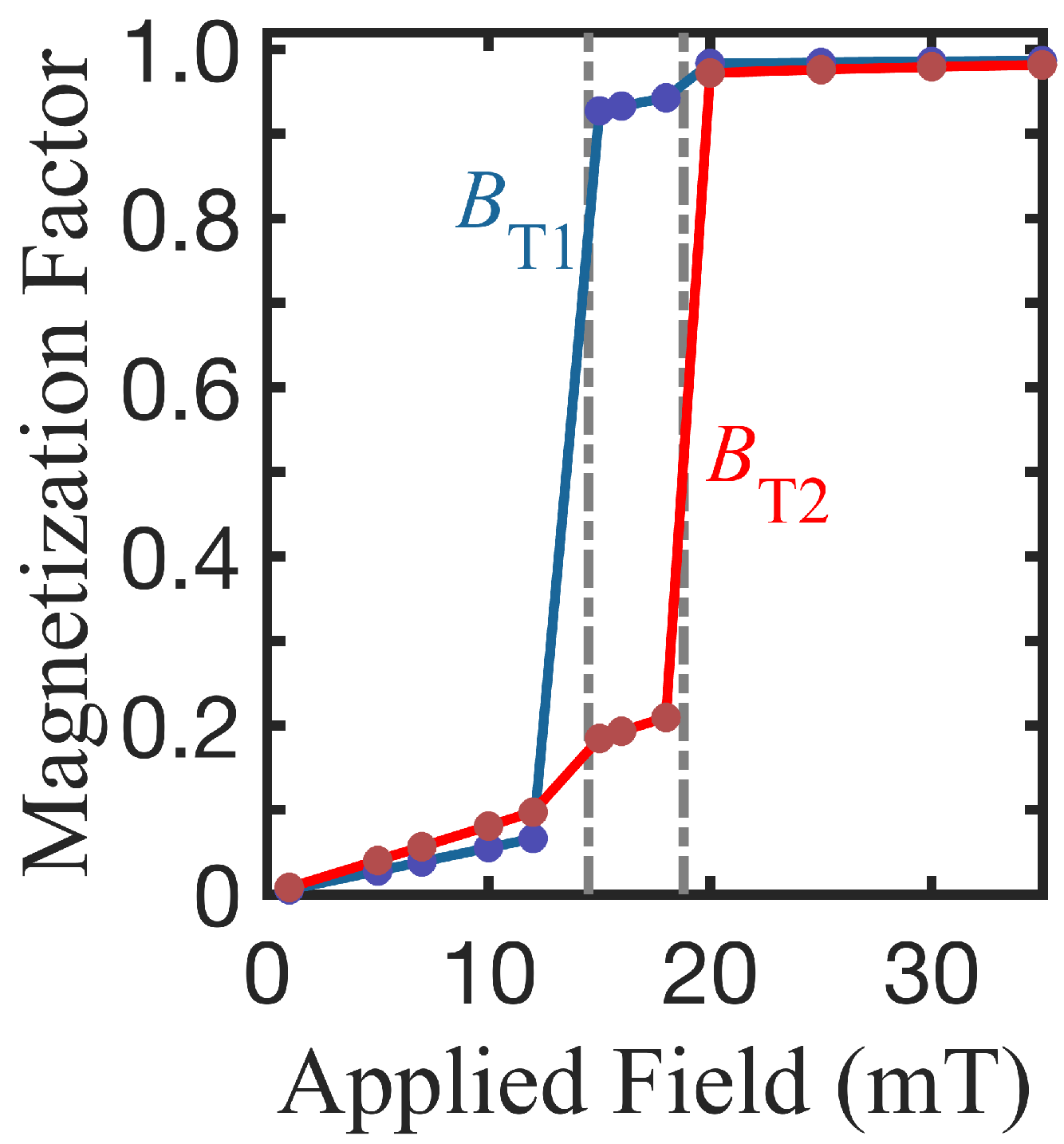
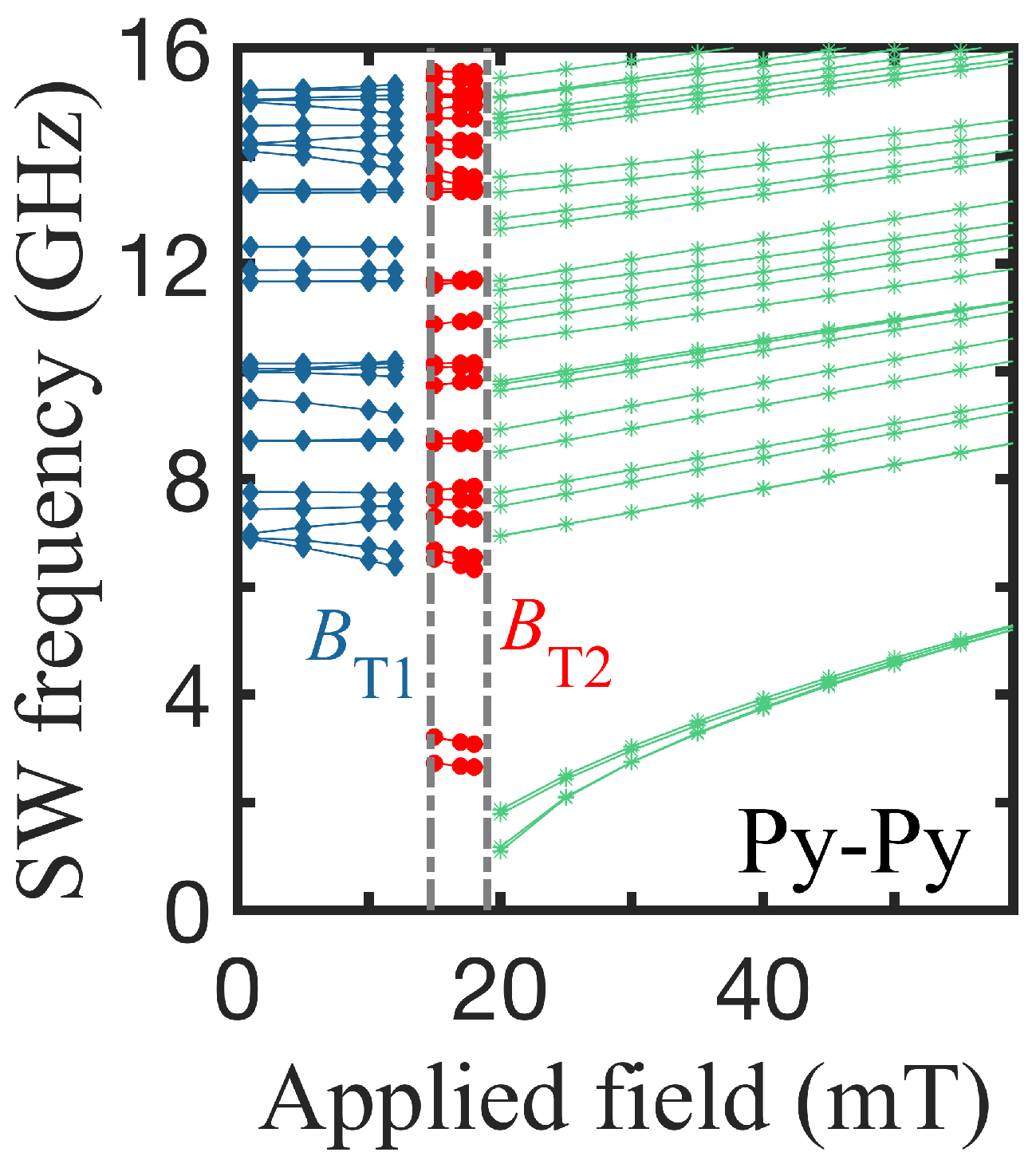
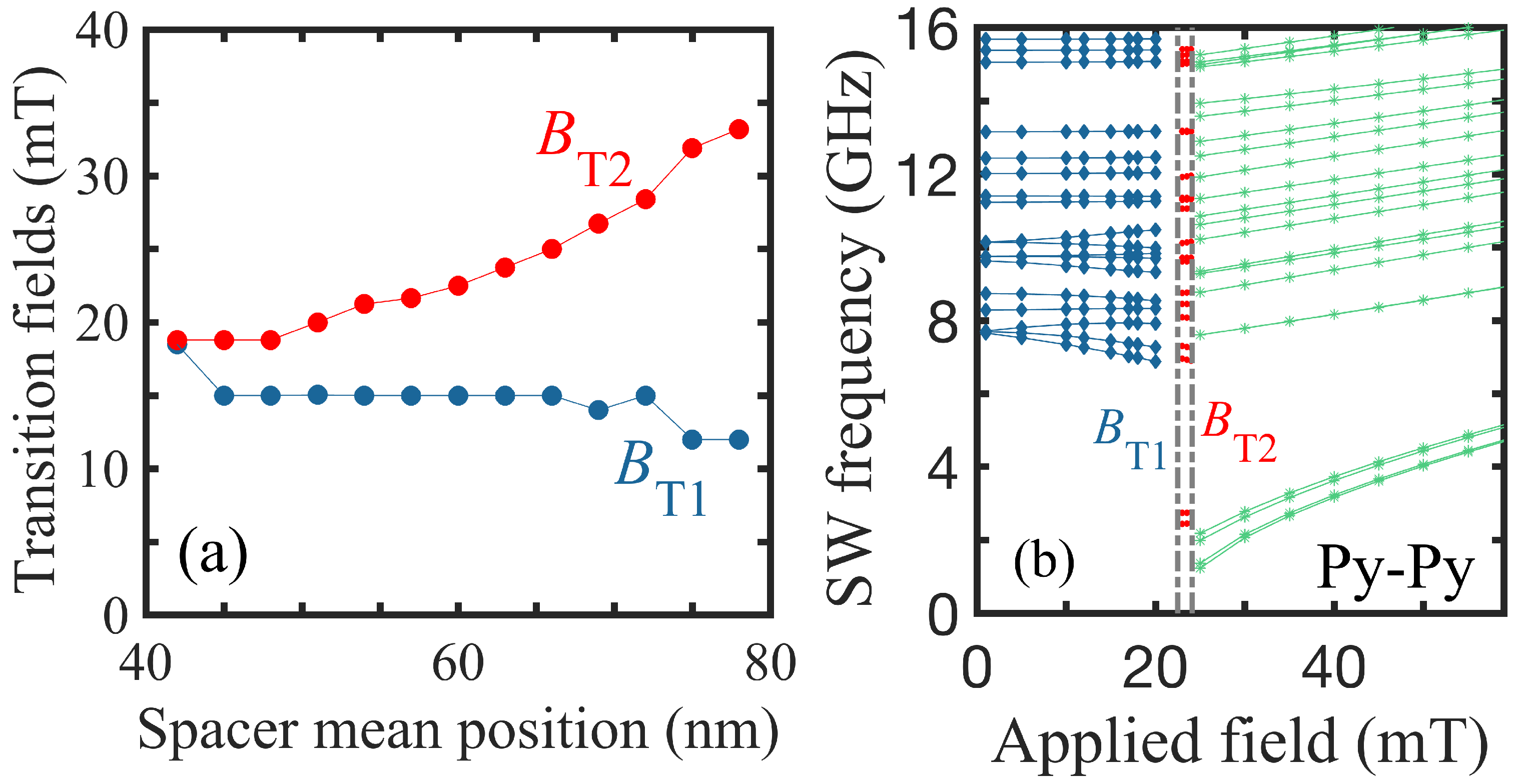
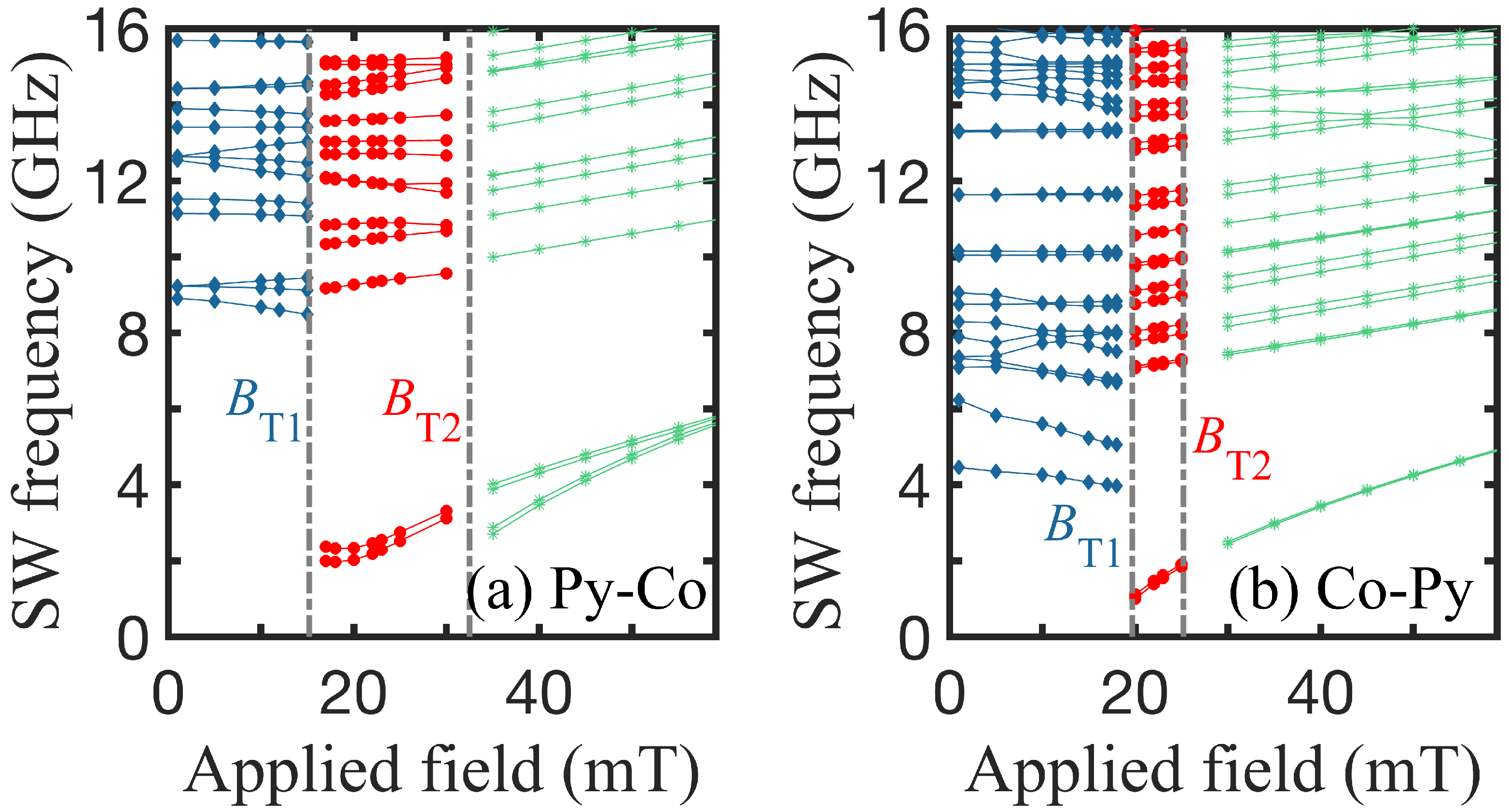
3. Results
3.1. Single-Component Structures
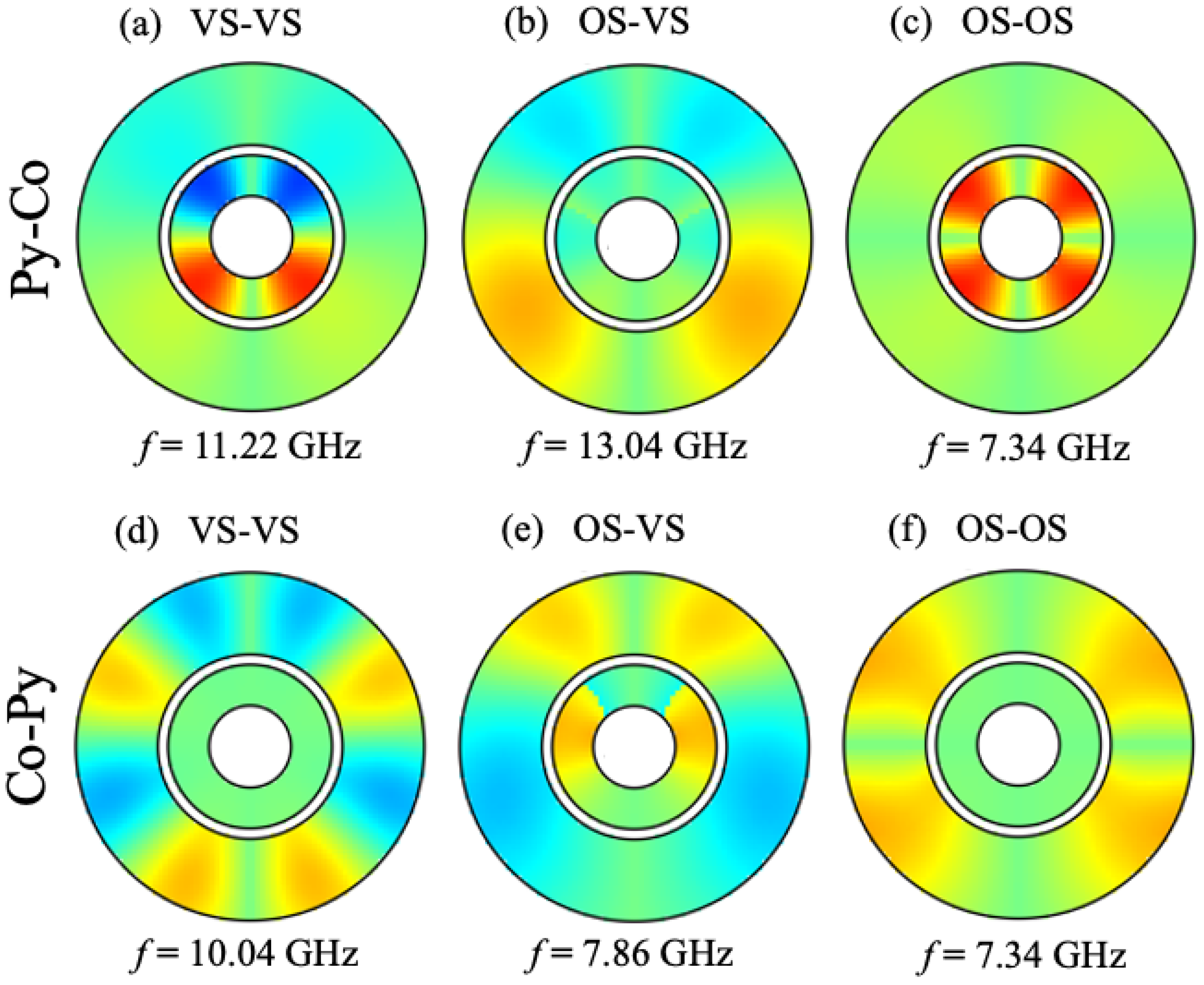
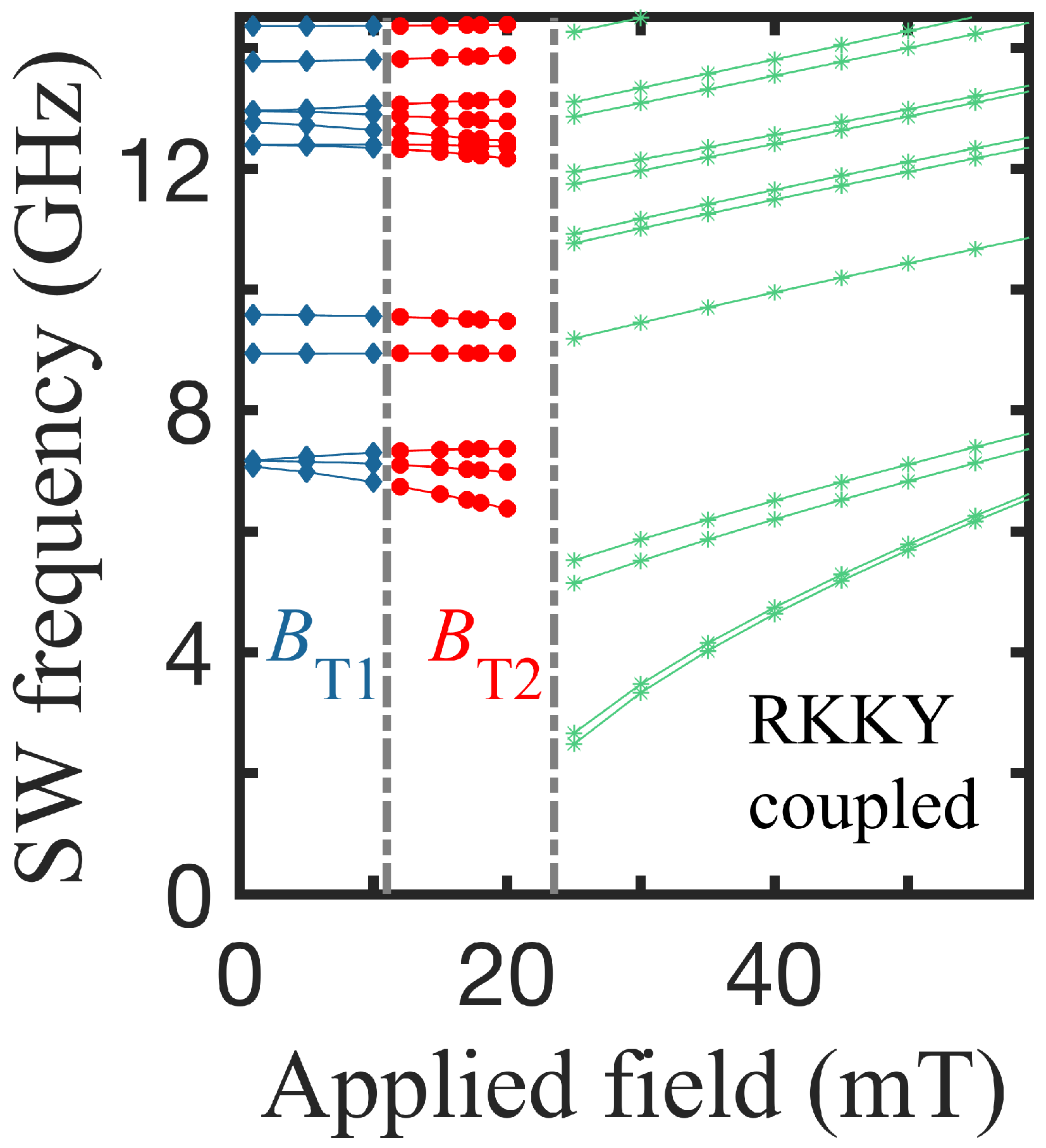
3.2. Bicomponent Structures
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Liu, X.L.; Yi, J.B.; Yang, Y.; Fan, H.M.; Ding, J. Stable vortex magnetite nanorings colloid: Micromagnetic simulation and experimental demonstration. J. Appl. Phys. 2012, 111, 044303. [Google Scholar] [CrossRef]
- Liu, X.L.; Yang, Y.; Ng, C.T.; Zhao, L.Y.; Zhang, Y.; Bay, B.H.; Fan, H.M.; Ding, J. Magnetic vortex nanorings: A new class of hyperthermia agent for highly efficient in vivo regression of tumors. Adv. Mater. 2015, 27, 1939. [Google Scholar] [CrossRef] [PubMed]
- Matatagui, D.; Kolokoltseva, O.V.; Qureshi, N.; Mejía-Uriartea, E.V.; Ordonez-Romero, C.L.; Vázquez-Olmos, A.; Saniger, J.M. Magnonic sensor array based on magnetic nanoparticles to detect, discriminate and classify toxic gases. Sens. Actuators B 2017, 240, 497. [Google Scholar] [CrossRef]
- Tong, G.; Liu, Y.; Cui, T.; Li, Y.; Zhao, Y.; Guan, J. Tunable dielectric properties and excellent microwave absorbing properties of elliptical Fe3O4 nanorings. Appl. Phys. Lett. 2016, 108, 072905. [Google Scholar] [CrossRef]
- Dias, C.S.B.; Hanchuk, T.D.M.; Wender, H.; Shigeyosi, W.T.; Kobarg, J.; Rossi, A.L.; Tanaka, M.N.; Cardoso, M.B.; Garcia, F. Shape tailored magnetic nanorings for intracellular hyperthermia cancer therapy. Sci. Rep. 2017, 7, 14843. [Google Scholar] [CrossRef] [PubMed]
- Chumak, A.V.; Serga, A.A.; Hillebrands, B. Magnonic crystals for data processing. J. Phys D Appl. Phys. 2017, 50, 244001. [Google Scholar] [CrossRef]
- Jung, H.; Choi, Y.S.; Lee, K.S.; Han, D.S.; Yu, Y.S.; Im, M.Y.; Fischer, P.; Kim, S.K. Logic operations based on magnetic-vortex-state networks. ACS Nano 2012, 6, 3712. [Google Scholar] [CrossRef]
- Hirohata, A.; Yamada, K.; Nakatani, Y.; Prejbeanu, I.L.; Diény, B.; Pirro, P.; Hillebrands, B. Review on spintronics: Principles and device applications. J. Magn. Magn. Mater. 2020, 509, 166711. [Google Scholar] [CrossRef]
- Gubbiotti, G. (Ed.) Three-Dimensional Magnonics; Jenny Stanford Publishing: Singapore, 2019; p. 1. [Google Scholar]
- Kudr, J.; Haddad, Y.; Richtera, L.; Heger, Z.; Cernak, M.; Adam, V.; Zitka, O. Magnetic nanoparticles: From design and synthesis to real world applications. Nanomaterials 2017, 7, 243. [Google Scholar] [CrossRef]
- Barman, A.; Mondal, S.; Sahoo, S.; De, A. Magnetization dynamics of nanoscale magnetic materials: A perspective. J. Appl. Phys. 2020, 128, 170901. [Google Scholar] [CrossRef]
- Hayward, T.J.; Llandro, J.; Balsod, R.B.; Bland, J.A.C.; Morecroft, D.; Castano, F.J.; Ross, C.A. Switching behavior of individual pseudo-spin-valve ring structures. Phys. Rev. B 2006, 74, 134405. [Google Scholar] [CrossRef]
- Mu, C.; Jing, J.; Dong, J.; Wang, W.; Xu, J.; Nie, A.; Xiang, J.; Wen, F.; Liu, Z. Static and dynamic characteristics of magnetism in permalloy oval nanoring by micromagnetic simulation. J. Magn. Magn. Mater. 2019, 474, 301–304. [Google Scholar] [CrossRef]
- Vaz, C.A.F.; Hayward, T.J.; Llandro, J.; Schackert, F.; Morecroft, D.; Bland, J.A.C.; Kläui, M.; Laufenberg, M.; Backes, D.; Rüdiger, U.; et al. Ferromagnetic nanorings. J. Phys. Condens. Matter 2007, 19, 255207. [Google Scholar] [CrossRef]
- Gubbiotti, G.; Madami, M.; Tacchi, S.; Carlotti, G.; Tanigawa, H.; Ono, T.; Giovannini, L.; Montoncello, F.; Nizzoli, F. Splitting of spin Excitations in nanometric rings induced by a magnetic field. Phys. Rev. Lett. 2006, 97, 247203. [Google Scholar] [CrossRef]
- Fonin, M.; Hartung, C.; Rüdiger, U.; Backes, D.; Heyderman, L.; Nolting, F.; Rodriguez, A.F.; Klaüi, M. Formation of magnetic domains and domain walls in epitaxial Fe3O4(100) elements. J. Appl. Phys. 2011, 109, 07D315. [Google Scholar] [CrossRef]
- Rothman, J.; Kläui, M.; Lopex-Diaz, L.; Vaz, C.A.F.; Bleloch, A.; Bland, J.A.C.; Cui, Z.; Speaks, R. Observation of a bi-domain state and nucleation free switching in mesoscopic ring magnets. Phys. Rev. Lett. 2001, 86, 1098. [Google Scholar] [CrossRef]
- Lopez-Diaz, L.; Rothman, J.; Klaüi, M.; Bland, J.A.C. Computational study of first magnetization curves in small rings. IEEE Trans. Magn. 2000, 36, 3155. [Google Scholar] [CrossRef]
- Klaüi, M.; Vaz, C.A.F.; Lopez-Diaz, L.; Bland, J.A.C. Vortex formation in narrow ferromagnetic rings. J. Phys. Condens. Matter 2003, 15, R985. [Google Scholar] [CrossRef]
- Cowburn, R.; Koltsov, D.; Adeyeye, A.; Welland, M.; Tricker, D. Single-domain circular nanomagnets. Phys. Rev. Lett. 1999, 83, 1042. [Google Scholar] [CrossRef]
- Hussain, B.; Haghshenasfard, Z.; Cottam, M.G. Spin waves in unsaturated single- and double-layered ferromagnetic nanorings. J. Phys. D Appl. Phys. 2021, 54, 165002. [Google Scholar] [CrossRef]
- Klaüi, M.; Jubert, P.O.; Allenspach, R.; Bischof, A.; Bland, J.A.C.; Faini, G.; Rüdiger, U.; Vaz, C.A.F.; Vila, L.; Vouille, C. Direct observation of domain-wall configurations transformed by spin currents. Phys. Rev. Lett. 2005, 95, 026601. [Google Scholar] [CrossRef] [PubMed]
- Guslienko, K.Y.; Hoffmann, A. Vortex magnetization reversal in double-layer ferromagnetic/ antiferromagnetic dots. J. Appl. Phys. 2007, 101, 093901. [Google Scholar] [CrossRef]
- Moreira, C.D.; Monteiro, M.G., Jr.; Toscano, D.; Leonel, S.A.; Sato, F. Decreasing the size limit for a stable magnetic vortex in modified permalloy nanodiscs. J. Mag. Magn. Mat. 2017, 443, 252. [Google Scholar] [CrossRef]
- Banerjee, C.; Saha, S.; Barman, S.; Rousseau, O.; Otani, Y.; Barman, A. Width dependent transition of quantized spin-wave modes in Ni80Fe20 square nanorings. J. Appl. Phys. 2014, 116, 163912. [Google Scholar] [CrossRef]
- Castano, F.J.; Ross, C.A.; Eilez, A. Magnetization reversal in elliptical-ring nanomagnets. J. Phys. D Appl. Phys. 2003, 36, 2031. [Google Scholar] [CrossRef]
- Mancilla-Almonacid, D.; Arias, R.E. Spin-wave modes in ferromagnetic nanodisks, their excitation via alternating currents and fields, and auto-oscillations. Phys. Rev. B 2017, 95, 214424. [Google Scholar] [CrossRef]
- Adeyeye, A.O.; Goolaup, S.; Singh, N.; Wang, C.C.; Gao, X.S.; Ross, C.A.; Jung, W.; Castano, F.J. Magnetostatic coupling in arrays of elongated Ni80Fe20 rings. J. Phys. D Appl. Phys 2007, 40, 6479–6483. [Google Scholar] [CrossRef]
- Raabe, J.; Pulwey, R.; Sattler, R.; Schweinbeck, T.; Zweck, J.; Weiss, D. Magnetization pattern of ferromagnetic nanodisks. J. Appl. Phys. 2000, 88, 4437. [Google Scholar] [CrossRef]
- Dumas, R.K.; Gredig, T.; Li, C.P.; Schuller, I.K.; Liu, K. Angular dependence of vortex-annihilation fields in asymmetric cobalt dots. Phys. Rev. B 2009, 80, 014416. [Google Scholar] [CrossRef]
- Shimon, G.; Adeyeye, A.O.; Ross, C.A. Comparative study of the ferromagnetic resonance behavior of coupled rectangular and circular Ni80Fe20 rings. Phys. Rev. B 2014, 89, 024302. [Google Scholar] [CrossRef]
- Vaz, C.A.F.; Athanasiou, C.; Bland, J.A.C.; Rowlands, G. Energetics of magnetic ring and disk elements: Uniform versus vortex state. Phys. Rev. B 2006, 73, 054411. [Google Scholar] [CrossRef]
- Madami, M.; Tacchi, S.; Gubbiotti, G.; Carlotti, G.; Montoncello, F.; Capuzzo, G.; Nizzoli, F. Magnetic normal modes of elliptical NiFe nanorings studied by micro-focused Brillouin light scattering. J. Phys. C Conf. Ser. 2010, 200, 042008. [Google Scholar] [CrossRef]
- Yu, C.; Chiang, T.W.; Chen, Y.S.; Cheng, K.W.; Chen, D.C.; Lee, S.F.; Liou, Y.; Hsu, J.H.; Yao, Y.D. Variation of magnetization reversal in pseudo-spin-valve elliptical rings. Appl. Phys. Lett. 2009, 94, 233103. [Google Scholar] [CrossRef]
- Cui, B.; Veres, T. Fabrication of metal nanoring array by nanoimprint lithography (NIL) and reactive ion etching. Microelectron. Eng. 2007, 84, 1544. [Google Scholar] [CrossRef]
- Castano, F.J.; Morecroft, D.; Ross, C.A. Low-field giant magnetoresistance in layered magnetic rings. Phys. Rev. B 2006, 74, 224401. [Google Scholar] [CrossRef]
- Zhu, M.; Mathieu, C.; Scholz, W.; Dubakka, S.; Kautzky, M. Vortex state formation and stability in single and double layer nanorings and nanodisks. J. Appl. Phys. 2013, 113, 17B905. [Google Scholar] [CrossRef]
- Podbielski, J.; Giesen, F.; Grundler, D. Spin-wave interference in microscopic rings. Phys. Rev. Lett. 2006, 96, 167207. [Google Scholar] [CrossRef]
- Podbielski, J.; Heitmann, D.; Grundler, D. Microwave-assisted switching of microscopic rings: Correlation between nonlinear spin dynamics and critical microwave fields. Phys. Rev. Lett. 2007, 99, 207202. [Google Scholar] [CrossRef]
- Jung, Y.S.; Jung, W.; Ross, C.A. Nanofabricated concentric ring structures by templated self-assembly of a diblock copolymer. Nano Lett. 2008, 8, 2975. [Google Scholar] [CrossRef]
- Jain, S.; Adeyeye, A.O. Aligned alternating head-to-head and tail-to-tail domain walls in ferromagnetic concentric rings. IEEE Trans. Mag. 2010, 46, 1595. [Google Scholar] [CrossRef]
- Avila, J.I.; Tumelero, M.A.; Pasa, A.A.; Viegas, A.D.C. Magnetoresistive system with concentric ferromagnetic asymmetric nanorings. J. Appl. Phys. 2015, 117, 103901. [Google Scholar] [CrossRef]
- McKeever, C.; Ogrin, F.Y.; Aziz, M.M. Dynamic susceptibility of concentric permalloy rings with opposite chirality vortices. J. Appl. Phys. 2017, 121, 203901. [Google Scholar] [CrossRef] [PubMed]
- Sahu, R.; Kotti, A.P.; Tandon, P.; Mishra, A.C. Static and dynamic magnetic characteristics in concentric permalloy nanorings. J. Mag. Magn. Mater. 2023, 581, 107973. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Cottam, M.G. Microscopic theory of spin-wave excitations in ferromagnetic nanorings. J. Appl. Phys. 2006, 99, 08J303. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Cottam, M.G. Spin-wave excitations in arrays of asymmetric ferromagnetic nanorings. J. Appl. Phys. 2008, 103, 07C503. [Google Scholar] [CrossRef]
- Tian, C.; Chauduri, U.; Singh, N.; Adeyeye, A.O. Direct mapping of spin wave modes of individual Ni80Fe20 nanorings. Nanotechnology 2020, 31, 145714. [Google Scholar] [CrossRef]
- Wang, Z.K.; Lim, H.S.; Liu, H.Y.; Ng, S.C.; Kuok, M.H.; Tay, L.L.; Lockwood, D.J.; Cottam, M.G.; Hobbs, K.L.; Larson, P.R.; et al. Spin waves in nickel nanorings of large aspect ratio. Phys. Rev. Lett. 2005, 94, 137208. [Google Scholar] [CrossRef]
- Neudecker, I.; Kläui, M.; Perzlmaier, K.; Backes, D.; Heyderman, L.J.; Vaz, C.A.F.; Bland, J.A.C.; Rüdiger, U.; Back, C.H. Spatially resolved dynamic eigenmode spectrum of Co rings. Phys. Rev. Lett. 2006, 96, 057207. [Google Scholar] [CrossRef]
- Hussain, B.; Cottam, M.G.; Baolai, G. Quasiperiodic spin waves in bi-component magnonic crystal arrays of nanowires. J. Phys. D Appl. Phys. 2019, 52, 095001. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Cottam, M.G. Spectral intensities and frequencies of spin waves in ferromagnetic cylinders: Application to nickel nanowires. Phys. Rev. B 2005, 72, 224415. [Google Scholar] [CrossRef]
- Lupo, P.; Haghshenasfard, Z.; Cottam, M.G.; Adeyeye, A.O. Ferromagnetic resonance study of interface coupling for spin waves in narrow NiFe/Ru/NiFe multilayer nanowires. Phys. Rev. B 2016, 118, 113902. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 1940, 58, 1098. [Google Scholar] [CrossRef]
- Gurevich, A.G.; Melkov, G.A. Magnetization Oscillation and Waves; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Stancil, D.D.; Prabhakar, A. Spin Waves: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Nguyen, T.M.; Cottam, M.G. Microscopic theory of dipole-exchange spin-wave excitations in ferromagnetic nanowires. Phys. Rev. B 2005, 71, 094406. [Google Scholar] [CrossRef]
- White, R.M. Quantum Theory of Magnetism: Magnetic Properties of Materials, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Gubbiotti, G.; Tacchi, S.; Nguyen, H.T.; Madami, M.; Carlotti, G.; Nakano, K.; Ono, T.; Cottam, M.G. Coupled spin waves in trilayer films and nanostripes of permalloy separated by nonmagnetic spacers: Brillouin light scattering and theory. Phys. Rev. B 2013, 87, 094406. [Google Scholar] [CrossRef]
- Klaüi, M.; Vaz, C.A.F.; Bland, J.A.C.; Heyderman, L.; Nolting, F.; Pavlovska, A.; Bauer, E.; Cherifi, S.; Heun, S.; Locatelli, A. Head-to-head domain-wall phase diagram in mesoscopic ring magnets. Appl. Phys. Lett. 2004, 85, 5637. [Google Scholar] [CrossRef]
- Muscas, G.; Menniti, M.; Brucas, R.; Jönsson, P.E. Mesoscopic magnetic rings: Complex magnetization reversal uncovered by FORC. J. Magn. Magn. Mater. 2020, 474, 166559. [Google Scholar] [CrossRef]
- Oliveira, L.L.; Nunes, M.S.; Souza, C.M.; Dantas, A.L.; Souza, I.Q.; Reboucas, G.O.G.; Carrico, A.S. Confinement of magnetic vortex and domain walls in dipolar-coupled concentric nanocylinders. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Moon, J.H.; Seo, S.M.; Lee, K.J.; Kim, K.W.; Ryu, J.; Lee, H.W.; McMichael, R.D.; Stiles, M.D. Spin-wave propagation in the presence of interfacial Dzyaloshinskii-Moriya interaction. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88, 184404. [Google Scholar] [CrossRef]
- Hussain, B.; Cottam, M.G. Dipole-exchange spin waves in unsaturated ferromagnetic nanorings with interfacial Dzyaloshinski-Moriya interactions. J. Appl. Phys. 2022, 132, 193901. [Google Scholar] [CrossRef]
- Zakeri, K.; Zhang, Y.; Prokop, J.; Chuang, T.H.; Sakr, N.; Tang, W.X.; Kirschner, J. Asymmetric spin-wave dispersion on Fe(110): Direct evidence of the Dzyaloshinskii-Moriya interaction. Phys. Rev. Lett. 2010, 104, 137203. [Google Scholar] [CrossRef]
- Chaurasiya, A.K.; Banerjee, C.; Pan, S.; Sahoo, S.; Choudhury, S.; Sinha, J.; Barman, A. Direct observation of interfacial Dzyaloshinskii-Moriya interaction from asymmetric spin-wave propagation in W/CoFeB/SiO2 heterostructures down to sub-nanometer CoFeB thickness. Sci. Rep. 2016, 6, 32592. [Google Scholar] [CrossRef] [PubMed]
- Camley, R.E.; Livesey, K.E. Consequences of the Dzyaloshinskii-Moriya interaction. Surf. Sci. Rep. 2023, 78, 100605. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, B.; Cottam, M.G. Magnetization States and Coupled Spin-Wave Modes in Concentric Double Nanorings. Nanomaterials 2024, 14, 1594. https://doi.org/10.3390/nano14191594
Hussain B, Cottam MG. Magnetization States and Coupled Spin-Wave Modes in Concentric Double Nanorings. Nanomaterials. 2024; 14(19):1594. https://doi.org/10.3390/nano14191594
Chicago/Turabian StyleHussain, Bushra, and Michael G. Cottam. 2024. "Magnetization States and Coupled Spin-Wave Modes in Concentric Double Nanorings" Nanomaterials 14, no. 19: 1594. https://doi.org/10.3390/nano14191594





