Physical Mechanism of Selective Healing of Nanopores in Condensed Matter under the Influence of Laser Irradiation and Plasma
Abstract
:1. Introduction
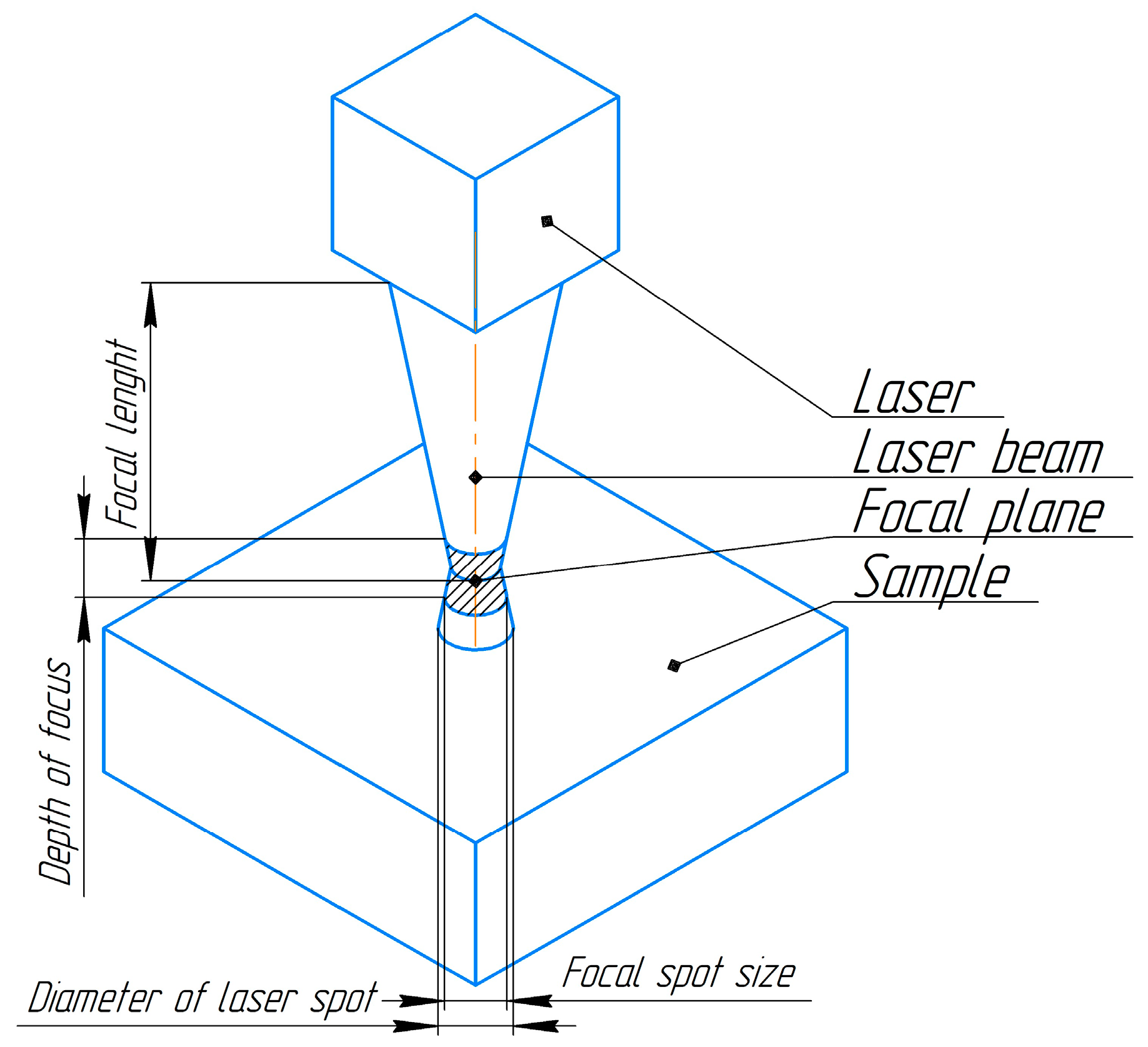
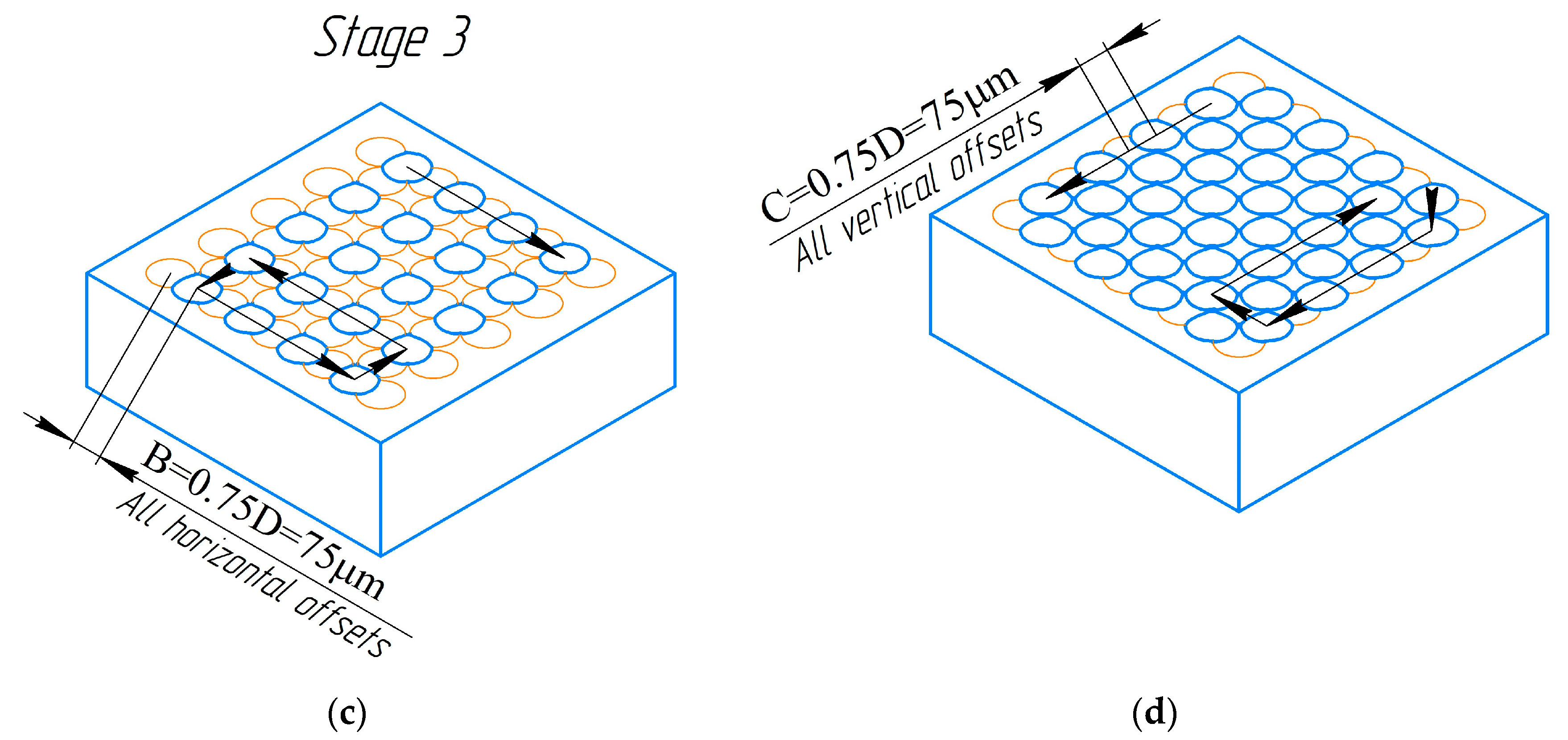
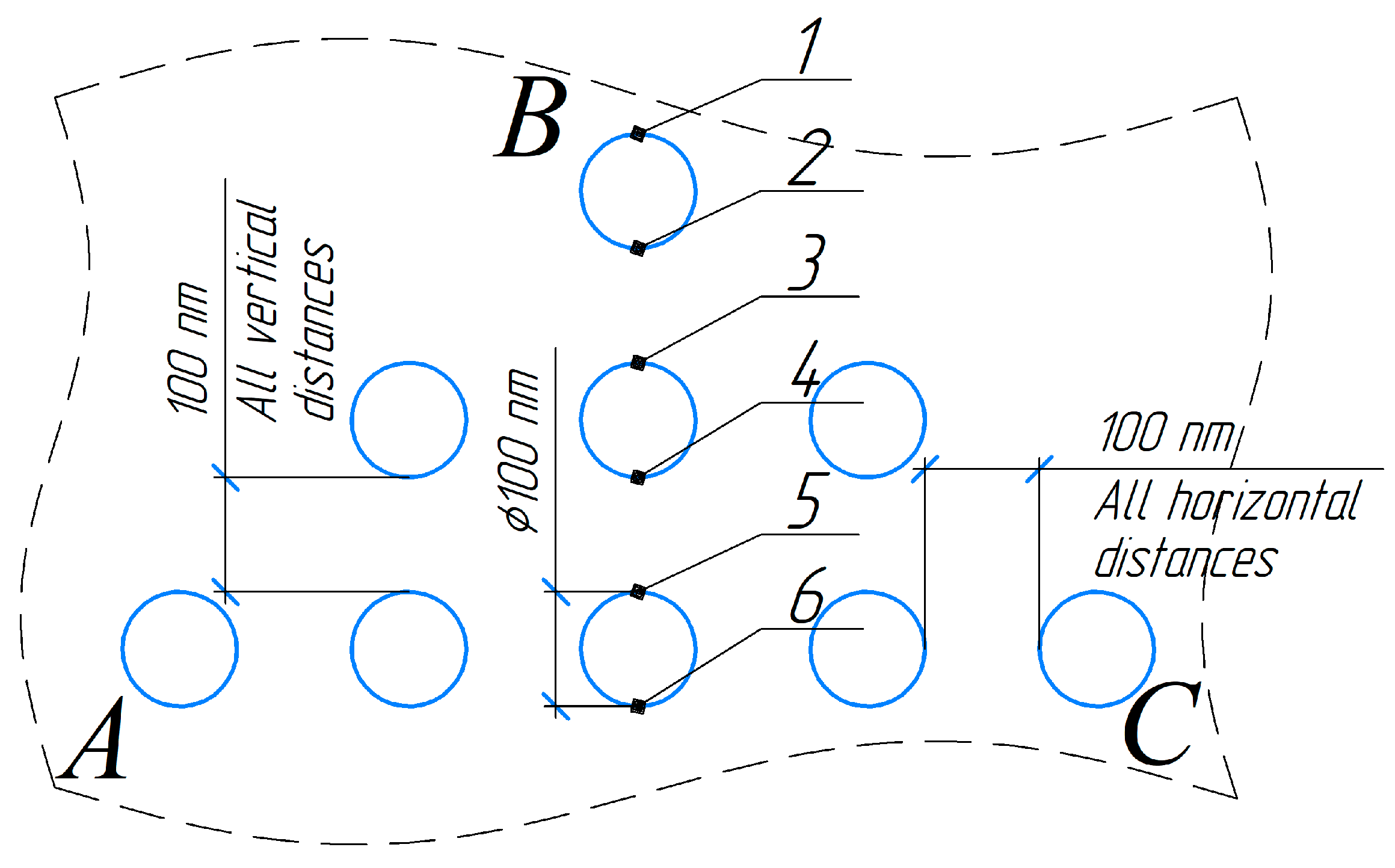
2. Materials and Methods
3. Results
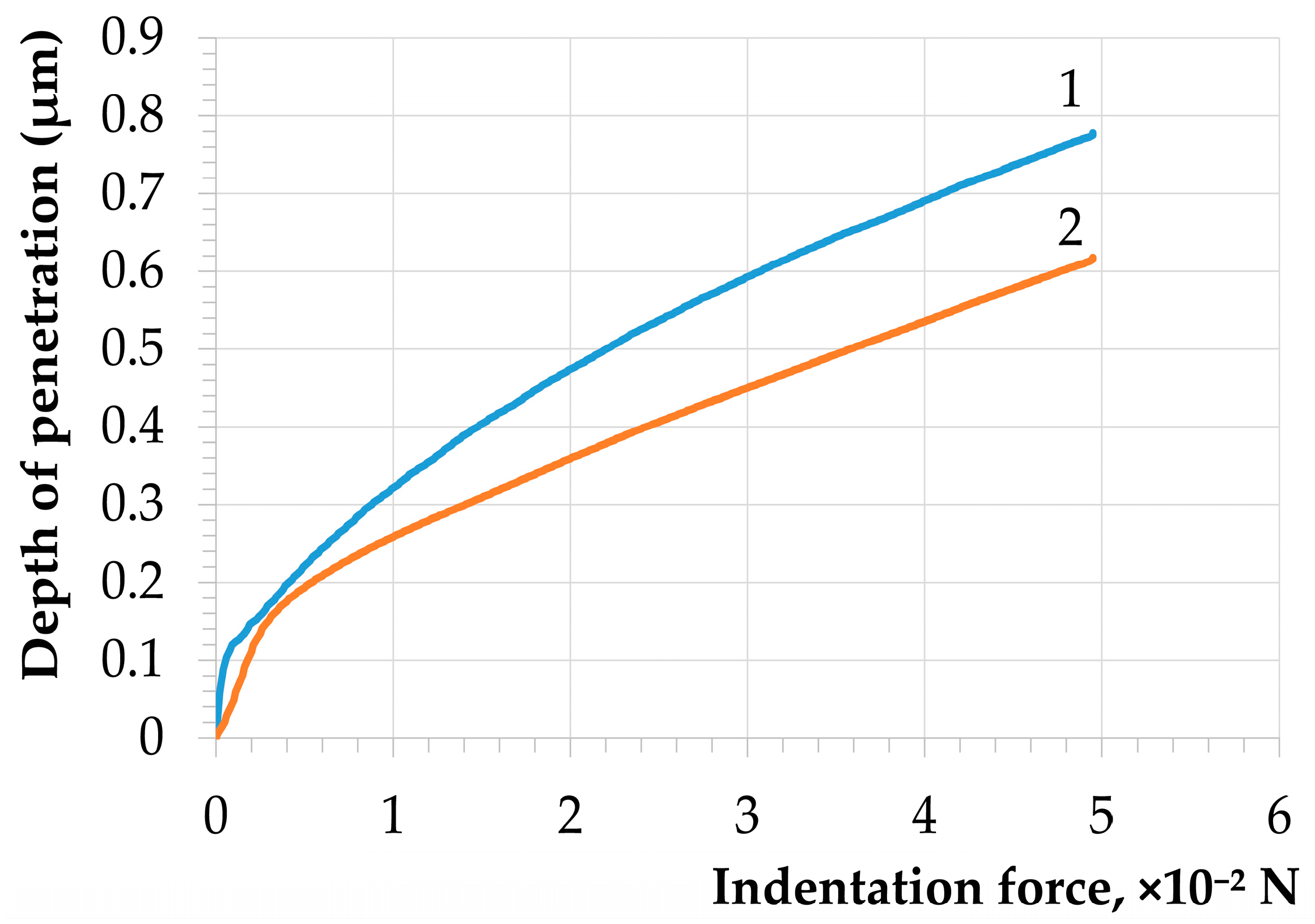
3.1. Experimental Results
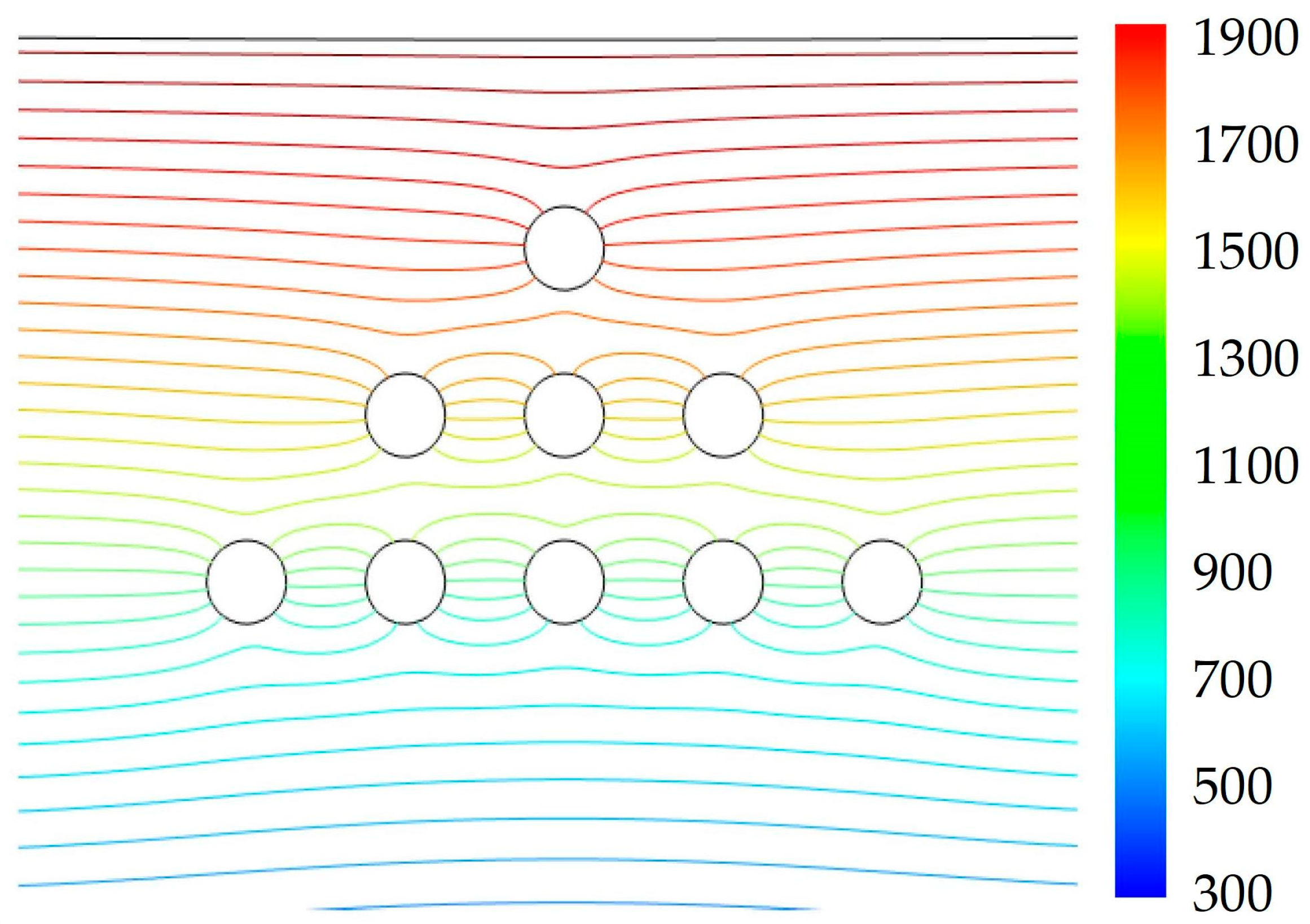
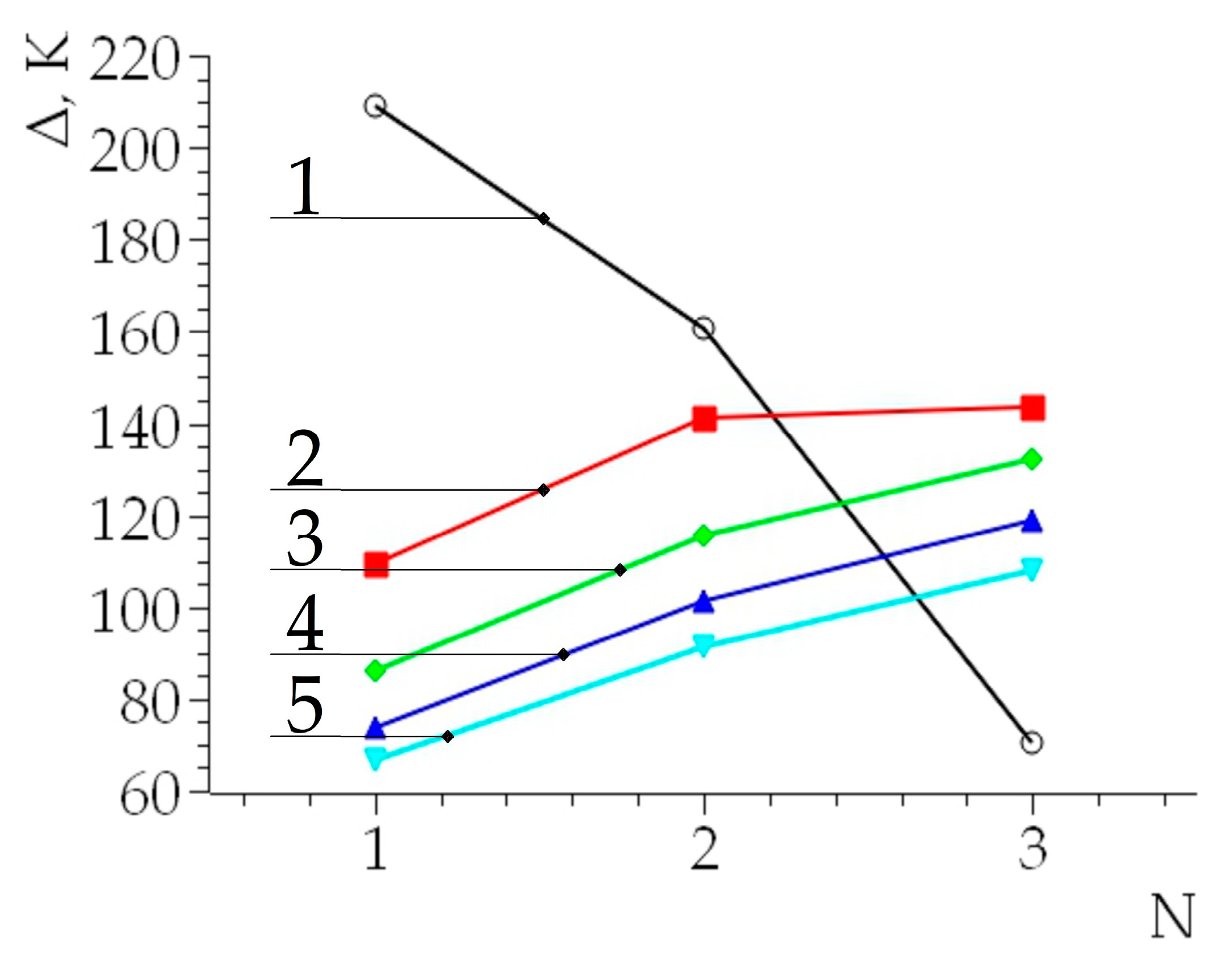
3.2. Theoretical Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aronin, A.; Abrosimova, G. Specific features of structure transformation and properties of amorphous-nanocrystalline alloys. Metals 2020, 10, 358. [Google Scholar] [CrossRef]
- Ushakov, I.V.; Safronov, I.S. Directed changing properties of amorphous and nanostructured metal alloys with help of nanosecond laser impulses. CIS Iron Steel Rev. 2021, 22, 77–81. [Google Scholar] [CrossRef]
- Savin, A.V.; Kosevich, Y.A.; Cantarero, A. Semiquantummolecular dynamics simulation of thermal properties and heattransport in low-dimensional nanostructures. Phys. Review. B Condens. Matter 2012, 86, 064305. [Google Scholar] [CrossRef]
- Shelyakov, A.; Sitnikov, N.; Zaletova, I.; Borodako, K.; Tabachkova, N. Study of structure and phase transformations in rejuvenated rapidly quenched TiNiCu alloys. Metals 2023, 13, 1175. [Google Scholar] [CrossRef]
- Wang, Z.; Ummethala, R.; Singh, N.; Tang, S.; Suryanarayana, C.; Eckert, J.; Prashanth, K.G. Selective laser melting of aluminum and its alloys. Materials 2020, 13, 4564. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Ushakov, I.V. How a crack and the defect material in its neighborhood affect the radiation strength of transparent materials. J. Opt. Technol. 2008, 75, 128–131. [Google Scholar] [CrossRef]
- Genin, F.Y.; Michlitsch, K.; Furr, J.; Kozlowski, M.R.; Krulevitch, P. Laser-induced damage of fused silica at 355 and 1064 nm initiated at aluminum contamination particles on the surface. Proc. SPIE. Proc. Int. Soc. Opt. Eng. 1997, 2966, 126–138. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Harmer, M.P.; Chou, Y.T. Laser-induced internal cracks in LiF single crystals. J. Mater. Sci. 1989, 24, 2756–2760. Available online: https://link.springer.com/article/10.1007/bf02385622 (accessed on 20 November 2020). [CrossRef]
- Kaputkina, L.M.; Kaputkin, D.E. Structure and phase transformations under quenching and tempering during heat and thermomechanical treatment of steels. Mater. Sci. Forum 2003, 426–432, 1119–1126. [Google Scholar] [CrossRef]
- Chichenev, N.A.; Gorbatyuk, S.M.; Naumova, M.G.; Morozova, I.G. Using the similarity theory for description of laser hardening processes. CIS Iron Steel Rev. 2020, 19, 44–47. [Google Scholar] [CrossRef]
- Li, R.; Chen, H.; Zhu, H.; Wang, M.; Chen, C. Tiechui Yuan Effect of aging treatment on the microstructure and mechanical properties of Al-3.02Mg-0.2Sc-0.1Zr alloy printed by selective laser melting. Mater. Des. 2019, 168, 107668. [Google Scholar] [CrossRef]
- Safronov, I.S.; Ushakov, A.I. Targeted alternation in properties of solid amorphous-nanocrystalline material in exposing to nanosecond laser radiation. Defect Diffus. Forum 2021, 410, 469–474. [Google Scholar] [CrossRef]
- Kaputkin, D.E. Application of focused optic irradiation for surface treatment of commercial steels. Mater. Sci. Forum 2003, 426–432, 1285–1288. [Google Scholar] [CrossRef]
- Vandzura, R.; Simkulet, V.; Gelatko, M.; Michal; Mitalova, Z. Effect of hardening temperature on maraging steel samples prepared by direct metal laser sintering process. Machines 2023, 11, 351. [Google Scholar] [CrossRef]
- Shinkaryov, A.S.; Ozherelkov, D.Y.; Pelevin, I.A.; Eremin, S.A.; Anikin, V.N.; Burmistrov, M.A.; Chernyshikhin, S.V.; Gromov, A.A.; Nalivaiko, A.Y. Laser fusion of aluminum powder coated with diamond particles via selective laser melting: Powder preparation and synthesis description. Coatings 2021, 11, 1219. [Google Scholar] [CrossRef]
- Yasa, E.; Kruth, J.-P. Microstructural investigation of selective laser melting 316L stainless steel parts exposed to laser re-melting. Procedia Eng. 2011, 19, 389–395. [Google Scholar] [CrossRef]
- Kolobov, Y.R.; Manokhin, S.S.; Odintsova, G.V.; Betekhtin, V.I.; Kadomtsev, A.G.; Narykova, M.V. Studying the influence of nanosecond pulsed laser action on the structure of submicrocrystalline titanium. Pisma v Zhurnal Tekhnicheskoi Fiz. 2021, 47, 21–25. [Google Scholar] [CrossRef]
- Manokhin, S.S.; Tokmacheva-Kolobova, A.Y.; Karlagina, Y.Y.; Betekhtin, V.I. Investigation of changes in the structure of submicrocrystalline titanium of VT1-0 brand under heat treatment and laser processing with nanosecond pulses. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2021, 15, 59–64. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, G.; Wang, Y.; Li, H.; Qin, Z.; Lu, X. Crack-free Fe-based amorphous coating synthesized by laser cladding. Mater. Lett. 2018, 210, 46–50. [Google Scholar] [CrossRef]
- Maharjan, N.; Wu, N.; Zhou, W. Hardening efficiency and microstructural changes during laser surface hardening of 50CrMo4 steel. Metals 2021, 11, 2015. [Google Scholar] [CrossRef]
- Zhao, Z.-Y.; Li, L.; Bai, P.-K.; Jin, Y.; Wu, L.-Y.; Li, J.; Guan, R.-G.; Qu, H.-Q. The heat treatment influence on the microstructure and hardness of TC4 titanium alloy manufactured via selective laser melting. Materials 2018, 11, 1318. [Google Scholar] [CrossRef] [PubMed]
- Ushakov, I.; Simonov, Y. Formation of surface properties of VT18u titanium alloy by laser pulse treatment. Mater. Today Proc. 2019, 19, 2051–2055. [Google Scholar] [CrossRef]
- Duan, X.; Long, T.; Zhu, K.; Li, W. Formation mechanism of pore defects and surface ripples under different process parameters via laser powder bed fusion by numerical simulation and experimental verification. Res. Sq. 2023, 2–23. [Google Scholar] [CrossRef]
- Betekhtin, V.I.; Kadomtsev, A.G.; Larionova, T.V.; Narykova, M.V. Effect of thermobaric treatment on the nanoporosity and properties of amorphous alloys. Met. Sci. Heat Treat. 2015, 56, 555–558. [Google Scholar] [CrossRef]
- Betekhtin, V.I.; Veselkov, S.Y.; Dal, Y.M.; Kadomtsev, A.G. Theoretical and experimental investigation of the effect of an applied load on pores in solids. Phys. Solid State 2003, 45, 649–655. [Google Scholar] [CrossRef]
- Sotov, A.V.; Agapovichev, A.V.; Smelov, V.G.; Kyarimov, R.R. Development algorithm of the technological process of manufacturing gas turbine parts by selective laser melting. IOP Conf. Ser. Mater. Sci. Eng. 2018, 302, 012065. [Google Scholar] [CrossRef]
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Prashanth, K.G.; Kolla, S.; Eckert, J. Additive manufacturing processes: Selective laser melting, electron beam melting and binder jetting—Selection guidelines. Materials 2017, 10, 672. [Google Scholar] [CrossRef]
- Deng, J.; Chen, C.; Zhang, W.; Li, Y.; Li, R.; Zhou, K. Densification, microstructure, and mechanical properties of additively manufactured 2124 Al–Cu alloy by selective laser melting. Materials 2020, 13, 4423. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef]
- Prashanth, K.G.; Scudino, S. Quasicrystallyne composites by additive manufacturing. Key Eng. Mater. 2019, 818, 72–76. [Google Scholar] [CrossRef]
- Markidonov, A.V.; Gostevskaya, A.N.; Gromov, V.E.; Starostenkov, M.D.; Zykov, P.A. Simulation of the structural changes in the surface layer of a deformed BCC crystal during a short-term external high-intense action. Russ. Metall. (Met.) 2022, 2022, 1090–1095. [Google Scholar] [CrossRef]
- Markidonov, A.V.; Starostenkov, M.D.; Lubyanoi, D.A.; Zakharov, P.V.; Lipunov, V.N. Modeling of healing cylindrical cavities exposed to shock waves in crystal subjected to shear deformation. Steel Transl. 2022, 52, 208–214. [Google Scholar] [CrossRef]
- Wang, H.-X.; Chen, X. Three-dimensional modelling of the laser-induced plasma plume characteristics in laser welding. J. Phys. D Appl. Phys. 2003, 36, 628–639. [Google Scholar] [CrossRef]
- Dudoladov, S.; Larionov, N. The condition for application of the crocco integral in the mathematical description of a laser welding plasma plume. St Petersburg Polytech. Univ. J. Phys. Math. 2021, 14, 60–75. [Google Scholar] [CrossRef]
- Smallman, R.E.; Ngan, A.H.W. Physical Metallurgy and Advanced Materials; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Gladkov, S.O.; Bogdanova, S.B. On the theory of nonlinear thermal conductivity. Tech. Phys. 2016, 61, 157–164. [Google Scholar] [CrossRef]
- Cheilytko, A. Finding of the generalized equation of thermal conductivity for porous heatinsulating materials. Technol. Audit. Prod. Reserves 2016, 5, 4–10. [Google Scholar] [CrossRef]
- Alexandrov, S.; Jeng, Y.-R. A method of finding stress solutions for a general plastic material under plane strain and plane stress conditions. J. Mech. 2020, 37, 100–107. [Google Scholar] [CrossRef]
- Lienhard, J.H., IV; Lienhard, J.H., V. A Heat Transfer Textbook, Version 5.10; Phlogiston Press: Cambridge, MA, USA, 2020; pp. 11–761. Available online: https://ahtt.mit.edu/wp-content/uploads/2020/08/AHTTv510.pdf (accessed on 15 September 2021).
- Kamrani, M.; Levitas, V.I.; Feng, B. FEM simulation of large deformation of copper in the quasi-constrain high-pressure-torsion setup. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2017, 705, 219–230. [Google Scholar] [CrossRef]




| Parameters | Value | Unit |
|---|---|---|
| Wavelength | 532 | nm |
| Energy | 75 | mJ |
| Pulse duration (FWHM) | 15–20 | ns |
| Pulse repetition rate | 50 | Hz |
| Beam divergence (Θ 0.86) | ≤0.7 | mrad |
| F, N | Untreated Surface, Pme | Laser-Treated Surface, Pme | Untreated Surface, HV | Laser-Treated Surface, HV |
|---|---|---|---|---|
| 0.49 ± 0.00735 | 0.2 | 0 | 218 ± 3.27 | 308 ± 4.62 |
| 0.98 ± 0.0147 | 0.25 | 0 | 250 ± 3.75 | 355 ± 5.325 |
| 1.47 ± 0.02205 | 0.3 | 0 | 265 ± 3.975 | 360 ± 5.4 |
| 1.96 ± 0.0294 | 0.35 | 0 | 270 ± 4.05 | 355 ± 5.325 |
| 2.94 ± 0.0441 | 0.4 | 0 | (260–290) ± 4.125 | (320–380) ± 5.25 |
| 3.92 ± 0.0588 | 0.45 | 0 | ||
| 4.9 ± 0.0735 | 0.55 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Ushakov, I.V.; Safronov, I.S.; Zuo, J. Physical Mechanism of Selective Healing of Nanopores in Condensed Matter under the Influence of Laser Irradiation and Plasma. Nanomaterials 2024, 14, 139. https://doi.org/10.3390/nano14020139
Wang Z, Ushakov IV, Safronov IS, Zuo J. Physical Mechanism of Selective Healing of Nanopores in Condensed Matter under the Influence of Laser Irradiation and Plasma. Nanomaterials. 2024; 14(2):139. https://doi.org/10.3390/nano14020139
Chicago/Turabian StyleWang, Zhiqiang, Ivan Vladimirovich Ushakov, Ivan Sergeevich Safronov, and Jianping Zuo. 2024. "Physical Mechanism of Selective Healing of Nanopores in Condensed Matter under the Influence of Laser Irradiation and Plasma" Nanomaterials 14, no. 2: 139. https://doi.org/10.3390/nano14020139






