Anomalous Dispersion in Reflection and Emission of Dye Molecules Strongly Coupled to Surface Plasmon Polaritons
Abstract
1. Introduction
2. Experimental Methods and Results
2.1. Sample Fabrication
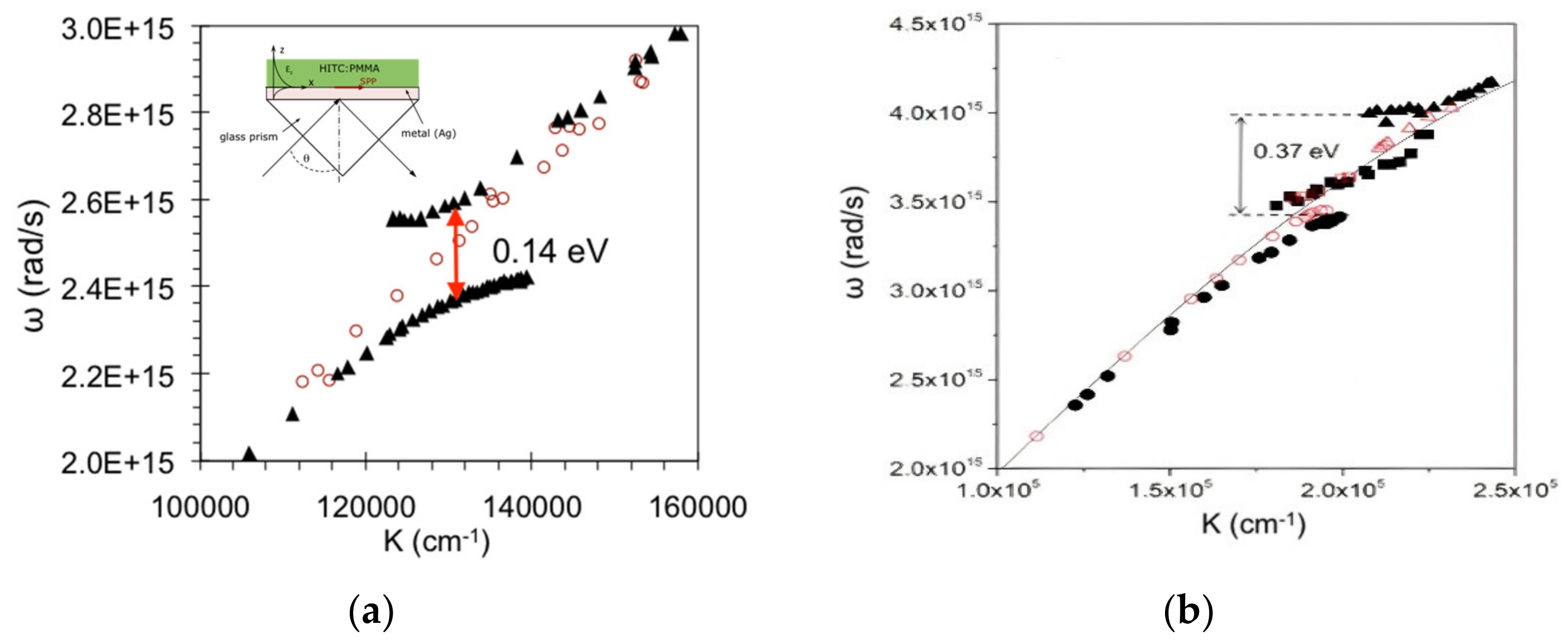
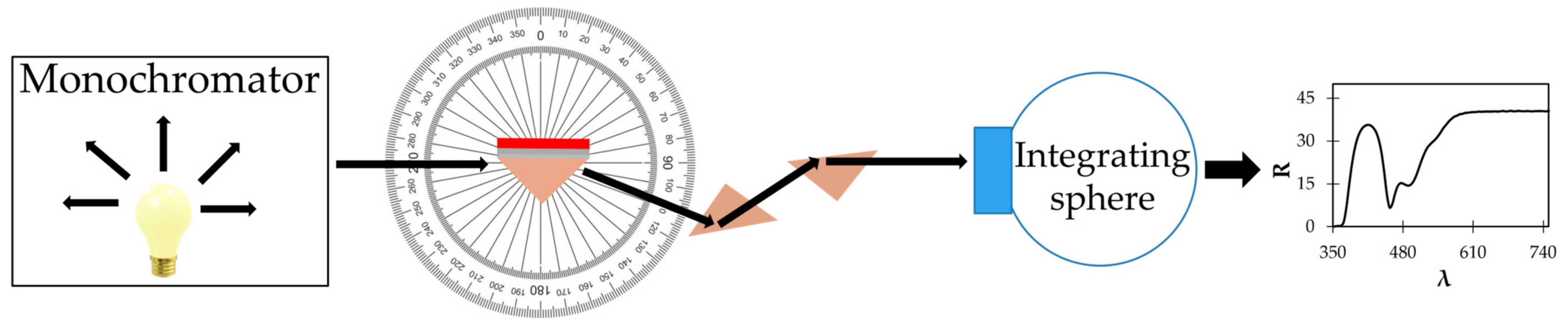
2.2. Dispersion Measurement in the Reflection Experiment
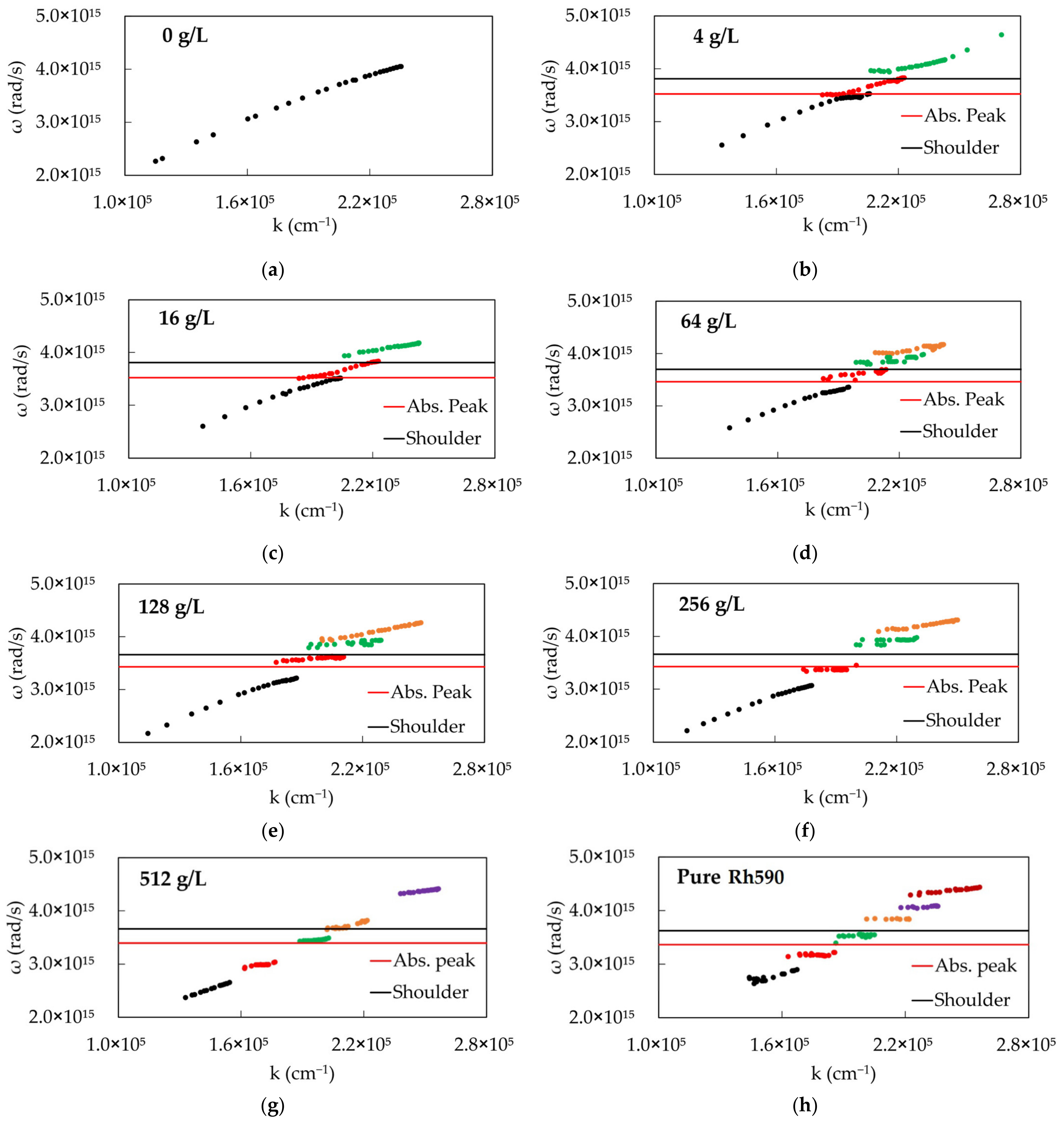
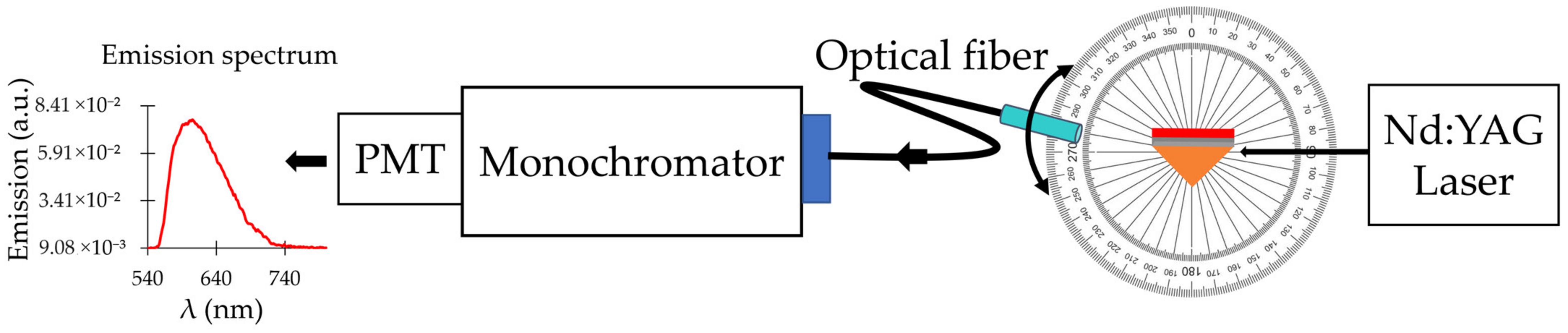
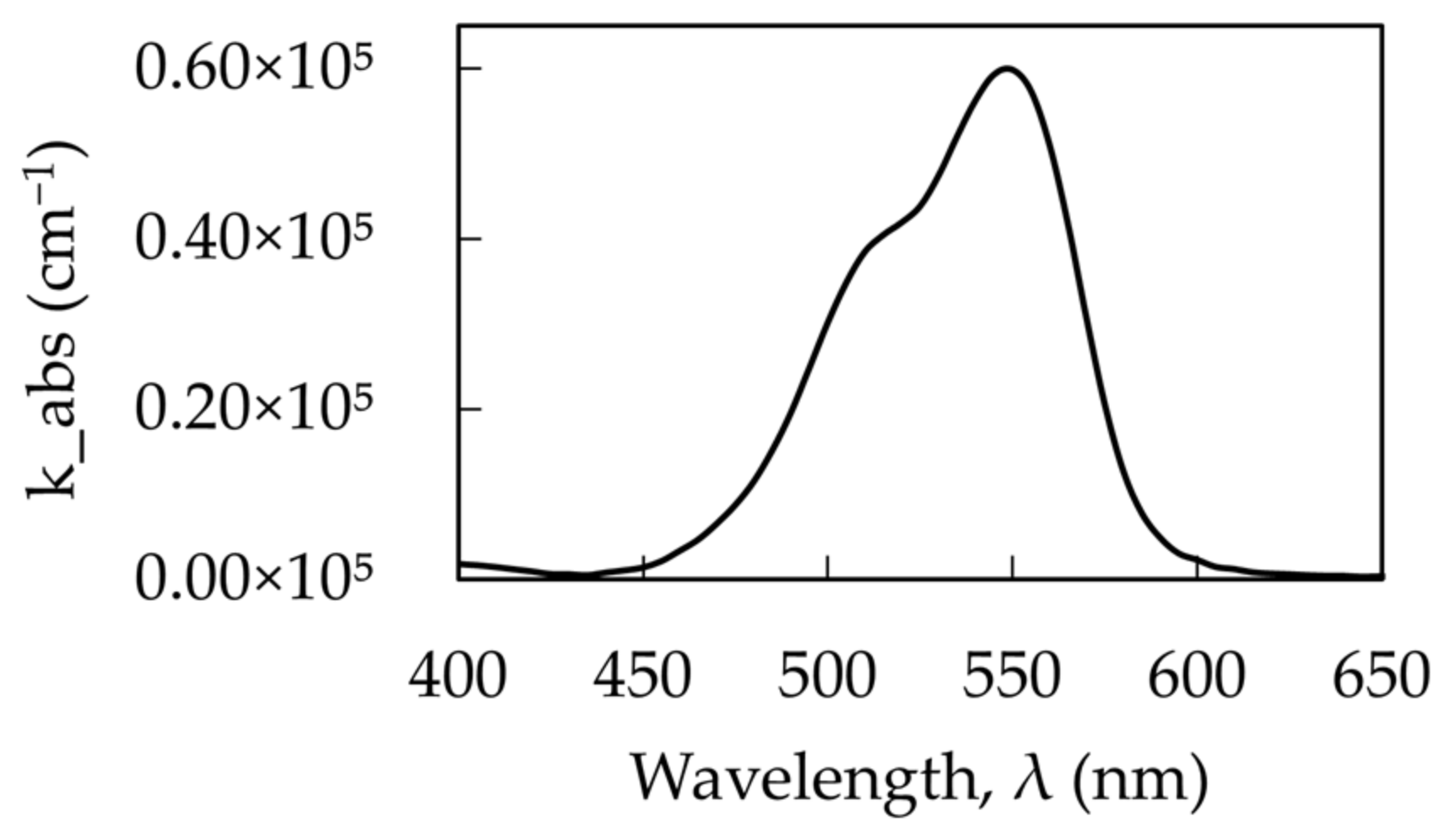
2.3. Dispersion Curves Obtained from the Emission Experiment
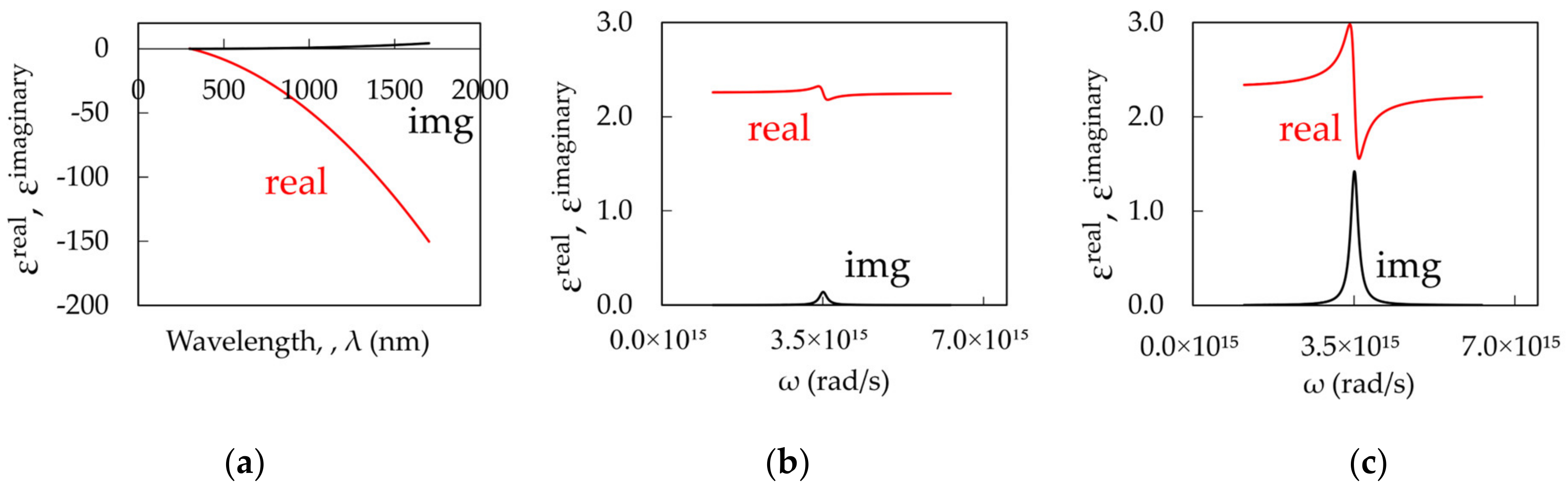
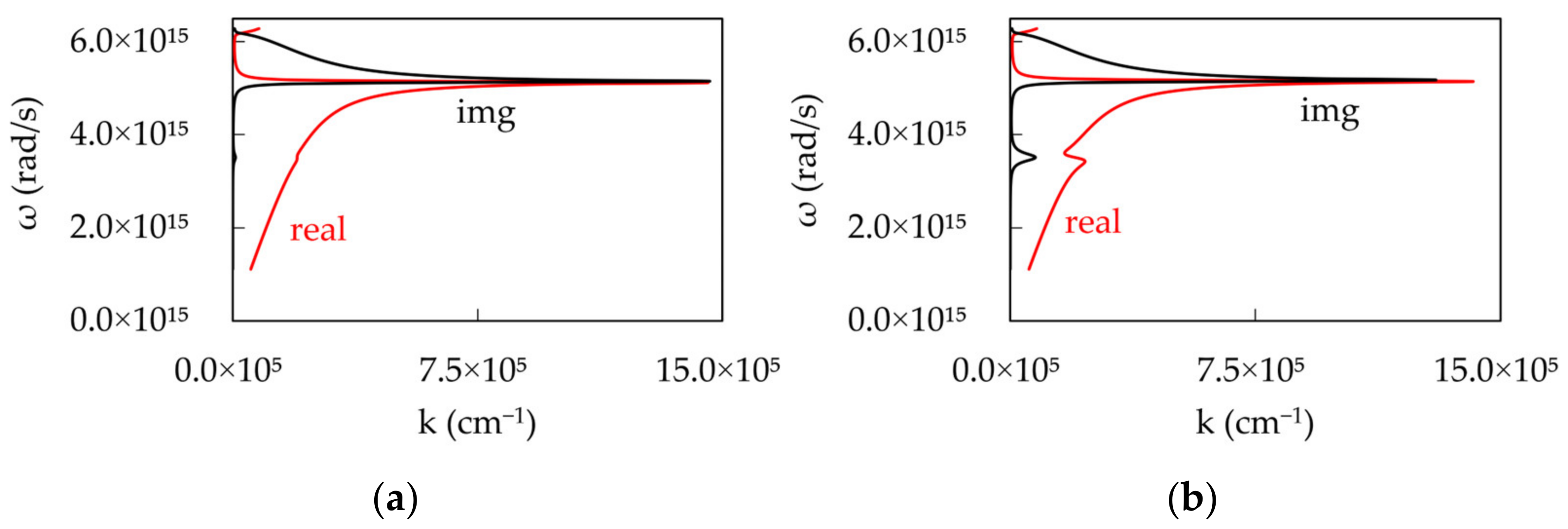
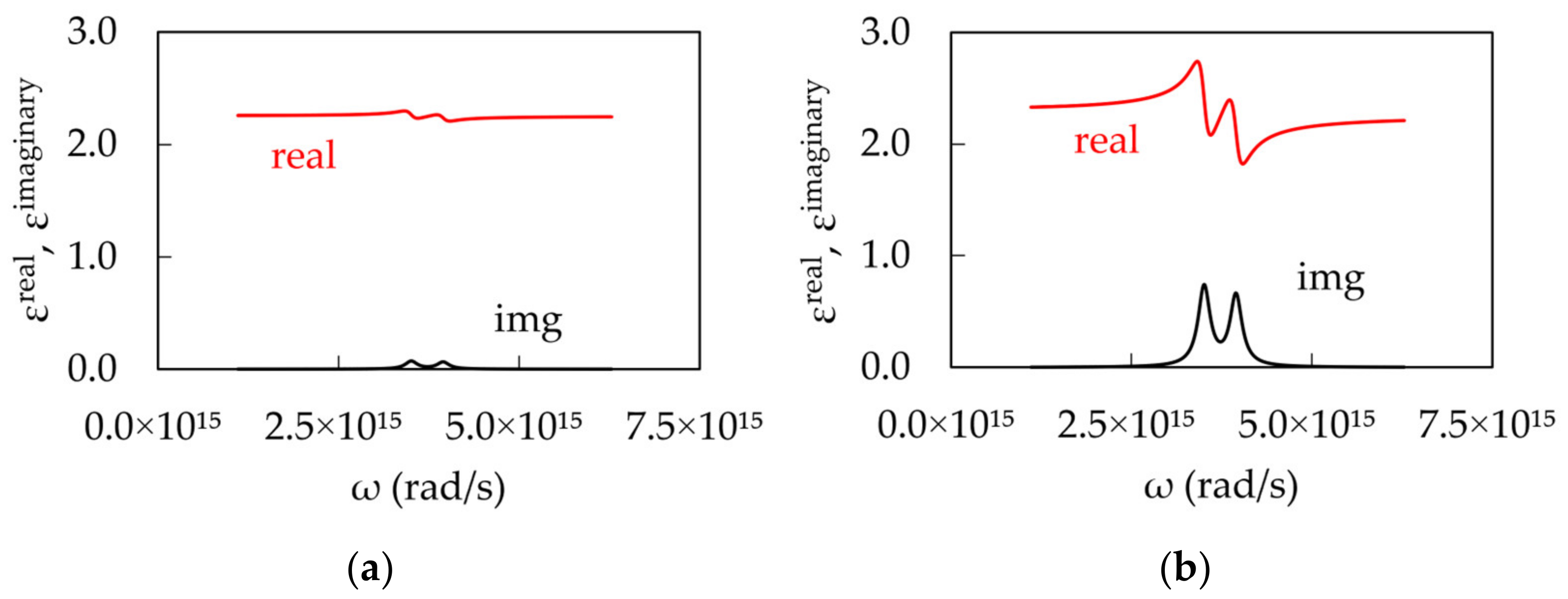
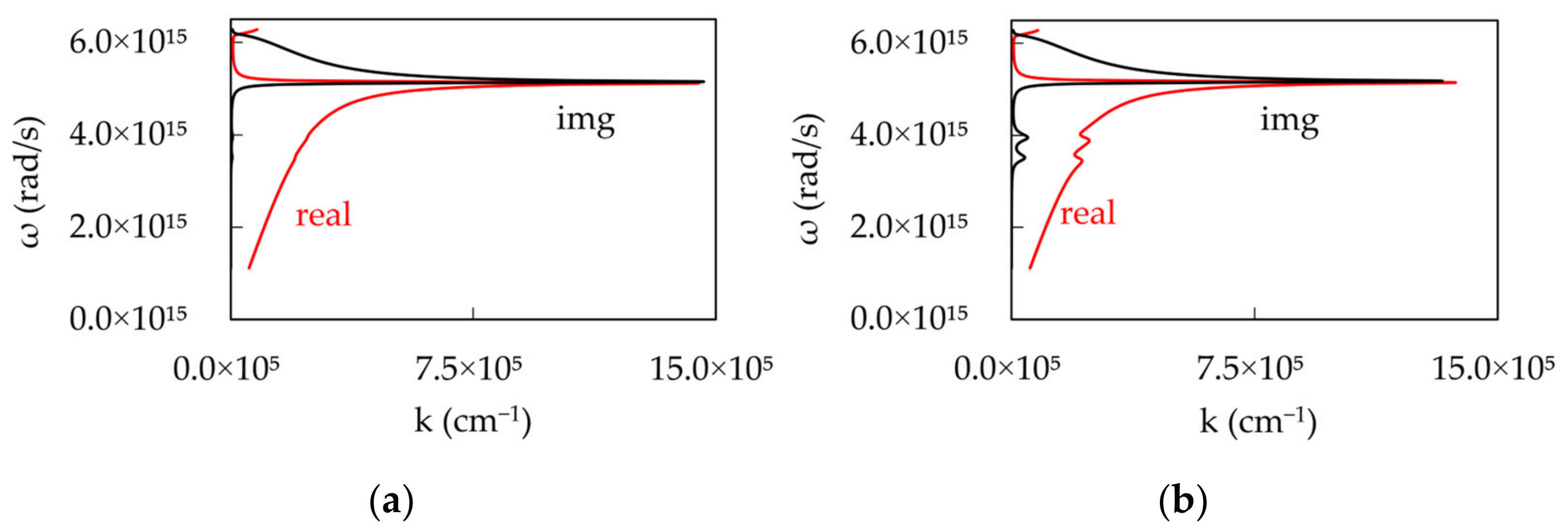
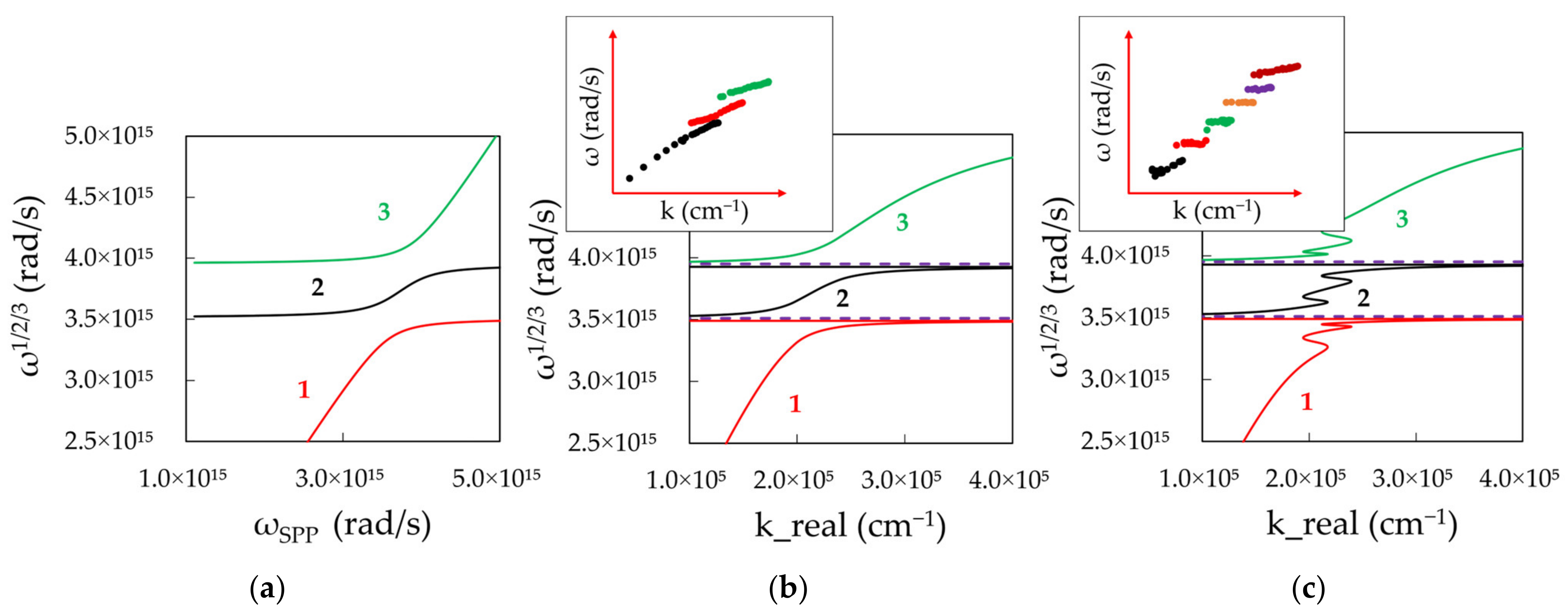
3. Theoretical Modeling
Strong Coupling between an Exciton and a Plasmon
4. Discussion
5. Summary
6. Methods: Sample Fabrication and Characterization [43]
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Assefa, S.; Xia, F.; Vlasov, Y.A. Reinventing germanium avalanche photodetector for nanophotonic on-chip optical interconnects. Nature 2010, 464, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Dregely, D.; Taubert, R.; Dorfmüller, J.; Vogelgesang, R.; Kern, K.; Giessen, H. 3D optical Yagi–Uda nanoantenna array. Nat. Commun. 2011, 2, 267. [Google Scholar] [CrossRef] [PubMed]
- Oulton, R.F.; Sorger, V.J.; Zentgraf, T.; Ma, R.M.; Gladden, C.; Dai, L.; Bartal, G.; Zhang, X. Plasmon lasers at deep subwavelength scale. Nature 2009, 461, 629–632. [Google Scholar] [CrossRef] [PubMed]
- Karelits, M.; Zalevsky, Z.; Karsenty, A. Nano polarimetry: Enhanced AFM-NSOM triple-mode polarimeter tip. Sci. Rep. 2020, 10, 16201. [Google Scholar] [CrossRef] [PubMed]
- Saha, T.; Mondal, J.; Khiste, S.; Lusic, H.; Hu, Z.W.; Jayabalan, R.; Hodgetts, K.J.; Jang, H.; Sengupta, S.; Lee, S.E.; et al. Nanotherapeutic approaches to overcome distinct drug resistance barriers in models of breast cancer. Nanophotonics 2021, 10, 3063–3073. [Google Scholar] [CrossRef] [PubMed]
- Atwater, H.A. Guiding Light; OE Magazine (SPIE): Bellingham, WA, USA, 2002; pp. 42–44. [Google Scholar]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; Volume 1, p. 245. [Google Scholar]
- Yin, L.; Vlasko-Vlasov, V.K.; Pearson, J.; Hiller, J.M.; Hua, J.; Welp, U.; Brown, D.E.; Kimball, C.W. Subwavelength focusing and guiding of surface plasmons. Nano Lett. 2005, 5, 1399–1402. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Ishihara, T. Subwavelength photolithography based on surface-plasmon polariton resonance. Opt. Express 2004, 12, 3055–3065. [Google Scholar] [CrossRef] [PubMed]
- Zijlstra, P.; Chon, J.W.; Gu, M. Five-dimensional optical recording mediated by surface plasmons in gold nanorods. Nature 2009, 459, 410–413. [Google Scholar] [CrossRef]
- Lezec, H.J.; Degiron, A.; Devaux, E.; Linke, R.A.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Ebbesen, T.W. Beaming light from a subwavelength aperture. Science 2002, 297, 820–822. [Google Scholar] [CrossRef]
- Ma, R.M.; Oulton, R.F.; Sorger, V.J.; Zhang, X. Plasmon lasers: Coherent light source at molecular scales. Laser Photonics Rev. 2013, 7, 1–21. [Google Scholar] [CrossRef]
- Guo, X. Surface plasmon resonance-based biosensor technique: A review. J. Biophotonics 2012, 5, 483–501. [Google Scholar] [CrossRef]
- Ferry, V.E.; Sweatlock, L.A.; Pacifici, D.; Atwater, H.A. Plasmonic nanostructure design for efficient light coupling into solar cells. Nano Lett. 2008, 8, 4391–4397. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Li, Z.; Huang, Y.; Zhang, S.; Nordlander, P.; Halas, N.J.; Xu, H. Branched silver nanowires as controllable plasmon routers. Nano Lett. 2010, 10, 1950–1954. [Google Scholar] [CrossRef]
- Juan, M.L.; Righini, M.; Quidant, R. Plasmon nano-optical tweezers. Nat. Photonics 2011, 5, 349–356. [Google Scholar] [CrossRef]
- Kshetrimayum, R.S. A brief intro to metamaterials. IEEE Potentials 2004, 23, 44–46. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction. Contemp. Phys. 2004, 45, 191–202. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Jacob, Z.; Alekseyev, L.V.; Narimanov, E. Optical hyperlens: Far-field imaging beyond the diffraction limit. Opt. Express 2006, 14, 8247–8256. [Google Scholar] [CrossRef]
- Pendry, J.B.; Smith, D.R. The quest for the superlens. Sci. Am. 2006, 295, 60–67. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Khitrova, G.; Gibbs, H.M.; Kira, M.; Koch, S.W.; Scherer, A. Vacuum Rabi splitting in semiconductors. Nat. Phys. 2006, 2, 81–90. [Google Scholar] [CrossRef]
- Törmä, P.; Barnes, W.L. Strong coupling between surface plasmon polaritons and emitters: A review. Rep. Prog. Phys. 2014, 78, 013901. [Google Scholar]
- Frisk Kockum, A.; Miranowicz, A.; De Liberato, S.; Savasta, S.; Nori, F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19–40. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005. [Google Scholar] [CrossRef]
- Hutchison, J.A.; Schwartz, T.; Genet, C.; Devaux, E.; Ebbesen, T.W. Modifying chemical landscapes by coupling to vacuum fields. Angew. Chem. Int. Ed. 2012, 51, 1592–1596. [Google Scholar] [CrossRef]
- Orgiu, E.; George, J.; Hutchison, J.A.; Devaux, E.; Dayen, J.F.; Doudin, B.; Stellacci, F.; Genet, C.; Schachenmayer, J.; Genes, C.; et al. Conductivity in organic semiconductors hybridized with the vacuum field. Nat. Mater. 2015, 14, 1123–1129. [Google Scholar] [CrossRef] [PubMed]
- Hutchison, J.A.; Liscio, A.; Schwartz, T.; Canaguier-Durand, A.; Genet, C.; Palermo, V.; Samorì, P.; Ebbesen, T.W. Tuning the work-function via strong coupling. Adv. Mater. 2013, 25, 2481–2485. [Google Scholar] [CrossRef]
- Wang, S.; Mika, A.; Hutchison, J.A.; Genet, C.; Jouaiti, A.; Hosseini, M.W.; Ebbesen, T.W. Phase transition of a perovskite strongly coupled to the vacuum field. Nanoscale 2014, 6, 7243–7248. [Google Scholar] [CrossRef]
- Hakala, T.K.; Toppari, J.J.; Kuzyk, A.; Pettersson, M.; Tikkanen, H.; Kunttu, H.; Törmä, P. Vacuum Rabi splitting and strong-coupling dynamics for surface-plasmon polaritons and rhodamine 6G molecules. Phys. Rev. Lett. 2009, 103, 053602. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Radiative decay of non radiative surface plasmons excited by light. Z. Für Naturforschung A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Raether, H. Surface plasmons on gratings. Surf. Plasmons Smooth Rough Surf. Gratings 2006, 111, 91–116. [Google Scholar]
- Bellessa, J.; Bonnand, C.; Plenet, J.C.; Mugnier, J. Strong coupling between surface plasmons and excitons in an organic semiconductor. Phys. Rev. Lett. 2004, 93, 036404. [Google Scholar] [CrossRef] [PubMed]
- Prayakarao, S.; Koutsares, S.R.; Bonner, C.E.; Noginov, M.A. Effect of nonlocal metal–dielectric environments on concentration quenching of HITC dye. JOSA B 2019, 36, 3579–3587. [Google Scholar] [CrossRef]
- Tumkur, T.U.; Zhu, G.; Noginov, M.A. Strong coupling of surface plasmon polaritons and ensembles of dye molecules. Opt. Express 2016, 24, 3921–3928. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Shalaev, V.M. Optical Metamaterials; Springer: New York, NY, USA, 2010; Volume 10. [Google Scholar]
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lidzey, D.G.; Coles, D.M. Strong coupling in organic and hybrid-semiconductor microcavity structures. In Organic and Hybrid Photonic Crystals; Springer: Cham, Switzerland, 2015; pp. 243–273. [Google Scholar]
- Cade, N.I.; Ritman-Meer, T.; Richards, D. Strong coupling of localized plasmons and molecular excitons in nanostructured silver films. Phys. Rev. B 2009, 79, 241404. [Google Scholar] [CrossRef]
- Tanyi, E.K.; Thuman, H.; Brown, N.; Koutsares, S.; Podolskiy, V.A.; Noginov, M.A. Control of the Stokes shift with strong coupling. Adv. Opt. Mater. 2017, 5, 1600941. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Mark, J.E. Physical Properties of Polymers Handbook; Springer: New York, NY, USA, 2007; Volume 1076, p. 825. [Google Scholar]
- Sultanova, N.; Kasarova, S.; Nikolov, I. Dispersion properties of optical polymers. Acta Phys. Pol. A 2009, 116, 585–587. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, M.G.R.; Hesami, L.; Khabir, K.M.; Howard, S.R.; Rab, M.A.; Noginova, N.; Noginov, M.A. Anomalous Dispersion in Reflection and Emission of Dye Molecules Strongly Coupled to Surface Plasmon Polaritons. Nanomaterials 2024, 14, 148. https://doi.org/10.3390/nano14020148
Chowdhury MGR, Hesami L, Khabir KM, Howard SR, Rab MA, Noginova N, Noginov MA. Anomalous Dispersion in Reflection and Emission of Dye Molecules Strongly Coupled to Surface Plasmon Polaritons. Nanomaterials. 2024; 14(2):148. https://doi.org/10.3390/nano14020148
Chicago/Turabian StyleChowdhury, Md Golam Rabbani, Leila Hesami, Kanij Mehtanin Khabir, Shamaar R. Howard, Md Afzalur Rab, Natalia Noginova, and Mikhail A. Noginov. 2024. "Anomalous Dispersion in Reflection and Emission of Dye Molecules Strongly Coupled to Surface Plasmon Polaritons" Nanomaterials 14, no. 2: 148. https://doi.org/10.3390/nano14020148
APA StyleChowdhury, M. G. R., Hesami, L., Khabir, K. M., Howard, S. R., Rab, M. A., Noginova, N., & Noginov, M. A. (2024). Anomalous Dispersion in Reflection and Emission of Dye Molecules Strongly Coupled to Surface Plasmon Polaritons. Nanomaterials, 14(2), 148. https://doi.org/10.3390/nano14020148






