Manipulating the Generation of Photonic Moiré Lattices Using Plasmonic Metasurfaces
Abstract
:1. Introduction
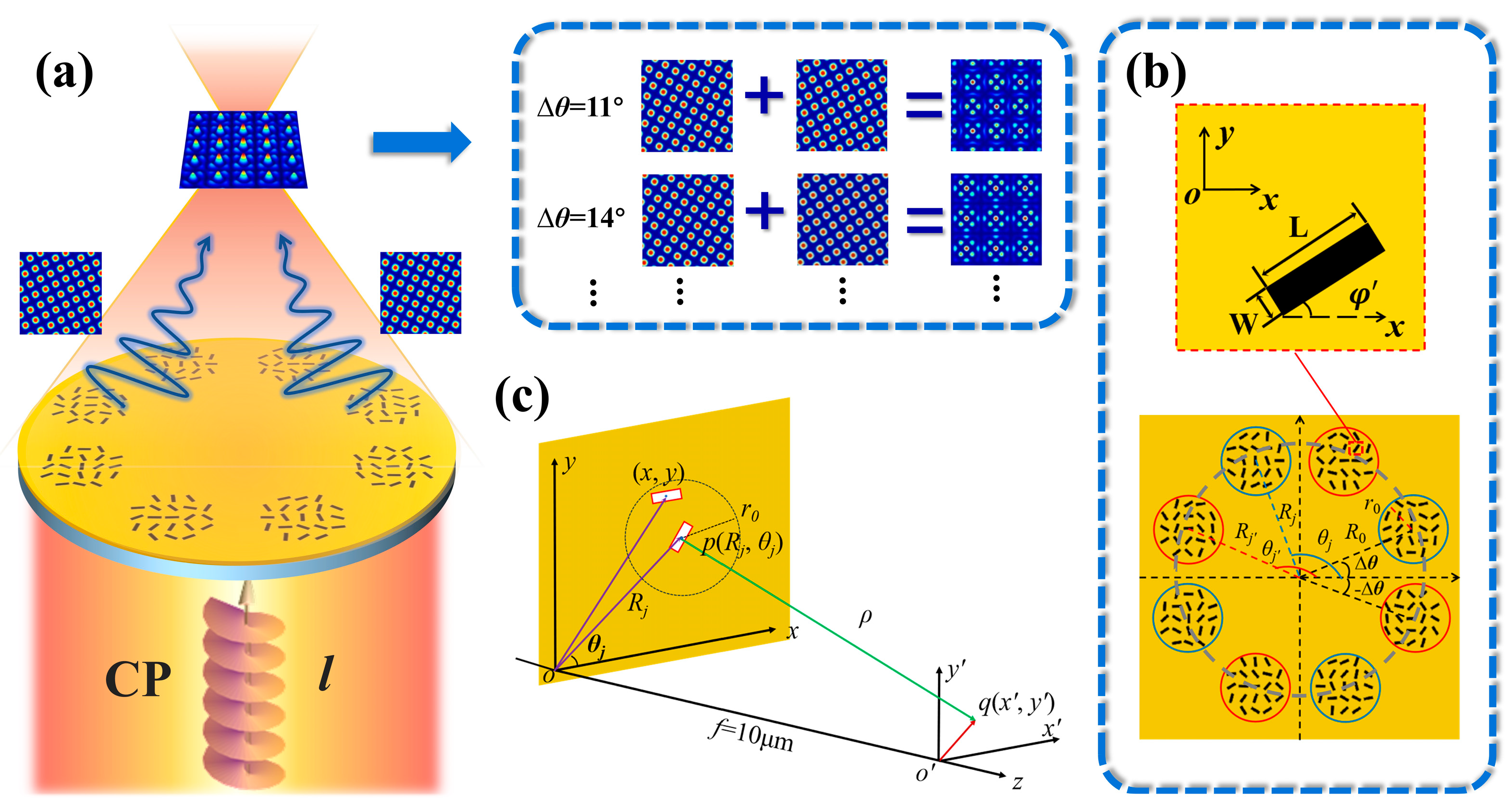
2. Materials and Methods
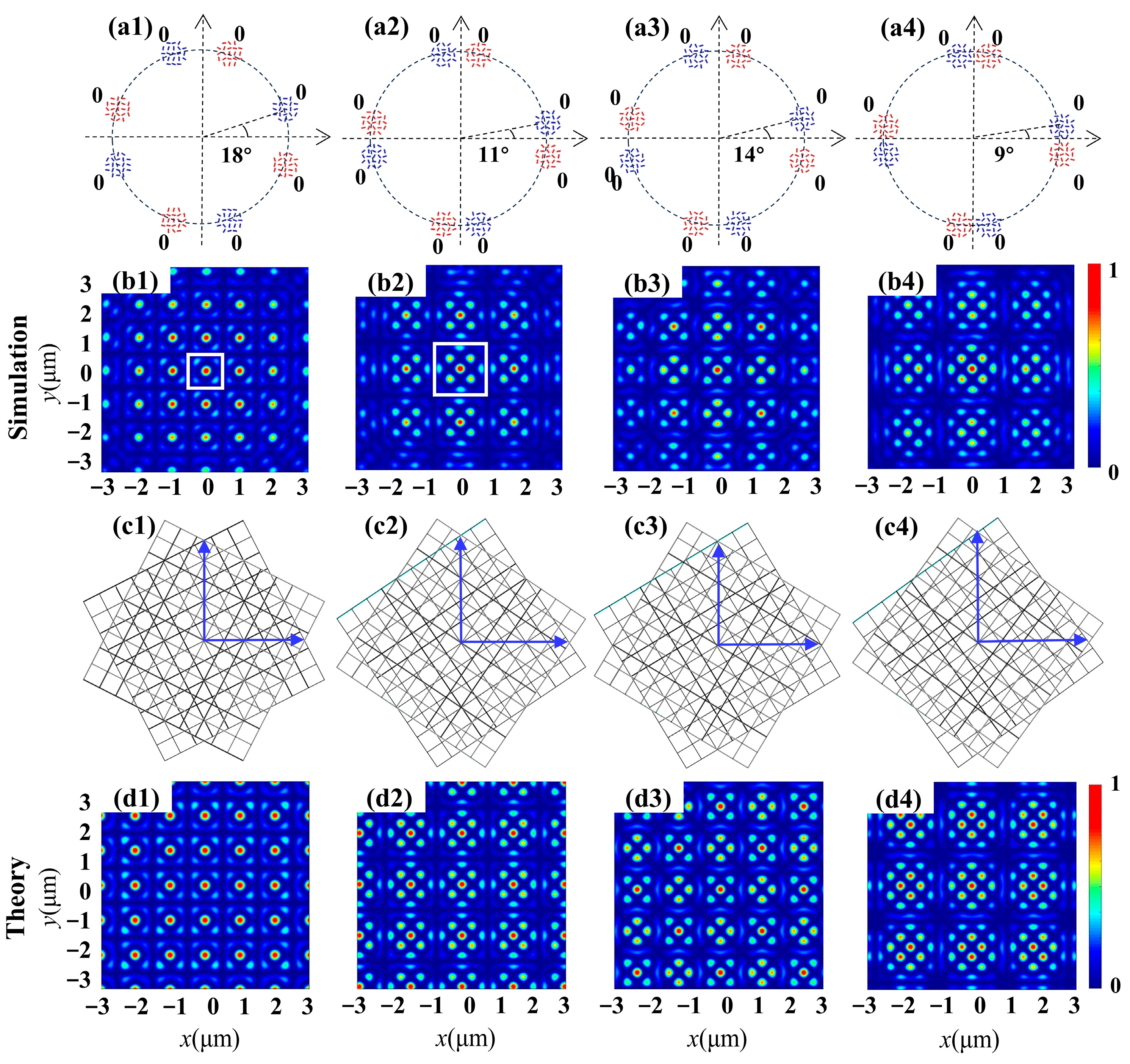
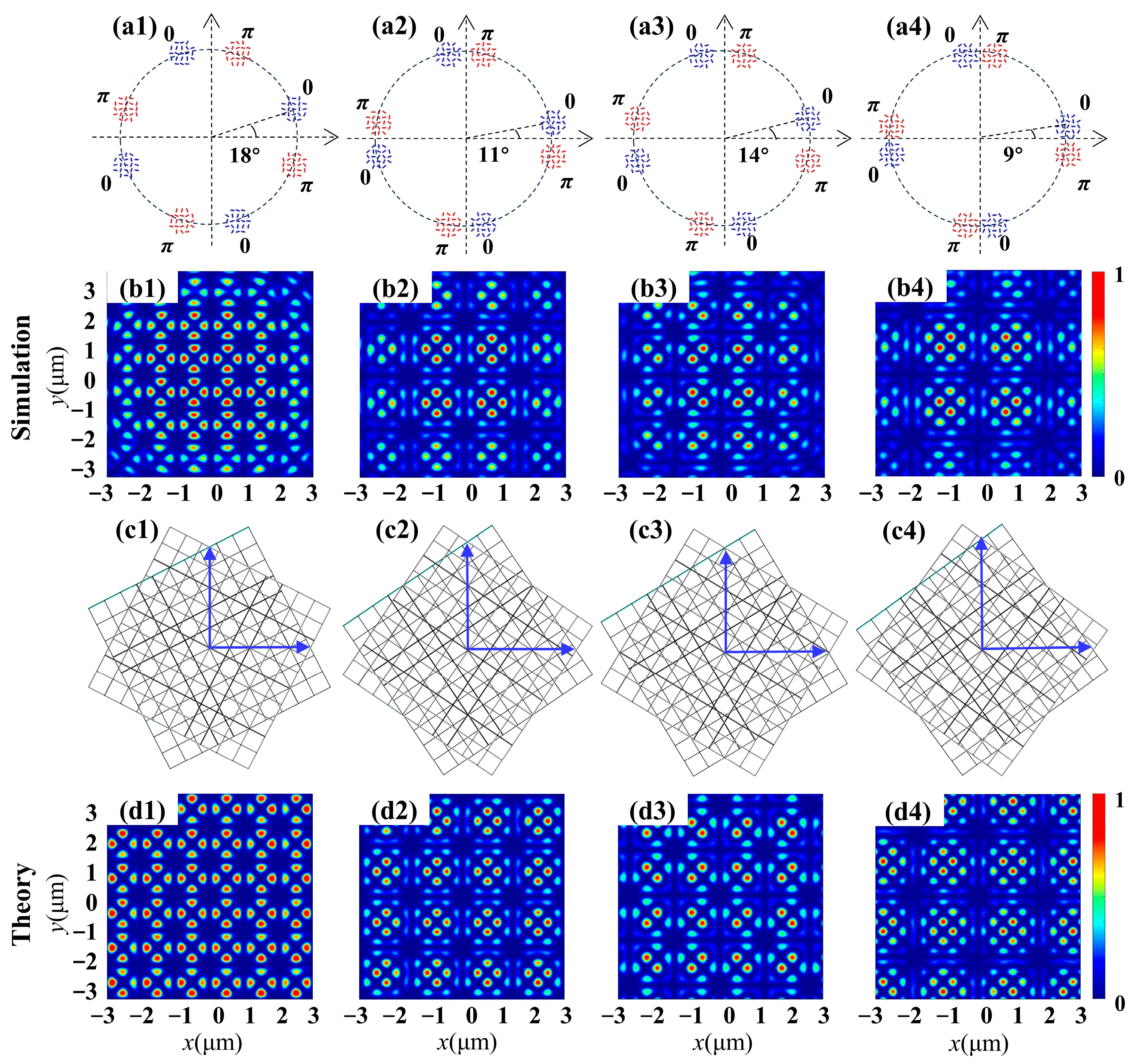
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Stepanov, P.; Yang, W.; Aamir, M.A.; Das, I.; Efetov, D.K. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 2019, 574, 653–657. [Google Scholar] [CrossRef] [PubMed]
- Oh, M.; Nuckolls, K.P.; Wong, D.; Lee, R.L.; Liu, X.; Watanabe, K.; Yazdani, A. Evidence for unconventional superconductivity in twisted bilayer graphene. Nature 2021, 600, 240–245. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.C.; Ma, X.; Liu, Z.; Watanabe, K.; Taniguchi, T.; Chu, J.H.; Yankowitz, M. Anomalous Hall effect at half filling in twisted bilayer graphene. Nat. Phys. 2022, 18, 1038–1042. [Google Scholar] [CrossRef]
- Geisenhof, F.R.; Winterer, F.; Seiler, A.M.; Lenz, J.; Xu, T.; Zhang, F.; Weitz, R.T. Quantum anomalous Hall octet driven by orbital magnetism in bilayer graphene. Nature 2021, 598, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.X.; Zhang, Y.H.; Morissette, E.; Wang, Z.; Liu, S.; Rhodes, D.; Li, J.I.A. Spin-orbit–driven ferromagnetism at half moiré filling in magic-angle twisted bilayer graphene. Science 2022, 375, 437–441. [Google Scholar] [CrossRef]
- Hu, G.; Ou, Q.; Si, G.; Wu, Y.; Wu, J.; Dai, Z.; Krasnok, A.; Mazor, Y.; Zhang, Q.; Bao, Q.; et al. Topological polaritons and photonic magic angles in twisted α-MoO3 bilayers. Nature 2020, 582, 209–213. [Google Scholar] [CrossRef]
- Chen, M.; Lin, X.; Dinh, T.H.; Zheng, Z.; Shen, J.; Ma, Q.; Chen, H.; Jarillo-Herrero, P.; Dai, S. Configurable phonon polaritons in twisted α-MoO3. Nat. Mater. 2020, 19, 1307–1311. [Google Scholar] [CrossRef]
- López, M.R.; Peñaranda, F.; Christensen, J.; San-Jose, P. Flat bands in magic-angle vibrating plates. Phys. Rev. Lett. 2020, 125, 214301. [Google Scholar] [CrossRef]
- Park, M.J.; Kim, Y.; Cho, G.Y.; Lee, S. Higher-order topological insulator in twisted bilayer graphene. Phys. Rev. Lett. 2019, 123, 216803. [Google Scholar] [CrossRef] [PubMed]
- Sunku, S.S.; Ni, G.; Jiang, B.Y.; Yoo, H.; Sternbach, A.; McLeod, A.S.; Basov, D.N. Photonic crystals for nano-light in moiré graphene superlattices. Science 2018, 362, 1153–1156. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Yang, S.; Li, S.; Lou, J.; Zhang, S.; Wang, S.; Li, B.; Gong, Y.; Song, L.; Zou, X.; et al. Conversion of non-van der Waals solids to 2D transition-metal chalcogenides. Nature 2020, 577, 492–496. [Google Scholar] [CrossRef] [PubMed]
- Domröse, T.; Danz, T.; Schaible, S.F.; Rossnagel, K.; Yalunin, S.V.; Ropers, C. Light-induced hexatic state in a layered quantum material. Nat. Mater. 2023, 22, 1345–1351. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Zheng, Y.; Chen, X.; Huang, C.; Kartashov, Y.V.; Torner, L.; Ye, F. Localization and delocalization of light in photonic moiré lattices. Nature 2020, 577, 42–46. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.; Fan, F.; Guan, S.; Wang, H.; Zhao, D.; Ji, Y.; Chang, S. Terahertz Spin-Conjugate Symmetry Breaking for Nonreciprocal Chirality and One-Way Transmission Based on Magneto-Optical Moiré Metasurface. Adv. Sci. 2023, 10, 2204916. [Google Scholar] [CrossRef] [PubMed]
- Hong, P.; Liang, Y.; Chen, Z.; Zhang, G. Robust moiré flatbands within a broad band-offset range. Adv. Photonics Nexus 2023, 2, 066001. [Google Scholar] [CrossRef]
- Gómez-Urrea, H.A.; Ospina-Medina, M.C.; Correa-Abad, J.D.; Mora-Ramos, M.E.; Caro-Lopera, F.J. Tunable band structure in 2D Bravais–Moiré photonic crystal lattices. Opt. Commun. 2020, 459, 125081. [Google Scholar] [CrossRef]
- Du, L.; Molas, M.R.; Huang, Z.; Zhang, G.; Wang, F.; Sun, Z. Moiré photonics and optoelectronics. Science 2023, 379, eadg0014. [Google Scholar] [CrossRef]
- Zeng, J.; Hu, Y.; Zhang, X.; Fu, S.; Yin, H.; Li, Z.; Chen, Z. Localization-to-delocalization transition of light in frequency-tuned photonic moiré lattices. Opt. Express. 2021, 29, 25388–25398. [Google Scholar] [CrossRef]
- Guan, J.; Hu, J.; Wang, Y.; Tan, M.J.; Schatz, G.C.; Odom, T.W. Far-field coupling between moiré photonic lattices. Nat. Nanotechnol. 2023, 18, 514–520. [Google Scholar] [CrossRef]
- Hu, G.; Krasnok, A.; Mazor, Y.; Qiu, C.W.; Alù, A. Moiré hyperbolic metasurfaces. Nano Lett. 2020, 20, 3217–3224. [Google Scholar] [CrossRef]
- Ivanov, S.K.; Konotop, V.V.; Kartashov, Y.V.; Torner, L. Vortex solitons in moiré optical lattices. Opt. Lett. 2023, 48, 3797–3800. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Wen, Z.; Zheng, L.; Zhao, L. Complex periodic non-diffracting beams generated by superposition of two identical periodic wave fields. Opt. Commun. 2017, 389, 123–127. [Google Scholar] [CrossRef]
- Lowell, D.; Hassan, S.; Sale, O.; Adewole, M.; Hurley, N.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-quasi-crystals with multiple-level gradients. Appl. Opt. 2018, 57, 6598–6604. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Zhang, W.; Zhang, X. Moiré quasibound states in the continuum. Phys. Rev. Lett. 2022, 128, 253901. [Google Scholar] [CrossRef] [PubMed]
- Salakhova, N.S.; Fradkin, I.M.; Dyakov, S.A.; Gippius, N.A. Twist-tunable moiré optical resonances. Phys. Rev. B 2023, 107, 155402. [Google Scholar] [CrossRef]
- Nguyen, D.X.; Letartre, X.; Drouard, E.; Viktorovitch, P.; Nguyen, H.C.; Nguyen, H.S. Magic configurations in moiré superlattice of bilayer photonic crystals: Almost-perfect flatbands and unconventional localization. Phys. Rev. Res. 2022, 4, L032031. [Google Scholar] [CrossRef]
- Shang, C.; Lu, C.; Tang, S.; Gao, Y.; Wen, Z. Generation of gradient photonic moiré lattice fields. Opt. Express. 2021, 29, 29116–29127. [Google Scholar] [CrossRef]
- Sale, O.; Hassan, S.; Hurley, N.; Alnasser, K.; Philipose, U.; Zhang, H.; Lin, Y. Holographic fabrication of octagon graded photonic supercrystal and potential applications in topological photonics. Front. Optoelectron. 2020, 13, 12–17. [Google Scholar] [CrossRef]
- Park, J.S.; Zhang, S.; She, A.; Chen, W.T.; Lin, P.; Yousef, K.M.; Capasso, F. All-glass, large metalens at visible wavelength using deep-ultraviolet projection lithography. Nano Lett. 2019, 19, 8673–8682. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Sun, Y.; Yu, Z.; Liu, X.; Chen, B.; Zhang, Y.; Zheng, Z. Dual-Functional Tunable Metasurface for Meta-Axicon with a Variable Depth of Focus and Continuous-Zoom Metalens. Nanomaterials 2023, 13, 2530. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Genevet, P. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 2986. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhang, Y.; Yuan, J.; Hong, Y.; Liu, H.; Guo, J.; Wei, Z. Three-Channel Metasurfaces for Multi-Wavelength Holography and Nanoprinting. Nanomaterials 2022, 13, 183. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Li, Z.; Cheng, H.; Tang, C.; Li, J.; Chen, S.; Tian, J. Energy-Tailorable Spin—Selective Multifunctional Metasurfaces with Full Fourier Components. Adv. Mater. 2019, 31, 1901729. [Google Scholar] [CrossRef] [PubMed]
- Solntsev, A.S.; Agarwal, G.S.; Kivshar, Y.S. Metasurfaces for quantum photonics. Nat. Photonics 2021, 15, 327–336. [Google Scholar] [CrossRef]
- Gao, H.; Li, Y.; Chen, L.; Jin, J.; Pu, M.; Li, X.; Gao, P.; Wang, C.; Luo, X.; Hong, M. Quasi-Talbot effect of orbital angular momentum beams for generation of optical vortex arrays by multiplexing metasurface design. Nanoscale 2018, 10, 666–671. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Ma, L.; Zeng, X.; Li, X.; Zhan, Z.; Cheng, C. Nanoscale optical lattices of arbitrary orders manipulated by plasmonic metasurfaces combining geometrical and dynamic phases. Nanoscale 2019, 11, 14024–14031. [Google Scholar] [CrossRef]
- Tsesses, S.; Ostrovsky, E.; Cohen, K.; Gjonaj, B.; Lindner, N.H.; Bartal, G. Optical skyrmion lattice in evanescent electromagnetic fields. Science 2018, 361, 993–996. [Google Scholar] [CrossRef]
- Tsesses, S.; Cohen, K.; Ostrovsky, E.; Gjonaj, B.; Bartal, G. Spin–orbit interaction of light in plasmonic lattices. Nano Lett. 2019, 19, 4010–4016. [Google Scholar] [CrossRef]
- Zhang, R.; Gu, M.; Sun, R.; Zeng, X.; Zhang, Y.; Zhang, Y.; Cheng, C. Plasmonic metasurfaces manipulating the two spin components from spin–orbit interactions of light with lattice field generations. Nanophotonics 2022, 11, 391–404. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, R.; Li, X.; Ma, L.; Liu, C.; He, C.; Cheng, C. Radially polarized plasmonic vector vortex generated by a metasurface spiral in gold film. Opt. Express 2019, 25, 32150–32160. [Google Scholar] [CrossRef]
- Lubin, S.M.; Zhou, W.; Hryn, A.J.; Huntington, M.D.; Odom, T.W. High-rotational symmetry lattices fabricated by moiré nanolithography. Nano Lett. 2012, 12, 4948–4952. [Google Scholar] [CrossRef]
- Tang, H.; Lou, B.; Du, F.; Zhang, M.; Ni, X.; Xu, W.; Mazur, E. Experimental probe of twist angle–dependent band structure of on-chip optical bilayer photonic crystal. Sci. Adv. 2023, 9, eadh8498. [Google Scholar] [CrossRef]
| Methods | Functionalities | Disadvantages |
|---|---|---|
| Computer holography | Can generate different moiré lattices. | (1) Require large-volume optical paths and complex algorithms. (2) Cannot manipulate the moiré lattices at subwavelength. |
| Polygon excitation slit | Can generate optical lattices (such as honeycomb, Kagome and hexagonal lattices) at subwavelength. | Cannot achieve the superposition of two-period sublattices and generate moiré lattices. |
| Moiré nanolithography | Can acquire the superposition of two hexagonal lattices with identical phases. | Cannot realize the superposition of other sublattices like square lattices and hexagonal vortex lattices. |
| Optical bilayer photonic crystal | Can obtain the superposition of two square and hexagonal lattices with identical phases. | Cannot modulate the phase difference between two superposed lattices. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, Z.; Zhang, Y.; An, J.; Zhang, X.; Zhou, H.; Song, H.; He, C.; Liu, G.; Cheng, C. Manipulating the Generation of Photonic Moiré Lattices Using Plasmonic Metasurfaces. Nanomaterials 2024, 14, 230. https://doi.org/10.3390/nano14020230
Mu Z, Zhang Y, An J, Zhang X, Zhou H, Song H, He C, Liu G, Cheng C. Manipulating the Generation of Photonic Moiré Lattices Using Plasmonic Metasurfaces. Nanomaterials. 2024; 14(2):230. https://doi.org/10.3390/nano14020230
Chicago/Turabian StyleMu, Zhanliang, Yuqin Zhang, Jianshan An, Xuehui Zhang, Haoran Zhou, Hongsheng Song, Changwei He, Guiyuan Liu, and Chuanfu Cheng. 2024. "Manipulating the Generation of Photonic Moiré Lattices Using Plasmonic Metasurfaces" Nanomaterials 14, no. 2: 230. https://doi.org/10.3390/nano14020230
APA StyleMu, Z., Zhang, Y., An, J., Zhang, X., Zhou, H., Song, H., He, C., Liu, G., & Cheng, C. (2024). Manipulating the Generation of Photonic Moiré Lattices Using Plasmonic Metasurfaces. Nanomaterials, 14(2), 230. https://doi.org/10.3390/nano14020230





