Diffusion-Induced Ordered Nanowire Growth: Mask Patterning Insights
Abstract
:1. Introduction
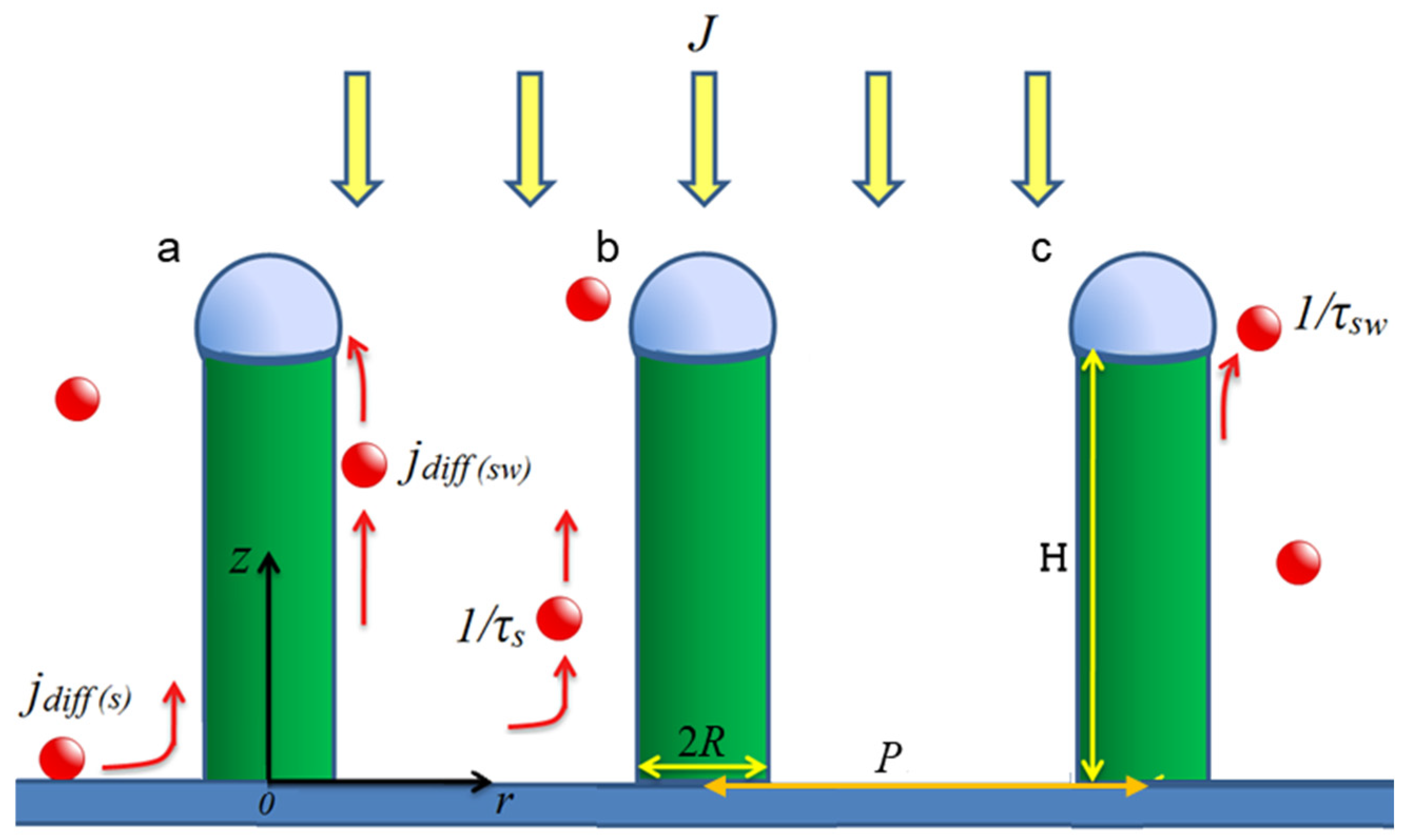
2. Model
3. Results
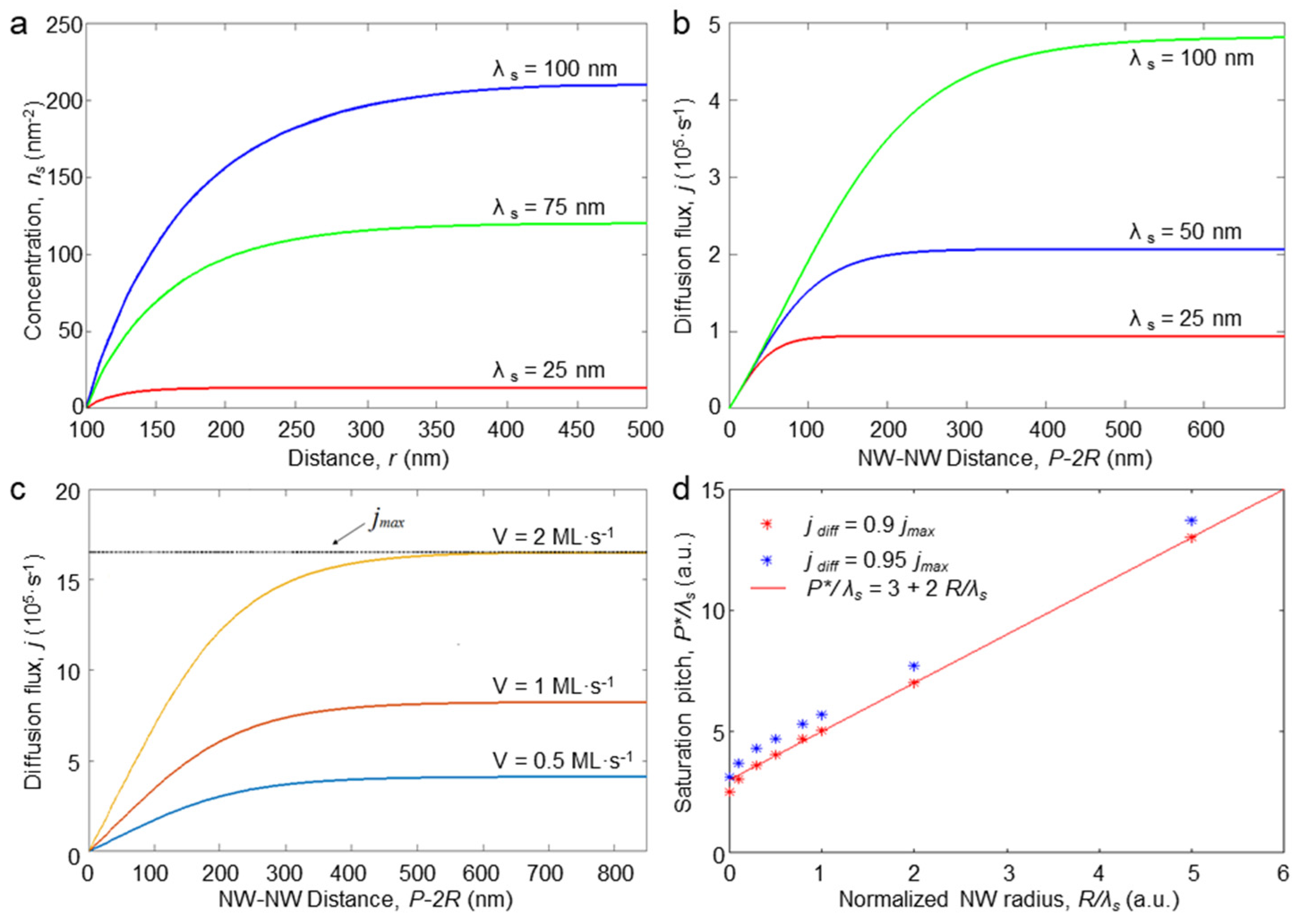
3.1. Diffusion on Substrate
- -
- NWs are cylinders with constant radii (in time and along the NW length), while the NWs are positioned regularly on the substrate with the pitch P between the neighboring NWs (see Figure 1);
- -
- The distribution of adatoms on the substrate around each NW has cylindrical symmetry (the closest case is hexagonal order of the NWs);
- -
- The deposition flux is perpendicular to the substrate (incident angle can be easily considered with geometrical coefficients);
- -
- The NW bottom perimeter and the catalyst droplet are ideal absorbers for the diffusing species.
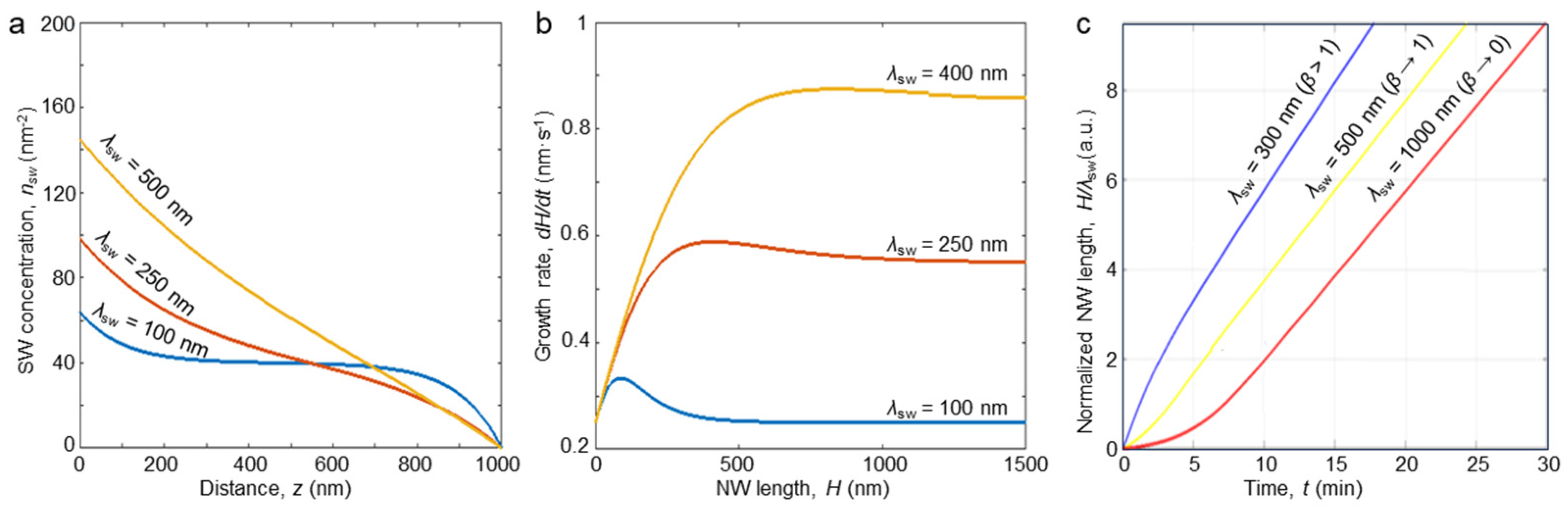
3.2. Diffusion on Sidewalls
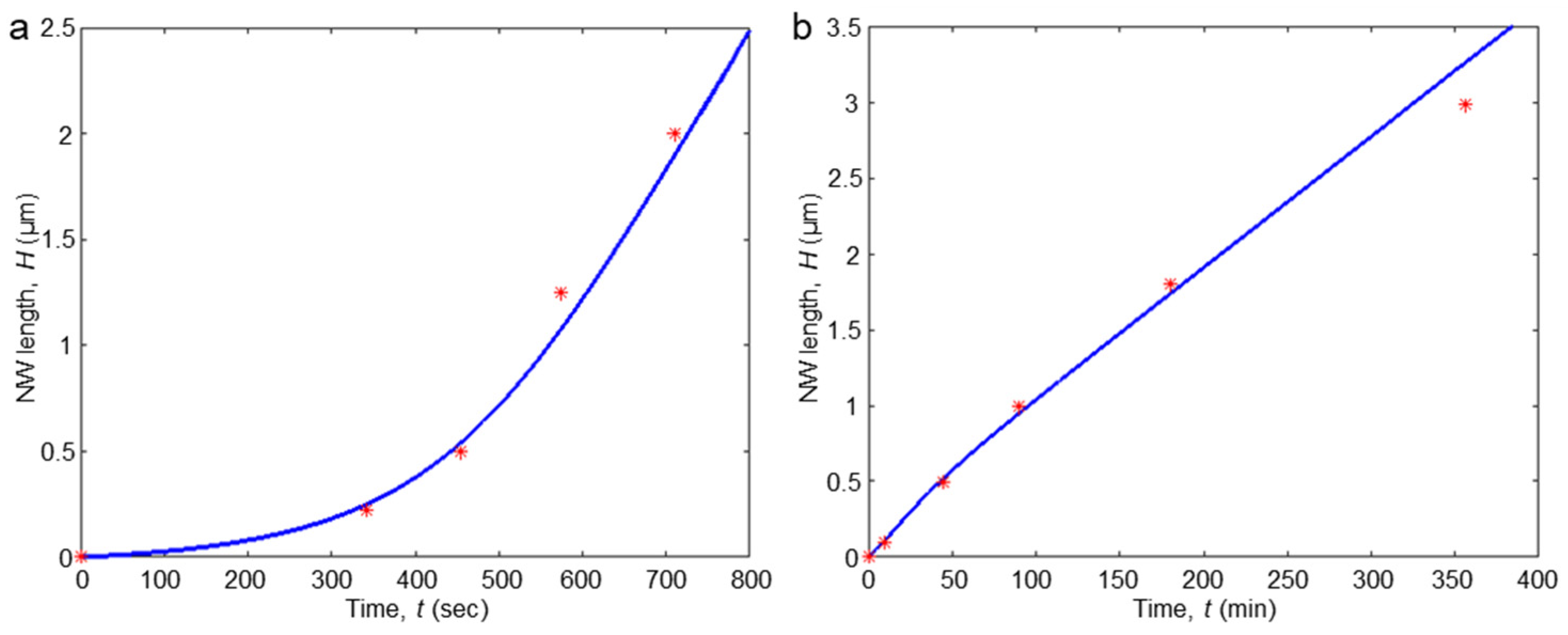
3.3. Experimental Data Fitting
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, A.Y.; Peters, J.; Huang, X.; Jung, D.; Norman, J.; Lee, M.L.; Gossard, A.C.; Bowers, J.E. Electrically pumped continuous-wave 1.3 μm quantum-dot lasers epitaxially grown on on-axis (001) GaP/Si. Opt. Lett. 2017, 42, 338–341. [Google Scholar] [CrossRef] [PubMed]
- Leandro, L.; Gunnarsson, C.P.; Reznik, R.; Jöns, K.D.; Shtrom, I.V.; Khrebtov, A.I.; Kasama, T.; Zwiller, V.; Cirlin, G.E.; Akopian, N. Nanowire quantum dots tuned to atomic resonances. Nano Lett. 2018, 18, 7217–7221. [Google Scholar] [CrossRef] [PubMed]
- Ishibe, T.; Tomeda, A.; Watanabe, K.; Kamakura, Y.; Mori, N.; Naruse, N.; Mera, Y.; Yamashita, Y.; Nakamura, Y. Methodology of thermoelectric power factor enhancement by controlling nanowire interface. ACS Appl. Mater. Interfaces 2018, 10, 37709–37716. [Google Scholar] [CrossRef] [PubMed]
- McCaughan, A.N.; Verma, V.B.; Buckley, S.M.; Allmaras, J.P.; Kozorezov, A.G.; Tait, A.N.; Nam, S.W.; Shainline, J.M. A superconducting thermal switch with ultrahigh impedance for interfacing superconductors to semiconductors. Nat. Electron. 2019, 2, 451–456. [Google Scholar] [CrossRef]
- McCaughan, A.N.; Verma, V.B.; Buckley, S.M.; Allmaras, J.P.; Kozorezov, A.G.; Tait, A.N.; Nam, S.W.; Shainline, J.M. Straining nanomembranes via highly mismatched heteroepitaxial growth: InAs islands on compliant Si substrates. ACS Nano 2012, 6, 10287–10295. [Google Scholar]
- Dubrovskii, V.G.; Cirlin, G.E.; Sibirev, N.V.; Jabeen, F.; Harmand, J.C.; Werner, P. New mode of vapor− liquid− solid nanowire growth. Nano Lett. 2011, 11, 1247–1253. [Google Scholar] [CrossRef]
- Sibirev, N.V.; Tchernycheva, M.; Timofeeva, M.A.; Harmand, J.-C.; Cirlin, G.E.; Dubrovskii, V.G. Influence of shadow effect on the growth and shape of InAs nanowires. J. Appl. Phys. 2012, 111, 104317. [Google Scholar] [CrossRef]
- Wagner, R.S.; Ellis, W.C. Vapor-liquid-solid mechanism of single crystal growth. Appl. Phys. Lett. 1964, 4, 89–90. [Google Scholar] [CrossRef]
- Cirlin, G.E.; Reznik, R.R.; Shtrom, I.V.; I Khrebtov, A.; Soshnikov, I.P.; A Kukushkin, S.; Leandro, L.; Kasama, T.; Akopian, N. AlGaAs and AlGaAs/GaAs/AlGaAs nanowires grown by molecular beam epitaxy on silicon substrates. J. Phys. D Appl. Phys. 2017, 50, 484003. [Google Scholar] [CrossRef]
- Lavenus, P.; Messanvi, A.; Rigutti, L.; De Luna Bugallo, A.; Zhang, H.; Bayle, F.; Julien, F.H.; Eymery, J.; Durand, C.; Tchernycheva, M. Experimental and theoretical analysis of transport properties of core–shell wire light emitting diodes probed by electron beam induced current microscopy. Nanotechnology 2014, 25, 255201. [Google Scholar] [CrossRef]
- Lauhon, L.J.; Gudiksen, M.S.; Wang, D.; Lieber, C.M. Epitaxial core–shell and core–multishell nanowire heterostructures. Nature 2002, 420, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.; Roy, P.; Kondratev, V.M.; Fedorov, V.V.; Kotlyar, K.P.; Reznik, R.R.; Vorobyev, A.A.; Mukhin, I.S.; Cirlin, G.E.; Bolshakov, A.D. Anisotropic Radiation in Heterostructured “Emitter in a Cavity” Nanowire. Nanomaterials 2022, 12, 241. [Google Scholar] [CrossRef] [PubMed]
- Kochetkov, F.M.; Neplokh, V.; Fedorov, V.V.; Bolshakov, A.D.; A Sharov, V.; E Eliseev, I.; Tchernycheva, M.; E Cirlin, G.; Nasibulin, A.G.; Islamova, R.M.; et al. Fabrication and electrical study of large area free-standing membrane with embedded GaP NWs for flexible devices. Nanotechnology 2020, 31, 46LT01. [Google Scholar] [CrossRef] [PubMed]
- Tchernycheva, M.; Neplokh, V.; Zhang, H.; Lavenus, P.; Rigutti, L.; Bayle, F.; Julien, F.H.; Babichev, A.; Jacopin, G.; Largeau, L.; et al. Core–shell InGaN/GaN nanowire light emitting diodes analyzed by electron beam induced current microscopy and cathodoluminescence mapping. Nanoscale 2015, 7, 11692–11701. [Google Scholar] [CrossRef]
- Matteini, F.; Dubrovskii, V.G.; Rüffer, D.; Tütüncüoglu, G.; Fontana, Y.; Morral, A.F.I. Tailoring the diameter and density of self-catalyzed GaAs nanowires on silicon. Nanotechnology 2015, 26, 105603. [Google Scholar] [CrossRef]
- Boulanger, J.P.; LaPierre, R.R. Patterned gold-assisted growth of GaP nanowires on Si. Semicond. Sci. Technol. 2012, 27, 035002. [Google Scholar] [CrossRef]
- Bauer, B.; Rudolph, A.; Soda, M.; Morral, A.F.I.; Zweck, J.; Schuh, D.; Reiger, E. Position controlled self-catalyzed growth of GaAs nanowires by molecular beam epitaxy. Nanotechnology 2010, 21, 435601. [Google Scholar] [CrossRef]
- He, X.; Zhang, J.; Wang, Z. STED direct laser writing of 45 nm width nanowire. Micromachines 2019, 10, 726. [Google Scholar] [CrossRef]
- Hwang, T.Y.; An, G.H.; Lim, J.H.; Myung, N.V.; Choa, Y.H. Morphology control of ordered Si nanowire arrays by nanosphere lithography and metal-assisted chemical etching. Jpn. J. Appl. Phys. 2014, 53, 05HA07. [Google Scholar] [CrossRef]
- Dvoretckaia, L.; Gridchin, V.; Mozharov, A.; Maksimova, A.; Dragunova, A.; Melnichenko, I.; Mitin, D.; Vinogradov, A.; Mukhin, I.; Cirlin, G. Light-emitting diodes based on InGaN/GaN nanowires on microsphere-lithography-patterned Si substrates. Nanomaterials 2022, 12, 1993. [Google Scholar] [CrossRef]
- Mårtensson, T.; Carlberg, P.; Borgström, M.; Montelius, L.; Seifert, W.; Samuelson, L. Nanowire arrays defined by nanoimprint lithography. Nano Lett. 2004, 4, 699–702. [Google Scholar] [CrossRef]
- Maliakkal, C.B.; Mårtensson, E.K.; Tornberg, M.U.; Jacobsson, D.; Persson, A.R.; Johansson, J.; Wallenberg, L.R.; Dick, K.A. Independent control of nucleation and layer growth in nanowires. ACS Nano 2020, 14, 3868–3875. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Dong, T.; Yu, L.; Xu, J.; Chen, K. Planar growth, integration, and applications of semiconducting nanowires. Adv. Mater. 2020, 32, 1903945. [Google Scholar] [CrossRef] [PubMed]
- McIntyre, P.C.; i Morral, A.F. Semiconductor nanowires: To grow or not to grow? Mater. Today Nano 2020, 9, 100058. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Bolshakov, A.D. Surface energy and modes of catalytic growth of semiconductor nanowhiskers. Tech. Phys. Lett. 2012, 38, 311–315. [Google Scholar] [CrossRef]
- Heiß, M.; Riedlberger, E.; Spirkoska, D.; Bichler, M.; Abstreiter, G.; i Morral, A.F. Growth mechanisms and optical properties of GaAs-based semiconductor microstructures by selective area epitaxy. J. Cryst. Growth 2008, 310, 1049–1056. [Google Scholar] [CrossRef]
- Hertenberger, S.; Rudolph, D.; Bichler, M.; Finley, J.J.; Abstreiter, G.; Koblmüller, G. Growth kinetics in position-controlled and catalyst-free InAs nanowire arrays on Si (111) grown by selective area molecular beam epitaxy. J. Appl. Phys. 2010, 108, 114316. [Google Scholar] [CrossRef]
- Madsen, M.H.; Krogstrup, P.; Johnson, E.; Venkatesan, S.; Mühlbauer, E.; Scheu, C.; Sørensen, C.B.; Nygård, J. Experimental determination of adatom diffusion lengths for growth of InAs nanowires. J. Cryst. Growth 2013, 364, 16–22. [Google Scholar] [CrossRef]
- Gotschke, T.; Schumann, T.; Limbach, F.; Stoica, T.; Calarco, R. Influence of the adatom diffusion on selective growth of GaN nanowire regular arrays. Appl. Phys. Lett. 2011, 98, 103102. [Google Scholar] [CrossRef]
- Oehler, F.; Cattoni, A.; Scaccabarozzi, A.; Patriarche, G.; Glas, F.; Harmand, J.C. Measuring and modeling the growth dynamics of self-catalyzed GaP nanowire arrays. Nano Lett. 2018, 18, 701–708. [Google Scholar] [CrossRef]
- Gibson, S.J.; LaPierre, R.R. Model of patterned self-assisted nanowire growth. Nanotechnology 2014, 25, 415304. [Google Scholar] [CrossRef] [PubMed]
- Dubrovskii, V.G.; Cirlin, G.E.; Ustinov, V.M. Semiconductor nanowhiskers: Synthesis, properties, and applications. Semiconductors 2009, 43, 1539. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Berdnikov, Y.; Schmidtbauer, J.; Borg, M.; Storm, K.; Deppert, K.; Johansson, J. Length distributions of nanowires growing by surface diffusion. Cryst. Growth Des. 2016, 16, 2167–2172. [Google Scholar] [CrossRef]
- Ruthand, V.; Hirth, J.P. Kinetics of diffusion-controlled whisker growth. J. Chem. Phys. 1964, 41, 3139. [Google Scholar]
- Dalacu, D.; Kam, A.; Austing, D.G.; Wu, X.; Lapointe, J.; Aers, G.C.; Poole, P.J. Selective-area vapour–liquid–solid growth of InP nanowires. Nanotechnology 2009, 20, 395602. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bikmeeva, K.R.; Bolshakov, A.D. Diffusion-Induced Ordered Nanowire Growth: Mask Patterning Insights. Nanomaterials 2024, 14, 1743. https://doi.org/10.3390/nano14211743
Bikmeeva KR, Bolshakov AD. Diffusion-Induced Ordered Nanowire Growth: Mask Patterning Insights. Nanomaterials. 2024; 14(21):1743. https://doi.org/10.3390/nano14211743
Chicago/Turabian StyleBikmeeva, Kamila R., and Alexey D. Bolshakov. 2024. "Diffusion-Induced Ordered Nanowire Growth: Mask Patterning Insights" Nanomaterials 14, no. 21: 1743. https://doi.org/10.3390/nano14211743
APA StyleBikmeeva, K. R., & Bolshakov, A. D. (2024). Diffusion-Induced Ordered Nanowire Growth: Mask Patterning Insights. Nanomaterials, 14(21), 1743. https://doi.org/10.3390/nano14211743




