Computational Design of the Electronic Response for Volatile Organic Compounds Interacting with Doped Graphene Substrates
Abstract
1. Introduction
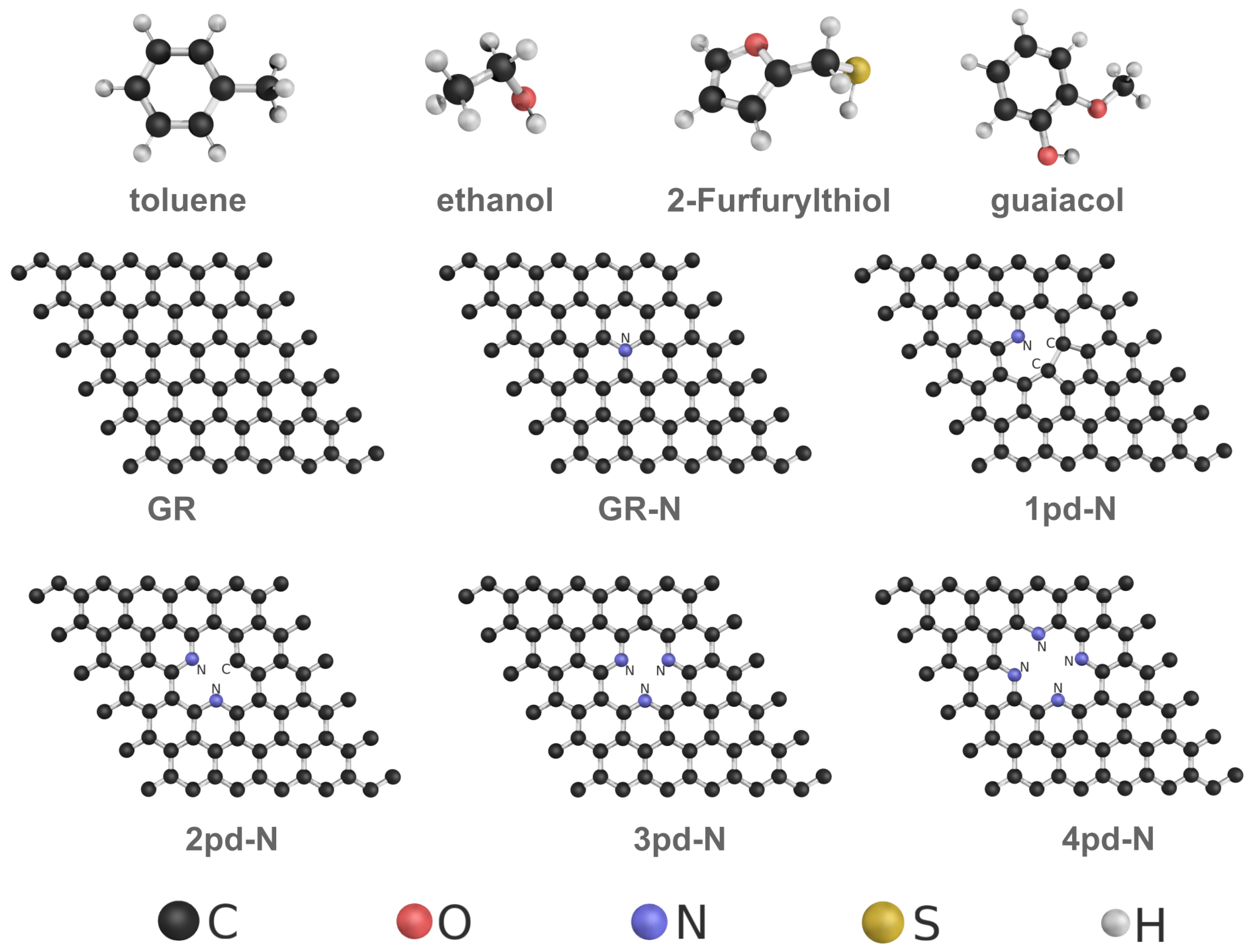
2. Computational Methods
3. Results and Discussion
3.1. Physisorption Interaction Type
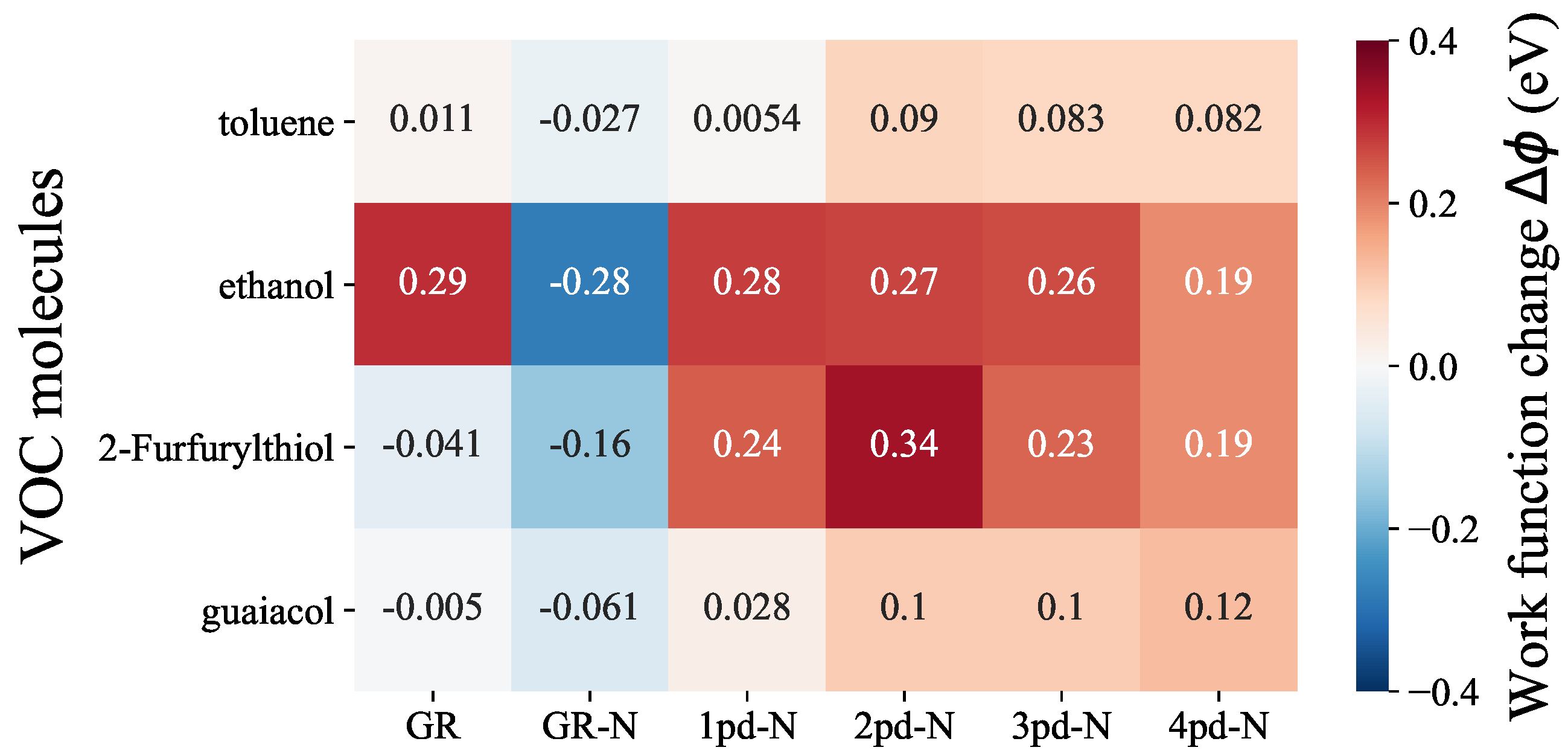
3.2. Work Function Change
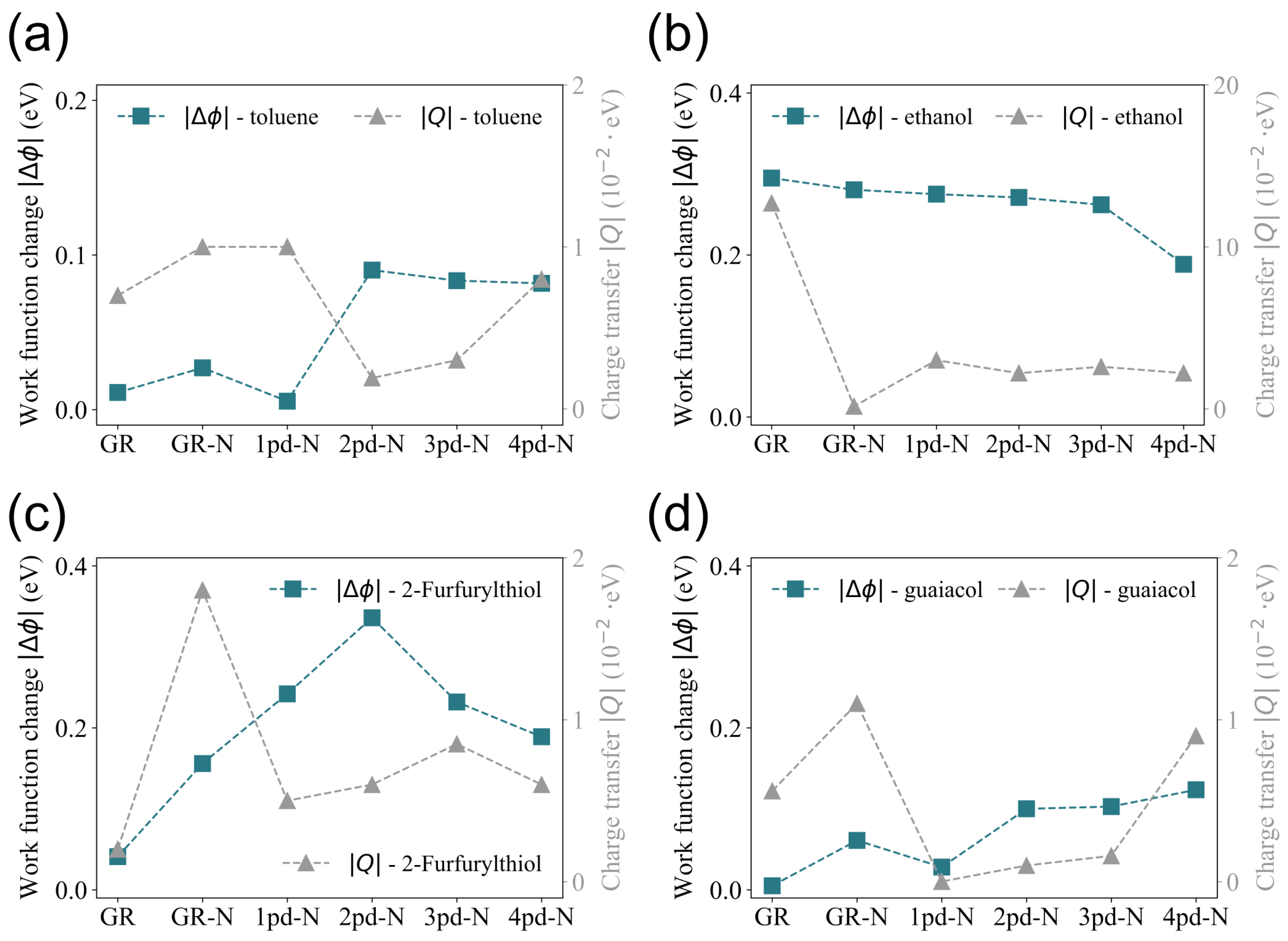
3.3. Charge Transfer vs. Work Function Change
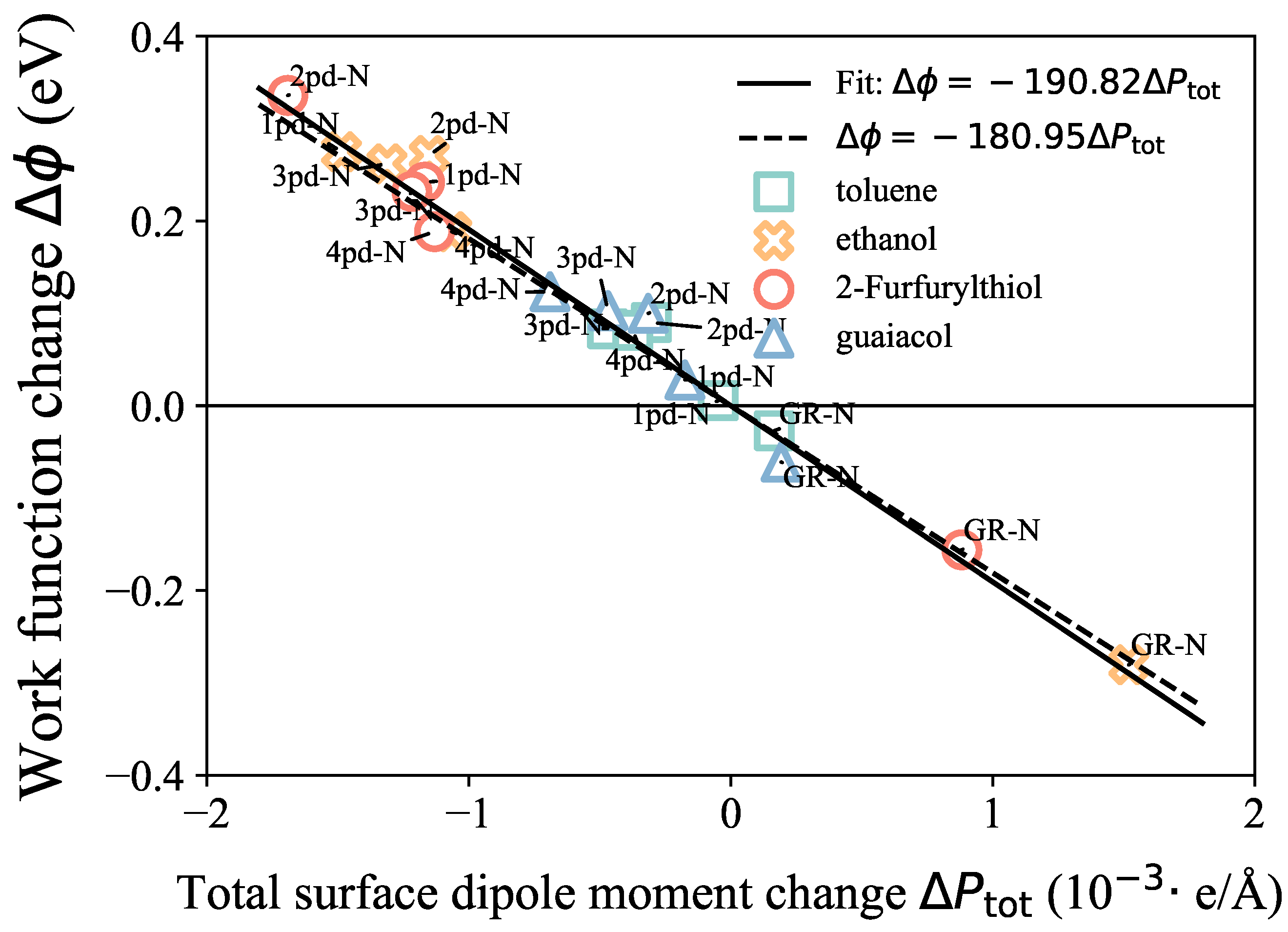
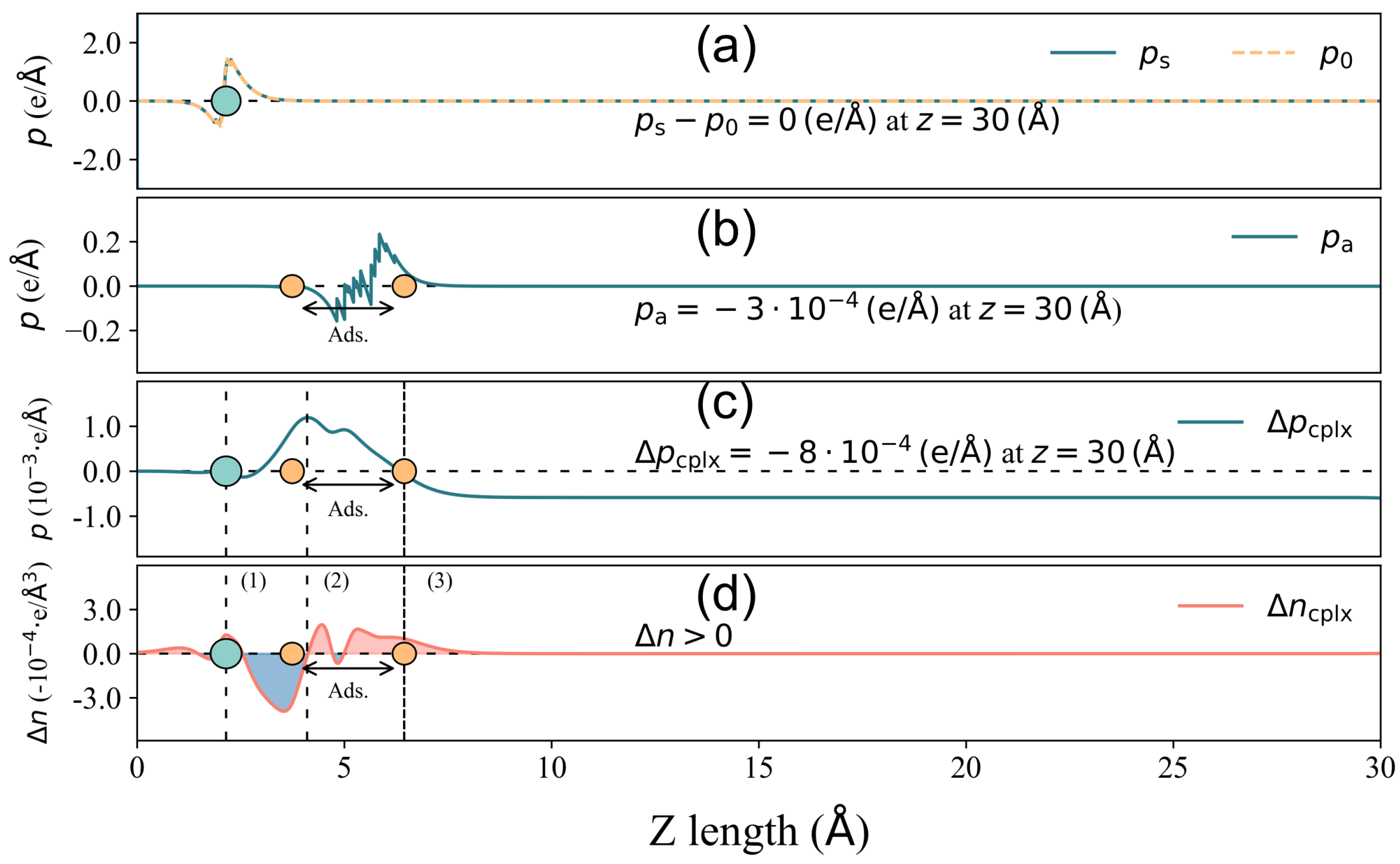
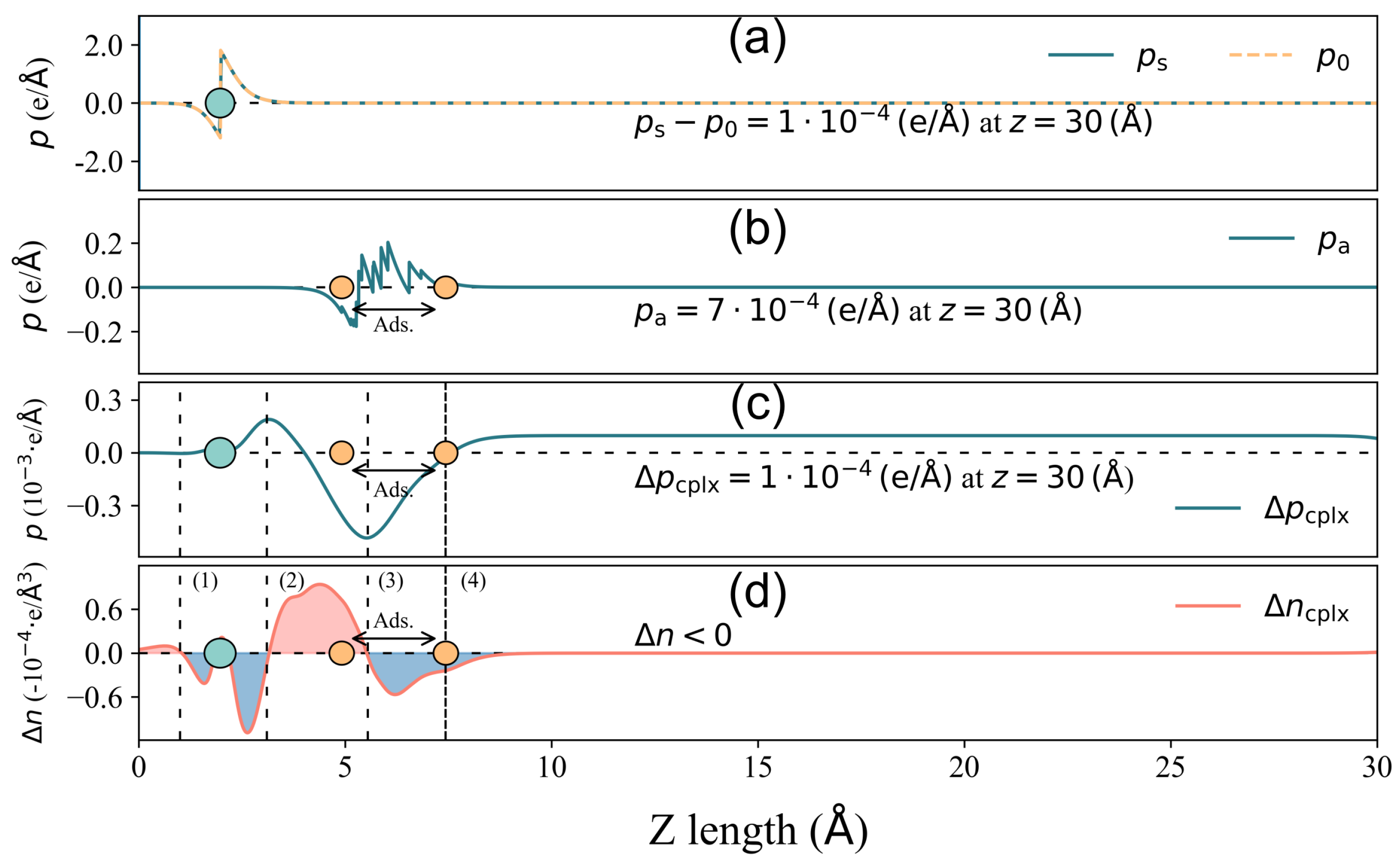
3.4. Surface Dipole Moment Change Validation
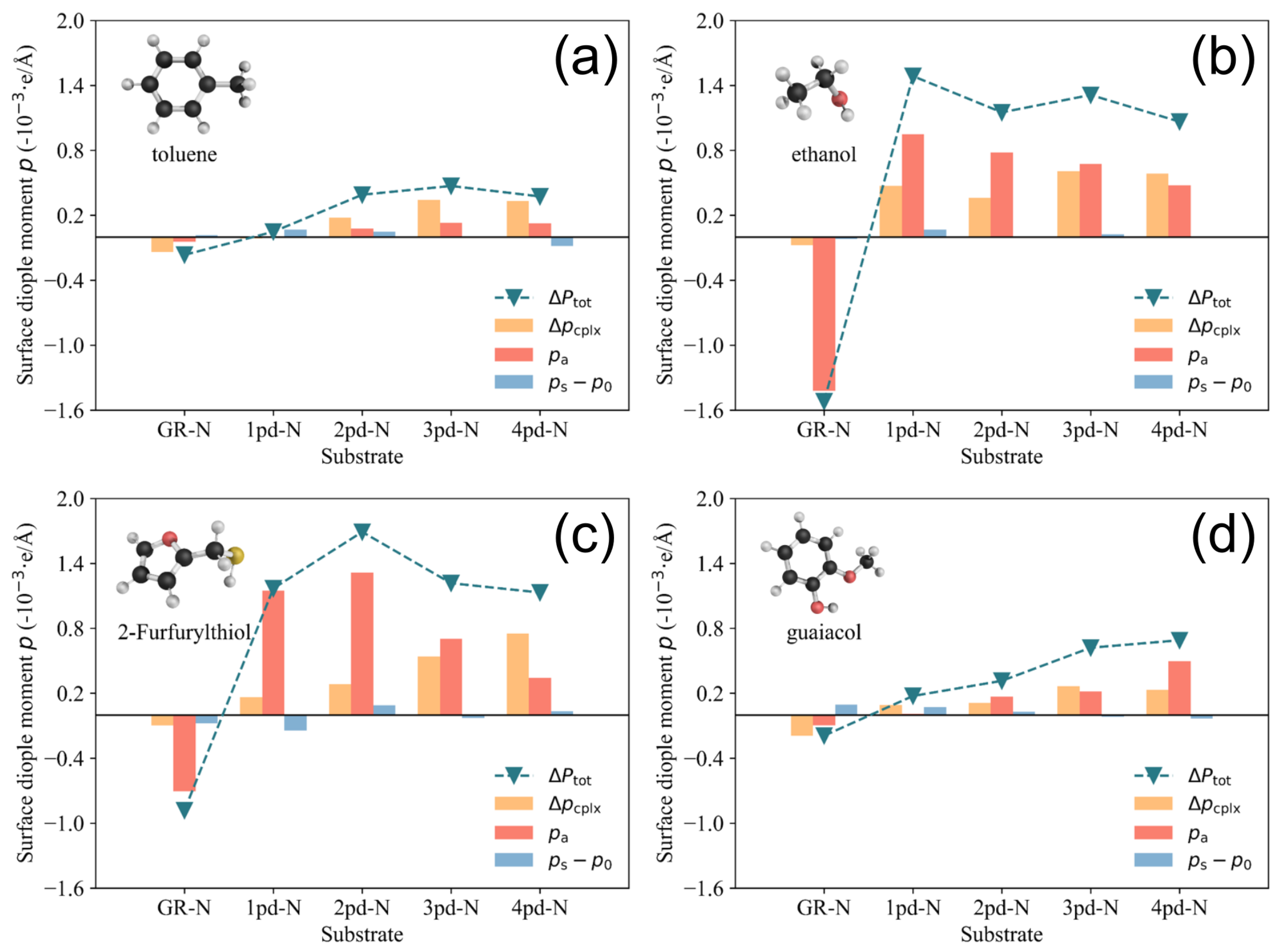
3.5. Surface Dipole Moment Change Decomposition
3.6. Design Principle of for VOC Sensing
- : One could induce multiple highly electronegative atoms into the adsorption site on the substrate, since it will bring more dangling bonds and yield charge redistribution, and vice versa, as reflected in the values presented in Figure 7.
- : While the out-of-plane dipole moment of VOC molecules can be tuned, adjusting the sign of by substituting different types of dopant atoms (e.g., pyridinic-N and pyrrolic-N) could further enhance the directional contrast of the difference.
- : Increasing the value is not recommended, even though this term also has a large influence on the value, as large deformation of the substrate is detrimental to the stability and durability of sensing materials.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Cheng, S.; Liu, H.; Hu, S.; Zhang, D.; Ning, H. A survey on gas sensing technology. Sensors 2012, 12, 9635–9665. [Google Scholar] [CrossRef] [PubMed]
- Pöschl, U.; Shiraiwa, M. Multiphase chemistry at the atmosphere–biosphere interface influencing climate and public health in the anthropocene. Chem. Rev. 2015, 115, 4440–4475. [Google Scholar]
- He, C.; Cheng, J.; Zhang, X.; Douthwaite, M.; Pattisson, S.; Hao, Z. Recent advances in the catalytic oxidation of volatile organic compounds: A review based on pollutant sorts and sources. Chem. Rev. 2019, 119, 4471–4568. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Jiang, C.; Wei, S.h. Gas sensing in 2D materials. Appl. Phys. Rev. 2017, 4, 021304. [Google Scholar] [CrossRef]
- Donarelli, M.; Ottaviano, L. 2D materials for gas sensing applications: A review on graphene oxide, MoS2, WS2 and phosphorene. Sensors 2018, 18, 3638. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Jacobs, R.; Ma, T.; Chen, D.; Booske, J.; Morgan, D. Work Function: Fundamentals, Measurement, Calculation, Engineering, and Applications. Phys. Rev. Appl. 2023, 19, 037001. [Google Scholar] [CrossRef]
- Gurlo, A.; Sahm, M.; Oprea, A.; Barsan, N.; Weimar, U. A p- to n-transition on α-Fe2O3-based thick film sensors studied by conductance and work function change measurements. Sens. Actuators B 2004, 102, 291–298. [Google Scholar] [CrossRef]
- Chou, P.C.; Chen, H.I.; Liu, I.P.; Chen, W.C.; Chen, C.C.; Liou, J.K.; Lai, C.J.; Liu, W.C. On a Schottky diode-type hydrogen sensor with pyramid-like Pd nanostructures. Int. J. Hydrogen Energy 2015, 40, 9006–9012. [Google Scholar] [CrossRef]
- Kumar, A. Palladium-based trench gate MOSFET for highly sensitive hydrogen gas sensor. Mater. Sci. Semicond. Process. 2020, 120, 105274. [Google Scholar] [CrossRef]
- Pour, G.B.; Aval, L.F.; Eslami, S. Sensitive capacitive-type hydrogen sensor based on Ni thin film in different hydrogen concentrations. Curr. Nanosci. 2018, 14, 136–142. [Google Scholar] [CrossRef]
- Sahm, T.; Gurlo, A.; Bârsan, N.; Weimar, U. Basics of oxygen and SnO2 interaction; work function change and conductivity measurements. Sens. Actuators B 2006, 118, 78–83. [Google Scholar] [CrossRef]
- Meng, J.; Li, Z. Schottky-Contacted Nanowire Sensors. Adv. Mater. 2020, 32, 2000130. [Google Scholar] [CrossRef] [PubMed]
- Li, J.H.; Wu, J.; Yu, Y.X. DFT exploration of sensor performances of two-dimensional WO3 to ten small gases in terms of work function and band gap changes and I-V responses. Appl. Surf. Sci. 2021, 546, 149104. [Google Scholar] [CrossRef]
- Nath, U.; Sarma, M. Pyridinic Dominance N-Doped Graphene: A Potential Material for SO2 Gas Detection. J. Phys. Chem. A 2023, 127, 1112–1123. [Google Scholar] [CrossRef] [PubMed]
- Cid, B.J.; Santana, J.E.; Arellano, L.G.; Miranda, Á.; Pérez-Figueroa, S.E.; Iturrios, M.I.; Pérez, L.A.; Cruz-Irisson, M. Metal-decorated siligene as work function type sensor for NH3 detection: A DFT approach. Appl. Surf. Sci. 2023, 610, 155541. [Google Scholar] [CrossRef]
- Kalwar, B.A.; Fangzong, W.; Soomro, A.M.; Naich, M.R.; Saeed, M.H.; Ahmed, I. Highly sensitive work function type room temperature gas sensor based on Ti doped hBN monolayer for sensing CO2, CO, H2S, HF and NO. A DFT study. RSC Adv. 2022, 12, 34185–34199. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.; Jia, P.; Peng, X.; Li, P. Adsorption and sensing of CO and C2H2 by S-defected SnS2 monolayer for DGA in transformer oil: A DFT study. Mater. Chem. Phys. 2020, 249, 123006. [Google Scholar] [CrossRef]
- Ni, J.; Wang, W.; Quintana, M.; Jia, F.; Song, S. Adsorption of small gas molecules on strained monolayer WSe2 doped with Pd, Ag, Au, and Pt: A computational investigation. Appl. Surf. Sci. 2020, 514, 145911. [Google Scholar] [CrossRef]
- Reji, R.P.; Balaji, S.K.C.; Sivalingam, Y.; Kawazoe, Y.; Velappa Jayaraman, S. First-principles density functional theory calculations on the potential of Sc2CO2 MXene nanosheets as a dual-mode sensor for detection of volatile organic compounds in exhaled human breath. ACS Appl. Nano Mater. 2023, 6, 5345–5356. [Google Scholar] [CrossRef]
- Lin, L.; Feng, Z.; Dong, Z.; Hu, C.; Han, L.; Tao, H. DFT study on the adsorption of CO, NO2, SO2 and NH3 by Te vacancy and metal atom doped MoTe2 monolayers. Phys. E 2023, 145, 115489. [Google Scholar] [CrossRef]
- Leung, C.; Kao, L.; Su, S.; Feng, J.; Chan, T. Relationship between surface dipole, work function and charge transfer: Some exceptions to an established rule. Phys. Rev. B Condens. Matter Mater. Phys. 2003, 68, 195408. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Xu, Y.; Lei, G.; Tsumori, K.; Isobe, M.; Shimizu, A.; Cui, Z.; Zhu, Y.; Hu, J.; et al. Theoretical calculation of cesium deposition and co-deposition with electronegative elements on the plasma grid in negative ion sources. Nucl. Mater. Energy 2023, 34, 101334. [Google Scholar] [CrossRef]
- Khazaei, M.; Arai, M.; Sasaki, T.; Ranjbar, A.; Liang, Y.; Yunoki, S. OH-terminated two-dimensional transition metal carbides and nitrides as ultralow work function materials. Phys. Rev. B Condens. Matter 2015, 92, 075411. [Google Scholar] [CrossRef]
- Gong, C.; Colombo, L.; Wallace, R.M.; Cho, K. The Unusual Mechanism of Partial Fermi Level Pinning at Metal–MoS2 Interfaces. Nano Lett. 2014, 14, 1714–1720. [Google Scholar] [CrossRef] [PubMed]
- Basera, P.; Traoré, B.; Even, J.; Katan, C. Interfacial engineering to modulate surface dipoles, work functions and dielectric confinement of halide perovskites. Nanoscale 2023, 15, 11884–11897. [Google Scholar] [CrossRef]
- Chen, W.Y.; Li, L.; Huang, T.; Yang, Z.X.; Zhang, T.; Huang, G.F.; Hu, W.; Huang, W.Q. Extending Schottky–Mott rule to van der Waals heterostructures of 2D Janus materials: Influence of intrinsic dipoles. Appl. Phys. Lett. 2023, 123, 171601. [Google Scholar] [CrossRef]
- Traoré, B.; Basera, P.; Ramadan, A.J.; Snaith, H.J.; Katan, C.; Even, J. A Theoretical Framework for Microscopic Surface and Interface Dipoles, Work Functions, and Valence Band Alignments in 2D and 3D Halide Perovskite Heterostructures. ACS Energy Lett. 2021, 7, 349–357. [Google Scholar] [CrossRef]
- Pappas, G.P.; Herbert, R.J.; Henderson, W.; Koenig, J.; Stover, B.; Barnhart, S. The respiratory effects of volatile organic compounds. Int. J. Occup. Environ. Health 2000, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Dorfner, R.; Ferge, T.; Kettrup, A.; Zimmermann, R.; Yeretzian, C. Real-time monitoring of 4-vinylguaiacol, guaiacol, and phenol during coffee roasting by resonant laser ionization time-of-flight mass spectrometry. J. Agric. Food Chem. 2003, 51, 5768–5773. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhang, J.M.; Xu, K.W.; Ji, V. Improving SO2 gas sensing properties of graphene by introducing dopant and defect: A first-principles study. Appl. Surf. Sci. 2014, 313, 405–410. [Google Scholar] [CrossRef]
- Tit, N.; Said, K.; Mahmoud, N.M.; Kouser, S.; Yamani, Z.H. Ab-initio investigation of adsorption of CO and CO2 molecules on graphene: Role of intrinsic defects on gas sensing. Appl. Surf. Sci. 2017, 394, 219–230. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Condens. Matter Phys. 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Condens. Matter Phys. 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; Gironcoli, S.D.; Delugas, P.; Ruffino, F.F.; et al. Quantum ESPRESSO toward the exascale. J. Condens. Matter Phys. 2020, 152, 154105. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B Condens. Matter 1996, 54, 16533. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Sohier, T.; Calandra, M.; Mauri, F. Density functional perturbation theory for gated two-dimensional heterostructures: Theoretical developments and application to flexural phonons in graphene. Phys. Rev. B Condens. Matter 2017, 96, 075448. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Itoh, T. Molecular structure of methylamine. J. Phys. Soc. Jpn. 1956, 11, 264–271. [Google Scholar] [CrossRef]
- Dzade, N.Y.; Roldan, A.; De Leeuw, N.H. Adsorption of methylamine on mackinawite (FeS) surfaces: A density functional theory study. J. Chem. Phys. 2013, 139, 124708. [Google Scholar] [CrossRef]
- Iijima, T.; Jimbo, H.; Taguchi, M. The molecular structure of methylamine in the vapour phase. J. Mol. Struct. 1986, 144, 381–383. [Google Scholar] [CrossRef]
- Yutomo, E.B.; Noor, F.A.; Winata, T. Effect of the number of nitrogen dopants on the electronic and magnetic properties of graphitic and pyridinic N-doped graphene–A density-functional study. RSC Adv. 2021, 11, 18371–18380. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Wang, K.; Yang, Z.; Wu, S.; Han, D. Quantum chemical study on the ozonolysis mechanism of guaiacol and the structure-reactivity relationship of phenols with hydroxyl, methoxy, and methyl substituents. Chem. Eng. J. 2021, 420, 127629. [Google Scholar] [CrossRef]
| GR | GR-N | 1pd-N | 2pd-N | 3pd-N | 4pd-N | |
|---|---|---|---|---|---|---|
| Toluene | 2.90 | 3.01 | 2.77 | 2.36 | 2.13 | 1.81 |
| Ethanol | 3.40 | 2.95 | 2.86 | 2.77 | 1.68 | 1.29 |
| 2-Furfurylthiol | 2.60 | 3.14 | 2.41 | 2.09 | 1.89 | 1.57 |
| Guaiacol | 2.58 | 2.60 | 2.46 | 2.32 | 2.16 | 1.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Bodesheim, D.; Ranjbar, A.; Dianat, A.; Biele, R.; Gutierrez, R.; Khazaei, M.; Cuniberti, G. Computational Design of the Electronic Response for Volatile Organic Compounds Interacting with Doped Graphene Substrates. Nanomaterials 2024, 14, 1778. https://doi.org/10.3390/nano14221778
Chen L, Bodesheim D, Ranjbar A, Dianat A, Biele R, Gutierrez R, Khazaei M, Cuniberti G. Computational Design of the Electronic Response for Volatile Organic Compounds Interacting with Doped Graphene Substrates. Nanomaterials. 2024; 14(22):1778. https://doi.org/10.3390/nano14221778
Chicago/Turabian StyleChen, Li, David Bodesheim, Ahmad Ranjbar, Arezoo Dianat, Robert Biele, Rafael Gutierrez, Mohammad Khazaei, and Gianaurelio Cuniberti. 2024. "Computational Design of the Electronic Response for Volatile Organic Compounds Interacting with Doped Graphene Substrates" Nanomaterials 14, no. 22: 1778. https://doi.org/10.3390/nano14221778
APA StyleChen, L., Bodesheim, D., Ranjbar, A., Dianat, A., Biele, R., Gutierrez, R., Khazaei, M., & Cuniberti, G. (2024). Computational Design of the Electronic Response for Volatile Organic Compounds Interacting with Doped Graphene Substrates. Nanomaterials, 14(22), 1778. https://doi.org/10.3390/nano14221778








