Simulation Study of High-Precision Characterization of MeV Electron Interactions for Advanced Nano-Imaging of Thick Biological Samples and Microchips
Abstract
1. Introduction
2. Results
2.1. Select Electron Energy
2.2. Monte Carlo Simulation
2.2.1. Using BNL-Monte Carlo Code
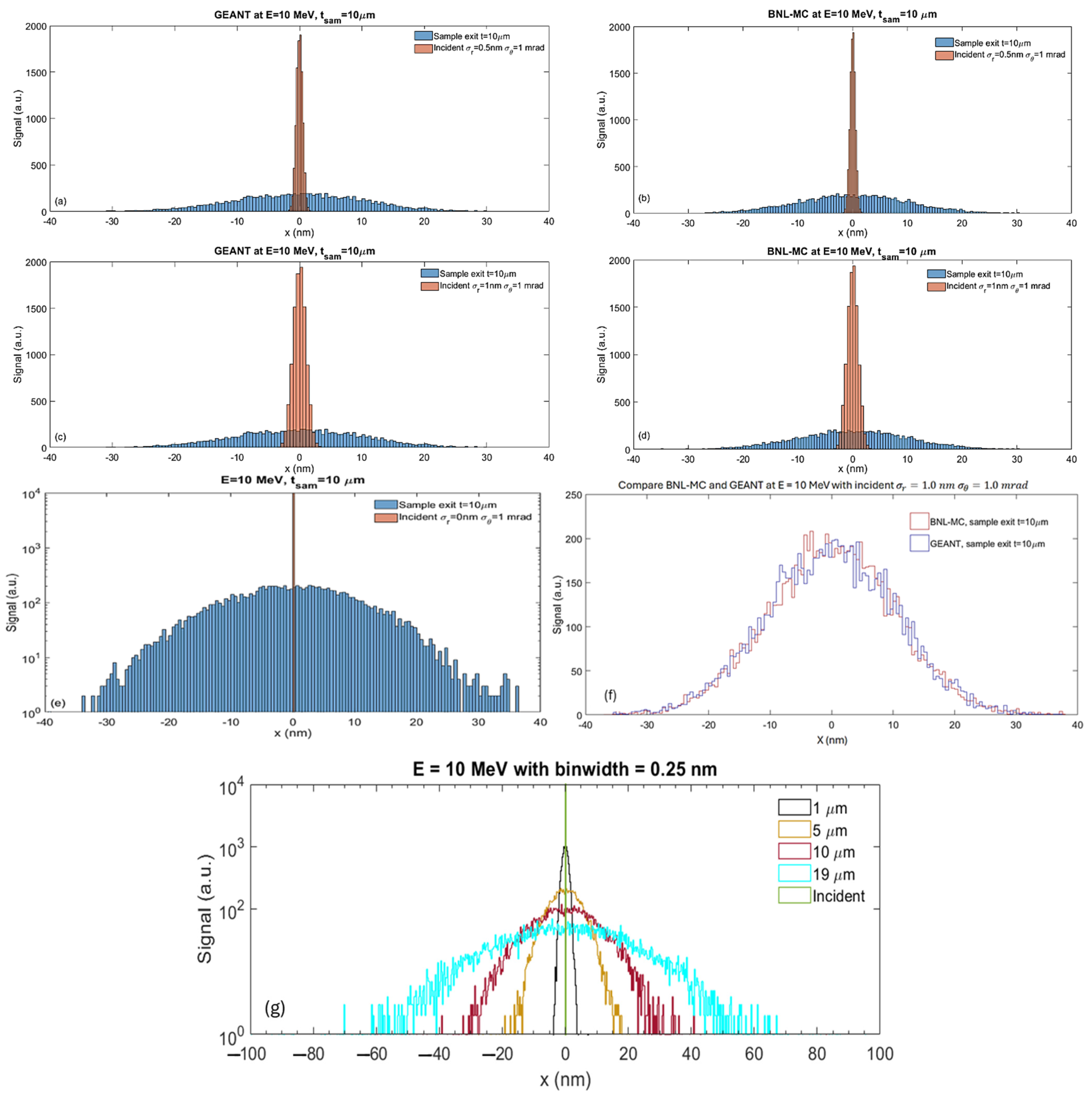
2.2.2. Comparing BNL-MC Code and GEANT
2.3. Numerical Evaluation of the Proposed Methodology
2.3.1. Study Objectives
2.3.2. Key Parameters for Measurement
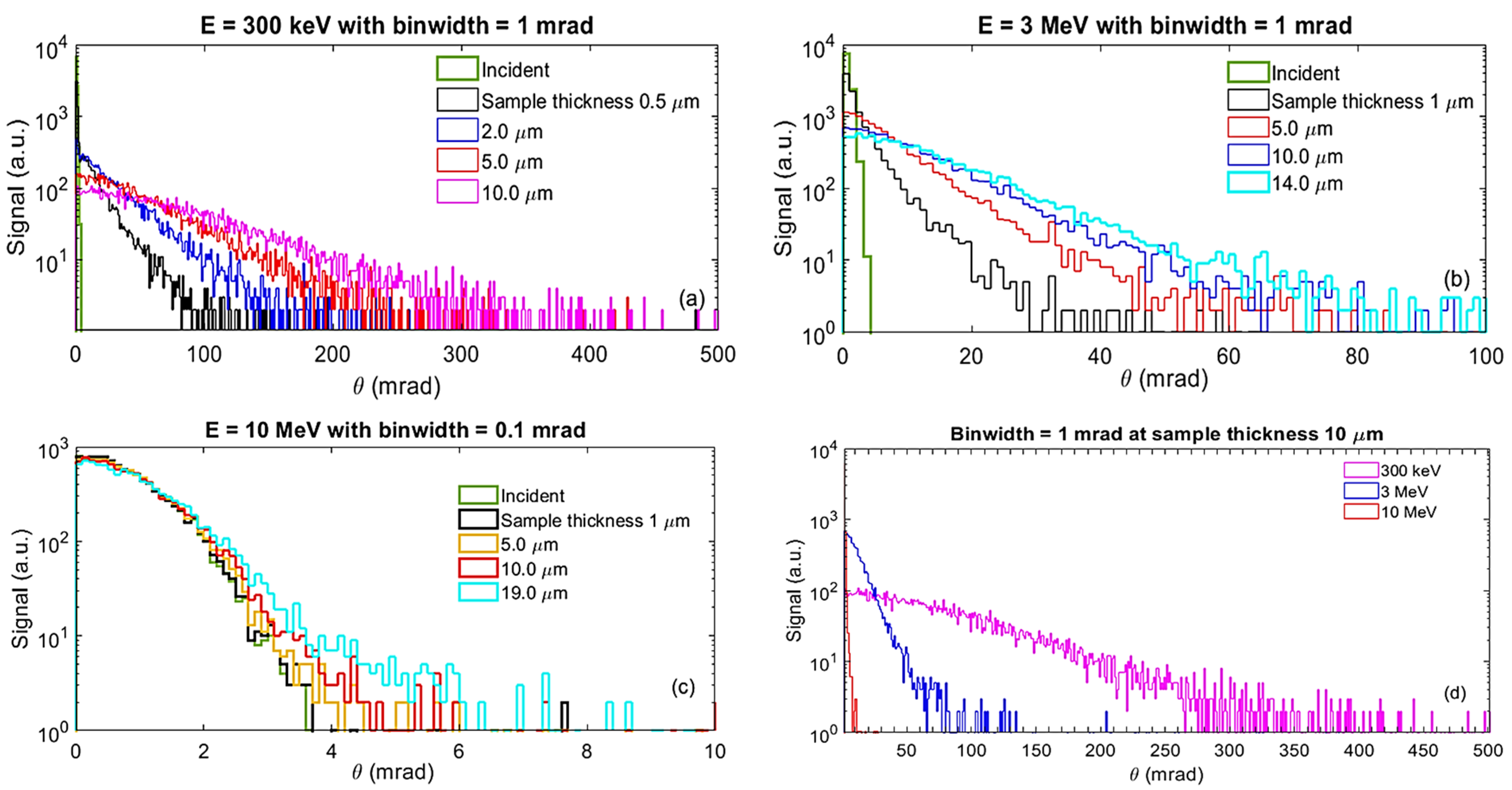
- Beam divergence: We will assess the divergence angle of the electron beam by varying the detector’s longitudinal position relative to the sample exit, analyzing how the beam profile changes with distance. Additionally, by steering the beam across a wedge-shaped sample with thicknesses ranging from 0 to 20 μm (see details in Section 2.3.5), we will quantify beam spread as a function of sample thickness.
- Beam intensity: We will measure electron beam attenuation through various sample thicknesses and materials by correlating these measurements with incident beam intensity.
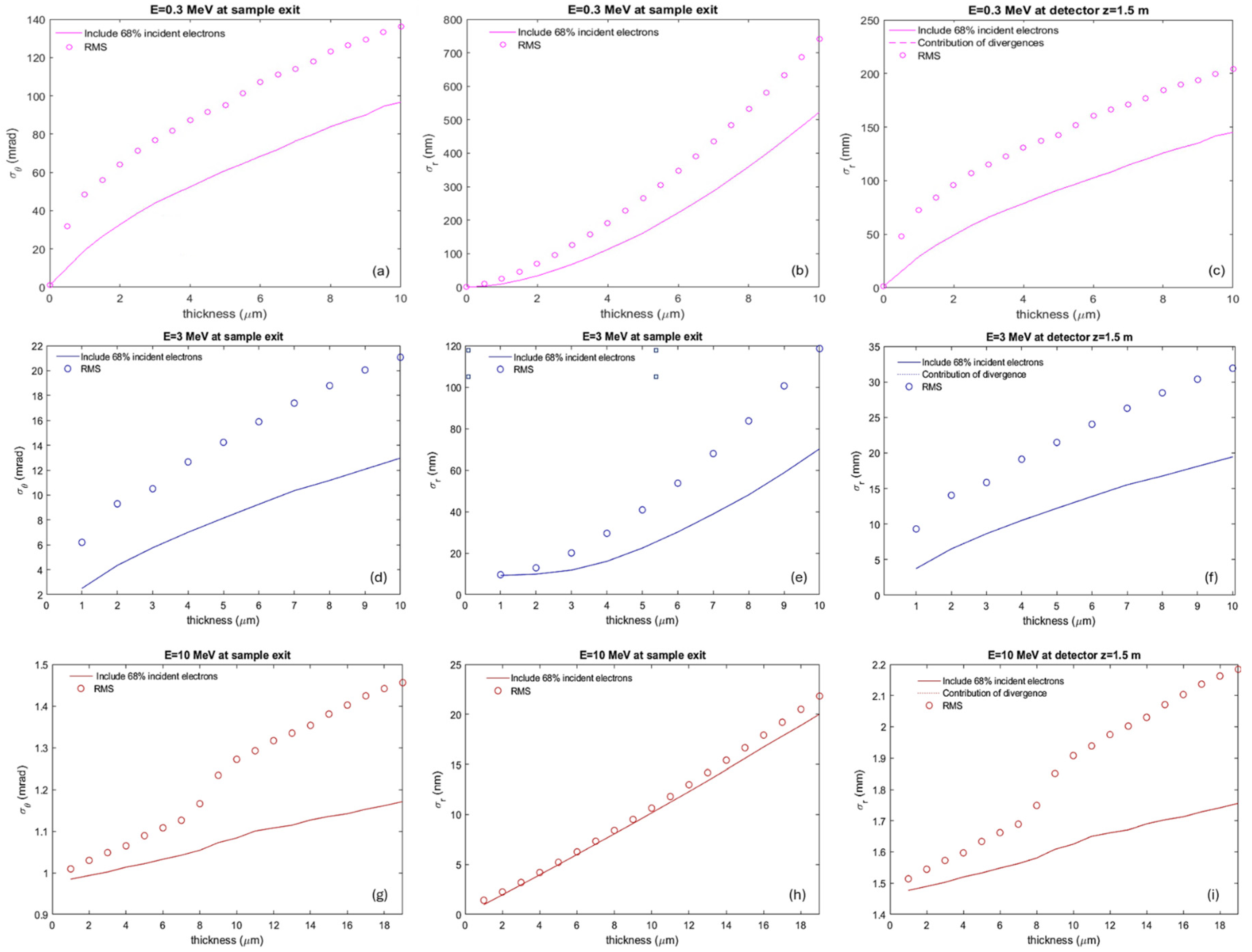
- Beam size at sample exit: Direct measurements of the projected beam size on the detector will be obtained from the 2-D image of the electron distribution. Using the measured beam divergence (details in the next section), we will calculate the beam size at the sample exit, as described by Equation (3) in Section 2.3.4.
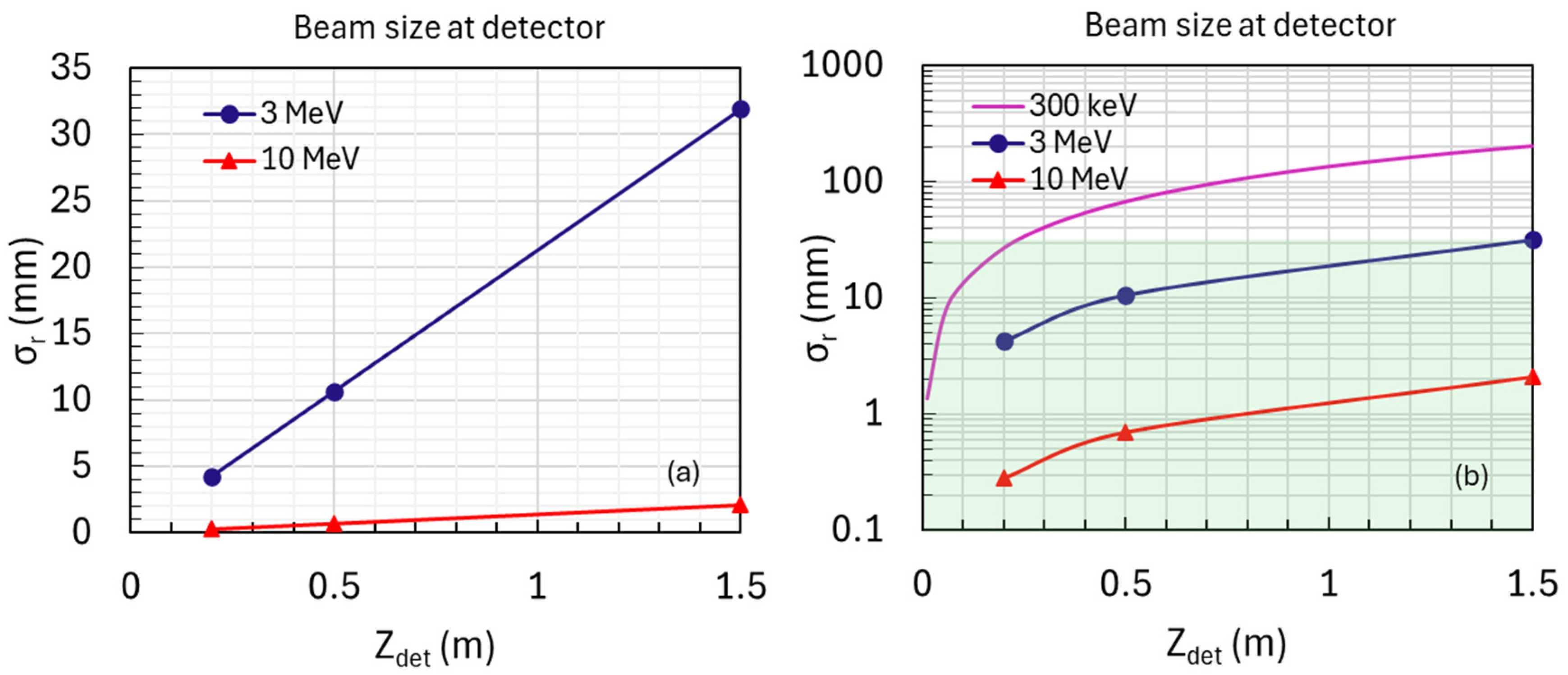
2.3.3. Detector Arrangement
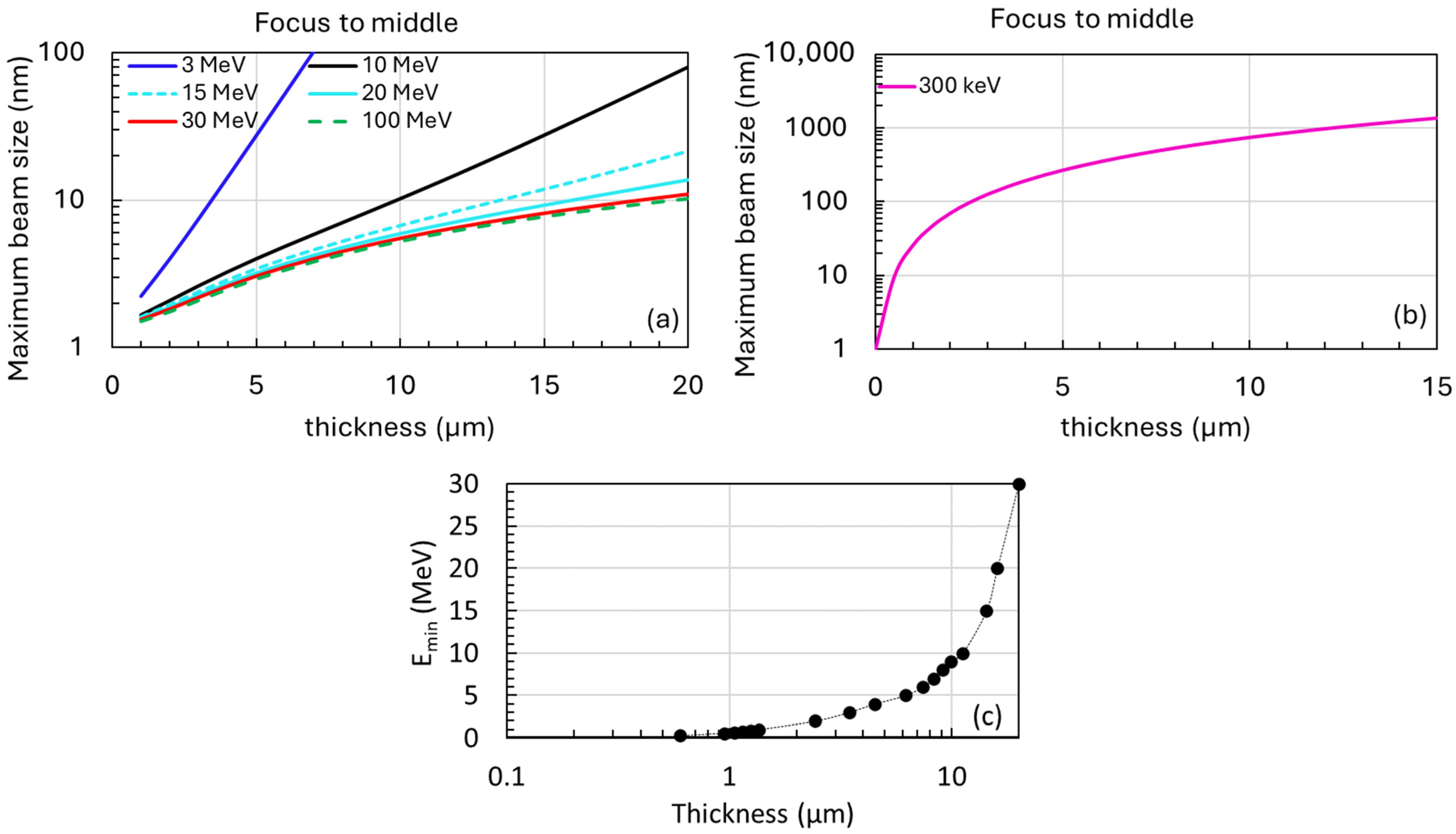
- Positions: The detector will be positioned at 0.2 m, 0.5 m, and 1.5 m from the sample exit for several MeV or higher energy levels (Figure 5a).
- Optimization: These positions were chosen based on simulations and previous studies to achieve optimal linear fits for accurate measurements of beam divergence and size.
- Constraints:
- ○
- Minimum distance (Zdet,min): Ensures that the beam size on the detector is sufficiently large for reliable measurements, considering pixel size and detector array dimensions.
- ○
- Maximum distance (Zdet,max): Prevents the beam from becoming too large to measure accurately.
2.3.4. Detector Performance Simulation
- Placing the detector closer than 0.2 m from the sample exit does not improve the precision of divergence measurements in high-energy cases (1–10 MeV).
- The selected positions at 0.2 m, 0.5 m, and 1.5 m offer optimal conditions for accurate measurements of beam divergence and size. However, if feasible, positioning the detector closer to the sample exit could further enhance the precision of beam size measurements.
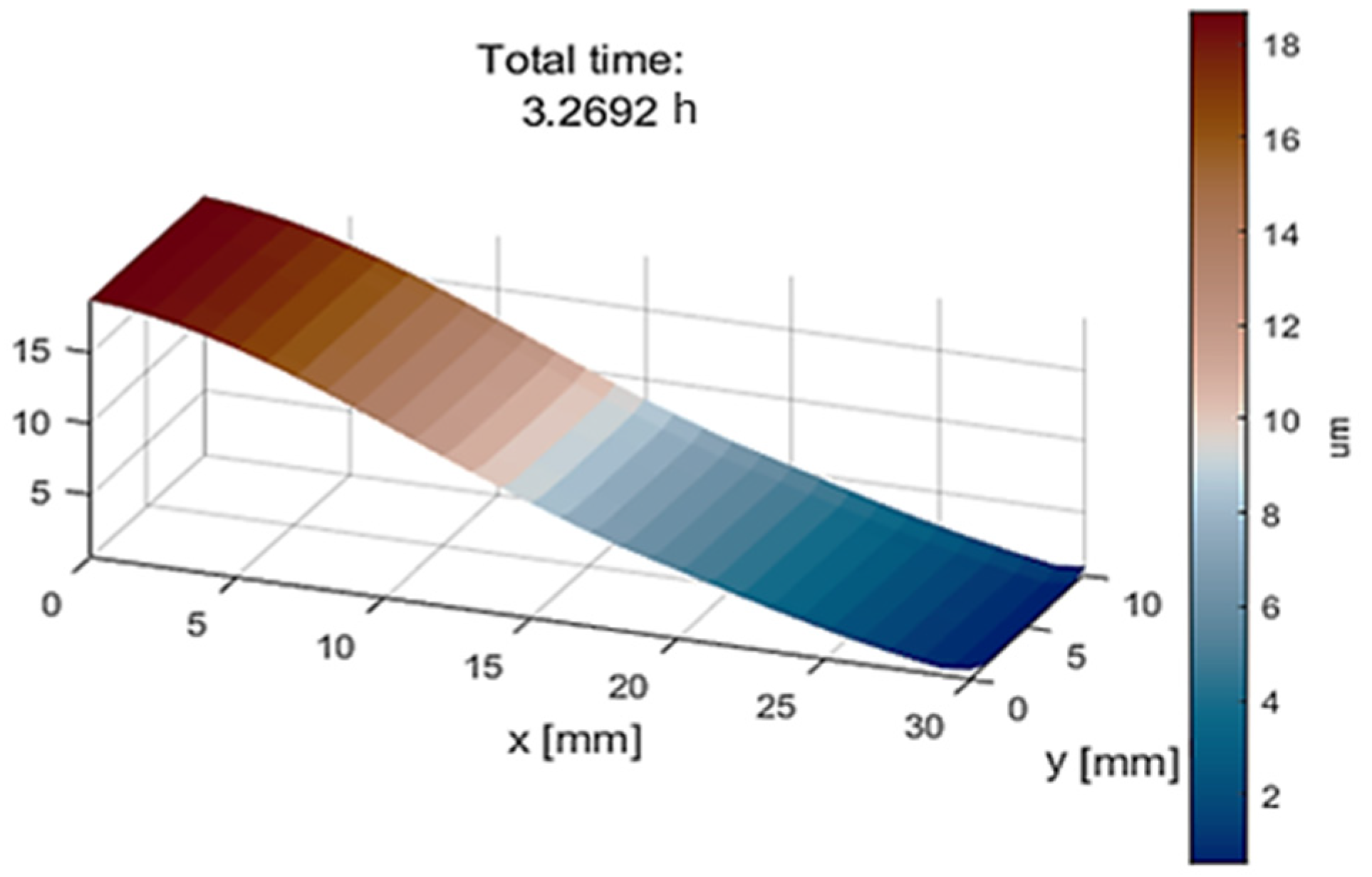
2.3.5. Numerical Assessment of Sample Fabrication
- The process begins with the silicon substrate.
- Achieving the desired slope of 0.67 μm/mm in the x-direction requires approximately 3.3 h, as illustrated in Figure 7.
2.4. Summary of Key Issues
3. Conclusions
- How do electron interactions with biological samples and microchip materials vary with beam energy, particularly concerning angular broadening? The standardized methodology will facilitate the precise determination of these critical angles.
- How does altering the electron bunch structure through the drive laser system affect radiation damage in biological samples, considering variation in bunch structure, energy, and intensity (see Figure A4 in the Appendix A.4)?
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Beam Energy Influence on TEM Resolution

Appendix A.2. Beam Energy Influence on Penetration Depth
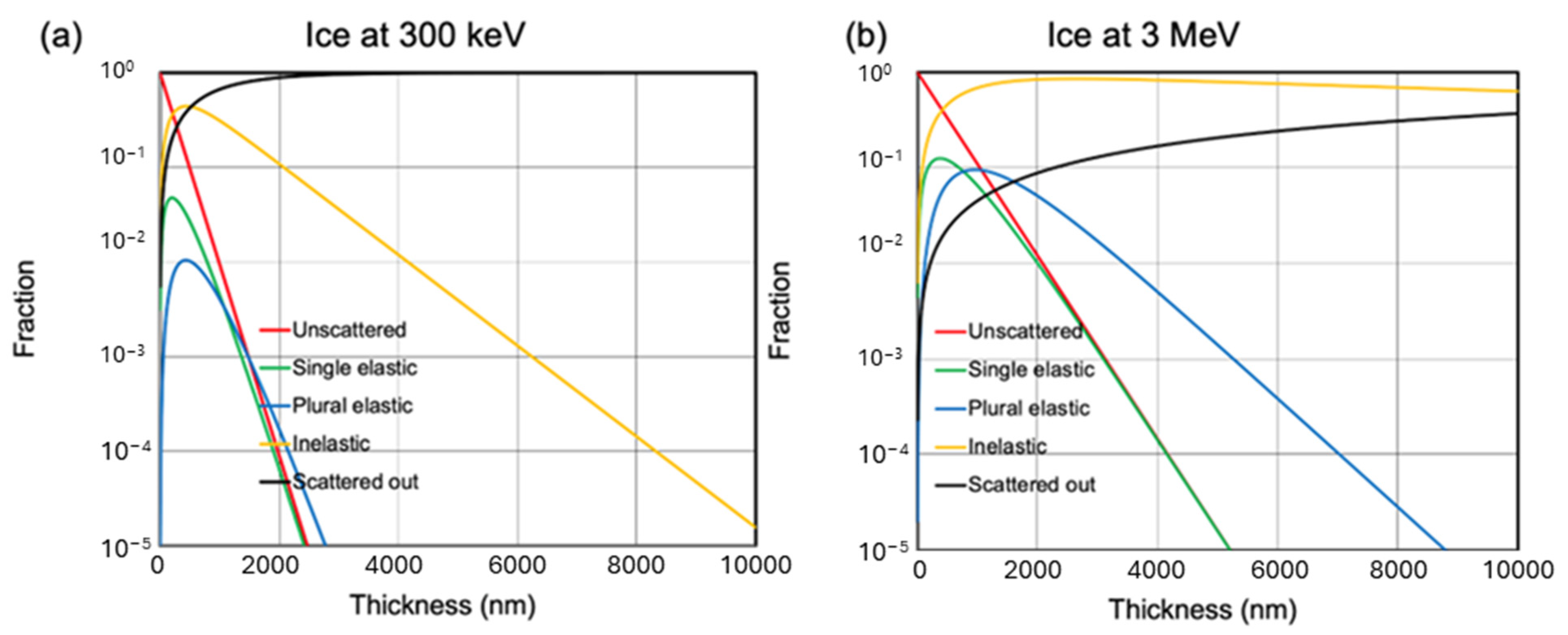
Appendix A.3. Validating MC Tool with Predictive Power

Appendix A.4. Study Radiation Damage

References
- Wang, N.S. Cell Fractionation Based on Density Gradient. 2023. Available online: https://user.eng.umd.edu/~nsw/ench485/lab10.htm (accessed on 13 February 2024).
- Yang, X.; Wang, L.; Maxson, J.; Bartnik, A.C.; Kaemingk, M.; Wan, W.; Cultrera, L.; Wu, L.; Smaluk, V.; Shaftan, T.; et al. Towards Construction of a Novel Nanometer-Resolution MeV-STEM for Imaging Thick Frozen Biological Samples. Photonics 2024, 11, 252. [Google Scholar] [CrossRef]
- Weiner, E.; Pinskey, J.M.; Nicastro, D.; Otegui, M.S. Electron microscopy for imaging organelles in plants and algae. Plant Physiol. 2022, 188, 713–725. [Google Scholar] [CrossRef]
- Böhning, J.; Bharat, T.A.M. Towards high-throughput in situ structural biology using electron cryotomography. Prog. Biophys. Mol. Biol. 2021, 160, 97–103. [Google Scholar] [CrossRef]
- Oikonomou, C.M.; Jensen, G.J. Cellular Electron Cryotomography: Toward Structural Biology In Situ. Annu. Rev. Biochem. 2017, 86, 873–896. [Google Scholar] [CrossRef]
- Otegui, M.S.; Pennington, J.G. Electron tomography in plant cell biology. Microscopy 2019, 68, 69–79. [Google Scholar] [CrossRef]
- Yang, X.; Wang, L.; Smaluk, V.; Shaftan, T. Optimize Electron Beam Energy toward In Situ Imaging of Thick Frozen Bio-Samples with Nanometer Resolution Using MeV-STEM. Nanomaterials 2024, 14, 803. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.G.; Shimoni, E.; Elbaum, M.; Houben, L. STEM tomography in biology. In Cellular Imaging: Electron Tomography and Related Techniques; Hanssen, E., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 33–60. [Google Scholar]
- Tanaka, N. Electron Nano-Imaging, 1st ed.; Springer: Tokyo, Japan, 2017. [Google Scholar]
- Du, M.; Jacobsen, C. Relative merits and limiting factors for x-ray and electron microscopy of thick, hydrated organic materials. Ultramicroscopy 2018, 184, 293–309. [Google Scholar] [CrossRef]
- Photoelectron Generated Amplified Spontaneous Radiation Source (PEGASUS). Available online: http://pbpl.physics.ucla.edu/pages/pegasus.html (accessed on 13 February 2024).
- Li, R.K.; Musumeci, P. Single-Shot MeV Transmission Electron Microscopy with Picosecond Temporal Resolution. Phys. Rev. Appl. 2014, 2, 024003. [Google Scholar] [CrossRef]
- Cesar, D.; Maxson, J.; Musumeci, P.; Sun, Y.; Harrison, J.; Frigola, P.; O’Shea, F.H.; To, H.; Alesini, D.; Li, R.K. Demonstration of Single-shot Picosecond Time-resolved MeV Electron Imaging Using a Compact Permanent Magnet Quadrupole Based Lens. Phys. Rev. Lett. 2016, 117, 024801. [Google Scholar] [CrossRef]
- Egerton, R.F. Choice of operating voltage for a transmission electron microscope. Ultramicroscopy 2014, 145, 85–93. [Google Scholar] [CrossRef]
- Raguin, E.; Weinkamer, R.; Schmitt, C.; Curcuraci, L.; Fratzl, P. Logistics of Bone Mineralization in the Chick Embryo Studied by 3D Cryo FIB-SEM Imaging. Adv. Sci. 2023, 10, e2301231. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yin, W.G.; Wu, L.; Zhu, P.; Konstantinova, T.; Tao, J.; Yang, J.; Cheong, S.W.; Carbone, F.; Misewich, J.A.; et al. Dichotomy in ultrafast atomic dynamics as direct evidence of polaron formation in manganites. npj Quantum Mater. 2016, 1, 16026. [Google Scholar] [CrossRef]
- Egerton, R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope, 3rd ed.; Springer: New York, NY, USA, 2011; ISBN 978-1-4419-9582-7. [Google Scholar] [CrossRef]
- Wolf, S.G.; Houben, L.; Elbaum, M. Cryo-scanning transmission electron tomography of vitrified cells. Nat. Methods 2014, 11, 423–428. [Google Scholar] [CrossRef] [PubMed]
- Durchschlag, H. Thermodynamic Data for Biochemistry and Biotechnology; Hinz, H.-J., Ed.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 45–128. [Google Scholar]
- Howard, J. Mechanics of Motor Proteins and the Cytoskeleton; Sinauer Associates, Inc.: Sunderland, MA, USA, 2001; Volume 30. [Google Scholar]
- Rickwood, D.; Chambers, J.A.A.; Barat, M. Isolation and preliminary characterisation of DNA-protein complexes from the mitochondria of Saccharomyces cerevisiae. Exp. Cell Res. 1981, 133, 1–13. [Google Scholar] [CrossRef]
- Baldwin, W.W.; Myer, R.; Powell, N.; Anderson, E.; Koch, A.L. Buoyant density of Escherichia coli is determined solely by the osmolarity of the culture medium. Arch Microbiol 1995, 164, 155–157. [Google Scholar] [CrossRef]
- Loferer-Krössbacher, M.; Klima, J.; Psenner, R. Determination of bacterial cell dry mass by transmission electron microscopy and densitometric image analysis. Appl Env. Microbiol 1998, 64, 688–694. [Google Scholar] [CrossRef]
- Langmore, J.P.; Smith, M.F. Quantitative energy-filtered electron-microscopy of biological molecules in ice. Ultramicroscopy 1992, 46, 349–373. [Google Scholar] [CrossRef]
- Jacobsen, C.; Medenwaldt, R.; Williams, S. X-Ray Microscopy and Spectromicroscopy: Status Report from the Fifth International Conference, Würzburg, 19–23 August 1996; Thieme, J., Schmahl, G., Rudolph, D., Umbach, E., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 197–206. [Google Scholar]
- Lee, H.; Cultrera, L.; Bazarov, I. Intrinsic emittance reduction in transmission mode photocathodes. Appl. Phys. Lett. 2016, 108, 124105. [Google Scholar] [CrossRef]
- Lee, H.; Liu, X.; Cultrera, L.; Dunham, B.; Kostroun, V.O.; Bazarov, I.V. A cryogenically cooled high voltage DC photoemission electron source. Rev. Sci. Instrum. 2018, 89, 083303. [Google Scholar] [CrossRef]
- Wan, W.; Chen, F.; Zhu, Y. Design of compact ultrafast microscopes for single- and multi-shot imaging with MeV electrons. Ultramicroscopy 2018, 194, 143–153. [Google Scholar] [CrossRef]
- Wang, L.; Yang, X. Monte Carlo Simulation of Electron Interactions in an MeV-STEM for Thick Frozen Biological Sample Imaging. Appl. Sci. 2024, 14, 1888. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.A.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Geant4 Documentation. Available online: https://geant4.web.cern.ch/docs/ (accessed on 13 February 2024).
- Reimer, L.; Kohl, H. Transmission Electron Microscopy, 5th ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Capua-Shenkar, J.; Varsano, N.; Itzhak, N.-R.; Kaplan-Ashiri, I.; Rechav, K.; Jin, X.; Niimi, M.; Fan, J.; Kruth, H.S.; Addadi, L. Examining atherosclerotic lesions in three dimensions at the nanometer scale with cryo-FIB-SEM. Proc. Natl. Acad. Sci. USA 2022, 119, e2205475119. [Google Scholar] [CrossRef]
- Schertel, A.; Snaidero, N.; Han, H.-M.; Ruhwedel, T.; Laue, M.; Grabenbauer, M.; Möbius, W. Cryo FIB-SEM: Volume imaging of cellular ultrastructure in native frozen specimens. J. Struct. Biol. 2013, 184, 355–360. [Google Scholar] [CrossRef]
- Spehner, D.; Steyer, A.M.; Bertinetti, L.; Orlov, I.; Benoit, L.; Pernet-Gallay, K.; Schertel, A.; Schultz, P. Cryo-FIB-SEM as a promising tool for localizing proteins in 3D. J. Struct. Biol. 2020, 211, 107528. [Google Scholar] [CrossRef]
- Vidavsky, N.; Akiva, A.; Kaplan-Ashiri, I.; Rechav, K.; Addadi, L.; Weiner, S.; Schertel, A. Cryo-FIB-SEM serial milling and block face imaging: Large volume structural analysis of biological tissues preserved close to their native state. J. Struct. Biol. 2016, 196, 487–495. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhu, Y.; Vogt, T.; Su, H.; Davenport, J.W.; Tafto, J. Valence-electron distribution in MgB2 by accurate diffraction measurements and first-principle calculations. Phys. Rev. B 2004, 69, 064501. [Google Scholar] [CrossRef]
- Hayashida, M.; Malac, M. High-Energy Electron Scattering in Thick Samples Evaluated by Bright-Field Transmission Electron Microscopy, Energy-Filtering Transmission Electron Microscopy, and Electron Tomography. Microsc. Microanal. 2022, 28, 659–671. [Google Scholar] [CrossRef]
- VandenBussche, E.J.; Flannigan, D.J. Reducing Radiation Damage in Soft Matter with Femtosecond-Timed Single-Electron Packets. Nano Lett. 2019, 19, 6687–6694. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N. Electron beam damage in oxides: A review. Rep. Prog. Phys. 2016, 79, 016501. [Google Scholar] [CrossRef] [PubMed]
- Karuppasamy, M.; Nejadasl, F.K.; Vulovic, M.; Koster, A.J.; Ravelli, R.B.G. Radiation damage in single-particle cryo-electron microscopy: Effects of dose and dose rate. J. Synchrotron Radiat. 2011, 18, 398–412. [Google Scholar] [CrossRef] [PubMed]
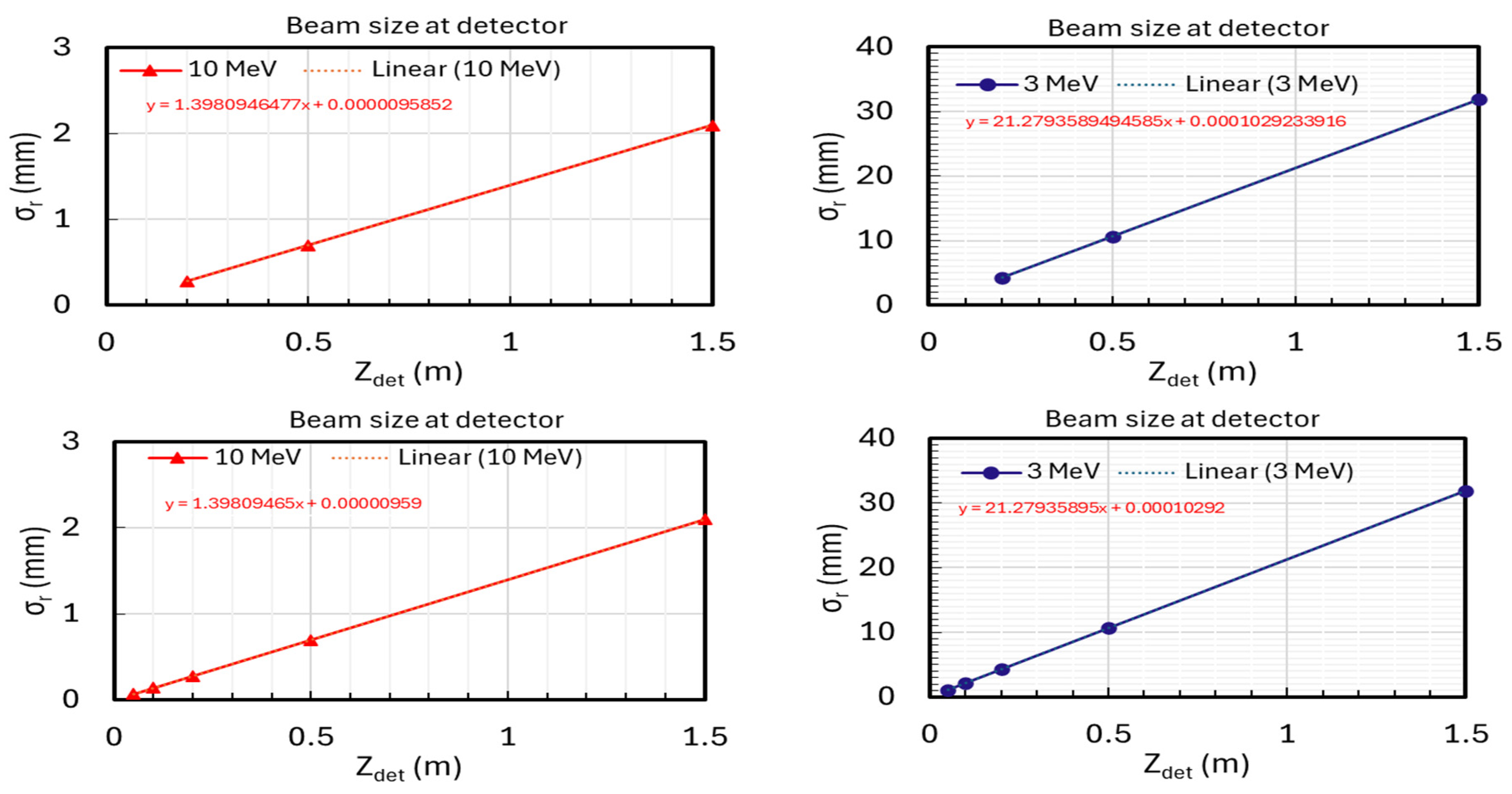
| E | Divergent Angle | Beam Size | E | Divergent Angle | Beam Size | |
|---|---|---|---|---|---|---|
| mrad | nm | mrad | nm | |||
| MC-simulation | 10 MeV | 1.397794 | 10.847086 | 3 MeV | 21.073517 | 118.607333 |
| Fitting detector data | 1.398095 | 9.585200 | 21.279359 | 102.923392 | ||
| Measurement error (%) | 0.021504 | 11.633414 | 0.976779 | 13.223416 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Wang, L.; Smaluk, V.; Shaftan, T.; Wang, T.; Bouet, N.; D’Amen, G.; Wan, W.; Musumeci, P. Simulation Study of High-Precision Characterization of MeV Electron Interactions for Advanced Nano-Imaging of Thick Biological Samples and Microchips. Nanomaterials 2024, 14, 1797. https://doi.org/10.3390/nano14221797
Yang X, Wang L, Smaluk V, Shaftan T, Wang T, Bouet N, D’Amen G, Wan W, Musumeci P. Simulation Study of High-Precision Characterization of MeV Electron Interactions for Advanced Nano-Imaging of Thick Biological Samples and Microchips. Nanomaterials. 2024; 14(22):1797. https://doi.org/10.3390/nano14221797
Chicago/Turabian StyleYang, Xi, Liguo Wang, Victor Smaluk, Timur Shaftan, Tianyi Wang, Nathalie Bouet, Gabriele D’Amen, Weishi Wan, and Pietro Musumeci. 2024. "Simulation Study of High-Precision Characterization of MeV Electron Interactions for Advanced Nano-Imaging of Thick Biological Samples and Microchips" Nanomaterials 14, no. 22: 1797. https://doi.org/10.3390/nano14221797
APA StyleYang, X., Wang, L., Smaluk, V., Shaftan, T., Wang, T., Bouet, N., D’Amen, G., Wan, W., & Musumeci, P. (2024). Simulation Study of High-Precision Characterization of MeV Electron Interactions for Advanced Nano-Imaging of Thick Biological Samples and Microchips. Nanomaterials, 14(22), 1797. https://doi.org/10.3390/nano14221797







