Nanograting p-n Junctions with Enhanced Charge Confinement
Abstract
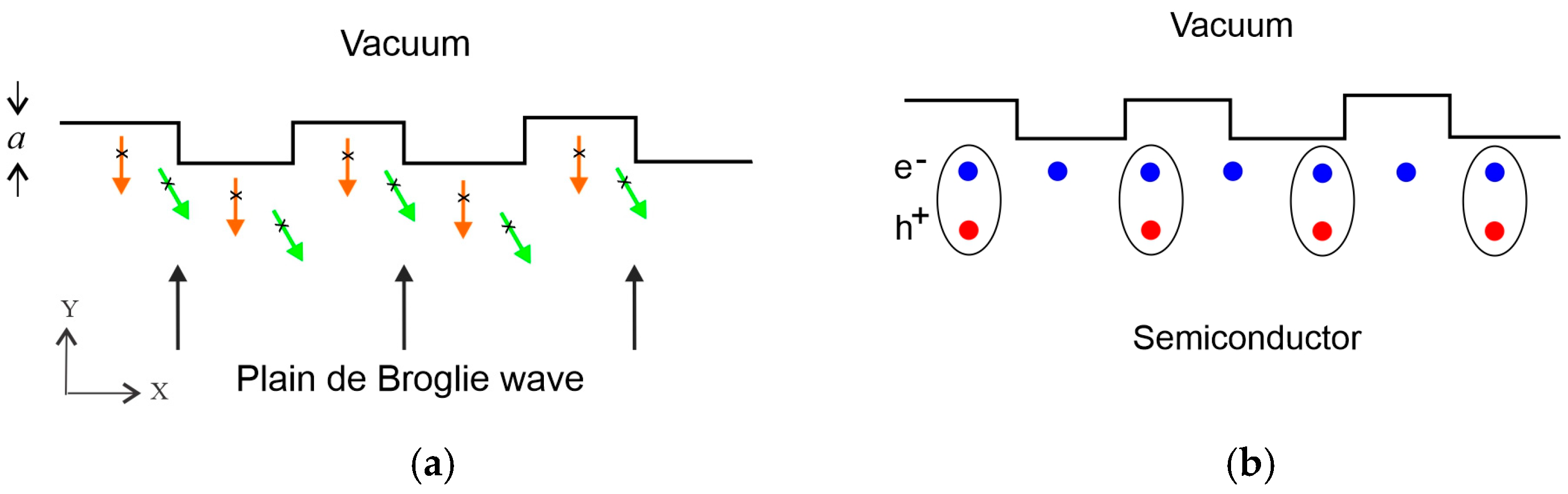
:1. Introduction
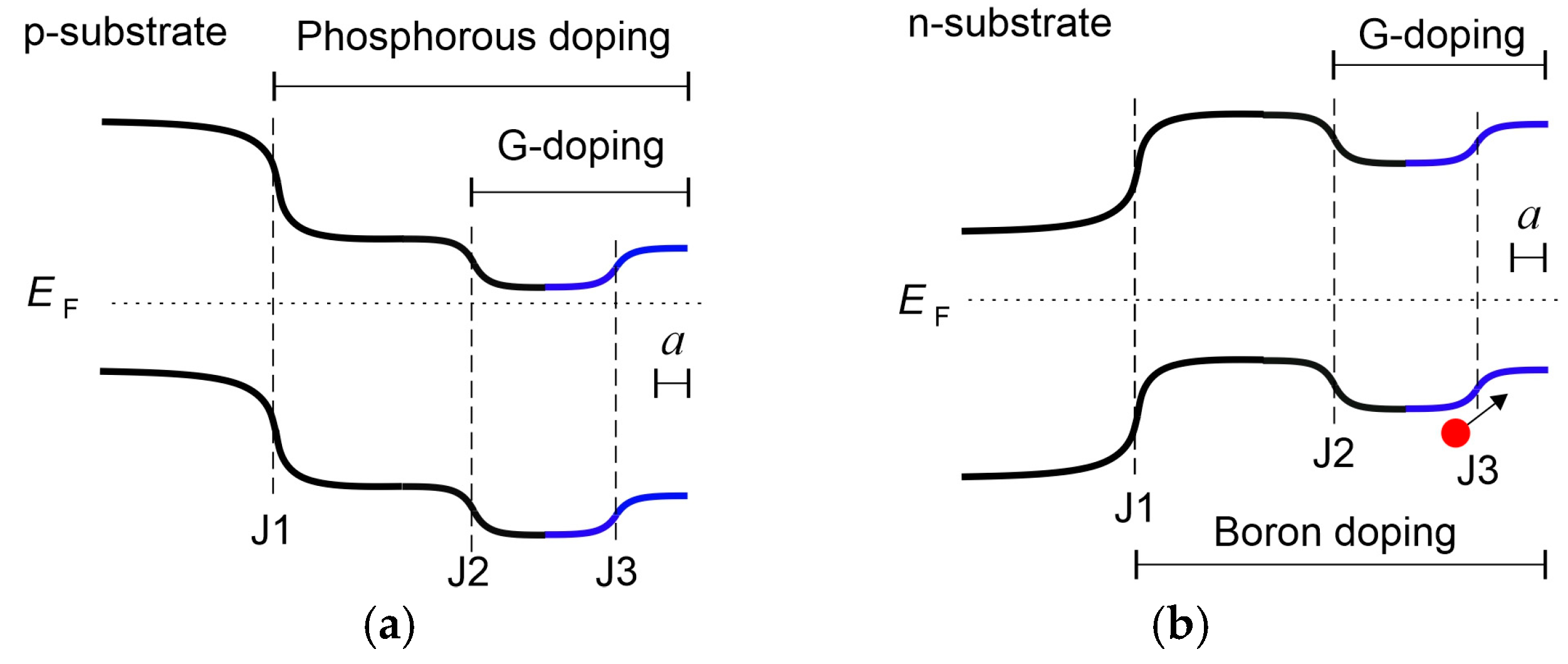
2. Materials and Methods
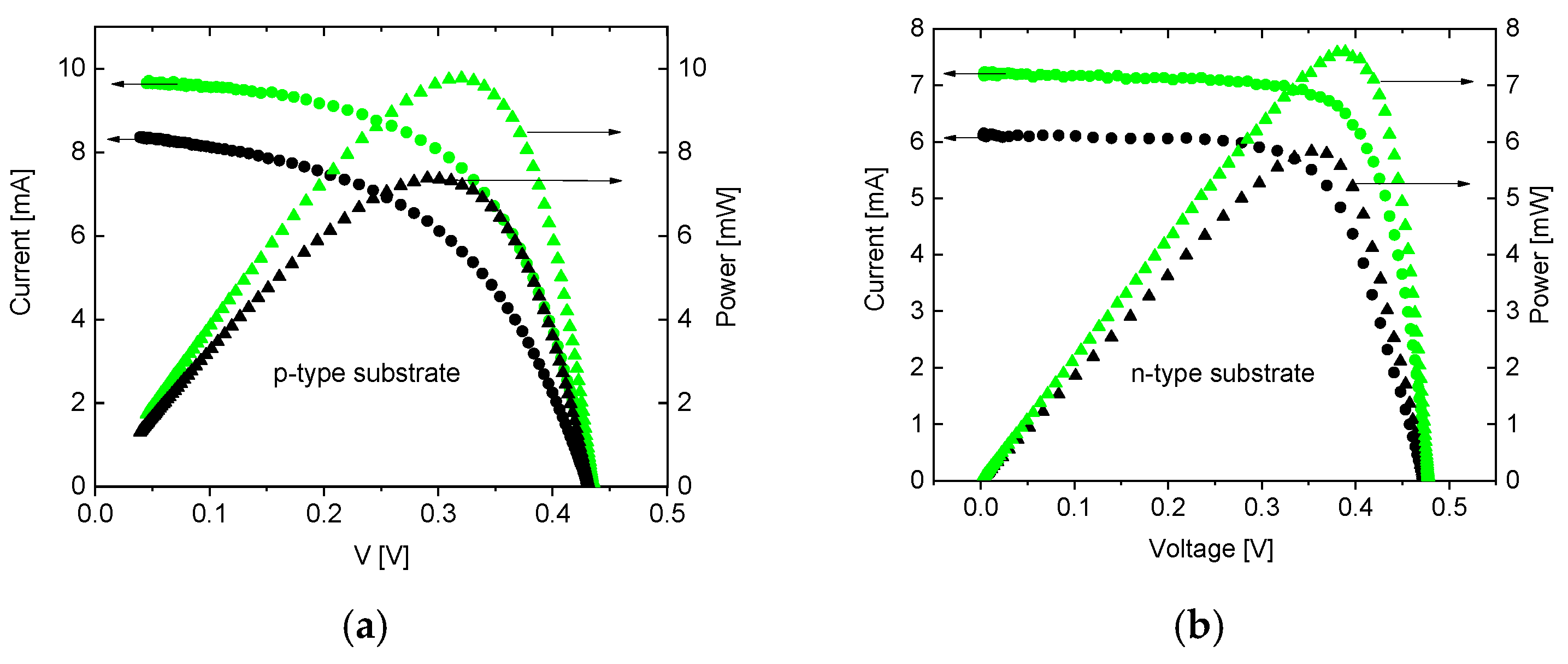
3. Results
3.1. Solar Cell-like p-n Junctionours
3.2. Photoluminescence from Nanograting Layers
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, R.; Cao, L.; Liu, D.; Wang, L.; Saeed, S.; Wang, Z. Laser Interference Lithography—A Method for the Fabrication of Controlled Periodic Structures. Nanomaterials 2023, 13, 1818. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Ma, Y.; Park, J.; Shin, B. Fabrication of uniform diffraction gratings using laser interference lithography for simultaneous measurement of refractive index. Jpn. J. Appl. Phys. 2021, 60, 105001. [Google Scholar] [CrossRef]
- Buhl, J.; Yoo, D.; Köpke, M.; Gerken, M. Two-Dimensional Nanograting Fabrication by Multistep Nanoimprint Lithography and Ion Beam Etching. Nanomanufacturing 2021, 1, 39–48. [Google Scholar] [CrossRef]
- Bashirpour, M.; Cui, W.; Gamouras, A.; Ménard, J.-M. Scalable Fabrication of Nanogratings on GaP for Efficient Diffraction of Near-Infrared Pulses and Enhanced Terahertz Generation by Optical Rectification. Crystals 2022, 12, 684. [Google Scholar] [CrossRef]
- Tavkhelidze, A.; Jangidze, L.; Mebonia, M.; Piotrowski, K.; Więckowski, J.; Taliashvili, Z.; Skhiladze, G.; Nadaraia, L. Geometry-induced quantum effects in periodic nanostructures. Phys. Status Solidi (a) 2017, 214, 1700334. [Google Scholar] [CrossRef]
- Liang, W.; Meng, S.; Zeng, Q.; Han, X. Intrinsic Connections between Thermionic Emission Cooling Effect and Emission Characteristics of W-La2O3 Cathodes at High Temperatures. Mater. Lett. 2022, 308, 131172. [Google Scholar] [CrossRef]
- Tavkhelidze, A. Geometry-induced electron doping in periodic semiconductor nanostructures. Phys. E 2014, 60, 4–10. [Google Scholar] [CrossRef]
- Chae, M.; Kim, S.; Han, Y.; Choi, D.; Choi, Y.; Kim, H.; Joo, M.K. High Temperature Carrier Scattering Mechanisms in Multilayer ReS2 Field-Effect Transistors. Appl. Sci. Converg. Technol. 2022, 31, 85–88. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, Y.; Miura, A.; Miyazaki, K.; Horita, Z.; Iikubo, S. Improving Thermoelectric Properties of Bi2Te3 by Straining under High Pressure: Experiment and DFT Calculation. Scr. Mater. 2024, 243, 115991. [Google Scholar] [CrossRef]
- Mamedov, N.; Tavkhelidze, A.; Bayramov, A.; Akhmedova, K.; Aliyeva, Y.; Eyyubov, G.; Jangidze, L.; Skhiladze, G. Spectroscopic planar diffraction ellipsometry of Si-based multilayer structure with subwavelength grating. Phys. Status Solidi C 2017, 14, 1700092. [Google Scholar] [CrossRef]
- Singh, A.K.; Kumar, J. Nano-gap planar metal electrodes: Fabrication and I–V characteristics. Nano Express 2021, 2, 020024. [Google Scholar] [CrossRef]
- Bayramov, A.; Alizade, E.; Mammadov, S.; Tavkhelidze, A.; Mamedov, N.; Aliyeva, Y.; Ahmedova, K.; Asadullayeva, S.; Jangidze, L.; Skhiladze, G. Optical properties of surface grated Si-based multilayer structure. J. Vac. Sci. Technol. B 2019, 37, 061807. [Google Scholar] [CrossRef]
- Du, L.; Zhao, Y.; Wu, L.; Hu, X.; Yao, L.; Wang, Y.; Bai, X.; Dai, Y.; Qiao, J.; Uddin, G.; et al. Giant anisotropic photonics in the 1D van der Waals semiconductor fibrous red phosphorus. Nat. Commun. 2021, 12, 4822. [Google Scholar] [CrossRef]
- Yeo, H.-S.; Lee, K.; Sim, Y.C.; Park, S.-H.; Cho, Y.-H. Strong and robust polarization anisotropy of site- and size-controlled single InGaN/GaN quantum wires. Sci. Rep. 2020, 10, 15371. [Google Scholar] [CrossRef]
- Fang, Z.; Zhao, Y.; Shao, J. Femtosecond Laser-Induced Periodic Surface Structure on Fused Silica Surface. Optik 2016, 127, 1171–1175. [Google Scholar] [CrossRef]
- Pérez, M.; Ramos, E.; de la Mora, M.; Santana, G.; Dutt, A. Absorption and Emission of Porous Silicon Based on Quantum Dots Models by TD-DFT: Experimental and Theoretical Approach. Mater. Lett. 2021, 302, 130411. [Google Scholar] [CrossRef]
- Tavkhelidze, A.; Bayramov, A.; Aliyeva, Y.; Jangidze, L.; Skhiladze, G.; Asadullayeva, S.; Alekperov, O.; Mamedov, N. Optical and electronic properties of periodic Si nanostructures. Phys. Status Solidi C 2017, 14, 1700093. [Google Scholar] [CrossRef]
- Taliashvili, Z.; Łusakowska, E.; Chusnutdinow, S.; Tavkhelidze, A.; Jangidze, L.; Sikharulidze, S.; Gorji, N.E.; Chubinidze, Z.; Melkadze, R. Optical Properties of Periodically and Aperiodically Nanostructured p-n Junctions. Opt. Quantum Electron. 2023, 55, 1028. [Google Scholar] [CrossRef]
- Mastellone, M.; Pace, M.L.; Curcio, M.; Caggiano, N.; De Bonis, A.; Teghil, R.; Dolce, P.; Mollica, D.; Orlando, S.; Santagata, A.; et al. LIPSS Applied to Wide Bandgap Semiconductors and Dielectrics: Assessment and Future Perspectives. Materials 2022, 15, 1378. [Google Scholar] [CrossRef]
- Wu, B.; Zheng, H.; Li, S.; Ding, J.; Zeng, Y.-J.; Liu, Z.; Liu, Y. Observation of Moiré Excitons in the Twisted WS2/WS2 Homostructure. Nanoscale 2022, 14, 12447–12454. [Google Scholar] [CrossRef]
- Rodríguez, Á.; Varillas, J.; Haider, G.; Kalbáč, M.; Frank, O. Complex Strain Scapes in Reconstructed Transition-Metal Dichalcogenide Moiré Superlattices. ACS Nano 2023, 17, 7787–7796. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zeng, C.; Yu, J.; Zhong, J.; Li, B.; Zhang, Z.; Liu, Z.; Wang, Z.M.; Pan, A.; Duan, X. Moiré Superlattices and Related Moiré Excitons in Twisted van der Waals Heterostructures. Chem. Soc. Rev. 2021, 50, 6401–6422. [Google Scholar] [CrossRef] [PubMed]
- Tran, K.; Moody, G.; Wu, F.; Lu, X.; Choi, J.; Kim, K.; Rai, A.; Sanchez, D.A.; Quan, J.; Singh, A.; et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 2019, 567, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Wu, B.; Li, S.; He, J.; Chen, K.; Liu, Z.; Liu, Y. Evidence for interlayer coupling and moiré excitons in twisted WS2/WS2 homostructure superlattices. Nano Res. 2022, 16, 3429–3434. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, B.; Li, S.; Ding, J.; He, J.; Liu, Z.; Wang, C.-T.; Wang, J.-T.; Pan, A.; Liu, Y. Localization-enhanced moiré exciton in twisted transition metal dichalcogenide heterotrilayer superlattices. Light Sci. Appl. 2023, 12, 117. [Google Scholar] [CrossRef]
- Adler, E.R.; Le, T.D.M.; Boulares, I.; Boyd, R.; He, Y.; Rhodes, D.; Van Keuren, E.; Barbara, P.; Najmaei, S. Observation of Multi-Phonon Emission in Monolayer WS2 on Various Substrates. Nanomaterials 2024, 14, 37. [Google Scholar] [CrossRef]
- Wu, S.; Tomić, S. Exciton States and Oscillator Strengths in a Cylindrical Quantum Wire with Finite Potential under Traverse Electric Field. J. Appl. Phys. 2012, 112, 033715. [Google Scholar] [CrossRef]
- Blancon, J.-C.; Stier, A.V.; Tsai, H.; Nie, W.; Stoumpos, C.C.; Traoré, B.; Pedesseau, L.; Kepenekian, M.; Katsutani, F.; Noe, G.T.; et al. Scaling law for excitons in 2D perovskite quantum wells. Nat. Commun. 2018, 9, 2254. [Google Scholar] [CrossRef]
- Kakulia, D.; Tavkhelidze, A.; Gogoberidze, V.; Mebonia, M. Density of quantum states in quasi-1D layers. Phys. E 2016, 78, 49–55. [Google Scholar] [CrossRef]
- Tavkhelidze, A.; Bibilashvili, A.; Jangidze, L.; Gorji, N.E. Fermi-Level Tuning of G-Doped Layers. Nanomaterials 2021, 11, 505. [Google Scholar] [CrossRef]
- Raja, A.; Waldecker, L.; Zipfel, J.; Cho, Y.; Brem, S.; Ziegler, J.D.; Kulig, M.; Taniguchi, T.; Watanabe, K.; Malic, E.; et al. Dielectric disorder in two-dimensional materials. Nat. Nanotechnol. 2019, 14, 832–837. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, C.-X.; Rao, J.-R.; Cao, L.; Ma, G.-Z.; Gao, M.; Chen, X.-C.; Shi, D. Spectroscopic Indications of Room-Temperature Electron-Hole Droplets in Optically Excited CH3NH3PbBr3 Single Crystals. Cell Rep. Phys. Sci. 2022, 3, 100896. [Google Scholar] [CrossRef]
- Tavkhelidze, A.; Jangidze, L.; Taliashvili, Z.; Gorji, N.E. G-Doping-Based Metal-Semiconductor Junction. Coatings 2021, 11, 945. [Google Scholar] [CrossRef]
- Revuelta, S.; Cánovas, E. Exciton formation dynamics at the SiO2/Si interface. Commun. Mater. 2023, 4, 97. [Google Scholar] [CrossRef]
- Saive, R. Light Trapping in Thin Silicon Solar Cells: A Review on Fundamentals and Technologies. Prog. Photovolt. Res. Appl. 2021, 29, 1125–1137. [Google Scholar] [CrossRef]
- Manzoor, S.; Filipič, M.; Onno, A.; Topič, M.; Holman, Z.C. Visualizing Light Trapping within Textured Silicon Solar Cells. J. Appl. Phys. 2020, 127, 063104. [Google Scholar] [CrossRef]
- Gatos, H.C. Crystalline Structure and Surface Reactivity: Atomistic models are unique tools for dealing with the chemical and physical properties of surfaces. Science 1962, 137, 311–322. [Google Scholar] [CrossRef]
- Saba, M.; Cadelano, M.; Marongiu, D.; Chen, F.; Sarritzu, V.; Sestu, N.; Figus, C.; Aresti, M.; Piras, R.G.; Lehmann, A.G.; et al. Correlated Correlated electron-hole plasma in organometal perovskites. Nat. Commun. 2014, 5, 5049. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tavkhelidze, A.; Jangidze, L.; Skhiladze, G.; Sikharulidze, S.; Dzneladze, K.; Kvesitadze, R.; Bibilashvili, A. Nanograting p-n Junctions with Enhanced Charge Confinement. Nanomaterials 2024, 14, 1889. https://doi.org/10.3390/nano14231889
Tavkhelidze A, Jangidze L, Skhiladze G, Sikharulidze S, Dzneladze K, Kvesitadze R, Bibilashvili A. Nanograting p-n Junctions with Enhanced Charge Confinement. Nanomaterials. 2024; 14(23):1889. https://doi.org/10.3390/nano14231889
Chicago/Turabian StyleTavkhelidze, Avtandil, Larisa Jangidze, Givi Skhiladze, Sergo Sikharulidze, Kristine Dzneladze, Rusudan Kvesitadze, and Amiran Bibilashvili. 2024. "Nanograting p-n Junctions with Enhanced Charge Confinement" Nanomaterials 14, no. 23: 1889. https://doi.org/10.3390/nano14231889
APA StyleTavkhelidze, A., Jangidze, L., Skhiladze, G., Sikharulidze, S., Dzneladze, K., Kvesitadze, R., & Bibilashvili, A. (2024). Nanograting p-n Junctions with Enhanced Charge Confinement. Nanomaterials, 14(23), 1889. https://doi.org/10.3390/nano14231889






