Superconductivity in Nb: Impact of Temperature, Dimensionality and Cooper-Pairing
Abstract
:1. Introduction
2. Tight-Binding and the Bogoliubov–de Gennes Method
3. Results
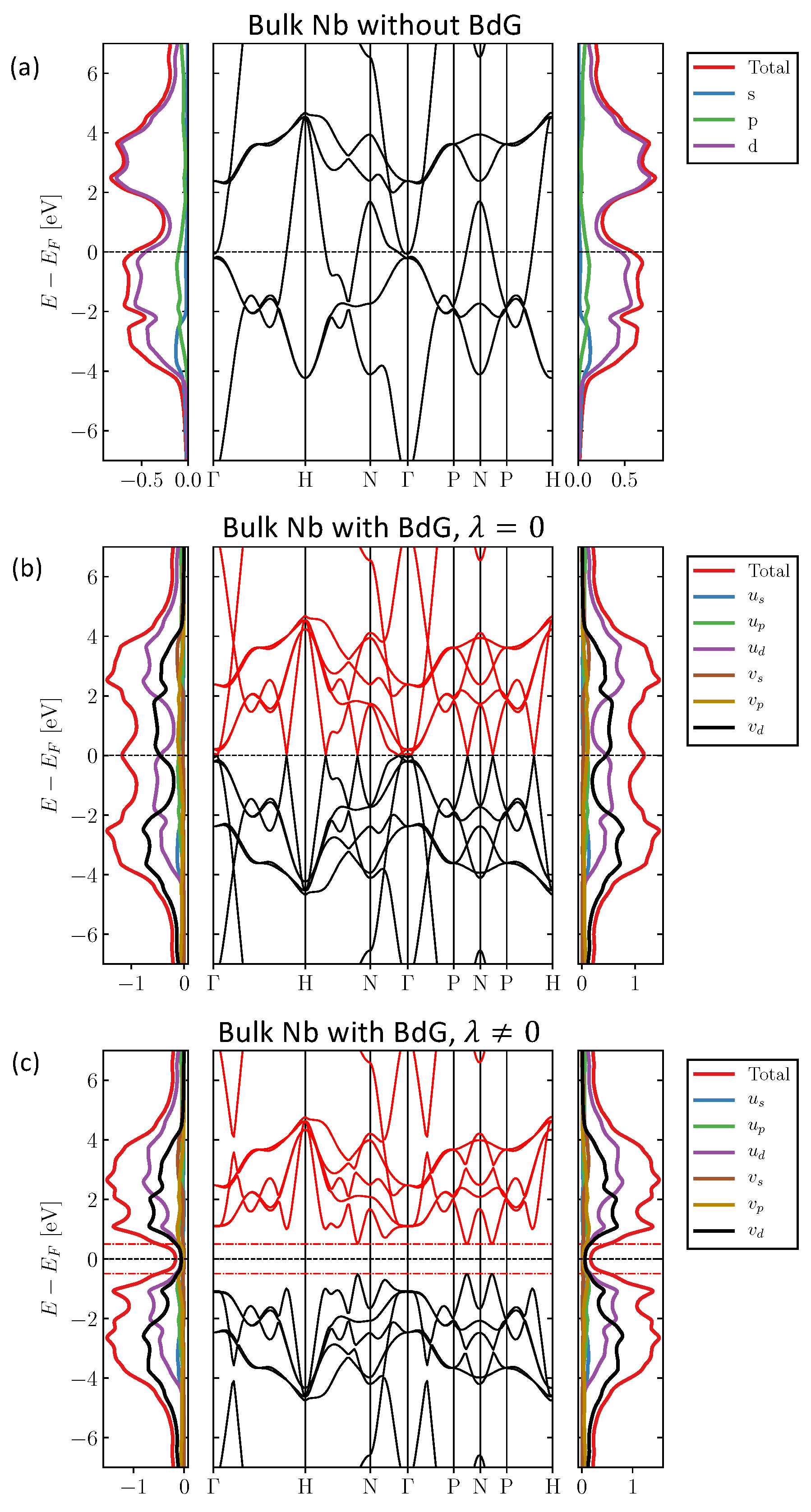
3.1. Bulk Superconducting Nb
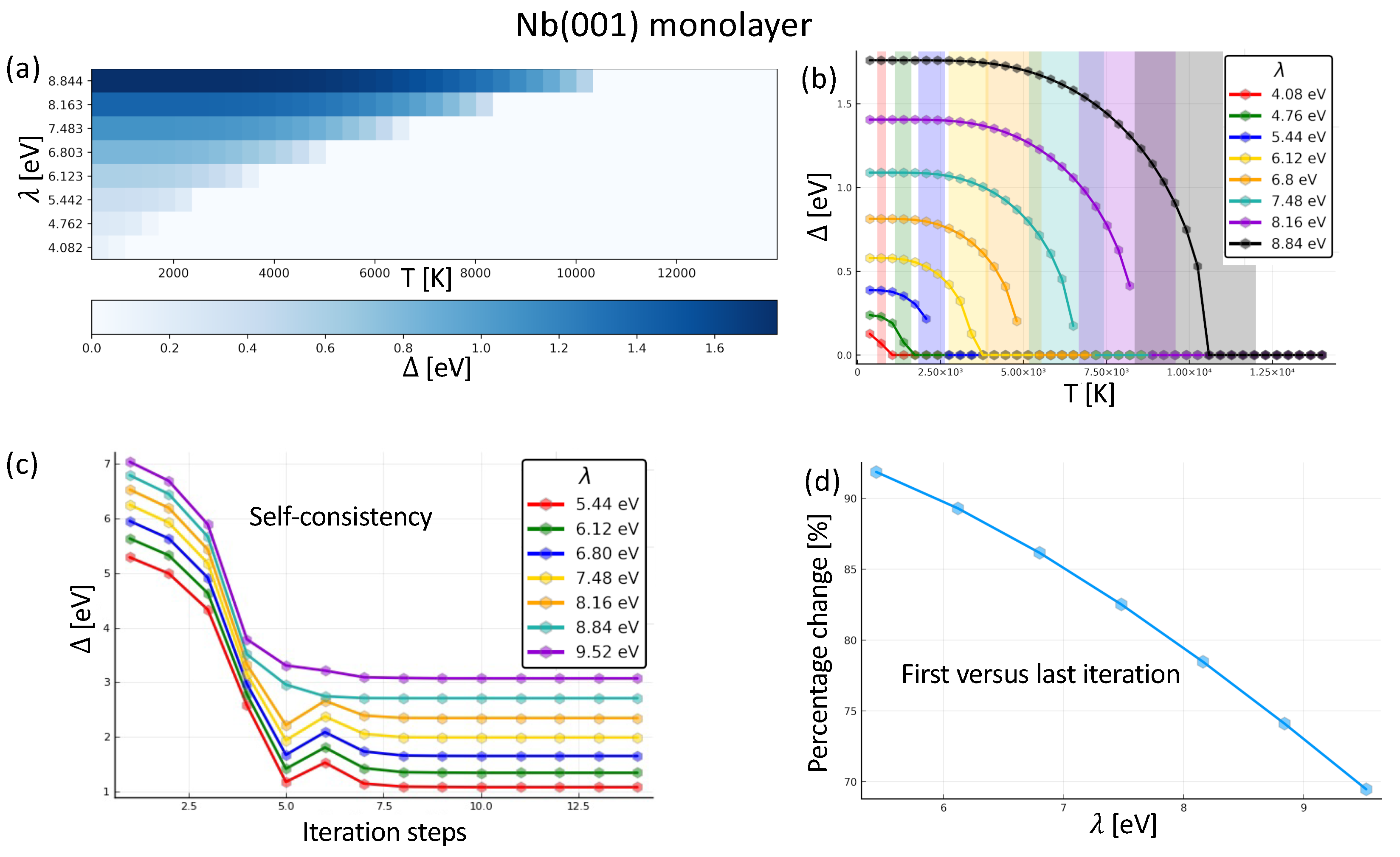
3.2. Superconducting Gap Tuning: Single Bcc (001) Nb Monolayer
3.3. Renormalization after Self-Consistency: Single Bcc (001) Nb Monolayer
3.4. Superconducting Nb (110) Monolayer
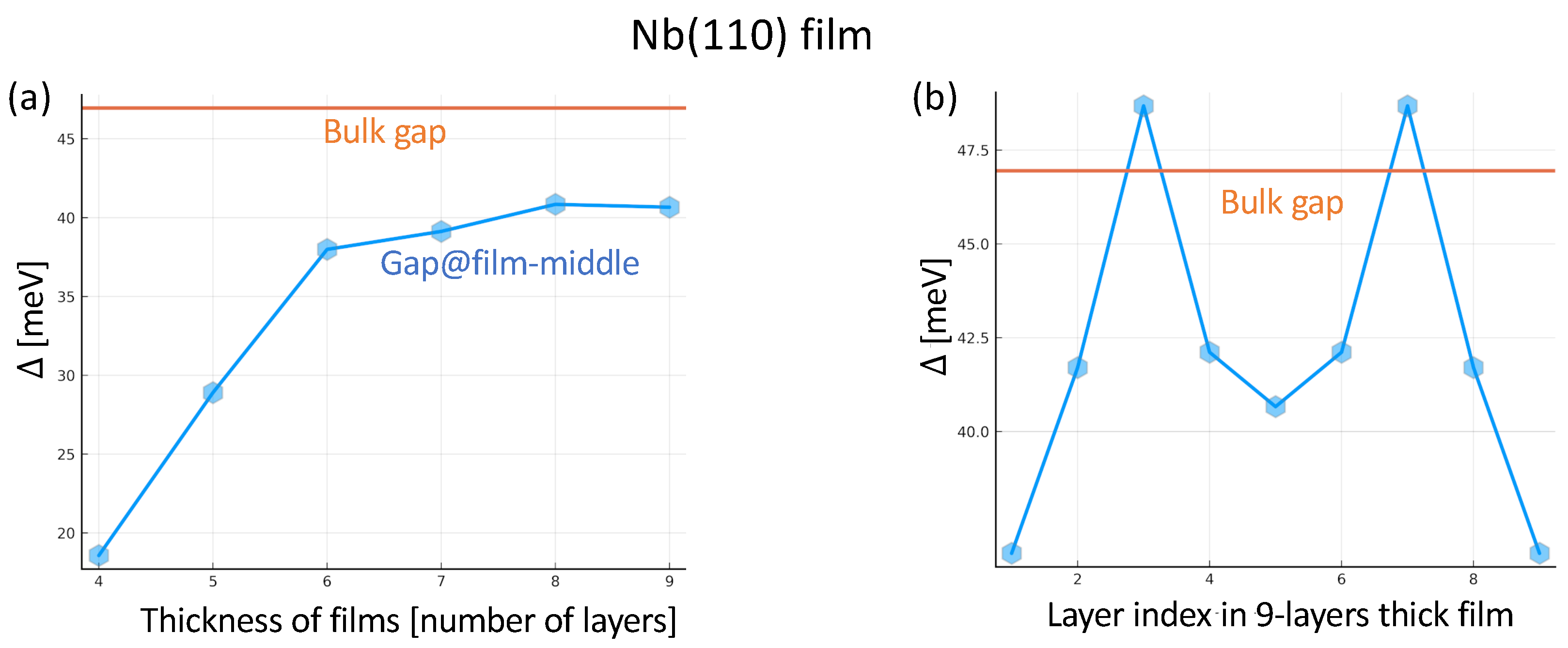
3.5. Superconducting Slab
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lahtinen, V.; Pachos, J.K. A Short Introduction to Topological Quantum Computation. SciPost Phys. 2017, 3, 021. [Google Scholar] [CrossRef]
- Mishra, A.; Simon, P.; Hyart, T.; Trif, M. Yu-Shiba-Rusinov Qubit. PRX Quantum 2021, 2, 040347. [Google Scholar] [CrossRef]
- Pavešić, L.; Žitko, R. Qubit based on spin-singlet Yu-Shiba-Rusinov states. Phys. Rev. B 2022, 105, 075129. [Google Scholar] [CrossRef]
- Linder, J.; Robinson, J.W.A. Superconducting spintronics. Nat. Phys. 2015, 11, 307–315. [Google Scholar] [CrossRef]
- Eschrig, M. Spin-polarized supercurrents for spintronics: A review of current progress. Rep. Prog. Phys. 2015, 78, 104501. [Google Scholar] [CrossRef]
- Buzdin, A.I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 2005, 77, 935–976. [Google Scholar] [CrossRef]
- Bergeret, F.S.; Silaev, M.; Virtanen, P.; Heikkilä, T.T. Colloquium: Nonequilibrium effects in superconductors with a spin-splitting field. Rev. Mod. Phys. 2018, 90, 041001. [Google Scholar] [CrossRef]
- Schneider, L.; Steinbrecher, M.; Rózsa, L.; Bouaziz, J.; Palotás, K.; dos Santos Dias, M.; Lounis, S.; Wiebe, J.; Wiesendanger, R. Magnetism and in-gap states of 3d transition metal atoms on superconducting Re. Npj Quantum Mater. 2019, 4, 42. [Google Scholar] [CrossRef]
- Beenakker, C. Search for Majorana Fermions in Superconductors. Annu. Rev. Condens. Matter Phys. 2013, 4, 113–136. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys.-Uspekhi 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Tanaka, Y.; Yokoyama, T.; Nagaosa, N. Manipulation of the Majorana Fermion, Andreev Reflection, and Josephson Current on Topological Insulators. Phys. Rev. Lett. 2009, 103, 107002. [Google Scholar] [CrossRef] [PubMed]
- Aguado, R.; Kouwenhoven, L.P. Majorana qubits for topological quantum computing. Phys. Today 2020, 73, 44–50. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Microscopic Theory of Superconductivity. Phys. Rev. 1957, 106, 162–164. [Google Scholar] [CrossRef]
- Bogoliubov, N. A New Method in the Theory of Superconductivity. I. J. Exp. Theor. Phys. 1958, 7, 41–46. [Google Scholar] [CrossRef]
- De Gennes, P.; Pincus, P. Superconductivity of Metals and Alloys; Advanced Books Classics; Avalon Publishing: New York, NY, USA, 1999. [Google Scholar]
- Alaberdin, E.R.; Vichorev, A.A.; Savchenko, A.M.; Sadovnikov, B.I. On Bogoliubov’s method in superconductivity. Theor. Math. Phys. 1996, 107, 523–532. [Google Scholar] [CrossRef]
- Zhu, J. Bogoliubov-de Gennes Method and Its Applications; Lecture Notes in Physics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Han, Q. A method of studying the Bogoliubov–de Gennes equations for the superconducting vortex lattice state. J. Phys. Condens. Matter 2009, 22, 035702. [Google Scholar] [CrossRef]
- Saunderson, T.G.; Gyorgypál, Z.; Annett, J.F.; Csire, G.; Újfalussy, B.; Gradhand, M. Real-space multiple scattering theory for superconductors with impurities. Phys. Rev. B 2020, 102, 245106. [Google Scholar] [CrossRef]
- Pellegrino, F.M.D.; Falci, G.; Paladino, E. Effect of dilute impurities on short graphene Josephson junctions. Commun. Phys. 2022, 5. [Google Scholar] [CrossRef]
- Stosiek, M.; Baretzky, C.; Balashov, T.; Evers, F.; Wulfhekel, W. Friedel oscillations and superconducting gap enhancement by impurity scattering. Phys. Rev. B 2022, 105, L140504. [Google Scholar] [CrossRef]
- Sato, M.; Ando, Y. Topological superconductors: A review. Rep. Prog. Phys. 2017, 80, 076501. [Google Scholar] [CrossRef]
- Feldman, B.E.; Randeria, M.T.; Li, J.; Jeon, S.; Xie, Y.; Wang, Z.; Drozdov, I.K.; Bernevig, B.A.; Yazdani, A. High-resolution studies of the Majorana atomic chain platform. Nat. Phys. 2016, 13, 286–291. [Google Scholar] [CrossRef]
- Schneider, L.; Brinker, S.; Steinbrecher, M.; Hermenau, J.; Posske, T.; dos Santos Dias, M.; Lounis, S.; Wiesendanger, R.; Wiebe, J. Controlling in-gap end states by linking nonmagnetic atoms and artificially-constructed spin chains on superconductors. Nat. Commun. 2020, 11, 4707. [Google Scholar] [CrossRef] [PubMed]
- Schneider, L.; Beck, P.; Posske, T.; Crawford, D.; Mascot, E.; Rachel, S.; Wiesendanger, R.; Wiebe, J. Topological Shiba bands in artificial spin chains on superconductors. Nat. Phys. 2021, 17, 943–948. [Google Scholar] [CrossRef]
- Schneider, L.; Beck, P.; Neuhaus-Steinmetz, J.; Rózsa, L.; Posske, T.; Wiebe, J.; Wiesendanger, R. Precursors of Majorana modes and their length-dependent energy oscillations probed at both ends of atomic Shiba chains. Nat. Nanotechnol. 2022, 17, 384–389. [Google Scholar] [CrossRef] [PubMed]
- Brinker, S.; Küster, F.; Parkin, S.S.P.; Sessi, P.; Lounis, S. Anomalous excitations of atomically crafted quantum magnets. Sci. Adv. 2022, 8, eabi7291. [Google Scholar] [CrossRef] [PubMed]
- Küster, F.; Brinker, S.; Hess, R.; Loss, D.; Parkin, S.S.P.; Klinovaja, J.; Lounis, S.; Sessi, P. Non-Majorana modes in diluted spin chains proximitized to a superconductor. Proc. Natl. Acad. Sci. USA 2022, 119, e2210589119. [Google Scholar] [CrossRef]
- Rüßmann, P.; Blügel, S. Density functional Bogoliubov-de Gennes analysis of superconducting Nb and Nb(110) surfaces. Phys. Rev. B 2022, 105, 125143. [Google Scholar] [CrossRef]
- Beck, P.; Schneider, L.; Rózsa, L.; Palotás, K.; Lászlóffy, A.; Szunyogh, L.; Wiebe, J.; Wiesendanger, R. Spin-orbit coupling induced splitting of Yu-Shiba-Rusinov states in antiferromagnetic dimers. Nat. Commun. 2021, 12, 2040. [Google Scholar] [CrossRef]
- Mier, C.; Choi, D.J.; Lorente, N. Calculations of in-gap states of ferromagnetic spin chains on s-wave wide-band superconductors. Phys. Rev. B 2021, 104, 245415. [Google Scholar] [CrossRef]
- Lászlóffy, A.; Nyári, B.; Csire, G.; Szunyogh, L.; Újfalussy, B. Topological superconductivity from first principles. II. Effects from manipulation of spin spirals: Topological fragmentation, braiding, and quasi-Majorana bound states. Phys. Rev. B 2023, 108, 134513. [Google Scholar] [CrossRef]
- Nyári, B.; Lászlóffy, A.; Csire, G.; Szunyogh, L.; Újfalussy, B. Topological superconductivity from first principles. I. Shiba band structure and topological edge states of artificial spin chains. Phys. Rev. B 2023, 108, 134512. [Google Scholar] [CrossRef]
- Rüßmann, P.; Bahari, M.; Blügel, S.; Trauzettel, B. Interorbital Cooper pairing at finite energies in Rashba surface states. Phys. Rev. Res. 2023, 5, 043181. [Google Scholar] [CrossRef]
- Oliveira, L.N.; Gross, E.K.U.; Kohn, W. Density-Functional Theory for Superconductors. Phys. Rev. Lett. 1988, 60, 2430–2433. [Google Scholar] [CrossRef] [PubMed]
- Lüders, M.; Marques, M.A.L.; Lathiotakis, N.N.; Floris, A.; Profeta, G.; Fast, L.; Continenza, A.; Massidda, S.; Gross, E.K.U. Ab initio theory of superconductivity. I. Density functional formalism and approximate functionals. Phys. Rev. B 2005, 72, 024545. [Google Scholar] [CrossRef]
- Marques, M.A.L.; Lüders, M.; Lathiotakis, N.N.; Profeta, G.; Floris, A.; Fast, L.; Continenza, A.; Gross, E.K.U.; Massidda, S. Ab initio theory of superconductivity. II. Application to elemental metals. Phys. Rev. B 2005, 72, 024546. [Google Scholar] [CrossRef]
- Essenberger, F.; Sanna, A.; Buczek, P.; Ernst, A.; Sandratskii, L.; Gross, E.K.U. Ab initio theory of iron-based superconductors. Phys. Rev. B 2016, 94, 014503. [Google Scholar] [CrossRef]
- Khaydukov, Y.N.; Vasenko, A.S.; Kravtsov, E.A.; Progliado, V.V.; Zhaketov, V.D.; Csik, A.; Nikitenko, Y.V.; Petrenko, A.V.; Keller, T.; Golubov, A.A.; et al. Magnetic and superconducting phase diagram of Nb/Gd/Nb trilayers. Phys. Rev. B 2018, 97, 144511. [Google Scholar] [CrossRef]
- Pal, B.; Chakraborty, A.; Sivakumar, P.K.; Davydova, M.; Gopi, A.K.; Pandeya, A.K.; Krieger, J.A.; Zhang, Y.; Date, M.; Ju, S.; et al. Josephson diode effect from Cooper pair momentum in a topological semimetal. Nat. Phys. 2022, 18, 1228–1233. [Google Scholar] [CrossRef]
- Odobesko, A.B.; Haldar, S.; Wilfert, S.; Hagen, J.; Jung, J.; Schmidt, N.; Sessi, P.; Vogt, M.; Heinze, S.; Bode, M. Preparation and electronic properties of clean superconducting Nb (110) surfaces. Phys. Rev. B 2019, 99, 115437. [Google Scholar] [CrossRef]
- Yu, L. Bound state in superconductors with paramagnetic impurities. Wu Li Hsueh Pao (China) Supersedes Chung-Kuo Wu Li Hsueh Engl. Transl. See Chin. J. Phys. (Peking) (Engl. Transl.) 1965, 21. [Google Scholar]
- Shiba, H. Classical Spins in Superconductors. Prog. Theor. Phys. 1968, 40, 435–451. [Google Scholar] [CrossRef]
- Rusinov, A. Theory of gapless superconductivity in alloys with paramagnetic impurities. Zh. Eksp. Theor. Fiz. 1969, 56, 2047–2056. [Google Scholar]
- Odobesko, A.; Di Sante, D.; Kowalski, A.; Wilfert, S.; Friedrich, F.; Thomale, R.; Sangiovanni, G.; Bode, M. Observation of tunable single-atom Yu-Shiba-Rusinov states. Phys. Rev. B 2020, 102, 174504. [Google Scholar] [CrossRef]
- Küster, F.; Brinker, S.; Lounis, S.; Parkin, S.S.P.; Sessi, P. Long range and highly tunable interaction between local spins coupled to a superconducting condensate. Nat. Commun. 2021, 12, 6722. [Google Scholar] [CrossRef] [PubMed]
- Küster, F.; Montero, A.M.; Guimarães, F.S.M.; Brinker, S.; Lounis, S.; Parkin, S.S.P.; Sessi, P. Correlating Josephson supercurrents and Shiba states in quantum spins unconventionally coupled to superconductors. Nat. Commun. 2021, 12, 1108. [Google Scholar] [CrossRef]
- Friedrich, F.; Boshuis, R.; Bode, M.; Odobesko, A. Coupling of Yu-Shiba-Rusinov states in one-dimensional chains of Fe atoms on Nb(110). Phys. Rev. B 2021, 103, 235437. [Google Scholar] [CrossRef]
- Soldini, M.O.; Küster, F.; Wagner, G.; Das, S.; Aldarawsheh, A.; Thomale, R.; Lounis, S.; Parkin, S.S.P.; Sessi, P.; Neupert, T. Two-dimensional Shiba lattices as a possible platform for crystalline topological superconductivity. Nat. Phys. 2023, 19, 1848–1854. [Google Scholar] [CrossRef]
- Goedecke, J.J.; Schneider, L.; Ma, Y.; That, K.T.; Wang, D.; Wiebe, J.; Wiesendanger, R. Correlation of Magnetism and Disordered Shiba Bands in Fe Monolayer Islands on Nb(110). ACS Nano 2022, 16, 14066–14074. [Google Scholar] [CrossRef]
- Beck, P.; Schneider, L.; Bachmann, L.; Wiebe, J.; Wiesendanger, R. Structural and superconducting properties of ultrathin Ir films on Nb(110). Phys. Rev. Mater. 2022, 6, 024801. [Google Scholar] [CrossRef]
- Lo Conte, R.; Bazarnik, M.; Palotás, K.; Rózsa, L.; Szunyogh, L.; Kubetzka, A.; von Bergmann, K.; Wiesendanger, R. Coexistence of antiferromagnetism and superconductivity in Mn/Nb(110). Phys. Rev. B 2022, 105, L100406. [Google Scholar] [CrossRef]
- Souza Mendes Guimarães, F.; Suckert, J.R.; Aceves Rodríguez, U.A.; Hamamera, H.; Brinker, S.; Bouaziz, J.; dos Santos Dias, M.; Lounis, S. TITAN. Zenodo 2023. [Google Scholar] [CrossRef]
- Guimarães, F.S.M.; dos Santos Dias, M.; Bouaziz, J.; Costa, A.T.; Muniz, R.B.; Lounis, S. Dynamical amplification of magnetoresistances and Hall currents up to the THz regime. Sci. Rep. 2017, 7, 3686. [Google Scholar] [CrossRef] [PubMed]
- Guimarães, F.S.M.; Suckert, J.R.; Chico, J.; Bouaziz, J.; dos Santos Dias, M.; Lounis, S. Comparative study of methodologies to compute the intrinsic Gilbert damping: Interrelations, validity and physical consequences. J. Phys. Condens. Matter 2019, 31, 255802. [Google Scholar] [CrossRef] [PubMed]
- Guimarães, F.S.M.; Bouaziz, J.; dos Santos Dias, M.; Lounis, S. Spin-orbit torques and their associated effective fields from gigahertz to terahertz. Commun. Phys. 2020, 3, 19. [Google Scholar] [CrossRef]
- Papaconstantopoulos, D. Handbook of the Band Structure of Elemental Solids: From Z = 1 To Z = 112, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Guimarães, F.S.M.; Lounis, S.; Costa, A.T.; Muniz, R.B. Dynamical current-induced ferromagnetic and antiferromagnetic resonances. Phys. Rev. B 2015, 92, 220410. [Google Scholar] [CrossRef]
- Hamamera, H.; Guimarães, F.S.M.; dos Santos Dias, M.; Lounis, S. Polarisation-dependent single-pulse ultrafast optical switching of an elementary ferromagnet. Commun. Phys. 2022, 5, 16. [Google Scholar] [CrossRef]
- Hamamera, H.; Guimarães, F.S.M.; dos Santos Dias, M.; Lounis, S. Ultrafast light-induced magnetization in non-magnetic films: From orbital and spin Hall phenomena to the inverse Faraday effect. arXiv 2023, arXiv:2312.07888. [Google Scholar] [CrossRef]
- Aceves Rodríguez, U.A.; Mendes Guimarães, F.S.; Brinker, S.; Lounis, S. Magnetic exchange interactions at the proximity of a superconductor. arXiv 2023, arXiv:2306.02906. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; Dover Books on Physics Series; Dover Publications: Garden City, NY, USA, 2004. [Google Scholar]
- Ikushima, A.; Mizusaki, T. Superconductivity in niobium and niobium-tantalum alloys. J. Phys. Chem. Solids 1969, 30, 873–879. [Google Scholar] [CrossRef]
- Veedu, S.; Popovic, Z.; Satpathy, S. Theoretical model for Rashba spin-orbit interaction in d electrons. Phys. Rev. B 2014, 90, 165108. [Google Scholar] [CrossRef]
- Csire, G.; Schönecker, S.; Újfalussy, B. First-principles approach to thin superconducting slabs and heterostructures. Phys. Rev. B 2016, 94, 140502. [Google Scholar] [CrossRef]
- McMillan, W.L. Transition Temperature of Strong-Coupled Superconductors. Phys. Rev. 1968, 167, 331–344. [Google Scholar] [CrossRef]
- Evans, R.; Gaspari, G.D.; Gyorffy, B.L. A simple theory of the electron-phonon mass enhancement in transition metals. J. Phys. F Met. Phys. 1973, 3, 39. [Google Scholar] [CrossRef]
- Savrasov, S.Y. Linear-response theory and lattice dynamics: A muffin-tin-orbital approach. Phys. Rev. B 1996, 54, 16470–16486. [Google Scholar] [CrossRef] [PubMed]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Klein, B.M.; Papaconstantopoulos, D.A. Electron-Phonon Interaction and Superconductivity in Transition Metals and Transition-Metal Carbides. Phys. Rev. Lett. 1974, 32, 1193–1195. [Google Scholar] [CrossRef]
- Saunderson, T.G.; Annett, J.F.; Újfalussy, B.; Csire, G.; Gradhand, M. Gap anisotropy in multiband superconductors based on multiple scattering theory. Phys. Rev. B 2020, 101, 064510. [Google Scholar] [CrossRef]
- Yildirim, T.; Gülseren, O.; Lynn, J.W.; Brown, C.M.; Udovic, T.J.; Huang, Q.; Rogado, N.; Regan, K.A.; Hayward, M.A.; Slusky, J.S.; et al. Giant Anharmonicity and Nonlinear Electron-Phonon Coupling in MgB2: A Combined First-Principles Calculation and Neutron Scattering Study. Phys. Rev. Lett. 2001, 87, 037001. [Google Scholar] [CrossRef]
- Lanzara, A.; Bogdanov, P.V.; Zhou, X.J.; Kellar, S.A.; Feng, D.L.; Lu, E.D.; Yoshida, T.; Eisaki, H.; Fujimori, A.; Kishio, K.; et al. Evidence for ubiquitous strong electron–phonon coupling in high-temperature superconductors. Nature 2001, 412, 510–514. [Google Scholar] [CrossRef]
- De Giovannini, U.; Hübener, H.; Sato, S.A.; Rubio, A. Direct Measurement of Electron-Phonon Coupling with Time-Resolved ARPES. Phys. Rev. Lett. 2020, 125, 136401. [Google Scholar] [CrossRef]
- Schackert, M.; Märkl, T.; Jandke, J.; Hölzer, M.; Ostanin, S.; Gross, E.K.U.; Ernst, A.; Wulfhekel, W. Local Measurement of the Eliashberg Function of Pb Islands: Enhancement of Electron-Phonon Coupling by Quantum Well States. Phys. Rev. Lett. 2015, 114, 047002. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Neupert, T.; Wang, Z.; MacDonald, A.H.; Yazdani, A.; Bernevig, B.A. Two-dimensional chiral topological superconductivity in Shiba lattices. Nat. Commun. 2016, 7, 12297. [Google Scholar] [CrossRef] [PubMed]
- Powell, M. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar] [CrossRef]
- Kodama, J.; Itoh, M.; Hirai, H. Superconducting transition temperature versus thickness of Nb film on various substrates. J. Appl. Phys. 1983, 54, 4050–4054. [Google Scholar] [CrossRef]
- Krause, D.; Thörnig, P. JURECA: Modular supercomputer at Jülich Supercomputing Centre. J. Large-Scale Res. Facil. JLSRF 2018, 4, A132. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aceves Rodriguez, U.A.; Guimarães, F.S.M.; Lounis, S. Superconductivity in Nb: Impact of Temperature, Dimensionality and Cooper-Pairing. Nanomaterials 2024, 14, 254. https://doi.org/10.3390/nano14030254
Aceves Rodriguez UA, Guimarães FSM, Lounis S. Superconductivity in Nb: Impact of Temperature, Dimensionality and Cooper-Pairing. Nanomaterials. 2024; 14(3):254. https://doi.org/10.3390/nano14030254
Chicago/Turabian StyleAceves Rodriguez, Uriel Allan, Filipe Souza Mendes Guimarães, and Samir Lounis. 2024. "Superconductivity in Nb: Impact of Temperature, Dimensionality and Cooper-Pairing" Nanomaterials 14, no. 3: 254. https://doi.org/10.3390/nano14030254
APA StyleAceves Rodriguez, U. A., Guimarães, F. S. M., & Lounis, S. (2024). Superconductivity in Nb: Impact of Temperature, Dimensionality and Cooper-Pairing. Nanomaterials, 14(3), 254. https://doi.org/10.3390/nano14030254





