Contacts at the Nanoscale and for Nanomaterials
Abstract
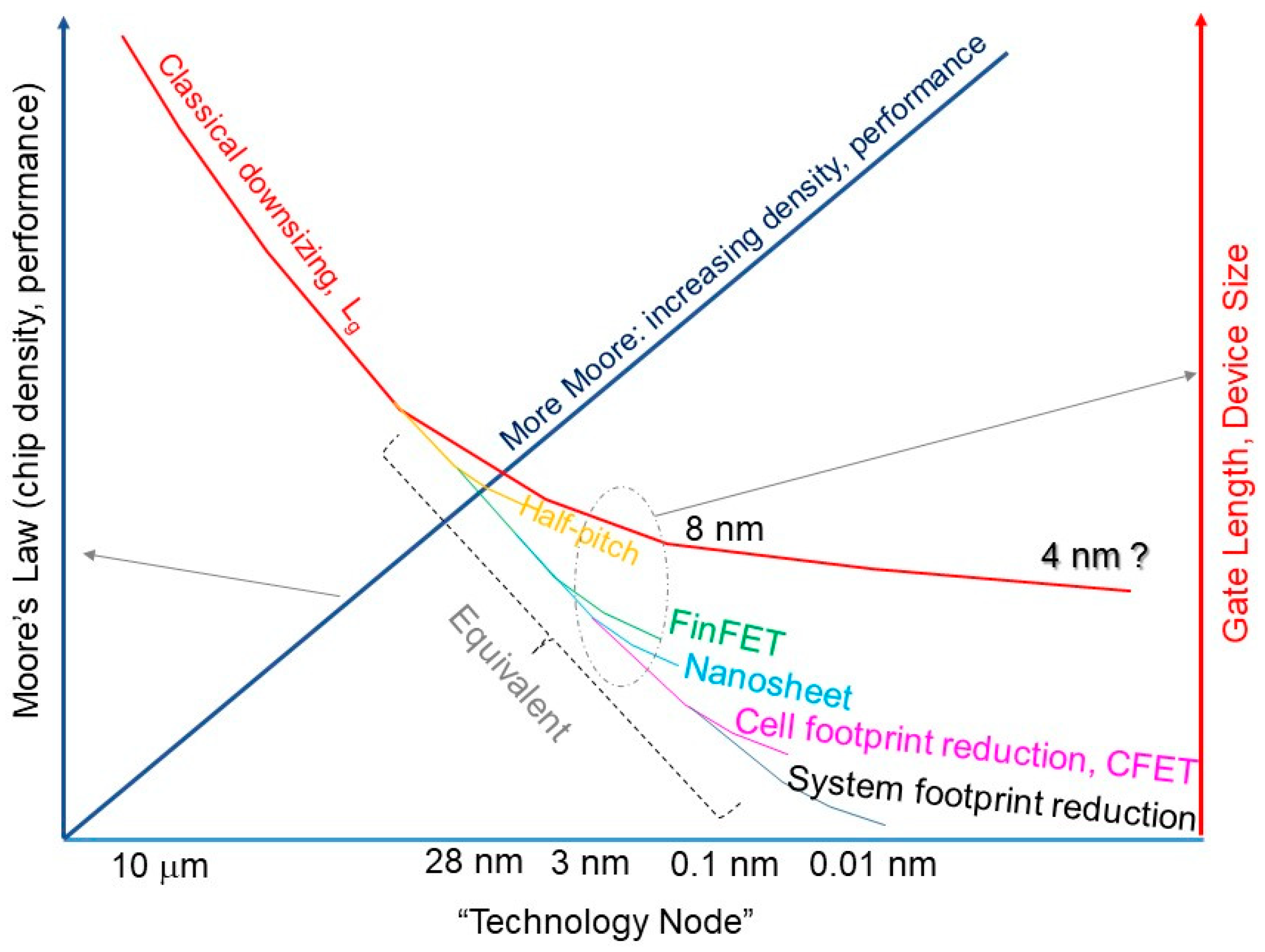
:1. Introduction
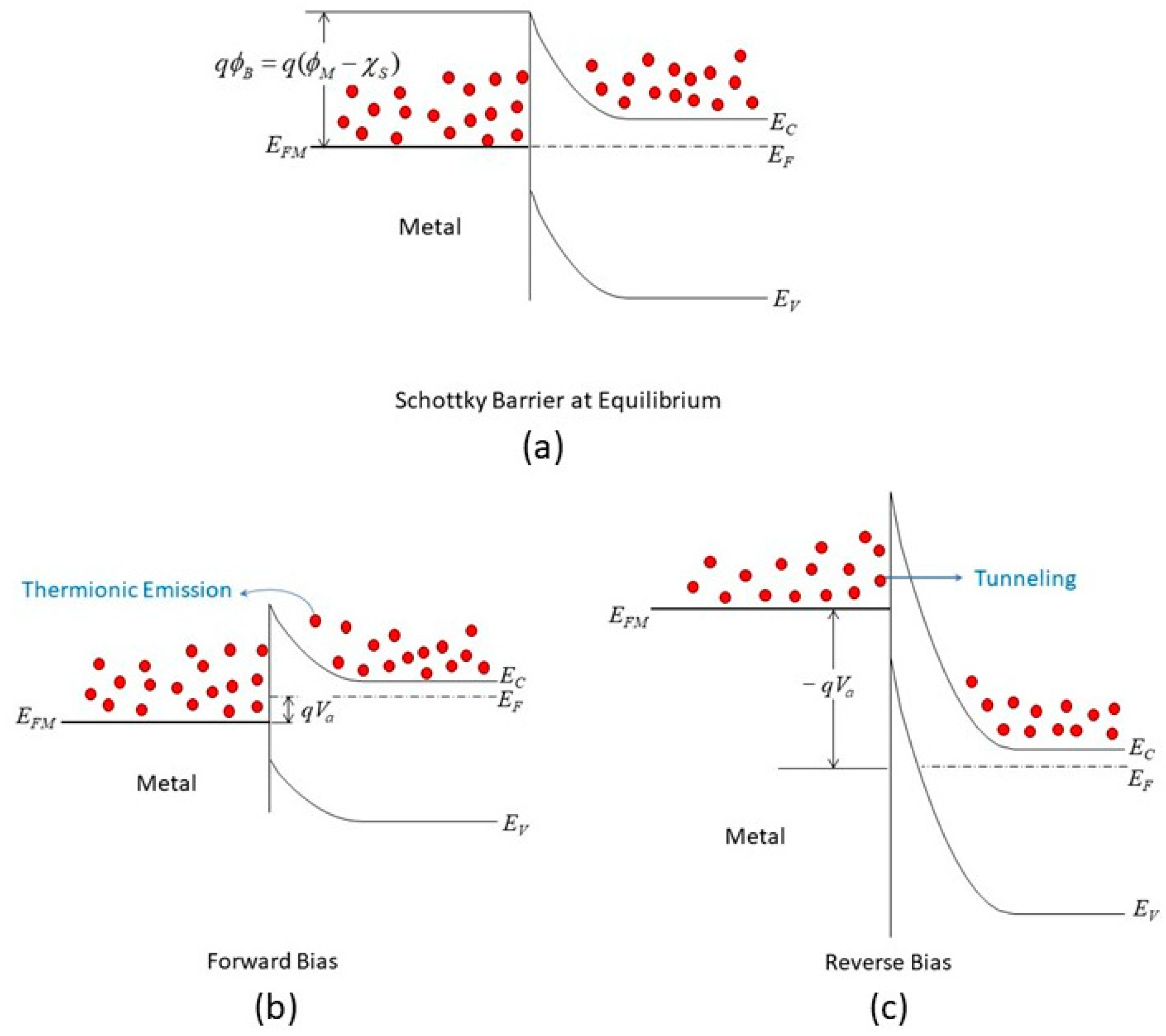
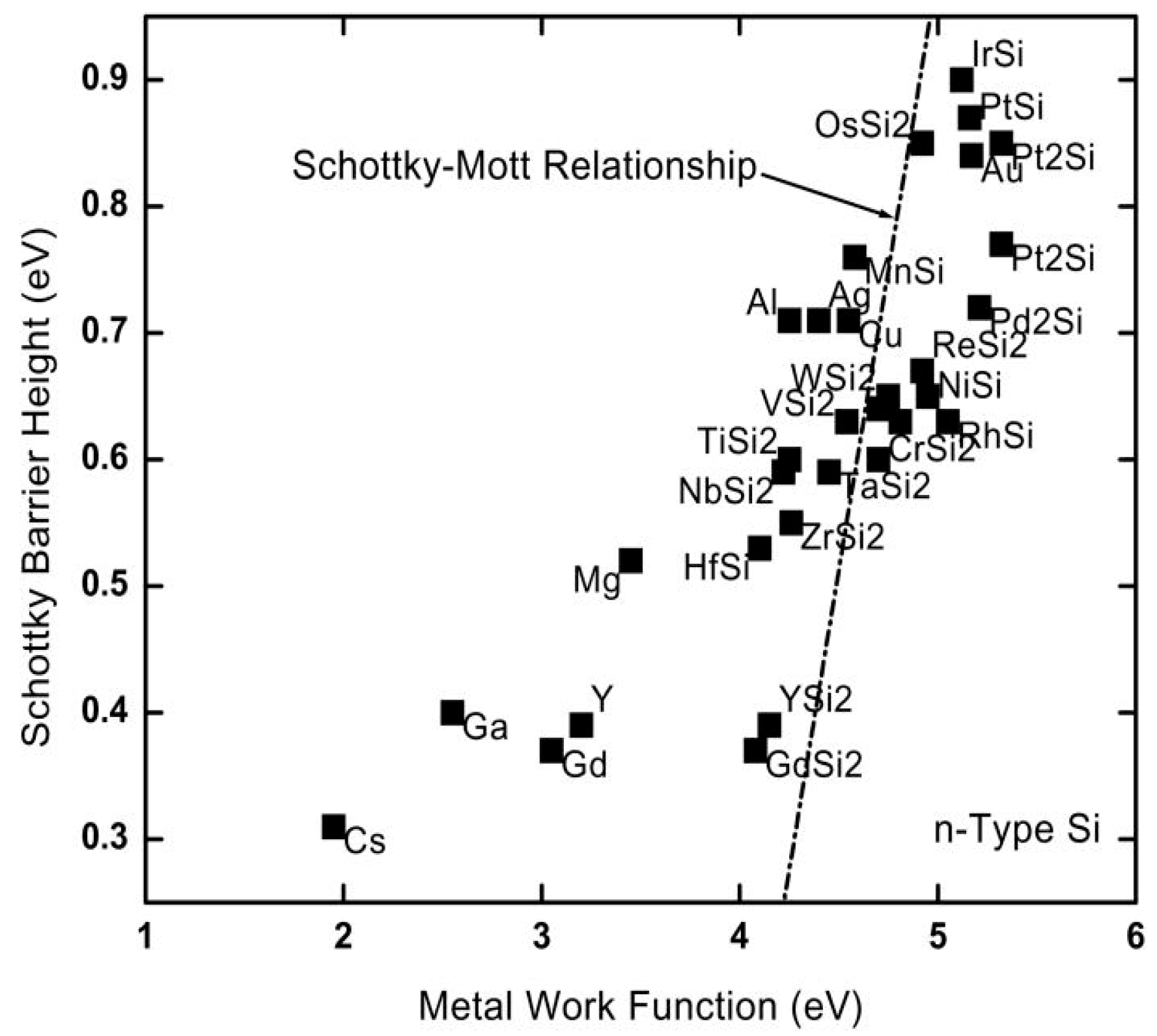
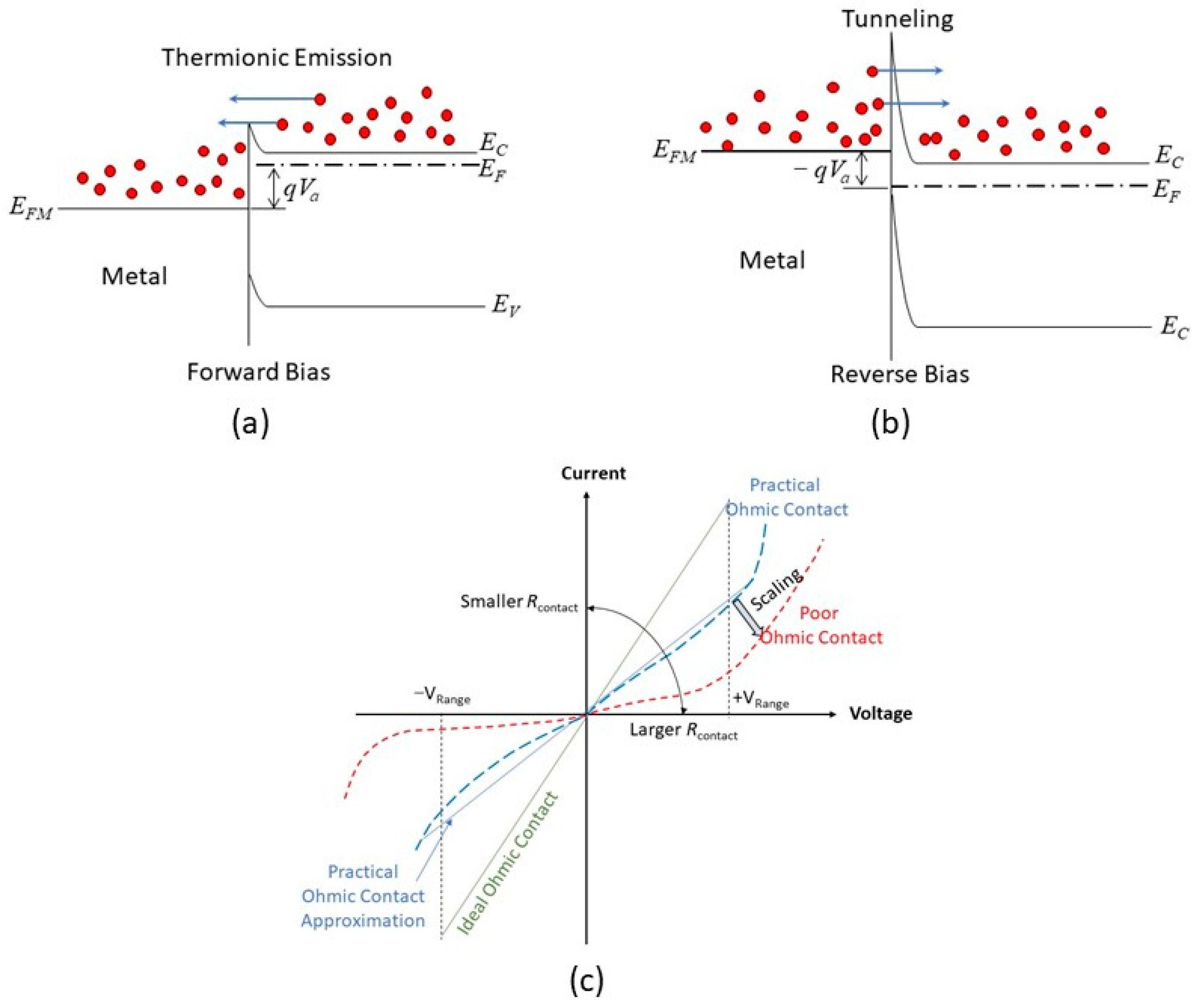
2. Schottky Junction
2.1. Schottky Equation
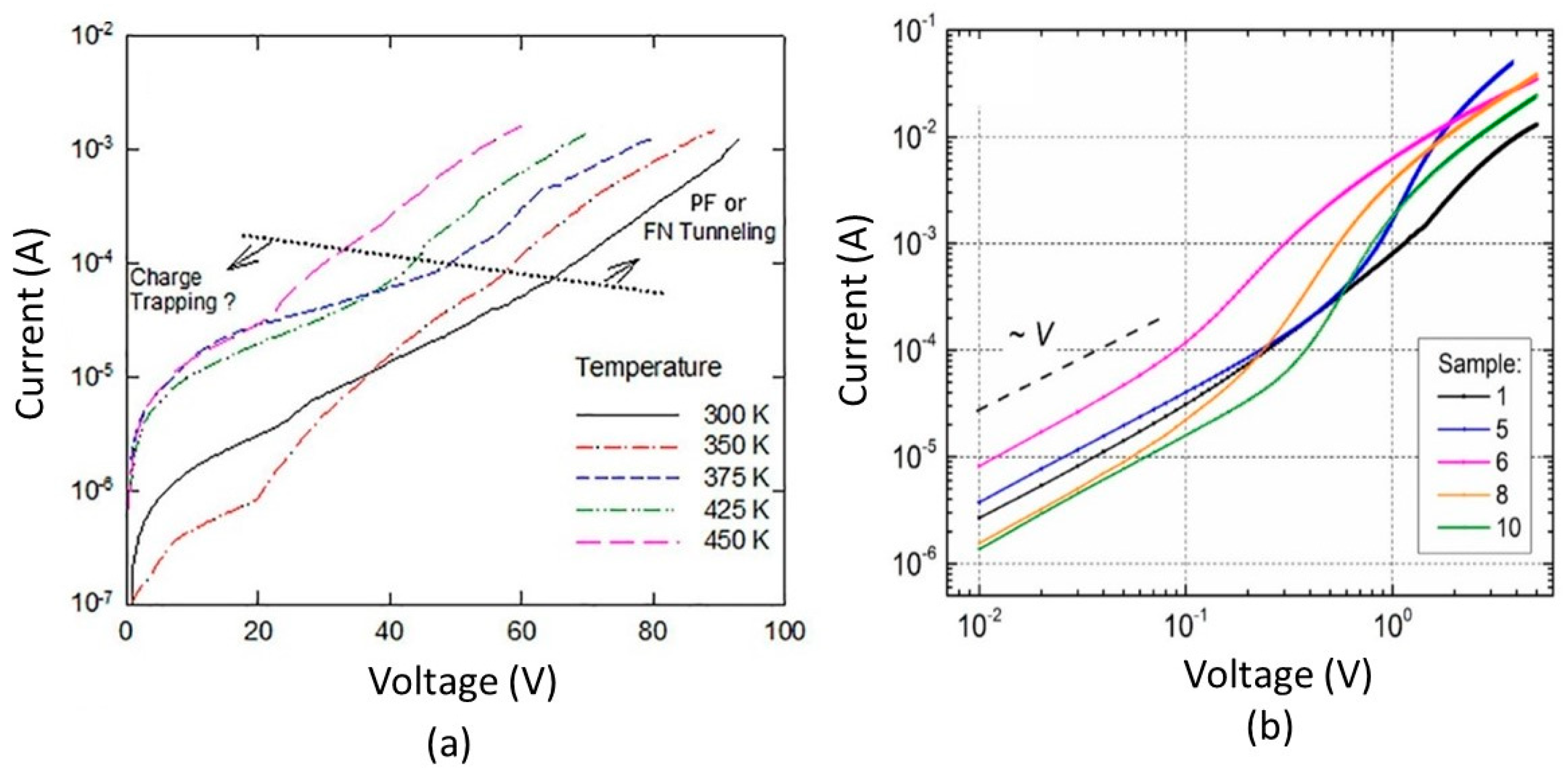
2.2. Current Conduction in an MIS Diode
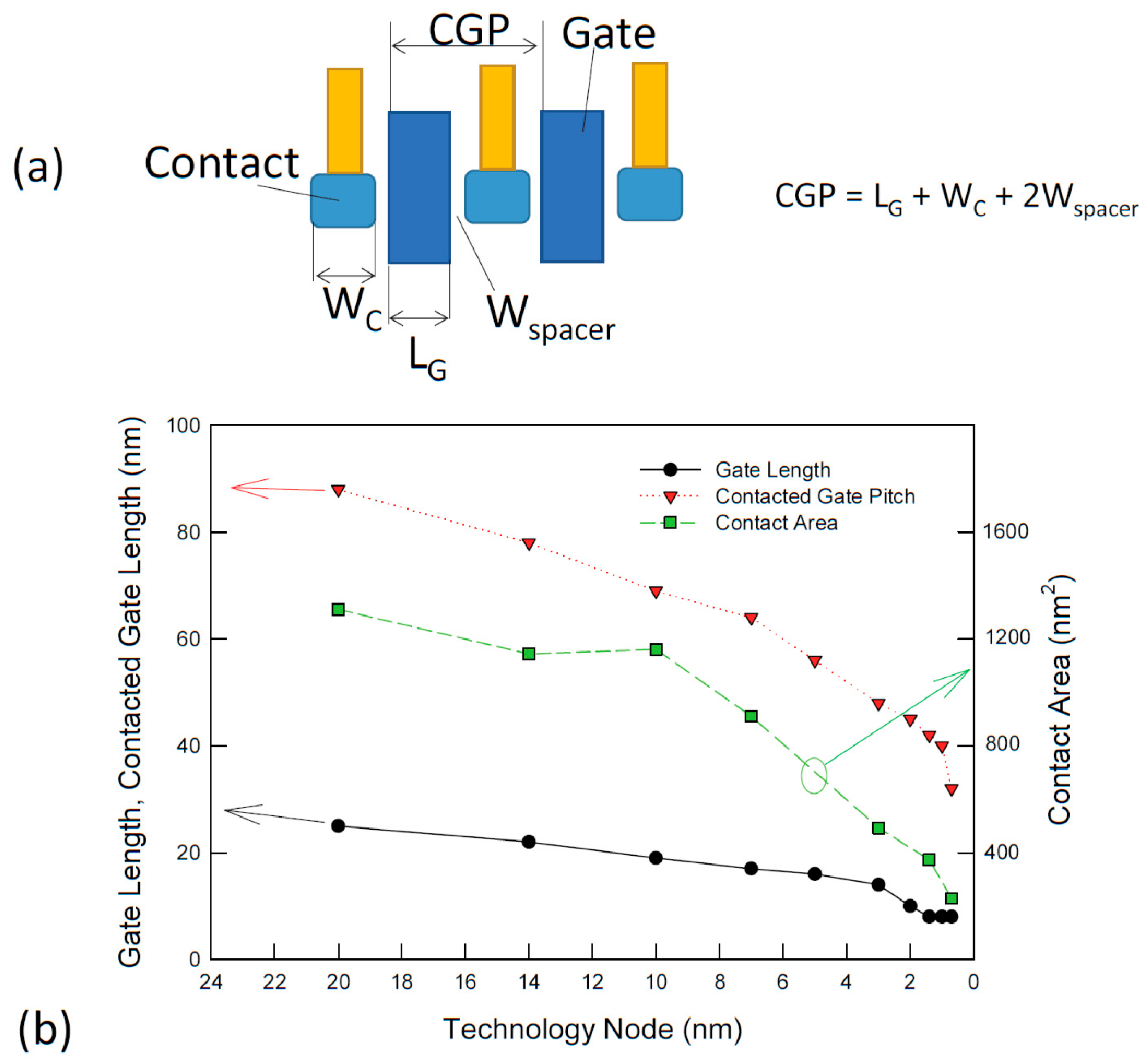
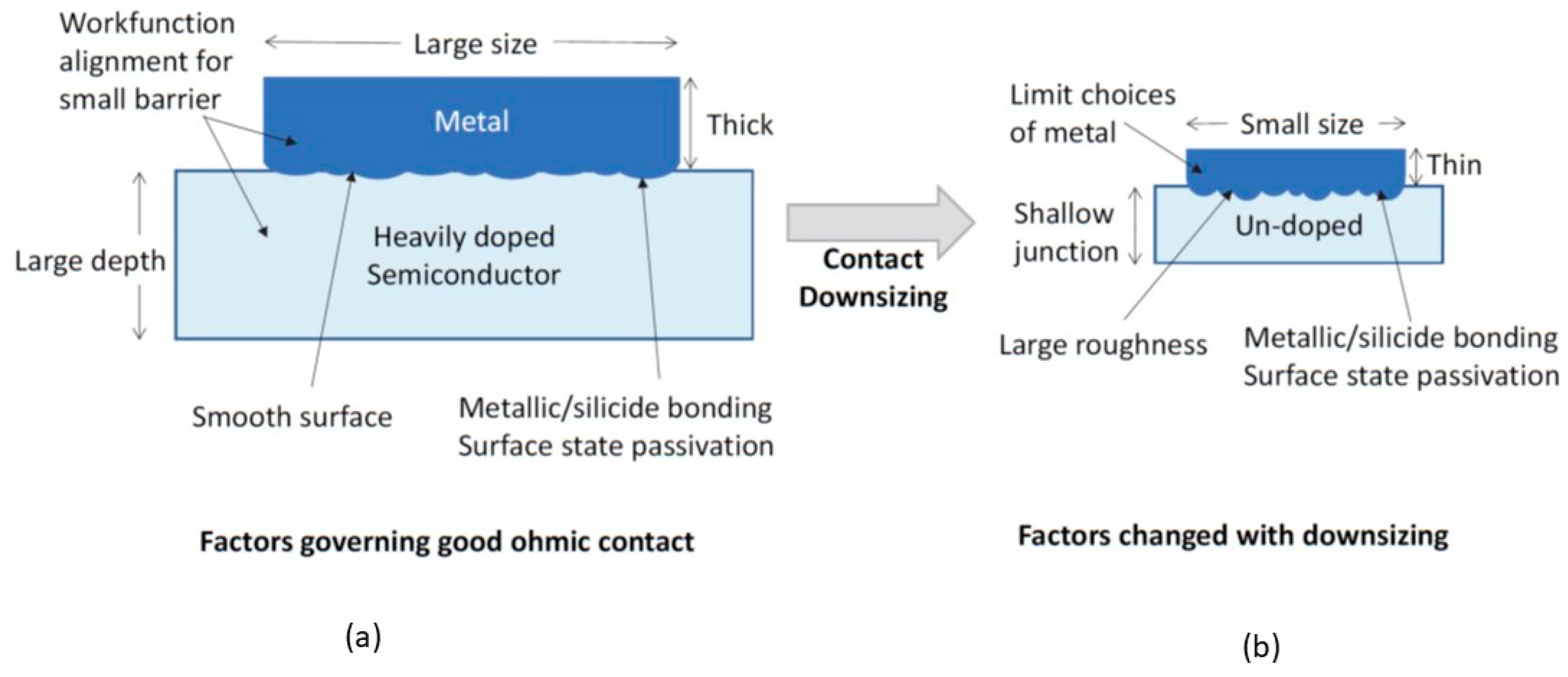
3. Ohmic Contact in the Nanoscale
- (1)
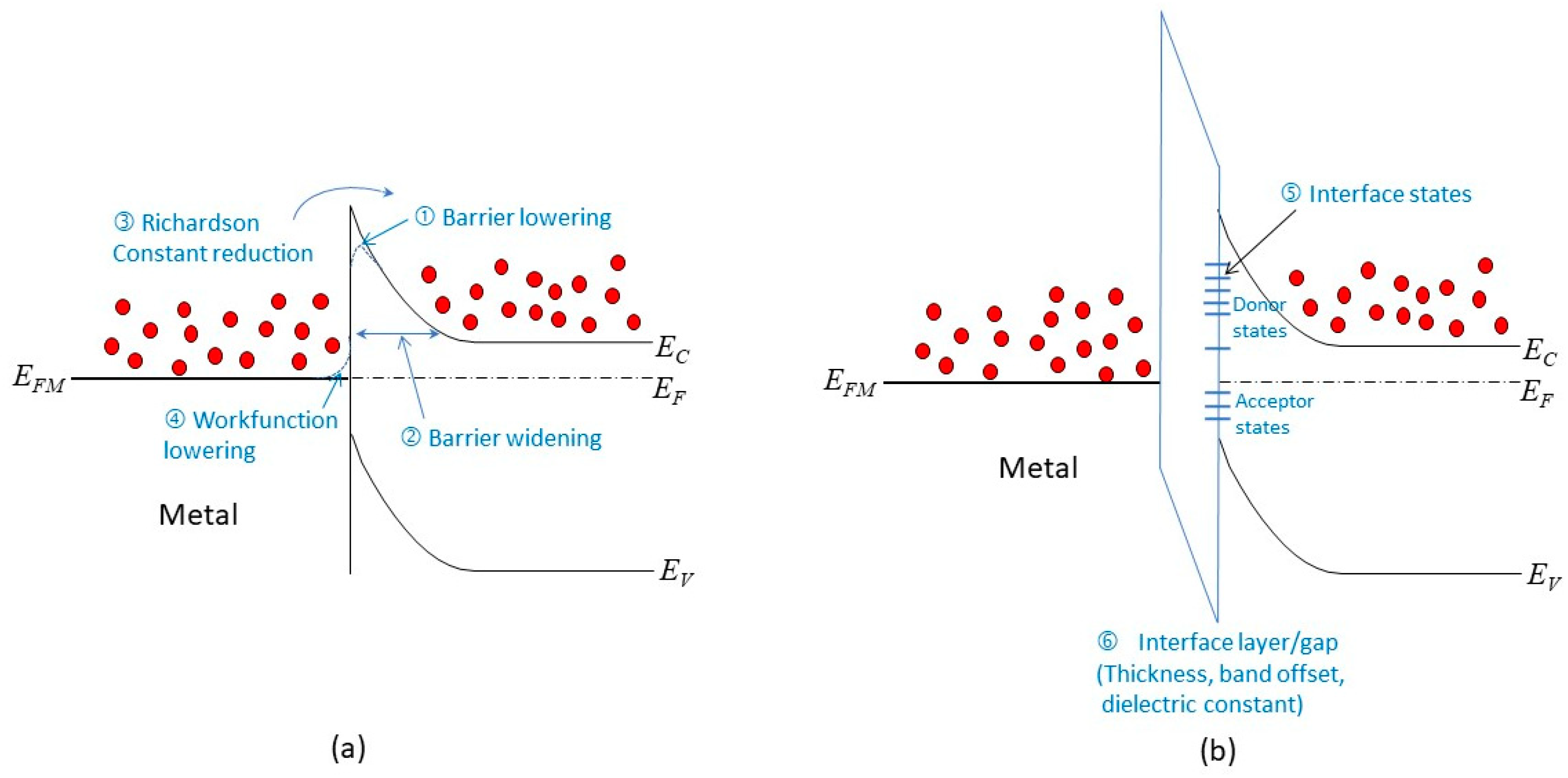
- Barrier lowering: The barrier height at the interface can be reduced by various factors, such as image force effects, metal workfunction variation, and surface roughness. These factors may be negligible in a large junction, but they can have significant impacts in a scaled junction. They can increase the forward current by lowering the potential barrier.
- (2)
- Barrier widening: The use of heavily doped contacts may not be possible in a scaled junction. This can result in a wider tunneling barrier, which reduces the conduction current under reverse bias.
- (3)
- Richardson constant reduction: Thinner metal films are used in a scaled junction, which can lead to a smaller value of the Richardson constant. This can decrease the forward current by reducing the thermionic emission.
- (4)
- Metal workfunction lowering: experimental results suggest that thinner metal films have lower workfunctions [46], which can also reduce the barrier height at the interface.
- (5)
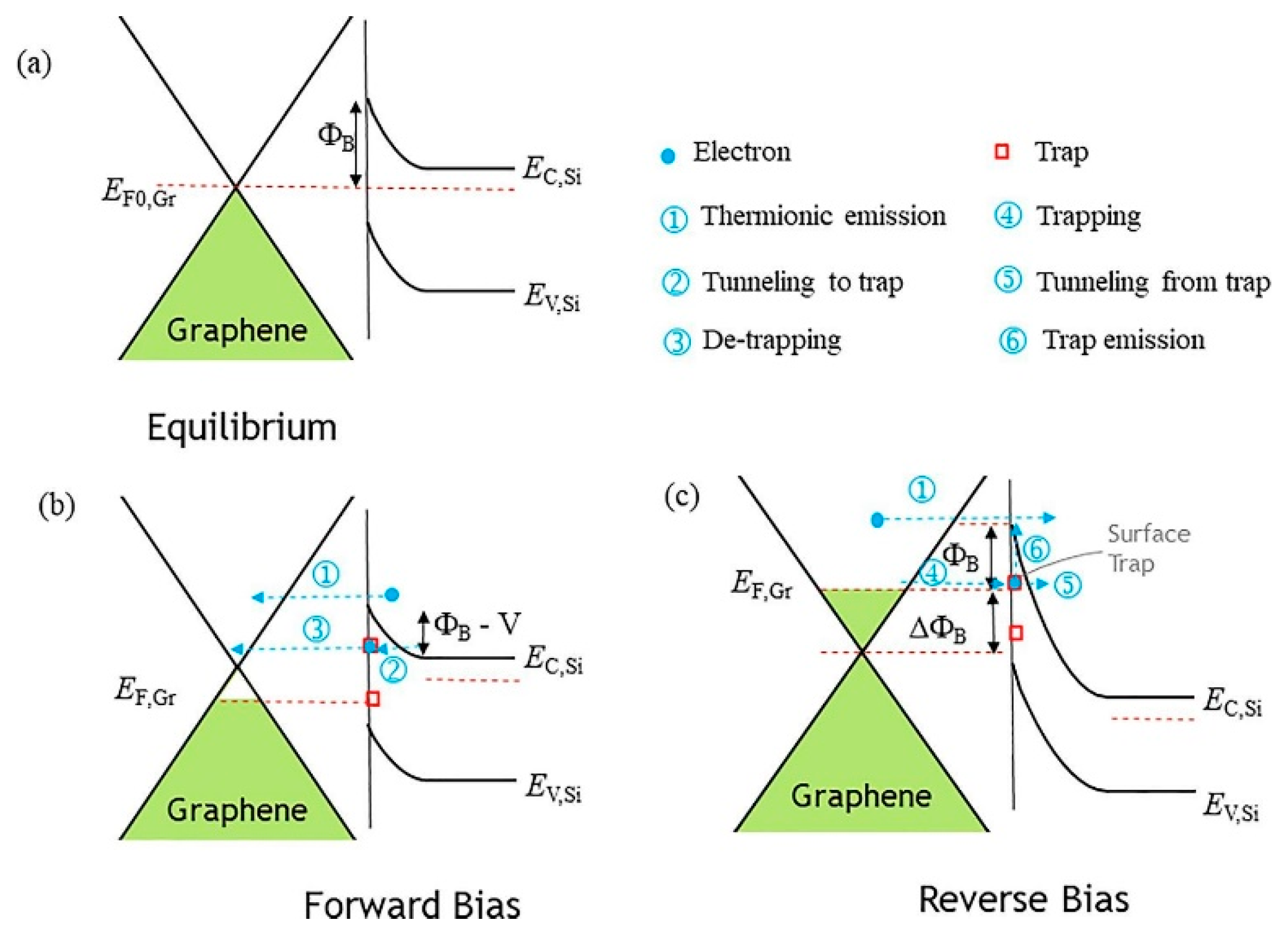
- Interface states: The presence of interface states can cause Fermi-level pinning, which affects the barrier height and the band bending. This effect is more pronounced in thinner films and in unpassivated surfaces.
- (6)
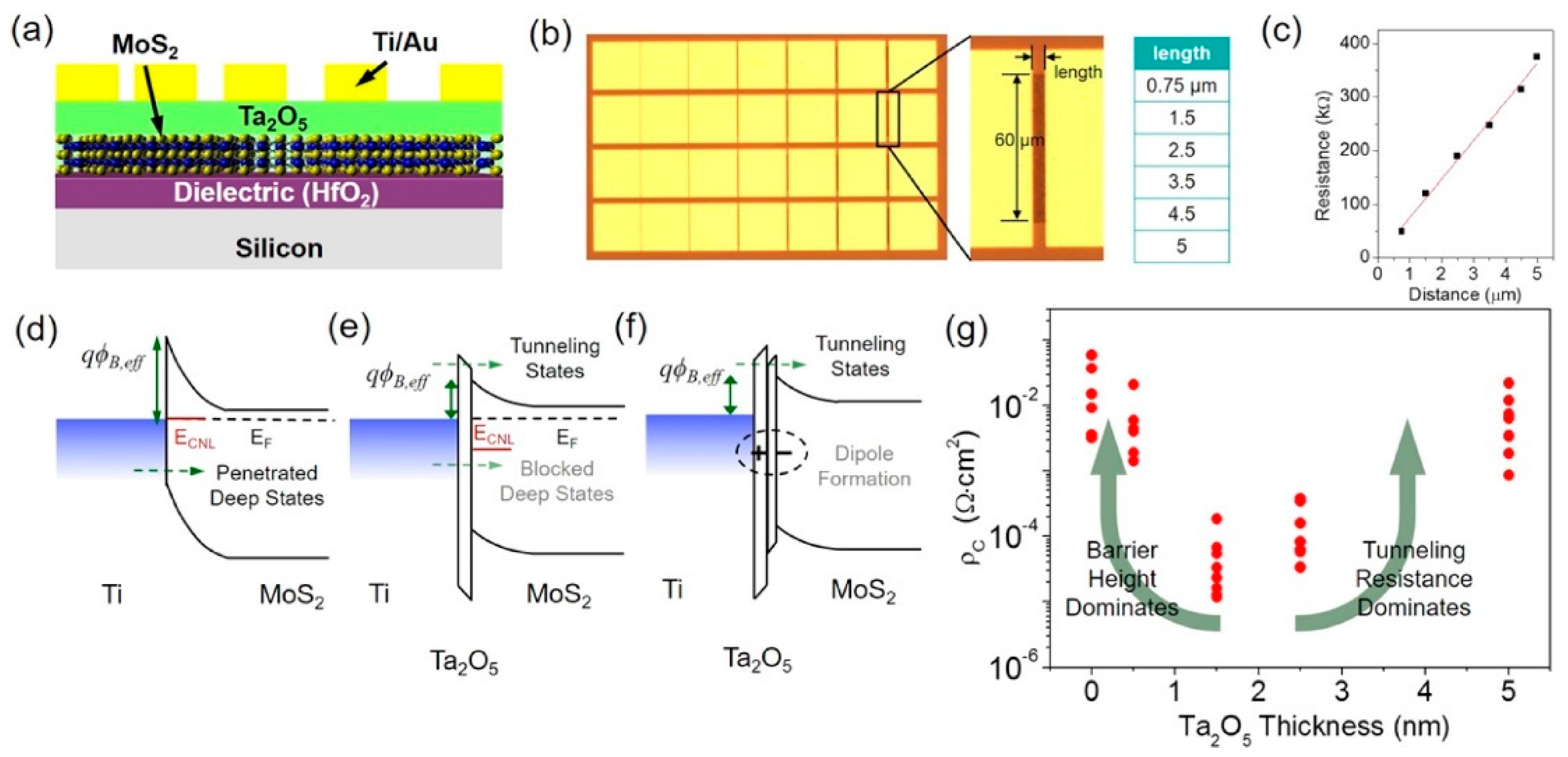
- Interface layer: To mitigate the Fermi-level pinning effect or to enable different circuit design options, such as using 2D materials as interlayer conductors (see Section 4.5), an interface layer may be used for passivation. This can affect the reverse currents by changing the tunneling characteristics. The thickness, band offset, and dielectric constant of the interface layer are important parameters for this effect.
3.1. Effects of Junction Doping
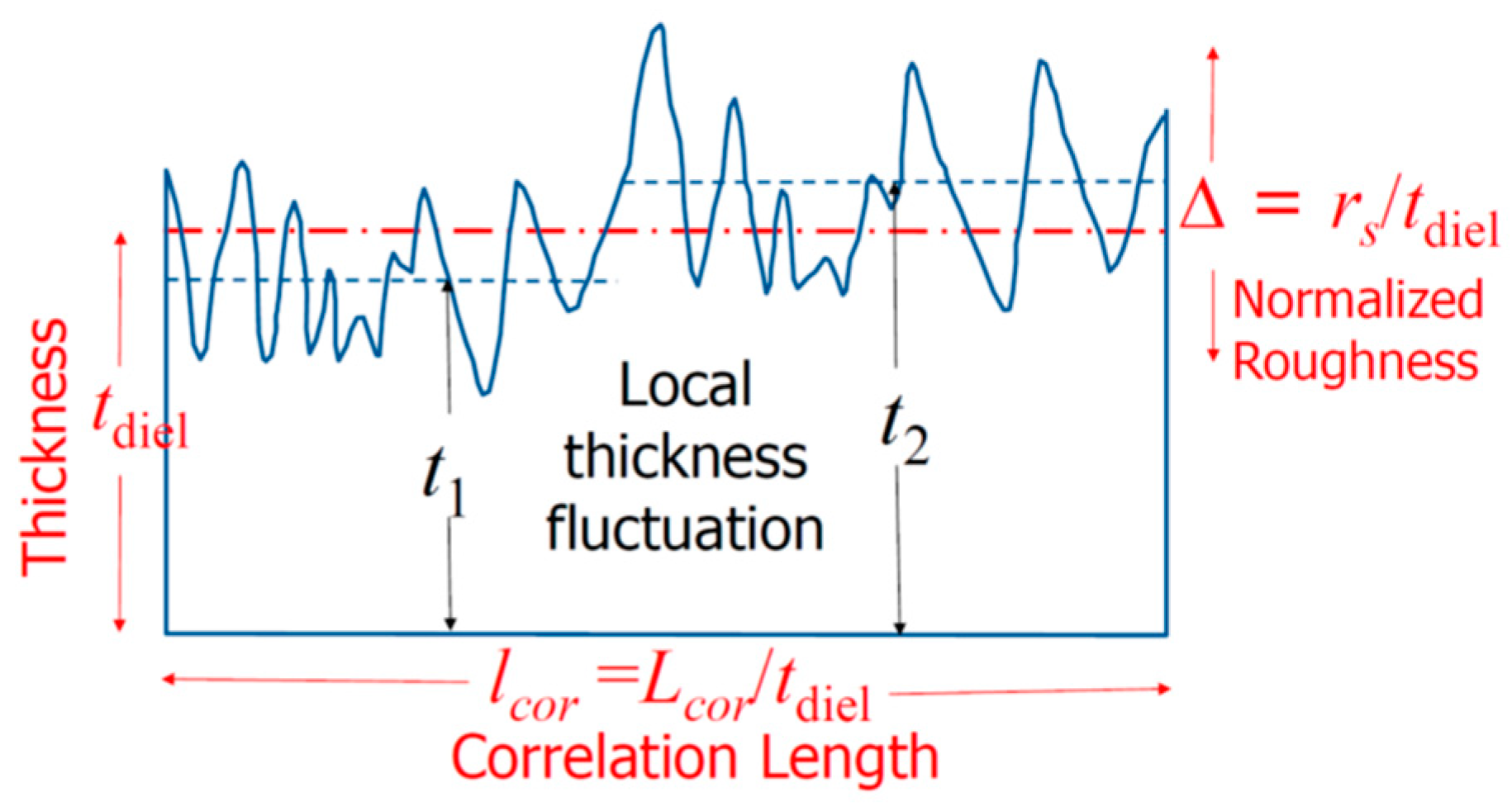
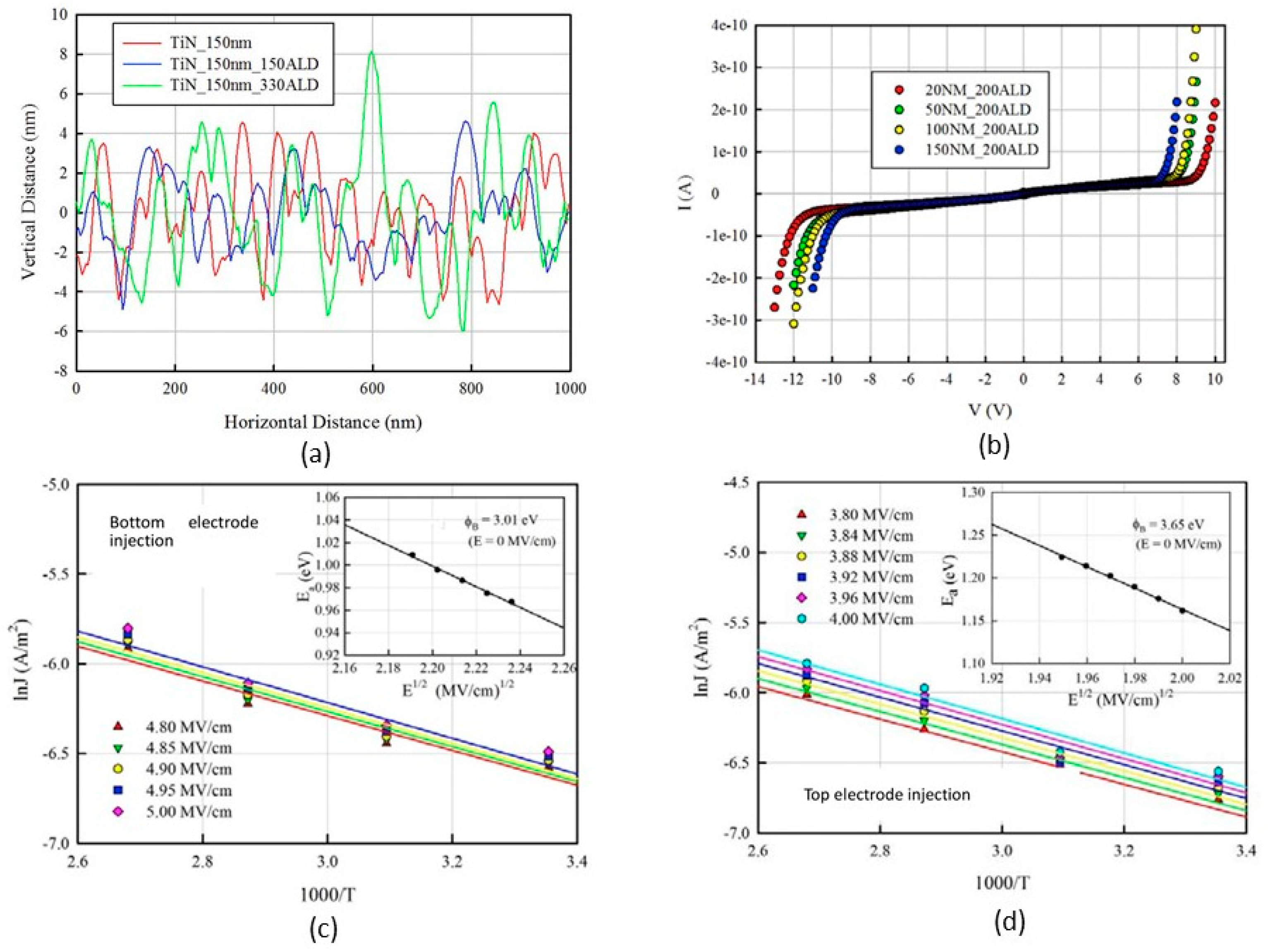
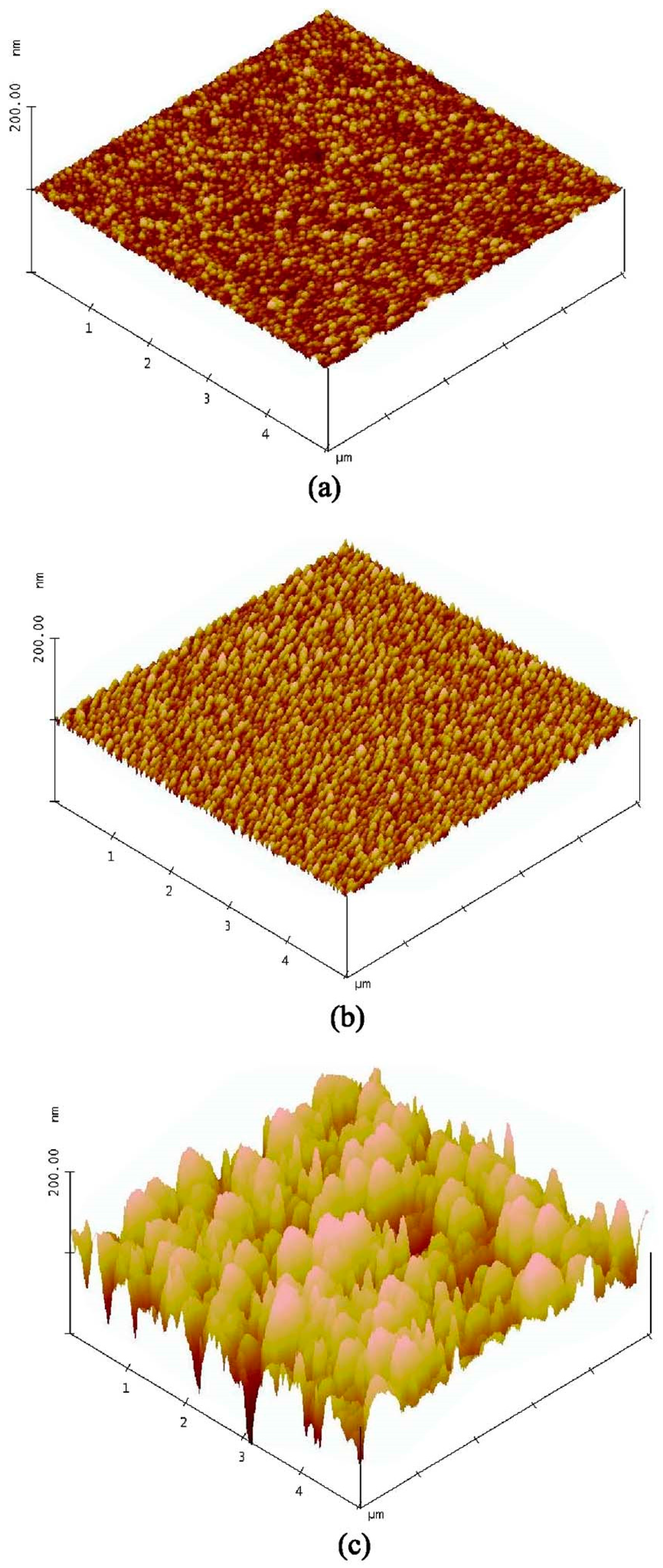
3.2. Effects of Interface Roughness
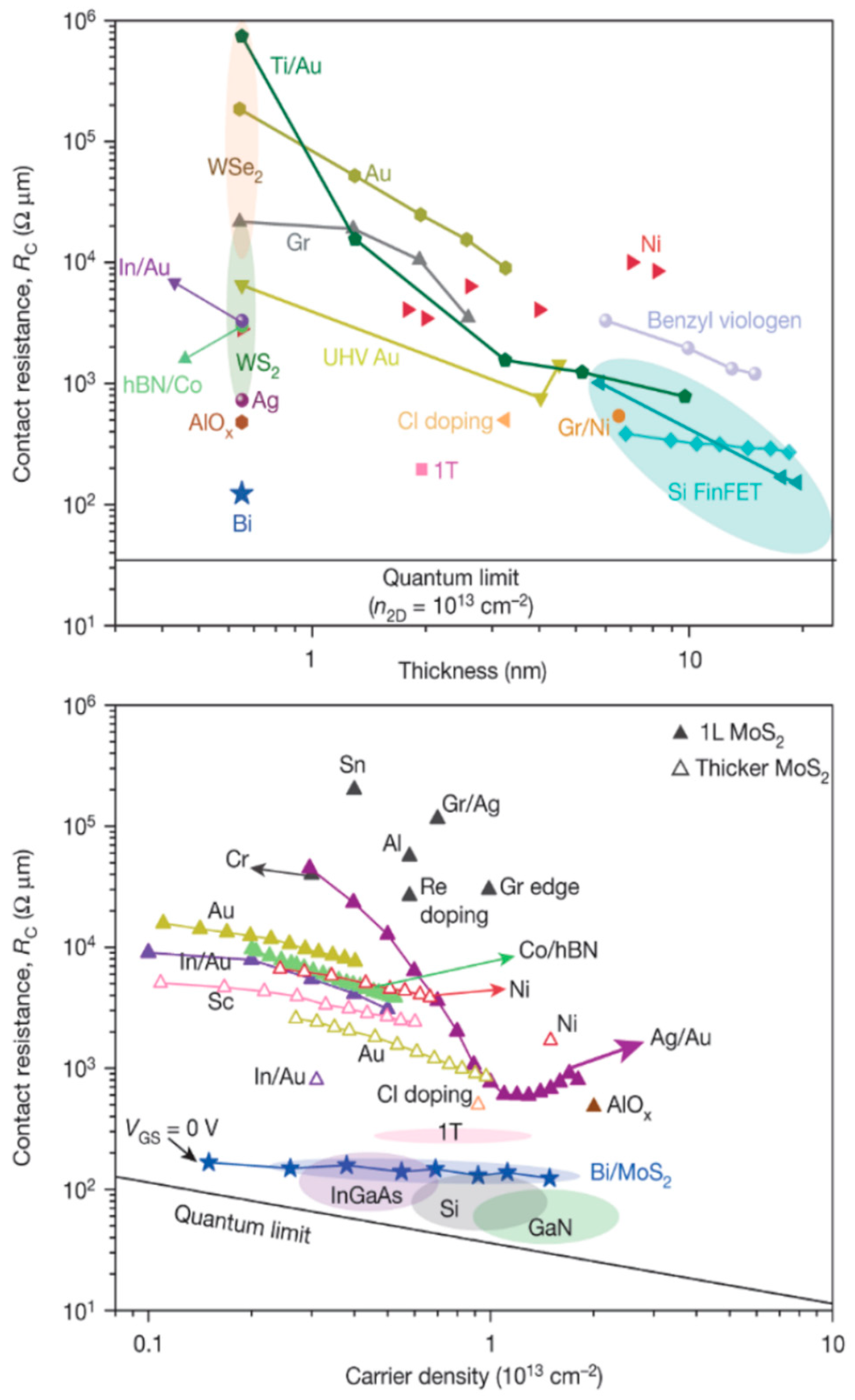
4. Contacts for 2D Materials
- (1)
- van der Waals gap: This is a tunneling barrier between the metal and the 2D material that allows for the tunneling of electrons. Some 2D materials may also form strong bonds with the metal or by overlapping their orbitals.
- (2)
- 2D contact: This is a common method of connecting 2D material from the top, but it has a high resistance per area because the current flows parallel to the 2D plane, not perpendicular to it. A top contact is easier to achieve because it involves depositing metal on the surface of the 2D materials and patterning it with standard photolithography.
- (3)
- Hybridization and edge contact: This is a better alternative to the 2D contact, as it creates a physical bond and a direct current path along the surface of the 2D material. However, it is challenging to achieve, because it requires the precise alignment and deposition of metal on very thin edges. Some 2D materials may also form strong bonds with the metal or by overlapping their orbitals.
- (4)
- Doping: 2D materials cannot be doped in the conventional ways, and it is hard to dope heavily.
- (5)
- Metal intercalation: This is a process of incorporating metal atoms into the gaps of multilayer 2D materials. The dopants contribute to the current’s conduction and can improve the contact’s conductivity.
- (6)
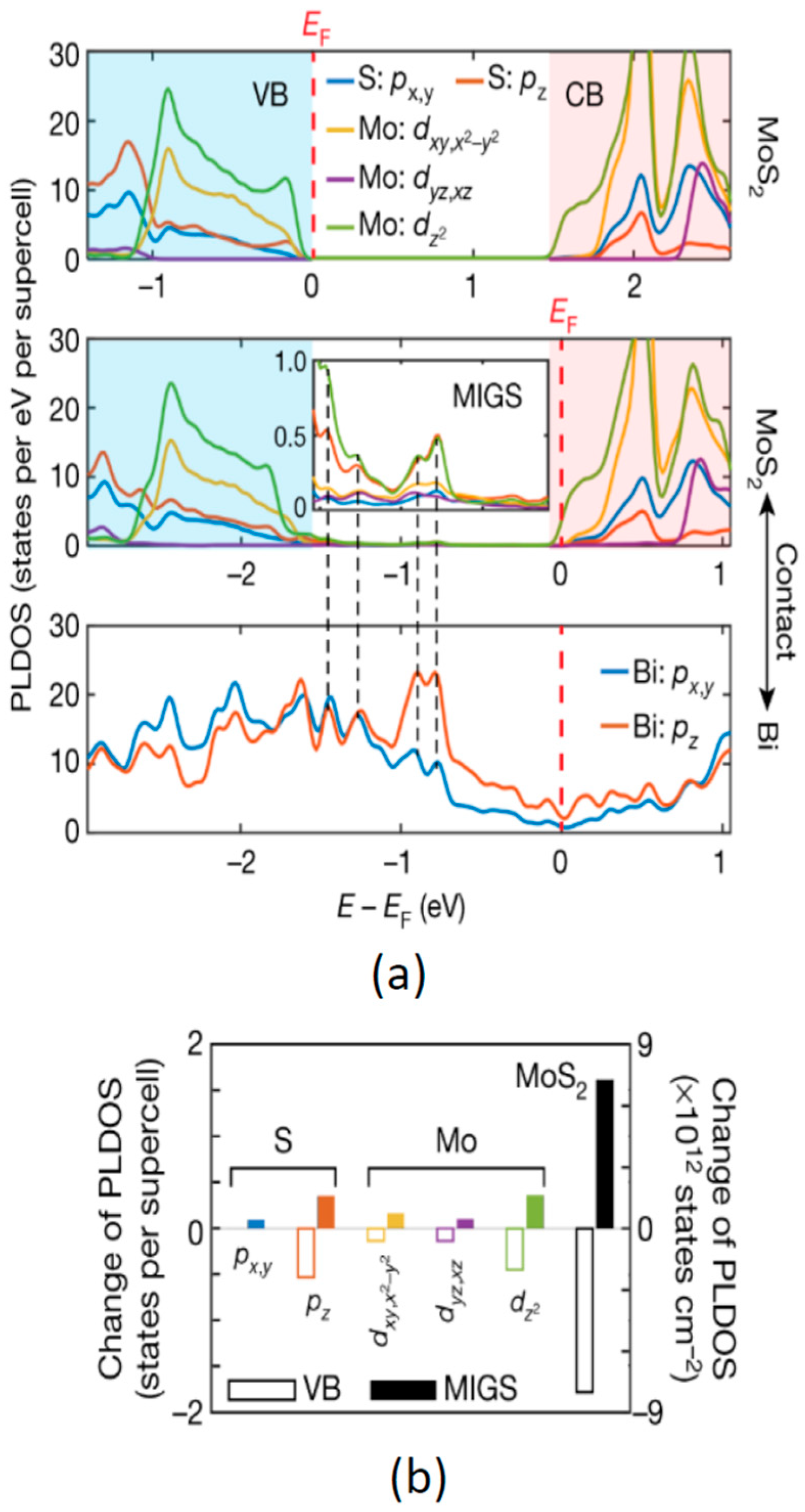
- Surface defects: These are imperfections, such as sulfur (S) vacancy in MoS2, on the 2D material surface that can trap charges and pin the Fermi level, affecting the contact potential and resistance.
- (7)
- Layer-dependent bandgap: The bandgap and the contact potential of the 2D material vary with the number of layers. This can be exploited to tune the contact properties by changing the layer thickness in the contact region.
- (8)
- Phase modification: Some 2D materials can switch among different phases that have distinct electrical properties. For instance, the 2H phase of TMDs is semiconducting, while the 1T and 1T0 phases are metallic. By changing the contact region to a metallic phase, the contact conductivity can be enhanced significantly.
- (9)
- Buffer layer insertion: inserting a buffer layer between the metal and the 2D material can help reduce the effects of the van der Waals gap and the metal-induced gap states.
- (10)
- Metal workfunction selection: To achieve good ohmic contact with both n-type and p-type 2D materials, various unconventional metals, such as In, Mg, Ag, Pd, Sc, and Ti, have been explored. However, not much work has addressed the issues of stability, reliability, and potential process contamination. For digital circuit applications, one must consider whether these metals can produce the desired threshold voltages for n-type and p-type transistors.
4.1. Metal van der Waals Contacts and Hybridized Contacts
4.2. Junction Doping
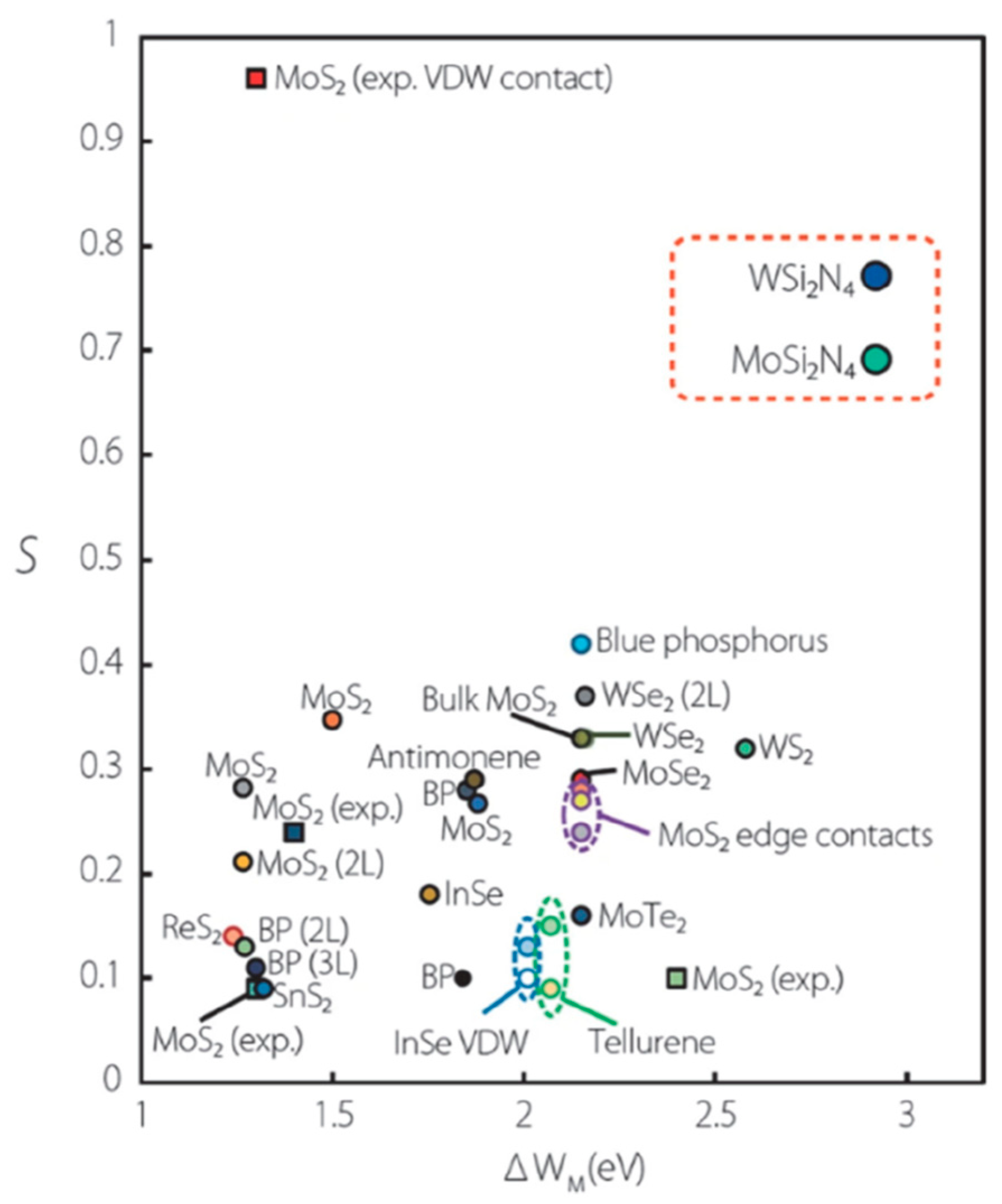
4.3. Bandgap Modification and Band Alignment
4.4. Phase Modification
4.5. Fermi-Level Pinning and Buffer Layer
5. 2D Contact with Silicon
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| 2D | Two Dimensional |
| 3D | Three Dimensional |
| ALD | Atomic Layer Deposition |
| AM | Amplitude Modulation |
| BN | Boron Nitride |
| CFET | Complementary Field-Effect Transistor |
| CGP | Contacted Gate Pitch |
| CMOS | Complementary Metal–Metal–Semiconductor |
| CPP | Contact-Poly Pitch |
| DCE | Dichloroethane |
| DFT | Density Functional Theory |
| FET | Field-Effect Transistor |
| FinFET | Fin Field-Effect Transistor |
| FLP | Fermi-Level Pinning |
| FN | Fowler–Nordheim |
| GAA | Gate-All-Around |
| GR | Generation and Recombination |
| HOMO | Highest-Occupied Molecular Orbital |
| IC | Integrated Circuit |
| ITRS | International Technology Roadmap for Semiconductors |
| I–V | Current–Voltage (Characteristics) |
| LDOS | Local Density of States |
| LED | Light-Emitting Diode |
| LUMO | Lowest Unoccupied Molecular Orbital |
| MIGS | Metal-Induced Gap States |
| MIM | Metal–Insulator–Metal |
| MIS | Metal–Insulator–Semiconductor |
| MOS | Metal-Oxide–Metal–Semiconductor |
| PDMS | Polydimethylsiloxane |
| PF | Poole–Frenkel (emission) |
| PLDOS | Projected Local Density of States |
| PMMA | Polymethylmethacrylate |
| SCTD | Spontaneous Charge Transfer Doping |
| STM | Scanning Tunneling Microscopy |
| STS | Scanning Tunneling Spectroscopy |
| TMD | Transition Metal Dichalcogenide |
| TSV | Through Silicon Via |
References
- Iwai, H.; Sze, S.M.; Taur, Y.; Wong, H. MOSFETs. In Guide to State-of-the-Art Electron Devices; Burghartz, J.N., Ed.; Wiley and IEEE: Hoboken, NJ, USA, 2013; pp. 21–36. [Google Scholar]
- Moore, G.E. Cramming More Components onto Integrated Circuits. Electronics 1965, 38, 114–117. [Google Scholar] [CrossRef]
- Wong, H.; Iwai, H. The road to miniaturization. Phys. World 2005, 18, 40. [Google Scholar] [CrossRef]
- Dennard, R.H.; Gaensslen, F.; Yu, H.-N.; Rideout, L.; Bassous, E.; LeBlanc, A. Design of ion-implanted MOSFET’s with very small physical dimensions. IEEE J. Solid-State Circuits 1974, 9, 256–268. [Google Scholar] [CrossRef]
- Semiconductor Industry Association, 2013 International Technology Roadmap for Semiconductors. Available online: https://www.semiconductors.org/resources/2013-international-technology-roadmap-for-semiconductors-itrs/ (accessed on 30 December 2019).
- Wong, H.; Iwai, H. On the Scaling of Subnanometer EOT Gate Dielectrics for Ultimate nano CMOS Technology. Microelectron. Eng. 2015, 138, 57–76. [Google Scholar] [CrossRef]
- Wong, H. On the CMOS Device Downsizing, More Moore, More than Moore, and More-than-Moore for More Moore. In Proceedings of the 2021 IEEE 32nd International Conference on Microelectronics (MIEL), Nis, Serbia, 12–14 September 2021; pp. 9–15. [Google Scholar]
- Wong, H.; Kakushima, K. Poole–Frenkel (PF)-MOS: A Proposal for the Ultimate Scale of an MOS Transistor. Nanomaterials 2023, 13, 411. [Google Scholar] [CrossRef] [PubMed]
- Ye, P.D.; Ernst, T.; Khare, M.V. The Nanosheet Transistor Is the Next and Maybe Last Step in Moores-Law. IEEE Spectr. 2019, 30. Available online: https://spectrum.ieee.org/the-nanosheet-transistor-is-the-next-and-maybe-last-step-in-moores-law (accessed on 22 January 2024).
- Wong, H.; Kakushima, K. On the Vertically Stacked Gate-All-Around Nanosheet and Nanowire Transistor Scaling beyond the 5 nm Technology Node. Nanomaterials 2022, 12, 1739. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Pan, Z.; Li, X.; Hao, W.; Miao, R.; Wang, A. Selective Overview of 3D Heterogeneity in CMOS. Nanomaterials 2022, 12, 2340. [Google Scholar] [CrossRef] [PubMed]
- Razavieh, A.; Zeitzoff, P.; Brown, D.E.; Karve, G.; Nowak, E.J. Scaling Challenges of FinFET Architecture below 40nm Contacted Gate Pitch. In Proceedings of the 2017 75th Annual Device Research Conference (DRC), South Bend, IN, USA, 25–28 June 2017; pp. 1–2. [Google Scholar]
- Afzalian, A.; Ahmed, Z.; Ryckaert, J. Towards Sub-30nm Contacted Gate Pitch, Forked Contact and Dynamically-Doped Nanosheets to Enhance Si and 2D Materials Device Scaling. arXiv 2022, arXiv:2203.06364. [Google Scholar] [CrossRef]
- Liu, Y.; Duan, X.; Shin, H.J.; Park, S.; Huang, Y.; Duan, X. Promises and Prospects of Two-Dimensional Transistors. Nature 2021, 591, 43–53. [Google Scholar] [CrossRef]
- Wong, H. Abridging CMOS Technology. Nanomaterials 2022, 12, 4245. [Google Scholar] [CrossRef] [PubMed]
- Elmourabit, F.; Dlimi, S.; El Moutaouakil, A.; Id Ouissaaden, F.; Khoukh, A.; Limouny, L.; Elkhatat, H.; El Kaaouachi, A. Nature of the Metal Insulator Transition in High-Mobility 2D Si-MOSFETs. Nanomaterials 2023, 13, 2047. [Google Scholar] [CrossRef] [PubMed]
- Knobloch, T.; Selberherr, S.; Grasser, T. Challenges for Nanoscale CMOS Logic based on Two-Dimensional Materials. Nanomaterials 2022, 12, 3548. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Wu, S.; Zhao, X.; Li, Z.; Yang, X.; Shen, Q.; Lu, M.; Xie, X.; Zhan, D.; Yan, J. Progress on Two-Dimensional Transitional Metal Dichalcogenides Alloy Materials: Growth, Characterisation, and Optoelectronic Applications. Nanomaterials 2023, 13, 2843. [Google Scholar] [CrossRef] [PubMed]
- Filipovic, L.; Selberherr, S. Application of Two-Dimensional Materials towards CMOS-Integrated Gas Sensors. Nanomaterials 2022, 12, 3651. [Google Scholar] [CrossRef] [PubMed]
- Kizhepat, S.; Rasal, A.S.; Chang, J.-Y.; Wu, H.-F. Development of Two-Dimensional Functional Nanomaterials for Biosensor Applications: Opportunities, Challenges, and Future Prospects. Nanomaterials 2023, 13, 1520. [Google Scholar] [CrossRef]
- Lemme, M.C.; Daus, A. Low-temperature MoS2 Growth on CMOS Wafers. Nat. Nanotechnol. 2023, 18, 446–447. [Google Scholar] [CrossRef]
- Pelella, A.; Kharsah, O.; Grillo, A.; Urban, F.; Passacantando, M.; Giubileo, F.; Iemmo, L.; Sleziona, S.; Pollmann, E.; Madauß, L.; et al. Electron Irradiation of Metal Contacts in Monolayer MoS2 Field-Effect Transistors. ACS Appl. Mater. Interfaces 2020, 12, 40532–40540. [Google Scholar] [CrossRef]
- Di Bartolomeo, A.; Kumar, A.; Durante, O.; Sessa, A.; Faella, E.; Viscardi, L.; Intonti, K.; Giubileo, F.; Martucciello, N.; Romano, P.; et al. Temperature-dependent Photoconductivity in Two-dimensional MoS2 Transistors. Mater. Today Nano 2023, 24, 100382. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, J.; Wang, Q.; Wan, J.; Liu, R. Homogeneous 2D MoTe2 CMOS Inverters and p–n Junctions Formed by Laser-Irradiation-Induced p-Type Doping. Small 2020, 16, 2001428. [Google Scholar] [CrossRef]
- Lim, J.Y.; Pezeshki, A.; Oh, S.; Kim, J.S.; Lee, Y.T.; Yu, S.; Hwang, D.K.; Lee, G.H.; Choi, H.J.; Im, S. Homogeneous 2D MoTe2 p–n Junctions and CMOS Inverters Formed by Atomic-Layer-Deposition-Induced Doping. Adv. Mater. 2017, 29, 1701798. [Google Scholar] [CrossRef]
- Patoary, N.H.; Xie, J.; Zhou, G.; Al Mamun, F.; Sayyad, M.; Tongay, S.; Esqueda, I.S. Improvements in 2D p-type WSe2 Transistors Towards Ultimate CMOS Scaling. Sci. Rep. 2023, 13, 3304. [Google Scholar] [CrossRef]
- Yu, L.; Zubair, A.; Santos, E.J.G.; Zhang, X.; Lin, Y.; Zhang, Y.; Palacios, T. High-performance WSe2 Complementary Metal Xxide Semiconductor Technology and Integrated Circuits. Nano Lett. 2015, 15, 4928–4934. [Google Scholar] [CrossRef]
- Grondahl, L.O. Twenty-Five Years of Copper-Copper Oxide Rectifiers. Trans. Am. Inst. Electr. Eng. 1948, 67 Pt I, 403–410. [Google Scholar] [CrossRef]
- Nordheim, L. Zur Theorie der Detektorwirkung. Z. Für Phys. 1932, 75, 434–441. [Google Scholar] [CrossRef]
- Frenkel, J.; Joffe, A. On the Electric and Photoelectric Properties of Contacts between a Metal and a Semiconductor. Phys. Rev. 1932, 39, 530–531. [Google Scholar] [CrossRef]
- Fowler, R.H. Statistical Mechanics; Cambridge University Press: Cambridge, UK, 1936. [Google Scholar]
- Schottky, W. Zur Halbleitertheorie der Sperrschicht- und Spitzengleichrichter. Z. Phys. 1939, 113, 367–414. [Google Scholar] [CrossRef]
- Mott, N.F. Note on the Contact between a Metal and an Insulator or Semiconductor. Math. Proc. Camb. Philos. Soc. 1938, 34, 568–572. [Google Scholar] [CrossRef]
- Richardson, O.W. On the Negative Radiation from Hot Platinum. In Proceedings of the Philosophical of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1901; Volume 11, pp. 286–295. [Google Scholar]
- Bardeen, J. Surface States and Rectification at a Metal Semi-conductor Contact. Phys. Rev. 1947, 71, 717–727. [Google Scholar] [CrossRef]
- Tung, R.T. Schottky Barrier Height—Do We Really Understand What We Measure? J. Vac. Sci. Technol. B 1993, 11, 1546–1552. [Google Scholar] [CrossRef]
- Tung, R.T. the physics and Chemistry of the Schottky Barrier Height. Appl. Phys. Rev. 2014, 1, 011304. [Google Scholar] [CrossRef]
- Crowell, C.R. the Richardson Constant for Thermionic Emission in Schottky Barrier Diodes. Solid-State Electron. 1965, 8, 395–399. [Google Scholar] [CrossRef]
- Shockley, W. The Theory of p-n Junctions in Semiconductors and p-n Junction Transistors. Bell Syst. Tech. J. 1949, 28, 435–489. [Google Scholar] [CrossRef]
- Schenk, A.; Krumbein, U. Coupled Defect-Level Recombination: Theory and Application to Anomalous Diode Characteristics. J. Appl. Phys. 1995, 78, 3185–3192. [Google Scholar] [CrossRef]
- Wong, H.; Anwar, M.A.; Dong, S. Effects of Silicon Surface Defects on the Graphene/Silicon Schottky Characteristics. Results Phys. 2021, 29, 104744. [Google Scholar] [CrossRef]
- Card, H.C.; Rhoderick, E.H. Studies of Tunnel MOS Diodes I. Interface Effects in Silicon Schottky Diodes. J. Phys. D Appl. Phys. 1971, 4, 1589–1601. [Google Scholar] [CrossRef]
- Ando, T.; Fowler, A.B.; Stern, F. Electronic Properties of Two-dimensional Systems. Rev. Mod. Phys. 1982, 54, 437. [Google Scholar] [CrossRef]
- Wong, H.; Iwai, H. Modeling and Characterization of Direct-Tunneling Current in Dual-Layer Ultrathin-Gate Dielectric Films. J. Vac. Sci. Technol. B 2006, 24, 1785–1793. [Google Scholar] [CrossRef]
- Yang, B.L.; Lai, P.T.; Wong, H. Conduction Mechanisms in MOS Gate Dielectric Films. Microelectron. Reliab. 2004, 44, 709–718. [Google Scholar] [CrossRef]
- Toyama, N. Variation in the Effective Richardson Constant of a Metal-Silicon Contact due to metal Film Thickness. J. Appl. Phys. 1988, 63, 2720–2724. [Google Scholar] [CrossRef]
- Yu, A. Electron Tunneling and Contact Resistance of Metal-Silicon Contact Barriers. Solid-State Electron. 1970, 13, 239–247. [Google Scholar] [CrossRef]
- Smoluchowski, R. Anisotropy of the Electronic Work Function of Metals. Phys. Rev. 1941, 60, 661–674. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Wang, G.C.; Lu, T.M.; Palasantzas, G.; de Hosson, J.T.M. Surface-Roughness Effect on Capacitance and Leakage Current of An Insulating Film. Phys. Rev. B 1999, 60, 9157–9164. [Google Scholar] [CrossRef]
- Wong, H.; Zhang, J.; Iwai, H.; Kakushima, K. Characteristic Variabilities of Subnanometer EOT La2O3 Gate Dielectric Film of Nano CMOS Devices. Nanomaterials 2021, 11, 2118. [Google Scholar] [CrossRef]
- Alimardani, N.; Conwell, E.W.; Wager, J.F.; Conley, J.F.; Evans, D.R.; Chin, M.; Kilpatrick, S.J.; Dubey, M. Impact of Electrode Roughness on Metal-Insulator-Metal Tunnel Diodes with Atomic Layer Deposited Al2O3 Tunnel Barriers. J. Vac. Sci. Technol. A 2012, 30, 01A113. [Google Scholar] [CrossRef]
- Du, L.; Wong, H.; Dong, S.; Lau, W.S.; Filip, V. AFM Study on the Surface Morphologies of Tin Films Prepared by Magnetron Sputtering and Al2O3 Films Prepared by Atomic Layer Deposition. Vacuum 2018, 153, 139–144. [Google Scholar] [CrossRef]
- Yu, D.Q.; Lau, W.S.; Wong, H.; Feng, X.; Dong, S.; Pey, K.L. the Variation of the Leakage Current Characteristics of W/Ta2O5/W MIM Capacitors with the Thickness of the Bottom W Electrode. Microelectron. Reliab. 2016, 61, 95–98. [Google Scholar] [CrossRef]
- Lau, W.S.; Zhang, J.; Wan, X.; Luo, J.K.; Xu, Y.; Wong, H. Surface Smoothing Effect of An Amorphous Thin Film Deposited by Atomic Layer Deposition on a Surface with Nano-Sized Roughness. AIP Adv. 2014, 4, 027120. [Google Scholar] [CrossRef]
- Liu, Y.; Kijima, S.; Sugimata, E.; Masahara, M.; Endo, K.; Matsukawa, T. Investigation of the Tin Gate Electrode with Tunable Work Function and Its Application for Finfet Fabrication. IEEE Trans. Nanotechnol. 2006, 5, 723–730. [Google Scholar] [CrossRef]
- Zheng, P.Y.; Zhou, T.; Engler, B.J.; Chawla, J.S.; Hull, R.; Gall, D. Surface Roughness Dependence of the Electrical Resistivity of W(001) Layers. J. Appl. Phys. 2017, 122, 095304. [Google Scholar] [CrossRef]
- Sami, S.N.; Diaz, L.; Sanati, M.; Joshi, R.P. Simulations of Field Emission from Copper Electrodes with Inclusion of Oxygen Surface Layer and Work Function Changes based on First-Principles Calculations. J. Appl. Phys. 2020, 128, 223302. [Google Scholar] [CrossRef]
- Li, Z.; Rahtu, A.; and Gordon, R.G. Atomic Layer Deposition of Ultrathin Copper Metal Films from a Liquid Copper(I) Amidinate Precursor. J. Electrochem. Soc. 2006, 153, C787–C794. [Google Scholar] [CrossRef]
- Shen, P.C.; Su, C.; Lin, Y.; Chou, A.S.; Cheng, C.C.; Park, J.H.; Chiu, M.H.; Lu, A.Y.; Tang, H.L.; Tavakoli, M.M.; et al. Ultralow Contact Resistance between Semimetal and Monolayer Semiconductors. Nature 2021, 593, 211–217. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, J.; Han, C.; Chen, W. Ohmic Contact Engineering for Two-Dimensional Materials. Cell Rep. Phys. Sci. 2021, 2, 100298. [Google Scholar] [CrossRef]
- Schulman, D.S.; Arnold, A.J.; Das, S. Contact Engineering for 2D Materials and Devices. Chem. Soc. Rev. 2018, 47, 3037–3058. [Google Scholar] [CrossRef]
- Wang, Q.; Cao, L.; Liang, S.-J.; Wu, W.; Wang, G.; Lee, C.H.; Ong, W.L.; Yang, H.Y.; Ang, L.K.; Yang, S.A.; et al. Efficient Ohmic Contacts and Built-In Atomic Sublayer Protection in MoSi2N4 and WSi2N4 Monolayers. npj 2D Mater. Appl. 2021, 5, 71. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, J.; Zhu, E.; Liao, L.; Lee, S.-J.; Ding, M.; Shakir, I.; Gambin, V.; Huang, Y.; Duan, X. Approaching the Schottky–Mott Limit in Van Der Waals Metal–Semiconductor Junctions. Nature 2018, 557, 696–700. [Google Scholar] [CrossRef]
- Wang, Y.; Kim, J.C.; Wu, R.J.; Martinez, J.; Song, X.; Yang, J.; Zhao, F.; Mkhoyan, A.; Jeong, H.Y.; Chhowalla, M. Van Der Waals Contacts between Three-Dimensional Metals and Two-Dimensional Semiconductors. Nature 2019, 568, 70–74. [Google Scholar] [CrossRef]
- Grillo, A.; DiBartolomeo, A. A Current–Voltage Model for Double Schottky Barrier Devices. Adv. Electron. Mater. 2021, 7, 2000979. [Google Scholar] [CrossRef]
- Wang, L.; Meric, I.; Huang, P.Y.; Gao, Q.; Gao, Y.; Tran, H.; Taniguchi, T.; Watanabe, K.; Campos, L.M.; Muller, D.A.; et al. One-Dimensional Electrical Contact to a Two-Dimensional Material. Science 2013, 342, 614–617. [Google Scholar] [CrossRef]
- Yang, Z.; Kim, C.; Lee, K.Y.; Lee, M.; Appalakondaiah, S.; Ra, C.H.; Watanabe, K.; Taniguchi, T.; Cho, K.; Hwang, E.; et al. A Fermi-Level-Pinning-Free 1D Electrical Contact at the Intrinsic 2D MoS2-Metal Junction. Adv. Mater. 2019, 31, e1808231. [Google Scholar] [CrossRef]
- Chu, C.H.; Lin, H.C.; Yeh, C.H.; Liang, Z.Y.; Chou, M.Y.; Chiu, P.W. Endbonded Metal Contacts on WSe2 Field-Effect Transistors. ACS Nano 2019, 13, 8146–8154. [Google Scholar] [CrossRef]
- Guimaraes, M.H.D.; Gao, H.; Han, Y.; Kang, K.; Xie, S.; Kim, C.J.; Muller, D.A.; Ralph, D.C.; Park, J. Atomically Thin Ohmic Edge Contacts between Two-Dimensional Materials. ACS Nano 2016, 10, 6392–6399. [Google Scholar] [CrossRef]
- McDonnell, S.; Smyth, C.; Hinkle, C.L.; Wallace, R.M. MoS2–Titanium Contact Interface Reactions. ACS Appl. Mater. Interfaces 2016, 8, 8289–8294. [Google Scholar] [CrossRef]
- English, C.D.; Shine, G.; Dorgan, V.E.; Saraswat, K.C.; Pop, E. Improved Contacts to MoS2 Transistors by Ultra-High Vacuum Metal Deposition. Nano Lett. 2016, 16, 3824–3830. [Google Scholar] [CrossRef]
- Liu, X.; Islam, A.; Guo, J.; Feng, P.X.-L. Controlling Polarity of MoTe2 Transistors for Monolithic Complementary Logic Via Schottky Contact Engineering. ACS Nano 2020, 14, 1457–1467. [Google Scholar] [CrossRef]
- Zhang, X.; Shao, Z.; Zhang, X.; He, Y.; Jie, J. Surface Charge Transfer Doping of Low-Dimensional Nanostructures Toward High-Performance Nanodevices. Adv. Mater. 2016, 28, 10409–10442. [Google Scholar] [CrossRef]
- Yang, L.; Majumdar, K.; Liu, H.; Du, Y.; Wu, H.; Hatzistergos, M.; Hung, P.Y.; Tieckelmann, R.; Tsai, W.; Hobbs, C.; et al. Chloride Molecular Doping Technique on 2D Materials: WS2 and MoS2. Nano Lett. 2014, 14, 6275–6280. [Google Scholar] [CrossRef]
- Tosun, M.; Chan, L.; Amani, M.; Roy, T.; Ahn, G.H.; Taheri, P.; Carraro, C.; Ager, J.W.; Maboudian, R.; Javey, A. Airstable N-Doping of Wse2 by Anion Vacancy Formation with Mild Plasma Treatment. ACS Nano 2016, 10, 6853–6860. [Google Scholar] [CrossRef]
- Kang, W.M.; Lee, S.T.; Cho, I.T.; Park, T.H.; Shin, H.; Hwang, C.S.; Lee, C.; Park, B.G.; Lee, J.H. Multi-Layer WSe2 Field Effect Transistor with Improved Carrier-Injection Contact by using Oxygen Plasma Treatment. Solid-State Electron. 2018, 140, 2–7. [Google Scholar] [CrossRef]
- Seo, S.Y.; Park, J.; Park, J.; Song, K.; Cha, S.; Sim, S.; Choi, S.Y.; Yeom, H.W.; Choi, H.; Jo, M.H. Writing Monolithic Integrated Circuits on a Two-Dimensional Semiconductor with a Scanning Light Probe. Nat. Electron. 2018, 1, 512–517. [Google Scholar] [CrossRef]
- Liu, X.; Qu, D.; Ryu, J.; Ahmed, F.; Yang, Z.; Lee, D.; Yoo, W.J. P-Type Polar Transition of Chemically Doped Multilayer MoS2 Transistor. Adv. Mater. 2016, 28, 2345–2351. [Google Scholar] [CrossRef]
- Kiriya, D.; Tosun, M.; Zhao, P.; Kang, J.S.; Javey, A. Air-Stable Surface Charge Transfer Doping of MoS2 by Benzyl Viologen. J. Am. Chem. Soc. 2014, 136, 7853–7856. [Google Scholar] [CrossRef]
- Yue, D.; Kim, C.; Lee, K.Y.; Yoo, W.J. Ohmic Contact in 2D Semiconductors via the Formation of a Benzyl Viologen Interlayer. Adv. Funct. Mater. 2019, 29, 1807338. [Google Scholar] [CrossRef]
- Fang, Q.; Zhao, X.; Huang, Y.; Xu, K.; Min, T.; Ma, F. Junction-Configuration-Dependent Interfacial Electronic States of a Monolayer Mos2/Metal Contact. J. Mater. Chem. C 2019, 7, 3607–3616. [Google Scholar] [CrossRef]
- Wickramaratne, D.; Weston, L.; Van de Walle, C.G. Monolayer to Bulk Properties of Hexagonal Boron Nitride. J. Phys. Chem. C 2018, 122, 25524–25529. [Google Scholar] [CrossRef]
- Li, S.L.; Komatsu, K.; Nakaharai, S.; Lin, Y.F.; Yamamoto, M.; Duan, X.; Tsukagoshi, K. Thickness Scaling Effect on Interfacial Barrier and Electrical Contact to Two-Dimensional MoS2 Layers. ACS Nano 2014, 8, 12836–12842. [Google Scholar] [CrossRef] [PubMed]
- Voiry, D.; Mohite, A.; Chhowalla, M. Phase Engineering of Transition Metal Dichalcogenides. Chem. Soc. Rev. 2015, 44, 2702–2712. [Google Scholar] [CrossRef]
- Kappera, R.; Voiry, D.; Yalcin, S.E.; Branch, B.; Gupta, G.; Mohite, A.D.; Chhowalla, M. Phase-Engineered Low-Resistance Contacts for Ultrathin MoS2 Transistors. Nat. Mater. 2014, 13, 1128–1134. [Google Scholar] [CrossRef]
- Sun, L.; Yan, X.; Zheng, J.; Yu, H.; Lu, Z.; Gao, S.P.; Liu, L.; Pan, X.; Wang, D.; Wang, Z.; et al. Layer-Dependent Chemically Induced Phase Transition of Two-Dimensional MoS2. Nano Lett. 2018, 18, 3435–3440. [Google Scholar] [CrossRef]
- Duerloo, K.A.N.; Li, Y.; Reed, E.J. Structural Phase Transitions in Two-Dimensional Mo- and W-Dichalcogenide Monolayers. Nat. Commun. 2014, 5, 4214. [Google Scholar] [CrossRef]
- Qi, D.; Wang, Q.; Han, C.; Jiang, J.; Zheng, Y.; Chen, W.; Zhang, W.; Wee, A.T.S. Reducing the Schottky Barrier between Few Layer MoTe2 and Gold. 2D Mater. 2017, 4, 045016. [Google Scholar] [CrossRef]
- Cho, S.; Kim, S.; Kim, J.H.; Zhao, J.; Seok, J.; Keum, D.H.; Baik, J.; Choe, D.H.; Chang, K.J.; Suenaga, K.; et al. Phase Patterning for Ohmic Homojunction Contact in MoTe2. Science 2015, 349, 625–628. [Google Scholar] [CrossRef] [PubMed]
- Addou, R.; McDonnell, S.; Barrera, D.; Guo, Z.; Azcatl, A.; Wang, J.; Zhu, H.; Hinkle, C.L.; Quevedo-Lopez, M.; Alshareef, H.N.; et al. Impurities and Electronic Property Variations of Natural MoS2 Crystal Surfaces. ACS Nano 2015, 9, 9124–9133. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Liu, D.; Robertson, J. 3D Behavior of Schottky Barriers of 2D Transition-Metal Dichalcogenides. ACS Appl. Mater. Interfaces 2015, 7, 25709–25715. [Google Scholar] [CrossRef] [PubMed]
- Kerelsky, A.; Nipane, A.; Edelberg, D.; Wang, D.; Zhou, X.; Motmaendadgar, A.; Gao, H.; Xie, S.; Kang, K.; Park, J.; et al. Absence of a Band Gap at the Interface of a Metal and Highly Doped Monolayer MoS2. Nano Lett. 2017, 17, 5962–5968. [Google Scholar] [CrossRef] [PubMed]
- Chee, S.S.; Seo, D.; Kim, H.; Jang, H.; Lee, S.; Moon, S.P.; Lee, K.H.; Kim, S.W.; Choi, H.; Ham, M.H. Lowering the Schottky Barrier Height by Graphene/Ag Electrodes for High-Mobility MoS2 Field-Effect Transistors. Adv. Mater. 2019, 31, e1804422. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Sim, Y.; Kim, S.Y.; Kim, J.H.; Oh, I.; Na, W.; Lee, D.H.; Wang, J.; Yan, S.; Liu, Y.; et al. Wafer-Scale Production of Patterned Transition Metal Ditelluride Layers for Two-Dimensional Metal–Semiconductor Contacts at the Schottky–Mott Limit. Nat. Electron. 2020, 3, 207–215. [Google Scholar] [CrossRef]
- Lee, C.S.; Oh, S.J.; Heo, H.; Seo, S.Y.; Kim, J.Y.; Kim, H.; Kim, D.; Ngome, O.F.; Shin, H.; Sung, J.H.; et al. Epitaxial Van Der Waals Contacts between Transition-Metal Dichalcogenide Monolayer Polymorphs. Nano Lett. 2019, 19, 1814–1820. [Google Scholar] [CrossRef]
- Shin, H.G.; Yoon, H.S.; Kim, J.S.; Kim, M.; Lim, J.Y.; Yu, S.; Park, J.H.; Yi, Y.; Kim, T.; Jun, S.C.; et al. Vertical and In-Plane Current Devices using NbS2/N-MoS2 Van Der Waals Schottky Junction and Graphene Contact. Nano Lett. 2018, 18, 1937–1945. [Google Scholar] [CrossRef]
- Jang, J.; Kim, Y.; Chee, S.S.; Kim, H.; Whang, D.; Kim, G.H.; Yun, S.J. Clean Interface Contact using a ZnO Interlayer for Low-Contact-Resistance MoS2 Transistors. ACS Appl. Mater. Interfaces 2020, 12, 5031–5039. [Google Scholar] [CrossRef]
- Chen, J.R.; Odenthal, P.M.; Swartz, A.G.; Floyd, G.C.; Wen, H.; Luo, K.Y.; Kawakami, R.K. Control of Schottky Barriers in Single Layer Mos2 Transistors with Ferromagnetic Contacts. Nano Lett. 2013, 13, 3106–3110. [Google Scholar] [CrossRef]
- Lee, S.; Tang, A.; Aloni, S.; Wong, H.S. Statistical Study on the Schottky Barrier Reduction of Tunneling Contacts to CVD Synthesized Mos2. Nano Lett. 2016, 16, 276–281. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yao, Q.; Huang, C.W.; Zou, X.; Liao, L.; Chen, S.; Fan, Z.; Zhang, K.; Wu, W.; Xiao, X.; et al. High Mobility MoS2 Transistor with Low Schottky Barrier Contact by using Atomic Thick H-BN As a Tunneling Layer. Adv. Mater. 2016, 28, 8302–8308. [Google Scholar] [CrossRef]
- Mleczko, M.J.; Yu, A.C.; Smyth, C.M.; Chen, V.; Shin, Y.C.; Chatterjee, S.; Tsai, Y.C.; Nishi, Y.; Wallace, R.M.; Pop, E. Contact Engineering High-Performance n-type MoTe2 Transistors. Nano Lett. 2019, 19, 6352–6362. [Google Scholar] [CrossRef]
- Cho, K.; Pak, J.; Kim, J.K.; Kang, K.; Kim, T.Y.; Shin, J.; Choi, B.Y.; Chung, S.; Lee, T. Contact-Engineered Electrical Properties of MoS2 Field-Effect Transistors via Selectively Deposited Thiol-molecules. Adv. Mater. 2018, 30, 1705540. [Google Scholar] [CrossRef]
- Wirth-Lima, A.J.; Alves-Sousa, P.P.; Bezerra-Fraga, W. Graphene/Silicon and 2D-MoS2/Silicon Solar Cells: A Review. Appl. Phys. A 2019, 125, 241. [Google Scholar] [CrossRef]
- Sinha, D.; Lee, J.U. Ideal Graphene/Silicon Schottky Junction Diodes. Nano Lett. 2014, 14, 4660–4664. [Google Scholar] [CrossRef] [PubMed]
- Di Bartolomeo, A. Graphene Schottky Diodes: An Experimental Review of the Rectifying Graphene/Semiconductor Heterojunction. Phys. Rep. 2016, 606, 1–58. [Google Scholar] [CrossRef]
- Wong, H.; Gritsenko, V.A. Defects in Silicon Oxynitride Gate Dielectric Films. Microelectron. Reliab. 2002, 42, 597–605. [Google Scholar] [CrossRef]
- Lenahan, P.; Conley, J., Jr. What Can Electron Paramagnetic Resonance Tell Us about the Si/SiO2 System? J. Vac. Sci. Technol. B 1998, 16, 2134–2153. [Google Scholar] [CrossRef]
- Wong, H.; Cheng, Y.C. Generation of Interface States at the Silicon/Oxide Interface due to Hot-Electron Injection. J. Appl. Phys. 1993, 74, 7364–7368. [Google Scholar] [CrossRef]
- Glemža, J.; Palenskis, V.; Gudaitis, R.; Jankauskas, Š.; Guobienė, A.; Vasiliauskas, A.; Meškinis, Š.; Pralgauskaitė, S.; Matukas, J. Low-frequency Noise of Directly Synthesized Graphene/Si(100) Junction. Diam. Relat. Mater. 2022, 127, 109207. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wong, H.; Zhang, J.; Liu, J. Contacts at the Nanoscale and for Nanomaterials. Nanomaterials 2024, 14, 386. https://doi.org/10.3390/nano14040386
Wong H, Zhang J, Liu J. Contacts at the Nanoscale and for Nanomaterials. Nanomaterials. 2024; 14(4):386. https://doi.org/10.3390/nano14040386
Chicago/Turabian StyleWong, Hei, Jieqiong Zhang, and Jun Liu. 2024. "Contacts at the Nanoscale and for Nanomaterials" Nanomaterials 14, no. 4: 386. https://doi.org/10.3390/nano14040386
APA StyleWong, H., Zhang, J., & Liu, J. (2024). Contacts at the Nanoscale and for Nanomaterials. Nanomaterials, 14(4), 386. https://doi.org/10.3390/nano14040386





