Qualitatively and Quantitatively Different Configurations of Nematic–Nanoparticle Mixtures
Abstract
:1. Introduction
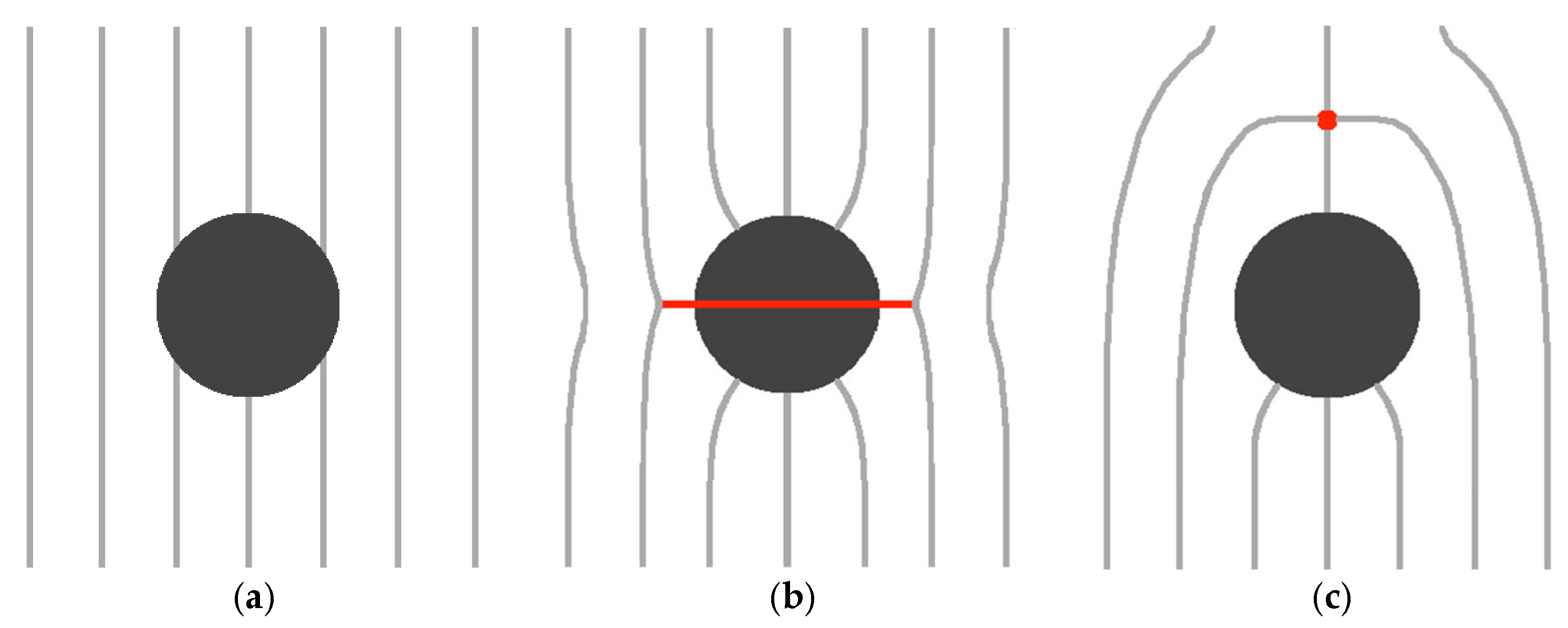
2. Mesoscopic Modelling
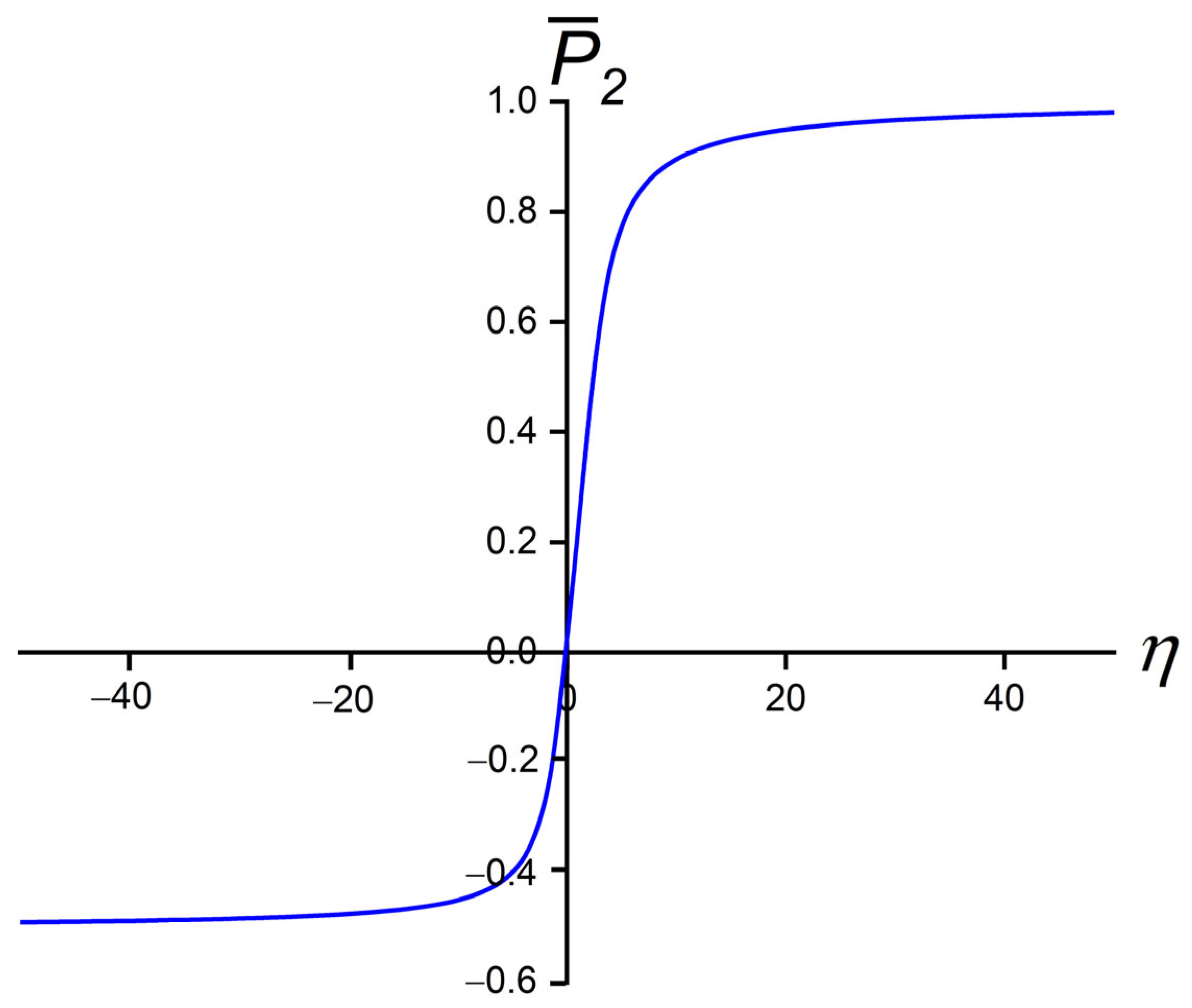
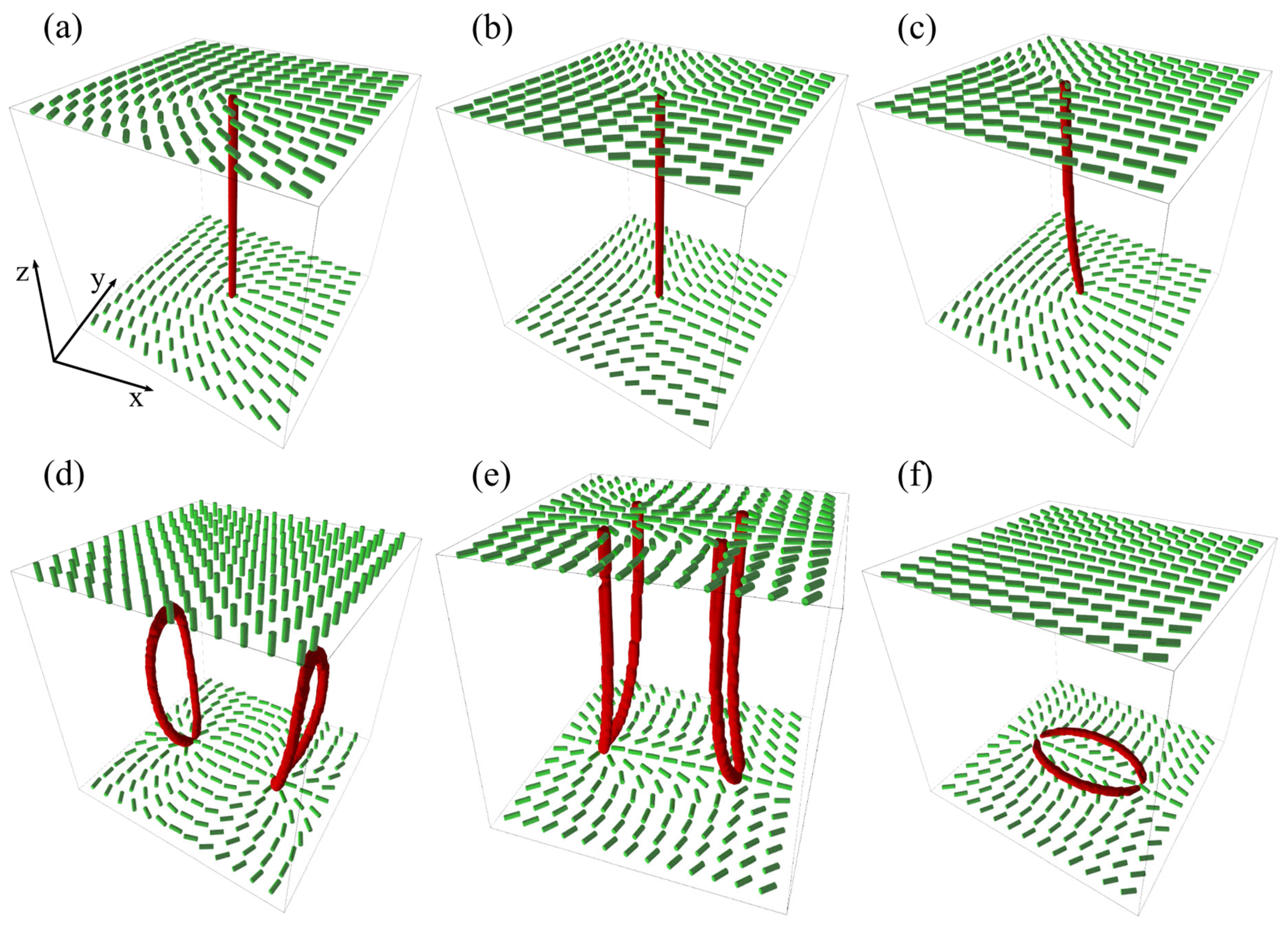
3. Phase and Structural Behaviour
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kleman, M.; Lavrentovich, O. Soft Matter Physics: An Introduction; Springer Science & Business Media: New York, NY, USA, 2004. [Google Scholar]
- Oswald, P.; Pieranski, P. Liquid Crystals: Concepts and Physical Properties Illustrated by Experiments, Two Volume Set, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Palffy-Muhoray, P. The diverse world of liquid crystals. Phys. Today 2007, 60, 54–60. [Google Scholar]
- Hamley, I.W. Nanotechnology with soft materials. Angew. Chem. Int. Ed. 2003, 42, 1692–1712. [Google Scholar] [CrossRef]
- Hegmann, T.; Qi, H.; Marx, V.M. Nanoparticles in liquid crystals: Synthesis, self-assembly, defect formation and potential applications. J. Inorg. Organomet. Polym. Mater. 2007, 17, 483–508. [Google Scholar] [CrossRef]
- Bisoyi, H.K.; Kumar, S. Liquid-crystal nanoscience: An emerging avenue of soft self-assembly. Chem. Soc. Rev. 2011, 40, 306–319. [Google Scholar] [CrossRef]
- Lagerwall, J.P.; Scalia, G. A new era for liquid crystal research: Applications of liquid crystals in soft matter nano-, bio-and microtechnology. Curr. Appl. Phys. 2012, 12, 1387–1412. [Google Scholar] [CrossRef]
- Smalyukh, I.I. Knots and other new topological effects in liquid crystals and colloids. Rep. Prog. Phys. 2020, 83, 106601. [Google Scholar] [CrossRef]
- Mundoor, H.; Park, S.; Senyuk, B.; Wensink, H.H.; Smalyukh, I.I. Hybrid molecular-colloidal liquid crystals. Science 2018, 360, 768–771. [Google Scholar] [CrossRef]
- Mundoor, H.; Wu, J.S.; Wensink, H.H.; Smalyukh, I.I. Thermally reconfigurable monoclinic nematic colloidal fluids. Nature 2021, 590, 268–274. [Google Scholar] [CrossRef]
- Zurek, W.-H. Cosmological experiments in superfluid helium? Nature 1985, 317, 505–508. [Google Scholar] [CrossRef]
- Duda, J. Framework for liquid crystal based particle models. arXiv 2021, arXiv:2108.07896. [Google Scholar]
- Dierking, I. Universal growth laws in liquid crystals far from equilibrium. Appl. Phys. A 2001, 72, 307–310. [Google Scholar] [CrossRef]
- Lagerwall, J.P.F.; Scalia, G. Liquid Crystals with Nano and Microparticles; World Scientific: Singapore, 2016; Volume 7. [Google Scholar]
- Hölbl, A.; Ranjkesh, A.; Abina, A.; Kralj, S.; Zidanšek, A. Phase behavior of nematic-nanoparticle mixtures. Front. Soft Matter 2023, 8, 1193904. [Google Scholar] [CrossRef]
- Lelidis, I.; Nobili, M.; Durand, G. Electric-field-induced change of the order parameter in a nematic liquid crystal. Phys. Rev. E 1993, 48, 3822–3824. [Google Scholar] [CrossRef]
- Pal, K.; Asthana, N.; Aljabali, A.A.; Bhardwaj, S.K.; Kralj, S.; Penkova, A.; Thomas, S.; Zaheer, T.; Souza, F.G. A critical review on multifunctional smart materials “nanographene” emerging avenue: Nano-imaging and biosensor applications. Crit. Rev. Solid State Mater. Sci. 2022, 47, 691–707. [Google Scholar] [CrossRef]
- Reshetnyak, V.Y.; Pinkevych, I.P.; Sluckin, T.J.; Urbas, A.M.; Evans, D.R. Effective medium theory for anisotropic media with plasmonic core-shell nanoparticle inclusions. Eur. Phys. J. Plus 2018, 133, 373–393. [Google Scholar] [CrossRef]
- Lavrentovich, O.D. Topological defects in dispersed words and worlds around liquid crystals, or liquid crystal drops. Liq. Cryst. 1998, 24, 117. [Google Scholar] [CrossRef]
- Smalyukh, I.-I.; Lansac, Y.; Clark, N.-A.; Trivedi, R.-P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids. Nat. Mater. 2010, 9, 139–145. [Google Scholar] [CrossRef]
- Tkalec, U.; Ravnik, M.; Čopar, S.; Žumer, S.; Muševič, I. Reconfigurable knots and links in chiral nematic colloids. Science 2011, 333, 62–65. [Google Scholar] [CrossRef]
- Čopar, S.; Ravnik, M.; Žumer, S. Introduction to colloidal and microfluidic nematic microstructures. Crystals 2021, 11, 956. [Google Scholar] [CrossRef]
- Fukuda, J.-I.; Žumer, S. Quasi-two-dimensional Skyrmion lattices in a chiral nematic liquid crystal. Nat. Commun. 2011, 2, 246. [Google Scholar] [CrossRef]
- Roshi, A.; Iannacchione, G.S.; Clegg, P.S.; Birgeneau, R. Evolution of the isotropic-to-nematic phase transition in octyloxycyanobiphenyl+aerosil dispersions. J. Phys. Rev. E 2004, 69, 031703. [Google Scholar] [CrossRef]
- Bellini, T.; Buscaglia, M.; Chiccoli, C.; Mantegazza, F.; Pasini, P.; Zannoni, C. Nematics with quenched disorder: What is left when long-range order is disrupted? Phys. Rev. Lett. 2000, 85, 1008–1011. [Google Scholar] [CrossRef]
- Chakrabarti, J. Simulation evidence of critical behavior of isotropic-nematic phase transition in a porous medium. Phys. Rev. Lett. 1998, 81, 385–388. [Google Scholar] [CrossRef]
- Leon, N.; Korb, J.P.; Bonalde, I.; Levitz, P. Universal nuclear spin relaxation and long-range order in nematics strongly confined in mass fractal silica gels. Phys. Rev. Lett. 2004, 92, 195504. [Google Scholar] [CrossRef]
- Jin, T.; Finotello, D. Aerosil dispersed in a liquid crystal: Magnetic order and random silica disorder. Phys. Rev. Lett. 2001, 86, 818–823. [Google Scholar] [CrossRef]
- Relaix, S.; Leheny, R.L.; Reven, L.; Sutton, M. Memory effect in composites of liquid crystal and silica aerosil. Phys. Rev. E 2011, 84, 061705. [Google Scholar] [CrossRef]
- Cordoyiannis, G.; Kralj, S.; Nounesis, G.; Žumer, S.; Kutnjak, Z. Soft-stiff regime crossover for an aerosil network dispersed in liquid crystals. Phys. Rev. E 2006, 73, 031707. [Google Scholar] [CrossRef]
- Kibble, T.-W.-B. Topology of cosmic domains and strings. J. Phys. A Math. Gen. 1976, 9, 1387–1398. [Google Scholar] [CrossRef]
- Poulin, P.; Stark, H.; Lubensky, T.-C.; Weitz, D.-A. Novel colloidal interactions in anisotropic fluids. Science 1997, 275, 1770–1773. [Google Scholar] [CrossRef]
- Liu, Q.; Cui, Y.; Gardner, D.; Li, X.; He, S.; Smalyukh, I.I. Self-alignment of plasmonic gold nanorods in reconfigurable anisotropic fluids for tunable bulk metamaterial applications. Nano Lett. 2010, 10, 1347–1353. [Google Scholar] [CrossRef]
- Liu, Q.; Yuan, Y.; Smalyukh, I.I. Electrically and optically tunable plasmonic guest-host liquid crystals with long-range ordered nanoparticles. Nano Lett. 2014, 14, 4071–4077. [Google Scholar] [CrossRef]
- Barbero, G.; Miraldi, E.; Stepanescu, A. Size and surface effect in nematic-isotropic phase transition of a liquid crystal. J. Appl. Phys. 1990, 68, 2063–2067. [Google Scholar] [CrossRef]
- Sen, A.K.; Sullivan, D.E. Landau–de Gennes theory of wetting and orientational transitions at a nematic-liquid–substrate interface. Phys. Rev. A 1987, 35, 1391–1403. [Google Scholar] [CrossRef]
- Nobili, M.; Durand, G. Disorientation-induced disordering at a nematic-liquid-crystal–solid interface. Phys. Rev. A 1992, 46, R6174–R6177. [Google Scholar] [CrossRef]
- Ravnik, M.; Žumer, S. Landau–de Gennes modelling of nematic liquid crystal colloids. Liq. Cryst. 2009, 36, 1201–1214. [Google Scholar] [CrossRef]
- Lynch, M.D.; Patrick, D.L. Organizing carbon nanotubes with liquid crystals. Nano Lett. 2002, 2, 1197–1201. [Google Scholar] [CrossRef]
- Lagerwall, J.P.; Scalia, G. Liquid Crystals with Nano and Microparticles (In 2 Volumes); Series In Soft Condensed Mater Book 7; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Mertelj, A.; Lisjak, D.; Drofenik, M.; Čopič, M. Ferromagnetism in suspensions of magnetic platelets in liquid crystal. Nature 2013, 504, 237–241. [Google Scholar] [CrossRef]
- Popa-Nita, V.; van der Schoot, P.; Kralj, S. Influence of a random field on particle fractionation and solidification in liquid-crystal colloid mixtures. Eur. Phys. J. E 2006, 21, 189–197. [Google Scholar] [CrossRef]
- Mermin, N.-D. The topological theory of defects in ordered media. Rev. Mod. Phys. 1979, 51, 591. [Google Scholar] [CrossRef]
- Kurik, M.-V.; Lavrentovich, O.-D. Defects in liquid crystals: Homotopy theory and experimental studies. Sov. Phys. Uspekhi 1988, 31, 196. [Google Scholar] [CrossRef]
- Volovik, G.-E.; Lavrentovich, O.-D. Topological dynamics of defects: Boojums in nematic drops. Zh. Eksp. Teor. Fiz. 1983, 85, 1997–2010. [Google Scholar]
- Skyrme, T.-H.-R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Chuang, I.; Durrer, R.; Turok, N.; Yurke, B. Cosmology in the laboratory: Defect dynamics in liquid crystals. Science 1991, 251, 1336–1342. [Google Scholar] [CrossRef]
- Lin, S.Z.; Wang, X.; Kamiya, Y.; Chern, G.-W.; Fan, F.; Fan, D.; Casas, B.; Liu, Y.; Kiryukhin, V.; Zurek, W.H.; et al. Topological defects as relics of emergent continuous symmetry and Higgs condensation of disorder in ferroelectrics. Nat. Phys. 2014, 10, 970–977. [Google Scholar] [CrossRef]
- Kosterlitz, J.-M.; Thouless, D.-J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181. [Google Scholar] [CrossRef]
- Afghah, S.; Selinger, R.-L.-B.; Selinger, J.-V. Visualising the crossover between 3D and 2D topological defects in nematic liquid crystals. Liq. Cryst. 2018, 45, 2022–2032. [Google Scholar] [CrossRef]
- Svenšek, D.; Žumer, S. Instability modes of high-strength disclinations in nematics. Phys. Rev. E 2004, 70, 061707. [Google Scholar] [CrossRef]
- Kralj, S.; Murray, B.-S.; Rosenblatt, C. Decomposition of strongly charged topological defects. Phys. Rev. E 2017, 95, 042702. [Google Scholar] [CrossRef]
- Cladis, P.-E.; Kleman, M. Non-singular disclinations of strength S=+ 1 in nematics. J. Phys. 1972, 33, 591–598. [Google Scholar] [CrossRef]
- Harkai, S.; Murray, B.-S.; Rosenblatt, C.; Kralj, S. Electric field driven reconfigurable multistable topological defect patterns. Phys. Rev. Res. 2020, 2, 013176. [Google Scholar] [CrossRef]
- Fukuda, J. Continuous transformation of a −1/2 wedge disclination line to a +1/2 one. Phys. Rev. E 2010, 81, 040701. [Google Scholar] [CrossRef]
- Lavrentovich, O.-D.; Terent’ev, E.-M. Phase transition altering the symmetry of topological point defects (hedgehogs) in a nematic liquid crystal. Zh. Eksp. Teor. Fiz. 1986, 91, 2084–2096. [Google Scholar]
- Kralj, S.; Virga, E.G. Universal fine structure of nematic hedgehogs. J. Phys. A Math. 2001, 34, 829. [Google Scholar] [CrossRef]
- Wang, X.; Miller, D.-S.; Bukusoglu, E.; De Pablo, J.-J.; Abbott, N.-L. Topological defects in liquid crystals as templates for molecular self-assembly. Nat. Mater. 2016, 15, 106–112. [Google Scholar] [CrossRef]
- Wang, X.; Kim, Y.K.; Bukusoglu, E.; Zhang, B.; Miller, D.S.; Abbott, N.L. Experimental insights into the nanostructure of the cores of topological defects in liquid crystals. Phys. Rev. Lett. 2016, 116, 147801. [Google Scholar] [CrossRef]
- Senyuk, B.; Liu, Q.; He, S.; Kamien, R.D.; Kusner, R.B.; Lubensky, T.C.; Smalyukh, I.I. Topological colloids. Nature 2013, 493, 200–205. [Google Scholar] [CrossRef]
- Schopohl, N.; Sluckin, T.-J. Defect core structure in nematic liquid crystals. Phys. Rev. Lett. 1987, 59, 2582–2584. [Google Scholar] [CrossRef]
- Zhou, S.; Shiyanovskii, S.-V.; Park, H.-S.; Lavrentovich, O.-D. Fine structure of the topological defect cores studied for disclinations in lyotropic chromonic liquid crystals. Nat. Commun. 2017, 8, 14974. [Google Scholar] [CrossRef]
- Pires, D.; Fleury, J.B.; Galerne, Y. Colloid particles in the interaction field of a disclination line in a nematic phase. Phys. Rev. Lett. 2007, 98, 247801. [Google Scholar] [CrossRef]
- Anderson, V.; Terentjev, E.; Meeker, S.; Crain, J.; Poon, W.C.K. Cellular solid behaviour of liquid crystal colloids 1. Phase separation and morphology. Eur. Phys. J. E 2001, 4, 11–20. [Google Scholar] [CrossRef]
- Kurioz, P.; Kralj, M.; Murray, B.; Rosenblatt, C.; Kralj, S. Nematic topological defects positionally controlled by geometry and external fields. Beilstein J. Nanotechnol. 2018, 9, 109–118. [Google Scholar] [CrossRef]
- Sethna, J.-P. Order parameters, broken symmetry, and topology. arXiv 1992, arXiv:cond-mat/9204009. [Google Scholar]
- Gaeta, G.; Virga, E.-G. Octupolar order in three dimensions. Eur. Phys. J. E 2016, 39, 113. [Google Scholar] [CrossRef]
- Machon, T.; Alexander, G.-P. Umbilic lines in orientational order. Phys. Rev. X 2016, 6, 011033. [Google Scholar] [CrossRef]
- Selinger, J.-V. Interpretation of saddle-splay and the Oseen-Frank free energy in liquid crystals. Liq. Cryst. Rev. 2018, 6, 129–142. [Google Scholar] [CrossRef]
- Selinger, J.-V. Director deformations, geometric frustration, and modulated phases in liquid crystals. Annu. Rev. Condens. Matter Phys. 2022, 13, 49–71. [Google Scholar] [CrossRef]
- Larkin, A.I. Effect of Inhomogeneties on the Structure of the Mixed State of Superconductors. Sov. Phys. JETP 1970, 31, 784–788. [Google Scholar]
- Imry, Y.; Ma, S.-K. Random-Field Instability of the Ordered State of Continuous Symmetry. Phys. Rev. Lett. 1975, 35, 1399–1401. [Google Scholar] [CrossRef]
- Dierking, I.; Blenkhorn, W.; Credland, E.; Drake, W.; Kociuruba, R.; Kayser, B.; Michael, T. Stabilising liquid crystalline blue phases. Soft Matter 2012, 8, 4355–4362. [Google Scholar] [CrossRef]
- Pišljar, J.; Ghosh, S.; Turlapati, S.; Rao, N.-V.-S.; Škarabot, M.; Mertelj, A.; Petelin, A.; Nych, A.; Marinčič, M.; Pusovnik, A.; et al. Blue phase III: Topological fluid of skyrmions. Phys. Rev. X 2022, 12, 011003. [Google Scholar] [CrossRef]
- Kikuchi, H.; Yokota, M.; Hisakado, Y.; Yang, H.; Kajiyama, T. Polymer-stabilized liquid crystal blue phases. Nat. Mater. 2002, 1, 64–68. [Google Scholar] [CrossRef]
- Yoshida, H.; Tanaka, Y.; Kawamoto, K.; Kubo, H.; Tsuda, T.; Fujii, A.; Kuwabata, S.; Kikuchi, H.; Ozaki, M. Nanoparticle-stabilized cholesteric blue phases. Appl. Phys. Express 2009, 2, 121501. [Google Scholar] [CrossRef]
- Cordoyiannis, G.; Jampani, V.S.R.; Kralj, S.; Dhara, S.; Tzitzios, V.; Basina, G.; Nounesis, G.; Kutnjak, Z.; Tripathi, C.S.P.; Losada-Perez, P.; et al. Different modulated structures of topological defects stabilized by adaptive targeting nanoparticles. Soft Matter 2013, 9, 3956–3964. [Google Scholar] [CrossRef]
- Coursault, D.; Grand, J.; Zappone, B.; Ayeb, H.; Levi, G.; F’elidj, N.; Lacaze, E. Linear Self-Assembly of Nanoparticles Within Liquid Crystal Defect Arrays. Adv. Mater. 2012, 24, 1461. [Google Scholar] [CrossRef]
- Ranjkesh, A.; Ambrozic, M.; Kralj, S.; Sluckin, T.J. Computational studies of history dependence in nematic liquid crystals in random environments. Phys. Rev. E 2014, 89, 022504. [Google Scholar] [CrossRef]
- Bray, A.J. Theory of phase-ordering kinetics. Adv. Phys. 2002, 51, 481–587. [Google Scholar] [CrossRef]
- Bradač, Z.; Kralj, S.; Žumer, S. Molecular dynamics study of isotropic-nematic quench. Phys. Rev. E 2022, 65, 021705–10. [Google Scholar] [CrossRef]
- Billeter, J.-L.; Smondyrev, A.-M.; Loriot, G.-B.; Pelcovits, R.-A. Phase-ordering dynamics of the Gay-Berne nematic liquid crystal. Phys. Rev. E 1999, 60, 6831–6840. [Google Scholar] [CrossRef]
- Sheng, P. Boundary-layer phase transition in nematic liquid crystals. Phys. Rev. A 1982, 26, 1610–1617. [Google Scholar] [CrossRef]
- Sluckin, T.J.; Poniewierski, A. Wetting and capillary condensation in liquid crystal systems. Mol. Cryst. Liq. Cryst. 1990, 179, 349–364. [Google Scholar] [CrossRef]
- Kralj, S.; Žumer, S.; Allender, D.W. Nematic-isotropic phase transition in a liquid-crystal droplet. Phys. Rev. A 1991, 43, 2943–2952. [Google Scholar] [CrossRef]
- Moses, T.; Shen, Y.R. Pretransitional surface ordering and disordering of a liquid crystal. Phys. Rev. Lett. 1991, 67, 2033–2036. [Google Scholar] [CrossRef]
- Boamfa, M.I.; Kim, M.W.; Maan, J.C.; Rasing, T. Observation of surface and bulk phase transitions in nematic liquid crystals. Nature 2003, 421, 149–152. [Google Scholar] [CrossRef]
- Kyrou, C.; Ambrožič, M.; Tsiourvas, D.; Kraj, S.; Atata, S.B.; Lelidis, I. Effect of quantum dots on the phase behavior and order of 8CB liquid crystal. J. Mol. Liq. 2023, 387, 122568. [Google Scholar] [CrossRef]
- Zidanšek, A.; Kralj, S.; Lahajnar, G.; Blinc, R. The deuterium NMR study of liquid crystals confined to aerogel matrices. Phys. Rev. E 1995, 51, 3332–3340. [Google Scholar] [CrossRef]
- Kralj, S.; Zidanšek, A.; Lahajnar, G.; Muševič, I.; Žumer, S.; Blinc, R.; Pintar, M.M. Nematic ordering in porous glasses: A deuterium NMR study. Phys. Rev. E 1996, 53, 3629–3638. [Google Scholar] [CrossRef]
- Dierking, I.; Scalia, G.; Morales, P. Liquid crystal–carbon nanotube dispersions. J. Appl. Phys. 2005, 97, 044309. [Google Scholar] [CrossRef]
- Lagerwall, J.; Scalia, G.; Haluska, M.; Dettlaff-Weglikowska, U.; Roth, S.; Giesselmann, F. Nanotube alignment using lyotropic liquid crystals. Adv. Mater. 2007, 19, 359–364. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zid, M.; Pal, K.; Harkai, S.; Abina, A.; Kralj, S.; Zidanšek, A. Qualitatively and Quantitatively Different Configurations of Nematic–Nanoparticle Mixtures. Nanomaterials 2024, 14, 436. https://doi.org/10.3390/nano14050436
Zid M, Pal K, Harkai S, Abina A, Kralj S, Zidanšek A. Qualitatively and Quantitatively Different Configurations of Nematic–Nanoparticle Mixtures. Nanomaterials. 2024; 14(5):436. https://doi.org/10.3390/nano14050436
Chicago/Turabian StyleZid, Maha, Kaushik Pal, Saša Harkai, Andreja Abina, Samo Kralj, and Aleksander Zidanšek. 2024. "Qualitatively and Quantitatively Different Configurations of Nematic–Nanoparticle Mixtures" Nanomaterials 14, no. 5: 436. https://doi.org/10.3390/nano14050436
APA StyleZid, M., Pal, K., Harkai, S., Abina, A., Kralj, S., & Zidanšek, A. (2024). Qualitatively and Quantitatively Different Configurations of Nematic–Nanoparticle Mixtures. Nanomaterials, 14(5), 436. https://doi.org/10.3390/nano14050436








